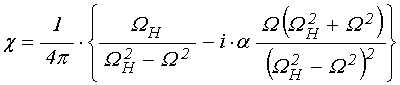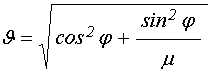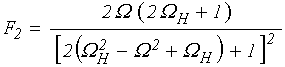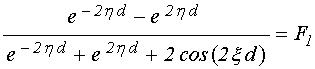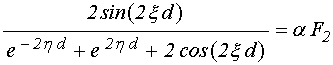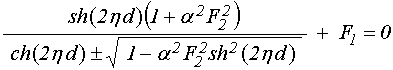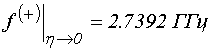УДК 537.874; 537.624
ВЛИЯНИЕ ДИССИПАЦИИ НА СВОЙСТВА ПОВЕРХНОСТНЫХ МАГНИТОСТАТИЧЕСКИХ ВОЛН В КАСАТЕЛЬНО НАМАГНИЧЕННОЙ ПЛАСТИНЕ ФЕРРИТА
П. А. Макаров 1, В. Г. Шавров 2, В. И. Щеглов 2
1 Сыктывкарский государственный университет, Сыктывкар, Россия
2 Институт радиотехники и электроники РАН, Москва, Россия
Статья получена 15 июля 2014 г.
Аннотация. На основе последовательного решения уравнения движения для намагниченности проведен учет затухания поверхностных магнитостатических волн (ПМСВ) в касательно намагниченной ферритовой пластине. Выявлено существование диссипативной ветви обратных ПМСВ, лежащей выше по частоте относительно основного спектра прямых ПМСВ, а также ограничение сверху предельных значений волнового числа для обоих ветвей спектра. Рассмотрено ограничение спектра по параметру затухания и роль толщины пластины в соотношении с длиной волны. Проведено сопоставление с опубликованными ранее экспериментальными результатами и даны рекомендации для проведения новых экспериментов.
Ключевые слова: феррит, магнитостатические волны, диссипация.
Abstract. By means of consistent solution of motion equation for magnetization the consideration of dissipation for magnetostatic surface waves (MSSW) propagating on in-plane magnetized ferrite plate is considered. It is revealed the existence of dissipative branch backward MSSW laying higher on frequency relative to the main spectrum of forward MSSW and so the limitation on top of wave number maximum values for both spectrum branches. It is investigated the limitation of spectrum by damping parameter and the plate thickness role in alignment of wave length. It is carried out the comparison with before published experimental results and the recommendations for the new experiments position are proposed.
Key words: ferrite, magnetostatic waves, dissipation.
Введение
Поверхностные магнитостатические волны (ПМСВ), распространяющиеся в пленках железоиттриевого граната (ЖИГ) [1], составляют основу широкого класса устройств аналоговой обработки информации в СВЧ диапазоне [2-5]. Традиционное устройство выполняется на основе линии передачи, представляющей собой пленку ЖИГ с расположенными на ее поверхности излучающим и приемным преобразователями, выполненными в виде антенн из тонкой проволоки. Пленка намагничена в плоскости постоянным полем, создаваемым внешним магнитом.
Типичный диапазон частот линии
передачи на ПМСВ составляет ![]() , диапазон
подмагничивающих полей –
, диапазон
подмагничивающих полей – ![]() , длина проводников
преобразователей –
, длина проводников
преобразователей – ![]() , расстояние между ними – того
же порядка. Типичная среда для распространения ПМСВ – пленки ЖИГ толщиной
, расстояние между ними – того
же порядка. Типичная среда для распространения ПМСВ – пленки ЖИГ толщиной ![]() , имеющие намагниченность насыщения
, имеющие намагниченность насыщения ![]() . При таких условиях длина ПМСВ составляет
от
. При таких условиях длина ПМСВ составляет
от ![]() до
до ![]() , что,
как правило, значительно меньше расстояния между преобразователями, поэтому
ослабление волны в процессе ее распространения за счет диссипативных процессов
в феррите может быть довольно значительным и составлять по мощности до нескольких
десятков децибел.
, что,
как правило, значительно меньше расстояния между преобразователями, поэтому
ослабление волны в процессе ее распространения за счет диссипативных процессов
в феррите может быть довольно значительным и составлять по мощности до нескольких
десятков децибел.
Несмотря на важность тематики и обилие работ по распространению ПМСВ в ферритах, в том числе в неоднородных полях [6-11] и сложных структурах [12-17], вопросам затухания ПМСВ уделяется внимания крайне недостаточно. В немногих работах на эту тему [18,19] показано, что наличие диссипации приводит к появлению в спектре ПМСВ обратных «диссипативных» волн, по частоте примыкающих к верхней границе спектра обычных прямых ПМСВ типа Дэймона-Эшбаха [1]. Кроме этого диссипация приводит к ограничению сверху возможного диапазона волновых чисел как для прямых, так и для обратных волн. Показано, что потери на распространение обратных волн значительно превышают подобные потери для прямых волн.
Однако проведенное в этих работах исследование является недостаточно полным. Рассмотрение базируется на анализе дисперсионного соотношения для ПМСВ, полученного без учета затухания, после чего затухание вводится через посредство комплексной добавки к частоте, что не является вполне последовательным. Полученные выражения не позволяют в достаточной степени выявить причину ограничения спектра ПМСВ не только по волновому числу, но также и по параметру затухания. Роль толщины ферритовой пластины в ее соотношении с длиной волны также остается не выясненной. Рассмотрение проведено в довольно общем виде, затрудняющем сопоставление полученных результатов с реальными экспериментами. Учет роли геометрии возбуждающего ПМСВ преобразователя полностью отсутствует.
Настоящая работа посвящена более подробному рассмотрению перечисленных вопросов, в том числе в непосредственной связи с условиями эксперимента.
1. Геометрия задачи
Общая геометрия задачи показана на рис.1.
Рис.1. Общая геометрия задачи.
Ферритовая пластина толщины ![]() намагничена в плоскости постоянным полем
намагничена в плоскости постоянным полем ![]() . Декартова система координат
. Декартова система координат ![]() выбрана таким образом, что ее начало,
точка
выбрана таким образом, что ее начало,
точка ![]() , находится на середине толщины пластины,
плоскость
, находится на середине толщины пластины,
плоскость ![]() параллельна плоскости пластины, а ось
параллельна плоскости пластины, а ось ![]() ей перпендикулярна. При этом координаты
плоскостей пластины по оси
ей перпендикулярна. При этом координаты
плоскостей пластины по оси ![]() равны
равны ![]() . Ось
. Ось ![]() ориентирована
вдоль поля
ориентирована
вдоль поля ![]() . В настоящей работе рассматриваются
поверхностные магнитостатические волны (ПМСВ), распространяющиеся вдоль верхней
поверхности пластины при
. В настоящей работе рассматриваются
поверхностные магнитостатические волны (ПМСВ), распространяющиеся вдоль верхней
поверхности пластины при ![]() . Волновой вектор
. Волновой вектор ![]() лежит в плоскости
лежит в плоскости ![]() и
составляет угол
и
составляет угол ![]() с осью
с осью ![]() ,
вектор групповой скорости
,
вектор групповой скорости ![]() лежит в той же
плоскости и составляет угол
лежит в той же
плоскости и составляет угол ![]() с осью
с осью ![]() .
.
2. Общий вид волновой функции и дисперсионного соотношения
Будем полагать, что среда
является изотропной, причем волны возбуждаются каким-то пространственно
локализованным источником, колеблющимся с заданной частотой ![]() . В этом случае волна распространяется
прямолинейно, а волновая функция имеет вид:
. В этом случае волна распространяется
прямолинейно, а волновая функция имеет вид:
![]() ,
(1)
,
(1)
где ![]() –
обобщенная координата вдоль направления распространения волны.
–
обобщенная координата вдоль направления распространения волны.
При этом, поскольку частота остается постоянной во времени, то амплитуда волны может уменьшаться только в том случае, если волновое число имеет мнимую добавку, то есть:
![]() ,
(2)
,
(2)
где ![]() и
и ![]() – действительные, причем для удобства
будем считать, что
– действительные, причем для удобства
будем считать, что ![]() и
и ![]() . При
этом волна (1) принимает вид:
. При
этом волна (1) принимает вид:
![]() ,
(3)
,
(3)
то есть распространяется в
положительном направлении оси координаты ![]() и при
таком распространении по амплитуде затухает.
и при
таком распространении по амплитуде затухает.
В этом случае длина волны ![]() , будучи определяемой соотношением:
, будучи определяемой соотношением:
![]() ,
(4)
,
(4)
не меняется и задается действительной
частью волнового числа ![]() .
.
Таким образом, для дальнейшего
рассмотрения примем определение закона дисперсии, как соотношения между
частотой ![]() и действительной частью волнового числа
и действительной частью волнового числа ![]() :
:
![]() , (5)
, (5)
где ![]() –
функция, определяемая параметрами среды, в том числе параметром затухания.
–
функция, определяемая параметрами среды, в том числе параметром затухания.
Кроме этого потребует
рассмотрения соотношение между частотой ![]() и мнимой
частью волнового числа
и мнимой
частью волнового числа ![]() :
:
![]() ,
(6)
,
(6)
которое будем называть «дисперсионным соотношением для диссипации».
3. Магнитная восприимчивость в среде с затуханием
Для описания движения вектора намагниченности в среде с потерями будем пользоваться уравнением Ландау-Лифшица с диссипативным членом в форме Гильберта [20-23]:
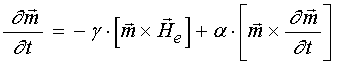 ,
(7)
,
(7)
где ![]() –
нормированный вектор намагниченности,
–
нормированный вектор намагниченности, ![]() –
намагниченность насыщения,
–
намагниченность насыщения, ![]() – гиромагнитная
постоянная (
– гиромагнитная
постоянная (![]() ),
), ![]() –
параметр затухания,
–
параметр затухания, ![]() – эффективное поле, равное:
– эффективное поле, равное:
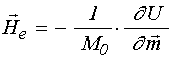 ,
(8)
,
(8)
где ![]() –
плотность магнитной энергии, в рассматриваемой геометрии равная:
–
плотность магнитной энергии, в рассматриваемой геометрии равная:
![]() .
(9)
.
(9)
Решение уравнения (7) дает компоненты магнитной восприимчивости, имеющие вид [20-23]:
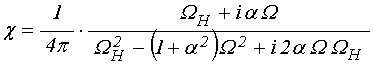 ;
(10)
;
(10)
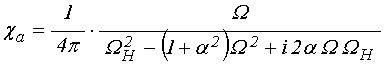 .
(11)
.
(11)
Будем далее считать потери
достаточно малыми, то есть положим ![]() . Отбрасывая слагаемые,
содержащие
. Отбрасывая слагаемые,
содержащие ![]() , по сравнению с единицей, освобождаясь от
мнимости в знаменателе и выделяя в явном виде действительную и мнимую части,
приводим компоненты восприимчивости к виду:
, по сравнению с единицей, освобождаясь от
мнимости в знаменателе и выделяя в явном виде действительную и мнимую части,
приводим компоненты восприимчивости к виду:
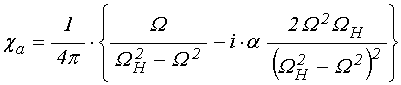 .
(13)
.
(13)
4. Полное дисперсионное соотношение
В описанной геометрии основное дисперсионное соотношение для поверхностных магнитостатических волн имеет вид:
где:
![]() ;
(16)
;
(16)
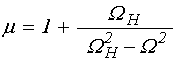 ;
(17)
;
(17)
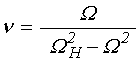 ;
(18)
;
(18)
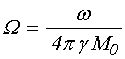 ;
(19)
;
(19)
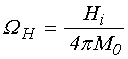 .
(20)
.
(20)
Это соотношение получено путем решения граничной задачи, впервые описанной в работе [1]. Приведенный здесь вид аналогичен полученному в [1], однако отличается удобством использования в задачах, касающихся распространения ПМСВ в пленках, намагниченных неоднородным полем [6-11].
Для целей настоящей работы дисперсионное соотношение (14) запишем в следующем более удобном виде:
где:
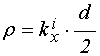 ; (22)
; (22)
![]() ;
(23)
;
(23)
![]() ,
(24)
,
(24)
где ![]() и
и ![]() определяются соотношениями (12)-(13), а компоненты
волнового вектора в полярной системе координат имеют вид:
определяются соотношениями (12)-(13), а компоненты
волнового вектора в полярной системе координат имеют вид:
![]() ;
(25)
;
(25)
![]() ;
(26)
;
(26)
![]() ;
(27)
;
(27)
![]() ,
(28)
,
(28)
где ![]() определяется
соотношением (15).
определяется
соотношением (15).
Для простоты ограничимся
рассмотрением волн, распространяющихся вдоль оси ![]() , для
чего положим
, для
чего положим ![]() . При этом выражения (25)-(28) принимают
вид:
. При этом выражения (25)-(28) принимают
вид:
![]() ;
(29)
;
(29)
![]() ;
(30)
;
(30)
![]() ;
(31)
;
(31)
![]() ;
(32)
;
(32)
![]() .
(33)
.
(33)
Подставляя (29)-(33) в (23)-(24) и далее в (21), приводим дисперсионное соотношение к виду:
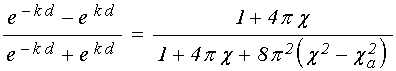 ;
(34)
;
(34)
Здесь левая часть зависит только
от волнового числа ![]() , тогда как правая, через посредство
(12)-(13), зависит только от частоты
, тогда как правая, через посредство
(12)-(13), зависит только от частоты ![]() (или
(или ![]() ), поэтому их можно рассмотреть независимо
по отдельности.
), поэтому их можно рассмотреть независимо
по отдельности.
Преобразуя обе части этого соотношения, освобождаясь от мнимости в знаменателе и выделяя в явном виде действительную и мнимую части, приводим дисперсионное соотношение к виду:
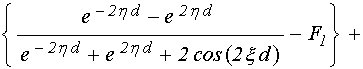
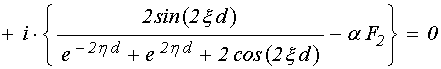 ,
(35)
,
(35)
где:
Приравнивая действительную и мнимую части этого выражения к нулю, получаем систему двух уравнений:
Правые части этих уравнений
содержат только частоты ![]() и
и ![]() .
.
В левые части входят только
действительная и мнимая компоненты волнового числа ![]() и
и ![]() .
.
Совокупность этих двух уравнений можно рассматривать как полное дисперсионное соотношение, включающее в себя зависимость от частоты как для действительной, так и мнимой частей волнового числа. Рассмотрим далее дисперсионные соотношения для действительной и мнимой частей волнового числа по отдельности. Для удобства различения этих двух видов соотношений будем называть первое – «дисперсионным соотношением для длины волны», а второе – «дисперсионным соотношением для диссипации».
5. Дисперсионное соотношение для действительной части волнового числа (для длины волны)
Поскольку частота ![]() задана постоянным полем (как параметр
среды), то есть неизменна, полученные уравнения (38)-(39) можно рассматривать
как систему, связывающую три переменных
задана постоянным полем (как параметр
среды), то есть неизменна, полученные уравнения (38)-(39) можно рассматривать
как систему, связывающую три переменных ![]() ,
, ![]() и
и ![]() .
Поскольку переменных три, а уравнений всего два, то одна из них может быть
задана произвольно. В соответствии с условием задачи (волна постоянной частоты
спадает в пространстве), частоту
.
Поскольку переменных три, а уравнений всего два, то одна из них может быть
задана произвольно. В соответствии с условием задачи (волна постоянной частоты
спадает в пространстве), частоту ![]() будем считать
заданной. Тогда (38)-(39) обращается в систему двух уравнений относительно
будем считать
заданной. Тогда (38)-(39) обращается в систему двух уравнений относительно ![]() и
и ![]() .
.
Положим, что основу будущего
дисперсионного соотношения, содержащего только действительную часть волнового
числа ![]() и частоту
и частоту ![]() ,
должно составить первое уравнение (38), которое однако содержит еще и
,
должно составить первое уравнение (38), которое однако содержит еще и ![]() в виде
в виде ![]() . Чтобы
исключить из первого уравнения мнимую компоненту волнового числа
. Чтобы
исключить из первого уравнения мнимую компоненту волнового числа ![]() , надо выразить ее из второго уравнения (39)
через действительную компоненту
, надо выразить ее из второго уравнения (39)
через действительную компоненту ![]() и функцию
и функцию ![]() . Это вполне можно сделать, так как
. Это вполне можно сделать, так как ![]() зависит только от частоты и компонент
волнового числа не содержит. Таким образом, из второго уравнения (39) надо
найти
зависит только от частоты и компонент
волнового числа не содержит. Таким образом, из второго уравнения (39) надо
найти ![]() , который затем и будет подставлен в
первое уравнение.
, который затем и будет подставлен в
первое уравнение.
Введем промежуточные обозначения:
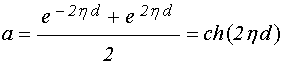 .
(40)
.
(40)
![]() ;
(41)
;
(41)
С этими обозначениями уравнение (39) принимает вид:
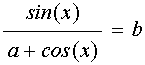 .
(43)
.
(43)
Выражая синус через косинус и возводя
в квадрат, получаем уравнение для ![]() :
:
![]() .
(44)
.
(44)
Это уравнение – квадратное. Его решение имеет вид:
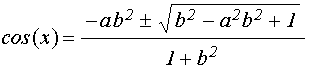 .
(45)
.
(45)
Подставляя обозначения (40)-(42) и учитывая соотношение:
![]() ,
(46)
,
(46)
где ![]() –
произвольное число, получаем:
–
произвольное число, получаем:
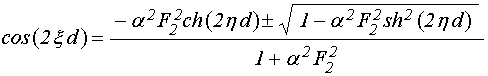 .
(47)
.
(47)
Подставляя это выражение в (38), получаем искомое дисперсионное соотношение для длины волны в виде:
где функции ![]() и
и
![]() определяются выражениями (36)-(37). Это
дисперсионное соотношение зависит только от
определяются выражениями (36)-(37). Это
дисперсионное соотношение зависит только от ![]() и
и ![]() , причем
, причем ![]() входит
как параметр.
входит
как параметр.
5.1. Предельные значения частот в отсутствие затухания
Рассмотрим сначала более простой
случай отсутствия затухания, позволяющий разрешить соотношение (48)
относительно частоты ![]() в явном виде. Действительно, при
в явном виде. Действительно, при
![]() дисперсионное соотношение (48) принимает
вид:
дисперсионное соотношение (48) принимает
вид:
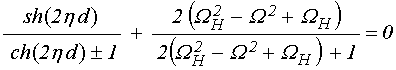 .
(49)
.
(49)
Введем вспомогательное обозначение:
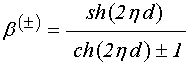 .
(50)
.
(50)
Разрешая (49) относительно частоты ![]() , получаем:
, получаем:
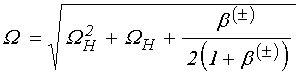 .
(51)
.
(51)
Из этого соотношения видно, что
зависимость нормированной частоты![]() от действительной
части волнового числа
от действительной
части волнового числа ![]() имеет две ветви, соответствующие
знакам «плюс» и «минус».
имеет две ветви, соответствующие
знакам «плюс» и «минус».
Рассмотрим предельные значения
частот обеих ветвей, определяемых этим дисперсионным соотношением при малых и
больших волновых числах, то есть при ![]() и
и ![]() . Приведем также корме нормированных
частот
. Приведем также корме нормированных
частот ![]() значения абсолютных частот
значения абсолютных частот ![]() . Полученные значения сведены в таблицу.
. Полученные значения сведены в таблицу.
Знак «ПЛЮС»:
![]() , при
этом
, при
этом ![]() :
:
![]() ;
(53)
;
(53)
![]() , при
этом
, при
этом ![]() :
:
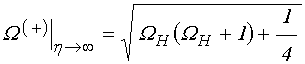 ;
(54)
;
(54)
![]() .
(55)
.
(55)
Знак «МИНУС»:
![]() , при
этом
, при
этом ![]() :
:
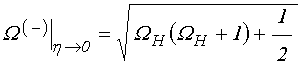 ;
(56)
;
(56)
![]() ;
(57)
;
(57)
![]() , при
этом
, при
этом ![]() :
:
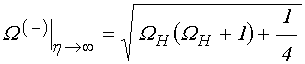 ;
(58)
;
(58)
![]() .
(59)
.
(59)
6. Дисперсионные кривые для длины волны при параметрах эксперимента
Полное дисперсионное соотношение
с учетом затухания (48) относительно частоты ![]() ,
по-видимому не разрешается. Поэтому его можно разрешить численно, задавая с
определенным шагом волновое число
,
по-видимому не разрешается. Поэтому его можно разрешить численно, задавая с
определенным шагом волновое число ![]() и находя на каждом
шаге частоту
и находя на каждом
шаге частоту ![]() с помощью алгоритма поиска нуля. Результаты
такого численного расчета приведены далее.
с помощью алгоритма поиска нуля. Результаты
такого численного расчета приведены далее.
Для определенности рассмотрим вид
дисперсионных кривых в условиях, близких к эксперименту [6-11], проводившемуся
на пленках железоиттриевого граната (ЖИГ), имеющих намагниченность насыщения ![]() и толщину
и толщину ![]() при
поле
при
поле ![]() (четверть от
(четверть от ![]() ).
).
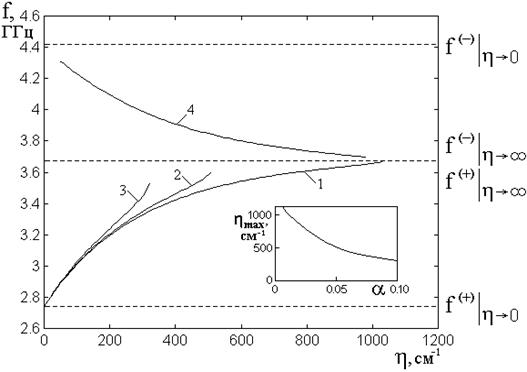
Рис.2. Дисперсионные кривые для
прямых (1,2,3) и обратных (4) ПМСВ при различных значениях параметра затухания ![]() :1 –
:1 – ![]() , 2 –
, 2 – ![]() , 3 –
, 3 – ![]() ,
,
4 – ![]() . Параметры:
. Параметры:
![]() ;
; ![]() ;
; ![]() .
.
На рис.2 приведены дисперсионные
кривые, построенные по формуле (48) при различных значениях параметра
затухания. Кривые 1-3 соответствуют знаку «плюс» перед корнем в выражении (48),
кривая 4 соответствует знаку «минус». Горизонтальными пунктирными линиями
показаны предельные значения частот в отсутствие затухания (![]() ), равные:
), равные:
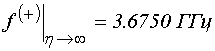 (
(![]() ); (61)
); (61)
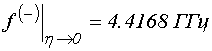 (
(![]() ); (62)
); (62)
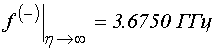 (
(![]() ). (63)
). (63)
Из рисунка видно, что волны,
соответствующие знаку «плюс», являются прямыми, тогда как волны,
соответствующие знаку «минус» являются обратными. Прямые волны существуют в
области частот между ![]() и
и ![]() ,
тогда как обратные – выше этой области между частотами
,
тогда как обратные – выше этой области между частотами ![]() и
и
![]() .
.
Ветви прямых волн (1-3) являются
аналогом классической волны Дэймона-Эшбаха [1] и отличаются от нее отклонением
в сторону более высоких частот по мере возрастания волнового числа, а также
ограничением в области больших волновых чисел, причем по мере возрастания
затухания эти отличия увеличиваются.
Ветвь обратных волн (4) в отсутствие затухания при ![]() не
существует, то есть ее наличие обусловлено именно затуханием. Вследствие этого,
аналогично [18,19], эту ветвь можно назвать «диссипативной». Приведенная на
рисунке ветвь обратных волн (4) соответствует
не
существует, то есть ее наличие обусловлено именно затуханием. Вследствие этого,
аналогично [18,19], эту ветвь можно назвать «диссипативной». Приведенная на
рисунке ветвь обратных волн (4) соответствует ![]() и не
является единственной, а лишь иллюстрирует пучок ветвей, расположенных в этой
области.
и не
является единственной, а лишь иллюстрирует пучок ветвей, расположенных в этой
области.
Все дисперсионные кривые со
стороны больших значений волнового числа ограничены предельным значением,
которое обозначим далее через ![]() . Так ветви 1-3 ограничиваются
при
. Так ветви 1-3 ограничиваются
при ![]() ,
, ![]() и
и ![]() соответственно, а ветвь 4 – при
соответственно, а ветвь 4 – при ![]() .
.
В математическом отношении ограничение действительной части волнового числа соответствует изменению знака подкоренного выражения в формуле (48), то есть условию:
![]() .
(64)
.
(64)
На врезке в рис.2 показана
зависимость ![]() от параметра затухания
от параметра затухания ![]() , построенная в соответствии с этим
условием при частоте
, построенная в соответствии с этим
условием при частоте 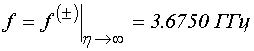 . Можно видеть, что при
увеличении затухания предельное значение волнового числа
. Можно видеть, что при
увеличении затухания предельное значение волнового числа ![]() уменьшается, стремясь к нулю. С другой
стороны, при
уменьшается, стремясь к нулю. С другой
стороны, при ![]() стремящемся к нулю
стремящемся к нулю ![]() бесконечно увеличивается.
бесконечно увеличивается.
Условие (64) содержит ограничение
не только по максимальной величине волнового числа, но также и при заданном
значении ![]() – ограничение по частоте. Вследствие
такого ограничения ветви 1-3, стремясь при увеличении
– ограничение по частоте. Вследствие
такого ограничения ветви 1-3, стремясь при увеличении ![]() вверх,
не доходят до частоты
вверх,
не доходят до частоты 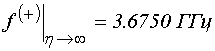 , а ограничиваются при
частотах
, а ограничиваются при
частотах ![]() ,
, ![]() и
и ![]() соответственно, а ветвь 4, стремясь при
увеличении
соответственно, а ветвь 4, стремясь при
увеличении ![]() вниз, также не доходит до
вниз, также не доходит до 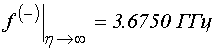 , а ограничивается при частоте
, а ограничивается при частоте ![]() .
.
Подобное ограничение существует и
по параметру затухания ![]() со стороны его больших
значений. Так прямые волны отсутствуют при
со стороны его больших
значений. Так прямые волны отсутствуют при ![]() , а обратные
– при
, а обратные
– при ![]() . Именно по этой причине на рис.2 ветвей
прямых волн при приведенных там значениях параметра
. Именно по этой причине на рис.2 ветвей
прямых волн при приведенных там значениях параметра ![]() ,
, ![]() и
и ![]() показано
три, а ветвь обратных волн – всего одна.
показано
три, а ветвь обратных волн – всего одна.
Можно отметить, что ограничения,
накладываемые соотношением (64), при заданных значениях частоты и параметра
затухания, сводятся к балансу между действительной частью волнового числа ![]() и толщиной пленки
и толщиной пленки ![]() .
То есть при задаваемом этим соотношением значении
.
То есть при задаваемом этим соотношением значении ![]() ограничение
становятся тем мягче, чем меньше толщина пленки
ограничение
становятся тем мягче, чем меньше толщина пленки ![]() . Из
этого следует, что при желании в эксперименте возбудить более короткие ПМСВ
надо выбирать толщину пленки как можно меньше.
. Из
этого следует, что при желании в эксперименте возбудить более короткие ПМСВ
надо выбирать толщину пленки как можно меньше.
Из сопоставления с экспериментами, описанными в работах [6-11] можно видеть, что там уверенно наблюдались только прямые ПМСВ, тогда как сообщения об обратных (диссипативных) волнах отсутствуют. С другой стороны, задача наблюдения обратных волн, имеющих по сравнению с прямыми противоположно направленную групповую скорость, в этих работах, по-видимому, не ставилась, то есть обнаружение диссипативных волн требует дополнительных исследований.
7. Дисперсионное соотношение для мнимой части волнового числа (для диссипации)
Рассмотрим теперь, как
сказываются потери, задаваемые параметром ![]() , на
амплитуде распространяющейся волны.
, на
амплитуде распространяющейся волны.
Полученное дисперсионное
соотношение (48) связывает частоту ![]() с действительной
частью волнового числа
с действительной
частью волнового числа ![]() , которая определяет только
длину распространяющейся волны, но не содержит информации о ее амплитуде. В
среде с диссипацией амплитуда волны по мере распространения уменьшается, что
определяется мнимой частью волнового числа
, которая определяет только
длину распространяющейся волны, но не содержит информации о ее амплитуде. В
среде с диссипацией амплитуда волны по мере распространения уменьшается, что
определяется мнимой частью волнового числа ![]() .
Получим теперь связь между частотой
.
Получим теперь связь между частотой ![]() и мнимой частью
волнового числа
и мнимой частью
волнового числа ![]() , то есть, как условлено ранее, «дисперсионное
соотношение для диссипации».
, то есть, как условлено ранее, «дисперсионное
соотношение для диссипации».
Будем исходить из системы уравнений (38)-(39), содержащей обе части волнового числа. Введем вспомогательные обозначения:
![]() ;
(65)
;
(65)
![]() ;
(66)
;
(66)
![]() ,
(67)
,
(67)
где ![]() определяется
соотношением (42).
определяется
соотношением (42).
В этих обозначениях система (38)-(39) принимает вид:
![]() ;
(68)
;
(68)
![]() .
(69)
.
(69)
Это – система двух квадратных
уравнений относительно ![]() . В ней кроме частоты
. В ней кроме частоты ![]() , содержатся также
, содержатся также ![]() и
и ![]() . Для
того, чтобы получить соотношение между
. Для
того, чтобы получить соотношение между ![]() и
и ![]() , из этой системы надо исключить
, из этой системы надо исключить ![]() . Учитывая, что в этих уравнениях
. Учитывая, что в этих уравнениях ![]() входит только через
входит только через ![]() в соответствии с (65), получаем, что из
системы (68)-(69) надо исключить
в соответствии с (65), получаем, что из
системы (68)-(69) надо исключить ![]() . Это вполне можно
сделать, например, если разрешить второе из этих уравнений (69) относительно
. Это вполне можно
сделать, например, если разрешить второе из этих уравнений (69) относительно ![]() и полученное выражение подставить в
первое уравнение (68).
и полученное выражение подставить в
первое уравнение (68).
Разрешая (69) относительно ![]() по формуле решения квадратного уравнения,
получаем:
по формуле решения квадратного уравнения,
получаем:
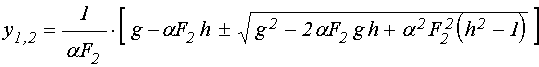 . (70)
. (70)
Подставляя (70) в (69) и приводя
подобные члены, получаем уравнение, не содержащее ![]() :
:
![]()
![]() . (71)
. (71)
Это – искомое дисперсионное соотношение для диссипации, записанное через вспомогательные обозначения (65)-(67).
Раскрывая вспомогательные
обозначения, получаем дисперсионное соотношение для диссипации, записанное в
явном виде относительно ![]() :
:
![]()
![]()
![]() . (72)
. (72)
Оно содержит мнимую часть волнового
числа ![]() , а также частоты
, а также частоты ![]() в
качестве переменной и
в
качестве переменной и ![]() в качестве параметра, входящие
в
в качестве параметра, входящие
в ![]() и
и ![]() в соответствии
с (36) и (37).
в соответствии
с (36) и (37).
В приведенном здесь виде (72) это
уравнение относительно ![]() или
или ![]() ,
по-видимому, не разрешается. Чтобы построить зависимость
,
по-видимому, не разрешается. Чтобы построить зависимость ![]() от
от ![]() в
численном виде, его можно разрешить, задавая с определенным шагом мнимую часть
волнового числа
в
численном виде, его можно разрешить, задавая с определенным шагом мнимую часть
волнового числа ![]() и находя на каждом шаге частоту
и находя на каждом шаге частоту
![]() с помощью алгоритма поиска нуля, что
сделано далее для конкретных параметров задачи, близких к эксперименту.
с помощью алгоритма поиска нуля, что
сделано далее для конкретных параметров задачи, близких к эксперименту.
8. Дисперсионные кривые для диссипации при параметрах эксперимента
Рассмотрим теперь вид дисперсионных кривых для диссипации в условиях, близких к эксперименту [6-11] на пленках ЖИГ, имеющих те же параметры, что и в предыдущем разделе.
На рис.3 показана зависимость
мнимой части волнового числа от частоты, построенная по формуле (72) при
параметре затухания ![]() . Вертикальными точечными
линиями показаны значения характерных граничных частот спектра ПМСВ,
определяемых соотношениями (52)-(59) и (60)-(63).
. Вертикальными точечными
линиями показаны значения характерных граничных частот спектра ПМСВ,
определяемых соотношениями (52)-(59) и (60)-(63).
Из рисунка видно, что мнимая
часть волнового числа ![]() в области прямых волн между
частотами
в области прямых волн между
частотами ![]() и
и ![]() возрастает,
сначала плавно, но при приближении частоты к верхней границе спектра
возрастает,
сначала плавно, но при приближении частоты к верхней границе спектра![]() – весьма резко. Это означает, что по мере
уменьшения длины волны прямых ПМСВ их затухание увеличивается, особенно резко
вблизи верхней границы частотного диапазона.
– весьма резко. Это означает, что по мере
уменьшения длины волны прямых ПМСВ их затухание увеличивается, особенно резко
вблизи верхней границы частотного диапазона.
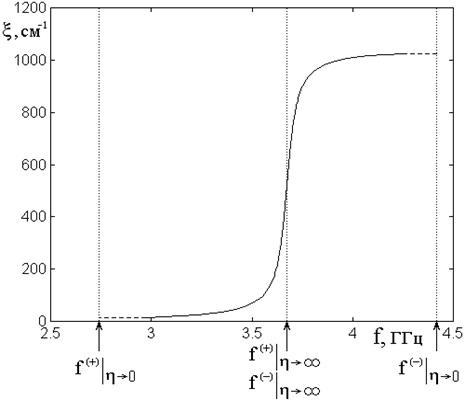
Рис.3. Зависимость мнимой части волнового числа от частоты.
Параметр затухания ![]() , остальные параметры – те же, что на рис.2.
, остальные параметры – те же, что на рис.2.
В области обратных
(диссипативных) волн между частотами ![]() и
и ![]() мнимая часть волнового числа
мнимая часть волнового числа ![]() также возрастает, причем особенно резко
вблизи нижней границы спектра
также возрастает, причем особенно резко
вблизи нижней границы спектра ![]() , после чего возрастание
замедляется. Это означает, что по мере уменьшения длины обратных (диссипативных)
ПМСВ их затухание также возрастает, особенно резко вблизи нижней границы
частотного диапазона.
, после чего возрастание
замедляется. Это означает, что по мере уменьшения длины обратных (диссипативных)
ПМСВ их затухание также возрастает, особенно резко вблизи нижней границы
частотного диапазона.
Сопоставляя с рис.2, можно видеть, что в обоих случаях затухание ПМСВ проявляется тем сильнее, чем действительная часть волнового числа больше то есть длина волны меньше. Другими словами, на одном и том же расстоянии пробега короткие волны затухают сильнее, чем длинные.
Из сравнения пологих участков
кривой на рис.3 можно видеть, что на частоте ![]() мнимая
часть волнового числа составляет около
мнимая
часть волнового числа составляет около ![]() , а на
частоте
, а на
частоте ![]() увеличивается до
увеличивается до ![]() ,
то есть при переходе от прямых ПМСВ к обратным отрицательный показатель
экспоненты в коэффициенте амплитуды ПМСВ увеличивается в 50 раз.,
,
то есть при переходе от прямых ПМСВ к обратным отрицательный показатель
экспоненты в коэффициенте амплитуды ПМСВ увеличивается в 50 раз.,
Следует заметить, что такое
превышение затухания обратных волн над прямыми соответствует значению параметра
затухания ![]() , при котором амплитуда волны уменьшается
на четыре порядка. В реальном эксперименте, например подобном описанному в [6-11],
это означает падение амплитуды волны практически до уровня шума, уже при
прохождении волной расстояния в
, при котором амплитуда волны уменьшается
на четыре порядка. В реальном эксперименте, например подобном описанному в [6-11],
это означает падение амплитуды волны практически до уровня шума, уже при
прохождении волной расстояния в ![]() . Для эксперимента
однако более типичным является расстояние порядка нескольких сантиметров, то
есть полученное здесь значение
. Для эксперимента
однако более типичным является расстояние порядка нескольких сантиметров, то
есть полученное здесь значение ![]() для прямых волн
является несколько завышенным. Вообще говоря, использованное при построении кривой
на рис.3 значение
для прямых волн
является несколько завышенным. Вообще говоря, использованное при построении кривой
на рис.3 значение ![]() выбрано только для удобства изображения
с целью более наглядно представить общий ход зависимости
выбрано только для удобства изображения
с целью более наглядно представить общий ход зависимости ![]() от частоты.
от частоты.
Более реальным для эксперимента
значением параметра затухания является ![]() (типичное
значение для хорошего монокристалла ЖИГ) [2-5]. В этом случае на частоте
(типичное
значение для хорошего монокристалла ЖИГ) [2-5]. В этом случае на частоте ![]() мнимая часть волнового числа составляет
около
мнимая часть волнового числа составляет
около ![]() , а на частоте
, а на частоте ![]() увеличивается
до
увеличивается
до ![]() , то есть при переходе от прямых ПМСВ к
обратным отрицательный показатель экспоненты в коэффициенте амплитуды ПМСВ
увеличивается почти в 700 раз, что говорит о крайне высоком затухании обратных
ПМСВ по сравнению с прямыми.
, то есть при переходе от прямых ПМСВ к
обратным отрицательный показатель экспоненты в коэффициенте амплитуды ПМСВ
увеличивается почти в 700 раз, что говорит о крайне высоком затухании обратных
ПМСВ по сравнению с прямыми.
С другой стороны при ![]() амплитуда прямой волны на частоте
амплитуда прямой волны на частоте ![]() при прохождении типичного для
эксперимента расстояния в
при прохождении типичного для
эксперимента расстояния в ![]() , в соответствии с
коэффициентом показателя экспоненты
, в соответствии с
коэффициентом показателя экспоненты ![]() , уменьшается примерно
в 20 раз, что в пересчете на мощность составляет около 40 дБ, что вполне
соответствует чувствительности реального измерительного тракта.
, уменьшается примерно
в 20 раз, что в пересчете на мощность составляет около 40 дБ, что вполне
соответствует чувствительности реального измерительного тракта.
9. Зависимости амплитуды ПМСВ от частоты
На основе полученной частотной зависимости мнимой части волнового числа для прямых и обратных волн рассмотрим теперь частотную зависимость амплитуды ПМСВ.
Рис.4. Зависимости от частоты амплитуды ПМСВ (утолщенная сплошная линия) и возбуждаемого преобразователем поля (пунктирные линии).
Расстояние пробега ПМСВ: ![]() . Ширина преобразователя:
. Ширина преобразователя: ![]() (кривая 1),
(кривая 1), ![]() (кривая
2),
(кривая
2), ![]() (кривая 3).
(кривая 3).
Вертикальные точечные линии – характерные частоты спектра ПМСВ.
Остальные параметры – те же, что на предыдущем рисунке.
На рис.4 утолщенной сплошной линией показана зависимость амплитуды ПМСВ соответствующая:
![]() ,
(73)
,
(73)
в единицах, нормированных на значение
амплитуды при ![]() . Расстояние пробега ПМСВ
выбрано равным
. Расстояние пробега ПМСВ
выбрано равным ![]() для удобства построения рисунка.
для удобства построения рисунка.
Из рисунка видно, что амплитуда прямых ПМСВ от нижней границы своего частотного диапазона в значительной части (до 80%) спадает незначительно, не более чем на 20%, тогда как в оставшейся части по мере приближения к верхней границе спадает резко то трех и более раз.
Амплитуда обратных (диссипативных) ПМСВ по мере удаления от нижней границы до 20% частотного интервала спадает резко, после чего спад замедляется и на остальной части частотного диапазона амплитуда составляет около 15% от начального низкочастотного значения.
Таким образом, амплитуда тех и других волн по мере увеличения частоты спадает, причем особенно сильно в области наиболее коротких ПМСВ. При этом амплитуда обратных (диссипативных) волн вблизи границы с прямыми волнами составляет не более 20% от максимальной амплитуды прямых волн, а в основной области составляет не более 5 %.
10. Возбуждение ПМСВ линейным преобразователем
Рассмотрим теперь эффективность возбуждения прямых ПМСВ, наблюдавшихся в экспериментах [6-11].
Поле магнитостатической волны в
ферритовой пластине, возбуждаемое преобразователем, представляющим собой
одиночный линейный проводник ширины ![]() , имеет вид [20-23]:
, имеет вид [20-23]:
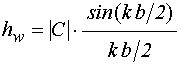 ,
(74)
,
(74)
где ![]() –
волновое число,
–
волновое число, ![]() – комплексная постоянная,
определяемая параметрами материала проводника и ферритовой пластины.
– комплексная постоянная,
определяемая параметрами материала проводника и ферритовой пластины.

Рис.5. Функция, описывающая поле в ферритовой пластине, возбуждаемое одиночным линейным преобразователем.
На рис.5 показана функция 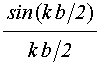 . Ширина основного лепестка на уровне половины
высоты близка к
. Ширина основного лепестка на уровне половины
высоты близка к ![]() , то есть:
, то есть:
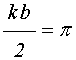 .
(75)
.
(75)
Полагая, что для наиболее эффективного возбуждения ширина лепестка должно равняться половине длины волны, получаем полную длину волны:
![]() .
(76)
.
(76)
Из рис.5 видно, что функция ![]() является знакопеременной. Однако амплитуда
возбуждаемых ПМСВ от фазы возбуждения не зависит, поэтому для оценки
эффективности возбуждения надо брать модуль этой функции
является знакопеременной. Однако амплитуда
возбуждаемых ПМСВ от фазы возбуждения не зависит, поэтому для оценки
эффективности возбуждения надо брать модуль этой функции ![]() , зависимость которого от частоты имеет
вид:
, зависимость которого от частоты имеет
вид:
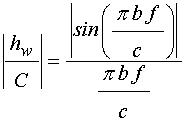 ,
(77)
,
(77)
где ![]() –
скорость электромагнитной волны, в пустом пространстве (над плоскостью магнитной
пластины) равная скорости света.
–
скорость электромагнитной волны, в пустом пространстве (над плоскостью магнитной
пластины) равная скорости света.
На рис.4 пунктирными линиями 1-3
показаны частотные зависимости функции поля ![]() ,
возбуждаемого преобразователями различной ширины. Кривые построены по формуле (77),
с нормировкой на значение, соответствующее низшей частоте спектра.
,
возбуждаемого преобразователями различной ширины. Кривые построены по формуле (77),
с нормировкой на значение, соответствующее низшей частоте спектра.
Из рисунка видно, что поле,
создаваемое преобразователем шириной ![]() (кривая 1) на уровне
0.5 от максимума, по частоте перекрывает практически весь диапазон прямых ПМСВ,
тогда как для преобразователя шириной
(кривая 1) на уровне
0.5 от максимума, по частоте перекрывает практически весь диапазон прямых ПМСВ,
тогда как для преобразователя шириной ![]() (кривая
2) перекрытие уменьшается до 90%, а для преобразователя шириной
(кривая
2) перекрытие уменьшается до 90%, а для преобразователя шириной ![]() (кривая 3) составляет всего 50%.
(кривая 3) составляет всего 50%.
Таким образом, можно полагать,
что для эффективного возбуждения ПМСВ в 90% диапазона прямых волн, ширина
преобразователя должна быть не более ![]() .
.
11. Замечание о наблюдении прямых ПМСВ в эксперименте
В экспериментах [6-11]
наблюдались прямые ПМСВ, для возбуждения которых использовался одиночный
линейный преобразователь из проволоки цилиндрического сечения с толщиной ![]() . При этом крайние частоты спектра прямых
ПМСВ равнялись:
. При этом крайние частоты спектра прямых
ПМСВ равнялись: ![]() ,
, ![]() .
.
Если считать, что толщина
цилиндрической проволоки эквивалентна ширине плоского преобразователя, то
получаем, что в этом случае полная длина волны равна ![]() .
Этой длине волны соответствует частота
.
Этой длине волны соответствует частота ![]() ,
которая весьма близка к верхней частоте спектра
,
которая весьма близка к верхней частоте спектра ![]() .
.
Однако в экспериментах [6-11] минимальная
длина волны, которую удавалось возбудить упомянутым преобразователем,
составляла всего ![]() при частоте
при частоте ![]() .
.
Таким образом, преобразователь
толщиной ![]() возбуждал волну, которую должен был бы
возбуждать преобразователь толщиной
возбуждал волну, которую должен был бы
возбуждать преобразователь толщиной ![]() .
.
Такое несоответствие, по-видимому, является следствием ограничения спектра прямых ПМСВ из-за затухания.
Действительно, из рис.4 можно
видеть, что амплитуда ПМСВ на частоте ![]() составляет
примерно 0.6 от амплитуды на начальном участке спектра. При этом поле на той же
частоте составляет около 0.95 от максимума. Если полагать, что амплитуда возбуждаемой
ПМСВ пропорциональна произведению этих величин, то получаем коэффициент 0.57.
составляет
примерно 0.6 от амплитуды на начальном участке спектра. При этом поле на той же
частоте составляет около 0.95 от максимума. Если полагать, что амплитуда возбуждаемой
ПМСВ пропорциональна произведению этих величин, то получаем коэффициент 0.57.
В экспериментах обычно измеряется
не амплитуда сигнала, а его мощность, пропорциональная квадрату амплитуды,
равная 0.32. Далее надо учесть, что в экспериментах ПМСВ не только
возбуждались, но и принимались подобным же преобразователем, то есть величину
0.32 надо возвести в квадрат, что дает ~ 0.10. Таким образом, получаем, что
даже без учета затухания волны при распространении, на частоте ![]() наблюдаемый сигнал составлял около 10% от
величины сигнала на начальной частоте спектра, то есть претерпевал ослабление
порядка 10 дБ.
наблюдаемый сигнал составлял около 10% от
величины сигнала на начальной частоте спектра, то есть претерпевал ослабление
порядка 10 дБ.
В экспериментах расстояние между
преобразователями составляло порядка единиц сантиметров, что давало возможность
наблюдать сигнал, соответствующий началу спектра, на уровне не более 10-20 дБ
выше уровня шума. Поэтому добавка к затуханию еще 10 дБ, обусловленных
ограничением спектра прямых ПМСВ из-за затухания, вполне могла приводить к
снижению уровня сигнала ниже уровня шума, что и не позволило наблюдать ПМСВ длиной
менее ![]() .
.
12. Некоторые рекомендации для наблюдения диссипативных ПМСВ в эксперименте
Предыдущее замечание касалось реально наблюдавшихся во множестве экспериментов прямых ПМСВ. Однако какие-либо сообщения о наблюдении диссипативных ПМСВ в литературе, известной авторам данной работы, по-видимому, отсутствуют. Из проведенного рассмотрения можно дать некоторые рекомендации для такого наблюдения.
Во-первых, благодаря обратному характеру диссипативных ПМСВ, направление их групповой скорости противоположно направлению групповой скорости прямых ПМСВ, то есть распространение надо наблюдать в направлении, противоположном направлению распространения прямых ПМСВ, для чего в простейшем случае излучающий и приемный преобразователи должны поменяться местами.
Очевидной рекомендацией является выбор для эксперимента пленок ЖИГ с как можно меньшим значением параметра затухания.
В то же время, исходя из общей крутизны дисперсионных кривых, показанных на рис.2, можно сделать вывод, что использование пленок большей толщины (десятки мкм) позволяет эффективнее возбуждать более длинные волны, обладающие однако большей скоростью, а в тонких пленках (единицы мкм) могут быть возбуждены более короткие волны, скорость которых значительно меньше.
Далее, благодаря чрезвычайно большому затуханию диссипативных волн при распространении, расстояние между преобразователями должно составлять не более нескольких десятков микрометров, что делает его сравнимым с толщиной используемых проволочных преобразователей. В этом случае возникает опасность сильного прямого просачивания электромагнитного сигнала с излучающего преобразователя на приемный, так что для предотвращения прямой наводки должны быть приняты специальные меры. По-видимому, в этом случае можно рекомендовать в качестве преобразователей использование микрополосковых проводников на достаточно широком основании [24,25]. Для таких структур, благодаря весьма высокой концентрации поля в области между полосковым проводником и подложкой, прямое излучение и связанная с ним наводка практически отсутствует, что позволяет их эффективно использовать при построении интегральных схем на СВЧ [26,27], в том числе с магнитными компонентами [28,29].
Другим возможным вариантом предотвращения опасности прямой наводки можно считать использование импульсного режима, издавна применяемого для исследования ферритовых линий задержки [30-35], что позволило бы разделить мешающий пролезающий и полезный задержанный сигналы во времени. Однако для наблюдения диссипативных волн, учитывая близость между излучающим и приемным преобразователями, время задержки, по-видимому, будет составлять не более десятков или в лучшем случае сотен наносекунд, что потребует использования импульсов еще меньшей длительности. Такие сверхкороткие импульсы потребуют значительного расширения полосы приемного тракта с вытекающим отсюда повышением уровня шумов и ослаблением чувствительности тракта в целом. Таким образом, использование импульсного режима требует компромиссной оценки между длительностью импульсов и чувствительностью тракта с учетом весьма большого затухания диссипативных волн.
Заключение
Для геометрии плоскопараллельной, намагниченной в плоскости ферритовой пластины получено дисперсионное соотношение для поверхностных магнитостатических волн, записанное через экспоненциальные функции от комплексного волнового числа и действительной частоты.
Подстановка в полученное соотношение комплексной магнитной восприимчивости найденной из решения уравнения движения для намагниченности Ландау-Лифшица с диссипативным членом в форме Гильберта, позволила в явном виде выделить компоненты, определяющие действительную и мнимую части комплексного волнового числа.
В качестве предварительной задачи выполнен анализ дисперсионного соотношения в отсутствие затухания, получены предельные значения характерных частот при стремлении действительной части волнового числа к нулю и к бесконечности.
На основе анализа полного дисперсионного соотношения получены две его ветви, разделенные по частоте предельным значением, соответствующим стремлению действительной части волнового числа к бесконечности.
Показано, что волны, лежащие по частоте ниже этого значения, являются прямыми и в пределе отсутствия затухания переходят в классические волны типа Дэймона-Эшбаха, тогда как волны, лежащие по частоте выше предельного значения, являются обратными, классического аналога не имеют и в среде без затухания отсутствуют. По аналогии с предшествующими работами эти волны названы «диссипативными».
Построены дисперсионные кривые при параметрах задачи, близких к условиям реального эксперимента. Продемонстрировано ограничение дисперсионных кривых со стороны максимального значения действительной части волнового числа. Выявлена математическая природа такого ограничения, получено математическое соотношение, являющееся условием существования обеих ветвей поверхностных магнитостатических волн, включающее в себя кроме волнового числа также параметр затухания и толщину магнитной пластины, по которым в свою очередь также имеются ограничения.
Получено дисперсионное соотношение для диссипации, представляющее собой связь между частотой и мнимой частью волнового числа. При параметрах, близких к условиям эксперимента, построена дисперсионная кривая для диссипации. На ее основе показано, что затухание при распространении обратных диссипативных ПМСВ может превышать подобное затухание для прямых ПМСВ по показателю экспоненты в сотни раз.
Рассмотрен вопрос о возможности
возбуждения прямых и обратных ПМСВ линейным преобразователем в условиях,
соответствующих экспериментальным. Показано, что для эффективного возбуждения
прямых ПМСВ длиной в десятки микрометров необходимы преобразователи, ширина
которых не превышает ![]() . На основе анализа конфигурации
поля преобразователя объяснена величина предельно малой достигнутой в
эксперименте длины ПМСВ, равной
. На основе анализа конфигурации
поля преобразователя объяснена величина предельно малой достигнутой в
эксперименте длины ПМСВ, равной ![]() .
.
Приведены некоторые рекомендации для наблюдения обратных диссипативных волн в эксперименте, состоящие в использовании микрополосковых преобразователей, а также импульсного режима возбуждения, требующего компромисса между длительностью импульса и шириной полосы пропускания приемного тракта в сочетании с ожидаемым высоким затуханием диссипативных волн.
Работа выполнена при финансовой поддержке РФФИ (гранты №12-02-01035-а, №13-02-01401-а).
Литература
1. Damon R.W., Eshbach J.R. // J. Phys. Chem. Solids. 1961. V.19 №3/4. P.308.
2. Адам Дж.Д. // ТИИЭР. 1988. Т.76. №2. С.73.
3. Исхак В.С. // ТИИЭР. 1988. Т.76. №2. С.86.
4. Шлеман Э.Ф. // ТИИЭР. 1988. Т.76. №2. С.105.
5. Adam J., Davis L., Dionne G., Schloemann E., Stitzer S. // IEEE Trans. on MTT. 2002. V.50. №3. P.721.
6. Вашковский А.В., Зубков В.И., Локк Э.Г., Щеглов В.И. // ПЖТФ. 1989. Т.15. №4. С.1.
7. Вашковский А.В., Зубков В.И., Локк Э.Г., Щеглов В.И. // ПЖТФ. 1989. Т.15. №4. С.5.
8. Вашковский А.В., Зубков В.И., Локк Э.Г., Щеглов В.И. // ЖТФ. 1990. Т.60. №7. С.138.
9. Зубков В.И., Локк Э.Г., Щеглов В.И. // РЭ. 1990. Т.35. №8. С.1617.
10. Vashkovsky A.V., Lock E.H., Shcheglov V.I., Zubkov V.I. // IEEE Trans. on Magn. 1990. V.26. №5. P.1480.
11. Вашковский А.В., Зубков В.И., Локк Э.Г., Щеглов В.И. // РЭ. 1991. Т.36. №1. С.18.
12. Зубков В.И., Щеглов В.И. // РЭ. 2000. Т.45. №4. С.471.
13. Зубков В.И., Щеглов В.И. // РЭ. 2001. Т.46. №4. С.433.
14. Зубков В.И., Щеглов В.И. // РЭ. 2006. Т.51. №3. С.328.
15. Зубков В.И., Щеглов В.И. // РЭ. 2007. Т.52. №6. С.701.
16. Зубков В.И., Щеглов В.И. // РЭ. 2009. Т.54. №9. С.1064.
17. Зубков В.И., Щеглов В.И. // РЭ. 2012. Т.57. №5. С.565.
18. Вызулин С.А., Розенсон А.Э., Шех С.А. // РЭ. 1991. Т.36. №1. С.164.
19. Вызулин С.А. Обобщенные плоские волны в задачах электродинамики магнитогиротропных сред. Диссертация. на соискание уч. ст. д.ф.-м.н. Краснодар. 2000.
20. Гуревич А.Г. Ферриты на сверхвысоких частотах. М.: Гос.Изд.физ.-мат.лит. 1960.
21. Гуревич А.Г. Магнитный резонанс в ферритах и антиферромагнетиках. М.: Наука. 1973.
22. Гуревич А.Г., Мелков Г.А. Магнитные колебания и волны. М.: Физматлит. 1994.
23. Gilbert T.L. // IEEE Trans. on Magn. V.40. №6. P.3443.
24. Изюмова Т.И. Свиридов В.Т. Волноводы, коаксиальные и полосковые линии. М.: Энергия. 1975.
25. Нефедов Е.И., Фиалковский А.Т. Полосковые линии передачи. М.: Наука. 1980.
26. Нефедов Е.И., Фиалковский А.Т. // ДАН СССР. 1978. Т.239. №2. С.315.
27. Нефедов Е.И., Санталов Н.П., Фиалковский А.Т. // РЭ. 1979. Т.24. №1. С.17.
28. Курушин Е.П., Нефедов Е.И. // Микроэлектроника. 1977. Т.6. №6. С.549.
29. Гуляев Ю.В., Зильберман П.Е. // РЭ. 1978. Т.23. №5. С.897.
30. Eshbach J.R. // JAP. 1963. V.34. №4. P.1298.
31. Eggers F.G., Strauss W. // JAP. 1963. V.34. №4. P.1180.
32. Schloemann E., Joseph R.I., Kohane T. // Proc. IEEE. 1965. V.53. №10. P.1495.
33. Шлёман Е., Джозеф К., Кохейн Т. // ТИИЭР. 1965. Т.53. №10. С.1685 (перевод [32]).
34. Есиков О.С., Фетисов Ю.К., Царьков А.Г. // ЖТФ. 1982. Т.52. №4. С.719.