Использование метода перенормировки с ограничением для восстановления искаженных изображений при наличии помех и шума с неизвестными параметрами

УДК 621.396

А. В. Кокошкин, В. А. Коротков, К. В. Коротков, Е. П. Новичихин

Институт радиотехники и электроники им. В.А. Котельникова РАН, Фрязинский филиал

Статья получена 22 июня 2015 г.

Аннотация. В работе предлагается метод перенормировки с ограничением для восстановления изображений, искажённых известной аппаратной функцией, при наличии неизвестных помех и шума.

Ключевые слова: аппаратная функция, восстановление изображений, помехи, шум.

Abstract. The method of renormalization limited to restore an image distorted by a known instrumental function in the presence of unknown interference and noise is proposed in the paper.

Key words: instrumental function, image restoration, interference, noise.

Введение

Задача восстановления искаженных аппаратной функцией (АФ) изображений при наличии шумов обычно решается с помощью различных способов фильтрации (например Винера или Тихонова) [1 – 5]. Помехи, имеющие в отличие от шумов некие регулярные свойства (спектрально-локальные), могут быть значительно ослаблены с помощью секвентного анализа. Секвентный анализ заключается в изучении спектральных (на основе преобразования Уолша) свойств помех с дальнейшим использованием этих свойств для фильтрации изображений [6, 7]. Альтернативным способом является метод опорного изображения (МОИ) [8 – 12], в котором существенным моментом является знание свойств спектра изображения. Помехами в этом случае являются те особенности пространственного спектра сформированного изображения, которые существенно энергетически превосходят величину спектра опорного изображения. При таком определении помех существенным моментом является спектр опорного изображения и определение порога, при превышении которого сигнал определяется как помеха. Использование универсального опорного спектра (УОС) [10 – 13] в качестве спектра опорного изображения частично решает задачу. Однако реальные амплитудные спектры могут заметно отличаться от УОС. В этом случае определение порога становится не простой задачей.

В данной работе предлагается применения метода перенормировки с ограничением (МПО) на основе УОС для решения задачи восстановления искаженных изображений при наличии неизвестных помех и шума.

2. Метод перенормировки с ограничением (МПО)

Рассмотрим сначала использование этого метода в задаче фильтрации от локально-спектральных помех.

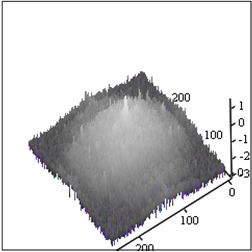
На Рис.1 представлено исходное изображение и его амплитудный спектр.

А Б

Рис.1. Неискаженное изображение – А и его спектр – Б.

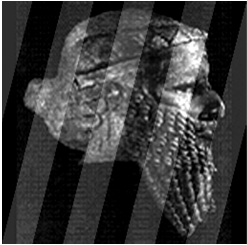
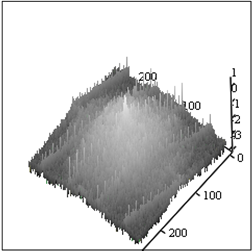
Добавим помеху в виде полос, яркость которых меняется от 0 до 50 (Рис.2). Эта помеха может появиться при изменении уровня «0» в регистрирующей изображение аппаратуре [6, 7, 12].

А Б

Рис.2. Изображение со спектрально – локальными помехами – А и его спектр – Б.

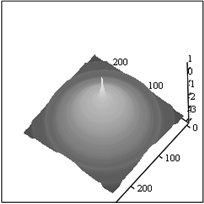
На спектре рис.2Б помеха проявляется в виде «гребня», который отсутствует на рис.1Б. Фильтрация с помощью УОС [11, 12] может быть проведена вполне успешно, однако результат в той или иной мере зависит от отличия реального спектра от УОС. Ранее [11, 12] для характеристики спектра использовался спектр, усредненный по спрайту 5х5 пикселов (УСС), причем усреднение производилось за исключением области диаметром 9 пикселов вблизи нуля. Такой спектр тоже можно использовать для фильтрации локально-спектральных помех. Но если область спектра, занятая помехой, превосходит 5х5 пикселов, то такой способ может быть не эффективен. Произведем осевое усреднение спектра на рис.2Б следующим образом. Значение усредненного спектра (УСК) равно среднему значению спектра в кольце с центром в нуле и шириной 5 пикселов. В окрестности нуля диаметром 9 пикселов значение спектра не усредняем. На рис. 3 представлен усредненный таким образом спектр в сравнении с УОС и УСС.

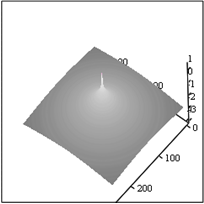
А Б В

Рис.3. Амплитудные спектры. УСС – А, УСК – Б, УОС - В.

Сравнение спектров на Рис.3 показывает, что в отличие от УСС, УОС и УСК радиально симметричны, хотя несколько отличаются по виду. УСС отличается не только отсутствием радиальной симметрии, но и небольшой «шероховатостью».

Изменим спектр изображения с помощью (1), делая его в среднем радиально симметричным.

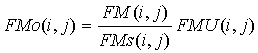, (1)

где и - пектры соответственно УСС и УСК, и - спектры соответственно изображения с помехой и преобразованный спектр. Так как в среднем спектр соответствует УСК, то превышение преобразованного спектра уровня УСК более чем в Ur раз интерпретируем как помеху. Ur выберем, как в работах [11 – 13], равным 4. Уменьшение Ur приводит к лучшей фильтрации, но и к потерям части информации об изображении. Спектральные значения, соответствующие помехе, приравниваем величине, в Ur раз меньше УСК на этой частоте, так как простое «зануление» амплитуды помехи может привести к появлению артефактов на изображении. В результате получается изображение, приведенное на рис. 4.

Сравнение рис.4 и рис.1 показывает, что удаление помехи произведено успешно. Небольшие отличия спектров рис.1Б и рис.4Б мало заметны на изображениях.

А Б

Рис.4. Восстановленное изображение со спектрально – локальными помехами – А и его спектр – Б.

Такой подход вполне применим и в случае с изображением, искаженным АФ с осесимметричным спектром.

Рассмотрим фильтрацию локально-спектральной помехи на искаженном анизотропной АФ изображении на примере АФ «смаз». На рис.5 представлено искаженное АФ «смаз» изображение. Величина S0=8 соответствует половине величины «смаза» изображения.

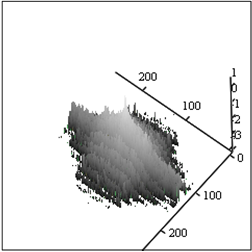
А Б

Рис.5. Искаженное АФ «смаз» изображение с S0=8 – А и его спектр – Б.

Наложим на изображение Рис.5 рассмотренную ранее локально-спектральную помеху. Полученное изображение представлено на Рис.6.

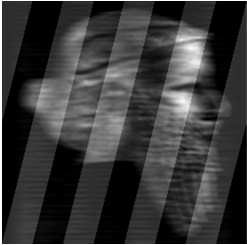
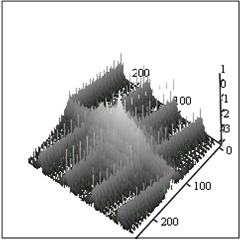
А Б

Рис.6. Искаженное АФ изображение со спектрально – локальными помехами – А и его спектр – Б.

На рис.6Б помеха проявляется так же, как и на рис.2Б – в виде «гребней». Если мы воспользуемся алгоритмом, описанным выше, то ослабим влияние спектрально-локальных помех, но не уберем искажение, внесенное АФ. На Рис.6Б помеха проявляется так же, как и на Рис.2Б – в виде «гребней». На Рис.7 представлены результаты фильтрации спектрально-локальных помех.

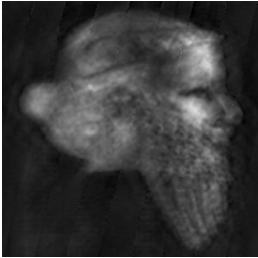
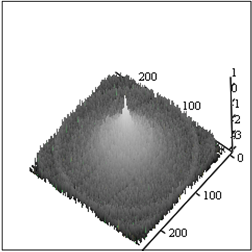
А Б

Рис.7. Восстановленное изображение рис.6А со спектрально – локальными помехами – А и его спектр – Б.

Рис.7А иллюстрирует хорошее подавление помех. Однако искажение, вызванное АФ, осталось. Отметим, что спектр рис.7Б отличается от спектра рис.4Б, несмотря на применение одного и того же алгоритма.

Следующий шаг в восстановлении рис.7А начинается с вычисления УСС - для применения перенормировки. Далее после инверсной фильтрации необходимо сделать перенормировку (2):

, (2)

где и соответственно спектр после инверсной фильтрации и УСС, и - соответственно нормированный спектр АФ и УОС, и - значения спектров при нулевой пространственной частоте, - перенормированный инверсно отфильтрованный спектр.

Так как в среднем это спектр должен соответствовать УОС, то превышение преобразованного спектра уровня УОС более чем в Ur раз интерпретируем как помеху. Ur выберем, как в работах [10 – 13], равным 4. В окрестности нуля диаметром 9 пикселов значение спектра не меняем. В результате получим изображение, представленное на Рис.8.

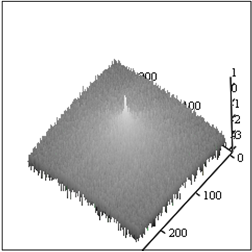
А Б

Рис.8. Восстановленное изображение Рис.7А со спектрально – локальными помехами – А и его спектр – Б.

Обратим внимание, что спектр рис.8Б напоминает УОС (рис.3В), а изображение рис.8А демонстрирует хорошее подавление помехи и искажение АФ.

Рассматриваемый метод перенормировки с ограничением достаточно устойчив не только к спектрально-локальным помехам, но и к действию белого шума. На рис.9 представлены результаты восстановления изображения рис.6А при различном уровне белого шума.

А (Sh=0) Б (Sh=0)

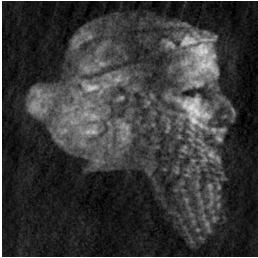
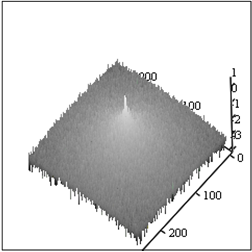
В (Sh=10) Г (Sh=10)

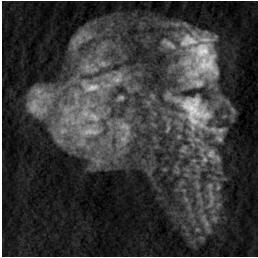
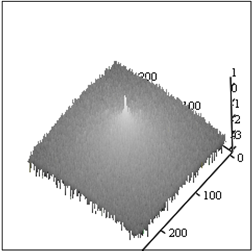
Д (Sh=20) Е (Sh=20)

Рис.9. Восстановление изображения рис.6А при наличии спектрально-локальной помехи (наклонные полосы)
и различных Sh - уровнях белого шума (удвоенная амплитуда).

Сравнение спектров на Рис.9 позволяет убедится в том, что рассмотренный алгоритм позволяет получить амплитудные спектры восстановленных изображений, слабо зависящие от уровня шума. Увеличение уровня шума приводит к увеличению артефактов на восстановленных изображениях и исчезновению (маскировке) мелких деталей изображения.

3. Выводы

Предложен метод перенормировки с ограничением (МПО) для восстановления изображений, искажённых известной аппаратной функцией, при наличии неизвестных помех и шума.

Проведено тестирование МПО, в результате которого констатируется высокая эффективность восстановления при одновременном присутствии на искажённом АФ изображении неизвестных шума и спектрально-локальных помех.

Литература

1. Р. Гонсалес, Р. Вудс. Цифровая обработка изображений. М. «Техносфера», 2005, 1071 стр.

2. Pratt W.K. Digital Image Processing. – John Wiley and Sons, Inc., USA, 1978.

3. Бейтс Р. Мак-Доннел М. Восстановление и реконструкция изображений. /Пер. с англ.к. ф-м н. Б.С. Кругликова и С.Л. Ярославского под редакцией д. ф-м н. Л.П. Ярославского. М.: «Мир», 1989, 487с.

4. Новейшие методы обработки изображений. / Под ред. А.А. Потапова. – М.: ФИЗМАТЛИТ, 2008, 496 с.

5. Журавель И.М. Краткий курс теории обработки изображений. URL: http://matlab.exponenta.ru/imageprocess/book2/index.php

6. В. А. Саблина «Разработка и исследование алгоритмов восстановления изображений методами секвентного анализа». Автореферат диссертации на соискание ученой степени кандидата технических наук. Рязань, 2009г.

7. Б. В. Костров «Теория и методология применения секвентного анализа для обработки аэрокосмических изображений». Автореферат диссертации на соискание ученой степени доктора технических наук, Рязань, 2012г.

8. А. Ю. Зражевский, А. В. Кокошкин, Е. П. Новичихин, С. В. Титов, «Повышение качества радиоизображений». «Нелинейный Мир», № 9, 2010г., с. 582-590.

9. Ю. В. Гуляев, А. Ю. Зражевский, А. В. Кокошкин, В. А. Коротков, В. А. Черепенин «Коррекция пространственного спектра, искаженного оптической системой, с помощью метода опорного изображения. Часть 2. Адаптивный метод опорного изображения (АМОИ)». // Журнал радиоэлектроники [электронный журнал]. 2013. №12. URL: http://jre.cplire.ru/jre/dec13/2/text.html

10. Ю. В. Гуляев, А. Ю. Зражевский, А. В. Кокошкин, В. А. Коротков, В. А. Черепенин «Коррекция пространственного спектра, искаженного оптической системой, с помощью метода опорного изображения. Часть 3. Универсальный опорный спектр». // Журнал радиоэлектроники [электронный журнал]. 2013. №12. URL: http://jre.cplire.ru/jre/dec13/3/text.html

11. А. Ю. Зражевский, А. В. Кокошкин, В. А. Коротков «Влияние спектрально-локальных помех на восстановление изображения методом опорного изображения». // Журнал радиоэлектроники [электронный журнал]. 2014. №1. URL: http://jre.cplire.ru/jre/jan14/9/text.html

12. Зражевский А. Ю., Кокошкин А. В., Коротков В. А., Коротков К. В.,

Новичихин Е.П. «Восстановление искажённых изображений при наличии спектрально-локальных помех». Доклады VIII Всероссийской научно-технической конференции "Радиолокация и радиосвязь", 24-26 ноября 2014г., Издание JRE – ИРЭ им. В.А.Котельникова РАН, Москва 2014 г., с.195.

13. Зражевский А. Ю., Кокошкин А. В., Коротков В. А., Коротков К. В., Новичихин Е.П. «Универсальный опорный спектр и его использование для нахождения аппаратной функции искажения и восстановления изображений». Доклады VIII Всероссийской научно-технической конференции "Радиолокация и радиосвязь", 24-26 ноября 2014г., Издание JRE – ИРЭ им. В.А.Котельникова РАН, Москва 2014г., с.191.