Термические эффекты воздействия электромагнитного излучения на проводящие частицы, интегрированные в диэлектрическую среду
П. С. Глазунов 1, В. А. Вдовин 2, А. И. Слепков 1
1 Московский государственный университет имени М.В. Ломоносова, физический факультет, кафедра общей физики
2 Институт радиотехники и электроники им. В.А.Котельникова РАН
Статья поступила в редакцию 6 июля 2016 г.
Аннотация. В работе проводится теоретическое исследование воздействия электромагнитного излучения на неоднородные среды типа «проводящие частицы в диэлектрике», а именно изучаются термические эффекты воздействия. Рассматриваются две идеализированные модели: первая представляет собой два полупространства «металл-диэлектрик», вторая - проводящий шар в диэлектрике. Считается, что напряженность электрического поля связана с токами проводимости законом Ома в дифференциальной форме, а функцию объемных источников тепла можно найти из закона Джоуля-Ленца. Для обеих моделей решается задача о прохождении падающей плоской гармонической электромагнитной волны вглубь металла. Для модели двух полупространств решение ищется в виде отраженной, прошедшей и падающей волн, для модели «шар в диэлектрике» решение находится с помощью функций Боргниса. Для первой модели с помощью преобразований Лапласа решается задача о распространении в ней тепла: выводится формула, описывающая температурный портрет в системе, а также асимптотическая формула, описывающая температуру на границе раздела сред «металл-диэлектрик» при достаточно больших временах. Для второй модели находится функция объемных источников тепла.
Ключевые слова: проводящие частицы, композитные среды, эффект селективного воздействия, термический эффект.
Abstract. This paper is devoted to theoretical research of impact of an electromagnetic radiation on the heterogeneous mediums such as "conductive particles in a dielectric", namely thermal effects of influence are studied. Two idealized models are considered: the first one represents two half-spaces "metal-dielectric", and the second one is conductive sphere in a dielectric. It is considered that the Ohm's law in a differential form is valid, and function of sources of heat can be found from the Joule-Lenz law. For both models the problem about passing of an incident plane harmonic electromagnetic wave into the metal is solved. For model of two half-spaces the solution is found in the form of the reflected, passed and falling waves, for the "sphere in a dielectric" model the solution is found by means of Borgnis's functions. For the first model by means of Laplace transformations the problem about distribution of heat is solved: the formula describing a temperature portrait in system and also the asymptotic formula describing temperature on a boundary of the metal-dielectric mediums at rather long periods of time are removed. For the second model a function of sources of heat is found.
Keywords: conductive particles, heterogeneous medium, the effect of selective impact, the thermal effect.
Введение
Настоящая работа посвящена теоретическому исследованию воздействия электромагнитного излучения на неоднородные среды, а именно на систему типа «проводящие частицы в диэлектрике». Цель воздействия - добиться селективного эффекта, заключающегося в следующем. При обработке электромагнитным излучением композитной среды из-за ее неоднородности происходят некоторые физические процессы, приводящие к возникновению механических напряжений на границах раздела сред металл-диэлектрик, что может привести к разрушению материала диэлектрика, причём преимущественно вокруг металлических частиц [1, 2].
Таким образом, обработка электромагнитным излучением может быть актуальна для решения широкого спектра прикладных задач в различных отраслях промышленности и медицине, среди которых: адресная доставка лекарств [1], дезинтеграция упорных минеральных руд [4], чистка поверхностей различных промышленных установок [3], разделение промышленных отходов для утилизации и переработки [3].
Физические процессы, возникающие при электромагнитной обработке, можно условно разделить на две группы: положительные и отрицательные, которые соответственно облегчают или затрудняют разделение композитных веществ на их составляющие. К положительным процессам, согласно [4], относятся такие как электрический пробой, шнурование тока, термомеханические напряжения, пондеромоторные силы. К отрицательным - перегрев комплекса: оплавление и спекание частиц, перегрев электродов.
Большинство процессов плохо изучено: для них не существует корректно работающих физических моделей, и сложно сказать, какие из них являются превалирующими, а какими можно пренебречь. Поэтому ясно, что в первую очередь должны исследоваться процессы, в существовании которых не приходится сомневаться. Таковым является нагрев проводящих частиц из-за наведенных в них токов, создаваемых проникшими вглубь проводника электромагнитными волнами. Актуальность исследования этого эффекта обусловлена и тем, что он может являться как положительным, так и отрицательным. Причем достоверно известно [4], что среди отрицательных эффектов он играет одну из главных ролей.
Детальное исследование разрушения композитных материалов под воздействием электромагнитного облучения является достаточно сложной задачей. Однако, во многих случаях для планирования и проведения экспериментальных исследований достаточно решения ряда идеализированных задач. Поэтому в работе исследовалось рассеяние лишь плоской гармонической электромагнитной волны. Рассматривались две модели: одномерная модель, состоящая из двух полупространств «металл-диэлектрик», и трехмерная модель: металлический шар в диэлектрике. Ставились две основные цели: во-первых, найти электромагнитное поле в системе с учетом его проникновения в проводник, во-вторых, рассчитать температурное распределение в системе.
1. Модель типа полупространства «металл – диэлектрик»
Методика решение задачи для одномерной модели состоит из следующих этапов.
1. Сведение системы исходных уравнений Максвелла к уравнениям Гельмгольца.
2. Решение задачи дифракции электромагнитных волн в исследуемой системе.
3. Решение краевой задачи теплопроводности в исследуемой системе.
1.1 Волновое уравнение для проводящих сред в стационарном случае
Запишем систему уравнения Максвелла в системе СИ (1)-(4). Пусть зависимость электромагнитных полей от времени гармоническая, а материальные уравнения имеют вид (5)-(7). Выведем волновое уравнение Гельмгольца для компонент вектора напряженности электромагнитного поля.
![]() (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
![]() (4)
(4)
![]() ,
, ![]() (5)
(5)
![]() ,
, ![]() (6)
(6)
![]() ,
,![]() (7)
(7)
Величины ![]() и
и ![]() будем предполагать действительными и зависящими от частоты
будем предполагать действительными и зависящими от частоты ![]() . Далее мы будем работать в описанных выше допущениях.
. Далее мы будем работать в описанных выше допущениях.
Заменяя производную по
времени умножением на ![]() , запишем уравнения Максвелла в следующем виде:
, запишем уравнения Максвелла в следующем виде:
![]() (8)
(8)
![]() (9)
(9)
![]() (10)
(10)
![]() (11)
(11)
Докажем, что ![]() . Беря ротор от (10), с учетом (5), (7) и того, что дивергенция ротора
любого вектора равна нулю, получаем:
. Беря ротор от (10), с учетом (5), (7) и того, что дивергенция ротора
любого вектора равна нулю, получаем:
![]() (12)
(12)
Выведем теперь уравнение Гельмгольца.
Возьмем ротор от (8), с учетом (5), (6), (12) и, используя известное
математическое тождество ![]() , получим:
, получим: ![]() .
.
Таким образом, для проводящей среды имеем:
![]() (13)
(13)
где ![]() .
.
Данная процедура является
типичной для задач дифракции электромагнитных волн, но в конкретном случае
имеется одна особенность: коэффициент ![]() в уравнении Гельмгольца (13) из-за
наличия проводимости комплексный.
в уравнении Гельмгольца (13) из-за
наличия проводимости комплексный.
1.2 Нахождение отражённой и прошедшей электромагнитных волн для одномерной модели
Сформулируем следующую
задачу. Рассмотрим отражение и прохождение плоской гармонической
электромагнитной волны, падающей нормально из диэлектрической среды I на проводящую среду II. Известны характеристики сред и
падающей волны, требуется найти характеристики прошедшей волны, а также
коэффициент ее прохождения ![]() .
.
Обозначим падающую, отражённую,
прошедшую волны соответственно: ![]() ,
,![]() ,
,![]() . Ища решение в виде плоских волн (14),
и подставляя их в граничные условия (15),
. Ища решение в виде плоских волн (14),
и подставляя их в граничные условия (15),
![]() ,
, ![]() ,
, ![]() (14)
(14)
![]() ,
, ![]() (15)
(15)
получаем решение (16)-(19), которое выражается через исходные
параметры задачи (![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ):
):
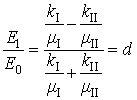 (16)
(16)
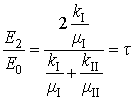 (17)
(17)
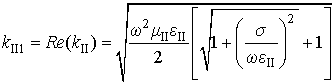 (18)
(18)
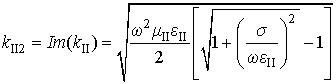 (19)
(19)
Приведём зависимость модуля коэффициента прохождения от частоты (рис. 1).
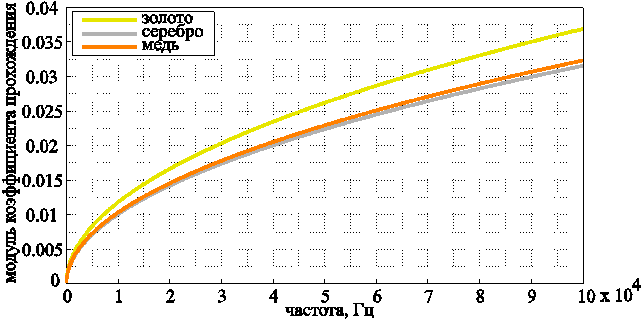
Рис. 1
С повышением проводимости среды, график становится более пологим. Это объясняется тем, что с ее повышением увеличивается концентрации свободных электронов в металле. Поэтому электромагнитная волна сильнее взаимодействует со средой, затухает в ней быстрее и, как следствие, волне «труднее» проникнуть вглубь среды.
1.3 Особенности определения температурного поля вблизи границы раздела сред «металл-диэлектрик».
Найти функцию объёмных источников
тела ![]() , выделяющегося в проводнике, можно по формуле:
, выделяющегося в проводнике, можно по формуле:
Для данной задачи эта функция имеет вид:
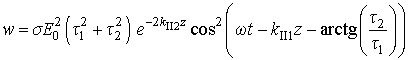 (21)
(21)
Нижние индексы 1 и 2 у величин ![]() и
и ![]() обозначают их действительную и мнимую
части соответственно. Для простоты положено, что амплитуда падающей волны
обозначают их действительную и мнимую
части соответственно. Для простоты положено, что амплитуда падающей волны ![]() вещественна.
вещественна.
Сформулируем теперь задачу о
нахождении тепла в нашей области: тепло выделяется только в среде II, на
границе ![]() есть тепловой контакт сред I и II.
есть тепловой контакт сред I и II.
Математически это
записывается как система двух уравнений в частных производных, связанных
условиями сопряжения при ![]() , с заданными начальными условиями при
, с заданными начальными условиями при ![]() и с естественными граничными условиями на бесконечности (
и с естественными граничными условиями на бесконечности (![]() –температура в градусах Кельвина):
–температура в градусах Кельвина):
![]() (22)
(22)
![]() (23)
(23)
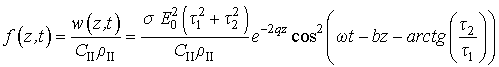 (24)
(24)
![]() (25)
(25)
Здесь ![]() - удельная теплоёмкость среды,
- удельная теплоёмкость среды, ![]() - плотность,
- плотность, ![]() - коэффициент теплопроводности,
- коэффициент теплопроводности, ![]() - коэффициент температуропроводности,
реальная и мнимая части волнового вектора во
- коэффициент температуропроводности,
реальная и мнимая части волнового вектора во ![]() среде обозначены, как
среде обозначены, как ![]() и
и ![]() соответственно. Прежде чем приступить к решению
системы (22)-(25), упростим выражение (24). Так как для электромагнитного
излучения, как правило,
соответственно. Прежде чем приступить к решению
системы (22)-(25), упростим выражение (24). Так как для электромагнитного
излучения, как правило, ![]() , а тепловой нагрев среды носит кумулятивный характер,
то на достаточно больших временах
, а тепловой нагрев среды носит кумулятивный характер,
то на достаточно больших временах![]() наблюдения
наблюдения ![]() уже будет не так важна периодическая зависимость
уже будет не так важна периодическая зависимость ![]() от времени. Поэтому усредним
от времени. Поэтому усредним ![]() по периоду ее колебаний, кроме того
обозначим
по периоду ее колебаний, кроме того
обозначим![]() . В таком случае:
. В таком случае: ![]() .
.
Далее будет получено аналитическое
решение для усреднённой функции ![]() .
.
Решать систему (22)-(25)
будем при помощи преобразования Лапласа. Из-за громоздкости выкладок опишем
решение схематично. К системе (22)-(25) применяется преобразование Лапласа, с
помощью которого от функций ![]() осуществляется переход к их изображениям:
осуществляется переход к их изображениям:
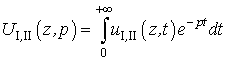 ,
,
и тем самым совершается переход от системы уравнений в частных производных к системе обыкновенных дифференциальных уравнений, решение которой находится тривиально. Затем, беря от него обратное преобразование Лапласа
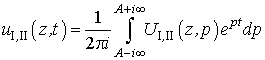 ,
,
получаем решение исходной задачи(22)-(25):
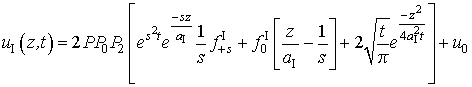 (26)
(26)
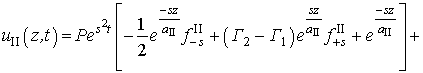
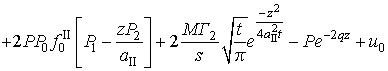 (27)
(27)
где: ![]() ,
, 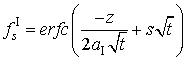 ,
, 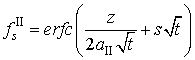 ,
, ![]() ,
,
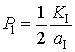 ,
, ![]() ,
, 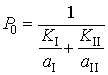 ,
, 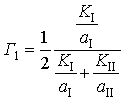 ,
, 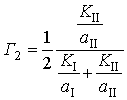 .
.
Формулы (26)-(27) значительно упрощаются при временах![]() . Например, для поведения температуры на границе раздела сред
«металл-диэлектрик» справедлива асимптотическая формула:
. Например, для поведения температуры на границе раздела сред
«металл-диэлектрик» справедлива асимптотическая формула:
![]() (28)
(28)
Формулы (26)-(27) были
проверены с помощью численного моделирования. Использовалась шести точечная
симметричная разностная схема (с безусловной сходимостью) с аппроксимацией ![]() . Бесконечное пространство заменялось конечным отрезком, на концах
которого ставились условия Дирихле. Сравнение аналитического и численного
решений проводится на рис. 2-3. Графики показывают распределение температуры в
реальной системе «золото-кварц» и соответствуют следующим параметрам задачи:
. Бесконечное пространство заменялось конечным отрезком, на концах
которого ставились условия Дирихле. Сравнение аналитического и численного
решений проводится на рис. 2-3. Графики показывают распределение температуры в
реальной системе «золото-кварц» и соответствуют следующим параметрам задачи:
![]() ,
, ![]() ,
,![]() МГц. Для построения
численного решения бралась не усреднённая по периоду своих колебаний функция
тепловых источников (24). На рис. 2 изображена выноска с увеличенным масштабом,
из которой видно, что усреднение не сильно сказывается на поведении решения. Из
рис.1 видно, что в выбранном диапазоне температур различия между решениями
малы: они составляют не более сотых долей градуса кельвина, что подтверждает
достоверность аналитического решения.
МГц. Для построения
численного решения бралась не усреднённая по периоду своих колебаний функция
тепловых источников (24). На рис. 2 изображена выноска с увеличенным масштабом,
из которой видно, что усреднение не сильно сказывается на поведении решения. Из
рис.1 видно, что в выбранном диапазоне температур различия между решениями
малы: они составляют не более сотых долей градуса кельвина, что подтверждает
достоверность аналитического решения.
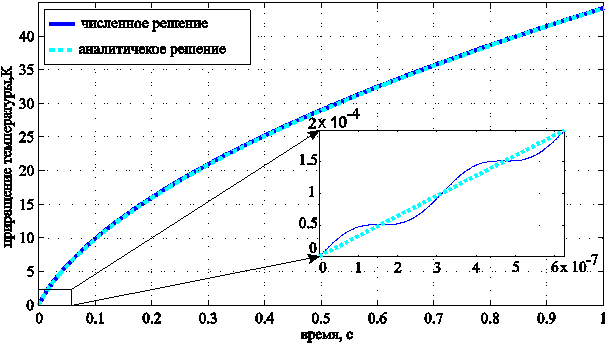
Рис. 2. График зависимости приращения температуры от времени на границе раздела сред «золото-кварц».
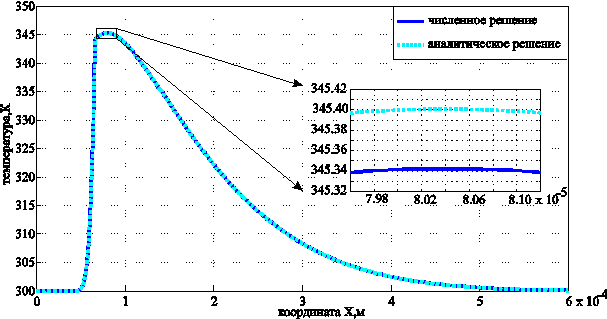
Рис. 3. Температурный портрет при времени равном 1 секунда для системы «золото-кварц».
2. Решение задачи дифракции на проводящем шаре
Схематично
опишем использованный метод решения. При гармонической зависимости электромагнитных
полей от времени можно уменьшить число неизвестных величин в системе уравнений
Максвелла и выразить компоненты электромагнитного поля всего через две
скалярные функции ![]() ,
, ![]() , которые называются функциями Боргниса [5]. В
сферических координатах компоненты напряжённости электрического поля выражаются
через них по следующим формулам:
, которые называются функциями Боргниса [5]. В
сферических координатах компоненты напряжённости электрического поля выражаются
через них по следующим формулам:
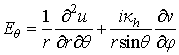 (29)
(29)
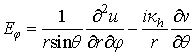 (30)
(30)
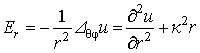 (31)
(31)
где ![]() ,
, ![]() ,
, ![]() .
.
Подобно тому, как электромагнитное поле должно удовлетворять уравнениям Максвелла, функции Боргниса должны удовлетворять уравнению Боргниса, вид которого в сферических координатах представлен следующей формулой:
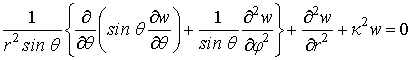 (32)
(32)
а также следующим граничным условиям:
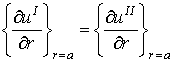 (33)
(33)
![]() (34)
(34)
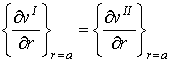 (35)
(35)
![]() (36)
(36)
Уравнение (32) заменой ![]() сводится к уравнению Гельмгольца в сферических координатах:
сводится к уравнению Гельмгольца в сферических координатах:
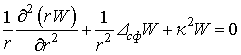 (37)
(37)
Решение уравнения (37) ищется в виде ряда:
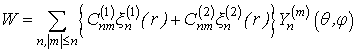 (38)
(38)
где ![]() ,
, ![]() - пара любых линейно независимых
сферических функций Бесселя.
- пара любых линейно независимых
сферических функций Бесселя.
Постановка задачи та же, что и ранее, но электромагнитная волна рассеивается теперь на металлическом шаре. Решение задачи (вектор напряженности электрического поля внутри шара) представлено тремя формулами ниже:
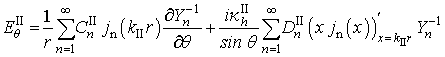 (39)
(39)
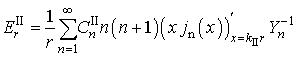 (40)
(40)
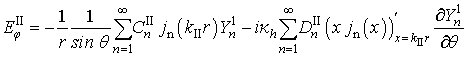 (41)
(41)
где коэффициенты ![]() и
и ![]() находятся из граничных условий (33)-(36).
находятся из граничных условий (33)-(36).
По формуле (20) можно найти и функцию тепловых источников. На рис. 4 показан её контурный график в сечении шара плоскостью, перпендикулярной фронту падающей волны.
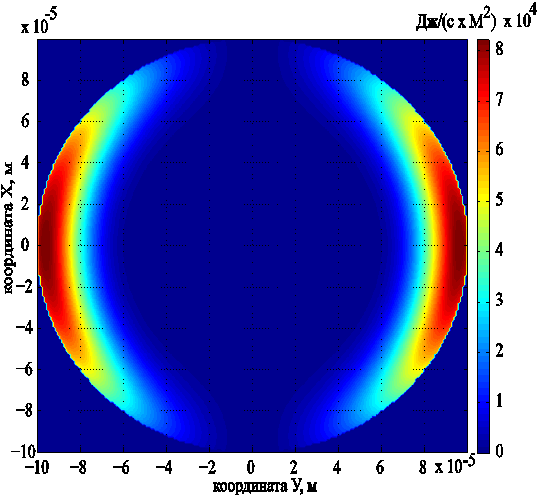
Рис. 4. Контурный график функции объемных тепловых источников.
В заключение скажем пару слов о границе применимости моделей. Формально, с математической точки зрения, радиус металлического шара ничем не ограничен. Однако в моделях не была учтена атомная структура вещества, поэтому (из-за возможности возникновения квантовых эффектов) радиус шара должен быть не менее десятков нанометров. Также характерная толщина скин-слоя должна быть много больше размеров кристаллической решётки проводника, поскольку из-за этого возможно возникновение аномального скин-эффекта.
Заключение
1. Для одномерной задачи (нормальное падение электромагнитной волны на границу раздела «диэлектрик-металл») создана математическая модель, позволяющая определять температурный портрет системы вблизи границы раздела.
2. Получены аналитическое и численное решения поставленной задачи: определена зависимость температуры среды от координаты рассматриваемой точки и от времени. Показано соответствие аналитических формул результатам численного моделирования.
3. Показано, что приращение температуры на границе раздела сред «металл-диэлектрик» ведет себя пропорционально корню квадратному от времени.
4.Для системы «металлический шар в диэлектрике» получено решение задачи дифракции плоской электромагнитной волны. Найдена функция тепловых источников, позволяющая ставить задачу о распределении температуры внутри и вне шарообразного проводника в зависимости от времени.
Работа проводилась при поддержке гранта РФФИ № 16-29-09581.
Литература
1. Гуляев Ю.В. и др. Дистанционная декапсуляция нанокомпозитных липосом, содержащих внедренные проводящие наночастицы, при воздействии импульсного электрического поля // Радиотехника и электроника, 2015, том 60, № 10, с. 1051-1063.
2. Чантурия В.А. и др. Использование мощных электромагнитных импульсов в процессах дезинтеграции и вскрытия упорного золотосодержащего сырья // Физико-технические проблемы обогащения полезных ископаемых, 2001, № 4, с. 95-106.
3. Isao Yoshimi et al. // Int. J. Mater. Eng. Resour. 2002.V.10, No.1, pp. 66–70.
4. В.А.Вдовин, Ю.В.Гуляев, В.А.Черепенин, В.А.Чантурия. Нетепловое воздействие мощных электромагнитных импульсов на золотосодержащую горную породу // Радиотехника и электроника. 2005. Т. 50. № 9. С. 1129-1133.
5. Топтыгин И.Н. Современная электродинамика, часть 2. Теория электромагнитных явлений в веществе: Учебное пособие. - Москва-Ижевск: НИЦ «Регулярная и хаотическая динамика», 2005. - 848 с.
6. А.В.Лыков Теория теплопроводности: Учебное пособие для студентов теплотехнических специальностей высших учебных заведений.-Издательство «Высшая школа», Москва, 1967.-600 c.