УДК 517.15: 517.95: 519.62: 535.4: 621.38
ИССЛЕДОВАНИЕ
ЭЛЕКТРОДИНАМИЧЕСКИХ СВОЙСТВ ПЛАНАРНОЙ ТОНКОПЛЕНОЧНОЙ ЛИНЗЫ ЛЮНЕБЕРГА
А.А. Егоров1, Л.А. Севастьянов2, А.Л. Севастьянов3
1 Институт
общей физики им. А.М. Прохорова РАН
2 Российский университет дружбы народов
3
Московский государственный университет им. М.В.Ломоносова
Получена
1 мая 2008 г., после доработки – 30 мая 2008 г.
Исследованы электродинамические свойства планарной тонкопленочной линзы Люнеберга. Тонкопленочная четырехслойная линза Люнеберга является частью интегральной волноводной диэлектрической структуры. Предложенный метод применим для анализа аналогичных структур из диэлектрических или магнитных материалов в достаточно широком диапазоне электромагнитных длин волн. Полученное решение может быть использовано для синтеза аналогичных структур с заданными свойствами, в том числе и из метаматериалов, а также – для неразрушающей, например, световой диагностики многослойной интегрально-оптической структуры по экспериментальным данным.
1. ВВЕДЕНИЕ
Анализу распространения плоской монохроматической световой волны в планарных многослойных маломодовых регулярных диэлектрических волноводах посвящено много работ (см., например, [1, 2] и цитированную там литературу). При наличии плавных волноводных нерегулярностей (показателей преломления слоев и/или их толщин) направляемая мода претерпевает возмущение. В отличие от направляемых мод регулярного волновода слабо возмущенные («квазиволноводные») моды плавно-нерегулярных волноводов могут обмениваться энергией между собой и с окружающей средой. Для анализа процессов трансформации квазиволноводных мод, сопровождающихся перекачкой энергии между модами и с окружающей средой, используются различные методы [2-19].
В нулевом порядке метода теории возмущений Саутвеллом [5] получены дисперсионные соотношения для тонкопленочной волноводной линзы Люнеберга. Асимптотический метод решения системы уравнений Максвелла [6] на наш взгляд лучше других подходит для описания процессов эволюции квазиволноводных мод. Для учета векторного характера задачи распространения монохроматического электромагнитного поля вдоль плавно-нерегулярных участков многослойного многомодового диэлектрического волновода предлагается сохранить в полученном решении слагаемые, пропорциональные градиенту диэлектрической проницаемости. Проблема векторного рассеяния направляемой волноводной моды в статистически нерегулярном диэлектрическом волноводе, в том числе и при наличии шума рассмотрена в работах [7-15], поэтому мы ее не рассматриваем в данной работе.
Задачу синтеза тонкопленочной волноводной линзы Люнеберга Саутвелл решил
с использованием горизонтальных граничных условий в точках наклона границ.
Правильные тангенциальные граничные условия учитывают локальные наклоны границы
и соответствующее изменение эффективных оптических характеристик, в частности
z-компоненты длины волны ![]() нерегулярного участка (
нерегулярного участка (![]() – длина волны монохроматического
излучения в вакууме;
– длина волны монохроматического
излучения в вакууме; ![]() –
продольная составляющая коэффициента фазового замедления
–
продольная составляющая коэффициента фазового замедления ![]() волноводной моды). Эти условия
отличаются от горизонтальных условий регулярной части на малую величину. Этот
факт приводит к возможности описания распространения электромагнитных волн в
плавно-нерегулярной части волноведущей интегральной структуры с помощью
асимптотического подхода, обобщающего метод ВКБ.
волноводной моды). Эти условия
отличаются от горизонтальных условий регулярной части на малую величину. Этот
факт приводит к возможности описания распространения электромагнитных волн в
плавно-нерегулярной части волноведущей интегральной структуры с помощью
асимптотического подхода, обобщающего метод ВКБ.
Проверка простейшего условия применимости ВКБ – метода
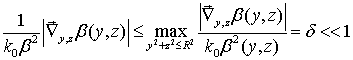
для тонкопленочной
волноводной линзы Люнеберга дает оценку: ![]() , где
, где ![]() – радиус области плавной нерегулярности –
собственно линзы в плоскости
– радиус области плавной нерегулярности –
собственно линзы в плоскости ![]() .
.
Как известно [5, 18, 19], волноводная линза Люнеберга является важнейшим функциональным элементом интегрально-оптических устройств, например, таких как интегрально-оптический ВЧ-спектроанализатор, работающий в реальном масштабе времени. Требование к точности расчета параметров аналогичных элементов интегральных структур при переходе в нанометровый диапазон сильно возрастает в связи с существованием ограничений обусловленных дифракционными эффектами.
2. ИСХОДНЫЕ УРАВНЕНИЯ. ПОСТАНОВКА ЗАДАЧИ
Уравнения Максвелла для электромагнитного поля в случае не поглощающей неоднородной линейной изотропной среды (в отсутствие токов и зарядов) в системе СИ сводятся к уравнениям [2]:
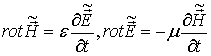 , (1)
, (1)
где ![]() –
диэлектрическая проницаемость среды;
–
диэлектрическая проницаемость среды; ![]() – магнитная проницаемость среды;
– магнитная проницаемость среды; ![]() ,
, ![]() – относительные диэлектрическая
и магнитная проницаемости соответственно (в немагнитной среде полагается
– относительные диэлектрическая
и магнитная проницаемости соответственно (в немагнитной среде полагается ![]() = 1);
= 1); ![]() и
и ![]() – это электрическая и магнитная
постоянные соответственно;
– это электрическая и магнитная
постоянные соответственно; ![]() =
= ![]() ,
, ![]() – показатель преломления среды (здесь и
далее – слоя рассматриваемой многослойной интегральной структуры),
– показатель преломления среды (здесь и
далее – слоя рассматриваемой многослойной интегральной структуры), ![]() ,
, ![]() ,
, ![]() – частота электромагнитного поля;
– частота электромагнитного поля; ![]() ,
, ![]() – вектора напряженностей
электрического и магнитного полей; символ тильда у векторов полей отражает их
комплексный характер. При выводе (1) учтено, что для линейной изотропной среды
справедливы соотношения:
– вектора напряженностей
электрического и магнитного полей; символ тильда у векторов полей отражает их
комплексный характер. При выводе (1) учтено, что для линейной изотропной среды
справедливы соотношения: ![]() ,
, ![]() , где
, где ![]() – вектор электрической индукции,
– вектор электрической индукции, ![]() – вектор магнитной
индукции.
– вектор магнитной
индукции.
В регулярном четырехслойном волноводе (см. Рис. 1) толщина ![]() второго волноведущего
слоя постоянна и собственные моды, распространяющиеся вдоль плоскости
второго волноведущего
слоя постоянна и собственные моды, распространяющиеся вдоль плоскости ![]() в направлении
в направлении ![]() , имеют хорошо известный
вид [1].
, имеют хорошо известный
вид [1].
В плавно-нерегулярном четырехслойном волноводе (см. Рис. 1) толщина
второго волноведущего слоя непостоянна ![]() , так что
, так что ![]() , но при этом полагаем, что эти производные
малы по абсолютной величине:
, но при этом полагаем, что эти производные
малы по абсолютной величине: ![]() . В этом случае метод Фурье разделения
переменных, как это делается в регулярном случае (см., например, [9-10]),
применить нельзя.
. В этом случае метод Фурье разделения
переменных, как это делается в регулярном случае (см., например, [9-10]),
применить нельзя.
В работе [17] использован асимптотический метод решения системы уравнений (1) для плавно-нерегулярной диэлектрической интегральной волноведущей структуры. В рамках этого подхода авторы оставили два вклада (см. ниже выражения (2а), (2б)), описывающие так называемое адиабатическое приближение [6]).
Для дальнейшей конкретизации модели был использован метод «частичного»
разделения переменных (метод Канторовича, известный как модифицированный метод
Галеркина [20] «частичного» разделения переменных). Решение уравнений Максвелла
с компонентами полей ![]() ,
зависящими от трех пространственных переменных, ищется в виде конечной суммы:
,
зависящими от трех пространственных переменных, ищется в виде конечной суммы:
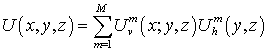 . (2)
. (2)
Ряд (2) содержит
множители ![]() ,
зависящие от горизонтальных переменных
,
зависящие от горизонтальных переменных ![]() и
и ![]() , и множители
, и множители ![]() , зависящие функционально от вертикальной
переменной
, зависящие функционально от вертикальной
переменной ![]() , и
параметрически зависящие от горизонтальных переменных. В регулярном случае
, и
параметрически зависящие от горизонтальных переменных. В регулярном случае ![]() = 1 и
= 1 и ![]() =
= ![]() .
Необходимым условием того, что можно пренебречь следующими членами с
.
Необходимым условием того, что можно пренебречь следующими членами с ![]() 1, является условие
1, является условие ![]() .
.
В итоге можно получить приближенные выражения, описывающие модель распространения электромагнитного поля в плавно-нерегулярном участке многослойного планарного диэлектрического волновода:
где ![]() – элемент длины луча.
– элемент длины луча.
На регулярном участке волновода вдоль оси ![]() могут распространяться направляемые TЕ- и ТМ-моды. Граница раздела
могут распространяться направляемые TЕ- и ТМ-моды. Граница раздела ![]() волноводного слоя и воздуха на регулярном
участке горизонтальна, и в любой точке
волноводного слоя и воздуха на регулярном
участке горизонтальна, и в любой точке ![]() касательная к ней плоскость совпадает с
плоскостью
касательная к ней плоскость совпадает с
плоскостью ![]() .
Тангенциальные граничные условия выполняются по отдельности для ТЕ- и для
ТМ-моды соответственно:
.
Тангенциальные граничные условия выполняются по отдельности для ТЕ- и для
ТМ-моды соответственно:
![]() ;
; ![]() .
.
Рис.1.
Поперечное сечение исследуемой интегральной структуры, образованной слоями 1–4.
Интегральный волновод образован средами 1, 2, 3. На рисунке обозначено: 1 –
обрамляющая среда или покровный слой (воздух) с показателем преломления ![]() ; 2 – волноводный слой
(регулярная часть интегральной структуры) с показателем преломления
; 2 – волноводный слой
(регулярная часть интегральной структуры) с показателем преломления ![]() ; 3 – подложка с
показателем преломления
; 3 – подложка с
показателем преломления![]() ; 4 – тонкопленочная волноводная линза
Люнеберга (нерегулярная часть интегральной структуры) с показателем преломления
; 4 – тонкопленочная волноводная линза
Люнеберга (нерегулярная часть интегральной структуры) с показателем преломления![]() ;
; ![]() – радиус апертура линзы;
– радиус апертура линзы; ![]() – толщина регулярной
части волноводной интегральной структуры;
– толщина регулярной
части волноводной интегральной структуры; ![]() – граница раздела волноводного слоя 4 и
воздуха 1.
– граница раздела волноводного слоя 4 и
воздуха 1.
На поверхности раздела ![]() нерегулярного участка волновода в точке
нерегулярного участка волновода в точке ![]() касательная плоскость
задается уравнением
касательная плоскость
задается уравнением ![]() =
0 и, в общем случае, не совпадает с горизонтальной плоскостью
=
0 и, в общем случае, не совпадает с горизонтальной плоскостью ![]() , задаваемой уравнением:
, задаваемой уравнением:
![]() = 0. При
этом тангенциальные граничные условия
= 0. При
этом тангенциальные граничные условия
![]() (3)
(3)
в общем случае
не выполняются раздельно для TM-мод и TЕ-мод.
Таким образом, именно граничные условия связывают две независимые волноводные
моды (так называемые квази-ТЕ и квази-ТМ моды) в одну слабосвязанную гибридную
моду. Связь является слабой в силу оценки ![]() . При этом у решений в плавно-нерегулярном
волноводе, также как и у мод регулярного волновода, присутствуют быстрые
осцилляции вдоль оси
. При этом у решений в плавно-нерегулярном
волноводе, также как и у мод регулярного волновода, присутствуют быстрые
осцилляции вдоль оси ![]() и
их число сохраняется при распространении мод.
и
их число сохраняется при распространении мод.
В работе [5] для тонкопленочной волноводной линзы Люнеберга, являющейся примером изучаемых нами плавно-нерегулярных интегральных волноводных структур, были получены дисперсионные соотношения в приближении, когда наклонные тангенциальные граничные условия были заменены их проекциями на горизонтальную плоскость.
Учет негоризонтальности тангенциальных граничных условий вносит в
соотношения Саутвелла малую поправку по параметру ![]() , определенному следующим образом:
, определенному следующим образом: ![]() (это двухмерный
волноводный аналог величины
(это двухмерный
волноводный аналог величины ![]() ).
).
В общем случае моды нерегулярного трехмерного диэлектрического и в частности оптического волновода – это гибридные моды, содержащие продольную составляющую как электрического, так и магнитного векторов.
3. КВАЗИВОЛНОВЫЕ УРАВНЕНИЯ ДЛЯ АДИАБАТИЧЕСКИХ МОД ПЛАВНО- НЕРЕГУЛЯРНОГО МНОГОСЛОЙНОГО ДИЭЛЕКТРИЧЕСКОГО ВОЛНОВОДА. ГРАНИЧНЫЕ УСЛОВИЯ И ДИСПЕРСИОННЫЕ СООТНОШЕНИЯ
С помощью дополнительных дифференцирований и с учетом адиабатичности
напряженностей поля из уравнений Максвелла (1) получаем выражения для компонент
поля ![]() и
квазиволновые уравнения для компонент поля
и
квазиволновые уравнения для компонент поля ![]() . Заметим, что квазиволновым называется
уравнение, имеющее вид волнового уравнения в левой части равенства, в правой
части которого вместо нуля находится выражение от неизвестной функции, первого
порядка малости
. Заметим, что квазиволновым называется
уравнение, имеющее вид волнового уравнения в левой части равенства, в правой
части которого вместо нуля находится выражение от неизвестной функции, первого
порядка малости ![]() по
сравнению с выражением в левой части.
по
сравнению с выражением в левой части.
В каждой из однородных областей
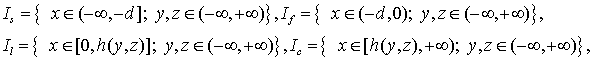 (4)
(4)
полученные
квазиволновые уравнения в нулевом по порядку малости ![]() приближении можно записать в виде
волновых уравнений:
приближении можно записать в виде
волновых уравнений:
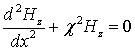 ,
(6)
,
(6)
где ![]() – поперечное волновое
число, равное в нулевом по порядку малости
– поперечное волновое
число, равное в нулевом по порядку малости ![]() приближении величине
приближении величине ![]() .
.
Решения уравнений (5), (6) имеют вид:
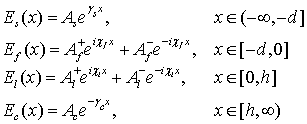 , (7)
, (7)
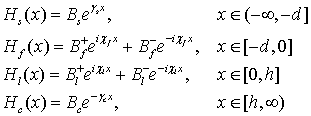 , (8)
, (8)
где:
![]() ,
, ![]() .
.
Далее находим горизонтальные граничные условия на плоскости ![]() и на плоскости
и на плоскости ![]() . «Негоризонтальные»
граничные условия находятся следующим образом. Электрическое поле,
тангенциальное к границе
. «Негоризонтальные»
граничные условия находятся следующим образом. Электрическое поле,
тангенциальное к границе ![]() раздела двух сред, имеет структуру
раздела двух сред, имеет структуру ![]() . Здесь через
. Здесь через ![]() обозначена нормальная
составляющая электрического поля к поверхности
обозначена нормальная
составляющая электрического поля к поверхности ![]() , ортогональная к касательной плоскости
, ортогональная к касательной плоскости ![]() , так что
, так что ![]() коллинеарно векторному
полю
коллинеарно векторному
полю 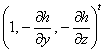 нормалей
к поверхности. Отсюда получаются выражения для тангенциальных компонент
напряженностей электрического поля
нормалей
к поверхности. Отсюда получаются выражения для тангенциальных компонент
напряженностей электрического поля ![]() ,
, ![]() и тангенциальных компонент напряженностей
магнитного поля
и тангенциальных компонент напряженностей
магнитного поля ![]() и
и
![]() .
.
Из трех компонент тангенциального поля ![]() лишь две линейно независимы.
Следовательно, вполне достаточно выписать граничные условия лишь
лишь две линейно независимы.
Следовательно, вполне достаточно выписать граничные условия лишь ![]() . Аналогично из трех
компонент магнитного поля лишь две
. Аналогично из трех
компонент магнитного поля лишь две ![]() и
и ![]() являются линейно независимыми.
Следовательно, граничные условия достаточно выписать лишь для них.
являются линейно независимыми.
Следовательно, граничные условия достаточно выписать лишь для них.
Группировка подобных членов позволяет получить искомые соотношения. Эти
соотношения и граничные условия на трех границах рассматриваемой интегральной
волноведущей структуры образуют однородную систему из двенадцати линейных
алгебраических уравнений для двенадцати неопределенных амплитудных
коэффициентов ![]() .
Эта система имеет нетривиальное решение, если она вырождена, т.е. если
детерминант данной матрицы
.
Эта система имеет нетривиальное решение, если она вырождена, т.е. если
детерминант данной матрицы ![]() равен нулю. Условие
равен нулю. Условие ![]() = 0 является, по
сути, дисперсионным соотношением для (гибридной) квазиволноводной моды в
плавно-нерегулярном участке диэлектрического волновода. Ниже для иллюстрации
приведен фрагмент полученной матрицы (столбцы 1-7; строки 1-12).
= 0 является, по
сути, дисперсионным соотношением для (гибридной) квазиволноводной моды в
плавно-нерегулярном участке диэлектрического волновода. Ниже для иллюстрации
приведен фрагмент полученной матрицы (столбцы 1-7; строки 1-12).
Как известно [21] определитель является линейной функцией любой своей строки. Следовательно, если имеются матрицы А, В и С, отличающиеся друг от друга только элементами одной из своих строк, а соответствующая строка матрицы А является линейной комбинацией этих же строк матриц B и С, то detА есть линейная комбинация с теми же коэффициентами определителей detВ и detС.
Используя это правило [21], мы можем показать, как преобразуется и в
некотором смысле упрощается полученная матрица ![]() в случае учета как нулевого, так и первого
порядков приближения по параметру
в случае учета как нулевого, так и первого
порядков приближения по параметру ![]() .
.
Граничные условия представляет собой систему алгебраических уравнений для
![]() и
и ![]() :
:
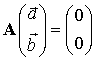 , (10)
, (10)
где вектор неопределенных коэффициентов состоит из двух шестимерных компонент:
![]() (11)
(11)
и
![]() . (12)
. (12)
Здесь мы переставили местами неопределенные коэффициенты ![]() и
и ![]() и уравнения для них, что привело
к перестановке строк и столбцов в матрице
и уравнения для них, что привело
к перестановке строк и столбцов в матрице ![]() . Данное представление позволяет в нулевом
приближении разделить дисперсионные соотношения для ТЕ- и ТМ-мод.
. Данное представление позволяет в нулевом
приближении разделить дисперсионные соотношения для ТЕ- и ТМ-мод.
Матрица ![]() данной
системы, размером 12
данной
системы, размером 12![]() 12
может быть представлена 12-ю столбцами вида:
12
может быть представлена 12-ю столбцами вида:
![]() . (13)
. (13)
Здесь вклады нулевого порядка малости по ![]() имеют вид:
имеют вид:
![]() = (
= (![]() ,
,![]() ,
,![]() ,0,0,0,0,0,0,0,0,0);
,0,0,0,0,0,0,0,0,0);
…………………………………………….;
![]() = (0,0,0,0,0,0,0,0,0,
= (0,0,0,0,0,0,0,0,0,![]() ,
,![]() ,
,![]() ).
).
А вклады первого порядка малости по ![]() имеют следующий вид:
имеют следующий вид:
![]() = (0,0,0,0,0,0,0,0,0,0,0,0);
= (0,0,0,0,0,0,0,0,0,0,0,0);
…………………………………………….;
![]() =
= ![]() ,0,0,
,0,0,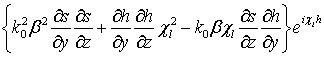 ,
, 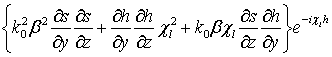 ,
,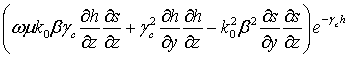 ,0,0,0,
,0,0,0,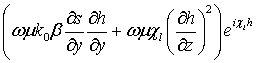 ,
,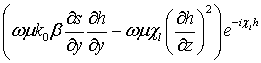 ,
, 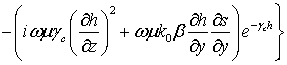 .
.
Отметим, что явный вид вкладов второго порядка малости по ![]() для данного изложения
значения не имеет.
для данного изложения
значения не имеет.
С целью изучения характерных черт и особенностей распределений коэффициентов
замедлений ![]() или
соответствующих им распределений продольных волновых чисел
или
соответствующих им распределений продольных волновых чисел ![]() и
и ![]() квазиволноводных мод проанализируем
зависимость дисперсионных соотношений от параметра малости
квазиволноводных мод проанализируем
зависимость дисперсионных соотношений от параметра малости ![]() .
.
Воспользуемся свойством линейности детерминанта по каждой из строк
матрицы ![]() :
:
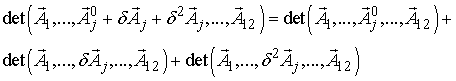 . (14)
. (14)
В третьем слагаемом правой части равенства имеется (j-й) столбец
с величинами порядка ![]() .
Весь третий детерминант является суммой произведений 12-ти матричных элементов
из разных столбцов, в каждом их которых присутствует сомножитель порядка
.
Весь третий детерминант является суммой произведений 12-ти матричных элементов
из разных столбцов, в каждом их которых присутствует сомножитель порядка ![]() из (j-го) столбца. Следовательно, третий детерминант является
линейной комбинацией малых величин порядка
из (j-го) столбца. Следовательно, третий детерминант является
линейной комбинацией малых величин порядка ![]() или выше по параметру
или выше по параметру ![]() . Второй детерминант в силу
аналогичных рассуждений является линейной комбинацией величин первого порядка
малости по
. Второй детерминант в силу
аналогичных рассуждений является линейной комбинацией величин первого порядка
малости по ![]() и
выше, а первый – нулевого порядка малости по
и
выше, а первый – нулевого порядка малости по ![]() и выше.
и выше.
Второй детерминант в силу линейности по другому столбцу можно записать в виде:
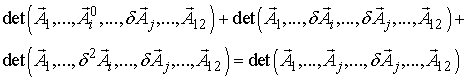 . (15)
. (15)
В силу
вышеприведенных рассуждений второй детерминант в разложении (15) является
суммой величин второго порядка малости и выше, а третий – суммой величин
третьего порядка малости и выше. Следовательно, для удержания в соотношении (14)
величин лишь нулевого и первого порядков малости по ![]() достаточно в разложении (15)
оставить лишь первый детерминант. Повторяя процедуру по оставшимся 10-ти
строкам получим, что вклады первого порядка содержатся лишь в детерминанте вида
достаточно в разложении (15)
оставить лишь первый детерминант. Повторяя процедуру по оставшимся 10-ти
строкам получим, что вклады первого порядка содержатся лишь в детерминанте вида
![]() с нулевыми
приближениями 11-ти столбцов и первого приближения одного столбца.
с нулевыми
приближениями 11-ти столбцов и первого приближения одного столбца.
В первом детерминанте разложения (15) воспользуемся его линейностью по i-тому
столбцу ![]() .
.
В таком разложении третий детерминант содержит вклады лишь второго и
более высоких порядков малости, второй детерминант содержит вклады лишь первого
и более высоких порядков малости. В силу этого третий детерминант отбрасываем,
для второго повторяем процедуру по оставшимся столбцам и оставляем лишь вклад ![]() .
.
Повторяя процедуру для первого детерминанта по оставшимся 10-ти столбцам,
получим в итоге сумму детерминантов, содержащих лишь величины нулевого и
первого порядков малости по ![]() :
:
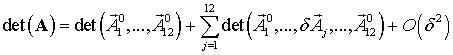 . (16)
. (16)
В представлении (9) дисперсионного соотношения (5) вклад нулевого порядка
малости по ![]() имеет
вид
имеет
вид
и эквивалентен
дисперсионному соотношению, приведенным в работе Саутвелла [5], а
дополнительные 12 вкладов первого порядка малости по ![]()
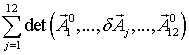 . (18)
. (18)
позволяют учесть (слабую) связь между ТЕ- и ТМ-модами, разрешенными дисперсионным соотношением (18).
4. РЕЗУЛЬТАТЫ ПРЕДВАРИТЕЛЬНЫХ ЧИСЛЕННЫХ РАСЧЕТОВ
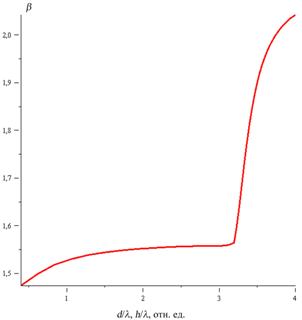
На рис. 2 приведены рассчитанные в соответствии с выражением (17)
зависимости коэффициентов фазового замедления ![]()
![]() - и
- и ![]() -моды от толщины волноводных слоев
четырехслойной интегрально-оптической структуры, состоящей из трехслойного
регулярного планарного волновода и четырехслойного плавно-нерегулярного волновода
(см. Рис. 1) с параметрами: коэффициент преломления подложки (SiO2)
-моды от толщины волноводных слоев
четырехслойной интегрально-оптической структуры, состоящей из трехслойного
регулярного планарного волновода и четырехслойного плавно-нерегулярного волновода
(см. Рис. 1) с параметрами: коэффициент преломления подложки (SiO2)
![]() = 1.470,
коэффициент преломления первого (регулярного) волноводного слоя (стекло марки Corning 7059)
= 1.470,
коэффициент преломления первого (регулярного) волноводного слоя (стекло марки Corning 7059) ![]() = 1.565, коэффициент преломления второго
волноводного слоя (Ta2O5)
переменной толщины h(y,
z)
= 1.565, коэффициент преломления второго
волноводного слоя (Ta2O5)
переменной толщины h(y,
z) ![]() = 2.100, коэффициент преломления
покровного слоя (воздух)
= 2.100, коэффициент преломления
покровного слоя (воздух) ![]() = 1.000.
= 1.000.
На дисперсионных зависимостях ![]() по вертикали отложены значения
коэффициента фазового замедления
по вертикали отложены значения
коэффициента фазового замедления ![]() , а по горизонтали – толщины волноводных
слоев в относительных единицах (
, а по горизонтали – толщины волноводных
слоев в относительных единицах (![]() и
и ![]() ), где
), где ![]() = 0.9 мкм. Таким образом, левая часть
рисунков (примерно от 0.0 до 3.0) является дисперсионной зависимостью
трехслойного регулярного волновода, а правая (от 3.0 до 3.8) – дисперсионной
зависимостью четырехслойного плавно-нерегулярного волновода, включающего линзу
Люнеберга. Аналогичные дисперсионные зависимости получены для других типов мод.
= 0.9 мкм. Таким образом, левая часть
рисунков (примерно от 0.0 до 3.0) является дисперсионной зависимостью
трехслойного регулярного волновода, а правая (от 3.0 до 3.8) – дисперсионной
зависимостью четырехслойного плавно-нерегулярного волновода, включающего линзу
Люнеберга. Аналогичные дисперсионные зависимости получены для других типов мод.
На рис.2 участки дисперсионной зависимости после 3.0 от ![]()
![]() 0.00 до
0.00 до ![]()
![]() 0.24 (в единицах
0.24 (в единицах ![]() ) отражают область некоторого
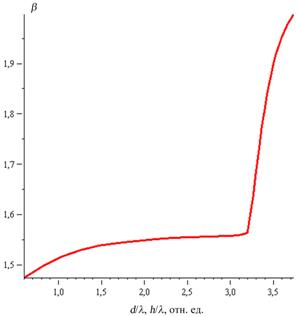
переходного режима в линзе Люнеберга. Более подробно эти участки изображены на
рис. 3 (примерно от 0.0 до 0.2).
) отражают область некоторого
переходного режима в линзе Люнеберга. Более подробно эти участки изображены на
рис. 3 (примерно от 0.0 до 0.2).
Эти расчеты удалось выполнить корректно на указанном участке лишь при
правильном учете перехода продольного волнового числа (![]() ) вдоль одной ветви двузначной
функции извлечения квадратного корня комплексного переменного при переходе
коэффициента фазового замедления
) вдоль одной ветви двузначной
функции извлечения квадратного корня комплексного переменного при переходе
коэффициента фазового замедления ![]() из области
из области ![]() в область
в область ![]() .
.
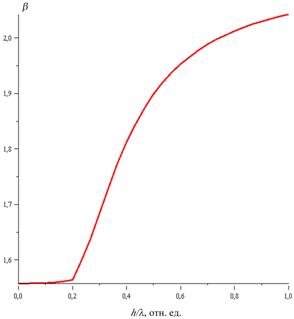
Ри.2. Дисперсионные зависимости четырехслойной интегрально-оптической
структуры, приведенной на Рис. 1: слева – для ![]() - моды, справа – для
- моды, справа – для ![]() -моды.
-моды.
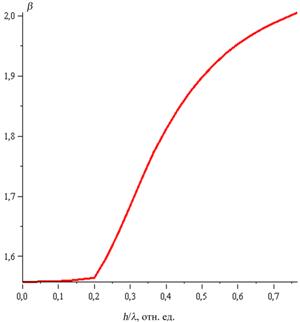
Ри.3. Дисперсионная зависимость четырехслойной
плавно-нерегулярной интегрально-оптической структуры, приведенной на Рис. 1, от
толщины второго волноводного слоя: слева – для ![]() - моды, справа – для
- моды, справа – для ![]() -моды.
-моды.
На рис. 4. приведен результат решения в соответствии с приближением (17) задачи
синтеза интегрально-оптической планарной линзы Люнеберга: при изменении
нормированного радиуса ![]() линзы от 0 до 1 найти вид распределения
профиля
линзы от 0 до 1 найти вид распределения
профиля ![]() (в
единицах
(в
единицах ![]() ).
).
Данная линза описывается радиальным распределением фазового замедления ![]() по
по ![]() в безразмерных единицах
в безразмерных единицах ![]() , где
, где ![]() – радиус линзы с
заданным фокусным расстоянием
– радиус линзы с
заданным фокусным расстоянием ![]() 1. Для расчета профиля толщины
нерегулярного волноводного слоя, необходимого для формирования волноводной
линзы Люнеберга, использовался программный пакет Maple,
позволяющий автоматизировать символьные, численные и графические вычисления.
Заметим, что аналогичные результаты получены для других типов мод и для
различных значений
1. Для расчета профиля толщины
нерегулярного волноводного слоя, необходимого для формирования волноводной
линзы Люнеберга, использовался программный пакет Maple,
позволяющий автоматизировать символьные, численные и графические вычисления.
Заметим, что аналогичные результаты получены для других типов мод и для
различных значений ![]() .
.
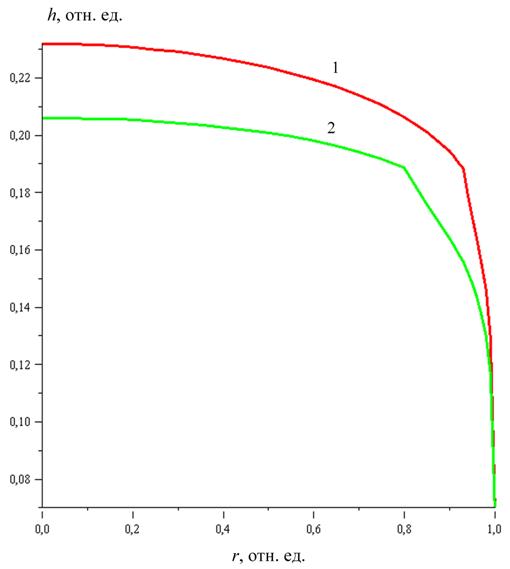
Ри.4. Профили синтезированных планарных линз Люнеберга: 1 –
фокусное расстояние ![]() =
5, 2 –
=
5, 2 – ![]() = 9;
показатели преломления сред интегральной структуры как на рис. 2.
= 9;
показатели преломления сред интегральной структуры как на рис. 2.
Заметим, что использование данного пакета для моделирования потребовала решить ряд проблем. В частности, решить проблему непрерывного роста объема оперативной памяти (в зависимости от количества точек сетки), необходимой для функционирования программы. Проблема неэффективного использования оперативной памяти является одним из существенных недостатков системы компьютерной математики Maple. При расчетах все промежуточные символьные цепочки сохраняются в оперативной памяти компьютера до выхода из системы Maple. Главная проблема здесь состоит в том, что требуется исправление внутренних алгоритмов Maple. Однако эта проблема в системе Maple, включая последние версии, пока не решена. Выполнение расчетов с поэтапным запоминанием промежуточных результатов[1] к радикальному улучшению процедуры расчетов пока не привели. Таким образом, преимущество символьных вычислений в случае достаточно сложных выражений оказывается серьезным препятствием для получения конечных численных результатов расчетов.
5. ВЫВОДЫ
В настоящей статье выполнено исследование электродинамических свойств планарной тонкопленочной линзы Люнеберга. Численное моделирование было выполнено для хорошо известной в интегральной оптике планарной линзы Люнеберга. Полученные результаты демонстрируют хорошую сходимость разработанного алгоритма решения поставленной электродинамической задачи в нулевом приближении используемого асимптотического метода. Первое приближение описываемого нами метода пока вызывает сложности при численной реализации.
В заключение необходимо подчеркнуть, что регулярный трехслойный и
четырехслойный волноводы являются частными случаями рассмотренной в настоящей
работе математической модели планарной линзы Люнеберга. Следует также отметить,
что предложенное нами теоретическое описание обобщается на случай
плавно-нерегулярной структуры из ![]() слоев, что является несомненным
преимуществом.
слоев, что является несомненным
преимуществом.
ЛИТЕРАТУРА
1. Дерюгин Л.Н., Марчук А.Н., Сотин В.Е. Свойства плоских несимметричных диэлектрических волноводов на подложке из диэлектрика // Изв. Вузов. Радиоэлектроника. 1967. Т. 10. С. 134-141.
2. Маркузе Д. Оптические волноводы. – М.: Мир, 1974.
3. Каценеленбаум Б.З. Теория нерегулярных волноводов с медленно изменяющимися параметрами. – М.: Изд. АН СССР, 1961.
4. Кинбер Б.Е., Кравцов Ю.А. Лучевая теория преобразования волн в многомодовых нерегулярных волноводах // Радиотехника и электроника. 1977. Т. 22. С. 2470-2483.
5. Southwell W.H. Inhomogeneous optical waveguide lens analysis // JOSA. 1977. V. 67. P. 1004-1014.
6. Бабич В.М., Булдырев В.С. Асимптотические методы в задачах дифракции коротких волн. – М.: Наука, 1972.
7. Шевченко В.В. Плавные переходы в открытых волноводах (Введение в теорию). – М.: Наука, 1969.
8. Шевченко В.В. О спектральном разложении по собственным и присоединенным функциям одной несамосопряженной задачи типа Штурма-Лиувилля на всей оси // Диф. Уравнения. 1979. Т. 15. С. 2004-2020.
9. Унгер Х.Г. Планарные и волоконные оптические волноводы. – М.: Мир, 1980.
10. Снайдер А., Лав Дж. Теория оптических волноводов. – М.: Радио и связь, 1987.
11. Содха М.С., Гхатак А.К. Неоднородные оптические волноводы. – М.: Связь, 1980.
12. Egorov A.A. Theory of laser radiation scattering in integrated optical waveguide with 3D-irregularities in presence of noise: vector consideration // Laser Physics Letters. 2004. V. 1. No. 12. P. 579-585.
13. Егоров А.А. Теория волноводного рассеяния света в интегрально-оптическом волноводе при наличии шума // Изв. Вузов. Радиофизика. 2005. Т. 48. С. 63-75.
14. Egorov A.A. Use of waveguide light scattering for precision measurements of the statistic parameters of irregularities of integrated optical waveguide materials // Optical Engineering. 2005. V. 44. P. 014601-1–014601-10.
15. Егоров А.А. Обратная задача рассеяния монохроматического света в статистически нерегулярном волноводе: теория и численное моделирование // Опт. и Спектр. 2007. Т. 103. C. 638-645.
16. Севастьянов Л.А. Дисс. … докт. физ.-мат. наук. – М.: РУДН, 1999.
17. Севастьянов Л.А., Егоров А.А. Теоретический анализ волноводного распространения электромагнитных волн в диэлектрических плавно-нерегулярных интегральных структурах. // Опт. и Спектр. 2008. (принята к печати).
18. Золотов Е.М., Киселев В.А., Сычугов В.А. Оптические явления в тонкопленочных волноводах // УФН. 1974. Т. 112. С. 231-273.
19. Хансперджер Р. Интегральная оптика. – М.: Мир, 1985.
20. Канторович Л.В., Крылов В.И. Приближенные методы высшего анализа. – Л.: Физматгиз, 1962.
21. Стренг Г. Линейная алгебра и ее применения. – М. Мир, 1980.
[1] Суть используемого способа состоит в следующем: в нижней строке состояния пакета отслеживается динамика использования памяти и при ее существенном увеличении все важные данные сохраняются на диске, после чего снова продолжают работу в новой сессии пакета Maple. Только такая процедура позволяет полностью освободить оперативную память компьютера.
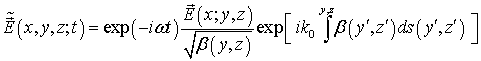 , (2а)
, (2а)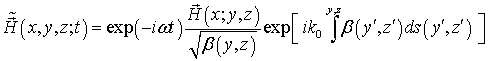 . (2б)
. (2б)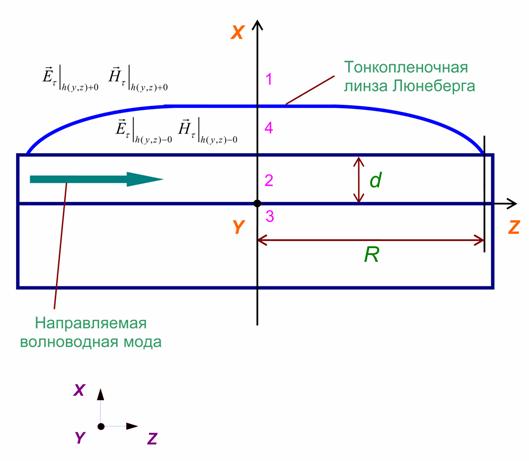
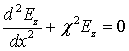 ,
(5)
,
(5)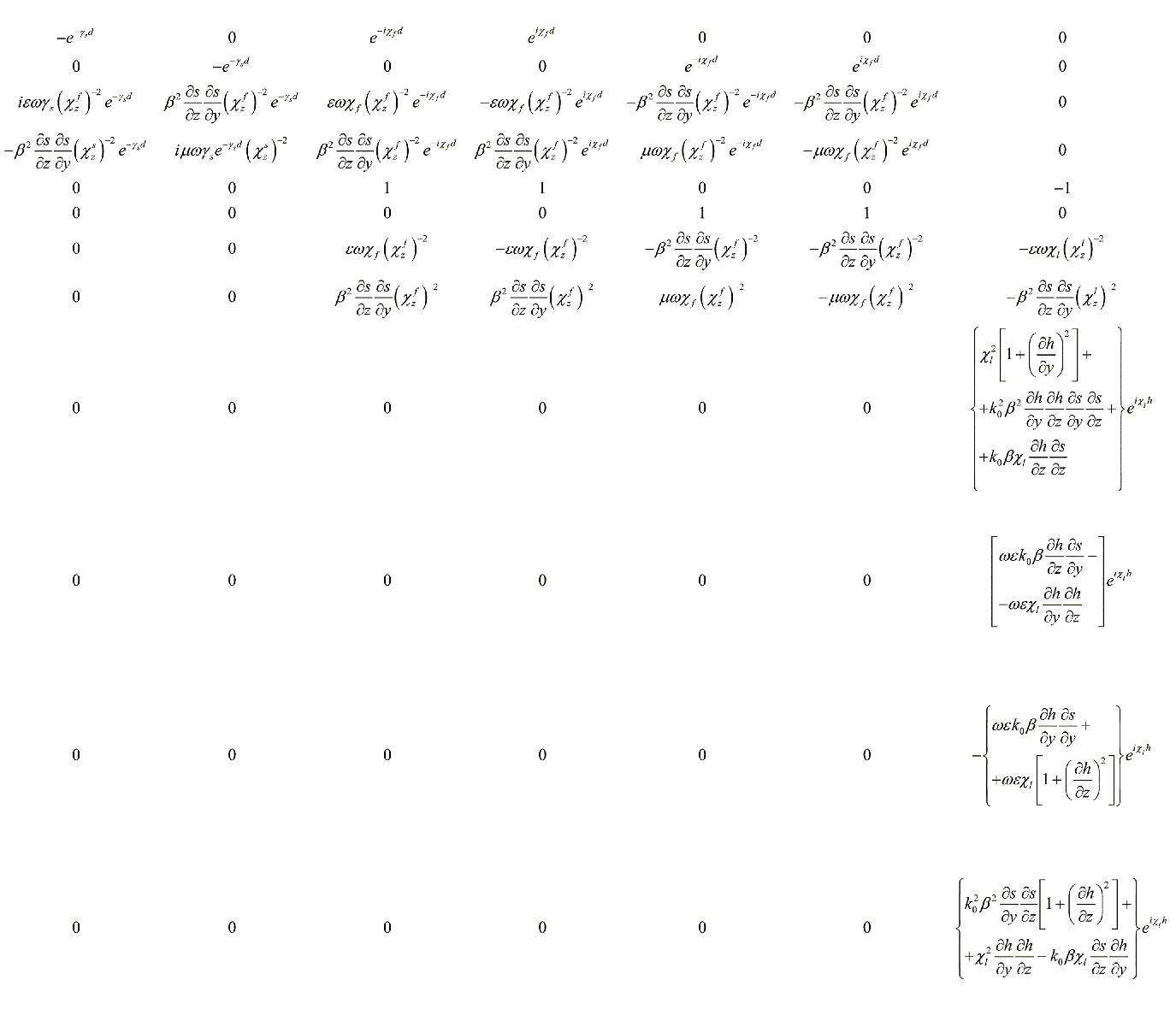 (9)
(9)