A Simple Adaptive Beamforming Algorithm
with
INTERFERENCE SUPRESSION
K. Meena alias Jeyanthi1, Dr. A. P. Kabilan2
1Department of Electronics and communication, PSNACET,
Dindigul
2Principal, Chettinad colledge of engineering & technology,
Karur
Received June 12, 2009
Modeling and simulation of uniform linear array using Matrix Inversion-Normalized Least Mean Square (MI-NLMS) adaptive beam forming with minimum Bit Error Rate (BER) is developed for smart antenna applications. We have modeled a linear array of antennas for 20°Half Power Beam Width (HPBW) and obtained the beam formation with digital modulation of 16 point Quadrature Amplitude Modulation (QAM).This modulation technique is used for the systems like CDMA,Wi-Fi (IEEE802.11) and WiMAX (IEEE 802.16).The algorithm have the advantage of both block adaptation and sample by sample techniques which shows that the performance of block adaptation and normalization of Least Mean Square (LMS) improves the system capacity and minimize bit error rate (BER) upto 10-4 for the signal to noise ratio of 13 dB’s. The Quadrature amplitude modulation (QAM) allows us to send more bits per symbol to achieve higher throughput and to overcome fading and other interferences. The simulation is done in MATLAB.
Keywords: simulation in electrodynamics, Matrix Inversion-Normalized Least Mean Square, smart antenna, WiMAX, bit error rate (BER).
Простой адаптивный алгоритм формирования пучка с подавлением ПОМЕХ
К. Мина Джеянти1, А. П.
Кабилан2
1Факультет электроники и связи колледжа PSNACET, Диндигул, Индия
2Инженерно-технический колледж Chettinad, Карур, Индия
Получена 12 июня 2009 г.
Моделирование однородного линейного массива с использованием
матрицы обратно-нормализованного наименьшего средних квадратов
(MI-NLMS) для адаптивного формирования пучка с минимумом частоты ошибок по битам
(BER) выполнено в приложении к смарт-антеннам. Мы смоделиовали линейный массив
антенн для 20°ширины пучка по уровню половинной мощности (HPBW) и добились
формирования пучка с цифровой модуляцией 16 точек квадратурной амплитудной
модуляции. Этот метод модуляции используется в системах типа CDMA, Wi-Fi
(IEEE802.11) and WiMAX (IEEE 802.16). Алгоритм имеет преимущество как адаптации
блока, так и технологии выборка к выборке, что показывает, что выполнение
адаптации блока и нормировка наименьшим средним квадратом улучшает пропускную
способность системы и минимизирует частоту ошибок по битам до 10-4
для отношения сигнал-шум 13 децибел. Квадратурная амплитудная модуляция
позволяет посылать больше бит на символ для того, чтобы достичь большей
пропускной способности и преодолеть затухание и другие помехи. Моделирование
было выполнено с помощью MATLAB.
Ключевые слова: смарт-антенна, моделирование в
электродинамике, частота ошибки по битам, матрица обратно-нормализованного
наименьшего средних квадратов, WiMAX.
I.
INTRODUCTION
Adaptive beamforming is a powerful technique of enhancing a signal of interest while suppressing the interference signal and the noise at the output of an array of sensors. A smart antenna system combines multiple antenna elements with a signal- processing capability to optimize its radiation and or reception pattern automatically in response to the signal environment. Matrix Inversion Normalized Least Mean Square (MI-NLMS) adaptive beamforming algorithm was developed for smart antenna application [4]. The Matrix inversion normalized least mean square combines the individual good aspects of Sample Matrix Inversion (SMI) and the Normalized Least Mean Square (NLMS) algorithms. There are a number of criteria for choosing the algorithm that will produce the optimum weights, they are closely relate to each other and therefore the choice of the one is critical in terms of its performance [6].The most mainly used adaptive algorithms include LMS(Least Mean Square),SMI(sample Matrix Inverse) and the RLS(Recursive least squares). The main figure of merit for measuring the quality of digital signals is called Bit error rate (BER) which is the ratio of number of bits received in error versus total number of bits sent [5]. The modulation scheme which we are using to calculate Bit error Rate (BER) is Quadrature Amplitude Modulation (QAM).
An array beamformer is a processor used in conjuction with an array of sensors to provide versatile form of spatial filtering.The sensor array collects spatial samples of propagation wave fields,which are processed by the beamformer.In case that,the desired signal and interfering signal occupy the same temporal frequency band, the conventional temporal filtering approach cannot be used to separate signal from interference.The desired signal and jammers originate from different spatial location [6]. This spatial separation can be exploited to separate signal from interference using a spatial filtering at the receiver.An adaptive array system can be employed to automatically adjust its directional response to null then interferer and thereby enhancing the reception of the desired signal.
II.
SMART
ANTENNAS
Smart antenna (also known as adaptive array antenna) refers to a system of antenna arrays with smart signal processing algorithms that are used to identify spatial signature such as direction of arrival (DOA) of the signal and it is used to calculate beamforming vectors, to track and locate the antenna beam on the mobile/target.
The two important categories are smart antennas. They are
- Switched Beam Antennas
Switched beam antenna systems form multiple fixed beams with heightened sensitivity in particular directions. These antenna systems detect signal strength, choose from one of several predetermined, fixed beams, and switch from one beam to another as the mobile moves throughout the sector.

Figure.1.Switchedbeam.
B. Adaptive Array Antenna
Only a small portion of the power transmitted in an omni directional manner is actually received by the intended user, while at the same time the rest,the ‘wasted’ power causes harmful interference to other potential users as shown in Fig 2. Hence it is obvious that the omni directional power transmission is inefficient both in terms of power and capacity. Exploiting the adaptive antenna spatial filtering properties, it is possible to confine the radio energy associated with a given user to a small addressed volume, thus reducing the interference from others. Adaptive array antenna technology represents the most advanced smart antenna approach. Using a variety of new signal-processing algorithms, the adaptive system takes advantage of its ability to effectively locate and track various types of signals to dynamically minimize interference and maximize intended signal reception.
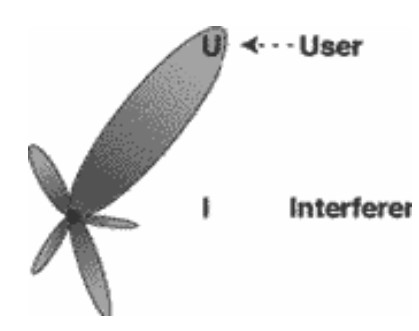
Figure.2.Adaptive Array.
III.
ADAPTIVE
BEAM FORMING
The purpose of beamforming is to form a multiple beams towards desired users while nulling the interferers at the same time, through the adjustment of the beamformer’s weight vectors. It is the process of altering the complex weight on-the-fly to maximize the quality of the communication channel. Fig.3 shows a generic adaptive beamforming system which requires a reference signal.
The signal x(n) received by multiple antenna elements is multiplied with the coefficients in a weight vector ‘w’ which adjust the phase and amplitude of the incoming signal accordingly. This weighted signal is summed up, resulting in the array output, y(n). An adaptive algorithm is then employed to minimize the error e(n) between a desired signal d(n) and the array output y(n).The complex weights wk for the antenna elements are carefully chosen to give the desired peaks and nulls in the radiation pattern of the array.the weights could then be slowly varied to steer the beam until maximum signal strength occurs and the direction to the signal source is found.
The use of multi-element antenna systems on both sides of the communication link has been proposed for extra ordinary increase of transmission rates [7]. Adaptive algorithms require less priori knowledge of the signal characteristics such as interference directions of arrival, bandwidth and also require high computational effort.
Linearly constrained LMS algorithm is the most widely used algorithm due to its simplicity,generally efficient and robust. It requires only the knowledge and the bandwidth of the signal.
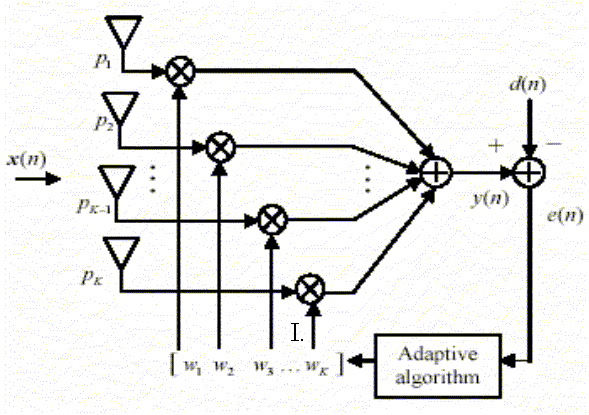
Figure.3.Block diagram of Adaptive beamforming
A. NLMS Algorithm
The normalized LMS filter is exactly the same as the standard LMS filter, as shown in the block diagram. Both adaptive filters are built around a transversal filter, but differ only in the way in which the weight controller is mechanized.
M-number of taps (filter length)
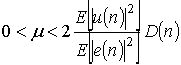 (3)
(3)
where ![]() =error signal power,
=error signal power, ![]() -adaptation constant,
-adaptation constant,
![]() is input signal power and
is input signal power and ![]() =mean-square deviation.
=mean-square deviation.
The input signal is u(n)=M by 1 tap input vector at time n,
d(n)=desired response at time step n,
The error signal, ![]() (4)
(4)
The estimate of tap weight at time step (n+1) is
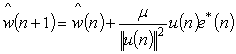 (5)
(5)
B. MI-NLMS Algorithm
In MI-NLMS algorithm, the SMI algorithm is utilized to determine the optimum weight vectors assigned to each of the antenna elements of the array instead of arbitrary value before calculating the final weight vector. The weight is calculated only for the first few samples or for a small block of incoming data. The weight coefficients derived by SMI algorithm are set as initial coefficients and are updated by introducing NLMS algorithm. To improve the stability of the system and convergence speed, NLMS method is used instead of LMS. By combining the above two algorithms, the novel optimum MI-NLMS algorithm update the weight vectors according to the following equations:
![]() where R is
the autocorrelation and r is the cross correlation matrix.
where R is
the autocorrelation and r is the cross correlation matrix.
The
output ![]() ,
(6)
,
(6)
The
error signal ![]() , (7)
, (7)
Estimate of tap weight at time step n+1,
![]()
![]()
=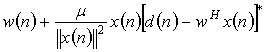 (8)
(8)
The final weight vector of the MI-NLMS algorithm is estimated from equation 8.In the MI-NLMS algorithm, advantages of both the block adaptive and sample by sample technique are employed.
C. Bit Error Rate (BER)
By considering 16-QAM, we can compute its Bit error rate (BER) using the concept of the distance. We have 16 symbols to transmit, with each symbol standing for 4 bits.
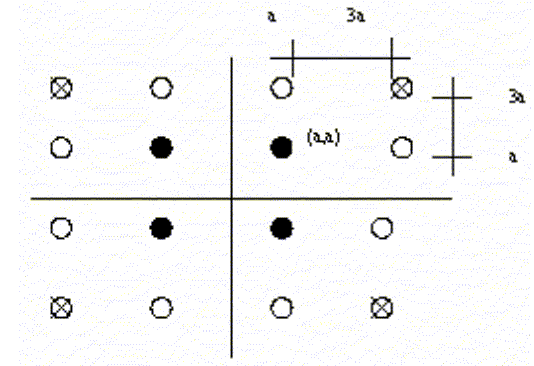
Fig.4. QAM constellations.
We assume that the inner most symbol is at (a,a) volts.
In this modulation, each symbol represents 4 bits, we have
![]() ,
,![]() (9)
(9)
Compare this to the inter-symbol distance of QPSK which is
![]()
BER of 16-QAM is
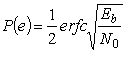 (10)
(10)
IV. RESULTS AND DISCUSSIONS
We considered a desired signal and interferers are operated in a frequency of 2.3GHz, the spacing between the antennas is one half wavelength. The received signals are modeled as MSK (Minimum Shift Keying) signals. Figure 5 show the array responses of NLMS which is scanning efficiently a single signal with very narrow main lobe beam width of 17θ HPBW.
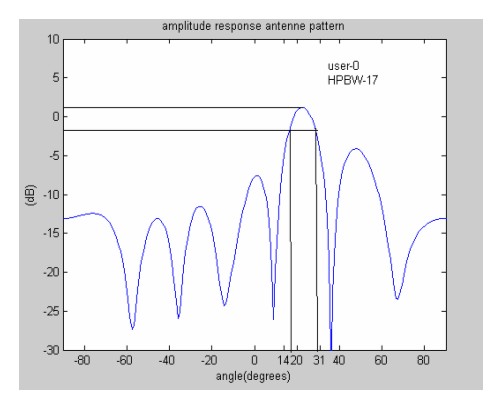
Figure.5.Beam pattern using NLMS.
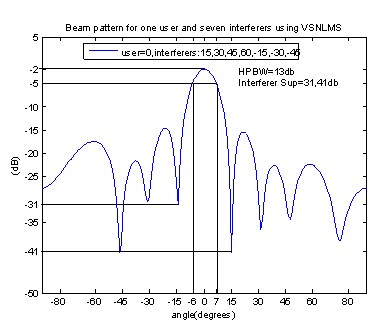
Figure.6.Beam pattern using NLMS.
Fig. 6 shows the amplitude pattern for Variable step size NLMS for seven interferers and the suppression of -31 and 41 dB’s. Fig. 7 shows the MI-NLMS algorithm for variable step size 0.0008 for the arrangement of 8 elements with 2 interferers at various angles with the HPBW of 30θ and interference suppression of 30 θ.
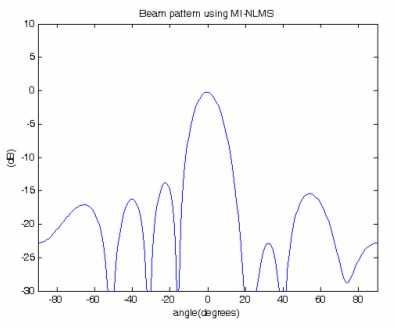
Figure .7 Array pattern
using MI-NLMS.
The results of MI-NLMS shows that the minimum side lobe level suppression of -30db is feasible in all the situation. The Half power beam width of 17 dB’s is maintained the desired signal. The side lobe level is 14 dB, that is indicated in the figure 8.Hence, the optimum performance is obtained through the proposed algorithm.
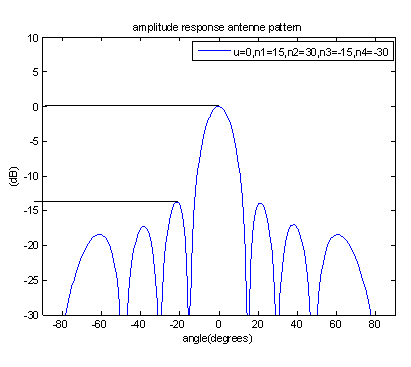
Figure 8 Array pattern with four interferers.
Figure
9 shows the Bit Error Rate (BER) using 16 point Quadrate Amplitude Modulation
(QAM). Bit error rate is like a “waterfall curve”. The BER is compared for NLMS
and the proposed MI-NLMS algorithm.In the graph given below, for 10dB ![]() there will be 1 error
for 10 bits. For 12dB
there will be 1 error
for 10 bits. For 12dB![]() ,
1 error for 1000 bits and thus for higher
,
1 error for 1000 bits and thus for higher![]() it converges to a small value.
it converges to a small value.
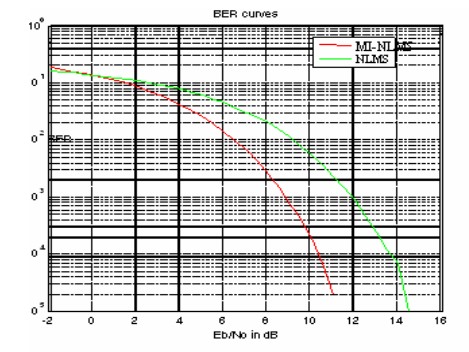
Figure .9. BER for 16-QAM.