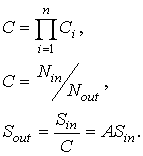УДК 621.396ИДЕНТИФИКАЦИОННЫЙ АЛГОРИТМ ДЕЦИМАЦИИ СИГНАЛОВ
Ю.Н. Кликушин1, Б.В. Кошекова2
1Омский государственный технический университет, Россия
2Северо-Казахстанский государственный университет им. М. Козыбаева, Петропавловск, Республика Казахстан
Получена 20 мая 2010 г.
Аннотация. Описан алгоритм и инструменты, ориентированные на решение задачи децимации и использующие в качестве критерия завершенности процедуры прореживания условие идентификационной эквивалентности исходного и выходного сигналов.
Ключевые слова: алгоритм, идентификационная эквивалентность, инструменты, децимация, компрессия, сигнал, спектр.
ВВЕДЕНИЕ
При решении задач анализа данных часто возникает проблема, связанная с компрессией (сжатием) исходной информации. Каждый пользователь персонального компьютера сталкивается с этой проблемой, когда необходимо на ограниченном объеме дискового пространства поместить максимальное число файлов. Для решения указанной проблемы используются инструменты, называемые архиваторами, качественные показатели которых определяются степенью сжатия, быстродействием и возможностями правильного восстановления информации.
В ряде важных практических случаях (обработка изображений, анализ звуковых, речевых, музыкальных и некоторых радиосигналов, мониторинг данных измерений в сейсмографии, медицинской и технической диагностике) не требуется абсолютно точно восстанавливать исходный сигнал. Главным условием выступает достижение максимальной компрессии при сохранении основных особенностей сигнала.
В качестве характерного примера можно привести задачу создания банка данных отпечатков пальцев. Предположим, что изображение папиллярных линий одного пальца человека занимает 1Мбайт. Тогда, чтобы сохранить отпечатки пальцев обеих рук населения 100 млн. человек, потребуется 109 Мбайт дискового пространства. Хотя принципиальных, технических проблем хранения такого большого объема информации не существует, возникают ограничения экономического характера. Именно с такой проблемой встретилось руководство ФБР при реализации программы, связанной с созданием общенационального банка данных отпечатков пальцев преступников в конце 20 века. В то время, наиболее удачное решение указанной проблемы было найдено на основе применения вейвлет – преобразования для сжатия изображений [1]. Хотя при этом восстановление изображения производится с некоторой погрешностью, зато компрессия получается максимальной.
Если исходная информация представлена в виде дискретного массива числовых данных, то задачу компрессии можно решить путем децимации (прореживания), смысл которой состоит в исключении «неинформативных» отсчетов. Возникает вопрос: Кто и как определяет принадлежность того или иного отсчета понятию информативности? В автоматизированных системах управления решение этого вопроса чаще всего является прерогативой эксперта (человека – специалиста данной предметной области), который, в зависимости от конкретной ситуации, может принимать определенные решения на основе интуитивного опыта и накопленных знаний. Однако, очевидно, что подобный алгоритм принятия решений является субъективным и, следовательно, не достаточно надежным.
Объективные методы децимации основаны на предварительном количественном анализе процесса. Наиболее простым является способ децимации, заключающийся в отбрасывании четных или нечетных отсчетов исходной выборки сигнала. Назовем этот способ прореживания классическим. Другой, распространенный вариант прореживания связан с агрегированием нескольких соседних отсчетов в один, например, с помощью вычисления среднего арифметического [2]. Интересный алгоритм децимации предложен в работе [3]. Однако свойства этого алгоритма исследованы еще недостаточно, чтобы можно было говорить о его реальных преимуществах, по сравнению с известными алгоритмами.
Далее описан алгоритм и инструменты, ориентированные на решение задачи децимации и использующие в качестве критерия завершенности процедуры прореживания условие идентификационной эквивалентности форм распределений исходного и выходного сигналов.
МЕТОДИКА И ИНСТРУМЕНТЫ ИССЛЕДОВАНИЙ
Методика исследований основана на компьютерном моделировании структурной схемы, представленной на рис. 1 и использующей принципы идентификационных измерений [4] сигналов.
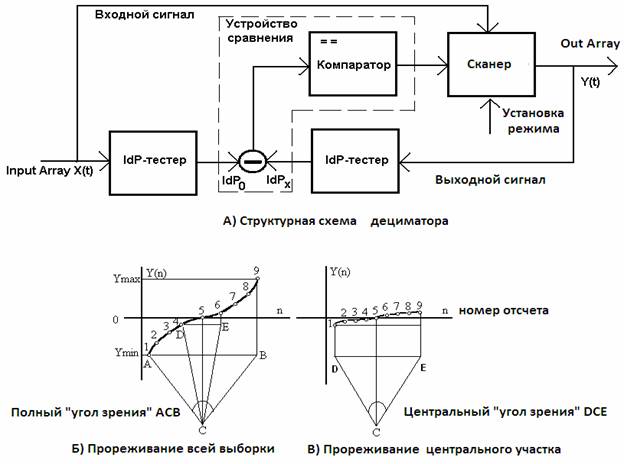
Структурная схема дециматора содержит два идентификационных тестера (IdP-тестер), устройство сравнения и сканер. Левый по схеме IdP-тестер измеряет форму распределения входного сигнала, представленного в виде массива Input Array. Правый IdP-тестер измеряет форму распределения выходного сигнала Out Array. Идентификационные числа IdP0, IdPx на выходах тестеров сравниваются устройством сравнения, выходной сигнал которого управляет работой сканера. В данном случае управление заключается в регулировании количества отсчетов, выбираемых сканером из входного массива. Установка режима работы сканера заключается в задании начального минимального объема порции сигнала.
На рис. 1 показан пример, когда эта порция составляет 9 отсчетов. Если пользователем задан режим прореживания полной выборки сигнала, имеющей исходный объем N отсчетов, то сканер равномерно выбирает по длине выборки только 9 отсчетов.
Рис. 1. Структурная схема модели дециматора и принцип его работы
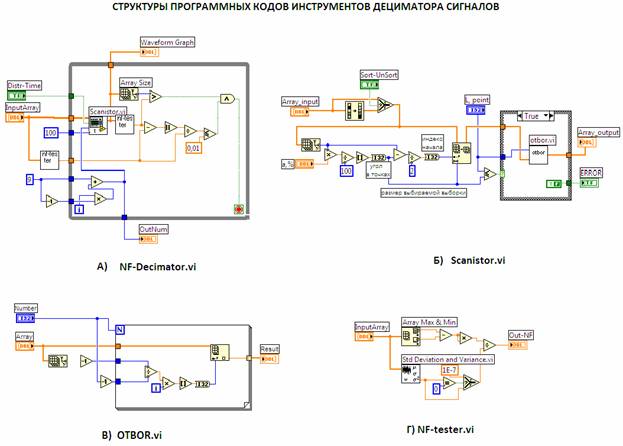
Таким образом, вместо N отсчетов на входе сканера, на его выходе сохраняются 9 отсчетов. С помощью правого IdP-тестера измеряется форма распределения данной «короткой» выборки. Полученное число IdPx сравнивается с результатом IdP0 измерения формы распределения всей выборки левым IdP-тестером. Если погрешность сравнения идентификационных чисел будет меньше заданной погрешности компаратора (по умолчанию эта погрешность установлена на уровне 1%), то работа дециматора заканчивается. В противном случае – первоначальный объем (n=9) порции увеличивается на 2 отсчета. Тем самым, при сканировании сохраняется неизменным положение средней линии «угла зрения» ACB и симметрия расположения отсчетов относительно центра выборочной реализации сигнала. В свою очередь данное условие обеспечивает минимальные вариации формы распределения из-за асимметричного расположения отсчетов. Еще один режим работы сканера связан с возможностью децимации не полной выборки, а ее центральной части в ограниченном «угле зрения», например, DCE, как показано на правой диаграмме рис. 1. Модель дециматора, выполненная в среде LabVIEW-7.1 (рис. 2), состоит из 3-х модулей: NF-Decimator.vi, Scanistor.vi, Otbor.vi, NF-tester.vi, которые совместно реализуют, описанный выше, алгоритм работы.
Рис. 2. Структуры программных кодов инструментов дециматора
Назначение модуля NF-Decimator.vi заключается в моделировании структурной схемы (рис. 1) дециматора, в целом. Блоки Scanistor.vi и Otbor.vi обеспечивают правильную работу сканера. Основными элементами структурной схемы дециматора являются IdP-тестеры, функциональная схема которых изображена на рис. 2, Г. Математической моделью тестера служит уравнение:
которое трактует обработку значений {X} сигнала как преобразование количества информации объема N на входе тестера в количество информации объема NF на выходе. В работе [5] показано, что численные оценки значения NF упорядочивают форму распределений случайных (2mod – двумодальное, asin – арксинусное, even – равномерное, simp – Симпсона, gaus – нормальное, lapl – Лапласа, kosh – Коши) и периодических (Squ – прямоугольный, Sine – синусоидальный, Tri – треугольный, Saw – пилообразный) сигналов, в соответствии с данными табл. 1.
Таблица 1
Распознавательная характеристика NF-тестера
IdP=NF, N=10000
Вид распределения случайного сигнала
2mod
asin
even
simp
gaus
lapl
kosh
Mean (NF)
4
8
12
24
60
150
>=N
Периодические аналоги
Squ
Sine
Tri, Saw
Физический смысл данной таблицы состоит в том, что численные оценки идентификационных чисел связывают между собой различные формы распределений в виде регулярной последовательности.
Изучение особенностей предложенного алгоритма проводилось по следующей программе. Во-первых, исследовалась возможность децимации сигналов разных типов (периодические, случайные, фрактальные, модулированные, аддитивные смеси) и разной формы. Во-вторых, изучались свойства алгоритма при варьировании объема выборки начальной порции. В-третьих, измерялся коэффициент сжатия и влияние на него объема выборки и погрешности сравнения компаратора (рис. 1). В-четвертых, оценивалось влияние децимации на спектр сигналов.
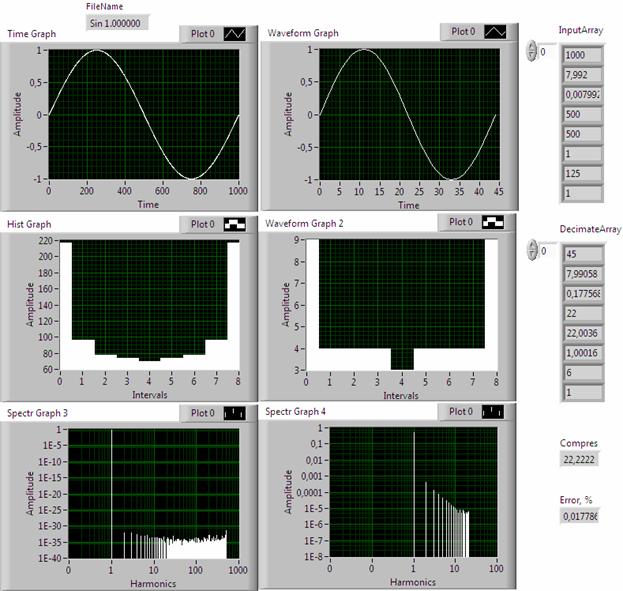
Правильность работы алгоритма децимации оценивалась визуально путем сравнения временных, вероятностных и спектральных функций входного и выходного сигналов. Достоверность результатов децимации оценивалась количественно измерениями погрешности сравнения. В качестве примера представления выходной информации, на рис. 3 изображен фрагмент передней панели виртуального прибора, предназначенного для тестирования дециматора.
На передней панели размещены дисплеи для отображения временной (Time), вероятностной (Hist) и спектральной (Spectr) характеристик входного (левая часть) и выходного, сжатого (правая часть) сигнала. Справа от дисплеев помещены окна вывода количественной информации. Первые три окна Input Array выводят результаты измерения объема N выборки, значение NF идентификационного числа и значение коэффициента Kf из уравнения (1) для временной функции. Последующие три окна отображают такие же параметры для спектральной функции. В седьмом и восьмом окнах выводятся условные параметры, характеризующие содержание виртуальных гармоник формы (Mf) и спектра (Ms), соответственно. При этом, чем больше указанные параметры, тем сложнее форма сигнала и его спектра. Тестовый пример (рис. 3) показывает, что фильтрующие свойства алгоритма проявляются, в первую очередь, в обрезании высокочастотной области спектра сигнала. При этом его верхняя граница сдвигается в низкочастотную область пропорционально коэффициенту сжатия. Для спектра, в частности, равенство Ms=1 говорит о том, что преобладающей является всего одна гармоника, а влияние остальных гармоник достаточно мало. Физический смысл этого параметра состоит в том, что он количественно оценивает свойство когерентности сигнала, учитывающей форму, ширину и спектральное содержание.
Рис. 3. Графики временной (Time), вероятностной (Hist) и спектральной (Spectr) характеристик входного (левая часть) и выходного (правая часть) синусоидального сигнала
Окна Decimate Array аналогичны по содержанию окнам Input Array. Контрольные окна типа Compres и Error% отображают оценки коэффициента сжатия и погрешности адекватности.
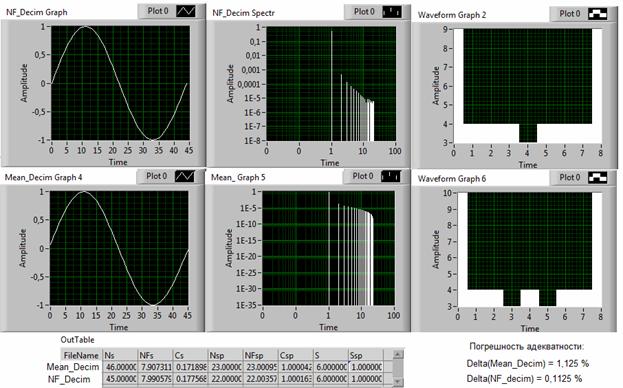
На рис. 4 представлены результаты измерений, предназначенные для сравнительного анализа предлагаемого, идентификационного метода децимации (NF_Decim) и классического метода (Mean_Decim), основанного на замене части соседних отсчетов их средним значением. Оба инструмента настраивались так, чтобы получить одинаковый коэффициент сжатия (C ≈ 22) исходного синусоидального сигнала, объема N=1000. Количественные оценки сравнения даны на этом же рисунке в таблице Out Table. Верхний ряд графиков отображает временную, спектральную и вероятностную функции выходного сигнала дециматора типа NF_Decim.
Рис. 4. Сравнение результатов децимации синусоидального сигнала предлагаемым (NF_Decim) и известным (Mean_Decim) методами
Нижний ряд графиков относится к среднеарифметическому дециматору. По данным, приведенным в таблице Out Table, по 7 показателям из 8 количественные оценки качества децимации в обоих методах практически одинаковы. Основное отличие состоит в погрешности воспроизведения формы сигнала (погрешности адекватности), которая примерно на порядок меньше в предлагаемом методе.
РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЯ
В предыдущем разделе была обоснована принципиальная возможность построения устройства (дециматора), предназначенного для прореживания сигналов и использующего в качестве критерия отбора отсчетов результаты идентификационных измерений формы входного сигнала.
При этом, анализ результатов контрольного (рис. 3) и сравнительного (рис. 4) примеров позволяет сформулировать следующие основные особенности предлагаемого алгоритма децимации. Во-первых, наблюдается хорошее соответствие (верхние два графика) между формами входного и децимированного сигнала, о чем говорит малое (δ≈0,02%) значение погрешности адекватности. Во-вторых, имеет место достаточно эффективная компрессия (Cd = Compres = Nin/Nd = 1000/45 ≈ 22 раза) входного сигнала. В-третьих, существенно сокращается (на величину компрессии) ширина высокочастотной области спектра (нижние графики), при этом низкочастотная часть спектра сохраняется. В-четвертых, хотя число шумовых компонент спектра сокращается, их уровень – возрастает. В-пятых, уровень основной (в данном случае, первой) гармоники уменьшается в 2 раза (с 1 до 0,5 Вольт), при этом размах сигнала сохраняется. Это говорит о том, что эффективный уровень шумов выходного сигнала меньше входного. В-шестых, форма распределения выходного сигнала сохраняет основные особенности формы распределения входного (средние графики). В-седьмых, предлагаемый алгоритм обеспечивает более высокую точность воспроизведения сигналов, по сравнению с методом прореживания с использованием средних значений.
Рассмотрим в качестве примера задачу каскадной децимации сигналов.
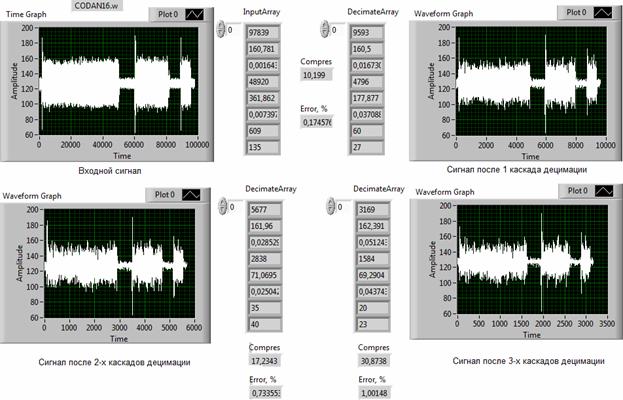
Рис. 5. Пример применения каскадирования при реализации процедуры децимации
Идея каскадной децимации основывается на фундаментальной зависимости погрешности адекватности от коэффициента сжатия. Общий характер этой зависимости таков: чем больше сжимается сигнал, тем больше погрешность адекватности. Поэтому, процедуру децимации можно последовательно применять несколько раз, пока текущее значение погрешности децимации не станет, равна заданной. На рис. 5 представлен пример применения каскадирования при реализации процедуры децимации. Входной сигнал (левый верхний график) после первого каскада децимации сжимается примерно в 10 раз и погрешность адекватности составляет ≈0,2% (правый верхний график). После третьего каскада децимации (нижний правый график), коэффициент сжатия достигает значения ≈ 31, а погрешность адекватности увеличивается до предельно допустимого значения 1%. Форма выходного сигнала при этом сохраняет основные особенности, присущие исходному сигналу. Настройка дециматора производится установкой заданного значения погрешности адекватности и указанием начального числа отсчетов сканера.
Данный пример интересен тем, что позволяет ввести некоторые аналитические соотношения между идентификационными параметрами входного и выходного сигналов. Для этого рассмотрим спектральное содержание гармоник формы и спектра (S, Ssp), количественные оценки которых выведены в двух последних окнах индикаторов Input Array и Decimate Array (табл. 2). Поскольку из двух идентификационных параметров (S, Ssp) при изменении коэффициента сжатия (С) монотонно изменяется только показатель S содержания гармоник формы, то несложно установить соотношения, связывающие форму и компрессию при каскадной децимации в виде следующих уравнений:
Здесь: Ci – коэффициент сжатия i-го каскада, 1≤i≤n, где n=3 – количество каскадов сжатия, Nin – объем выборки на входе, Nout – объем выборки на выходе, Sin – количество гармоник формы на входе, Sout – количество гармоник формы на выходе, A – коэффициент передачи дециматора.
Результаты каскадной децимации
№ п/п
Параметр
Входной сигнал
Выходные сигналы
1 каскад
2 каскад
3 каскад
1
Объем выборки, N
97839
9593
5677
3169
2
Коэффициент сжатия, C
1
10 (10)
17 (1,7)
31 (1,8)
3
Погрешность адекватности, δ,%
0
0,175
0,73
1
4
Кол-во гармоник формы, S
609
60
35
20
5
Кол-во гармоник спектра, Ssp
135
27
40
23
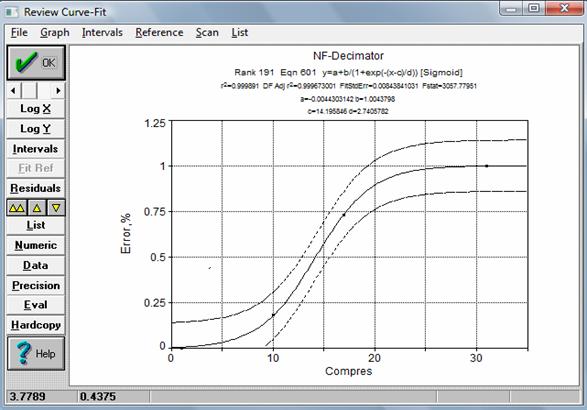
На рис. 6 представлен вид аналитической зависимости погрешности адекватности от коэффициента сжатия. Данная зависимость построена в среде TCWin в режиме подбора аналитических моделей по минимуму среднеквадратического отклонения с учетом сложности и удобства использования уравнения при расчетах. Предельно допустимая погрешность адекватности в 1% соответствует внутренней настройке дециматора, но может быть изменена в большую или меньшую стороны. В этом случае придется снова производить подбор модели. Таким образом, если в методе среднеарифметического агрегирования коэффициент сжатия задается выбором объема усреднения, а погрешность адекватности никак не контролируется, то в предлагаемом методе, наоборот, погрешность адекватности задается и, в соответствие с ней, устанавливается та или иная степень компрессии.
Рис. 6. Модель связи погрешности адекватности с коэффициентом сжатия (допустимая погрешность 1%)
При одинаковом сжатии, погрешность адекватности описанного алгоритма всегда меньше, чем у классического или среднеарифметического методов децимации. Указанные достоинства позволяют рекомендовать идентификационный алгоритм для построения автоматизированных систем, использующих процедуру децимации для компрессии количественной информации.
ЛИТЕРАТУРА
1. Левкович-Маслюк Л. Дайджест вейвлет-анализа.// Компьютерра, №8, 1998, с.31-39.
2. Басараб М.А. Цифровая обработка сигналов на основе теоремы Уиттекера-Котельникова-Шеннона. – М.: Радиотехника, 2004. – 72 с.
3. Цыганенко В.Н., Белик А.Г. Дискретизация измерительных сигналов на основе прикладных функциональных моделей //Цифровая обработка сигналов. – М.: 2009. - №2. – С.58-60.
4. Кликушин Ю.Н. Идентификационные инструменты анализа и синтеза формы сигналов: Монография. – Омск: Изд-во ОмГТУ, 2010. – 216 с.
5. Кликушин Ю.Н. Классификационные шкалы для распределений вероятности. Интернет издание. – М.: Журнал Радиоэлектроники, ИРЭ РАН, № 11 (ноябрь), 2000. http://jre.cplire.ru/jre/nov00/4/text.html
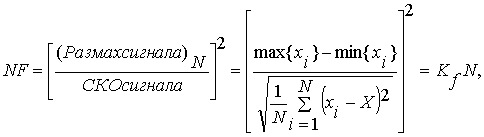 (1)
(1)