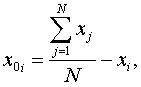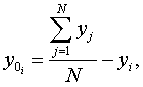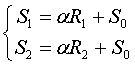УДК 621.396

Фокусировка инверсно-синтезируемых двумерных радиолокационных изображений объектов при измерениях в условиях открытых полигонов

С. И. Моряков, С. М. Нестеров, И. А. Скородумов

Научно-исследовательской институт ВВКО Минобороны России

Статья поступила в редакцию 13 мая 2016 г., после доработки – 30 мая 2016 г.

Аннотация. Современные широкополосные радиолокационные системы и средства, использующие эффективные методы цифровой обработки сигналов, позволяют формировать двумерные радиолокационные изображения (РЛИ) наблюдаемых объектов, обеспечивая новое качество радиолокационной информации для решения задач селекции, идентификации и дефектоскопии объектов. Разработка и совершенствование таких систем неразрывно связаны с теоретическими и экспериментальными исследованиями в данной области. Важное практическое значение при этом имеет экспериментальное синтезирование радиолокационных изображений натурных образцов или их масштабных моделей с небольшим коэффициентом масштабирования, которое, в силу больших размеров и веса таких объектов, проводится на полигонах открытого типа, оборудованных необходимыми механизмами подъёма и вращения крупногабаритных объектов, а также обеспечивающих необходимую дальность до них. Динамические нагрузки во время проведения измерений на открытом полигоне с гибкой системой подвеса объектов являются причиной перемещения объекта в измерительном поле и, соответственно, дополнительных фазовых набегов в принимаемом измерительной аппаратурой сигнале. Это приводит к расфокусировке и искажениям получаемых изображений как по метрике, так и по интенсивности элементов разрешения. В работе предложены алгоритмы оценки смещения по дальности оси вращения объекта измерений, закрепленного на гибкой системе подвеса в условиях открытого полигона. Алгоритмы основаны на математической обработке данных о координатах закреплённых на объекте маркеров, измеряемых оптической системой координатной привязки, и обеспечивают компенсацию дополнительных фазовых набегов в широких угловых секторах синтезирования. Оценка качества фокусируемых изображений объектов проверена путем корреляционной обработки экспериментальных РЛИ металлических сфер с РЛИ тех же объектов, рассчитанных строгим методом собственных функций. Показано, что полученные результаты обеспечивают формирование сфокусированных РЛИ объектов в широких угловых секторах синтезирования по результатам измерений в условиях открытых полигонов с гибкой системой подвеса объектов.

Ключевые слова: инверсное синтезирование апертуры, радиолокационные изображения, корреляционная обработка.

Abstract. Modern wideband radar systems and tools with digital signal processing and inverse synthetic aperture radar imaging capabilities provide a new quality of radar information to solve identification and flaw detection problem. Development and improvement of these systems are inseparably linked with theoretical and experimental research in this area. The experimental inverse synthetic aperture radar imaging of full-scale objects and scale model of the object on outdoor measurements facilities with mount and rotating system, which provides the necessary range and load-carrying capacity, is of great practical importance. The dynamics load during measurements on outdoor facility with flexible mount system leads to the displacement of the object and respectively to phase errors in receiving signal. As a result, wide-angle inverse synthetic aperture radar images are defocused, distorted and blurred. In the paper algorithms of object axis of rotation distance offset estimation in outdoor measurements facility with flexible mount system are proposed. Algorithms are based on marker coordinate data processing and provide phase shifts compensation needed to focus wide-angle inverse synthetic aperture radar images. We propose solutions of various locations of markers on the object to create well-focused inverse synthetic aperture radar images. The assessment of quality of focused inverse synthetic aperture radar images is conducted by cross-correlation with eigenfunction analytical solution of calibration object. In the paper it is shown that results provide well focused wide-angle inverse synthetic aperture radar imaging on outdoor measurements facility with flexible mount system. Focused inverse synthetic aperture radar images are nessesary for development and improvement of modern wideband radar systems with digital signal capabilities.

Key words: inverse synthetic aperture, radar images, radar cross section, correlation processing.

В настоящее время все большее применение получают широкополосные радиолокационные системы с режимом формирования двумерных изображений объектов методом инверсного синтезирования апертуры [1-5]. Для разработки и совершенствования таких систем необходимы радиолокационные изображения (РЛИ) типовых объектов, получаемые на радиолокационных стендах и измерительных комплексах. Важное практическое значение при этом имеет экспериментальное синтезирование РЛИ натурных образцов или их масштабных моделей с небольшим коэффициентом масштабирования, которое, в силу больших размеров и веса таких объектов измерений, проводится на полигонах открытого типа, оборудованных необходимыми механизмами подъёма и вращения крупногабаритных объектов, а также обеспечивающих необходимую дальность до них.

Рассмотрим открытый полигон с системой подвеса объектов измерений, где влияние паразитных фоновых отражений минимизируется за счёт подъёма объекта на значительную высоту (порядка 30 м), установки отсекающих экранов вдоль измерительной трассы (длиной порядка 800 м) и использования малоотражающих лент и шнуров для подвеса объекта к тросу и для нижнего крепления объекта к расположенному на земле механизму вращения. На рис.1 приведена примерная схема размещения объекта (1 – трос, 3 – верхнее крепление, 2 – нижние растяжки) в границах рабочей зоны измерений порядка 15 м, которая обозначена на рисунке пунктиром.

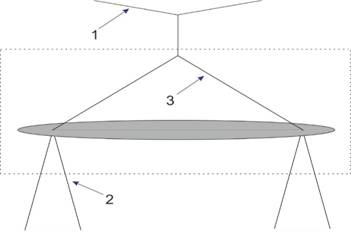
Рис. 1. Схема размещения объекта на гибкой системе подвеса

Гибкая система подвеса с её значительными размерами приводит к тому, что при задании вращения его ось перемещается в пространстве, при отсутствии ветра, по некому конусу с вершиной в точке подвеса к тросу – или более сложным образом при ветровой нагрузке, так что объект помимо вращательного движения получает и перемещения по дальности, то есть дополнительные фазовые набеги в отраженном сигнале. Без их устранения формируемые по результатам измерений двумерные РЛИ оказываются расфокусированными.

Цель работы – обеспечить получение сфокусированных РЛИ объектов в широких угловых секторах синтезирования по результатам измерений в условиях открытых полигонов с гибкой системой подвеса объектов.

Рассмотрим подвешенный объект в виде двух эталонных отражателей (металлических сфер диаметром 30см) и соединяющего их малоотражающего устройства длиной 5,5м. Объекту задано равномерное вращение в измерительном поле широкополосной измерительной установки (ШИУ). Положение объекта (относительная дальность и угол поворота) отслеживается оптической системой координатной привязки (СКП) при помощи установленных квадроцентрических маркеров (рис. 2) [6].

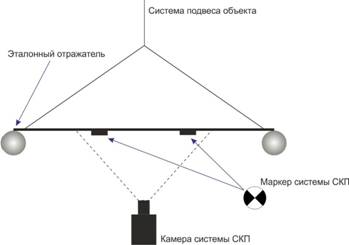
Рис. 2. Схема размещения на объекте маркеров системы СКП

Согласно алгоритму формирования РЛИ за счет инверсного синтезирования апертуры [7], требуется, чтобы дальность до объекта за время синтезирования не менялась, в противном случае получаемое РЛИ не будет сфокусировано.

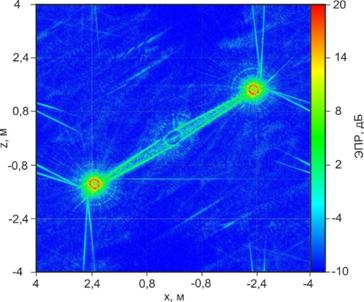
На рис.3 приведено двумерное РЛИ объекта в круговом секторе углов синтезирования, полученное по результатам измерений в практически штилевую погоду после выполнения предварительной фокусировки объекта к центру кадра [4]. Интенсивность элементов разрешения на изображении показана цветовой палитрой относительно единиц ЭПР. Видно, что полученное РЛИ существенно расфокусировано.

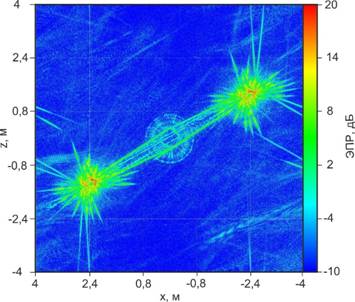
Рис. 3. Двумерное РЛИ объекта после предварительной фокусировки

На рис. 4 приведены траектории движения маркеров за один оборот вращения объекта. При идеальном вращении траектории маркеров должны описывать окружности. Полученные траектории имеют незначительные эллиптичность и высокочастотные осцилляции, показывающие наличие радиальных перемещений объекта (дополнительных фазовых набегов), которые приводят к расфокусировке и искажениям РЛИ как по метрике, так и по интенсивности.

Для устранения искажений и фокусировки РЛИ объектов предлагается использовать получаемые координаты маркеров системы СКП, вычислять дополнительные фазовые набеги за время синтезирования и удалять их из зарегистрированного отражённого от объекта сигнала.

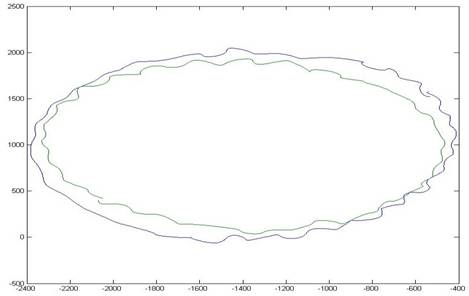
Рис. 4. Траектории движения маркеров системы СКП

В рассматриваемом примере маркеры СКП были установлены на примерно равном расстоянии от предполагаемой оси вращения, что иллюстрируют описывающие их движение траектории на рис.4.

При такой установке маркеров можно использовать следующие простые вычисления (алгоритм 1) оценки дополнительных набегов по дальности в каждом кадре за время синтезирования РЛИ:

(1)

(2),

где

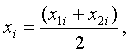
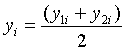– оценка координат точки оси вращения в плоскости вращения;

, – координаты первого маркера, измеренные системой СКП;

, - координаты второго маркера, измеренные системой СКП;

i – номер кадра;

N – число кадров системы СКП;

- угол направления на ШИУ в системе координат СКП.

Однако, априорное определение вероятного положения оси вращения объекта на гибкой системе подвеса и соответственная установка маркеров системы СКП на одинаковом от неё расстоянии не всегда возможны.

Для устранения дополнительных фазовых набегов, вызванных перемещением оси вращения, в общем случае требуется определить её вероятное местоположение относительно объекта, что реализует излагаемый ниже алгоритм 2.

Будем полагать, что точка вращения 0 (точка пересечения оси вращения с плоскостью вращения) не меняет своего положения относительно точек маркеров 1 и 2 на объекте, так что эти три точки составляют треугольник с неизменными сторонами в плоскости вращения (рис.5).

Пусть за время синтезирования объект повернулся на угол , а вершины 0, 1 и 2 рассматриваемого треугольника прошли пути , и .

Полагая, что пути точек 1 и 2 складываются из вращательного движения вокруг точки 0 с радиусами и и равного для всех точек объекта радиального пути , имеем два уравнения

(3)

относительно трёх неизвестных , и .

Неизвестные радиусы вращения и можно найти численно, определив их минимально возможные и и максимально возможные значения и .

Максимально возможные значения радиусов находятся в предположения нулевого радиального перемещения:

, .

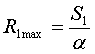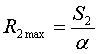Минимально возможные значения радиусов связаны равенством , где - расстояние между маркерами 1 и 2, откуда с учётом (3) получаем

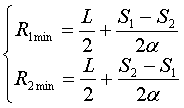
При решении задачи численного поиска неизвестных радиусов в рассчитанных границах снова обратимся к системе (3), из которой следует, что промежуточное изменение значения одного из радиусов влечёт такое же изменение значений второго радиуса. Тем самым имеем задачу численного поиска значения параметра , где по критерию минимума пути, как функции этого параметра, точки, принимаемой в качестве оси вращения, расстояние от которой до маркеров 1 и 2 равно и .

Расчёт пути, проходимого этой точкой за время синтезирования, выполняется, исходя из её текущих координат. При этом необходимо учесть, что искомая точка может располагаться как по одну, так и по другую сторону от линии, соединяющей маркеры 1 и 2, и проверять на минимум длину путей, которые проходят обе точки.

Координаты этих точек вычисляются по известным координатам маркеров:

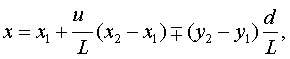
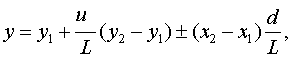
где

;

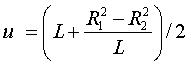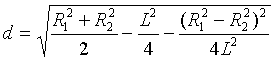и – текущие значения радиусов вращения (рис. 5).

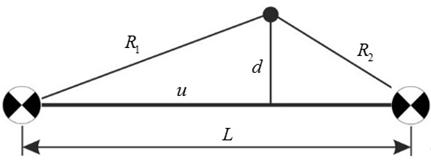
Рис. 5. Пояснения к алгоритму 2

Указанные вычисления выполним для каждого кадра системы СКП, после чего, аналогично (1) - (2), получим набеги дальности , которые необходимо компенсировать.

Результаты оценки смещений по дальности оси вращения объекта по двум представленным алгоритмам приведены на рисунке 6. Отличия результатов определения смещения оси вращения алгоритмами достигают 120 мм.

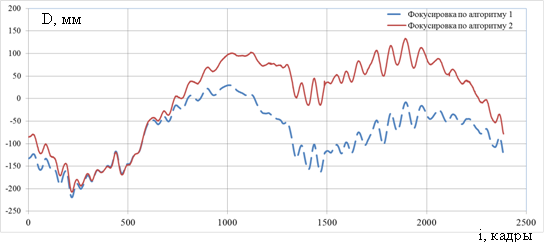
Рис. 6. Результаты оценки смещений по дальности оси вращения объекта

Результат формирования РЛИ с учетом смещений приведены на рисунке 7. Несмотря на то, что отражатели на РЛИ приобрели правильную форму, их диаметры значительно превышают истинные. Этот эффект может быть устранен путем дополнительной фокусировки сигнала для совмещения оси вращения объекта и центра кадра РЛИ при помощи алгоритма максимума контраста РЛИ [6]. Точность алгоритма должна соответствовать точности алгоритмов оценки смещений по дальности оси вращения.

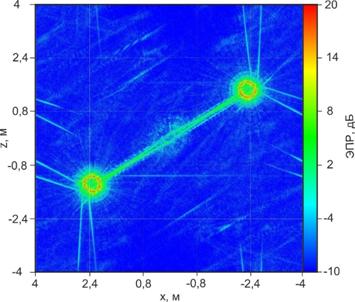
Рис. 7. Двумерное РЛИ объекта с учетом смещений

Результаты формирования РЛИ с учетом дополнительной фокусировки приведены на рисунке 8 (рис. 8а – фокусировка к центру между маркерами согласно алгоритма 1, рис. 8б – фокусировка с определением точки вращения согласно алгоритма 2).

(а)

(б)

Рис. 8. Двумерное РЛИ объекта после дополнительной фокусировки

На представленных РЛИ четко различаются эталонные отражатели. Оценка качества сфокусированных РЛИ производилась по результатам вычисления коэффициента корреляции с эталонным РЛИ сферы (рис. 9), полученным расчётом строгим методом собственных функций.

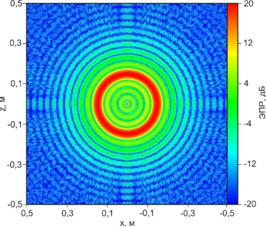
Рис. 9. Эталонное двумерное РЛИ сферы

Результаты построения функции коэффициентов корреляции для РЛИ с поправкой к центру между маркерами (алгоритм 1) и с расчётом координат точки вращения (алгоритм 2) приведены на рисунках 10 и 11 соответственно.

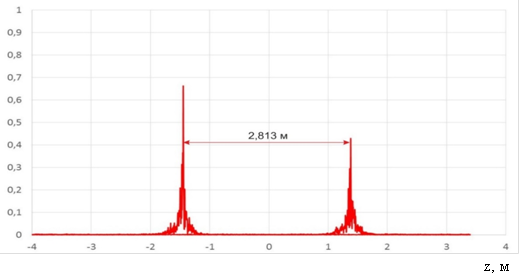
Рис. 10. Функция коэффициента корреляции для РЛИ с поправкой к центру между маркерами (алгоритм 1)

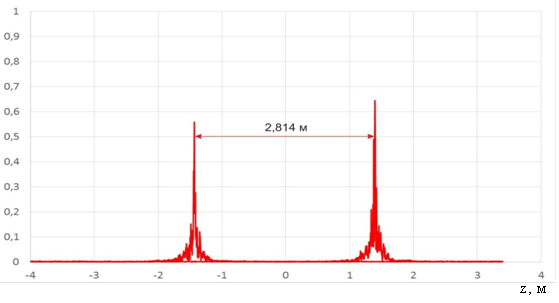
Рис. 11. Функция коэффициента корреляции для РЛИ с расчётом координат точки вращения (алгоритм 2)

Фокусировка РЛИ по второму алгоритму приводит к близким значениям максимумов коэффициентов корреляции для каждого из шаров (0,57 и 0,63). Фокусировка РЛИ по первому алгоритму показывает максимальное значение коэффициента корреляции 0,66 для одного из шаров, однако для другого шара он не превышает 0,42. По расстоянию между максимумами коэффициента корреляции можно определить расстояние между эталонными объектами на РЛИ. Как в первом, так и во втором случае были определены расстояния между максимумами ~2,81 м (рис.10, 11), что с учетом поворота объекта на РЛИ на 59,2 градуса дало расстояние между эталонными сферами 5,5 м. Данная оценка свидетельствует об отсутствии геометрических искажений на РЛИ. В то же время искажения на РЛИ полностью не устранены, что показывает форма основного лепестка функции коэффициента корреляции. На рисунке 12 приведены фрагменты функции коэффициента корреляции для алгоритмов 1 и 2 в сравнении с автокорреляционной функцией эталона.

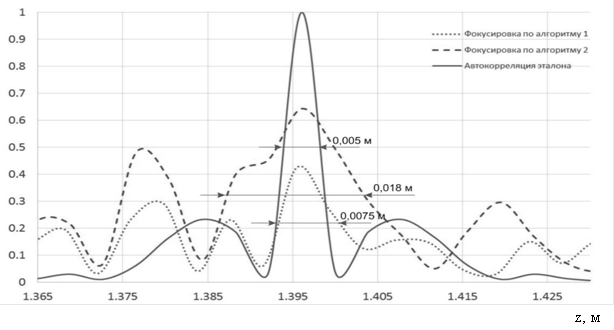
Рис. 12. Фрагмент функции коэффициента корреляции для алгоритмов 1 и 2 в сравнении с автокорреляционной функцией эталона

Выводы

Предложены алгоритмы оценки смещения по дальности оси вращения объекта измерений на гибкой системе подвеса в условиях открытого полигона. Алгоритмы основаны на математической обработке координат закреплённых на объекте маркеров, измеряемых оптической системой, и обеспечивают компенсацию дополнительных фазовых набегов по дальности, необходимую для фокусировки инверсно-синтезируемых двумерных РЛИ объектов в широких угловых секторах синтезирования.

Оценка качества фокусируемых РЛИ объектов проверена путем корреляционной обработки экспериментальных РЛИ металлических сфер с РЛИ тех же объектов, рассчитанных строгим методом собственных функций.

Литература

1. Ковалев С.В., Нестеров С.М., Скородумов И.А. Двумерные радиолокационные изображения эталонных объектов // Радиотехника и Электроника. 2011. Т.56. №2.

2. Моряков С.И., Нестеров С.М., Скородумов И.А., Приймаков С.Н. Оценка точностных параметров радиолокационных изображений исследуемых объектов // «Журнал радиоэлектроники»: электронный журнал. 2014. №.6. URL: http://jre.cplire.ru/jre/jun14/8/text.pdf.

3. Гузенко О.Б., Моряков С.И., Нестеров С.М., Скородумов И.А. К описанию функции неопределенности сигнала при инверсном синтезировании двумерных радиолокационных изображений объектов. 2015. №.3. URL: http://jre.cplire.ru/mac/mar15/10/text.pdf.

4. Cumming, I.G., Wong F.H Digital Processing of Synthetic Aperture Radar Data. - Norwood, MA.: Artech House, 2005.

5. Ozdemir Caner. Inverse synthetic aperture radar imaging with MATLAB. – Hoboken, NJ.: John Wiley & Sons, 2012.

6. Радиолокационные характеристии объектов. Методы исследования. Монография / Под ред. С.М. Нестерова. – М.: Радиотехника, 2015.

7. Ковалев С.В., Нестеров С.М., Скородумов И.А. Способ получения двумерного радиолокационного изображения объекта при многочастотном импульсном зондировании // Патент RU 2422851 C1, кл. G01S 13/89, 2011.

References

1. Kovalev S.V., Nesterov S.M., Skorodumov I. A. 2D Radar Images of Template Objects. Journal of Communications Technology and Electronics, 2011, Vol.56, No 2, pp.183-188. DOI: 10.1134/S1064226911020082

2. Moryakov C. I., Nesterov S.M., Skorodumov I. A. Estimating the precision parameters radar systems offering to generate radar images. Zhurnal radioelectroniki - Journal of Radio Electronics, 2014, No. 6. Available at http://jre.cplire.ru/jun14/8/text.pdf. (In Russian)

3. Guzenko O.B., Moryakov S. I., Nesterov S. M. , Skorodumov I. A. Description of the ambiguity function of the signal by objects ISA Rimaging.
Zhurnal radioelectroniki - Journal of Radio Electronics, 2015, No. 3. Available at http://jre.cplire.ru/jre/mar15/10/text.pdf (In Russian)

4. Cumming, I.G., Wong F.H Digital Processing of Synthetic Aperture Radar Data. - Norwood, MA.: Artech House, 2005.

5. Ozdemir Caner. Inverse synthetic aperture radar imaging with MATLAB. – Hoboken, NJ.: John Wiley & Sons, 2012.

6. Edited by Nesterov S.M. Radiolokatsionnye kharakteristiki obyektov. Metody issledovaniya. [Radar characteristics of objects. Research methods]. Moscow, Radiotekhnika Publ. 2015. (In Russian)

7. Kovalev S.V., Nesterov S.M., Skorodumov I. A. Sposob polucheniya dvumernogo radiolokatsionnogo izbrazheniya obyekta pri mnogochastotnom impulsnom zondirovanii. [A method of obtaining 2D radar image of the object at the multi frequency pulse sensing.] Patent RF, 2422851 C1, G01S 13/89, 2011. (In Russian)