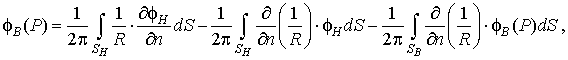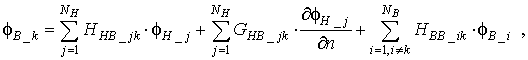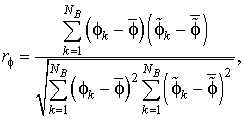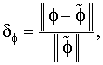Анализ погрешности расчета электрических потенциалов, создаваемых поверхностным источником в проводящем цилиндре конечной длины
М. Н. Крамм, Ю. А. Палютина, Н. О. Стрелков
Национальный исследовательский университет «МЭИ»
Статья поступила в редакцию 20 мая 2016 г.
Аннотация. Целью данной работы является анализ погрешности расчета электрических потенциалов на поверхности проводящего цилиндра, возбуждаемых поверхностным источником внутри этого цилиндра. Необходимость этого анализа связана с решением обратной задачи электрокардиографии (ЭКГ) − задачи реконструкции источника по ЭКГ-сигналам, создаваемым этим источником и регистрируемым в точках размещения электродов на поверхности торса. Поскольку в основе решения обратной задачи лежит прямой расчет поверхностных потенциалов, то важно оценить погрешность расчета потенциалов, связанную с дискретизацией поверхности, на которой распределен эквивалентный электрический источник. В данной работе рассматривается погрешность расчета потенциалов на поверхности проводящего цилиндра конечной длины, возбуждаемых распределением потенциала и его нормальной производной на внутренней сферической поверхности (сферическая модель квазиэпикарда в ЭКГ). Анализируется влияние числа разбиений, типа источника и формы цилиндра на погрешность расчета потенциалов.
Ключевые слова: электрокардиография, электрические потенциалы, модель торса, квазиэпикард, поверхностные источники, поверхностные интегралы.
Abstract. The aim of this work is the analysis of the error of the electrical potential calculation on the surface of the conductive cylinder, excited by surface source inside the cylinder. The necessity оf this comparison is connected with the solution of the inverse problem of electrocardiography − the task of reconstruction of the source by ECG signals created by this source and recorded at the points of electrodes placement on the body surface. As in basis of the solution of the inverse problem is the direct calculation of surface potentials, it is important to estimate the error of the calculation of the potentials, associated with the discretization of the surface of equivalent electrical source distribution. In this paper we considered the error of calculation of potentials on the surface of the conductive cylinder with finite length excited by a distribution of potential and its normal derivative on the inner spherical surface (a spherical model of quasi-epicardium in ECG). As a model source producing surface potentials we used dipole located inside the sphere of the epicardium. The electric potential on the torso surface was calculated by the boundary element method, in this case we compared the contribution to the error of calculation, which yields the integration of the potential, its normal derivative on the surface of the spherical epicardium and the integration of the potential on the cylindrical torso surface. The impacts of the number of segmentations, type of source and shape of the cylinder on the error of potentials calculation were analyzed.
Key words: electrocardiography, electric potentials, model of torso, quasi-epicardium, surface sources, surface integrals.
Введение
Для повышения информативности диагностических исследований электрической деятельности сердца актуальным является решение обратной задачи электрокардиографии, которая связана с пересчетом электрических потенциалов, измеренных на поверхности грудной клетки (ГК) человека, в распределение эквивалентных источников на поверхности эпикарда [1, 2, 3]. Поскольку в основе решения обратной задачи лежит прямой расчет поверхностных потенциалов грудной клетки (ПП для ГК) на основе распределения поверхностных источников эпикарда (ПИЭ), то представляет интерес оценка погрешности расчета ПП для ГК, обусловленная дискретизацией поверхности эпикарда при различных типах ПИЭ. Ограничение количества разбиений поверхности связано с желаемым уменьшением количества электродов и временных затрат. Также представляет интерес вопрос о погрешности расчета ПП, обусловленной неравномерным распределением электродов на поверхности ГК, что связано с размещением электродов лишь на боковой поверхности торса.
Для анализа влияния отмеченных выше факторов нами
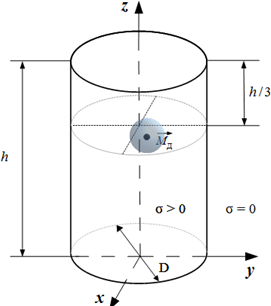
рассмотрена модельная задача, когда поверхность торса описана цилиндром
конечной длины, а поверхностные источники рассматриваются на сферической
поверхности квазиэпикарда, окружающей эпикард [1, 2] (рис. 1). Поскольку основной вклад в ПП для ГК дает
дипольный член разложения ПП, то модельный поверхностный источник на
квазиэпикарде формировался диполем различной ориентации с вектором момента ![]() , расположенным внутри сферы квазиэпикарда.
, расположенным внутри сферы квазиэпикарда.
|
а) |
б) |
|
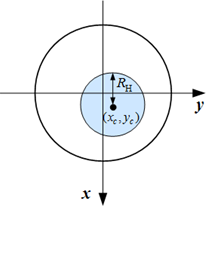
Рис. 1. Модель тела человека в форме кругового цилиндра с системой электродов а – в объеме, б – вид сверху. |
|
Расчет распределений потенциалов. Математические аспекты
Рассмотрим ситуацию, когда внутренней неоднородностью среды между торсом и квазиэпикардом можно пренебречь [4]. При этом электрический потенциал на поверхности торса можно определить с помощью следующих поверхностных интегралов [1, 2]:
|
|
(1) |
где ![]() – точка
наблюдения,
– точка
наблюдения, ![]() ,
, ![]() –
поверхности интегрирования, соответственно для торса и квазиэпикарда,
–
поверхности интегрирования, соответственно для торса и квазиэпикарда, ![]() – расстояние между точкой
наблюдения и точкой на поверхности интегрирования,
– расстояние между точкой
наблюдения и точкой на поверхности интегрирования, ![]() –
производная по направлению внешней нормали к поверхности интегрирования
(внешней нормали по отношению к среде между поверхностями интегрирования),
–
производная по направлению внешней нормали к поверхности интегрирования
(внешней нормали по отношению к среде между поверхностями интегрирования), ![]() – дифференциальный элемент
поверхности. Существенно, что в (1) учтено условие электрической изоляции торса
– дифференциальный элемент
поверхности. Существенно, что в (1) учтено условие электрической изоляции торса
![]() ; также в (1) малую окрестность точки
наблюдения
; также в (1) малую окрестность точки
наблюдения ![]() надо исключить из интеграла по
поверхности
надо исключить из интеграла по
поверхности ![]() . В соответствии с (1) эквивалентные
источники измеряемых потенциалов на поверхности грудной клетки описываются
распределениями
. В соответствии с (1) эквивалентные
источники измеряемых потенциалов на поверхности грудной клетки описываются
распределениями ![]() и
и ![]() на
поверхности эпикарда, причем имеются перекрестные связи между ПП для ГК (третий
интеграл в (1)).
на
поверхности эпикарда, причем имеются перекрестные связи между ПП для ГК (третий
интеграл в (1)).
В рамках метода
граничных элементов [5] поверхности ![]() и
и ![]() можно
разбить на
можно
разбить на ![]() и
и ![]() элементов,
соответственно, и прийти к системе линейных алгебраических уравнений (СЛАУ):
элементов,
соответственно, и прийти к системе линейных алгебраических уравнений (СЛАУ):
где ![]()
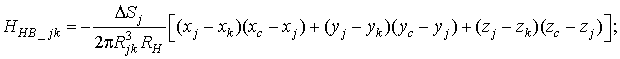
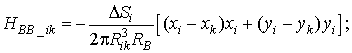
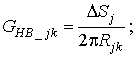
![]() – расстояние между центрами граничных
элементов поверхностей
– расстояние между центрами граничных
элементов поверхностей ![]() и
и ![]() с
координатами
с
координатами ![]() и
и ![]() аналогично
определяется расстояние
аналогично
определяется расстояние ![]() для граничных
элементов на поверхности
для граничных
элементов на поверхности ![]() ;
; ![]() – координаты центра сферы квазиэпикарда;
– координаты центра сферы квазиэпикарда; ![]() ,
, ![]() –
площади соответствующих граничных элементов.
–
площади соответствующих граничных элементов.
Методика анализа погрешности расчета поверхностных потенциалов
Нас интересовала погрешность дискретизации
поверхности при расчете ПП для ГК с использованием соотношения (2). Для оценки
погрешности получаемые по формуле (2) поверхностные потенциалы ![]() , сравнивались с потенциалами
, сравнивались с потенциалами ![]() , рассчитанными стандартным методом
конечных элементов с достаточно мелкой сеткой (порядка 107
элементов). При этом в правой части (2) использовались поверхностные
распределения
, рассчитанными стандартным методом
конечных элементов с достаточно мелкой сеткой (порядка 107
элементов). При этом в правой части (2) использовались поверхностные
распределения ![]() ,
, ![]() и
и ![]() , рассчитанные методом конечных элементов для
модельного источника дипольного типа, расположенного внутри сферы квазиэпикарда
при различной ориентации диполя. Разбиение поверхностей интегрирования
проводилось так, чтобы площади граничных элементов
, рассчитанные методом конечных элементов для
модельного источника дипольного типа, расположенного внутри сферы квазиэпикарда
при различной ориентации диполя. Разбиение поверхностей интегрирования
проводилось так, чтобы площади граничных элементов ![]() (аналогично
(аналогично
![]() ) были одинаковы. Поскольку в реальных
обследованиях потенциалы
) были одинаковы. Поскольку в реальных
обследованиях потенциалы ![]() измеряются на боковой
поверхности торса, то суммирование в (2) и оценка погрешности проводились на
боковой поверхности цилиндрической модели торса.
измеряются на боковой
поверхности торса, то суммирование в (2) и оценка погрешности проводились на
боковой поверхности цилиндрической модели торса.
Для сравнения распределений потенциалов во всех случаях использовались следующие количественные характеристики:
– коэффициент корреляции Пирсона (КК)
|
|
(3) |
где 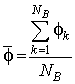 и
и 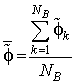 – средние значения распределений
– средние значения распределений ![]() и
и ![]() ,
заданных в виде вектора длиной
,
заданных в виде вектора длиной ![]() ;
;
– относительное отклонение (ОО)
|
|
(4) |
где 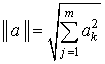 – норма матрицы;
– норма матрицы;
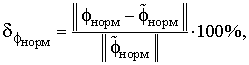
– относительное отклонение нормированных потенциалов (ООН)
|
|
(5) |
где 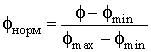 и
и 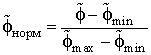 – нормированные распределения потенциалов.
– нормированные распределения потенциалов.
Параметры КК и ООН позволяют сделать вывод относительно сходства или различия распределений потенциалов по форме.
Результаты анализа погрешности расчета поверхностных потенциалов
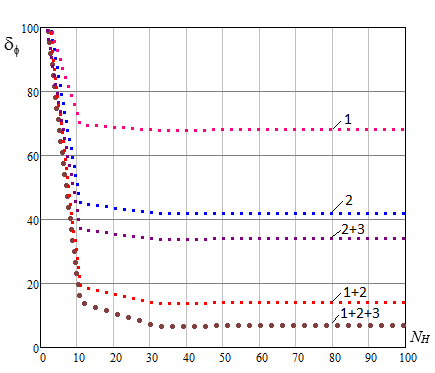
На рис. 2 представлены зависимости
относительного отклонения (ОО) ПП для ГК от количества разбиений
поверхности квазиэпикарда ![]() . При этом также анализировался вклад в погрешность различных
комбинаций поверхностных источников в правой части уравнения (2). Рассматривалась
модельная задача, в которой диаметр цилиндрической модели торса
. При этом также анализировался вклад в погрешность различных
комбинаций поверхностных источников в правой части уравнения (2). Рассматривалась
модельная задача, в которой диаметр цилиндрической модели торса ![]() м, высота цилиндра
м, высота цилиндра ![]() м, радиус сферы квазиэпикарда
м, радиус сферы квазиэпикарда ![]() м, координаты центра сферы
м, координаты центра сферы ![]() м,
м, ![]() м,
м,
![]() м; исходный дипольный источник располагался
в центре сферы и был ориентирован в поперечной плоскости, вдоль оси y (в
дальнейшем y-диполь). На основании представленных графиков можно
заключить, что при числе граничных элементов
м; исходный дипольный источник располагался
в центре сферы и был ориентирован в поперечной плоскости, вдоль оси y (в
дальнейшем y-диполь). На основании представленных графиков можно
заключить, что при числе граничных элементов ![]() дискретизация
поверхности квазиэпикарда практически перестает влиять на погрешность расчета
ПП. Наибольший вклад в карты ПП вносят распределения потенциала и производной
потенциала на поверхности квазиэпикарда (1 и 2 слагаемые в (2)).
дискретизация
поверхности квазиэпикарда практически перестает влиять на погрешность расчета
ПП. Наибольший вклад в карты ПП вносят распределения потенциала и производной
потенциала на поверхности квазиэпикарда (1 и 2 слагаемые в (2)).
На графиках рис. 2 цифрой 1 обозначен
вклад первого слагаемого 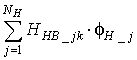 из формулы (2),
цифрой 2 – вклад
из формулы (2),
цифрой 2 – вклад 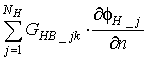 из формулы (2) и цифрой 3 –
вклад
из формулы (2) и цифрой 3 –
вклад 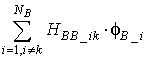 из формулы (2).
из формулы (2).
|
|
|
Рис. 2. Зависимость относительного отклонения от
числа разбиений при учете различных поверхностных источников; 1-учет 1+2-учет |
Остаточная погрешность при ![]() , которая наблюдается даже при учете всех поверхностных интегралов
в (2), связана с суммированием в третьем слагаемом (2) только по боковой
поверхности торса (реально потенциалы
, которая наблюдается даже при учете всех поверхностных интегралов
в (2), связана с суммированием в третьем слагаемом (2) только по боковой
поверхности торса (реально потенциалы ![]() измеряются
на боковой поверхности торса). В результате погрешность расчета ПП для ГК
(параметры ОО и ООН) зависит от соотношения высоты и диаметра цилиндра торса
измеряются
на боковой поверхности торса). В результате погрешность расчета ПП для ГК
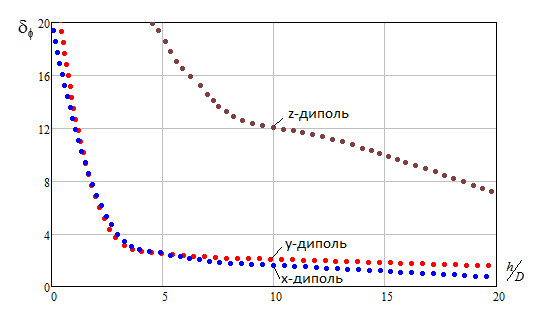
(параметры ОО и ООН) зависит от соотношения высоты и диаметра цилиндра торса ![]() а также от ориентации исходного
дипольного источника. Влияние этих факторов иллюстрируют рис. 3 и таблица 1.
а также от ориентации исходного
дипольного источника. Влияние этих факторов иллюстрируют рис. 3 и таблица 1.
|
|
|
Рис. 3. Влияние ориентации диполя и длины цилиндра на погрешность |
Отмечается заметное снижение погрешности при ![]() . Наибольшее среднеквадратическое
отклонение потенциала наблюдается для диполя, ориентированного вдоль оси торса
(z-диполь). Оценка возможного снижения погрешности расчета ПП для ГК следует из таблицы 2, где представлены параметры отклонения ПП,
полученные при суммировании в (2) только по боковой поверхности цилиндра
высотой
. Наибольшее среднеквадратическое
отклонение потенциала наблюдается для диполя, ориентированного вдоль оси торса
(z-диполь). Оценка возможного снижения погрешности расчета ПП для ГК следует из таблицы 2, где представлены параметры отклонения ПП,
полученные при суммировании в (2) только по боковой поверхности цилиндра
высотой ![]() (верхняя строка таблицы) и с учетом
суммирования по торцевым поверхностям (нижняя строка). Основной вклад в
погрешность вносит верхняя торцевая поверхность, так как источник расположен
ближе к ней (
(верхняя строка таблицы) и с учетом
суммирования по торцевым поверхностям (нижняя строка). Основной вклад в
погрешность вносит верхняя торцевая поверхность, так как источник расположен
ближе к ней (![]() ). В целом учет суммирования по торцевым
поверхностям снижает относительное отклонение в 4-5 раз. Следует отметить, что
даже без проведения суммирования по торцевым поверхностям относительное
отклонение нормированных потенциалов (ООН) не превышает величины порядка 2 %, а коэффициент корреляции не ниже 0.99, что свидетельствует о
высокой схожести сравниваемых распределений поверхностных потенциалов.
). В целом учет суммирования по торцевым
поверхностям снижает относительное отклонение в 4-5 раз. Следует отметить, что
даже без проведения суммирования по торцевым поверхностям относительное
отклонение нормированных потенциалов (ООН) не превышает величины порядка 2 %, а коэффициент корреляции не ниже 0.99, что свидетельствует о
высокой схожести сравниваемых распределений поверхностных потенциалов.
Таблица 1. Влияние высоты цилиндра и ориентации диполя
|
|
x-диполь |
y-диполь |
z-диполь |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
1.8 |
7.73 |
2.36 |
0.028 |
7.96 |
2.52 |
0.027 |
32.6 |
9.56 |
0.011 |
|
3.6 |
1.98 |
0.112 |
2.34·10-5 |
2.99 |
0.345 |
6.34·10-5 |
22.1 |
10.7 |
0.01 |
|
7.2 |
2.20 |
0.307 |
6.85·10-4 |
1.89 |
0.189 |
4.12·10-5 |
14.8 |
7.88 |
0.0064 |
|
21.7 |
1.42 |
0.356 |
4.12·10-5 |
0.613 |
0.073 |
1.67 10-5 |
6.45 |
4.39 |
0.0018 |
Таблица 2. Влияние учета торцевых поверхностей
|
Цилиндр |
x-диполь |
y-диполь |
z-диполь |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
Без торцев |
7.73 |
2.36 |
0.028 |
7.96 |
2.52 |
0.027 |
32.6 |
9.56 |
0.011 |
|
С торцами |
1.84 |
0.39 |
5.8·10-5 |
1.80 |
0.40 |
5.7·10-5 |
6.52 |
1.61 |
2.2·10-4 |
Выводы
Таким образом, на основании полученных модельных результатов можно сделать вывод, что увеличение числа граничных элементов на поверхности квазиэпикарда до величины, превышающей 20-30, не приводит к дальнейшему заметному уменьшению погрешности расчета потенциалов на поверхности грудной клетки. Наибольший вклад в карты поверхностных потенциалов вносят распределения потенциала и производной потенциала на поверхности квазиэпикарда.
Литература
1. Титомир Л. И., Кнеппо П. Математическое моделирование биоэлектрического генератора сердца. – М.: Наука., 1999. – 447 с.
2. Титомир Л.И., Электрический генератор сердца. – М.: Наука, 1980. – 372 с.
3. Rudy Y., Messinger-Rapport B.J. The inverse problem in electrocardiography: Solutions in terms of epicardial potentials // CRC Crit. Rev. Biomed. Eng. - 1988.- Vol. 16, No. 7. P. 216-268.
4. Стрелков Н.О., Крамм М.Н., Жихарева Г.В. Неоднородная электродинамическая модель грудной клетки человека в форме эллиптического цилиндра // Журнал радиоэлектроники [электронный журнал]. 2011. № 7. URL: http://jre.cplire.ru/jre/jul11/4/text.html
5. Бреббия К., Теллес Ж., Вроубел Л. Методы граничных элементов: Пер. с англ. М.: Мир, 1987 - 524 с.
References
1. Titomir L.I., Kneppo P. Matematicheskoe modelirovanie bioelektricheskogo generatora serdca. [Mathematical modeling of heart's bioelectric generator]. Moscow, Nauka Publ. 1999. 447 p. (In Russian)
2. Titomir L.I. Elektricheskij generator serdca. [Electric Heart generator]. Moscow, Nauka Publ. 1980. 372 p. (In Russian)
3. Rudy Y., Messinger-Rapport B.J. The inverse problem in electrocardiography: Solutions in terms of epicardial potentials. CRC Crit. Rev. Biomed. Eng. 1988, No. 16, pp. 216-268
4. Strelkov N. O., Kramm M.N., Zhikhareva G.V., Inhomogeneous electrodynamic model of human chest in the form of an elliptical cylinder. Zhurnal Radioelektroniki - Journal of Radio Electronics, 2011, Vol. 16, No. 7. Available at http://jre.cplire.ru/jre/jul11/4/text.pdf. (In Russian)
5. Brebbia C., Telles J., Vroubel L., Metody granichnyx elementov. [Boundary element methods], Moscow, Mir Publ. 1987. 524 p. (In Russian)