Архитектура высокочастотного дельта-сигма модулятора в основе полностью цифрового гигагерцового передатчика

 

О. Д. Субботин

Московский физико-технический институт (государственный университет)

НПП «САИТ»

 

Статья поступила в редакцию 30 мая 2016 г.

 

Аннотация. В работе представлена улучшенная архитектура построения дельта-сигма модулятора, лежащего в основе полностью цифрового передатчика, работающая на гигагерцовых несущих. Представлена блок-схема обработки сигнала, выполнено полифазное разложения ДСМ модуляторов 1 и 2 порядков. Реализован ДСМ 1 и 2 порядка с использованием полифазного представления на основе микросхемы Kintex 7 фирмы Xilinx. Для каждого модулятора выполнена оптимизации логики. Полученные на основе оптимизации высокочастотная архитектура ДСМ 1 порядка исключает наличие обратной связи в явном виде, уменьшает сложность комбинационной логики. Данная схема позволяет реализовать логику как для 4, так и для 8 и более фаз без уменьшения частоты тактирования схемы. Максимальная частота для стандартной схемы составила 194МГц для 4 фазного разложения, высокочастотной для 8 фаз – 316МГц. Оптимизация архитектуры ДСМ 2 выполнена за счет дополнительной параллелизации вычислений с использованием мультиплексоров. В результате реализации стандартной архитектуры максимальная частота для 4 фаз – 119 МГц, высокочастотной архитектуры для 4 фаз – 223МГц, для 8 фаз – 134 МГц. Представлены результаты реализации для полифазной и высокочастотной схемы с учетом уровня шумов ДСМ для коэффициентов передискретизации 64 и 128.

Ключевые слова: ДСМ, полифазное представление, высокочастотная архитектура, OSR.

 Abstract. An improved architecture of building a delta-sigma modulator, which is the basis of fully digital transmitter operating at gigahertz carrier, is presented. A block diagram of signal processing is represented, a polyphase decomposition of DSM modulators 1 and 2 orders is carried out.  DSM 1 and 2 orders are implemented in chip Kintex 7 firm Xilinx, using polyphase conception. Logic optimization is executed for each modulator. The high frequency architecture of DSM 1 order, which is obtained on optimization, excludes feedback in an explicit form, has less complexity of combinational logic. The scheme allows to create logic with 4, 8 and more phases without decreasing clock frequency. The maximum frequency of realization for standart architecture with 4 phases is 194Mhz, for high frequency architecture with 8 phases – 316Mhz. Optimization architecture DSM 2 order is made by additional parallelization of calculations using multiplexer. As a result, the maximum frequency of the standard architecture for phases 4 is 119 MHz, high-frequency architecture for 4 phases  - 223MGts, 8 phases - 134 MHz. The results of the implementation of a polyphase and high-frequency circuits, including DSM noise, are represented for oversampling ratios 64 and 128.

Keywords: DSM, polyphaser decomposition, high-frequency architecture, OSR.

 

Введение

Цифро-аналоговый преобразователь (ЦАП) является генератором аналогового сигнала, находясь в начале цепи распространения сигнала; высокий уровень шумов ЦАП снижает характеристики всей схемы в целом.

 На рисунке 1 представлена классическая схема QAM, в которой перенос на несущую частоту осуществляется путем перемножения входного аналогового сигнала с гармоническим сигналом на несущей частоте. В идеале два канала ортогональны и не влияют друг на друга. В реальных схемах несоответствие фазового сдвига и коэффициента усиления между каналами приводит к просачиванию зеркального канала и снижению соотношения сигнал/шум(SNR). Текущие схемы создания аналоговых квадратурных модуляторов, работающих на частотах в единицах ГГц, имеют соотношение сигнал/шум не более 30-35 дБ.

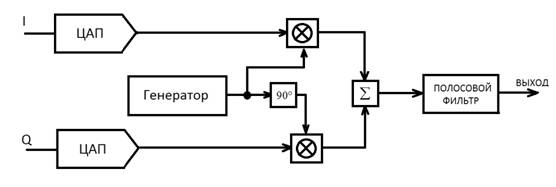
Рис. 1. Схема квадратурной амплитудной модуляции(QAM)

Одним из методов улучшения характеристик выходного сигнала ЦАП является реализация полностью цифрового преобразователя на основе дельта-сигма модуляции(ДСМ) [1,2]. Такой способ позволяет исключить искажения, вносимые нелинейной характеристикой ЦАП, выполнить квадратурную модуляцию в цифровом виде [3], исключив аналоговые искажения. Подобная реализации требует больших скоростей вычислений и возможности генерировать высокоскоростные потоки на выходе схемы.

В данной статье представлена архитектура построения ДСМ, способная генерировать сигнал, уровень сигнал/шум которых выше 70дБ на несущих вплоть до 2.525ГГц для ДСМ 1 порядка, 1.072 ГГц для ДСМ 2 порядка, реализованные на ПЛИС Kintex 7 фирмы Xilinx.

2. Дельта-сигма модулятор

Для начала рассмотрим основной элемент цепи обработки сигнала - ДСМ (подробное описание схем и характеристик можно найти в [4]). В цифровой логике ДСМ нужен для переквантования входного сигнала, в данном случае для перехода от многоразрядного сигнала на входе к битовому потоку на выходе (см. Рисунок 2). В результате падения разрядности к выходному сигналу прибавляется шум квантования, обратная связь переносит энергию шума в высокочастотную область (“noiseshaping”).

 

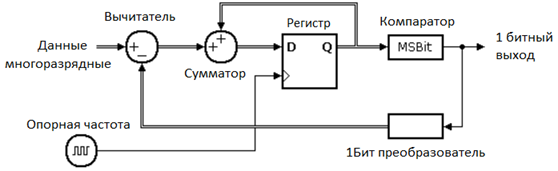
Рис. 2. Цифровой ДСМ 1 порядка

Соотношение сигнал/шум квантования (SQNR)зависит от коэффициента передискретизации (OSR), порядка модулятора. Именно SQNR ДСМ будет определять уровень шума всей цифровой схемы. Теоретически соотношение SQNR для идеального гармонического сигнала можно оценить по формуле

Для ДСМ 1 порядка:

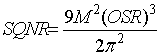                                                                                   (1)

 

Для ДСМ 2 порядка:

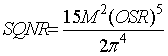                                                                                  (2)

 

M - амплитуда входного сигнала.

Из данных соотношений получим при OSR = 128, M = 1 для ДСМ 1 порядка – 60дБ, 2 порядка - 94 дБ. Данные характеристики является несколько завышенными, так как идеальный гармонический сигнал имеет высокую автокорреляцию, соответственно будет высокая корреляции ошибок, генерируемых квантователем, которые обратной отрицательной связью будут сокращены. Как следствие, при создании цифровым ДСМ стоит учитывать этот фактор, однако полученные при помощи формул (1), (2) значения можно рассматривать как минимальный уровень шума. Итак, перейдем к схеме обработки цифрового сигнала.

3. Цифровая квадратурная амплитудная модуляция

Блок схема полностью цифрового передатчика на основе ДСМ представлена на рисунке 3. По аналогии с аналоговым квадратурным модулятором, входные отсчеты разбиваются на 2 канала: синфазный и квадратурный. По каждому из каналов выполняется интерполяция (IF) с увеличением частоты дискретизации в OSR раз, далее проходит через низкочастотный ДСМ (LPDSM) [5,6] в результате чего из входного многоразрядного сигнала  получаем одноразрядный выход.  При построении интерполяционного фильтра стоит учитывать, что скорость нарастания шума квантования составляет 20 дБ/декада для ДСМ 1 порядка, 40дБ/декада для ДСМ 2 порядка, соответственно высокочастотный сигнал будет утерян на фоне шумов. Выходы обоих каналов подаются на вход квадратурного модулятора (I/Q). Все описанные выше стадии выполняются в цифровой форме, соответственно никакой фазовой шум между каналами не возникает и ошибки квадратурная модуляция не вносит. В аналоговую часть входит двухуровневый DAC (нелинейные искажения исключены) и полосовой фильтр (BPF), необходимый для передачи по радиоканалу.

 

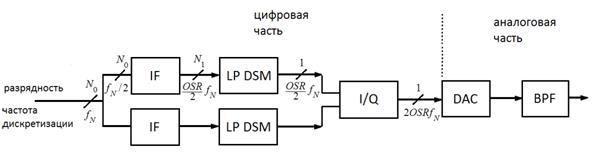
Рис. 3. Блок схема обработки сигнала

 

4.1. Полифазное представление

Использование ПЛИС для реализации высокочастотных схем позволяет изменить характеристики интерполяционных фильтров, перестроить или оптимизировать логику реализации ДСМ; частота тактирования схемы определяется уровнем логики, определяемым максимальным количеством комбинационных элементов на самом длинном пути. Для кристалла Kintex 7 (7 серия кристаллов Xilinx) максимальная частота тактирования элементарной логики составляет 470Мгц. Если такой частотой мы ограничим максимальную скорость генерации битового потока на выходе ДСМ, то максимальная выходная скорость составит 1880 Мбит/с, частота несущей 470МГц.

Полифазное разложение [7] позволяет распараллелить вычисления, таким образом увеличить скорость выходного потока, частоту несущей и частоту данных на входе, для ее выполнения рассмотрим некоторую передаточную функцию H(z) (КИХ или БИХ фильтр). От линейного представления можно перейти к матричному (см.  Рисунок 4).  - полифазные компоненты матрицы, получаемые из H(z):

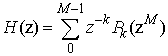                                                                                        (3)

 

До полифазного разложения вход представляет линейный поток данных I(n), после - преобразуется в многопоточное. Выход:

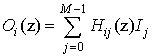                                                                                            (4)

 

 

 

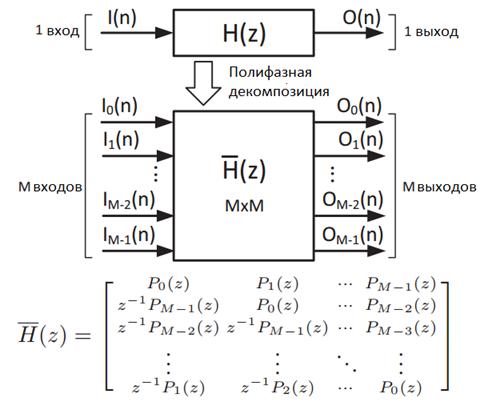
Рис. 4. Схема полифазного разложения

Полифазное представление позволяет увеличить скорость на входе ДСМ, переходя от линейной структуры,  для которой каждому такту соответствовало одно значение на выходе, к структуре, в которой в результате распараллеливания на каждый такт вырабатывается M значений. Однако использование полифазного представления увеличивает сложность комбинационной логики, как следствие, падает максимальная тактовая частота работы ДСМ.

4.2.Полифазное разложение ДСМ 1 порядка

Применим данный метод на ДСМ 1 порядка. В качестве функции для полифазного представления может рассматриваться как интегратор, так и элемент задержки (см. Рисунок 5).

 

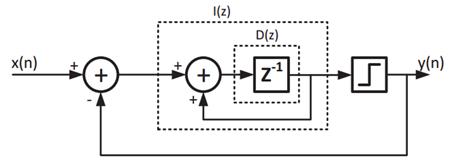
Рис. 5. Функции полифазного разложения ДСМ 1 порядка

 

Используем функции интегрирования для распараллеливания на 4 фазы. На основании формулы (3):

 

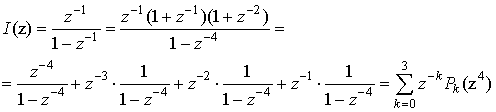                       (5)

 

Матрица:

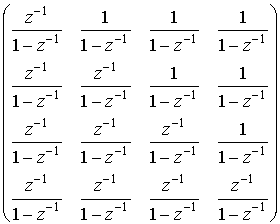                                                                 (6)

Выходной сигнал для каждой из фаз определяется суммой интеграторов и интеграторов с задержкой на линии. Такая система значительно сложнее в реализации относительно линейной, но теоретически может увеличить скорость обработки данных в 4 раза, однако из-за сложности реализации, ввиду высокого уровня комбинационной логики, максимальная тактовая частота значительно падает. Чтобы уменьшить уровень логики в качестве функции для разложения, стоит взять элемент задержки:

                                                                                                         (7)

Матрица :

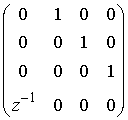                                                                                                (8)

Как результат: зависимость каждого входа только от одного выхода, cущественное снижения уровня комбинационной логики, что позволяет увеличить частоту тактирования схемы. На основе элементов матрицы полифазного представления построим схему для ДСМ 1 порядка (см. Рисунок 6).

 

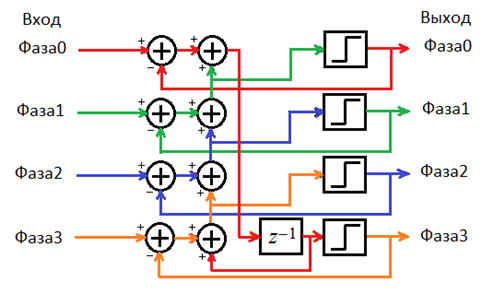
Рис. 6. Схема 4 фазового ДСМ 1 порядка

В данной схеме наличие элемента задержки только на выходе интегратора на фазе 0 означает, все операции суммирования выполняются в течение одного такта.  Добавление элементов задержки в схему для сдвига выхода на несколько тактов может привести к тому, что данные на выходе будут генерироваться раз в N тактов, где N – количество дополнительных элементов задержки. Однако снизить уровень логики и соответственно увеличить частоту тактирования можно, оптимизировав логику следующим образом.

4.3.Высокочастотная архитектура ДСМ 1 порядка

Рассмотрим цифровой ДСМ, предварительно изменив диапазон входных значений. Стандартно для ДСМ вход изменяется в диапазоне (-1;+1), тогда выход сумматора лежал в диапазоне (-2;+2). Изменим входной диапазон (0;1) (так как выход интерполятора знаковый, то необходимый диапазон достигается путем добавления константы, соответственно спектр не изменяется). На рисунке 7 представлены все переменные в цифровом формате. Операция вычитания выполняется в дополнительном коде, соответственно старший бит отвечает за знак, так как входное значение положительное первый бит 0. Разрядность на выходе сумматора совпадает со входом (с учетом знака), это стало возможным за счет того, что выход сумматора  лежит в диапазоне (-1;1). По обратной связи в соответствии с входным диапазоном возвращается либо 0, либо -1, что в дополнительном коде соответствует 100… В итоге получаем

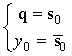                                                                                                           (9)     

Отсюда следует, что следующее значение сумматора:

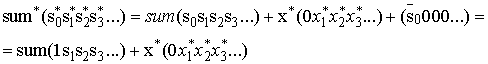                        (10)

В независимости от предыдущего значения, на выходе сумматора sum при следующей операции суммирования в старшем разряде всегда 1 с предыдущей операции (10).

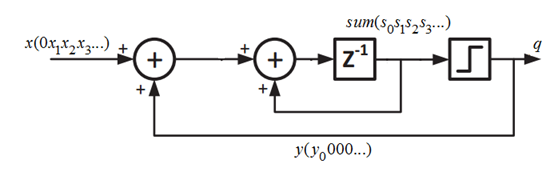
Рис. 7. Битовое представление ДСМ 1 порядка

В результате схему полифазного представления можно преобразовать в следующий вид (см. Рисунок 8). Преимущество реализации данной схемы заключается в полном отсутствии обратной связи в явном виде, как следствие, уровень логики схемы не увеличивается с увеличением количества фаз. Максимально на пути распространения сигнала выполняется 2 операции суммирования, максимальная частота тактирования будет одинакова как для 4 фаз, так и для 8 и 16, если необходимо.

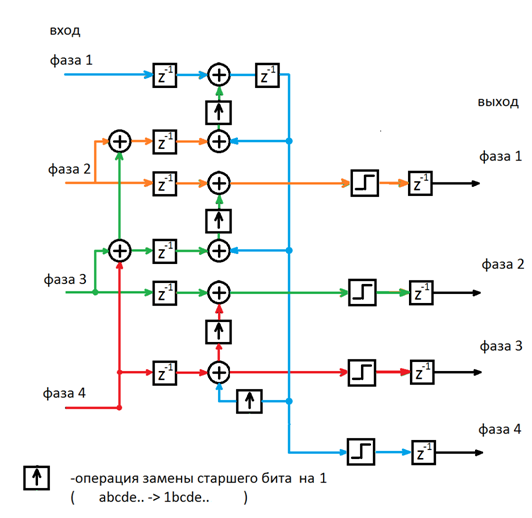
Рис. 8. Оптимизированная схема ДСМ 1 порядка

Для представленной на рисунках 6,8 логик была выполнена реализация на кристалле Kintex 7. В таблице 1 указаны результаты реализации полностью цифрового преобразователя для ДСМ 1 порядка, в правом столбце результат разводки для стандартной логики (см. Рисунок 6). Как следствие, уже для 4 фаз уровень логики 11, что снизило максимальную частоту тактирования до 194 МГц. Оптимизированная схема реализована для 8 фаз, уровень логики 5, что позволяет развести схему на более высокой частоте 316 МГц. Как указывалось ранее, при данной реализации вне зависимости от количество фаз уровень комбинационной логики не увеличивается (здесь используется именно 8 фаз, так как при большем количестве схему невозможно реализовать из-за ограничения скорости на выходе GTXмодуля, предельная скорость которого для Kintex 7 составляют 12 Гбит). Соответственно, подсчитанное ранее значение для шума квантования (1) для OSR = 128 указано таблице. Скорость потока данных определяется разделением битовой скорости с выхода ДСМ на OSR. Максимальная частота несущей определяется при выполнении квадратурной модуляции в цифровом виде без уменьшения символьной скорости за счет дополнительных отсчетов [3] (частота дискретизации на выходе полностью цифрового преобразователя в 4 раза превышает частоту Найквиста).

 

Таблица 1.

Тип архитектуры	высокочастотная	стандартная
Количество фаз	8	4
Коэффициент передискретизации (OSR)	128	128
Максимальная тактовая частота разводки схемы дельта-сигма модулятора 1 порядка	316МГц	194МГц
Уровень комбинационной логики	5	11
Максимальная битовая скорость на выходе(OSR=128)	10.1Гбит	3.1Гбит
Максимальная символьная скорость	39.5МБод	12.13MБод
Соотношение сигнал/шум квантования (SQNR)	60дБ	60дБ
Максимальная частота несущей	2.525ГГц	775МГц

 

5.1.Полифазное разложение ДСМ 2 порядка

Воспользуемся полифазным представлением для распараллеливания вычислений ДСМ 2 порядка на 4 фазы. Так же как для ДСМ 1 порядка, в качестве функции возьмем элемент задержки (7), стоящий на выходе схемы. Выполнив разложение, получим следующую архитектуру построения ДСМ 2 порядка (см. Рисунок 9).

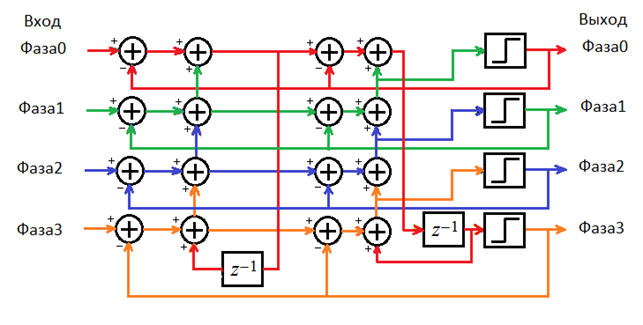
Рис. 9. Полифазная схема ДСМ 2 порядка

 

Теперь наличие обратной связи имеет в 2 раза больший эффект (для каждой фазы присутствует в цепи 2-ух сумматоров); добавление нового интегратора на входе привело к размножению сумматора на каждую из фаз. Как следствие, попытка напрямую реализовать подобную структуру схемы приведет к существенному снижению частоты тактирования (подробные характеристики описаны в таблице ниже), не говоря об использовании 8 фаз.

Вторым существенным отличием является устойчивость ДСМ 2 порядка. Вне зависимости от уровня ограничений на вход, всегда найдутся колебания, приводящие к бесконечному возрастанию значения выходного сумматора схемы. Для этого необходима синхронизация частоты колебаний входа с внутренней частотой схемы, несмотря на это, для выходного сумматора можно ввести следующее ограничение (подробное описание в [4]):

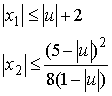                                                                                             (9)

- выходы 1-го и 2-го сумматора соответственно (см. Рисунок 10).

 

5.2.Высокочастотная архитектура ДСМ 1 порядка

По аналогии с проделанным ранее, рассмотрим цифровой ДСМ 2 порядка. Вычисление также выполняются в дополнительном коде, входной диапазон установим [0;0.5], возвращаемое по обратной связи значение либо 0, либо -1 (см. Рисунок 10).

Так как для входа ограничение , из условия (9) следует, что количество дополнительных бит должно быть N=3, чтобы не происходило переполнение.  Следовательно, количество ненулевых бит, передающихся по обратной связи, равно 4(1111000… или 0000…).

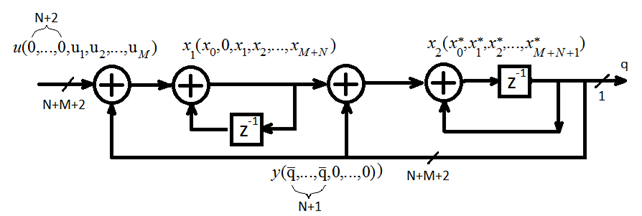
Рис. 10. Битовое представление ДСМ 2 порядка

Предлагается модифицировать полифазную схему следующим образом. Наличие цепи обратной связи приводит к тому, что каждая следующая фаза зависит от результатов предыдущих, за исключением ДСМ 1 порядка, результат модификаций которого позволил полностью исключить обратную связь (см.  Рисунок 7). В данном модулятора такое невозможно сделать, однако для каждой фазы можно провести расчеты заранее, вычислив значения выходного сумматора для каждого результата обратной связи (см. Рисунок 11). Представленная схема для каждой фазы вычисляет выходы внутренних сумматоров параллельно, вне зависимости от результата обратной связи. Выходные сумматоры выполняет суммирование вычисленного значения с выходом мультиплексора.

 

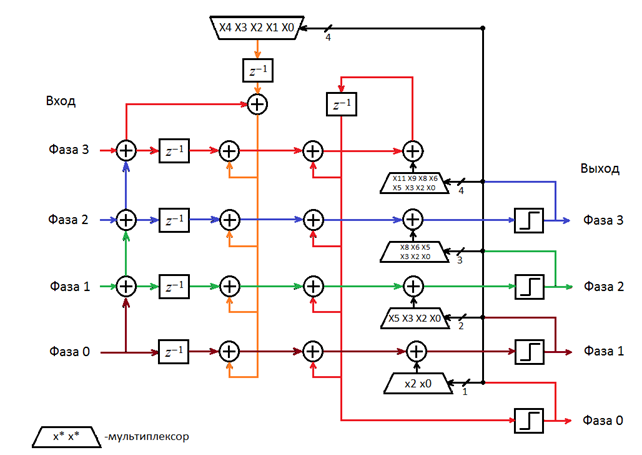
Рис. 11. Оптимизированная схема ДСМ 2 порядка

Выход мультиплексора задается управляющим сигналом, определяемым обратными связями предыдущих фаз (с увеличением фазы разрядность управляющего сигнала возрастает). Коэффициенты внутри мультиплексора определяют множитель для значения передаваемого по обратной связи значения: 1111000….(см. Рисунок  10). Такая реализация позволила прежде всего часть вычислений на входе перенести в последовательную логику, что снизило нагрузку на вычисления комбинационной логики (наличие дополнительных элементов задержки на входе), и частично распараллелить вычисления, сдвинув влияние обратной связи только на конечный результат по каждой из фаз.

Результаты реализации полностью цифрового преобразователя на основе ДСМ 2 порядка для микросхемы Kintex 7 указаны в Таблице 2.

 

Таблица 2.

Тип архитектуры	высокочастотная		стандартная
Количество фаз	4	8	4
Коэффициент передискретизации(OSR)	64	128	64
Максимальная тактовая частота разводки схемы дельта-сигма модулятора 2 порядка	223МГц	134МГц	119МГц
Уровень комбинационной логики	8	14	14
Максимальная битовая скорость на выходе(для соответствующих OSR)	3.568Гбит	4.288Гбит	1.904Гбит
Максимальная символьная скорость	27.875Мбод	16.75Мбод	14.87Мбод
Соотношение сигнал/шум квантования(SQNR)	79дБ	94дБ	79дБ
Максимальная частота несущей	892МГц	1.072ГГц	476МГц

 

Вывод

Проведено исследование архитектуры низкочастотных ДСМ модуляторов 1 и 2 порядка для реализации полностью цифрового передатчика, способного работать на несущих частотах в единицах ГГц при соотношении сигнал/шум выше 70дБ.

В ходе работы выполнено полифазное разложение ДСМ 1 и 2 порядка, оптимизация логики позволила реализовать высокочастотную архитектуру ДСМ, которая обладает следующими преимуществами по сравнению с обычной реализацией: для 1 порядка – отсутствие обратной связи в явном виде, как следствие возможность увеличения количество фаз без уменьшения частоты тактирования схемы, для 2 порядка – уменьшение сложности комбинационной логики, увеличение тактовой частоты за счет дополнительной параллелизации вычислений.

В результате реализации на микросхеме Kintex 7 фирмы Xilinx получены следующие характеристики:

для ДСМ 1 порядка: максимальная тактовая частота для стандартной схемы  4 фазового представления - 194 МГц (уровень логики 11); высокочастотная схема для 8 фаз - 316Мгц (уровень логики 5);

для ДСМ 2 порядка: стандартная схема для 4 фаз - 119МГц; высокочастотная для 4 фаз - 223МГц, для 8 фаз – 134МГц.

 

Литература

1. M.Nielsen and T.Larsen. A transmitter architecture based on delta-sigma modulation and switch-mode power amplification // IEEE Trans. Circuits Syst. II: Exp. Briefs, vol. 54, no. 8, pp. 735–739, Aug. 2007.

2. P. Wagh, P. Midya, P. Rakers, J. Caldwell, and T. Schooler. An all digital niversal RF transmitter // in Proc. IEEE Custom Integr. Circuits
Conf., Oct. 2004, pp. 549–552.

3. M. Helaoui, S. Hatami, R. Negra, F. Ghannouchi. A Novel Architecture of Delta-Sigma Modulator Enabling All-Digital Multiband Multistandard RF Transmitters Design //  IEEE Trans. ON Circuits Syst. II: Exp. Briefs, vol. 55, no. 11, pp.1129-33, nov. 2008.

4. R. Schreier, G.C. Temes. Understanding Delta-Sigma Data Converters // Wiley-IEEE Press, pp. 36-39, Nov. 2004

5. M. A. Morin. A 1.6 Gb/s delta-sigma modulator with integrated wideband mixer for RF applications // in Proc. Bipolar/BiCMOS Circuits Technol. Meeting, pp.148–151,Sep.1998.
6. A. Jerng and C. G. Sodini. A wideband delta-sigma digital-RF modulator for high data rate transmitters//  IEEE J. Solid-State Circuits, vol.42, no. 8, pp. 1710–1722, Aug. 2007

7. P.P. Vaidyanathan. Multirate digital filters, filter banks, polyphase networks, and applications: a tutorial // Proceedings of the IEEE, VOL. 78, NO. 1, pp. 56-93, Jan. 1990

 

References

1. Nielsen M. and Larsen T. A transmitter architecture based on delta-sigma modulation and switch-mode power amplification. IEEE Trans. Circuits Syst. II: Exp. Briefs, vol. 54, no. 8, pp. 735–739, Aug. 2007.

2. Wagh  P., Midya  P., Rakers  P., Caldwell J., Schooler  T. An all digital universal RF transmitter. in Proc. IEEE Custom Integr. Circuits
Conf., Oct. 2004, pp. 549–552.

3. Helaoui M., Hatami S., Negra R., Ghannouchi F. A Novel Architecture of Delta-Sigma Modulator Enabling All-Digital Multiband Multistandard RF Transmitters Design.  IEEE Trans. ON Circuits Syst. II: Exp. Briefs, vol. 55, no. 11, pp.1129-33, nov. 2008.

4. Schreier R., Temes G.C. Understanding Delta-Sigma Data Converters. Wiley-IEEE Press, pp. 36-39, Nov. 2004

5. Morin M. A. A 1.6 Gb/s delta-sigma modulator with integrated wideband mixer for RF applications. in Proc. Bipolar/BiCMOS Circuits Technol. Meeting, pp.148–151,Sep.1998.
6. Jerng A. and Sodini C. G. A wideband delta-sigma digital-RF modulator for high data rate transmitters. IEEE J. Solid-State Circuits, vol.42, no. 8, pp. 1710–1722, Aug. 2007

7. Vaidyanathan P.P. Multirate digital filters, filter banks, polyphase networks, and applications: a tutorial. Proceedings of the IEEE, VOL. 78, NO. 1, pp. 56-93, Jan. 1990