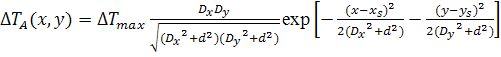Использование априорной информации в решении динамических обратных задач акустотермометрии
А. А. Аносов 1, 2
1 Институт радиотехники и электроники им. В.А. Котельникова РАН
2 Первый Московский Государственный Медицинский Университет им. И.М. Сеченова
Статья поступила в редакцию 1 июня 2016 г.
Аннотация. Представлены результаты экспериментального восстановления температурных распределений в модельных объектах и в теле человека методом акустотермометрии. В рассмотренных алгоритмах использована априорная информация о виде распределения температуры. Восстанавливается глубинная температура, меняющаяся во времени, поэтому время одного измерения ограничено 10-ю секундами. Точность определения геометрических (около 1–2 мм) и температурных (около 0.5–1 К) параметров распределений приемлема для медицинских приложений метода. Результаты были представлены на IX Всероссийской конференции «Радиолокация и радиосвязь».
Ключевые слова: тепловое акустическое излучение, акустотермометрия, априорная информация, обратные задачи.
Abstract. Experimental results of temperature distribution reconstruction in the model plasticine objects and the human body were obtained with the help of passive acoustic thermometry. The objects under the study were heated and cooled and could be moved relatively receiving array. The array consisted of 14 probes based on broadband 1.6–2.5 MHz disc-shaped ultrasonic detectors with an 8 mm aperture. The probe threshold sensitivity was 0.3 K for the integration time in 10 s. The portable computer thermograph was used to measure the surface temperature of the human body. The temperature was measured in five experiments with the cooled fixed cylinder and forefinger (1), shifted heated cylinder (2), heated fixed parallelepiped (3), cooled the fixed parallelepiped and hand (4), heated fixed sphere (5). A priory information about the temperature distributions was used in reconstruction algorithms. Тhe temperature distributions were approximated by 1D, 2D, 3D Gaussians with time-varying parameters. The algorithms allowed to reconstruct four (in the 1–3 experiments) or five parameters (in the 5 experiment): the two or three spatial coordinates, size or two sizes and maximum temperature of heated region. The symmetrical distribution was reconstructed in the fourth experiment. In this case the only parameter was detected. The electronic journal format allows to demonstrate the time-varying temperature distributions with the help of an animation. The detection accuracy of the geometrical (about 1-2 mm) and temperature (about 0.5-1 K) parameters of the temperature distributions is acceptable for medical applications. The results were presented at Conference "Radars and Communications 9".
Key words: thermal acoustic radiation, acoustic thermometry, a priory information, inverse problems.
Введение
Задача неинвазивных безболезненных измерений глубинной температуры тела человека актуальна для медицинской практики [1]. В настоящее время разрабатываются различные методы ее решения [2-4]. Все они имеют свои преимущества и недостатки. В частности, потенциально, использование для этой цели магниторезонансной томографии позволит получать пространственное распределение глубинной температуры во всем теле [5]. Однако в конкретных случаях использование столь дорогостоящего оборудования неэффективно. Рассмотрим задачу мониторинга температуры при локальной гипертермии участка тела человека [6]. Врач осуществляет нагрев (например, с помощью лазерного излучения, передаваемого вглубь организма по световоду) и нуждается в контроле температуры (см. рис. 1). Ему нужен достаточно простой и удобный способ измерения температуры, отвечающий по точности медицинским требованиям. Меняющееся температурное распределение может иметь достаточно сложный вид, но для практических целей врачу достаточно знать два параметра: максимальную температуру и размер нагретой области. Если неизвестно положение нагретой области, то восстанавливать надо еще три параметра: координаты центра нагретой области. Врачу необходимо знать, как меняются искомые параметры во времени, чтобы вовремя завершить процедуру: недогрев не даст терапевтического эффекта, перегрев опасен для окружающих здоровых тканей пациента.
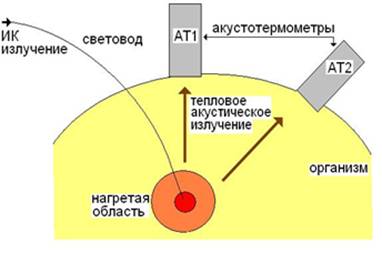
Рис. 1. Схема акустотермометрии при глубинной лазерной гипертермии.
Для измерений глубинной температуры предлагается использовать пассивную акустическую термометрию [7-9], основанную на регистрации собственного теплового акустического излучения организма человека в мегагерцовом диапазоне [10-13]. Акустотермометрия востребована при измерениях локальных изменений температуры (в объеме нескольких кубических сантиметров) с использованием небольшого количества (около десяти) датчиков [14-16]. При таких ограничениях задача восстановления температуры с надлежащей точностью является некорректной и для ее решения необходимо использовать априорную информацию [17-21]. При этом, в акустической термометрии следует учитывать аппаратную функцию приемного датчика, потому что ее характерный размер может быть близок к размеру нагретой области [22-24]. В литературе предлагаются и альтернативные способы восстановления температурного распределения по данным корреляционного [25-30] и фокусированного [31-33] приема, многочастотного зондирования [34-36] теплового акустического излучения.
Предлагаемые алгоритмы восстановления температуры проверены в экспериментах на модельных объектах, а также при изменении температуры участков тела человека. Формат электронного журнала позволяет наглядно показать меняющие во времени температурные распределения с помощью анимации.
Экспериментальная установка
В экспериментах использовался многоканальный акустотермограф (рис. 2), разработанный в ИПФ РАН группой А.Д. Мансфельда [37-39]: полоса пропускания 1.6-2.5 МГц, пороговая чувствительность при времени интегрирования 10 с – 0.3 К, диаметр датчиков 8 мм. Принимаемые акустические сигналы преобразовывались в электрические, которые усиливались и проходили через квадратичный детектор. С выхода акустотермографа сигналы подавались на 14-ти разрядный многоканальный АЦП Е14-140 (ЗАО «L-Card») с частотой дискретизации 1 кГц на один канал и поступали в компьютер. Разработанная аспирантом ИРЭ им. В.А. Котельникова РАН А.С. Казанским [40] программа проводила дальнейшее усреднение и оптимальное представление данных.
Рис. 2. Многоканальный акустотермограф, разработанный в ИПФ РАН.
Для измерений поверхностной температуры участков тела человека использовался портативный компьютерный термограф ИРТИС-2000 (ООО "Иртис", Москва, Россия) с чувствительностью к перепаду температур (на уровне 30°С) 0.05 К, регистрировавший тепловое электромагнитное излучение в диапазоне 3-5 мкм [41].
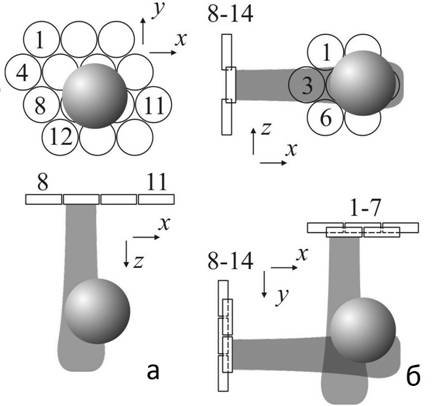
Рис. 3. Геометрия экспериментов. В качестве исследуемого тела представлен пластилиновый шар, температура которого менялась.
В акустических измерениях использовались две схемы расположения датчиков: двумерная решетка (рис. 3а) размером 45 ´ 34 мм из четырнадцати датчиков и две расположенные перпендикулярно решетки (рис. 3б) размером 30 ´ 26 мм из семи датчиков каждая [42]. Решетки были расположены в аквариуме, заполненном водой. Измерялось тепловое акустическое излучение модельных пластилиновых объектов различной формы, которые помещали в аквариум, а также излучение, идущее из тела человека: из кисти и из пальца, опущенных в воду. Длительность одного измерения составляла 10 с.
Аппаратная функция акустотермометрического датчика
Изначальным
требованием к приемнику теплового акустического излучения является его широкополосность, т.к. пороговая
чувствительность прибора зависит от ширины полосы пропускания [8]. В работе [43]
была исследована аппаратная функция широкополосного акустотермометрического
датчика. В частности, было
показано, что для использованных в эксперименте круглых датчиков Æ 8 мм дифракционное расширение аппаратной функции начинается с
расстояния в 20 мм от датчика. При этом поперечный размер (по уровню 0.5 от максимального) w (z) аппаратной функции определяется
выражением 
, где l
– длина волны, соответствующая средней частоте полосы пропускания датчика, z – расстояние по акустической оси
датчика, а – радиус датчика. Для используемых в эксперименте датчиков (а
= 4 мм, l = 0.73 мм) поперечный размер аппаратной функции датчика (в диапазоне z = [20, 100] мм) определяется (с точностью до 0.1 мм) выражением
Аппаратная функция приближалась гауссианом, поперечный размер которого менялся вдоль акустической оси (оси z) и определялся (по уровню 0.5 от максимального) выражением (1). Аппаратная функция i-го датчика, центр которого расположен в точке (xri, yri, 0), а акустическая ось направлена вдоль оси z, определялась выражением:
где
–
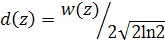(2б)
характерный
поперечный размер (меняющийся из-за дифракционной расходимости) аппаратной
функции на расстоянии z от приемника. Аппаратная
функция нормирована так, что интеграл по площади от выражения (2а) равен
единице при любом z: 
.
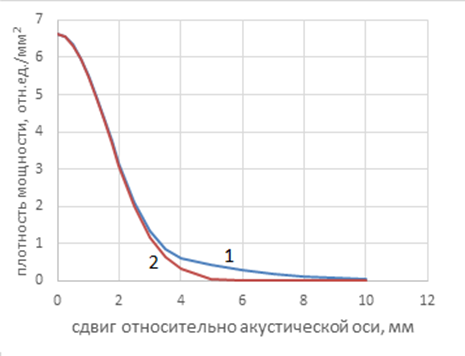
Рис. 4. Рассчитанная в работе [43] аппаратная функция на расстоянии 50 мм от датчика (1) и ее приближение гауссианом (2).
Преимуществом такого приближения является простота деконволюции измеренного сигнала: восстановления из распределения акустояркостной температуры распределения термодинамической температуры. Недостатком является то, что реальная аппаратная функция при увеличении сдвига от акустической оси не снижается так быстро, как спадает гауссиан. На рис. 4 видна систематическая ошибка приближения в диапазоне отклонений от акустической оси от 3 до 8 мм.
Акустояркостная температура
Измеряемый акустотермометрическим датчиком сигнал – инкремент DTA акустояркостной температуры TA – связан с инкрементом DT термодинамической температуры T выражением [44]:
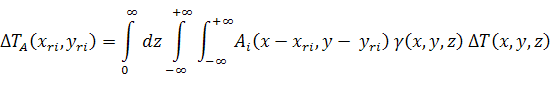
, (3)
где g – коэффициент поглощения ультразвука по интенсивности, DTA = TA – T0, DT = T – T0, T0 – температура окружающей среды, в нашем случае – температура аквариума.
Целесообразно рассмотреть частные случаи, когда можно упростить выражение (3). Во-первых, если температура исследуемого объекта постоянна T = T0, то его акустояркостная температура равна термодинамической TA = T0. Указанное свойство следует из определения акустояркостной температуры [44]: это температура акустического черного тела, испускающего тепловое излучение такой же интенсивности, как и исследуемый объект. На основе этого определения и получено выражение (3).
Часто рассматривается
плоскослоистая среда [7, 10, 20], в которой зависимости температуры и
коэффициента поглощения меняются только вдоль оси z,
направленной вглубь объекта: 
и 
. В этом случае акустояркостная
температура не зависит от аппаратной функции:
Если при этом положить коэффициент поглощения постоянным, то инкремент акустояркостной температуры равен
. (4б)
Если рассмотреть тела, обладающие большим поглощением (например, пластилин: коэффициент поглощения на частоте 2 МГц при температуре 20°С составляет 0.41 мм-1 [20]), находящиеся в практически непоглощающей среде (например, в воде: коэффициент поглощения на частоте 2 МГц при температуре 20°С составляет 2×10-4 мм-1 [45]), то выражение (3) можно упростить [38]:
Здесь 
– распределение температуры на некоторой глубине z.
Математические модели: использование априорной информации
Модель 1. В экспериментах 1 и 2 использовались протяженные вдоль оси y (расположение оси y см. рис. 3а) пластилиновые цилиндры. При этом, согласно условиям эксперимента, считалось, что температура не меняется вдоль оси y. Искомая проекция инкремента температурного распределения DТ на плоскость xy в цилиндре задавалась одномерным гауссианом:
где DTmax – максимальная температура, xs (y) – координата оси цилиндра, Dx – характерный размер (вдоль оси x) нагретой области. Введение зависимости для координаты оси цилиндра связано с тем, что исследуемые протяженные цилиндры могли располагаться не строго вертикально, а с небольшим наклоном. Поэтому для координаты xs использовали линейную зависимость
xs = ay + b, (7а)
которую характеризовали углом j наклона цилиндра
. (7б)
В этом случае, согласно выражению (5), измеряемая i-м (i = 1, …, 14) датчиком величина (инкремент акустояркостной температуры DTAi) является результатом свертки аппаратной функции (2) приемника и искомого температурного распределения (6):
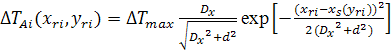, (8а)
где величина d определяется по известному расстоянию z между решеткой датчиков и осью цилиндра с помощью выражений (1) и (2б).
Выражение (8а) определяет инкремент акустояркостной
температуры, измеренный i-м
датчиком, центр которого имеет координаты 
. Можно расширить выражение (8а) на всю плоскость x, y и получить распределение инкремента акустояркостной
температуры в этой плоскости:
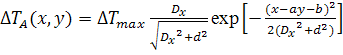. (8б)
Отметим, что распределение (8б) акустояркостной температуры ниже и шире
распределения (6) термодинамической температуры, но интегралы по x от обоих выражений равны 
.
Выражения (8а) и (8б) содержат четыре искомых
параметра, которые надо найти: 
, 
, a и b. Алгоритм их определения состоял из двух этапов,
аналогично методу, представленному в работе [42]. Сначала рассчитывались
параметры a и b. Для этого путем интерполяции измеренных инкрементов
акустояркостной температуры строилась карта распределения акустояркостной
температуры (рис. 5а). Затем для каждого значения y (шаг по оси y составлял 1 мм) определялась координата xs максимума акустояркостной
температуры (маркеры на рис. 5а). Полученный набор xs аппроксимировали прямой, тем самым
получая искомые параметры a
и b. На втором этапе построенная карта аппроксимировалась
выражением (8б), где параметры a и b уже были определены. Эта
аппроксимация позволяла рассчитать недостающие параметры и (аппроксимированная функция показана на рис. 5б). Отметим, что можно
было искать четыре параметра распределения (используя четырнадцать
экспериментальных данных) одновременно, не разбивая алгоритм на два этапа.
Однако в этом случае ошибка восстановления параметров была существенно выше.
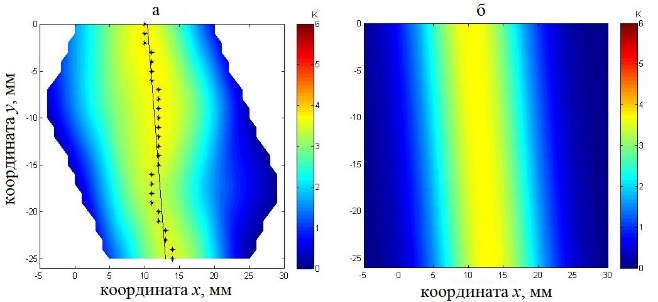
Рис. 5. Карта распределения акустояркостной температуры (а). Маркеры – координаты максимумов акустояркостной температуры при разных значениях координаты y. Линия – аппроксимация оси цилиндра. Распределение акустояркостной температуры (б), аппроксимированное гауссианом (8б).
В модели использовалась априорная информация о форме исследуемого объекта (протяженный цилиндр) и характере температурного распределения (температура не менялась вдоль оси цилиндра). Это дало возможность задать температурное распределение в форме гауссиана (6). Информация о том, что цилиндр может быть отклонен от вертикального положения, была использована, чтобы ограничить выбор положений центра нагретой области. Информация о поглощении в исследуемой среде (большое поглощение в пластилиновом объекте и малое в окружающей воде) позволила задать распределение акустояркостной температуры с помощью выражения (8б), и получить однозначную связь между измеряемыми и восстанавливаемыми величинами.
Модель 2. В эксперименте 3 восстанавливалась 2D проекция температурного распределения в нагретых пластилиновых объектах, имевших разные размеры по осям x и y. В этом случае искомая проекция температурного распределения DТ на плоскость xy также задавалась гауссианом:
где по сравнению с выражением (6) добавлялся параметр
Dy –
характерный размер нагретой области вдоль оси y.
Параметры xs и ys определяли координаты центра нагретой области. Параметры DTmax
и Dx определялись так же, как и в
выражении (6). Наличие сильно поглощающего объекта, находящегося в слабо-поглощающей
среде, позволяло использовать для расчета акустояркостной температуры выражение
(5). В этом случае измеряемая величина (инкремент акустояркостной температуры DTAi)
является результатом свертки аппаратной функции (2) и искомого температурного
распределения (9). Эту функцию, изначально заданную в точках с координатами 
, можно расширить на всю плоскость xy и получить распределение инкремента акустояркостной
температуры, заданное на плоскости xy:
Распределение (10) акустояркостной температуры ниже и шире распределения
(9) для термодинамической температуры, но двумерные интегралы по x и по y от обоих выражений равны 
.
Таким образом,
речь идет о восстановлении пяти параметров. Расчеты показали, что при
одновременном восстановлении всех параметров возникают неприемлемые погрешности.
Поэтому использовался подход, описанный выше: алгоритм восстановления был
разбит на два этапа. Сначала определялись координаты центра нагретой области,
которые совпадают с координатами максимума распределения акустояркостной
температуры. Для этого путем интерполяции измеренных инкрементов
акустояркостной температуры строилась карта акустояркостной температуры (рис.
6а) и находился максимум распределения (маркер на рис. 6а). Вторым шагом было одновременное
определение остальных трех параметров распределения: максимальной температуры 
и размеров 
и 
нагретой
области. Для этого карта акустояркостной температуры (рис. 6а) аппроксимировалась
выражением (10), и получалось распределение температуры, представленное на рис.
6б.
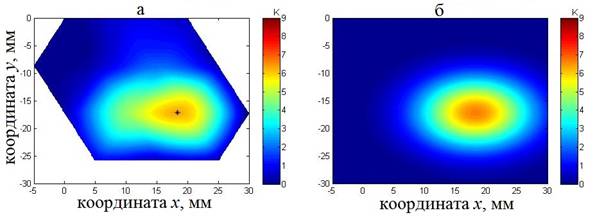
Рис. 6. Карта распределения акустояркостной температуры (а). Маркер – координата максимума акустояркостной температуры. Распределение акустояркостной температуры (б), аппроксимированное гауссианом (10).
В модели использовалась априорная информация о нагреве исследуемого объекта: использовался один источник нагрева, нагретое тело имело разные размеры по осям x и y. Это дало возможность задать температурное распределение в виде двумерного гауссиана (9). Как и в модели 1, информация о поглощении в исследуемой среде позволила задать акустояркостную температуру путем свертки аппаратной функции (2а) и гауссиана (9).
Модель 3. В эксперименте 5 с помощью двух приемных решеток (рис. 3б) восстанавливалось 3D температурное распределение в нагретом пластилиновом шаре. Искомое температурное распределение было задано центрально-симметричным гауссианом:
, (11)
где новые по сравнению с выражениями (6) и (9) параметры: zs – координата z центра, D – характерный размер нагретой области. Наличие двух плоских приемных решеток позволяло восстановить проекции температурного распределения (11) в плоскости xz
(12а)
и в плоскости yz
, (12б)
Благодаря чему решение 3D задачи свелось к решению двух 2D задач. Проекция (12а) была восстановлена с помощью первой приемной решетки, а проекция (12б) – с помощью второй приемной решетки. Описание решения 2D задачи представлено в модели 2 с одним упрощением: в модели 3 нагретая область считалась центрально-симметричной, и вместо двух характерных размеров необходимо было найти ее единственный характерный размер. Как и в модели 2, наличие сильно поглощающего объекта, находящегося в слабо-поглощающей среде, позволяло использовать для расчета акустояркостных температур выражение (5). Функции акустояркостных температур, заданные в точках, можно расширить на плоскость xz и на плоскость yz и получить распределения инкрементов акустояркостных температур:
, (13а)
. (13б)
Как и для модели 2, распределение (13а) (распределение (13б)) ниже и шире
проекции (12а) (проекции (12б)), но двумерные интегралы от обоих выражений
равны 
.
С помощью
измерений на одной приемной решетке восстанавливались четыре параметра. При
этом три параметра (, D и 
) независимо восстанавливались с помощью обеих решеток. Это давало
возможность сравнить результаты восстановления. Дополнительно с помощью первой
решетки восстанавливался параметр 
, а с помощью второй – параметр 
.
Использованная в модели 3 априорная информация аналогична информации, на которой была построена модель 2, с одним добавлением: было рассмотрено нагретое центрально-симметричное тело. Можно сказать, что вторая и третья модели на практике соответствуют локальному нагреву участка тела человека с использованием точечного источника, который находится внутри тела. Рассмотренная далее модель 4 предполагает гипер/гипотермию, когда источник нагрева/охлаждения находится вне организма.
Модель 4. В эксперименте 4 восстанавливались изменения температуры нагретой пластилиновой пластины и кисти руки (размеры обоих объектов превышали размеры решетки), которые помещались в аквариум с водой. Математическая модель восстановления выбиралась исходя из следующего соображения: она должна была соответствовать условиям эксперимента и для пластилина, и для кисти. Точки пересечения акустических осей датчиков с поверхностью исследуемых объектов имели координаты (x, y). По показаниям каждого датчика были рассчитаны температурные профили T(x, y, z) вдоль оси z, идущей от центра датчика перпендикулярно поверхности вглубь объекта (z = 0 и z = d - координаты поверхностей объекта, d - толщина объекта). Форма симметричного профиля определялась суммой двух экспонент:
где Tsurf - температура на поверхности объекта
(температура аквариума), одинаковая для всех x и y:
, Tdepth - характерный температурный параметр
распределения: для пластилина эта величина равна начальной температуре
нагретого относительно аквариума пластилина, для кисти – температуре теплового
ядра тела человека (Tdepth =37°С), a=a(x,y) - параметр, определяющий быстроту изменения температуры в пространстве.
Если a(x,y) d << 1,
то 
. Набор профилей позволил получить 3D температурное распределение.
Согласно результатам, представленным в работах [46, 47], профиль температуры в кисти несимметричен: в среднем максимум температуры сдвинут на 3 ± 2 мм в сторону ладони. Требование симметричности профиля обусловлено условиями эксперимента: использовалась только одна решетка датчиков, находящаяся напротив ладони. Это давало возможность восстанавливать только один параметр температурного профиля [48].
Инкремент акустояркостной температуры DTA определялся по формуле (4б), где интегрирование было ограничено толщиной пластилина (кисти). В данной модели предполагалось, что кисть акустически однородна, рассеянием ультразвука можно пренебречь [49] и считалось, что коэффициент поглощения не меняется. Несмотря на то, что в кисти мягкая мышечная ткань соседствует с костной, с кожей, сухожилиями и т.п., важно не само наличие неоднородностей, а их влияние на измеряемый сигнал. В работе [20] было исследовано влияние акустических неоднородностей на измеряемую акустояркостную температуру для модельного объекта (пластилина): результаты показали, что влияние неоднородностей несущественно. Это связано с тем, что акустояркостная температура является интегральной характеристикой исследуемой среды.
Результат интегрирования выражения (4б) представлялся в виде композиции элементарных функций и определялся единственным параметром a, т.е. являлся нелинейным алгебраическим уравнением относительно a, которое решалось численно.
Использованная в модели априорная информация связана с предположением о симметричности температурного профиля в исследуемых объектах. Это дало возможность использовать для определения профиля уравнение (14) с единственным восстанавливаемым параметром.
Экспериментальные результаты
С использованием модели 1 была восстановлена температура протяженных пластилиновых цилиндров, неподвижных и перемещающихся в пространстве, а также температура пальца, помещенного в воду.
Эксперимент 1: а) остывающий неподвижный цилиндр и б) указательный палец. Нагретый до температуры 41.8°С пластилиновый цилиндр длиной 170 мм (это в пять раз больше размера решетки) и диаметром 9 мм был помещен вертикально на расстоянии 44 мм от приемной решетки в аквариум с водой температурой 19.8°С. В течение 110 с датчики регистрировали тепловое излучение остывающего тела. Результаты измерений и восстановления температуры цилиндра показаны с помощью анимации (рис. 7 и 8). Результаты измерений представлены на рис. 7 слева, изменение инкрементов температуры представлено цветовой шкалой в Кельвинах: 0 – соответствует температуре 19.8°С. Карта инкрементов акустояркостных температур получена следующим образом: результаты измерений четырнадцати датчиков были помещены в точках, где расположены центры этих датчиков. По этим четырнадцати точкам была осуществлена линейная двумерная интерполяция. Аппроксимирующий распределение акустояркостной температуры гауссиан (8б) показан справа. На рис. 8 результат аппроксимации показан в виде вертикального цилиндра. Изменение положения цилиндра связано с ошибками в определении координаты его оси xs: в идеале цилиндр не должен двигаться. Изменения диаметра цилиндра связаны с ошибками восстановления размера нагретой области: в идеале диаметр цилиндра не должен меняться. Чем ярче цвет цилиндра, тем выше его температура.
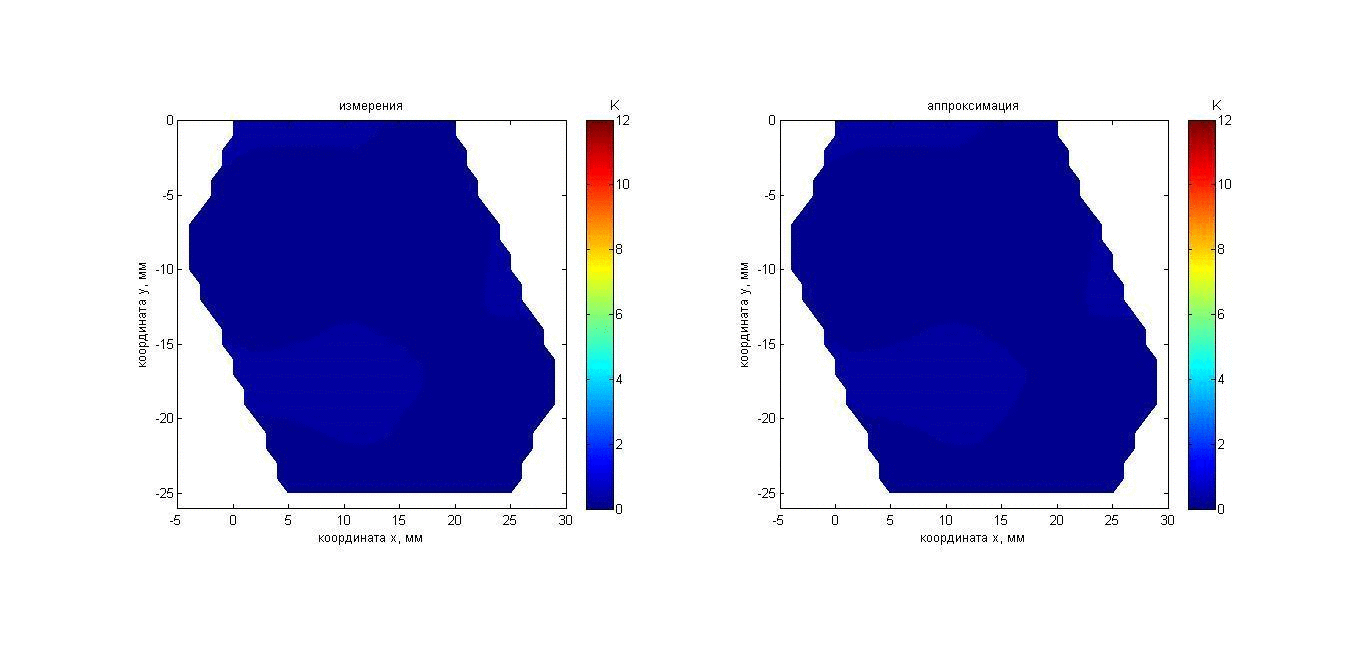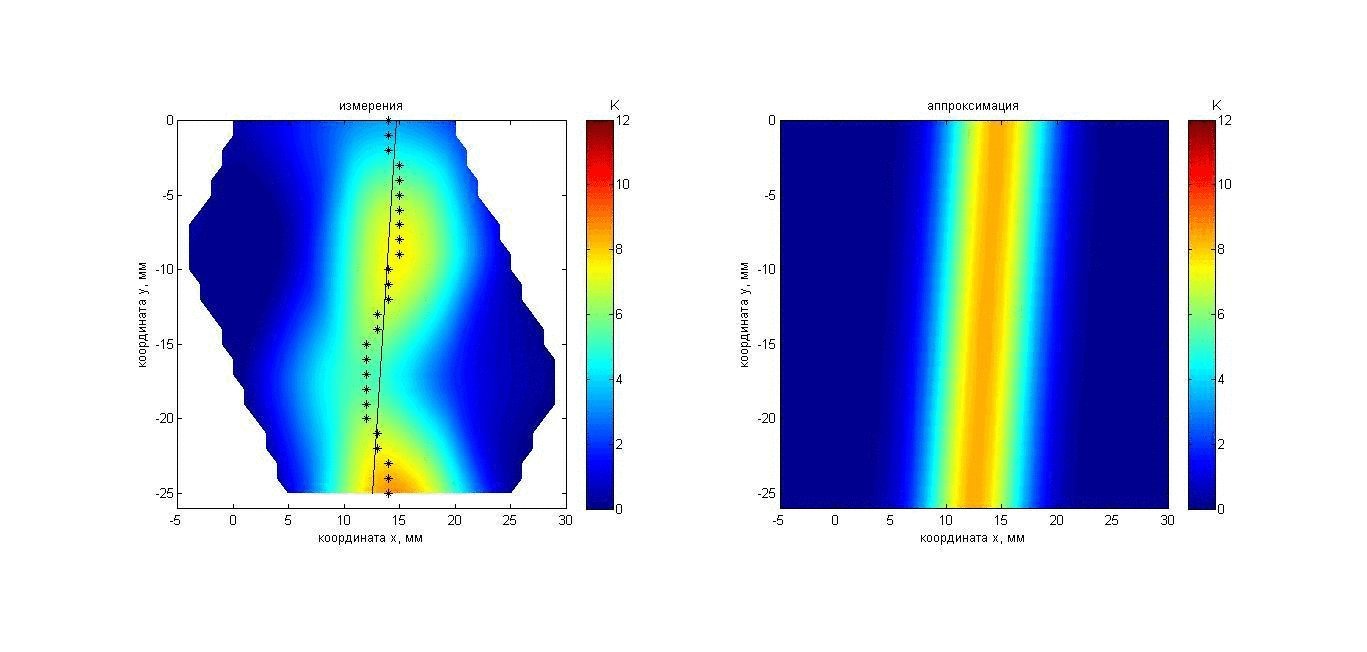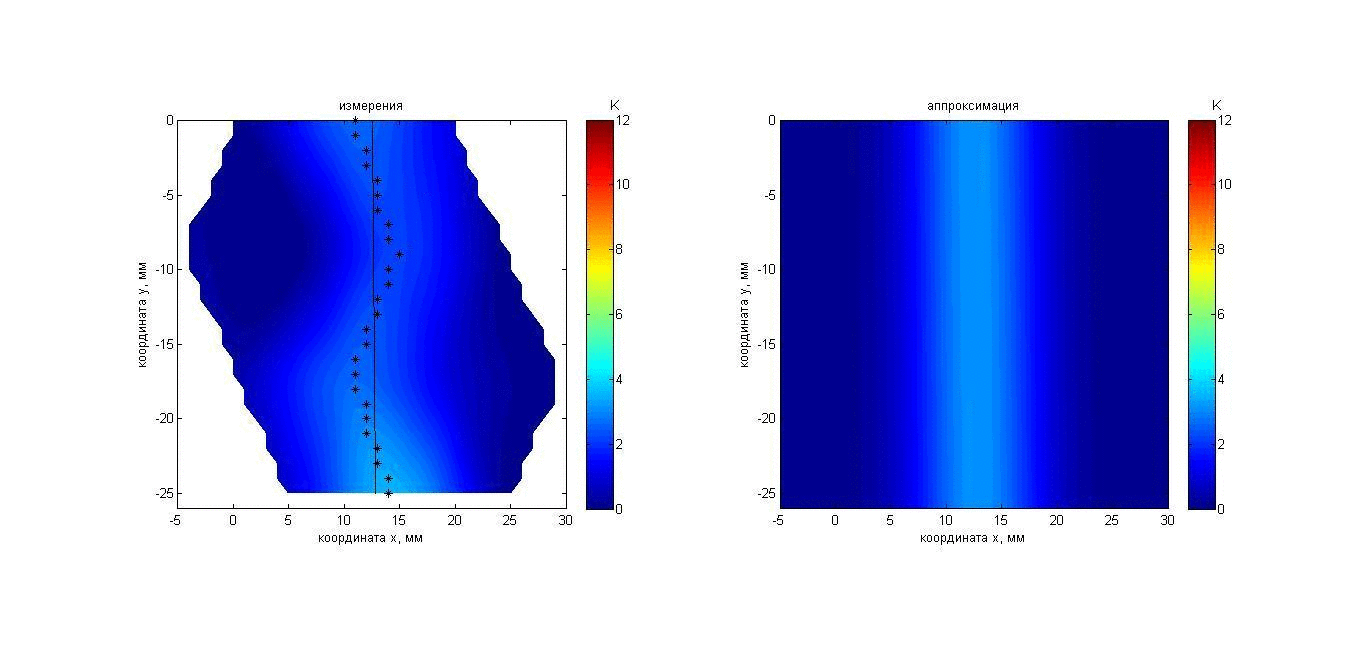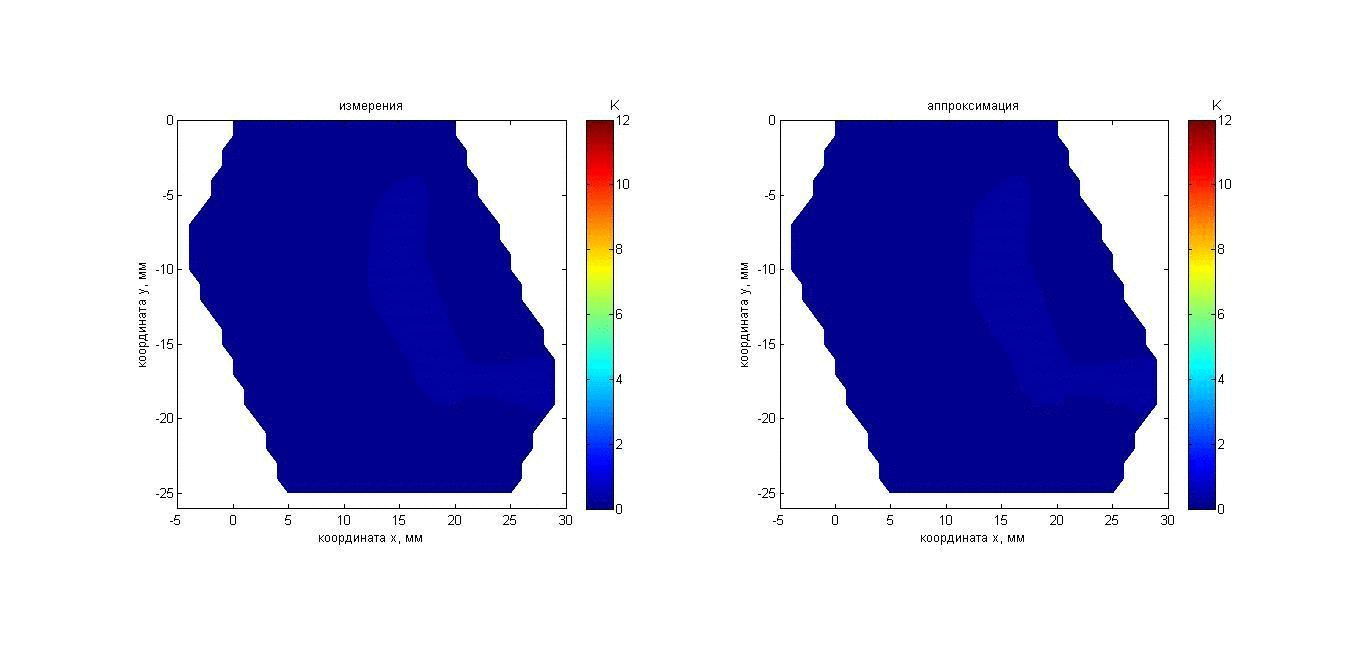
Рис. 7. Анимация меняющихся во времени распределения акустояркостной температуры неподвижного пластилинового цилиндра (слева) и аппроксимации этого распределения гауссианом (справа). Пояснения о маркерах и линии представлены на рис. 5. Здесь и далее – реальная длительность каждого кадра анимации равна времени интегрирования – 10 с.
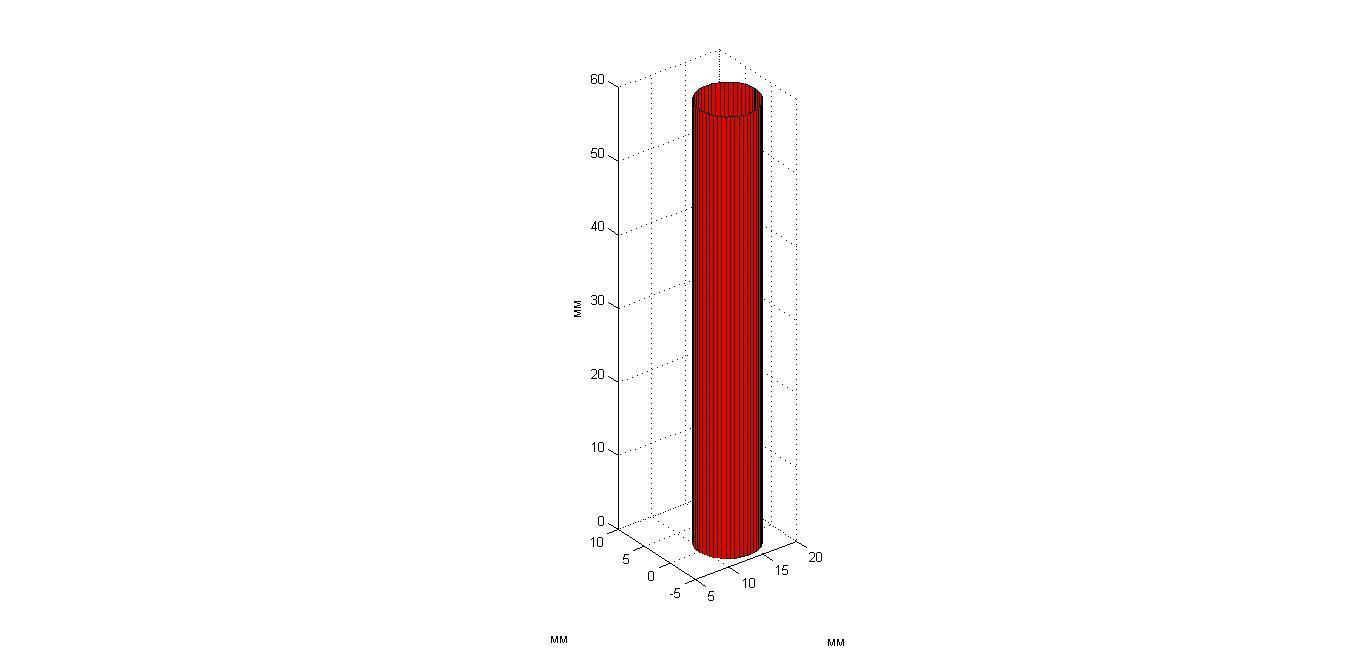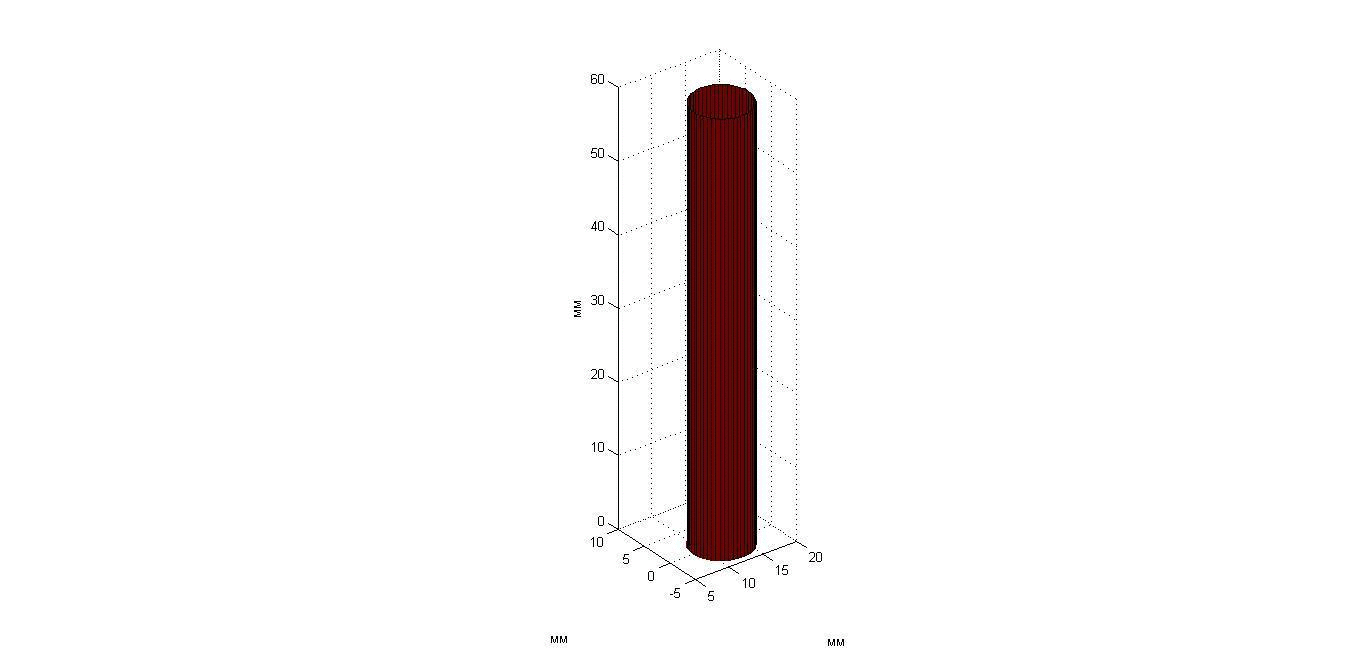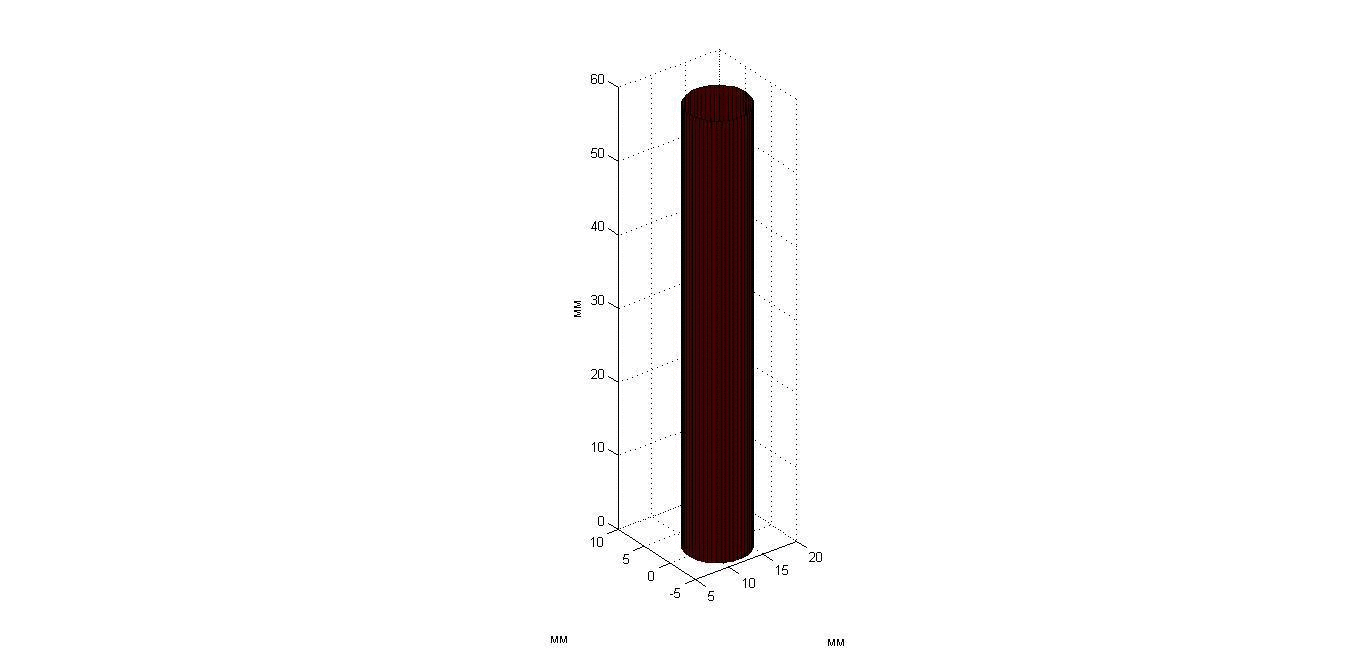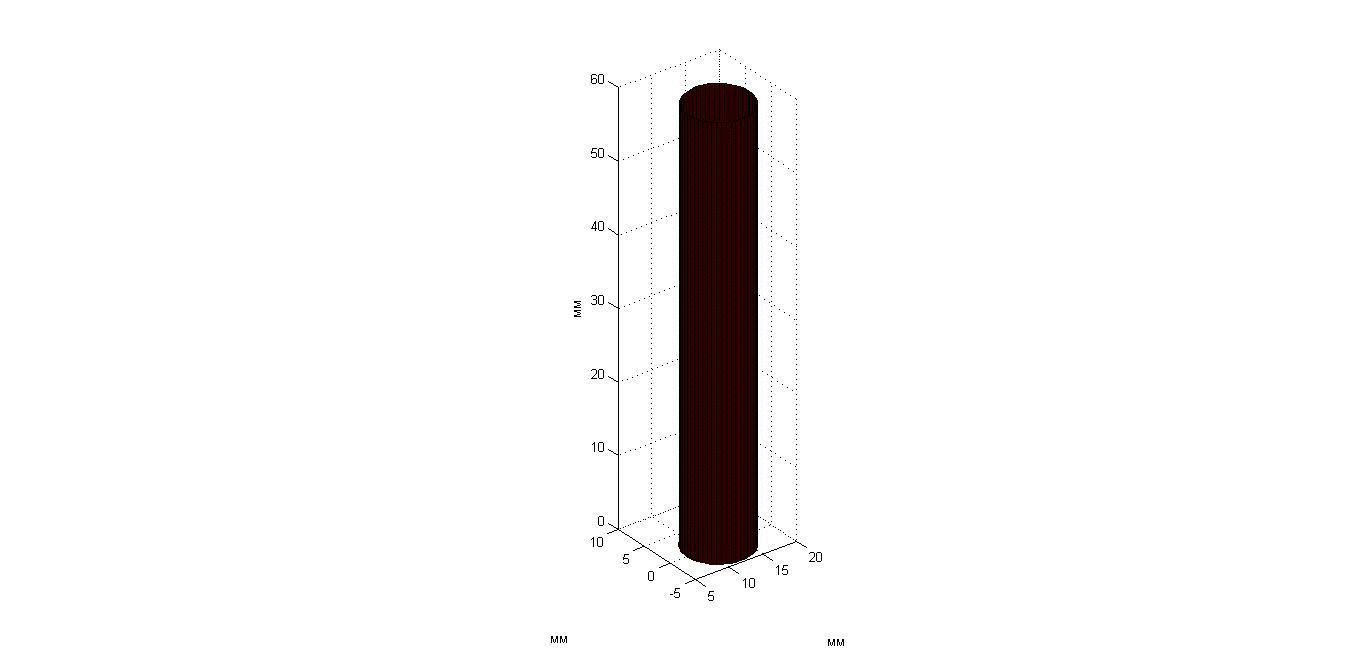
Рис. 8. Анимация меняющегося во времени температурного распределения неподвижного остывающего пластилинового цилиндра.
Изменения во времени восстановленных параметров показаны на рис. 9. В эксперименте исследовался неподвижный объект, у которого снижалась температура. Три параметра (координата оси, наклон, размер), определяющие положение объекта в пространстве, флуктуировали относительно средних значений.
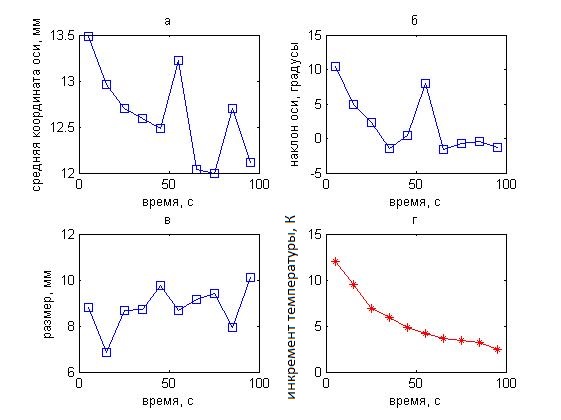
Рис. 9. Изменения восстанавливаемых параметров (а – средней координаты оси, б – наклона оси, в – диаметра, г – максимальной температуры цилиндра) температурного распределения в неподвижном остывающем пластилиновом цилиндре во времени.
Средняя координата оси цилиндра (рис. 9а) равна среднему значению xs координат максимумов акустояркостной
температуры (маркеры слева на рис. 7). Изменения этой величины показывают
ошибку восстановления центра нагретой области, которая составляет ± 0.5 мм.
Наклон оси 2 ± 4° (рис. 9б) показывает
ошибку, возникающую при установке исследуемого объекта. Вертикальность цилиндра
оценивалась визуально: среднее значение наклона (2°) показывает точность такой оценки. Ошибка (± 4°) в определении наклона показывает точность
использованного алгоритма восстановления. На рис. 9в показаны флуктуации в
определении границ размера (диаметра) нагретой области, где температура снижается
вдвое: 8.8 ± 0.9 мм. Этот размер практически совпадает с
диаметром цилиндра. Снижение со временем инкремента максимальной температуры 
объекта показано на рис. 9г. Отметим, что
наибольшее восстановленное значение инкремента максимальной температуры
составляет 12 К, в то время как соответствующая исходная разница в
температурах тела и аквариума составляла 22 К. Ошибка связана с тем, что
восстанавливать максимальную температуру «толстого» (по оси z, рис. 3а) объекта с большим поглощением, используя
выражение (5), не вполне корректно. Из такого объекта (в виду большого
поглощения) излучение выходит (и достигает приемника) из приповерхностных
областей, где температура приближена к температуре окружающей воды.
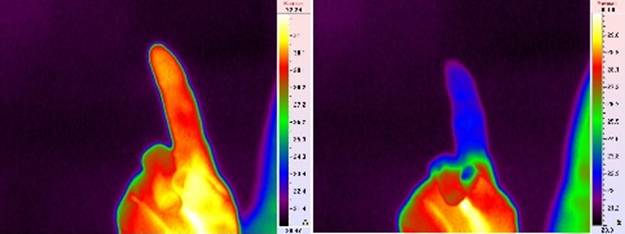
Рис. 10. Поверхностная температура пальца, измеренная термографом
ИРТИС-2000,
до помещения пальца в воду и после того, как палец вынули из воды,
слева и справа, соответственно.
После эксперимента с модельным объектом были проведены аналогичные измерения теплового акустического излучения из участка тела человека. Указательный палец правой руки был помещен на 50 с в воду температурой 19.6°С ладонной стороной (ногтем вниз) к приемной решетке в 33 мм от датчиков. Поверхностная температура пальца, измеренная термографом ИРТИС-2000 (аналогичные измерения проделаны в работах [41, 48, 50]), до помещения в воду (около 29°С) и после того, как палец вынули из воды (около 23°С), показана на рис. 10 слева и справа, соответственно. Результаты измерений акустояркостной температуры пальца показаны с помощью анимации на рис. 11. Карта инкрементов (0 К соответствует температуре 19.6°С) акустояркостных температур, полученная так же, как и в эксперименте 1а, представлена на рис. 11 слева. Аппроксимирующий распределение акустояркостной температуры гауссиан (8б) показан справа.
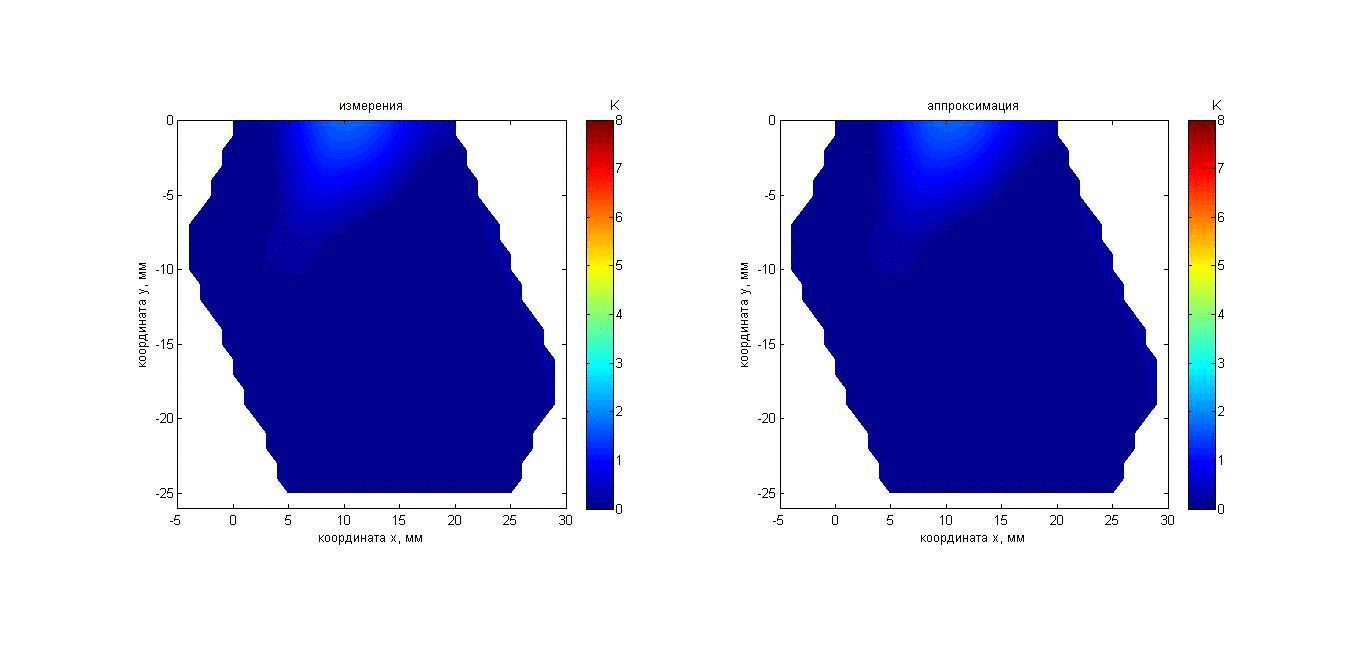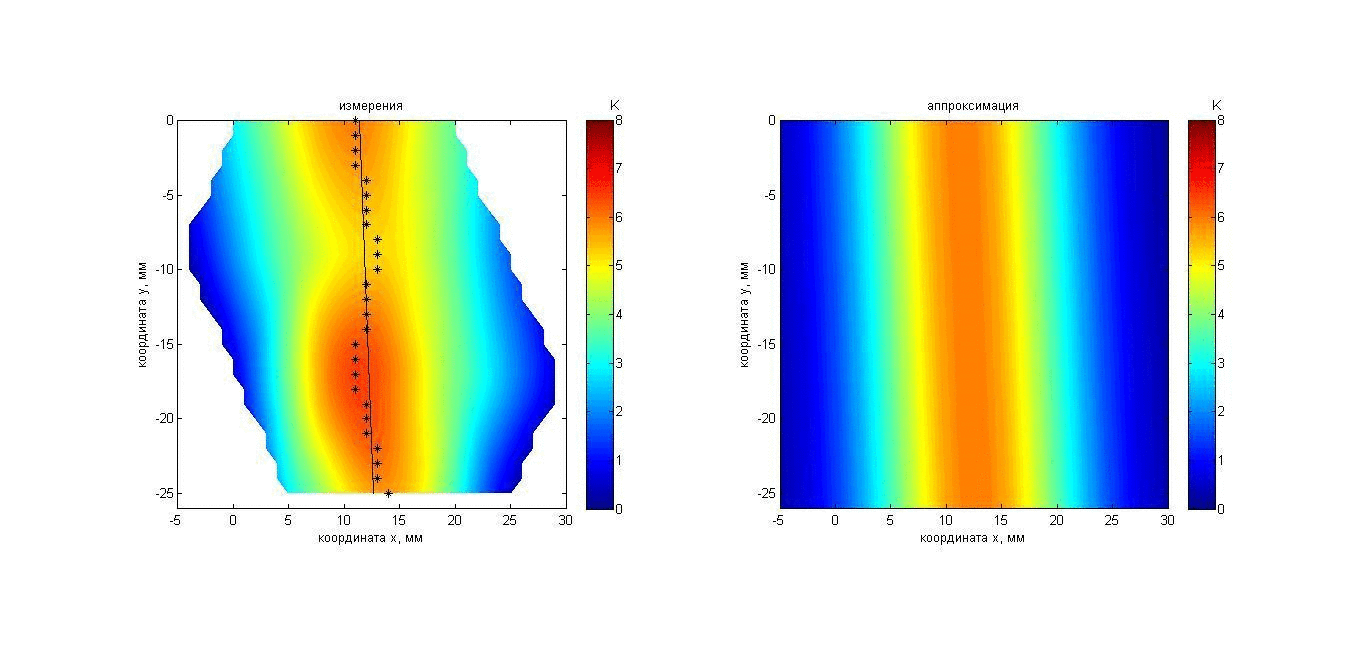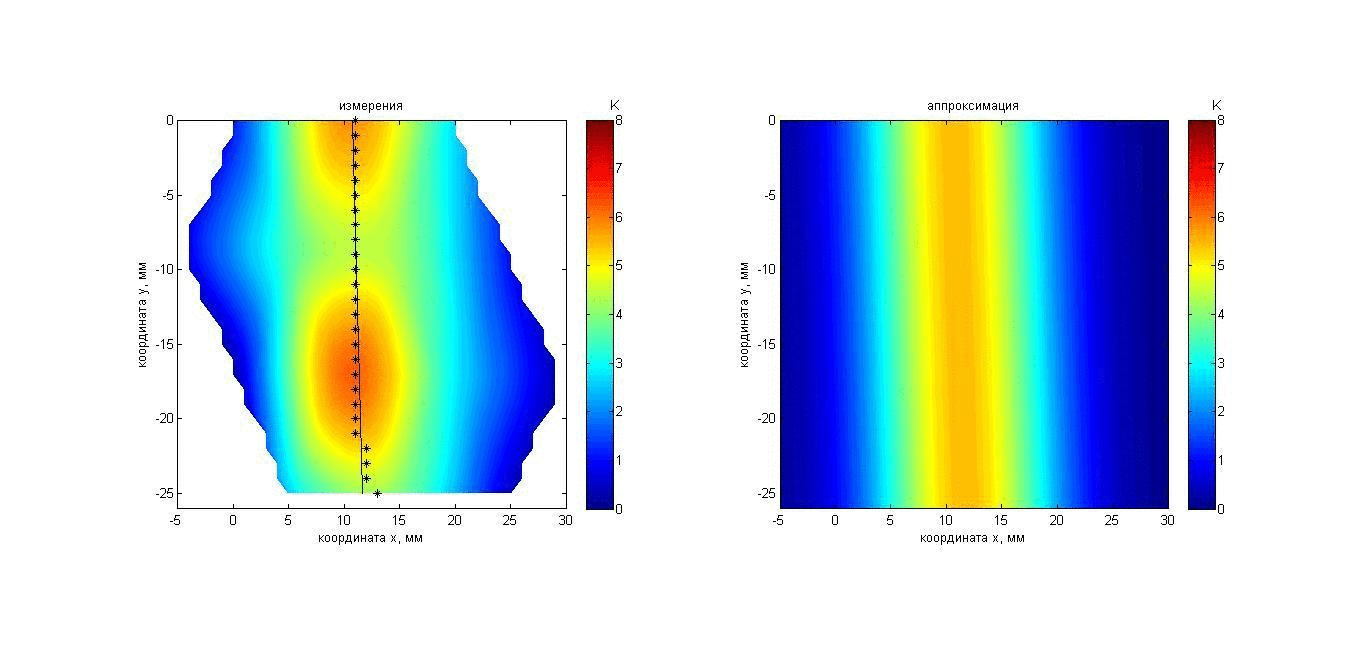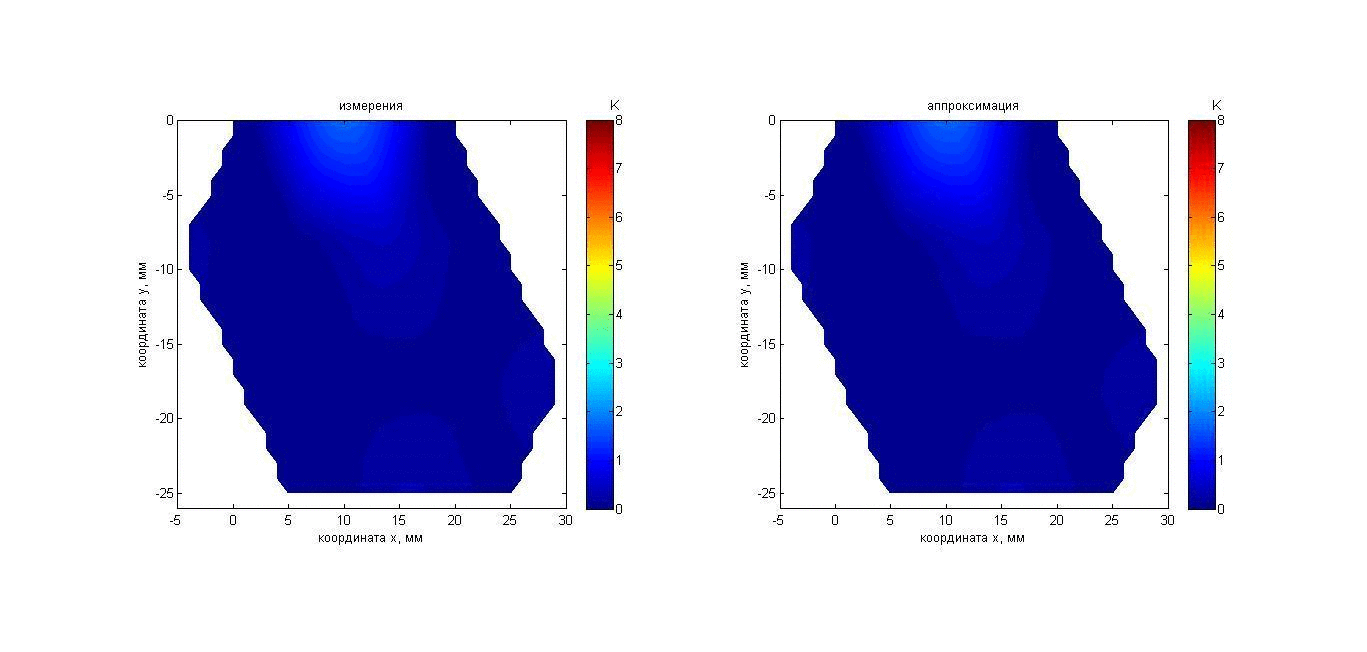
Рис. 11. Анимация меняющихся во времени распределения акустояркостной температуры указательного пальца (слева) и аппроксимации этого распределения гауссианом (справа). Пояснения о маркерах и линии представлены на рис. 5.
Изменения во времени
восстановленных параметров (палец рассматривался как протяженный цилиндр) показаны
на рис. 12. Ошибка восстановления средней координаты оси (рис. 12а) составляет ± 1.4 мм.
Наклон оси (рис. 12б) пальца (если его рассматривать как цилиндр) составляет
1 ± 5°. Размер пальца (рис.
12в), точнее диаметр нагретой области, где температура снижается вдвое, равен 15 ± 2 мм.
Средняя толщина указательного пальца испытуемого составляла Df = 17 мм. Изменение со временем инкремента максимальной
температуры объекта показано на рис. 12, г: в течение
40 с глубинная температура пальца не менялась, после чего резко снизилась.
Этот эффект можно объяснить изменением кровотока в конечности, помещенной в
прохладную воду. Отметим, что наибольшее восстановленное значение инкремента
максимальной температуры (рис. 12, г, кривая 1) составляет около 6 К, что
с учетом температуры аквариума составляет около 26°С, что заведомо меньше реальной глубинной температуры пальца. Максимальную
глубинную температуру пальца можно уточнить, если учесть, что поглощение
ультразвука в пальце много меньше, чем в пластилине. Для оценки поглощения в
пальце использовались данные о поглощении в кисти из работы [47]: коэффициент
поглощения по интенсивности на частоте 2 МГц составил g = 0.047 мм-1. Согласно интегралу
(4б), акустояркостная температура 
слоя толщиной Df
меньше температуры 
слоя из-за
конечности поглощения в слое: 
. Если эту поправку учесть, то глубинной
температуры пальца составит около 31°С
(рис. 12, г, кривая 2), что отвечает физиологическим данным [51].
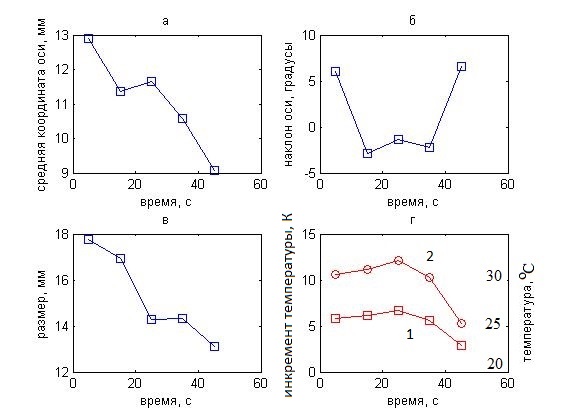
Рис. 12. Изменения восстанавливаемых параметров (а – средней координаты оси, б – наклона оси, в – диаметра, г – максимальной температуры цилиндра) температурного распределения указательного пальца (представленного цилиндром), помещенного в воду, во времени. 1 – восстановление, проведенное на основании модели 1, 2 – восстановление с учетом поглощения ультразвука.
Эксперимент 2: перемещаемый
нагретый цилиндр. Тот же самый пластилиновый цилиндр, как в эксперименте 1а,
нагретый благодаря расположенному внутри сопротивлению, через которое пропускался
ток, был помещен вертикально в аквариум с водой температурой 18.7°С. Цилиндр перемещался горизонтально (при
этом расстояние в 89 мм между центром цилиндра и приемной решеткой не менялось)
с шагом 2 мм. Длительность измерений на каждом шаге составляла 10 с. Результаты
измерений и восстановления температуры цилиндра показаны с помощью анимации
(рис. 13 и 14). Карта инкрементов (0 К соответствует температуре аквариума)
акустояркостных температур, полученная так же, как и в эксперименте 1, представлена
на рис. 13, слева. Аппроксимирующий распределение акустояркостной температуры
гауссиан (8б) показан справа. На рис. 14 результат аппроксимации представлен в
виде вертикального цилиндра. За 10 шагов цилиндр сдвигался на 20 мм. Изменения
диаметра цилиндра связаны с ошибками восстановления размера нагретой области Dx: в идеале диаметр цилиндра не должен
меняться. Чем ярче цвет цилиндра, тем выше его температура: по условиям
эксперимента температура цилиндра не меняется, следовательно, изменения яркости
свидетельствуют об ошибках восстановления максимальной температуры .
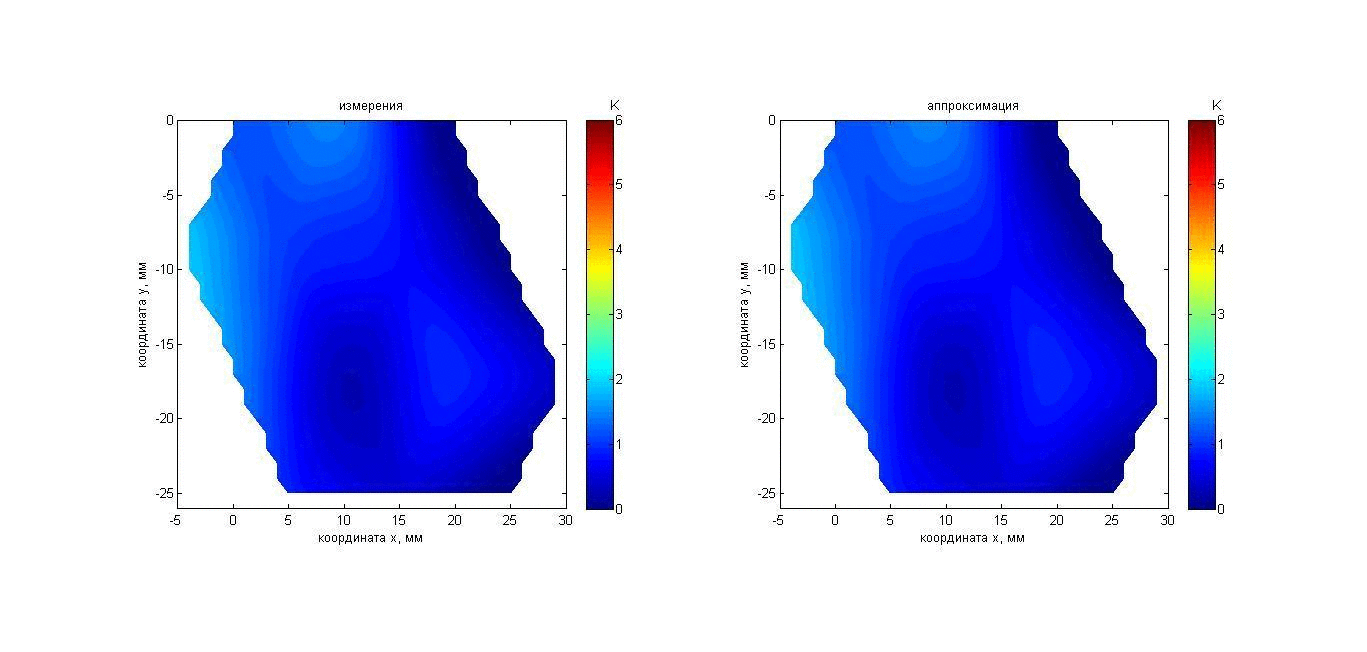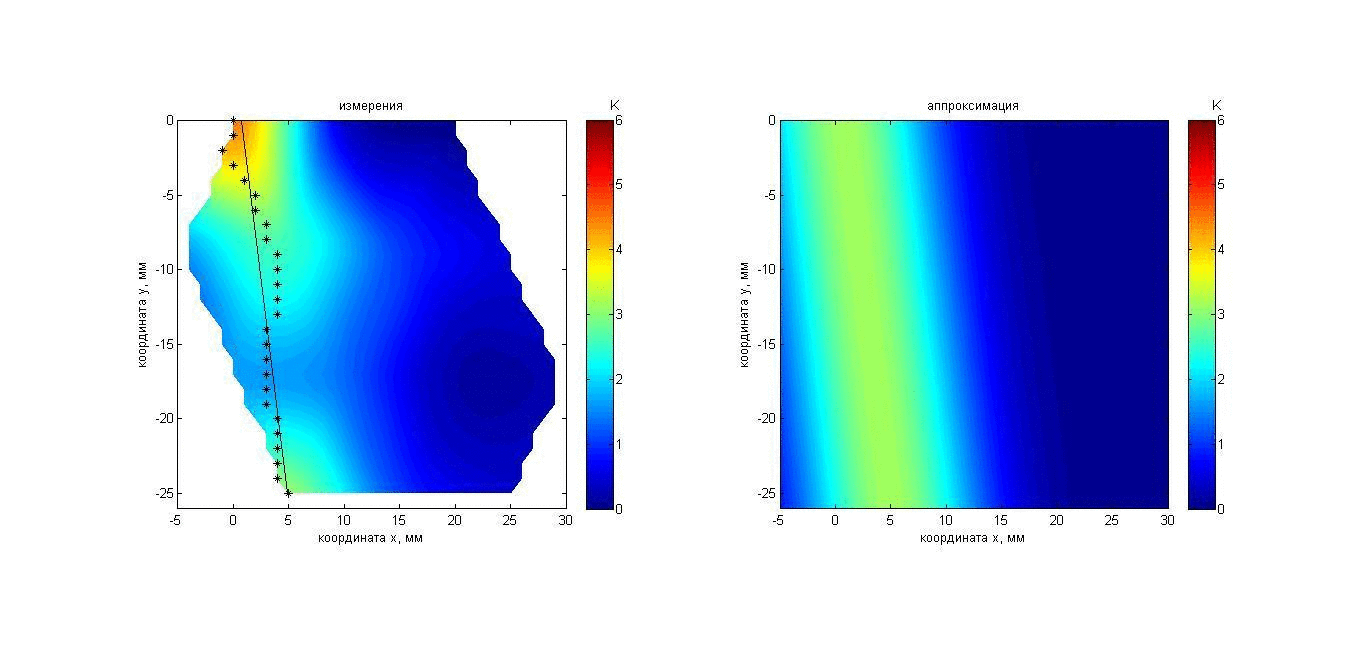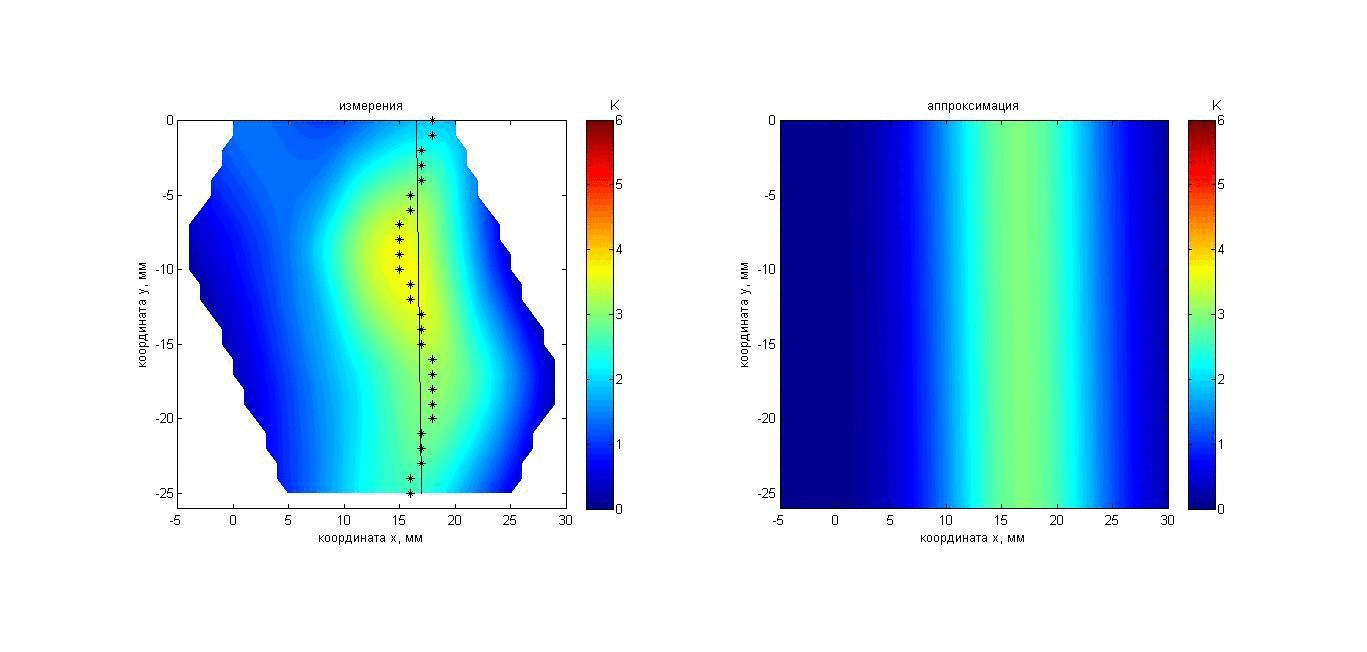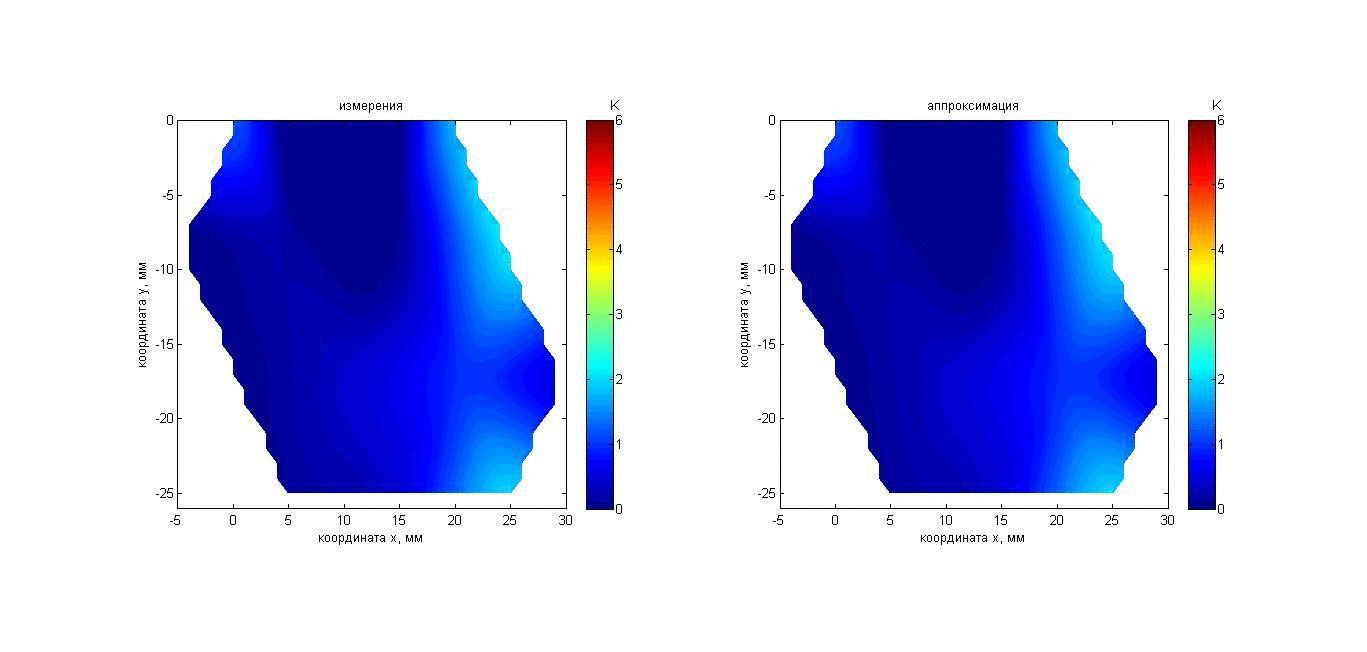
Рис. 13. Анимация меняющихся во времени распределения акустояркостной температуры перемещаемого пластилинового цилиндра (слева) и аппроксимации этого распределения гауссианом (справа). Пояснения о маркерах и линии представлены на рис. 5.
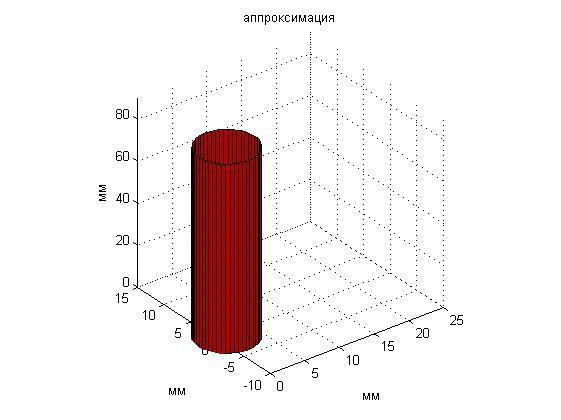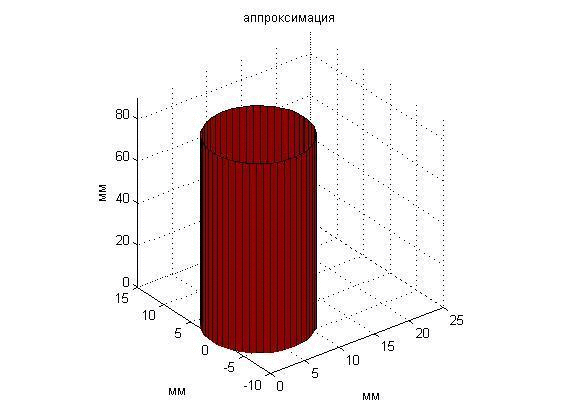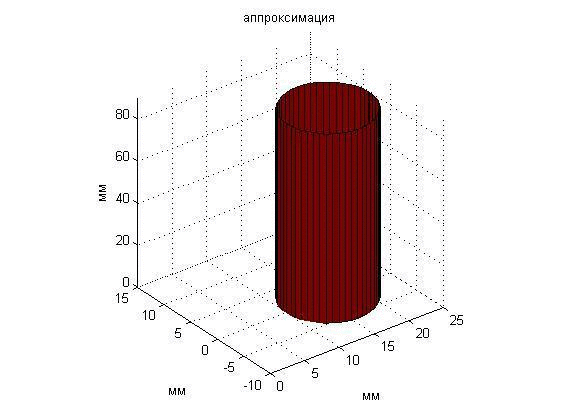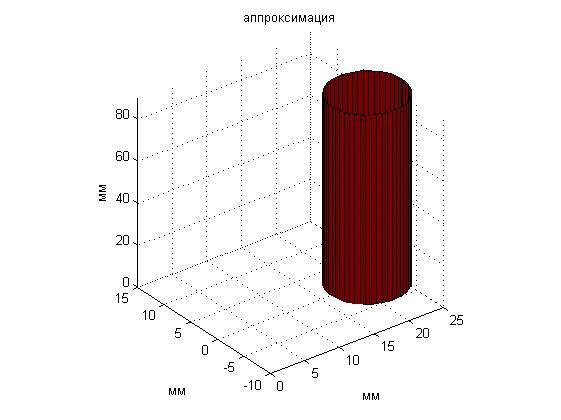
Рис. 14. Анимация перемещаемого пластилинового цилиндра постоянной температуры.
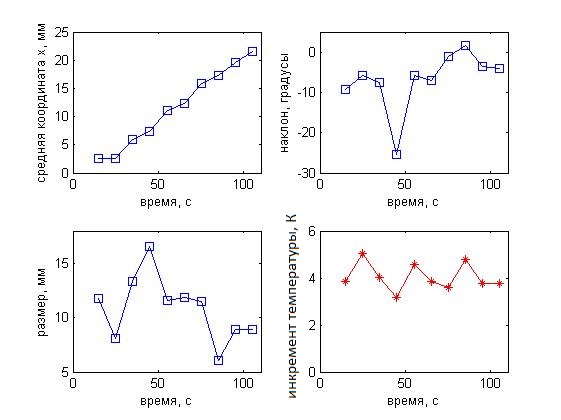
Рис. 15. Изменения восстанавливаемых параметров (а – средней координаты оси, б – наклона оси, в – диаметра, г – максимальной температуры цилиндра) температурного распределения в перемещаемом пластилиновом цилиндре со временем.
Изменения во времени восстановленных параметров показаны на рис. 15. Исследовался перемещаемый объект, температуру которого поддерживали постоянной. Таким образом, три восстанавливаемых параметра (наклон, размер и максимальная температура) флуктуировали относительно средних значений, а средняя координата оси цилиндра (рис. 15а) возрастала со средней скоростью 0.2 мм/с. Наибольший интерес представляет точность восстановления размера (взятого по уровню ½ от максимальной температуры) 10 ± 3 мм (реальный диаметр цилиндра 9 мм) и максимальной температуры 4.0 ± 0.6 К нагретой области.
Эксперимент 3: нагреваемые неподвижные а) параллелепипед и б) шар. Пластилиновый прямоугольный параллелепипед размером 23´16´16 мм располагался в аквариуме с водой температурой 21.2°С перед решеткой датчиков на расстоянии 70 мм (к датчикам он был повернут гранью 23´16 мм). В течение 60 с объект нагревался в глубине на приблизительно 15 К относительно аквариума благодаря помещенному в пластилин сопротивлению. При этом температура поверхности параллелепипеда была близка температуре аквариума. Общая продолжительность измерений теплового излучения тела при нагреве и дальнейшем охлаждении составила 120 с. Результаты измерений и восстановления температуры показаны с помощью анимации на рис. 16. Карта инкрементов акустояркостных температур (рис. 16, слева) получена так же, как и в предыдущих экспериментах. Аппроксимирующий распределение акустояркостной температуры 2D гауссиан (10) показан на рис. 16, справа.
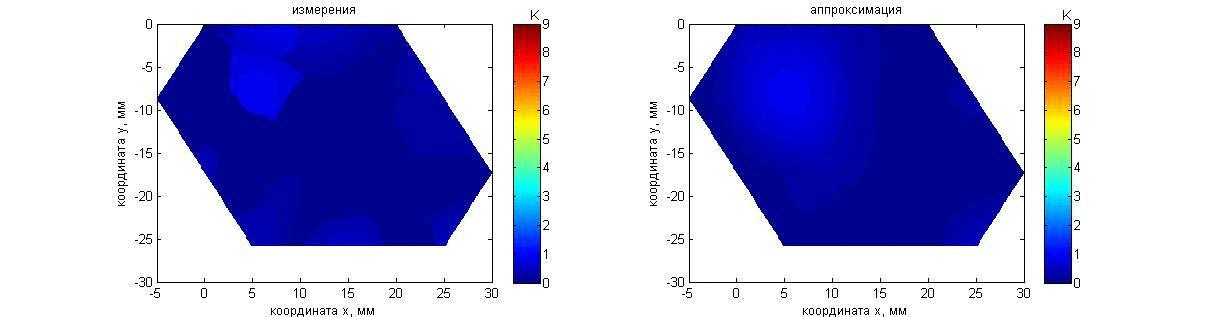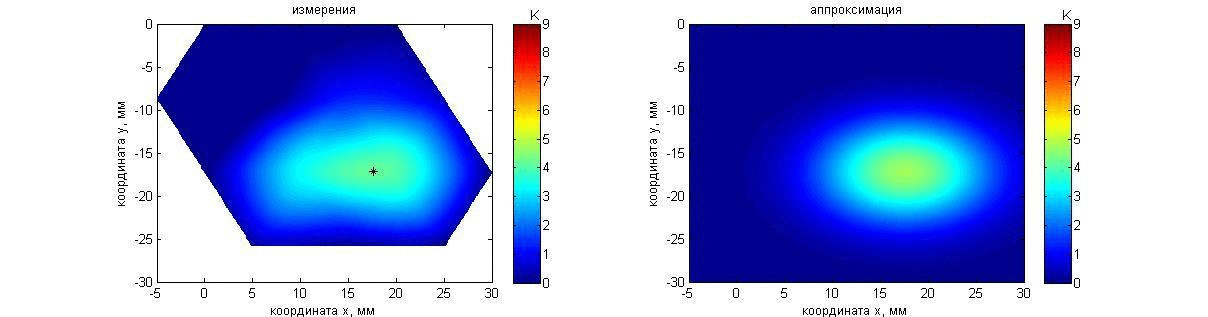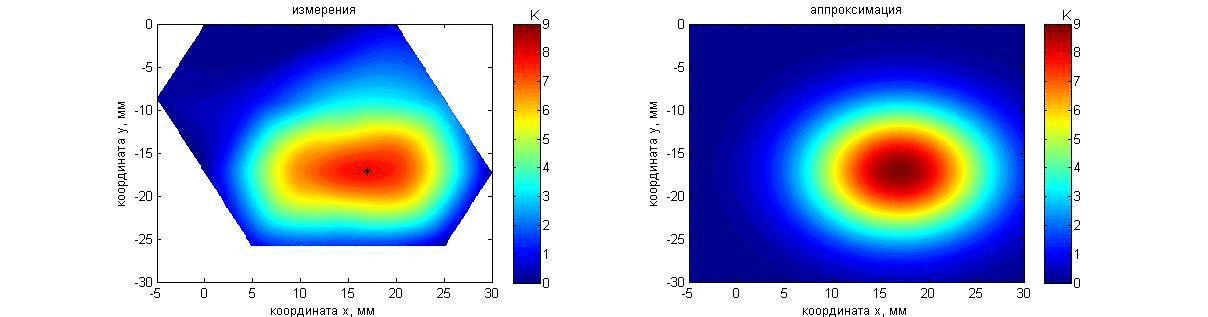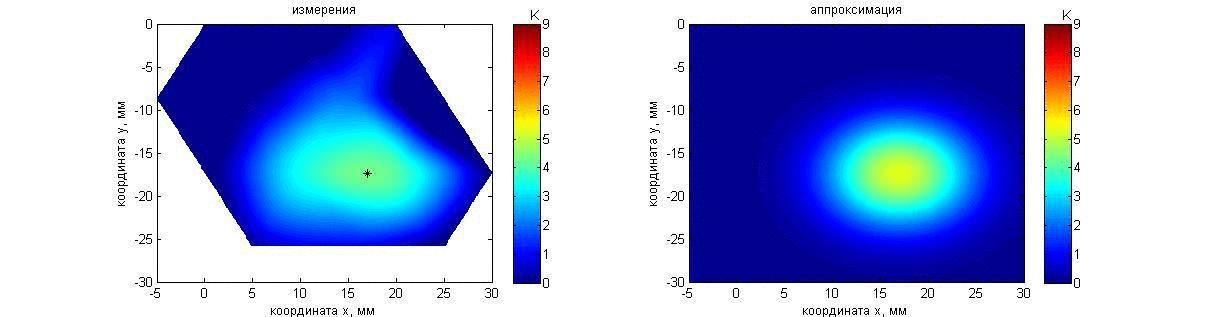
Рис. 16. Анимация меняющихся во времени распределения акустояркостной температуры пластилинового прямоугольного параллелепипеда (слева) и аппроксимации этого распределения гауссианом (справа). Пояснения о маркере представлены на рис. 6.
Изменение во времени
восстановленных параметров показано на рис. 17. Исследовался неподвижный
объект, у которого менялась температура. Поэтому четыре параметра (координаты центра
, 
и размеры нагретого объекта)
флуктуировали относительно средних значений: = 17.4 ± 0.8 мм, = – 17.2 ± 0.2
мм, размеры по x и по y нагретой области, взятые по уровню, где температура
снижается вдвое, были равны 15.9 ± 1.2 и 10.0 ± 1.5 мм,
соответственно. Соответствующие размеры пластилинового параллелепипеда были
равны 23 и 16 мм. Восстановленное наибольшее значение инкремента максимальной
температуры составило 12.2 К.
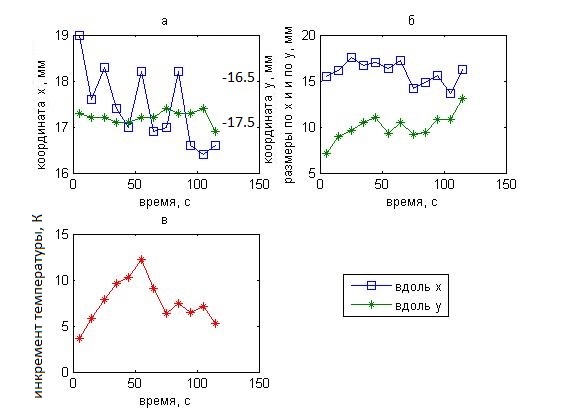
Рис. 17. Восстановленные параметры (а – координаты центра, б – размеры, в – максимальная температура нагретой области) температурного распределения неподвижного нагреваемого (после 50-й секунды остывающего) пластилинового параллелепипеда.
Тот же алгоритм использовался для восстановления температуры неподвижного пластилинового шара диаметром 16 мм, который был помещен в аквариум с водой температурой 17.6°С перед решеткой датчиков на расстоянии 50 мм. То есть, хотя было априори известно о симметрии задачи, эта информация не была учтена. Это позволило проверить точность восстановления размеров нагретой области. В течение 80 с шар нагревался в глубине на приблизительно 10 К относительно аквариума. При этом температура поверхности шара оставалась приблизительно равной температуре аквариума. Результаты измерений и восстановления температуры шара показаны с помощью анимации на рис. 18. Карта инкрементов акустояркостных температур (рис. 18, слева) получена так же, как и в предыдущем эксперименте с параллелепипедом. Аппроксимирующий распределение акустояркостной температуры 2D гауссиан (10) показан на рис. 18, справа.
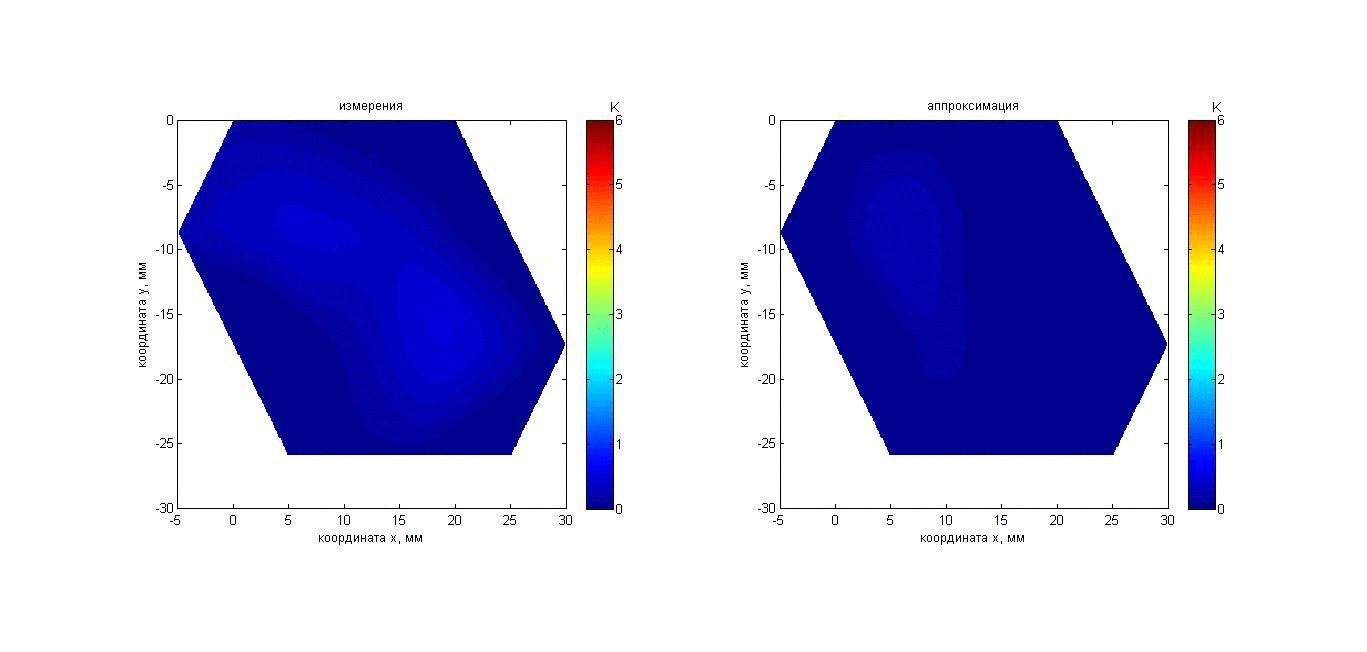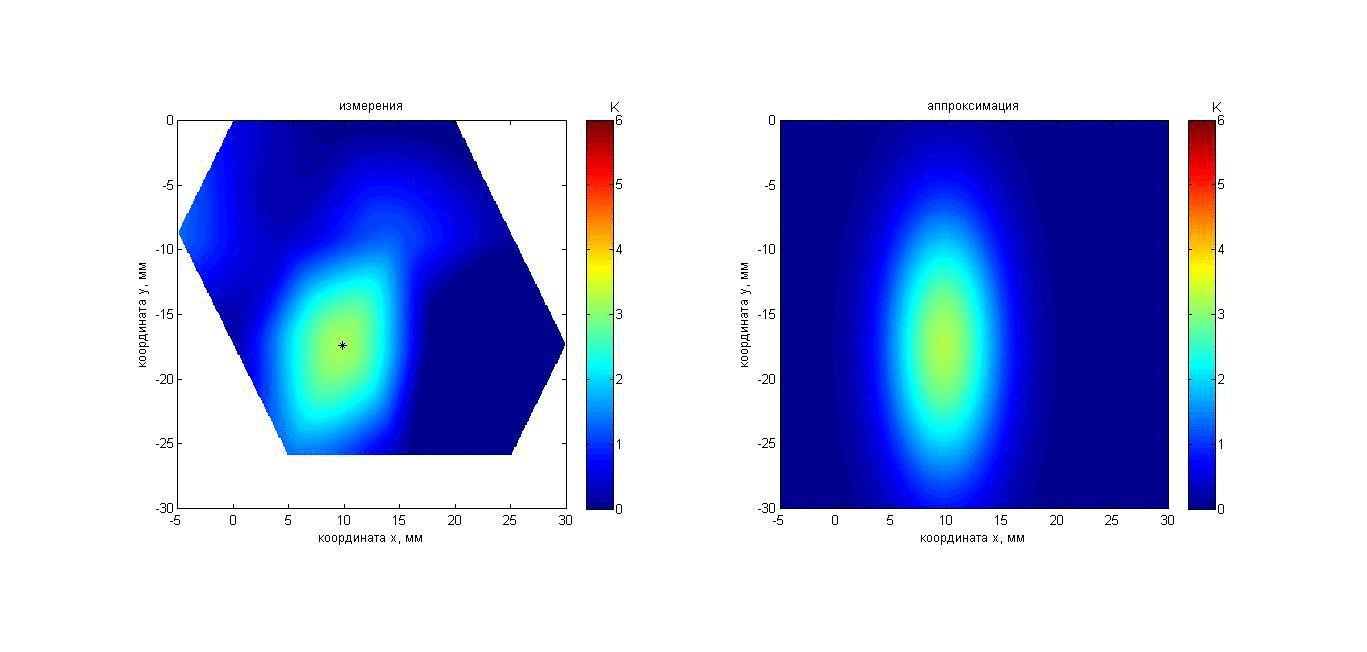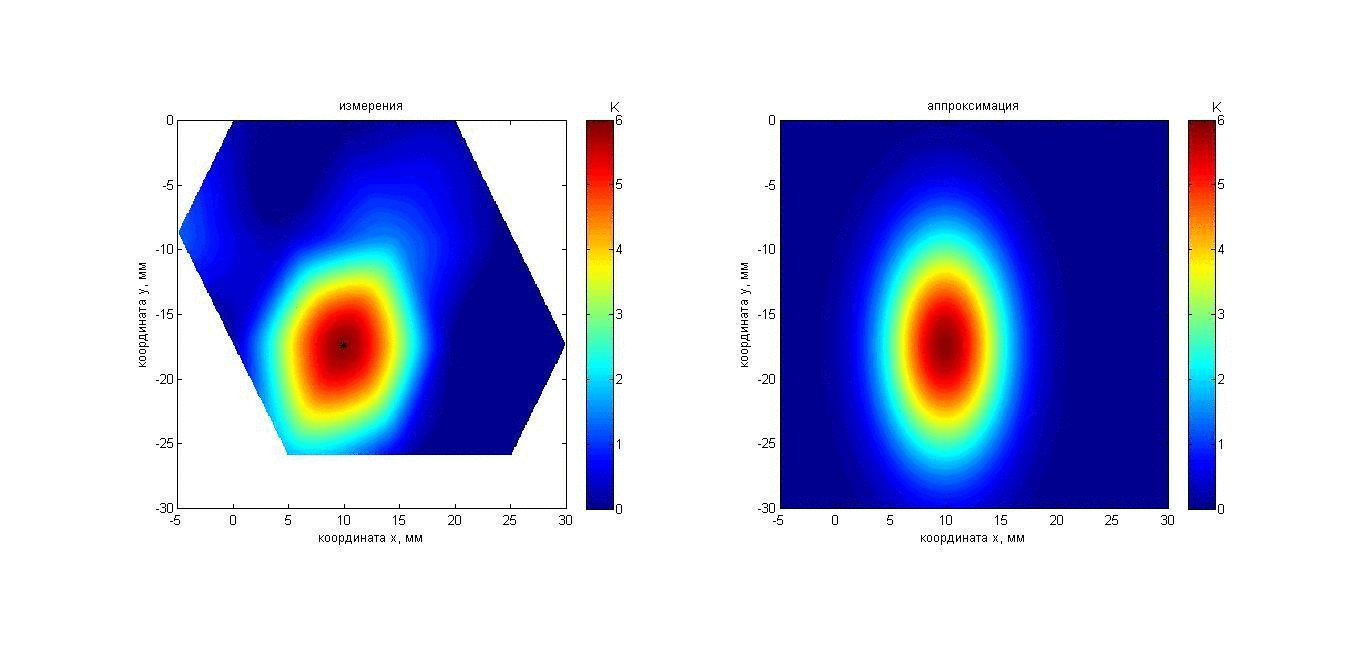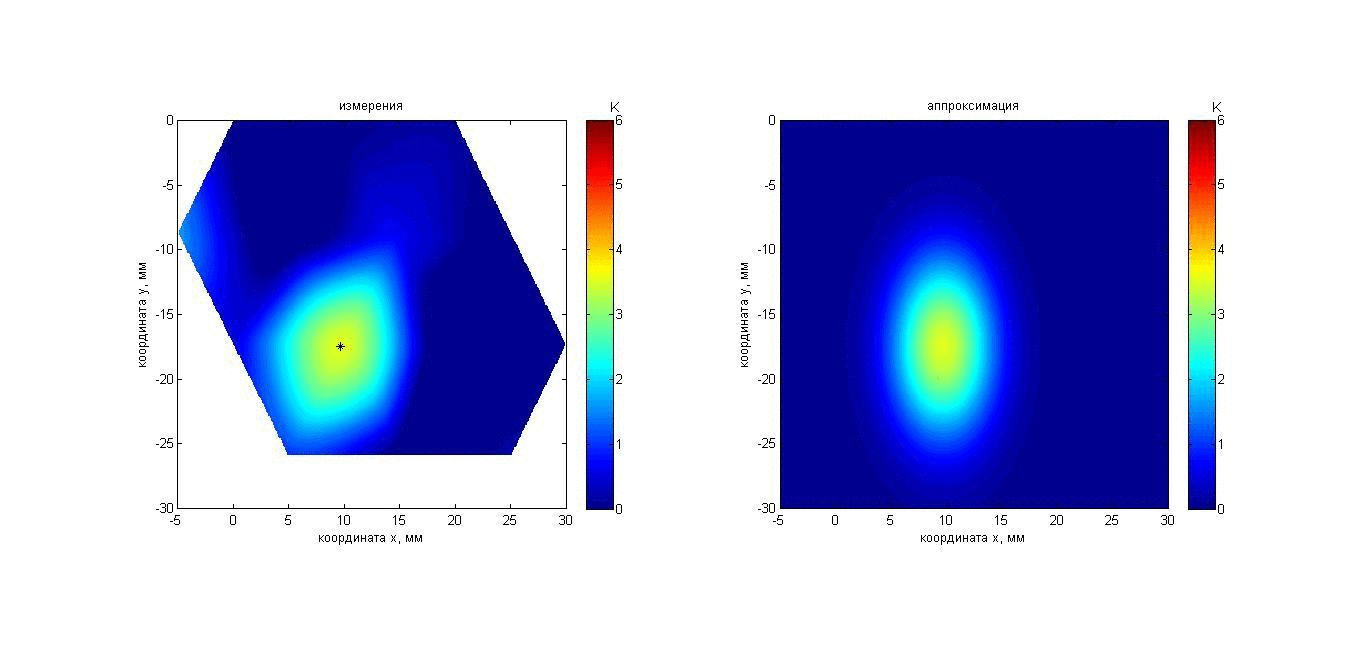
Рис. 18. Анимация меняющихся во времени распределения акустояркостной
температуры пластилинового шара (слева) и аппроксимации этого распределения
гауссианом (справа). Пояснения о маркере представлены
на рис. 6.
Изменения во времени восстановленных
параметров показаны на рис. 19. Отметим, что, как и в предыдущем эксперименте,
исследовался неподвижный объект, у которого менялась температура. Точно так же,
четыре параметра флуктуировали относительно средних значений: = 9.8 ± 0.2, = –17.6 ± 0.2 мм, размеры по x и по y нагретой области,
взятые по уровню, где температура снижается вдвое, были равны 8.4 ± 0.7
и 10.9 ± 1.0 мм, соответственно. Систематическая ошибка в определении
размеров составила 2.5 мм. Восстановленное наибольшее значение инкремента
максимальной температуры составило 7.5 К.
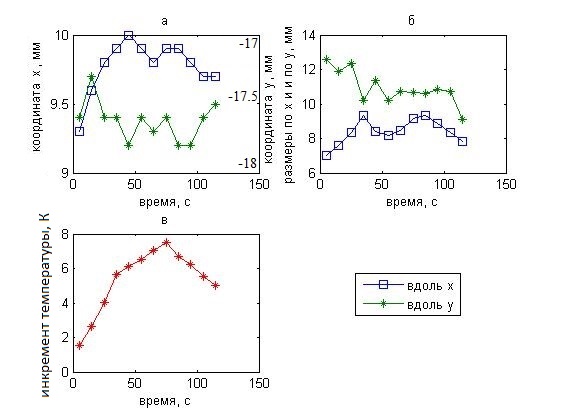
Рис. 19. Восстановленные параметры (а
– координаты центра, б – размеры, в – максимальная температура нагретой
области)
нагреваемого (после 80-й секунды остывающего) шара.
Эксперимент 4: а) пластилин и б) рука, помещенные в воду. В аквариум с водой температурой 20°С помещался нагретый пластилиновый параллелепипед размером 150 ´ 80 ´ 16 мм (к приемной решетке параллелепипед был повернут стороной 150 ´ 80 мм) или кисть (ладонью к приемной решетке), и в течение 50-и секунд проводились измерения исследуемого объекта. Начальная температура пластилина (36.5°С) была приблизительно равна температуре в глубине кисти (около 35°С). Для восстановления температурного распределения сигнал от исследуемых объектов усреднялся в течение 10 с. Таким образом, за 50 с были получены пять наборов данных для пластилина и кисти, которые позволили составить 2D карты распределения акустояркостных температур, представленные на рис. 20 с помощью анимации. Изображения получены путем интерполяции по трем точкам с помощью кусочно-линейной функции. На рис. 20, слева видно, что инкремент акустояркостной температуры пластилина за 50 с снижается с 14 до 9 К. Акустояркостная температура кисти за то же время снижается значительно медленнее с 9 до 7 К. То, что акустояркостная температура пластилина выше, объясняется тем, что в кисти (по сравнению с пластилином) ниже поглощение ультразвука. То, что акустояркостная температура кисти за 50 с изменяется незначительно, связано с существующим источником тепла – с притекающей в кисть кровью.
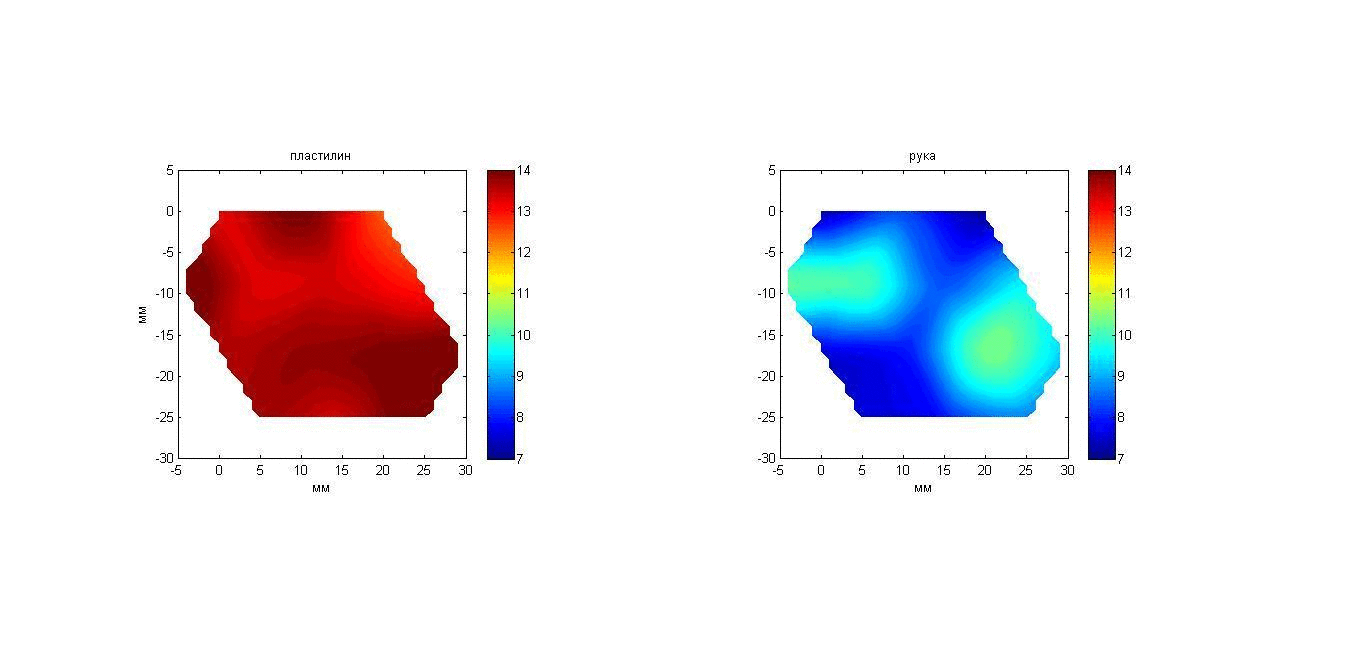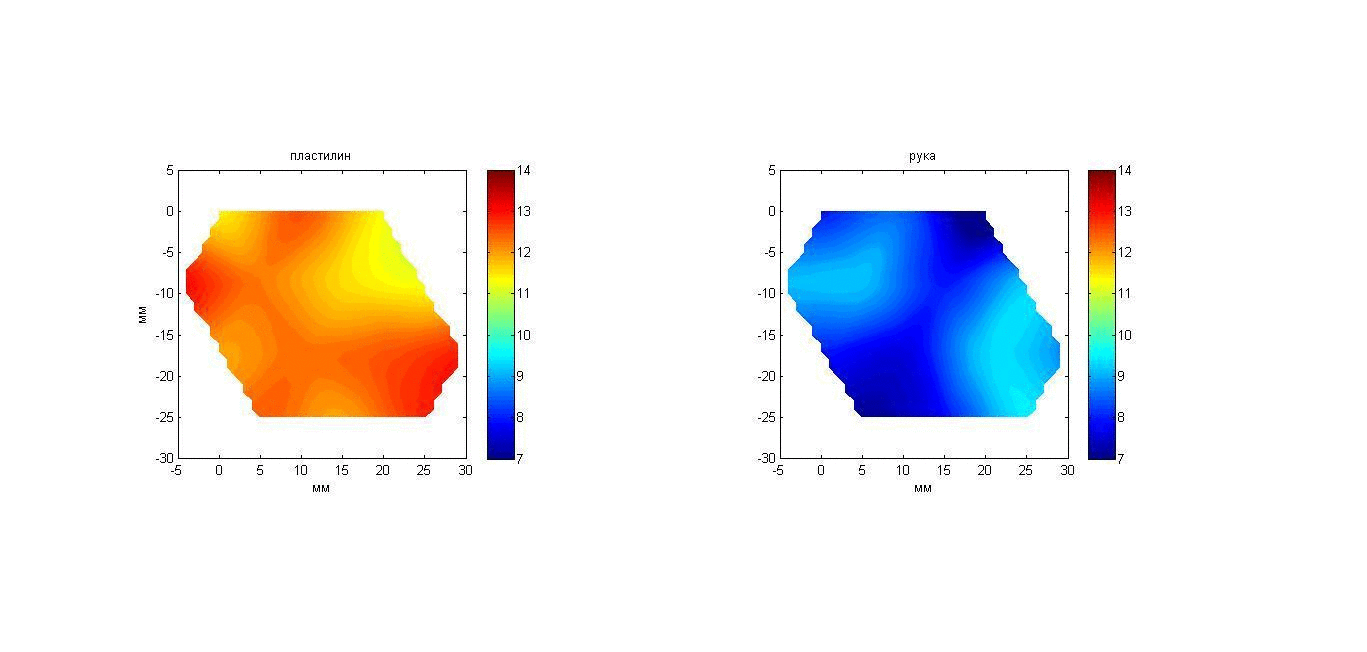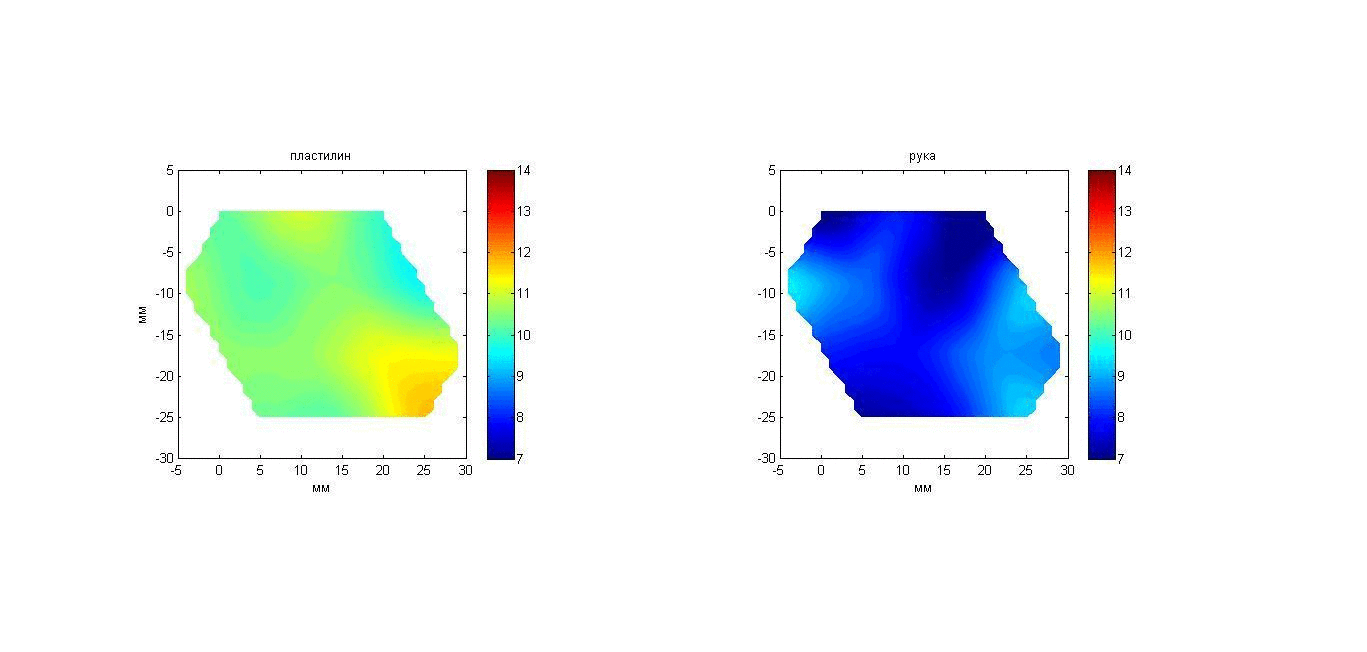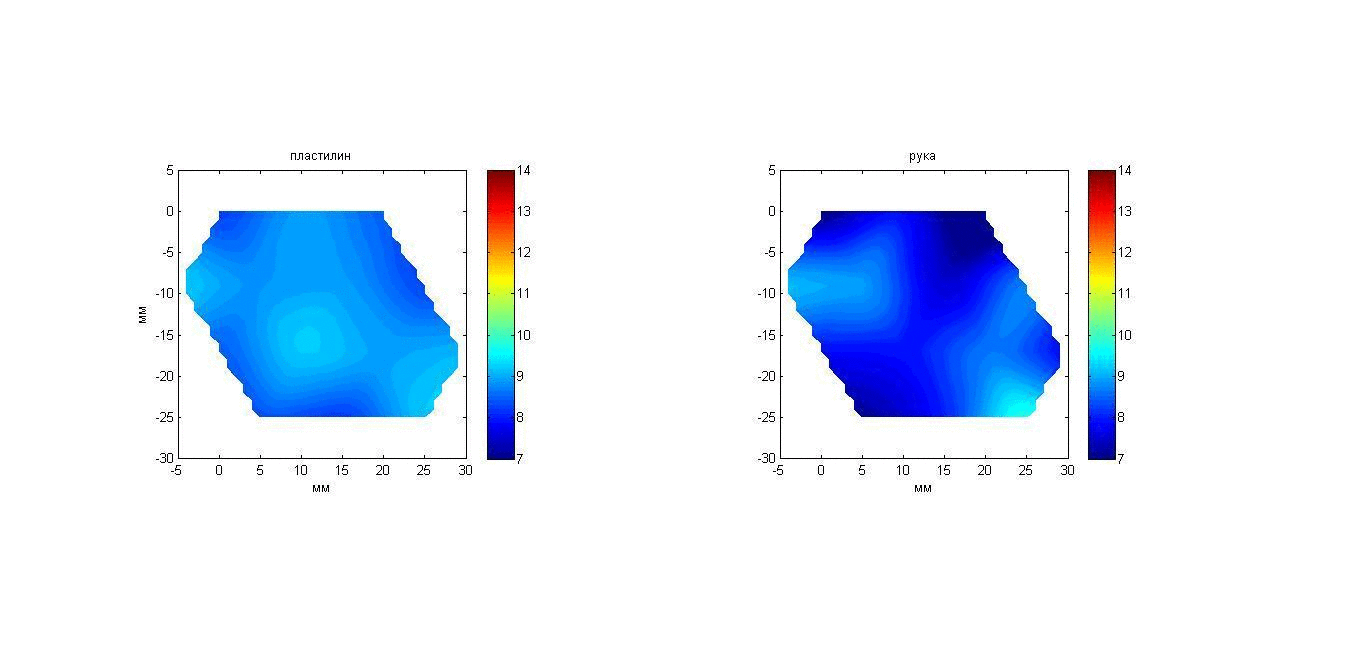
Рис. 20. Анимация меняющихся во времени 2D распределений акустояркостной температуры в пластилиновом параллелепипеде (слева) и в ладони (справа).
На картах для пластилина разброс температуры является случайным и обусловлен погрешностью измерений. На картах для кисти видны две нагретых области, возможно, связанные с расположением в кисти поверхностной ладонной дуги arcus palmaris superficialis. Для сравнения на рис. 21 представлены ИК термограммы кисти перед тем, как ее опустили в воду, и после того, как ее вынули из воды. Видно, что температура поверхности кисти снизилась с приблизительно 34 до 32°С, однако поверхностная температура (в отличие от акустояркостной) не дает информации о наличии в глубине кисти нагретых областей.
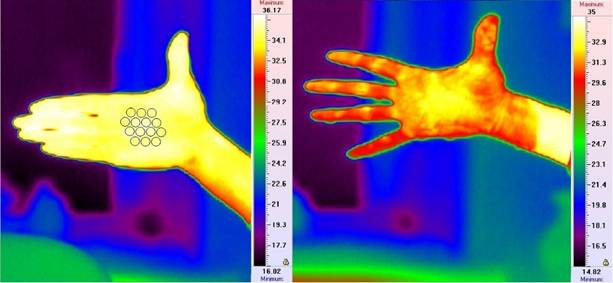
Рис. 21. Поверхностная температура ладони, измеренная термографом ИРТИС-2000, до помещения кисти в воду и после того, как кисть вынули из воды, слева и справа, соответственно. Кружки показывают расположение датчиков (Æ 8 мм) приемной решетки.
Для того, чтобы восстановить температурные профили, надо знать поглощение ультразвука в пластилине и в кисти. Для этого были использованы результаты, полученные в работах [20, 47]: на частоте около 2 МГц (средняя частота приема датчиков) измеренные коэффициенты поглощения для пластилина и кисти составили 0.41 и 0.047 мм-1, соответственно. Полученные значения инкрементов акустояркостной температуры позволили рассчитать значения параметра a(x,y) и по формуле (14) построить профили температуры в глубине объекта. Восстановленные профили глубинной температуры дали возможность получить 3D температурное распределение в пластилине и в кисти. Изменение во времени пространственных распределений температур пластилина и кисти показано с помощью анимации на рис. 22, слева и справа, соответственно. Изображать на плоскости функцию трех переменных достаточно сложно. На рис. 22 показаны температурные сечения в трех взаимно перпендикулярных плоскостях, общая точка которых расположена в центре исследуемой области. Вертикальная ось направлена вглубь поверхности объекта, поэтому сверху (при z = 16 мм для пластилина и 30 мм для кисти) и снизу (при z = 0 мм) температура минимальна (близка температуре аквариума). В середине (в горизонтальной плоскости) температура максимальна.
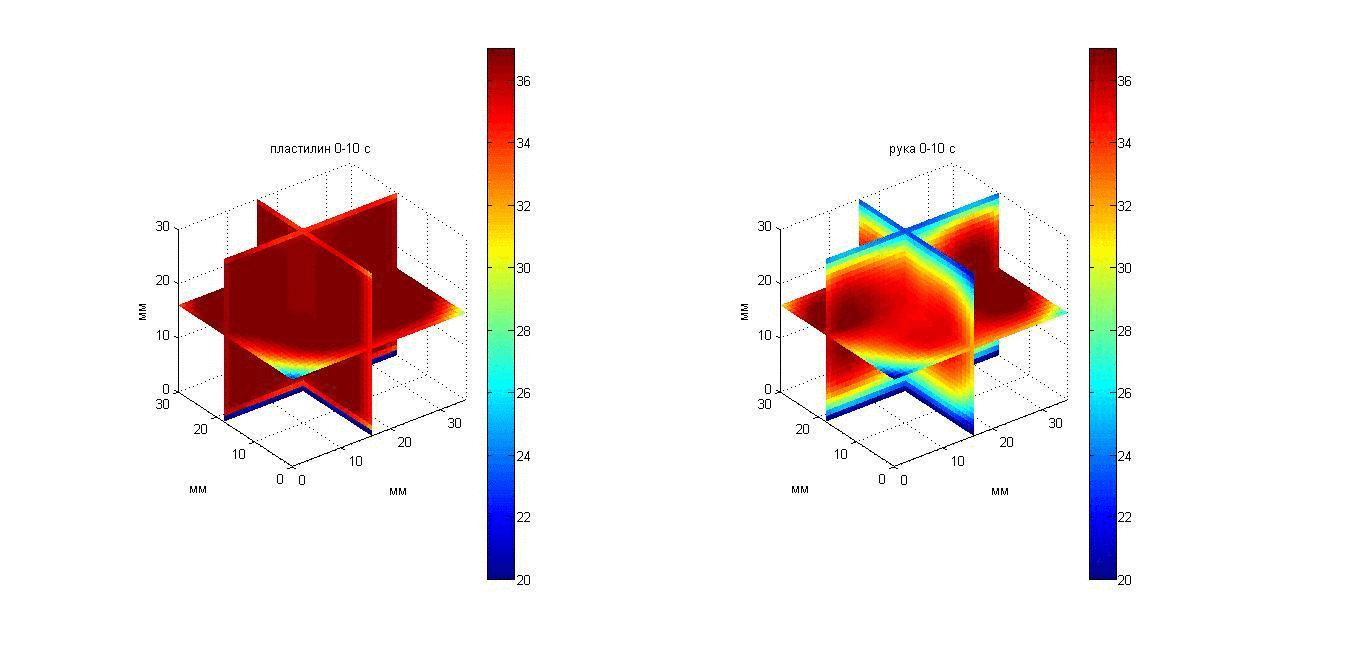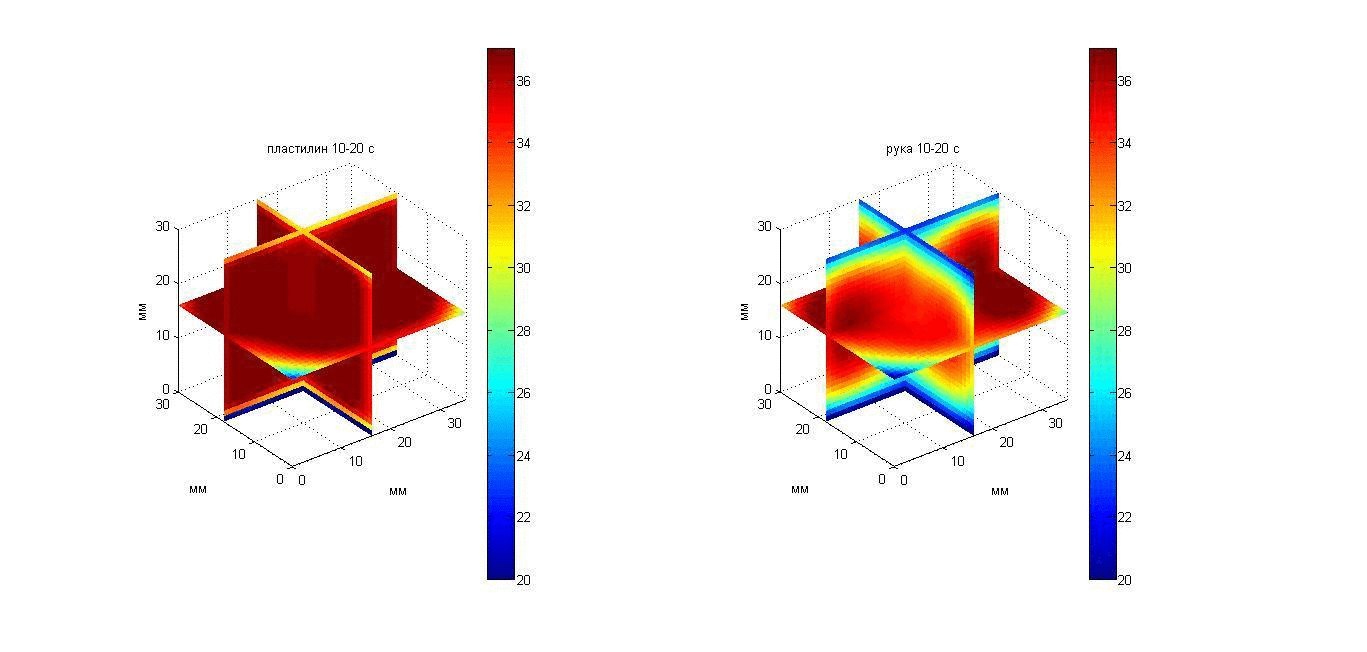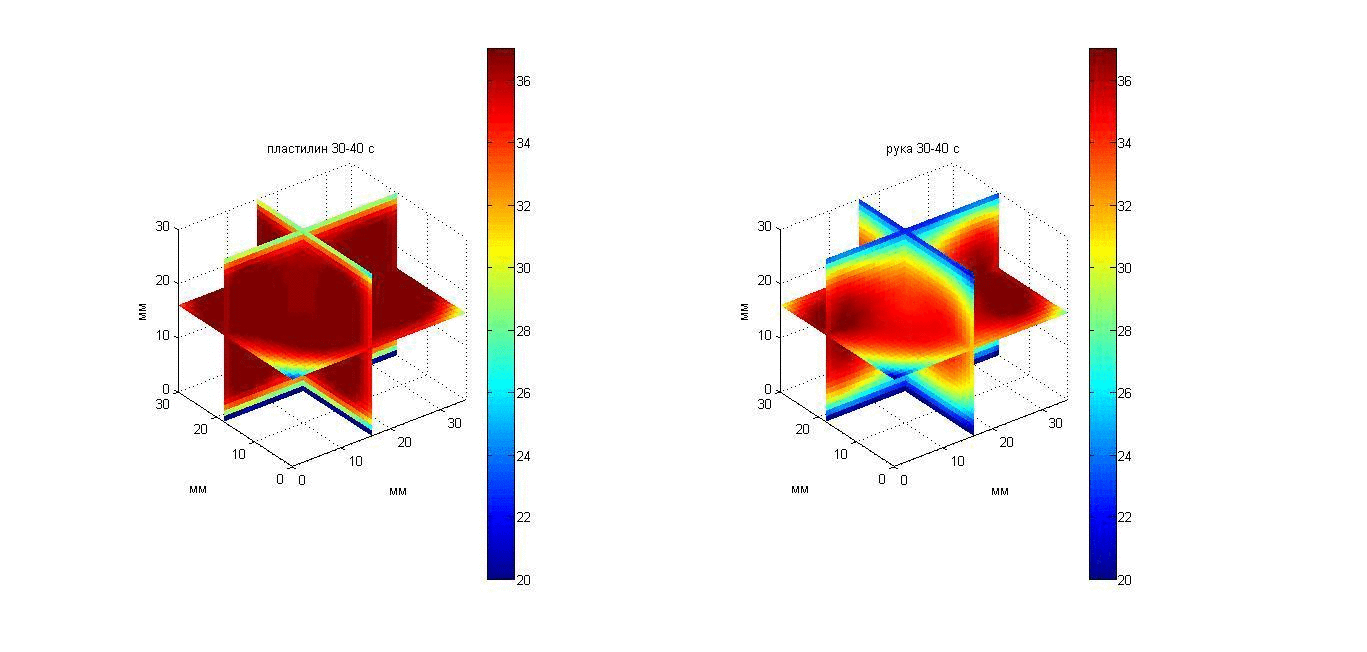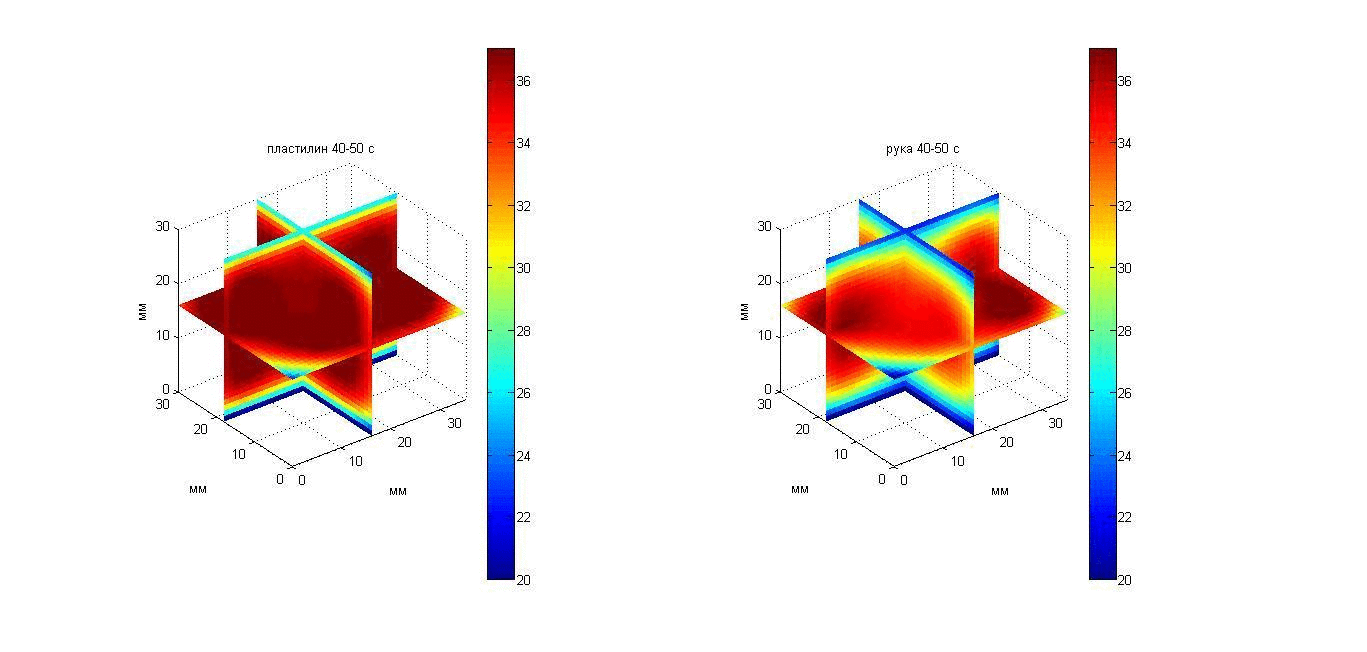
Рис. 22. Анимация меняющихся во времени 3D распределений температуры в пластилиновом параллелепипеде (слева) и в кисти (справа).
В пластилин были вставлены термопары MS6501 (Mastech, Гонконг, Китай), независимо измерявшие его температуру. Среднеквадратическая ошибка акустотермометрического восстановления температуры составила 0.5 К. Такая ошибка допустима в медицинских приложениях метода. Определить погрешность восстановления температуры в кисти невозможно без независимых инвазивных измерений, которые, по понятным причинам, не проводились.
На рис. 23 (чтобы показать, как снижается температура кисти при длительном нахождении в воде) представлена анимация меняющегося во времени 3D распределения температуры в кисти, помещенной на 11 мин в воду температурой 18°С.
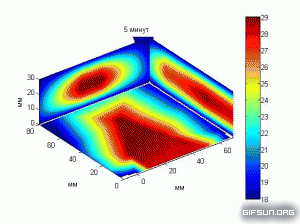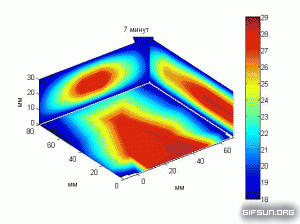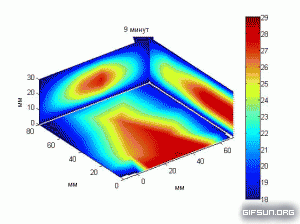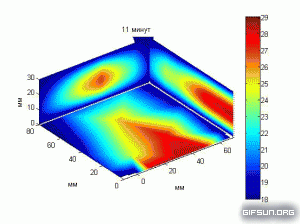
Рис. 23. Анимация меняющегося во времени 3D распределения температуры в кисти, помещенной на 11 мин в воду температурой 18°С.
Эксперимент 5: нагреваемый неподвижный шар. Рассмотрим эксперимент, проведенный с двумя приемными решетками с семью датчиками каждая (рис. 3, б). Пластилиновый шар диаметром 19 мм располагался в аквариуме с водой температурой 20°С. Шар нагревался на приблизительно 15 К относительно аквариума. Расстояние от центра шара до приемных антенн равнялось 44 мм. Эксперимент длился 200 с, прогрев начинался на 50-ой секунде и отключался на 100-ой секунде. При этом температура поверхности шара была близка температуре аквариума. Результаты измерений акустояркостной температуры показаны с помощью анимации на рис. 24. Карты инкрементов акустояркостных температур построены на двух перпендикулярных плоскостях (показанных на рис. 24 в изометрической проекции). Каждая карта получена (по результатам измерений одной решетки) с помощью модели 3. На рис. 25 результат восстановления распределения температуры показан в виде двух сфер. Изменения положения и диаметра сфер связаны с ошибками восстановления: в идеале сферы не должны двигаться и менять свои размеры. Цвет сфер определяется восстанавливаемой приемными решетками температурой: во-первых, чем ярче цвет, тем выше температура, во-вторых, в идеале яркость двух сфер должна быть одинаковой.
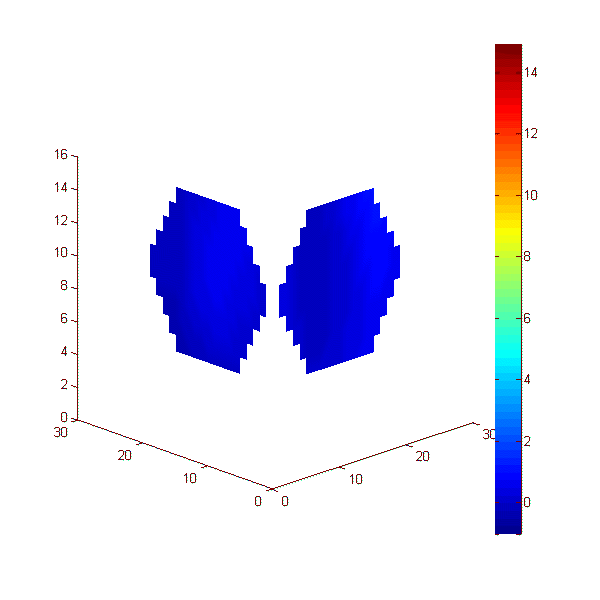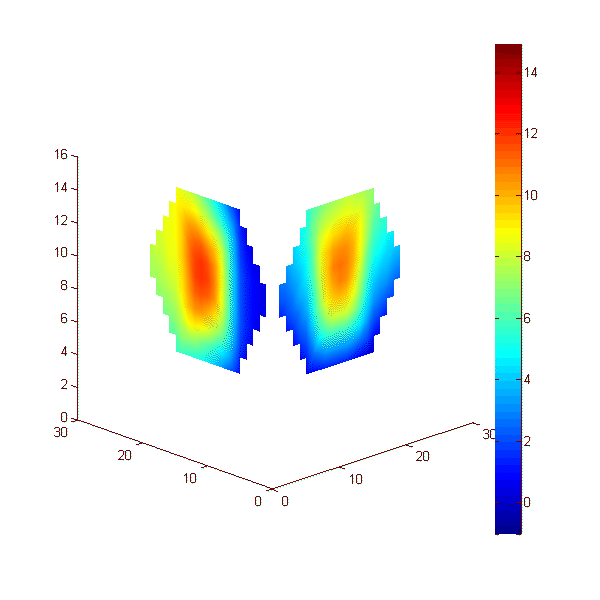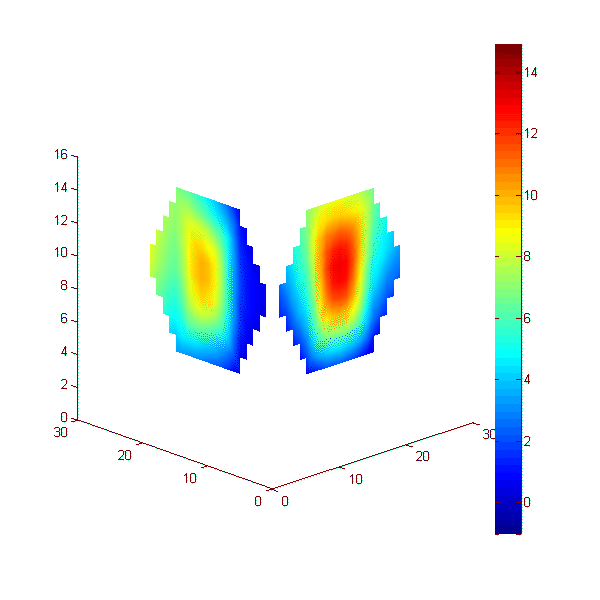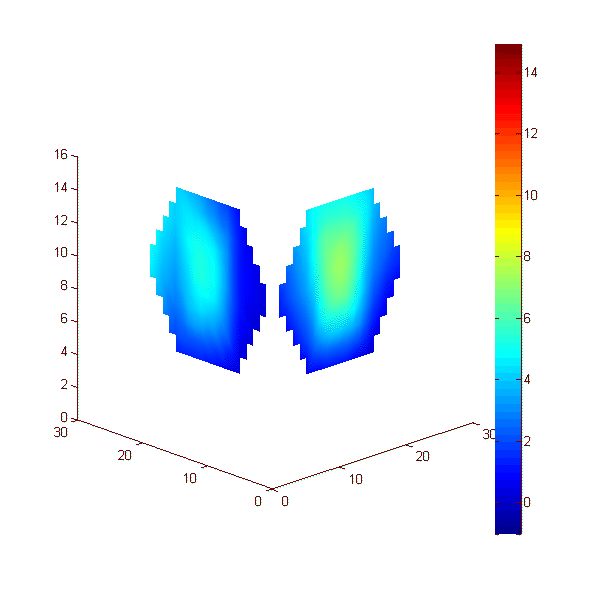
Рис. 24. Анимация меняющихся во времени 2D распределений акустояркостной температуры пластилинового шара, полученных двумя приемными решетками. Расстояния по осям – в мм, цветовая шкала – в К.
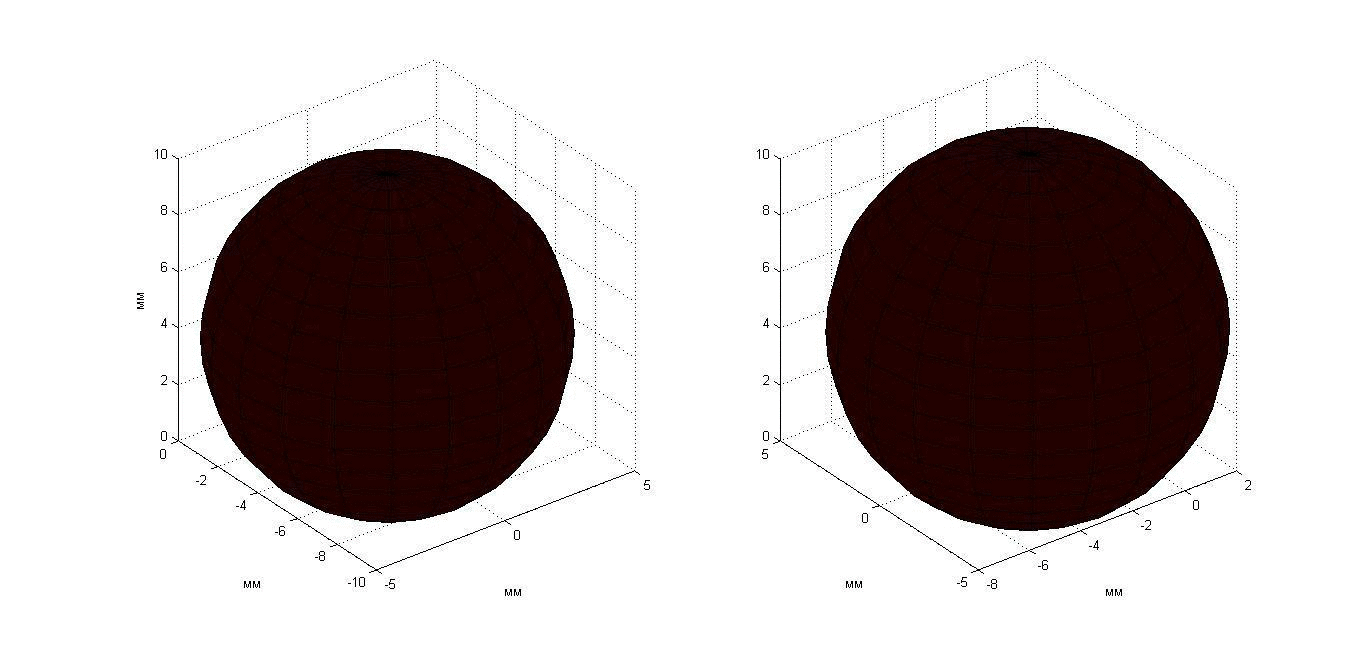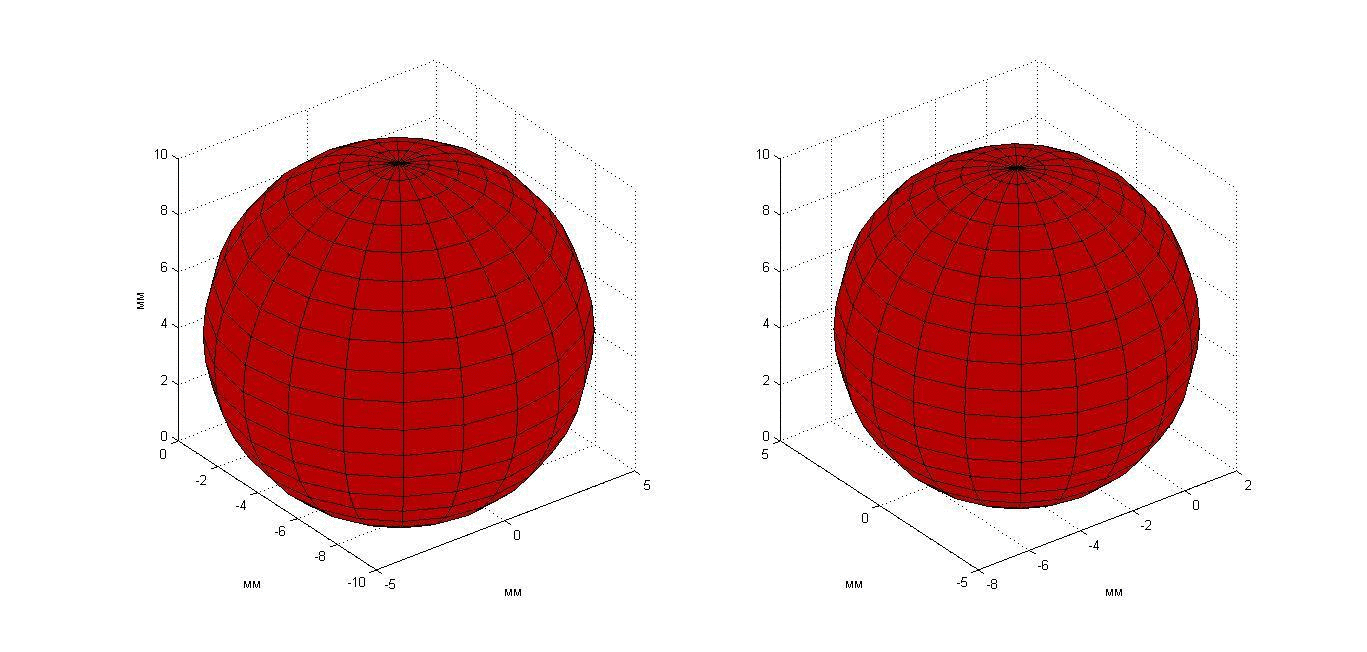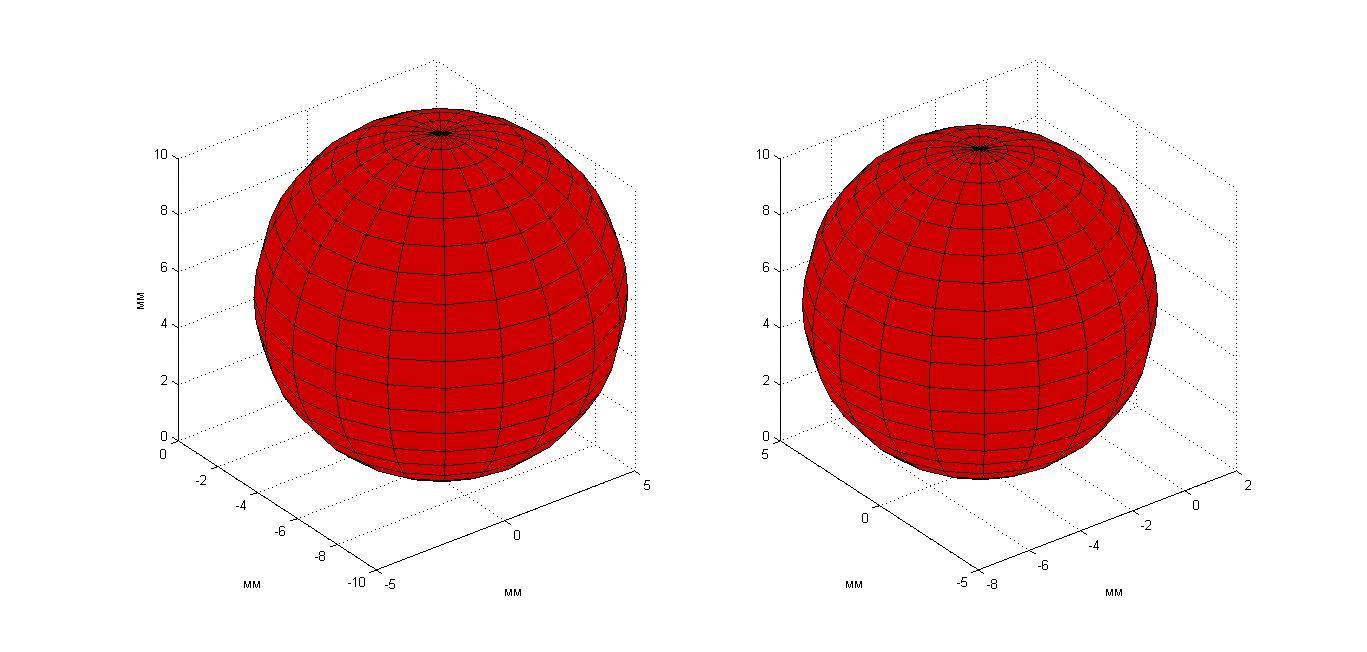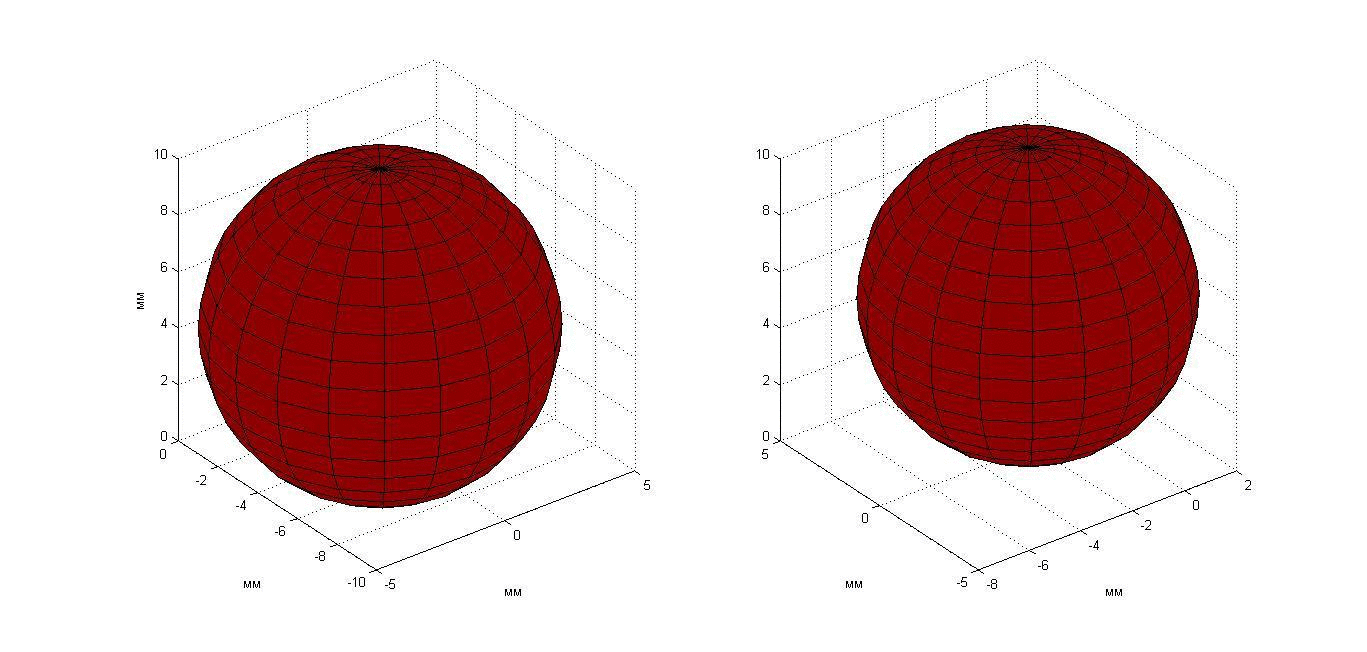
Рис. 25. Анимация меняющегося во времени температурного распределения неподвижного пластилинового шара, полученного двумя приемными решетками.
img width=587 height=469 id="Рисунок 9" src="text.files/image071.jpg">
Рис. 26. Восстановленные параметры (а, б – координаты центра, в – размер, г – инкремент максимальной температуры нагретой области) нагреваемого (после 100-й секунды остывающего) шара. Данные 1 (2) получены с помощью первой (второй) приемной решетки, соответственно. Данные 3 получены с помощью обеих решеток.
Изменения восстановленных
параметров показаны на рис. 26. Так как исследовался неподвижный объект, у
которого менялась температура, то четыре восстанавливаемых в модели 3 параметра
флуктуировали относительно средних значений. Координаты центра нагретой области
(рис. 26, а и б) были равны = 3.8 ± 0.6 мм, = –0.1 ± 0.4 мм, 
= 1.0 ± 0.4 и 2.2 ± 0.5
мм, по результатам измерений первой и второй решетками, соответственно. Таким
образом, точность определения центра нагретой области в пространстве составила
не более 1.5 мм, что полностью удовлетворяет медицинским требованиям. Размеры
нагретой области (рис. 26, в), взятые по уровню, где температура снижается
вдвое, полученные с помощью первой (1) и второй (2) решетки, практически
совпали: 13.1 ± 0.6 и 13.6 ± 0.7 мм,
соответственно. Если использовать для определения размера результаты,
полученные с помощью обеих решеток (3), то размер нагретой области составляет
13.2 ± 0.6 мм. Этот результат соответствует диаметру нагретого
пластилинового шара 19 мм. Восстановленные наибольшие значения инкремента максимальной
температуры (рис. 26, г) составили 19 и 18 К, с помощью первой и второй
решетки, соответственно. Изменения максимальной температуры, полученные по
результатам независимых измерений с помощью первой (1) и второй (2) решеток, различаются
не сильно: среднее различие составляет 1.1 ± 0.5 К.
Восстановленная с использованием первой и второй решетки температура (3)
показана на рис. 26, г.
Обсуждение
Результаты, определяющие точность
восстановления параметров нагретой области, сведены в таблицу. Из таблицы
(столбец 2) видно, что случайная ошибка восстановления (за время измерения 10
с) положения центра нагретой области составляет около 1 мм. На первый
взгляд, возникает парадоксальная ситуация: апертура датчика равна 8 мм, а
ошибка в определении пространственных параметров температурного распределения
гораздо меньше. Проблема решается следующим образом: если априорная информация
о геометрии распределения не используется, именно апертура датчика (с учетом
дифракционной расходимости) в основном определяет пространственное разрешение
метода. Например, в модели 4 (эксперименты 4а и 4б) никаких ограничений на проекцию
распределения температуры в плоскости xy не было. Поэтому пространственное разрешение
определялось расстоянием между центрами датчиков в решетке и составляло около
± 5 мм. В моделях 1 – 3 априорно предполагалось наличие одного
источника тепла. Теоретическую оценку пространственного разрешения в таком
случае можно дать, исходя из следующего рассуждения: задача определения
положения центра нагретой области с помощью решетки из N датчиков аналогична задаче
нахождения среднего при проведении N измерений. В этом случае погрешность определения центра нагретой области
составляет около ± 5/
мм. Такая величина и получена (при N = 7 и 14) в экспериментах. За повышение точности
«заплачено» ограничениями модели: если реально источников нагрева несколько, то
модель перестает быть адекватной. Систематическую ошибку при определении
положения центра нагретой области можно оценить, используя данные эксперимента
5: разница в координате z,
которая определялась независимо первой и второй решетками, составила около 1
мм. Вместе со случайной ошибкой (± 1 мм) этого вполне достаточно для
медицинских приложений метода.
|
эксперимент |
ошибка определения координаты, мм |
восстановленный размер, мм |
реальный размер, мм |
ошибка определения температуры, К |
|
1а |
± 0.5 |
9 ± 1 |
9 |
|
|
1б |
± 1.4 |
15 ± 2 |
17 |
|
|
2 |
|
10 ± 3 |
9 |
± 0.6 |
|
3а по оси х по оси y |
± 0.8 ± 0.2 |
15.9 ± 1.2 10.0 ± 1.5 |
23 16 |
|
|
3б по оси х по оси y |
± 0.2 ± 0.2 |
8.4 ± 0.7 11 ± 1 |
16 16 |
|
|
4а |
|
|
|
± 0.5 |
|
5 |
± 0.6* ± 0.4** 1.2 ± 0.6*** |
13.1 ± 0.6**** 13.6 ± 0.6***** |
19 |
1.0 ± 0.5 |
* по оси х
** по оси y
*** по оси z
**** по измерениям с помощью первой решетки
***** по измерениям с помощью второй решетки
Аналогичная ситуация наблюдается при определении характерного размера области (таблица, столбец 3): случайная ошибка восстановления не превышает ± (2 – 3) мм. Систематическую ошибку измерений размера области можно оценить, используя данные экспериментов 3б, в котором восстанавливали размеры (в двух взаимно-перпендикулярных направлениях) центрально-симметричного объекта, и 5, в котором диаметр шара восстанавливали независимо двумя решетками. Разница в размерах (реально одинаковых) не превышает 2.6 мм – эта величина характеризует систематическую ошибку измерений. Существует еще систематическая ошибка моделирования: температурное распределение восстанавливается гауссианом, и определяется размер гауссиана, где температура спадает вдвое. Для анализа адекватности модельного представления необходимо сравнивать третий и четвертый столбцы таблицы. При восстановлении в экспериментах 1 и 2 одномерного гауссиана его размер практически равен (разница не превышала 2 мм) размеру нагретого тела. При восстановлении в экспериментах 3 и 5 двумерного гауссиана его размер в 1.5 ± 0.2 раза больше размера нагретого тела.
Точность восстановления температуры определяется данными, представленными в таблице, столбец 5. В эксперименте 2 температура исследуемого объекта была постоянна. Это дало возможность оценить случайную ошибку восстановления: 0.6 К. Систематическую ошибку измерений можно оценить по данным эксперимента 5: разница значений максимальной температуры, определенных двумя решетками, составляет 1.0 ± 0.5 К.
Таким образом, использование априорной информации при восстановлении распределения внутренней температуры объекта позволяет получить точность, приемлемую для медицинских приложений, за время, позволяющее отслеживать временные изменения температуры.
Литература
1. Годик Э.Э., Гуляев Ю.В. Человек “глазами радиофизики”. Радиотехника. 1991. №8. С. 51-62.
2. Inoue T., Shimizu H., Fujimura M., Saito A., Yoshioka Y., Matsuda T., Tominaga T. Noninvasive measurement of human brain temperature adjacent to arteriovenous malformation using 3.0 T magnetic resonance spectroscopy. Clinical Neurology and Neurosurgery. 2013. 115 (4): 445-449.
3. R. Maass-Moreno, C. A. Damianou. Noninvasive temperature estimation in tissue via ultrasound echo-shifts. Part I. Analytical model. J. Acoust. Soc. Am. 1996. V. 100. P. 2514.
4. L. Dubois, J.-P. Sozanski, V. Tessier, J.-C. Camart, J.-J. Fabre, J. Pribetich, M. Chive. Temperature control and thermal dosimetry by microwave radiometry in hyperthermia. IEEE Trans. Microwave Theory Tech. 1996. V. 44. P. 1755-1761.
5. V. Rieke and K. Butts Pauly. MR Thermometry. J. Magn. Reson. Imaging 2008. V. 27. P. 376–390.
6. Аносов А.А., Сергеева Т.В., Алехин А.И., Беляев Р.В., Вилков В.А., Иванникова О.Н., Казанский А.С, Кузнецова О.С., Лесс Ю.А., Мансфельд А.Д., Санин А.Г., Шаракшанэ А.С., Луковкин А.В. Акустотермометрическое сопровождение лазериндуцированной интерстициальной гипертермии молочной и щитовидной желез. Биомедицинская радиоэлектроника. 2008. №5. С. 67-72.
7. Бабий В.И. Перенос акустической энергии в поглощающей и излучающей среде. Мор. гидрофиз. исслед. 1974. №2 (65) С.189-192.
8. Bowen T. Passive remote temperature sensor system. U.S. Patent 4246784. Jan. 27. 1981.
9. Гуляев Ю.В., Годик Э.Э., Дементиенко В.В., Пасечник В.И., Рубцов А.А. О возможностях акустотермографии биологических объектов. Докл. АН СССР. 1985. Т.283. №6. С.1495-1499.
10.Bowen T. Acoustic radiation temperature for noninvasive thermometry. Automedica (UK). 1987. V. 8. #4. P. 247–267.
11.Миргородский В.И., Герасимов В.В., Пешин С.В. Исследования пространственного распределения источников некогерентного излучения с помощью корреляционной обработки. Письма в ЖЭТФ. 1995. Т. 62. Вып. 3. С. 236-241.
12.Passechnik V.I., Bograchev K.M., Anosov A.A. Fundamentals and prospects of passive thermoacoustic tomography. Critical Reviews in Biomedical Engineering. 2000. V. 28. #3–4. P. 603–640.
13.Буров В.А., Дариалашвили П.И., Румянцева О.Д. Активно-пассивная термоакустическая томография. Акуст. журн. 2002. Т.48. №4. С.474-484.
14.Аносов А.А., Пасечник В.И., Исрефилов М.Г. Восстановление двумерного распределения внутренней температуры модельного объекта методом пассивной термоакустической томографии. Акуст. журн. 1999. Т. 45. № 1. С. 20.
15.Аносов А.А., Беляев Р.В., Вилков В.А., Казанский А.С., Мансфельд А.Д., Субочев П.В. Динамическое восстановление глубинной температуры методом акустотермографии с помощью нейронных сетей. Акуст. журн. 2013. Т. 59. № 6. С. 768.
16.Krotov E.V., Zhadobov M.V., Reyman A.M., Volkov G.P., Zharov V.P. Detection of thermal acoustic radiation from laser-heated deep tissue. Appl. Phys. Lett. 2002. V. 81. P. 3918-3920.
17.Гуляев Ю.В., Бограчев К.М., Боровиков И.П., Обухов Ю.В., Пасечник В.И. Пассивная термоакустическая томография – методы и подходы. Радиотехника и электроника. 1998. Т. 43. №9 С. 140-146.
18.Бограчев К.М., Пасечник В.И. Метод стандартного источника в пассивной акустической термотомографии. Акуст. журн. 2003. Т. 49. № 4. С. 477–480.
19.Bosnyakov M.S., Obukhov Yu.V. Optimum wavelet basis for representation of the functions satisfying the head conduction equation. Pattern Recognition and Image Analysis. 2003. V. 13. #1. P. 621–624.
20.Аносов А.А., Беляев Р.В., Вилков В.А., Дворникова М.В., Дворникова В.В., Казанский А.С., Курятникова Н.А., Мансфельд А.Д. Акустотермометрическое восстановление профиля глубинной температуры с использованием уравнения теплопроводности. Акуст. журн. 2012. Т. 58. № 5. С. 592.
21.Аносов А.А., Беляев Р.В., Вилков В.А., Закарян А.В., Казанский А.С., Мансфельд А.Д., Субочев П.В. Восстановление глубинной температуры методом акустотермометри с учетом уравнения теплопроводности. Радиотехника и электроника. 2015. Т. 60. № 8. С. 855.
22.Ксенофонтов С.Ю., Мансфельд А.Д., Рейман А.М. Реконструктивная акустическая термотомография биологических объектов. Изв. ВУЗов РАДИОФИЗИКА. 1997. Т. XL. №6. С. 752-760.
23.Кротов Е.В., Ксенофонтов С.Ю., Мансфельд А.Д., Рейман А.М., Санин А.Г., Прудников М.Б. Экспериментальные исследования возможностей многоканальной акустической термотомографии. Изв. ВУЗов. Радиофизика. 1999. Т. XLII. № 5. С. 479–484.
24.Аносов А.А., Казанский А.С., Мансфельд А.Д., Шаракшанэ А.С. Определение положения и размера нагретой области методом динамической акустотермографии. // Журнал радиоэлектроники: электронный журнал. 2013. № 3. С. 10. URL: http://jre.cplire.ru/jre/mar13/11/text.pdf.
25.R. A. Hessemer, T. Perper, T. Bowen. Correlation thermotomography. US Patent 4416552. 1983.
26.Аносов А.А., Барабаненков Ю.Н., Сельский А.Г. Корреляционный прием теплового акустического излучения. Акуст. журн. 2003. Т. 49. № 6. С. 725-730.
27.Weaver R.L., Lobkis O.I. Elastic wave thermal fluctuations, ultrasonic waveforms by correlation of thermal phonons. J. Acoust. Soc. Am. 2003. V. 113 P. 2611–2621.
28.Буров В.А., Дариалашвили П.И., Евтухов С.Н., Румянцева О.Д. Экспериментальное моделирование процессов активно-пассивной термоакустической томографии. Акуст. журн. 2004. Т. 50 № 3. С. 298–310.
29.Миргородский В.И., Герасимов В.В., Пешин С.В. Экспериментальные исследования особенностей пассивной корреляционной томографии источников некогерентного акустического излучения мегагерцового диапазона. Акуст. журн. 2006. Т. 52. № 5. С. 606–612.
30.Godin O.A. Retrieval of Green’s functions of elastic waves from thermal fluctuations of fluid-solid systems. J. Acoust. Soc. Am. 2009. V. 125 P. 1960–1970.
31.Аносов А.А., Пасечник В.И., Шаблинский В.В. Пространственная разрешающая способность акустотермографии и СВЧ-радиометрии. Акустический журнал. 1991. Т. 37. № 4. С. 610.
32.Вилков В.А., Кротов Е.В., Мансфельд А.Д., Рейман А.М. Применение фокусируемых антенн для задач акустояркостной термометрии. Акуст. журн. 2005. Т.51 №1 С.63-70.
33.Кротов Е.В., Рейман А.М., Субочев П.В. Синтез акустической линзы Френеля для акустояркостной термометрии. Акуст. журн. 2007. Т.53. №6. С. 779-785.
34.Субочев П.В., Мансфельд А.Д., Беляев Р.В. Многочастотная акустическая термотомография при лазерной гипертермии: физическое моделирование. Вестник Нижегородского университета им. Н.И. Лобачевского. 2010. № 5 (1). С. 67-74.
35.Anosov A.A., Kazansky A.S., Subochev P.V., Mansfel'd A.D., Klinshov V.V. Passive estimation of internal temperatures making use of broadband ultrasound radiated by the body. J. Acoust. Soc. Am. 2015. Т. 137. № 4. С. 1667-1674.
36.Аносов А.А., Беляев Р.В., Клиньшов В.В., Мансфельд А.Д., Субочев П.В. Пассивная широкополосная акустическая термометрия. Журнал технической физики. 2016. Т. 86. № 4. С. 119-124.
37.Мансфельд А.Д. Акустотермометрия. Состояние и перспективы. Акуст. журн. 2009. Т. 55. № 4-5. С. 536-547.
38.Аносов А.Н., Беляев Р.В., Вилков В.А., Казанский А.С., Мансфельд А.Д., Шаракшанэ А.С. Определение динамики изменения температуры в модельном объекте методом акустотермографии. Акуст. журн. 2008. Т.54. №4. С. 540-545.
39.Аносов А.А., Немченко О.Ю., Лесс Ю.А., Казанский А.С., Мансфельд А.Д. Возможности акустотермометрии для контроля адресной доставки лекарств. Акуст. журн. 2015. Т. 61. № 4. С. 535.
40.Казанский А.С. Обработка акустотермометрических данных при помощи искусственных нейронных сетей. Нелинейный мир. 2011. Т. 9. №2 С. 112-113.
41.Аносов А.А., Балашов И.С., Беляев Р.В., Вилков В.А., Гарсков Р.В., Казанский А.С., Мансфельд А.Д., Щербаков М.И. Акустическая термометрия головного мозга пациентов с черепно-мозговой травмой. Биофизика. 2014. Т. 59. № 3. С. 545-551.
42.Аносов А.А., Беляев Р.В., Вилков В.А., Казанский А.С., Мансфельд А.Д., Шаракшанэ А.С. Динамическая акустотермография. Акуст. журн. 2009. Т. 55. № 4-5. С. 436-444.
43.А.А. Аносов, А.А. Шаракшанэ, А.С. Казанский, А.Д. Мансфельд, А.Г. Санин, А.С. Шаракшанэ Аппаратная функция широкополосного акустотермометрического датчика. Акуст. журн. 2016. Т. 62. № 6. В печати.
44.Passechnik V.I. Verification of the Physical basis of acoustothermography. Ultrasonics. 1994. V.32. P. 293-299.
45.F. Duck Physical properties of tissue. London. Academic Press. 1990. 346 P.
46.Аносов А.А., Пасечник В.И., Бограчев К.М. Пассивная термоакустическая томография кисти руки человека. Акуст. журн. 1998. Т. 44. № 6. С. 725-730.
47.Аносов А.А., Беляев Р.В., Вилков В.А., Дворникова М.В., Дворникова В.В., Казанский А.С., Курятникова Н.А., Мансфельд А.Д. Акустотермометрический контроль кисти человека при гипертермии и гипотермии. Акуст. журн. 2013. Т. 59. № 1. С. 109-114.
48.Аносов А.А., Казанский А.С., Мансфельд А.Д., Шаракшанэ А.С. Акустотермометрическое восстановление меняющегося во времени температурного распределения. Акуст. журн. 2016. Т. 62. № 2. С. 259.
49. V. I. Passechnik. The influence of sound scattering on the acoustobrightness temperature. Ultrasonics. 1996. V. 34. P. 677-685.
50.Аносов А.А., Беляев Р.В., Вилков В.А., Казанский А.С., Курятникова Н.А., Мансфельд А.Д. Акустотермометрические данные о кровотоке и теплопродукции в предплечье при физической нагрузке. Акуст. журн. 2013. Т. 59. № 4. С. 539.
51.Г. Ульмер, К. Брюк, Ф. Вальдек, О. Гарт, Г. Тевс Физиология человека: в 4-х томах. Т. 4. Пер. с англ. Под ред. Р. Шмидта и Г. Гевса. – М.: Мир, 1986. С. 23.
References
1. Godik E.E., Gulyaev Yu.V. Radiophysics looks at a human body. Radiotechnika – Radio engineering, 1991, No. 8, pp. 51-62. (In Russian)
2. Inoue T., Shimizu H., Fujimura M., Saito A., Yoshioka Y., Matsuda T., Tominaga T. Noninvasive measurement of human brain temperature adjacent to arteriovenous malformation using 3.0 T magnetic resonance spectroscopy. Clinical Neurology and Neurosurgery, 2013, Vol. 115, No. 4, pp. 445-449. DOI: http://dx.doi.org/10.1016/j.clineuro.2012.06.022
3. Maass-Moreno R., Damianou C.A. Noninvasive temperature estimation in tissue via ultrasound echo-shifts. Part I. Analytical model. J. Acoust. Soc. Am., 1996, Vol. 100, No.4, pp. 2514. Available at: http://dx.doi.org/10.1121/1.417359
4. Dubois L., Sozanski J.-P., Tessier V., Camart J.-C., Fabre J.-J., Pribetich J., Chive M. Temperature control and thermal dosimetry by microwave radiometry in hyperthermia. IEEE Trans. Microwave Theory Tech., 1996, Vol. 44, No. 10, pp. 1755-1761. DOI: 10.1109/22.539932
5. Rieke V., Butts Pauly K. MR Thermometry. J. Magn. Reson. Imaging, 2008, Vol. 27, No. 2, pp. 376–390.
6. Anosov A.A., Sergeeva T.V., Alekhin A.I., Belyaev R.V., Vilkov V.A., Ivannikova O.N., Kazanskii A.S., Kuznetsova O.S., Less Yu.A., Mansfel’d A.D., Obukhov Yu.V., Sanin A.G., Sharakshane A.S., Lukovkin A.V. Acoustothermometric accompaniment of the laser-induced interstitial hyperthermia of mammary and thyroid glands. Biomed. Radioelektr. – Biomed. Radionics, 2008, No. 5, pp. 67-73. (In Russian)
7. Babii V.I. The transfer of acoustic energy in the absorbing and emitting medium. Mor. Gidrofiz. Issled. – Marine hydrophysical study, 1974, No. 2, pp. 189-192. (In Russian)
8. Bowen T. Passive remote temperature sensor system. US Patent 4246784. Jan. 27. 1981.
9. Gulyaev Yu.V., Godik E.E., Dementienko V.V., Pasechnik V.I., Rubtsov A.A. On the possibilities of the acoustothermography of biological objects. Dokl. Akad. Nauk SSSR – Reports of the Academy of Sciences, 1985, Vol. 283, No. 6, pp. 1495-1499. (In Russian)
10.Bowen T. Acoustic radiation temperature for noninvasive thermometry. Automedica (UK), 1987, Vol. 8, No. 4, pp.247–267.
11.Mirgorodskii V.I., Gerasimov V.V., Peshin S.V. Spatial distribution of incoherent radiation sources by correlation processing. JETP Letters, 1995, Vol. 62, No. 3, pp. 252-257.
12.Passechnik V.I., Bograchev K.M., Anosov A.A. Fundamentals and prospects of passive thermoacoustic tomography. Critical Reviews in Biomedical Engineering, 2000, Vol. 28, No. 3–4, pp. 603–640. DOI: 10.1615/CritRevBiomedEng.v28.i34.410
13.Burov V.A., Darialashvili P.I., Rumyantseva O.D. Active-passive thermoacoustic tomography. Acoust. Phys., 2002, Vol. 48, No. 4, pp. 412-422. DOI: 10.1134/1.1494019
14.Anosov A.A., Pasechnik V.I., Isrefilov M.G. Reconstruction of a two-dimensional distribution of the internal temperature of a model object by passive thermoacoustic tomography. Acoust. Phys., 1999, Vol. 45, No. 1, pp. 14-18.
15.Anosov A.A., Belyaev R.V., Vilkov V.A., Kazanskii A.S., Mansfel’d A.D., Subochev P.V. Dynamic deep temperature recovery by acoustic thermography using neural networks. Acoust. Phys., 2013, Vol. 59, No. 6, pp. 717-721. DOI: 10.1134/S1063771013050011
16.Krotov E.V., Zhadobov M.V., Reyman A.M., Volkov G.P., Zharov V.P. Detection of thermal acoustic radiation from laser-heated deep tissue. Appl. Phys. Lett., 2002, Vol. 81, No. 21, pp. 3918-3920. Available at: http://dx.doi.org/10.1063/1.1521245
17.Gulyaev Yu.V., Bograchev K.M., Borovikov I.P., Obukhov Yu.V., Passechnik V.I. Passive thermoacoustic tomography: methods and approaches. Journal of communications technology and electronics, 1998, Vol. 43, No. 9, pp. 1061-1067.
18.Bograchev K.M., Passechnik V.I. Standard source method in passive acoustic thermal tomography. Acoust. Phys., 2003, Vol. 49, No. 4, pp. 396–401. DOI: 10.1134/1.1591293
19.Bosnyakov M.S., Obukhov Yu.V. Optimum wavelet basis for representation of the functions satisfying the head conduction equation. Pattern Recognition and Image Analysis, 2003, Vol. 13, No. 1, pp. 621–624.
20.Anosov A.A., Belyaev R.V., Vilkov V.A., Dvornikova M.V., Dvornikova V.V., Kazanskii A.S., Kuryatnikova N.A., Mansfel’d A.D. Acousto-thermometric recovery of the deep temperature profile using heat conduction equation. Acoust. Phys., 2012, Vol. 58, No. 5, pp. 542-548. DOI: 10.1134/S1063771012030037
21.Anosov A.A., Belyaev R.V., Vilkov V.A., Zakaryan A.V., Kazanskii A.S., Mansfel’d A.D., Subochev P.V. Reconstruction of the deep temperature by the acoustothermometric method and with consideration for the heat conduction equation. Journal of Communications Technology and Electronics, 2015, Vol. 60, No. 8, pp. 919-927. DOI: 10.1134/S106422691508001X
22.Ksenofontov S.Yu., Mansfel’d A.D., Reiman A.M. Reconstructive acoustic thermotomography of biological objects. Radiophysics and Quantum Electronics, 1997, Vol. 40, No. 6, pp. 498-503. DOI: 10.1007/BF02675926
23.Krotov E.V., Ksenofontov S.Yu., Mansfel’d A.D., Reiman A.M., Sanin A.G., Prudnikov M.B. Experimental study of the potential of multichannel acoustic thermotomography. Radiophysics and Quantum Electronics, 1999, Vol. 42, No. 5, pp. 425-430. DOI: 10.1007/BF02677623
24.Anosov A.A., Kazanskii A.S., Mansfel’d A.D., Sharakshane A.S. Detection of heated region's location and size by dynamical acoustical thermography. Zhurnal Radioelektroniki - Journal of Radio Electronics, 2013, No. 3. Available at: URL: http://jre.cplire.ru/jre/mar13/11/text.pdf. (In Russian)
25.R. A. Hessemer, T. Perper, T. Bowen. Correlation thermotomography. US Patent 4416552. 1983.
26.Anosov A.A., Barabanenkov Yu.N., Sel’skii A.G. Correlation reception of thermal acoustic radiation. Acoust. Phys., 2003, Vol. 49, No. 6, pp. 615-619. DOI: 10.1134/1.1626171
27.Weaver R.L., Lobkis O.I. Elastic wave thermal fluctuations, ultrasonic waveforms by correlation of thermal phonons. J. Acoust. Soc. Am., 2003, Vol. 113, No.5, pp. 2611–2621. Available at: http://dx.doi.org/10.1121/1.1564017
28.Burov V.A., Darialashvili P.I., Evtukhov S.N., Rumyantseva O.D. Experimental modeling of the processes of active-passive thermoacoustic tomography. Acoust. Phys., 2004, Vol. 50, No. 3, pp. 243-254. DOI: 10.1134/1.1739492
29.Mirgorodskii V.I., Gerasimov V.V., Peshin S.V. Experimental studies of passive correlation tomography of incoherent acoustic sources in the megahertz frequency band. Acoust. Phys., 2006, Vol. 52, No. 5, pp. 606-612. DOI: 10.1134/S1063771006050150
30.Godin O.A. Retrieval of Green’s functions of elastic waves from thermal fluctuations of fluid-solid systems. J. Acoust. Soc. Am., 2009, Vol. 125, No. 4, pp. 1960–1970. Available at: http://dx.doi.org/10.1121/1.3082101
31.Anosov A.A., Pasechnik V.I., Shablinskii V.V. Spatial resolution of acoustotermography and microwave radiometry. Akust. Zhurn. – Acoust. Phys., 1991, Vol. 37, No. 4, pp. 610-615. (In Russian)
32.Vilkov V.A., Krotov E.V., Mansfel’d A.D., Reiman A.M. Application of focusing arrays to the problems of acoustic brightness thermometry. Acoust. Phys., 2005, Vol. 51, No. 1, pp. 63-70. DOI: 10.1134/1.1851630
33.Krotov E.V., Reiman A.M., Subochev P.V. Synthesis of a Fresnel acoustic lens for acoustic brightness thermometry. Acoust. Phys. 2007, Vol. 53, No. 6, pp. 688-693. DOI: 10.1134/S1063771007060061
34.Subochev P.V., Mansfel’d A.D., Belyaev R.V. Multifrequency acoustic thermography during laser hyperthermia: physical modeling. Vestn. NNGU im N. I. Lobachevskogo – Vestnik of Lobachevsky state university of Nizni Novgorod, 2010, No. 5 (1), pp. 67-74. (In Russian)
35.Anosov A.A., Kazansky A.S., Subochev P.V., Mansfel'd A.D., Klinshov V.V. Passive estimation of internal temperatures making use of broadband ultrasound radiated by the body. J. Acoust. Soc. Am., 2015, Vol. 137, No. 4, pp. 1667-1674. DOI: 10.1121/1.4915483
36.Anosov A.A., Belyaev R.V., Klinshov V.V., Mansfel’d A.D., Subochev P.V. Passive broadband acoustic thermometry. Technical physics, 2016, Vol. 86, No. 4, pp. 597-602. DOI: 10.1134/S1063784216040058
37.Mansfel’d A. D. Acoustothermometry: current status and prospects. Acoust. Phys., 2009, Vol. 55, No. 4-5, pp. 556-566. DOI: 10.1134/S1063771009040125
38.Anosov A.A., Belyaev R.V., Vilkov V.A., Kazanskii A.S., Mansfel’d A.D., Sharakshane A.S. Determination of the dynamics of temperature variation in a modal object by acoustic thermography. Acoust. Phys., 2008, Vol. 54, No. 4, pp. 464-468. DOI: 10.1134/S1063771008040040
39.Anosov A.A., Nemchenko O.Yu., Less Yu.A., Kazanskii A.S., Mansfel’d A.D. Possibilities of acoustic thermometry for controlling targeted drug delivery. Acoust. Phys., 2015, Vol. 61, No. 4, pp. 488-493. DOI: 10.1134/S1063771015040028
40.Kazansky A.S. Using artificial neural networks for processing acoustothermometrical data. Nelineinyi mir – Nonlinear World, 2011, Vol. 9, No. 2, pp. 112-113. (In Russian)
41.Anosov A.A., Balashov I.S., Belyaev R.V., Vilkov V.A., Garskov R.V., Kazanskii A.S., Mansfel’d A.D., Shcherbakov M.I. Acoustic thermometry of the patient brain with traumatic brain injury. Biophysics, 2014, Vol. 59, No. 3, pp. 447-452. DOI: 10.1134/S0006350914030026
42.Anosov A.A., Belyaev R.V., Vilkov V.A., Kazanskii A.S., Mansfel’d A.D., Sharakshane A.S. Dynamic acoustothermography. Acoust. Phys., 2009, Vol. 55, No. 4-5, pp. 454-462. DOI: 10.1134/S1063771009040022
43.Anosov A.A., Sharakshane A.A., Kazanskii A.S., Mansfel’d A.D., Sanin A.G., Sharakshane A.S. Directional pattern of broadband acoustothermometric sensor. Acoust. Phys., 2016, Vol. 62. In press.
44.Passechnik V.I. Verification of the physical basis of acoustothermography. Ultrasonics, 1994, Vol. 32, No. 4, pp. 293-299. Available at: http://dx.doi.org/10.1016/0041-624X(94)90009-4
45.Duck F. Physical properties of tissue. London, Academic Press. 1990. 346 p.
46.Anosov A.A., Pasechnik V.I., Bograchev K.M. Passive thermoacoustic tomography of a human hand. Acoust. Phys., 1998, Vol. 44, No. 6, pp. 629-634.
47.Anosov A.A., Belyaev R.V., Vilkov V.A., Dvornikova M.V., Dvornikova V.V., Kazanskii A.S., Kuryatnikova N.A., Mansfel’d A.D. Acoustothermometric study of the human hand under hyperthermia and hypothermia. Acoust. Phys., 2013, Vol. 59, No. 1, pp. 103-108. DOI: 10.1134/S1063771013010028
48.Anosov A.A., Kazanskii A.S., Mansfel’d A.D., Sharakshane A.S. Acoustic Thermometric Reconstruction of a Time-Varying Temperature Profile. Acoust. Phys., 2016, Vol. 62, No. 2, pp. 255-261. DOI: 10.1134/S1063771016020032
49. Passechnik V.I. The influence of sound scattering on the acoustobrightness temperature. Ultrasonics, 1996, Vol. 34, No. 6, pp. 677-685. DOI:10.1016/0041-624X(96)00051-0
50.Anosov A.A., Belyaev R.V., Vilkov V.A., Kazanskii A.S., Kuryatnikova N.A., Mansfel’d A.D. Acoustic thermometric data on blood flow and thermal output in forearm under physical pressure. Acoust. Phys., 2013, Vol. 59, No. 4, pp. 482-487. DOI: 10.1134/S1063771013040027
51.Schmidt R.F., Thews G. (eds) Human Physiology. 2nd ed. Berlin, Springer-Verlag. 1989. 828 p.