Делители квазиоптического пучка на тонких диэлектрических пленках в миллиметровом и субмиллиметровом диапазонах длин волн.

Делители квазиоптического пучка на тонких диэлектрических пленках в миллиметровом и субмиллиметровом диапазонах длин волн

Е. Е. Чигряй, Г. И. Хохлов, И. П. Никитин

Институт радиотехники и электроники им. В.А. Котельникова РАН, Фрязинский филиал, г. Фрязино

Статья поступила в редакцию 14 июня 2016 г.

Аннотация. Разработан оригинальный способ определения тангенса угла потерь (tgδ) тонких диэлектрических пластин и пленок в миллиметровом и субмиллиметровом диапазонах длин волн. Этот способ основан на сравнении добротностей пустого полусимметричного конфокального открытого резонатора и резонатора, в котором рядом с плоским зеркалом расположен измеряемый образец. Изменение потерь в резонаторе при внесении образца представляется как разница между потерями при отражении от плоского зеркала и от образца, расположенного перед зеркалом. При этом дополнительный фазовый набег, связанный с внесением в резонатор образца, компенсируется уменьшением длины резонатора. Измерения тангенса угла потерь tgδ тонких пленок были проведены в резонаторе на частоте 69.4 ГГц. Для определения показателя преломления пленок предлагается метод, основанный на измерении отражений от образца при падении на него плоской электромагнитной волны, сформированной системой рупор-линза. Показатель преломления измерялся на частоте 103.1 ГГц. Описанная методика применялась для измерения параметров лавсановых пленок различных марок и толщин (от 20 до 250 мкм), выбранных случайным образом. Полученные данные позволили рассчитать характеристики делителей квазиоптических пучков (коэффициента отражения в боковой канал и прохождения в рабочем канале). Создан алгоритм расчета характеристик делителей и проведены измерения делителей на пленках различной толщины на частоте 92 ГГц. Сравнивались коэффициенты отражения пленкой и металлической пластиной при падении волны под углом 45^о для ТЕ-волны и для ТМ-волны. При измерении коэффициента пропускания измерялся уровень прошедшей волны с пленкой, расположенной под углом 45^о к падающей волне, и без неё.

Ключевые слова: диэлектрические пленки, диэлектрическая проницаемость, открытый резонатор, квазиоптические методы измерений, миллиметровые волны.

Abstract. An original method is developed for determining the loss tangent (tand) of thin dielectric plates and films in the millimeter and submillimeter ranges. The method is based on comparing the Q factors of an empty semisymmetric confocal open resonator and a resonator in which a sample under test is placed near the plane mirror. The change of losses in the resonator due to the insertion of a sample is represented as a difference between the reflection losses from the plane mirror and from the sample placed in front of the mirror. The additional phase shift due to the insertion of a sample into the resonator is compensated for by a decrease in the resonator length. The loss tangent tand of thin films was measured in the cavity resonator at 69.4 GHz. To determine the refraction index of the films, a method is proposed that is based on measuring the reflection coefficient of a plane electromagnetic wave formed by the horn-lens system incident on a sample. The refraction index is measured at frequency of 103.1 GHz. The method is applied to measuring the parameters of Mylar films of various types and thickness (from 20 to 250 mm). The data obtained allowed one to calculate the characteristics of quasioptical beam splitters (the reflection coefficient into a side channel and transmission through the working channel). An algorithm is developed for calculating the characteristics of beam splitters, and the characteristics of beam splitters are measured for films of various thicknesses at frequency of 92 GHz. The reflection coefficients of the film and a metal plate are compared for TE and TM waves incident at 45^o. When measuring the transmission coefficient, the amplitude of the transmitted wave is measured for a film situated at 45^o to the incident wave and without the film.

Key words: dielectric films, dielectric permittivity, open resonator, quasioptical methods of measurement, millimeter waves.

1. Введение

В устройствах и в измерительных схемах миллиметровых и субмиллиметровых длин волн нашли применение различные диэлектрические пленки. Они используются для разделения квазиоптических пучков. На основе диэлектрической пленки, установленной на пути волнового пучка под углом 45^о, можно создать несколько измерительных схем, таких как контроль проходящей мощности (или опорный канал), схему для измерения отражения образцами, интерферометр и т.д. С помощью диэлектрических пленок можно разделить поток на несколько каналов [1]. Для расчетов подобных устройств необходимо знать диэлектрическую проницаемость пленки и её толщину. При этом, поскольку при изготовлении пленок они испытывают большие физические нагрузки (в том числе и температурные), их оптические свойства оказываются трудно воспроизводимыми. Это вызывает необходимость оперативного контроля оптических свойств пленок. Существуют методы измерения диэлектрических параметров пленок с использованием высокодобротных резонаторов Фабри-Перо [2]. Созданы установки и методики, позволяющие измерять диэлектрические параметры пленок без измерения их толщины, что значительно уменьшает погрешность измерений. При этом чувствительность этих комплексов позволяет определять показатель преломления тефлоновых пленок толщиной 5-20 мкм и замечать поглощение в них. Ввиду уникальности упомянутых измерительных установок воспроизведение их и доступ к ним ограничены.

Авторами разработаны модификации резонаторных методик и методик, основанных на амплитудных измерениях. Они дают значения диэлектрических параметров пленок с погрешностями, приемлемыми для практических применений этих пленок.

2. Измерение потерь в диэлектрических пленках в резонаторе

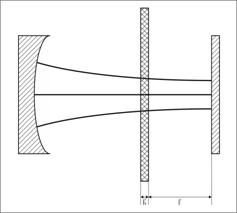
Рассмотрим случай расположения пленки в полусимметричном конфокальном резонаторе на расстоянии от плоского зеркала. Конфигурация резонатора и размещённой в нём пленки представлена на рис. 1.

Рис. 1. Расположение плёнки в резонаторе.

Связь внешнего электромагнитного поля с объёмом резонатора осуществляется через отверстия связи в сферическом зеркале. Выражение для добротности резонатора без пленки имеет вид:

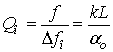, (1)

где L - длина пустого резонатора, соответствующая резонансу на частоте , k = 2π/c, с - скорость света,- ширина резонансной кривой на уровне 0.5, ₀- потери энергии в резонаторе. После внесения плёнки и настройки резонатора на резонанс путем уменьшения физической длины электрическая длина резонатора не изменяется. Добротность резонатора с пленкой может быть записана так:

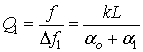, (2)

где - дополнительные потери энергии в резонаторе, вызванные внесением пленки в резонатор. Из (1) и (2) эти потери можно определить так:

. (3)

Эти потери можно представить как потери при отражении от пленки, расположенной на расстоянии от плоского зеркала

a = 1 - |r|², (4)

где коэффициент отражения r равен

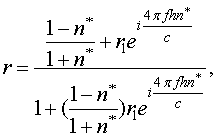(5)

Здесь n*=n + ik – комплексный показатель преломления материала пленки, h - толщина пленки, а r₁ определяется выражением

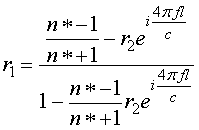Здесь – коэффициент отражения плоского зеркала резонатора. Этот коэффициент, согласно [3], равен

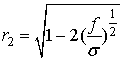, (6)

где - проводимость материала зеркала на частоте 60 ГГц. Для алюминиевого зеркала . Значение для алюминия равно 3.8 10⁷ [4].

Мнимая часть показателя преломления k находится графическим решением уравнения

x(k) = |a(k) - a₁ - a₂| = 0. (7)

Здесь - потери энергии при отражении металлическим зеркалом,

a₂ = 8.3 × 10^-⁴.

Тангенс угла диэлектрических потерь tgδ равен

tg δ = 2k / n. (8)

Потери энергии в резонаторе с плёнкой зависят от расстояния l между пленкой и плоским зеркалом.

Так, если лавсановая пленка толщиной 20 мкм расположена вплотную к плоскому зеркалу, отношение составляет 1.01 (электрическое поле вблизи металла мало), а если l = l/4, то это отношение равно 1.23, т.е. резонатор становится более чувствительным к внесению пленки. При более толстых пленках расстояние l меньше, чем l/4. В любом случае оптимальное расстояние пленки от плоского зеркала можно найти, построив зависимость a от l и определить l, при котором отклик резонатора будет максимальным. При этом l_maxслабо зависит отk.

Измерение показателя преломления пленки

Рассмотрим способ определения показателя преломления n из измерения отражения пленкой при нормальном падении плоской волны, сформированной системой рупор-линза. Коэффициент отражения равен

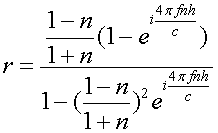. (9)

Показатель преломления находится графическим решением уравнения

, (10)

где R - измеренное значение коэффициента отражения.

3. Результаты измерений и расчетов

В таблице 1 приведены результаты измерений коэффициента преломления и тангенса угла потерь различных лавсановых пленок. Выбор пленок был случайным, поэтому и характеристики пленок значительно разнятся. Измерения tgδ были проведены в резонаторе на частоте 69.4 ГГц, а показатель преломления измерялся на частоте 103.1 ГГц.

Таблица 1.

Толщина пленки, мкм

253

n (103.1 ГГц)

1.82

1.85

1.808

1.805

tgδ (69.4 ГГц)

56 × 10^-⁴

52 × 10^-⁴

12 × 10^-³

63 × 10^-⁴

33 × 10^-⁴

В таблице 2 приведены величины рассчитанных и измеренных параметров пленочных делителей квазиоптических пучков. Измерения проводились на частоте 92 ГГц. Сравнивались коэффициенты отражения пленкой и металлической пластиной при падении волны под углом 45^о, для ТЕ-волны, и для ТМ-волны. При измерении коэффициента прохождения измеряется уровень прошедшей волны с пленкой, расположенной под углом 45^о к падающей волне и без неё.

Таблица 2.

Толщина пленки, мкм	ТЕ-волна					ТМ-волна
	эксперимент			расчёт		эксперимент			расчет
	R, dB	T, dB	R, dB		T, dB		R, dB	T, dB		R ,dB	T ,dB
50	-16.3	-0.1	-16.2		-0.12		-25.1	-0.1		-25.2	-0.02
97	-10.2	-0.5	-11.0		-0.38		-19.8	-0.1		-19.9	-0.6
253	-4.8	-2.0	-4.9		-1.73		-12.4	-0.3		-12.6	-0.26

Расчёты коэффициентов отражения и прохождения пленки выполнены по формулам [3]:

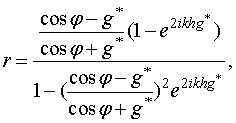
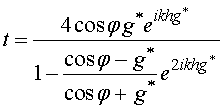. (11)

Здесь g*=u + iv = n*cosψ, ψ - угол преломления. Можно выразить u и v через угол падения φ и параметры пленки n и k:

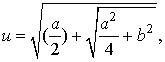v = b/u,

где a² = k²- sin²φ, b = nk.

Для ТМ-волны r и t имеют вид:

, .

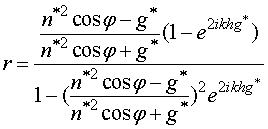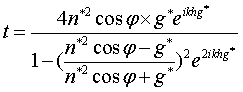В таблице коэффициенты отражения и прохождения приведены в dB:

R = 20log|r|, T = 20log|t|.

4. Заключение

Получены количественные характеристики делителей квазиоптических пучков миллиметровых волн. Для расчета характеристик были разработаны методы и проведены измерения электрических характеристик (показателя преломления (n) и тангенса диэлектрических потерь (tgδ)) некоторых лавсановых пленок различной толщины. Погрешности измерения параметров делителей пучков и диэлектрических свойств пленок находятся в допустимых пределах для практических применений.

Литература

1. Е.Е. Чигряй, Б.Г. Игнатов, Г.И. Хохлов и др. Радиоволновый интроскоп в миллиметровом диапазоне. Электромагнитные волны и электронные системы. 2010. Т. 15. № 1. стр. 50–54.

2. С.Н. Власов, В.В. Паршин, Е.А. Серов, Методы исследования тонких пленок в миллиметровом диапазоне. ЖТФ. 2010. Т. 80. Вып. 12. стр. 73–79.

3. М. Борн, Э. Вольф. Основы оптики. М.: Наука, 1970, 855с.

4. В.Г. Герасимов, П.Г. Грудинский, П.А. Жуков. Электротехнический справочник. В 3-х томах. Т. 1. Общие вопросы. Электротехнические материалы / под общей редакцией профессоров МЭИ.- 6-е издание.- М.: Энергия. 1982. С. 364.