|
|
"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 3, 2002 |
|
Исследование механизма формирования колебаний виртуального катода методами стохастического моделирования.
В.Н.Корниенко, А.П.Привезенцев
Получена 1 марта 2002 г.
В работе рассмотрена простая стохастическая модельная система, параметры которой обладают гистерезисными свойствами. Показано, что поведение такой системы близко к поведению устройств с виртуальным катодом и позволяет понять механизм формирования колебательных режимов потока заряженных частиц. В Приложении представлена программная реализация предложенной стохастической модели.
Динамика интенсивного потока заряженных частиц в диодном промежутке в режиме сверхкритического тока является типичным примером поведения нелинейной системы вдали от равновесия. Временная эволюция параметров пространственного заряда при сформировавшемся виртуальном катоде представляет сложную суперпозицию когерентной структуры с периодом порядка времени пролета заряда через промежуток и динамического хаоса на меньших временных масштабах [1,2]. В настоящей работе рассмотрена простая стохастическая модельная система, исследование которой позволяет понять механизм формирования колебательных режимов потока заряженных частиц с виртуальным катодом.
Рассмотрим плоский эквипотенциальный пролетный промежуток, в который инжектируется ток, превышающий критический. Как известно [3] самосогласованные уравнения движения зарядов в собственном кулоновском поле допускают в таком случае стационарное решение с частичным прохождением потока через промежуток и отражением его части от виртуального катода. Плотности инжектируемого
Ji прошедшего Jt и отраженного Jr тока связаны равенством Ji=Jt+Jr. При этом стационарное состояние образовано частицами с двумя принципиально различными типами траектории (пролетные и отраженные частицы). Времена движения в промежутке пролетных и отраженных частиц постоянны. Разделение общего числа (ni) инжектируемых частиц на пролетные (nt) и отраженные (nr) для произвольного интервала времени влета в стационарном потоке происходит в строго заданной пропорции nr / nt = Jr / Jt. Такое разделение обеспечивает сохранение стационарного баланса кулоновских сил отталкивания, изменения энергии частиц и их импульсов.Рассматриваемый стационарный поток неустойчив. В режиме сверхкритического тока формируется нестационарное состояние, в котором времена движения пролетных и отраженных частиц изменяются в достаточно широких пределах [1]. В нестационарном потоке происходит близкое к периодическому чередование процессов накопления (преобладают отражаемые частицы) и сброса заряда (преобладают пролетные частицы). Это
приводит к тому, что временные реализации параметров потока содержат интенсивную периодическую компоненту. Распределение по типам траекторий для инжектируемых частиц при этом происходит сложным образом. В каждом промежутке времени влета имеются частицы с различными типами траекторий, однако пропорции разделения на пролетные и возвратные выдерживаются “в среднем” лишь на достаточно больших промежутках времени. Для коротких интервалов времени, по-видимому, наблюдаются большие флуктуации, и разделение по типам траекторий изменяется непредсказуемым образом. Возникает ситуация, характерная для неустойчивых динамических систем с хаотическим режимом, когда детерминированное описание, предполагающее точное задание начальных условий становится недопустимой идеализацией [5]. Это обстоятельство является причиной того, что временные реализации параметров нестационарного потока имеют фрактальный характер [2,4].Рассмотренные особенности потока с виртуальным катодом определили выбор его стохастической модели, которая является модификацией классической схемы случайных блужданий [6]. Пусть частицы равномерно инжектируются в промежуток
0 Ј x Ј 1 в точке х = 0 с интервалом D t. Скорость частиц при влете v = 1. Закон движения частиц в дискретном времени задается выражениемгде
0 Ј xk ,i Ј 1 - координата к -ой частицы в i -ый момент времени, vk,i - ее скорость, к = 1,2,…,N, N – полное число частиц в текущий момент времени. Величина очередного шага по времени изменяется случайным образом D tk,i=D t | gi| , где gi - случайная величина распределенная по нормальному закону с нулевым средним и единичной дисперсией. При прохождении частицей через точку xc , определяющую положение центра масс системы,
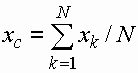
скорость частицы может случайным образом изменить знак с вероятностью P(v = -1) = q или остаться неизменной с вероятностью P(v = 1) = p, p + q = 1. Таким образом моделируется разделение частиц на пролетные и возвратные. Чередование процессов накопления и сброса зарядов моделируется введением зависимости вероятностей перехода p и q от положения центра масс. Эта зависимость имеет характер гистерезиса
где
xr > xl , pf > 1/2, pb < 1/2 . Гистерезис p(xc) обуславливает периодичность процесса “в среднем”, поскольку каждый раз при достижении центром масс границы гистерезиса направление его среднего перемещения, определяемое разностью p-q, изменяется.Анализ динамики системы проводился по временным реализациям координаты центра масс. Для оценки соответствия стохастической модели результатам расчетов в рамках детерминированного подхода, основанного на гамильтоновой модели плоских листов [1.2], сравнивались спектральные и фрактальные характеристики временных реализаций для этих моделей. Спектры мощности вычислялись с использованием быстрого преобразования Фурье. Анализ фрактальных свойств реализации проводился путем вычисления стандартного среднеквадратичного отключения приращений процесса D x(t) = x(t0+t) - x(t0) как функции сдвига по времени t. Такой метод используется в теории фрактальных временных рядов [7,8]. Зависимость среднеквадратичного отклонения приращений координаты от сдвига по времени для фрактального (обобщенного) броуновского движения, введенного Мальдебротом и Ван Нессом, определяется с помощью параметра H
где
Е[x] означает математическое ожидание величины х, s - положительная константа. Случай H = 1/2 соответствует винеровскому процессу (обычное броуновское движение), который является марковским. Фрактальное броуновское движение для H № 1/2 марковским свойством не обладает и при H > 1/2 является персистентным (сохраняющим тенденцию) случайным процессом. Величина параметра H связана с фрактальной размерностью d графика реализации процесса x(t) соотношением d = 2 - H .а) б)
Рис.1. Спектральная плотность мощности
Рассмотрим результаты численного моделирования. На рис.1 представлены спектральные плотности мощности S(n) как функции номера гармоники дискретного преобразования Фурье. График на рис.1 а) представляет спектральную плотность наведенного тока колебаний потока пространственного заряда с виртуальным катодом, рассчитанному по гамильтоновской модели плоских листов [1,2]. Приведенный график соответствует току инжекции Ji=3.56Jкр, где Jкр- критическое значение тока при котором происходит срыв режима стационарного потока через пролетный промежуток и начинает формироваться виртуальный катод. Спектр на рис.1. б) представляет колебания центра масс для стохастической модели (1) описанной выше. Период колебаний в этом процессе определяется средним временем первого достижения границы гистерезиса хr(xl) после очередной смены ветви гистерезиса в зависимости вероятности перехода p(xс) от положения центра масс (2). Вероятностный характер рассматриваемого процесса аналогичен классической задаче о первом достижении границы процессом диффузии (задача о разорении) [6]. Таким образом, частота периодической компоненты колебаний центра масс и, следовательно, положение максимумов в спектре мощности определяется величиной разности хr - xl . Увеличение расстояния между границами гистерезиса приводит к увеличению времени первого достижения и уменьшению частоты колебаний. Уменьшение xl при неизменном значении хr приводит к уменьшению номера гармоники с максимумом спектра nmax по закону, близкому к линейному nmax = k xl , с уменьшением хr - xl частота колебаний xc возрастает.
Отмеченная зависимость частоты колебаний центра масс от ширины области гистерезиса позволяет выбрать параметры стохастической модели хr и xl так, что положение максимумов спектра, определяющих регулярную компоненту колебаний в сравниваемых моделях практически совпадают, как это видно на рис.1.
Известно, что с увеличением тока инжекции положение виртуального катода приближается к электроду через который производится инжекция. При этом область локализации виртуального катода уменьшается, а частота его колебаний увеличивается. Росту степени надкритичности Ji/Jкр в рассматриваемой модели соответствует приближение правой границы гистерезиса хr к плоскости инжекции ( x = 0 ) и, в силу условия 0 < xl < хr , естественное уменьшение разности хr - xl ,которое приводит к увеличению частоты колебаний хc . Отмеченное обстоятельство подтверждает, что предлагаемая модель правильно передает особенности динамики виртуального катода.
Возможность формирования периодической структуры критически зависит от величины правой границы гистерезиса хr . При переходе хr за середину промежутка хr > 0.51 , колебательный режим с интенсивной периодической составляющей переходит в режим хаотических биений со спектром близким к сплошному.
Острота пиков спектра зависит также от величины вероятностей перехода при значениях pf » 0.8, pb» 0.2 дисперсия времени достижения границы гистерезиса сравнивается с его средним значением и периодическая компонента поглощается флуктуациями.
Рис.2. Зависимость стандартного отклонения от сдвига по времени
На рис.2 представлена зависимость логарифма стандартного отклонения
Ln(std(t)) как функция логарифма временного сдвига Ln(t), рассчитанная по алгоритму, описанному в [8]. Сплошная линия представляет результаты обработки процесса персистентных случайных блужданий центра масс, в исследуемой стохастической системе (1). Отмеченная крестиками штриховая линия соответствует временной реализации наведенного тока для гамильтоновской формы модели плоских листов. Полученные кривые наглядно демонстрируют существование области сдвигов по времени, где выполняется соотношение скейлингаLn(std(t)) = H Ln(t) + C
с
H = 0.886, C = -4,728 . Достаточно хорошее совпадение кривых в области скейлинга свидетельствует о том, что на этих масштабах времени динамика виртуального катода действительно может рассматриваться как случайный процесс и величину периода его колебаний можно интерпретировать в рамках вероятностной задачи о времени первого достижения границы частицей, совершающей случайные блуждания.Отметим, что рассмотренная задача является иллюстрацией общего для неустойчивых нелинейных систем явления – возникновения необратимого стохастического поведения при численном моделировании в рамках детерминированной модели [9].
Авторы выражают благодарность С.В.Гигинейшвили за многочисленные консультации и Р.И.Новиковой за внимание к работе.
ПРИЛОЖЕНИЕ.
Реализация стохастической модели.
Программа, написанная на языке
JAVA, позволяет получать временную зависимость положения центра масс системы для различных значений параметров:вероятности
pf (Вероятность "1", изменяется в интервале от 0 до 1)вероятности pb (Вероятность "2", изменяется в интервале от 0 до 1)
левой границы положения центра масс (изменяется от 0 до 1, причем должна быть меньше значения правой границы)
правой границы положения центра масс (изменяется от 0 до 1 и должна быть больше левой границы)
Рассматривается единичный интервал расстояния и предполагается, что модуль скорости частиц равен единице. Изменяя параметры системы, можно убедится в существовании разнообразных режимов движения центра масс системы.
СПИСОК ЛИТЕРАТУРЫ