|
|
"JOURNAL OF RADIOELECTRONICS" N 3, 2002 |
|
METHODOLOGY OF INDISTINCT IDENTIFICATION FOR IDENTIFICATION OF ELECTRONIC TRAFFIC CONTROL SYSTEMS
O.Svegzda 1) , e-mail: ly1df@one.lt,
V.Bagdonas1) , e-mail: valtek@eaf.ktu.lt
T. Magyla 1,2) , e-mail: Tomas.Magyla@eaf.ktu.lt
1)Kaunas Technology University KTU, Kaunas, Lithuania
2)Railways Infrastructure Modernization Group,
Lithuanian Railways LG PIU, Kaunas, Lithuania
Received on March 20, 2002.
This article contains development of an indistinct (fuzzy) methodology for identification of electronic systems, identification criteria form and a sample application of proposed methodology for evaluation of implementation impact of a centralized electronic traffic control system in LG. The proposed methodology performs solution of identification problem by the help of indistinct sets and expert evaluations. Therefore the intellect of an expert is treated as an instrument of measurement, which is used for evaluation of identification criteria. The identification of criteria in proposed methodology is performed in a trapezoid form of a membership function. Created methodology enables to evaluate influence of implementation of one or another electronic system and characterizes how good one or another decision alternative is suitable for evaluation needs, according to the formulated criteria of evaluation. The developed methodology was used for evaluation and analysis of implementation influence of a centralized traffic control system in LG, as dependence set of technical, social and other factors.
1. Introduction
3. The Methodology of Evaluation
4. results
5. CONCLUSIONS
6. References
Increasing complexity in electronic system hierarchy has caused a huge interest in using knowledge-based “fuzzy” identification. “Fuzzy” identification is based on new approaches to generation and selection of fuzzy logic families [1, 2, 3, 4, 5, 6]. The role of inference with uncertainty is becoming more and more important in real-time electronic processes. The efforts for building fuzzy decision-making systems to assist decision in non-standard situations have been widely discussed [7, 8, 9]. Different types of expert systems have been used for this or similar purposes, based on different approaches to fuzzy logics data acquisition. The corner stone of the fuzzy inference mechanism is fuzzy algorithm [10, 11] which consists from the following procedures: conversion of the input identification indistinct data from the research object (process, action) to the universal scale with rated values; processing of the universal scale rated input values by using fuzzy rule system to the output values of universal rated scale; conversion of the output rated values to the normal dimension output signals for inference or formation of the control output signal. Almost the same idea is used in expert systems [12, 13, 14, 15, 16] where experts perform initial evaluation of the parameter by evaluating that parameter in fuzzy numbers with different form of a membership function (the process of “fuzzification”); on the next phase, the data array is processed by applying fuzzy rules; and on the end the received fuzzy expression is “defuzzificated” thus obtaining alternatives for inference or the final result of identification or evaluation.
So far no comprehensive approach exists for evaluating and finding objective overall impact of implementation of a new railway electronics projects, among the most complicated decision/evaluation problems that exist. In complicated railway electronics, decision-making situations where research objects are huge electronic traffic interlocking or centralized traffic control systems, evaluation and optimization, based on classical methods, is impossible, as the only one acceptable way for identification of evaluation facets (from our point of view) is by using the abovementioned fuzzy algorithm idea adopted for expert inference mechanism. In most of fuzzy expert systems the standard identification and inference methods [12, 13, 17] are used. Processing of expert submitted evaluation data can be based on a fuzzy analytic hierarchy pair-wise comparison method [2, 13, 15], weight coefficient space transformation method [18], or other robust methods of analysis [19, 20]; some of direct calculation methods are based on the fuzzy inference software packages (FuzzyCalc, Mathlab Fuzzy workbench, Fagoal). No one of these standard methods have enough strength to withstand the inadequateness, caused by the non-linearity of the expert utility function, as in most of these methods expert initial evaluation results are taken for granted. We have proved many times, that inadequateness, caused by the shortage of expert experience or non-linearity of expert utility function can mutilate both intermediate results of inference process, and the final result of identification or evaluation [21, 22, 23]. Therefore the modified methodology, free from the abovementioned shortcomings has been proposed in this article. We have proposed to evaluate the utility of implementation of electronic centralized traffic control system by using expert evaluations in indistinct numbers, in a form of a trapezoid membership function, as we are confident about advantages, obtained by using this evaluation method. The methodology of evaluation and weighting of criteria in a trapezoid membership form is proposed in this article, together with the results of a sample evaluation in railways electronics.
2. Factors of Evaluation
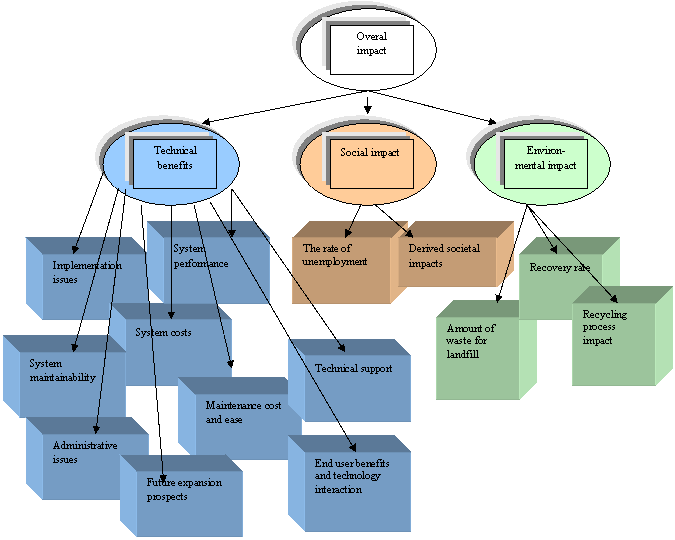
The implementation result of a new electronic traffic control system usually means maximum throughput capacity, optimal time tables, comfortable traffic data filtering and analysis, minimum human supervision, therefore minimum expenses for maintenance and so on. All the possible benefits taken together minus the cost of the system project, permission for construction work, manufacturing, installation, commissioning, maintenance, and the possible shortcomings of the new system gives the understanding of the system implementation overall impact. A new comprehensive system does not always means a better one. If all of the possible positive effects, taken together are equal to or dominate over the negative side of the implementation issues. For instance [22], after the detailed analysis by applying mathematical modeling and expert evaluations to a railways electronic auto-block system, as a research object, it turned out, that the implementation impact of a modern auto-block system (instead of the existing relay semi-automatic block system) will deliver traffic throughput capacity approx. one and a half times higher than the old one. This is an impressive indicator, but by the help of an expert system, applied to the prognosis of traffic growth, it was sorted out, that at the moment of research the old semi-automatic block system was able to handle at least three times higher throughput capacity, compared with statistics of that time. The railways growth prognosis was such, that the maximum capacity will only be reached in a decade or so, and it was a fact, that speaking in monetary terms, the implementation of a new automated-block system was not reasonable. The lesson is, that as many factors, as possible have to be included into the set of evaluation facets, interacting the final goal, but factors must not be redundant or overlapping [18]. The expansion and innovation process of railway traffic control systems results in many positive technical issues: better administrative, organizational and technical performance of railways, reliability, technical interaction, lower capital, operating and maintenance costs, ease of implementation and maintenance, many useful new features of a network and an integration performance, psychological impression to the end user. In different performance evaluation methodologies these positive issues are taken for granted, and usually only different alternatives of positive impacts are being analyzed [15, 17, 24, 25, 26]. But the implementation of a new traffic control system also has an inward-effect: environmental impact, job loses, and other derived societal shortcomings (see Fig 1).
Fig. 1
Environmental issues of railways electronics has long been considered as positive and environmental-friendly, therefore no effective measures have been taken to prevent waste growth, however, there is an increasing recognition, that many processes used to produce electronic systems do have environmental consequences (as a result of materials used, power consumed, or end-of life product consideration); some electronic products do have increasing disposal problems [17, 27, 28]. The replacement of old relay-based circuits with newly developed electronic computerized traffic control systems will result in a huge amount of electronics waste, designated for landfill. An effective, decision-based recycling is one option that may aid in reducing the volume of electronics waste designated for landfill disposal, with the possible decision model, which can be motivated on using expert evaluations.
The other unwanted effect of implementation of centralized electronic traffic control systems- job loses, that are related to the declining human supervision demand in new electronic traffic control systems. As experience shows, electronics and computer technology boosts with an exponential acceleration, and a new Artificial Intellect mindset will be the engine for inference. Human supervision demand in the wide area Centralized Traffic Control Systems [29] is declining and needed only for occasional system maintenance procedures, but not for daily influence. That results job loses and in turn, job loses result in many unwanted societal sideband effects.
The abovementioned problems are quite important in railway electronics. Proper measures can compensate or even eliminate unwanted effects of system level decisions, if applied to a planned situation. The situation can be planned, by referring to a prognosis of evaluation. Our aim in this article is to propose a methodology that is capable to adequately identify the relationships between attributes and objectives of both technical and institutional issues of electronic traffic control systems in railways.
3. The Methodology of Evaluation
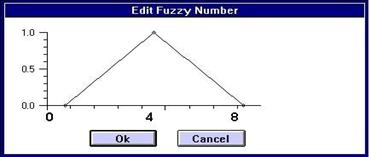
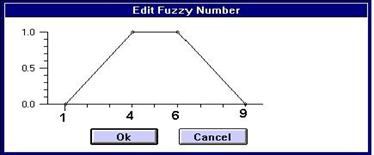
In simple electronic traffic control systems simulation of the electronic network throughput capacity could be an efficient way out for evaluating the impact of the given system [22]. It is quite informative, especially for a single layer hierarchy system. But in multi-attribute multi-layer electronic traffic control systems complexity overruns informative issues. Therefore the ordinary way for performing multi-criteria evaluation of the research object (electronic traffic control systems) is by using group expert evaluations, submitted in expressions with indistinct numbers, characterized by “triangle” [6, 22] type membership function. Every facet from the developed decision problem hierarchy is evaluated separately by providing it with corresponding membership form. Fig 2 represents a well-known example of indistinct number in a form of triangular membership.
Fig. 2
If we analyze it in more details, we’ll notice, that the triangular membership function (see Fig 2.) is derived from expert evaluation information, and can be formalized as follows:
1.
submitted probability
p,
which is usually in a form of interval
![]() ,
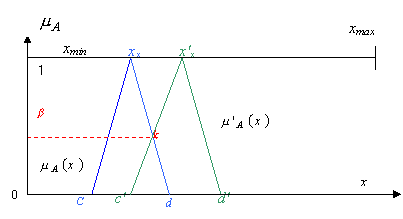
where the value of the evaluated hierarchy criterion A may be (see
Fig 3, a detail view of a triangle membership);
,
where the value of the evaluated hierarchy criterion A may be (see
Fig 3, a detail view of a triangle membership);
2. typical and most expected fuzzy value x of evaluated criterion, by the opinion of an expert.
In that case the evaluation of criterion A can be formulated like this:
Fig. 3
This form is quite desirable for the knowledge engineer, but psychologically is inconvenient for an expert, performing the evaluation: it may be hard to interpret separate parts of the membership function. Due to this and some other reasons (some of these reasons are quite personal characteristics of the expert), statistics is usually used to characterize the perfection of an expert [15, 30, 31]. But in some new and un-traditional decision problems statistics data may not exist. Our experiments show [6, 21, 23], that evaluations, performed by a single expert, may fluctuate a lot, depending on expert experience, and may not be time-constant, therefore such methodology of evaluation is imprecise and does not worth to pay much attention. Therefore we propose a weight coefficient (kind of expert “calibration” procedure), which is engaged to characterize expert’s ability to evaluate precisely. Moreover, we suggest engage a group evaluation:
where
![]() -
is a direct evaluation of evaluation facet A by the j-th
expert (
-
is a direct evaluation of evaluation facet A by the j-th
expert (![]() - index of the expert); the index of the goal for
this separate case in multi-facet evaluations is
- index of the expert); the index of the goal for
this separate case in multi-facet evaluations is
![]() .
A weight coefficient, characterizing expert’s utility function and expert’s
ability to evaluate precisely is engaged, thus obtaining complex expression of
the evaluation
.
A weight coefficient, characterizing expert’s utility function and expert’s
ability to evaluate precisely is engaged, thus obtaining complex expression of
the evaluation
![]() :
:
where
![]() -
the complex expert weight coefficient. Then a
complete rated indistinct expression for a group evaluation
-
the complex expert weight coefficient. Then a
complete rated indistinct expression for a group evaluation
![]() is
as follows:
is
as follows:
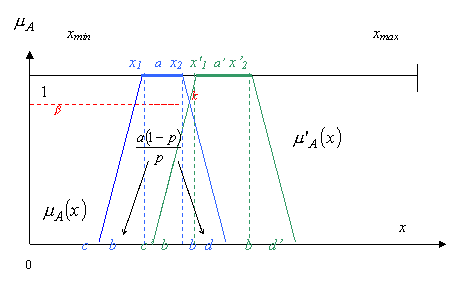
But from psychological point of view a more convenient way (see Fig 4) is to use indistinct evaluations in trapezoid membership. In that case an expert is asked to point out:
- an
interval
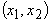 ,
where the most typical value of the criterion A is, by the opinion of
an expert (see Fig 5);
,
where the most typical value of the criterion A is, by the opinion of
an expert (see Fig 5); -
subjective probability p (which is in a form of an interval
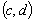 )
under which the expert is right.
)
under which the expert is right.
In that case the evaluation of the indication A is as follows:
Fig. 4
Then a group expert evaluation in a trapezoid membership is as follows:
Fig. 5
A trapezoid
type membership function expression
![]() from
equation (5) can be formulated as follows (see Fig 5):
from
equation (5) can be formulated as follows (see Fig 5):
where
We can easily notice, that formula (7) is valid only if:
For the
ease of calculations, we’ll make an assumption, that
![]() ;
or else the membership formula (7) has to be modified.
;
or else the membership formula (7) has to be modified.
Modification 1): if
![]() ;
then
;
then
Modification 2): if
![]() ;
then
;
then
Modification 3): if b>2x1; then
where
![]()
Modification 4): if b>2(1-x2); then
where
![]() .
.
As we can clearly see from Fig 3 and Fig 5,
evaluation in a trapezoid membership function posses the same functionality,
like evaluations in a triangle membership function, if only
![]() and
and
![]() .
When
.
When
![]() (
(![]() ),
an error appears. If
),
an error appears. If
![]() is
acceptable, an error may be regarded as unimportant. Then the
abovementioned psychologically convenient evaluations, submitted in trapezoid
membership function, are processed by applying a derived methodology, which is
based on a triangle membership evaluation method.
is
acceptable, an error may be regarded as unimportant. Then the
abovementioned psychologically convenient evaluations, submitted in trapezoid
membership function, are processed by applying a derived methodology, which is
based on a triangle membership evaluation method.
Let us assume, that expert evaluations are of a real-life,
and inadequateness, which is dependent upon the non-linearity of expert’s
subjective efficiency function [23] is present together with
other expert shortages. Non-linearity of expert’s subjective efficiency
function is characteristic for non-typical decisions, projects, reforms, where
expert conservatism takes place; also in making decisions where an expert is a
concerned person. Trying to diminish or eliminate the mistakes derived from
non-linearity of the expert’s subjective efficiency function, a correction
procedure is needed: both the expert’s submitted direct evaluation of
evaluation facet A
![]() and
a Parett set of partial evaluation facets
and
a Parett set of partial evaluation facets
![]() have
to be enlarged by the number
have
to be enlarged by the number
![]() ,
equal to the j-th expert risk (evaluating object, process or action
A) supplement function, to become “complete”-
,
equal to the j-th expert risk (evaluating object, process or action
A) supplement function, to become “complete”-
![]() .
The “incompleteness” elimination procedure for submitted
evaluations
.
The “incompleteness” elimination procedure for submitted
evaluations
![]() and
and
![]() ,
can be formulated as follows [23]:
,
can be formulated as follows [23]:
Actually, the expert risk supplement function is calculated only after
obtaining the expert’s efficiency function. This function depends on the
evaluated factor A and can be time dependant. Due to this reason
efficiency function has to be measured at the time of performing expert
interviewing. The procedure of efficiency function measurement is quite
complicated, therefore it is purposeful to measure it at single point and only
then (with acceptable error) the expert’s turn for non-risk can be considered
as constant:
![]() .
The expert’s
.
The expert’s
![]() can
also be calculated by using classical lottery methods [23].
In general case a weight coefficient for summing up expert’s efficiency
function must be included into the complete rated indistinct expression for a
group evaluation (formula (4)), and in that case it must be
as follows:
can
also be calculated by using classical lottery methods [23].
In general case a weight coefficient for summing up expert’s efficiency
function must be included into the complete rated indistinct expression for a
group evaluation (formula (4)), and in that case it must be
as follows:
where:
![]() -
direct evaluation of evaluation object A by the j-th
expert;
-
direct evaluation of evaluation object A by the j-th
expert;
j =
![]() -
index of the expert (the index of the goal in
multi-attribute evaluations is
-
index of the expert (the index of the goal in
multi-attribute evaluations is
![]() );
);
![]() -
complex expert weight coefficient. For the
triangular membership case it can be formulated as following:
-
complex expert weight coefficient. For the
triangular membership case it can be formulated as following:
where
![]() is
a weight coefficient, characterizing expert’s experience level (“ability to
evaluate in chime’);
is
a weight coefficient, characterizing expert’s experience level (“ability to
evaluate in chime’);
![]() is
a weight coefficient, characterizing expert’s distinctness of evaluations;
is
a weight coefficient, characterizing expert’s distinctness of evaluations;
![]() is
a weight coefficient, characterizing expert’s efficiency function (its
expression was discussed earlier).
is
a weight coefficient, characterizing expert’s efficiency function (its
expression was discussed earlier).
For the
triangle membership case, the best illustration of
![]() is
from geometrical point of view- it is a magnitude of intersection point k
of both triangles
is
from geometrical point of view- it is a magnitude of intersection point k
of both triangles
![]() and
and
![]() (see
Fig 3). Triangle
(see
Fig 3). Triangle
![]() represents
direct evaluation
represents
direct evaluation
![]() of
our research facet, and
of
our research facet, and
![]() represents
indirect (summarized) evaluation
represents
indirect (summarized) evaluation
![]() of
the Parett set of facets. The coefficient
of
the Parett set of facets. The coefficient
![]() can
be found as the rate of the area of intersection of these triangles:
can
be found as the rate of the area of intersection of these triangles:
The bigger
is the area, the more distinct is expert evaluation.
The same idea can be used for the trapezoid
membership case (see Fig 5). From geometrical point of
view,
![]() is
a magnitude of an intersection point k of trapezoids
is
a magnitude of an intersection point k of trapezoids
![]() and
and
![]() .
Trapezoid
.
Trapezoid
![]() represents
direct evaluation
represents
direct evaluation
![]() of
evaluation facet A and a trapezoid
of
evaluation facet A and a trapezoid
![]() represents
summarized evaluation
represents
summarized evaluation
![]() of
the Parett set of partial facets. Coefficient
of
the Parett set of partial facets. Coefficient
![]() is
found as the rate of the area of intersection of these trapezoids:
is
found as the rate of the area of intersection of these trapezoids:
The bigger is the area of intersection, the more distinct is expert evaluation. For the trapezoid case, we would like to propose to calculate weight coefficient, characterizing expert’s experience level by applying fuzzy integral (so called “fuzzy” expected value”) expression [32, 33]:
where:
![]() -
fuzzy integral [32] of
-
fuzzy integral [32] of
![]() by
indistinct measure x(.) (“
by
indistinct measure x(.) (“![]() ”
means “minimum”);
”
means “minimum”);
![]() and
and
![]() -indistinct
evaluations, characterized by their membership functions, correspondingly
-indistinct
evaluations, characterized by their membership functions, correspondingly
![]() and
and
![]() ;
where
;
where
![]() represents
(trapezoid
represents
(trapezoid
![]() )
direct evaluation of A, and
)
direct evaluation of A, and
![]() represents
(trapezoid
represents
(trapezoid
![]() )
summarized (Parett) evaluation of A.
)
summarized (Parett) evaluation of A.
Weight
coefficient
![]() ,
characterizing distinctness of expert’s evaluations, (for a trapezoid case) is
formulated by applying fuzzy integral expression and by using the same
conception as for the triangular membership case:
,
characterizing distinctness of expert’s evaluations, (for a trapezoid case) is
formulated by applying fuzzy integral expression and by using the same
conception as for the triangular membership case:
Finally, a
coefficient is needed (lets us call it
![]() )
to eliminate the transformation “triangle to trapezoid” influence. This
influence is depending only on the trapezoid top length a, namely on
the interval
)
to eliminate the transformation “triangle to trapezoid” influence. This
influence is depending only on the trapezoid top length a, namely on
the interval![]() .
If we split this interval into two equal parts
.
If we split this interval into two equal parts
![]() and
and
![]() ,
the central point x can be treated like a median value of the triangle,
the transformation triangle-to-trapezoid influence instantly becomes reduced
twice. Coefficient
,
the central point x can be treated like a median value of the triangle,
the transformation triangle-to-trapezoid influence instantly becomes reduced
twice. Coefficient
![]() is
as follows:
is
as follows:
where
![]() is
a minimal average length of trapezoid top
is
a minimal average length of trapezoid top
![]() from
submitted expert evaluations;
from
submitted expert evaluations;
![]() .
Then the complex weight coefficient for a trapezoid membership function is as
follows:
.
Then the complex weight coefficient for a trapezoid membership function is as
follows:
Then the complex indistinct evaluation of an object, process or action A with a trapezoid membership function is characterized by:
As a result of our proposed methodology, an expression of a complex indistinct evaluation of implementation expediency for centralized electronic traffic control system, where subsequent hierarchy facets are characterized with a trapezoid membership function, was obtained (formula (23)). Formula (23) was experimentally tested and obtained results were compared with experimentally (by the help of formula (15)) obtained results of evaluation in triangular membership, and results of mathematical simulation by applying GPSS [22]. The comparison has proved precision of calculations and low indistinctness of prognosis by using (23) formula. Comparison procedure was executed by applying developed formulas to a small electronic centralized traffic control network between two nodes, as GPSS is not suitable for more complex solutions.
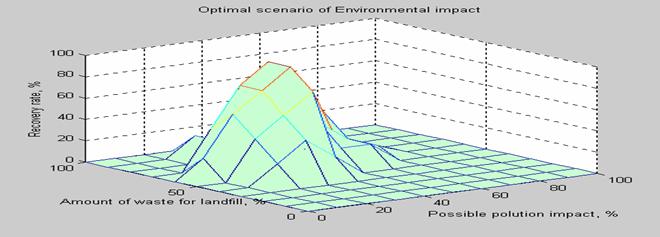
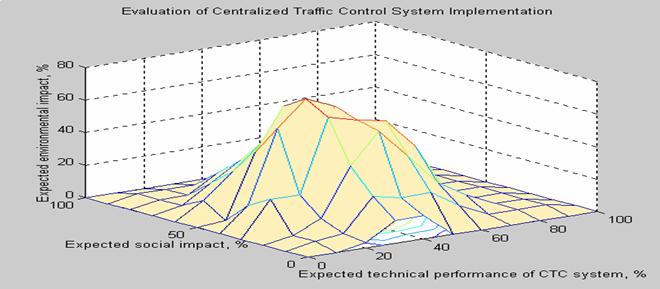
The second phase of experiments included results, obtained after the evaluation of a centralized electronic traffic control system (CTC) EbiScreen. As an example of attribute hierarchy for EbiScreen, attributes of electronic interlocking Ebilock 950, experimentally examined earlier [13], were chosen. For the evaluation of CTC EbiScreen we decided on three main branches of evaluation attributes: technical, environmental and social attribute branches (Fig 1). The process of evaluation of electronic CTC EbiScreen has included evaluation of the overall impact of CTC implementation as a sum impact value of the main three attribute branches versus the utility of the existing old CTC system. Expert submitted evaluations have been processed by applying formula (23). The branch of technical attributes have been scaled down to a lower hierarchy facets: implementation issues, system costs, system performance, technical benefits and technology interaction for the end user, system maintainability, maintenance cost and ease, technical support, administrative issues, future expansion prospects and other facets, scaled down to a lower branch of hierarchy (see Fig 1). The branch of environmental attributes: amount of waste for landfill (slag, ash, non-recyclable materials), recycling process impacts (global warming, acidification, photochemical ozone creation, possible photo-smog), recovery rate and cost of the recycled materials as a function of recycling scenario (Ag, Al, Cu, Fe, Hg, Pb and others). Recovery rate is mostly dependent on the amount of recovered metals and on the cost of recycling [28]. Different scenarios of end-of-life electronics recycling have been analyzed, during the evaluation of environmental issue. Due to the limitations of this article scope the evaluation results have been reviewed quite shortly, and the main environmental dependency impacts can be seen from the picture (see Fig 6).
Fig. 6
Fig. 7
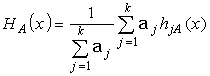
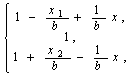
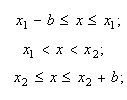
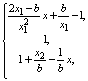
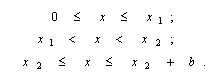
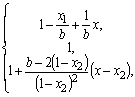
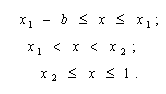
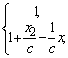
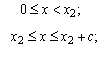
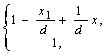
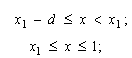
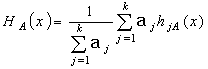
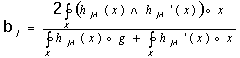 ;
;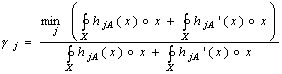
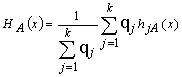 .
.