 |
"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 3, 2004 |
 |
Сверхразрешение в системах радиовидения миллиметрового диапазона
Пирогов Ю.А., Гладун В.В., Тищенко Д.А., Тимановский А.Л.,
Шлемин И.В., Джен С.Ф.
Лаборатория микроволновой радиометрии
физического факультета МГУ им. М.В. Ломоносова
Получена 29.03.2004 г.
Рассмотрены принципы построения пассивных систем радиовидения. Произведен анализ путей улучшения основных характеристик систем пассивного радиовидения. Представлены численные методы улучшения разрешения получаемых изображений. Затронут вопрос корректной дискретизации изображения при повышении разрешения. Приведены результаты численных экспериментов по восстановлению изображений, а также результаты обработки реальных данных.
Содержание
Сверхразрешение в системах радиовидения миллиметрового диапазона..
2 Принципы построения систем пассивного радиовидения
3.4 Дискретизация в условиях сверхразрешения
3.5.2 Экспериментальные данные
1 Введение
К настоящему времени системы радиовидения используются во многих областях науки и техники, и интерес к ним продолжает расти. Существует еще множество областей, где они могут использоваться в будущем. Широкое распространение систем радиовидения и, особенно, систем пассивного радиовидения невозможно без достижения характеристик, конкурентноспособных по сравнению с системами инфракрасного и оптического диапазонов. К важнейшим характеристикам, требующим особого внимания, относятся угловое разрешение, быстродействие и чувствительность. В данной работе представлены методы улучшения указанных характеристик систем пассивного радиовидения.
Одним из наиболее заметных узких мест таких систем является их быстродействие, скорость получения конечного изображения. Эта скорость ограничена самим принципом радиометрии. Как известно [1], радиометрический выигрыш пропорционален корню квадратному из постоянной времени интегрирования выходного каскада радиометра. Так, для повышения чувствительности в два раза требуется увеличить выходное время интегрирования в четыре раза при прочих постоянных параметрах. Типичным значением постоянной времени интегрирования является величина около 0.1 с, при этом интегратор может быть реализован как аналоговый фильтр или как цифровая обработка сигнала. Такие значения постоянной времени означают, что за секунду будет измерено 10 пикселов (минимальных элементов изображения), а на получение изображения 200 на 200 пикселов понадобится около часа. Если же учесть время необходимое для осуществления механического сканирования, то общее время измерения еще более возрастет.
При заданной чувствительности есть несколько способов увеличить скорость получения изображения. Один из способов – уменьшение времени интегрирования за счет изменения характеристик остальных систем радиометра. Возможно, например, увеличение ширины входной полосы частот радиометра, понижение собственных шумов радиометра за счет использования охлаждаемых детекторов, и т.п. Другим подходом является применение многоканальных систем [2], в которых одновременно работают несколько каналов радиометра. Применение, например, десятиканальной системы радиовидения позволяет ускорить процесс получения изображения в десять раз по сравнению с аналогичной одноканальной системой.
Другой проблемой в системах радиовидения является угловое
разрешение 
,
оно ограничено рэлеевским пределом 
[1] ,
где 
- рабочая длина волны, D – входная апертура. Повысить угловое разрешение можно
двумя путями: варьируя параметры
и D, или
применяя методы сверхразрешения, основанные на математической обработке
измеренных радиометрических данных. Цель такой обработки – компенсировать
искажения изображения, вызванные конечным угловым разрешением системы, путем
математического решения обратной задачи. В то время как уменьшение рабочей
длины волны и увеличение апертуры является либо дорогостоящим, либо вообще
невозможным по техническим причинам, сверхразрешение может быть применено практически
в любой системе радиовидения. Однако, как известно, алгоритмы сверхразрешения
требуют значительных вычислительных ресурсов.
2 Принципы построения систем пассивного радиовидения
Принцип действия всех систем пассивного радиовидения основан
на регистрации собственного теплового электромагнитного излучения исследуемых
объектов. Тепловое излучение носит шумовой характер и в области радиоволн имеет
весьма низкую интенсивность. Спектральная плотность потока излучения абсолютно
черного тела (АЧТ) дается формулой Планка
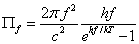[3]
.
Согласно этой формуле, излучение в миллиметровой области имеет порядок ~10-15 Вт/(Гц·м2). Для детектирования столь слабых сигналов применяются радиометры – сверхчувствительные приемники, принцип действия которых основан на накоплении полезного сигнала. В современных условиях при комнатной температуре удается достичь чувствительности в десятые и сотые доли Кельвина.
В области радиоволн, где 
формула Планка переходит в Формулу
Рэлея-Джинса 
.
Таким образом, интенсивность
микроволнового излучения пропорциональна физической температуре черного тела,
что ведет к заметному упрощению методов радиометрии и интерпретации данных. Для
реальных тел вводят понятие радиояркостной температуры 
, которая по определению равна
физической температуре такого АЧТ, которое создавало бы излучение такой же
интенсивности в исследуемом диапазоне частот [1].
Рабочий диапазон частот систем пассивного радиовидения обычно выбирается в окне прозрачности атмосферы, для того чтобы минимизировать потери сигнала в атмосфере и, тем самым, увеличить дальность действия и всепогодные характеристики систем. В лаборатории микроволновой радиометрии МГУ широко используются системы трех- и восьми-миллиметрового диапазонов.
Рассмотрим антенную часть систем радиовидения. Задача антенной системы сформировать как можно более узкую аппаратную функцию – «луч», сосредоточенный преимущественно в одном направлении.
Антенная система может быть построена различным образом, но самыми распространенными являются следующие:
· зеркальная система;
· линзовая система;
· с электронным управлением лучом (фазированные антенные решетки);
· с использованием апертурного синтеза.
На рис.1 представлен пример многоканальной системы радиовидения. Излучение от исследуемого объекта фокусируется линзой в фокальной плоскости, где располагается линейка облучателей на входе сенсоров.
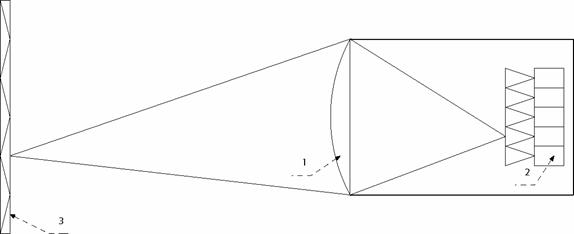
Рисунок 1. Оптическая схема многоканальной системы радиовидения: 1 - диэлектрическая линза, 2 - линейная решетка сенсоров, 3 – наблюдаемый объект.
Для получения полного радиометрического изображения объекта необходимо произвести измерения при различных направления «луча», т.е. провести сканирование объекта. В рассматриваемой системе и ей подобных сканирование осуществляется механическим поворотом системы в горизонтальном и вертикальном направлениях. После установки в заданное положение производится радиометрическое измерение интенсивности излучения. Результатом описанной процедуры является одна точка (пиксел) изображения и ассоциированная с ней пара угловых координат. Совокупность достаточно большого числа таких измерений позволяет сформировать из них изображение, соответствующее распределению радиояркостной температуры. Обычно сканирование производится по равномерной прямоугольной сетке.
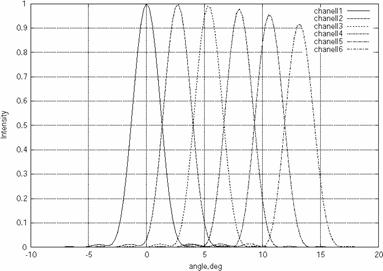
Рисунок 2. Аппаратные функции шести различных каналов в E-плоскости.
В реальных системах из-за дифракционных ограничений результат измерения интенсивности всегда является усреднением по некоторой области вблизи направления основного максимума. Численной характеристикой направленности является аппаратная функция системы, она равна отклику системы на единичный входной сигнал в зависимости от его положения относительно оптической оси системы. На рис. 2 в представлены аппаратные функции 6 из 11 каналов многоканальной системы пассивного радиовидения 8-мм диапазона. Как видно, в данном случае их ширина (по полувысоте) составляет примерно 2.5°.
3 Сверхразрешение
3.1 Обзор проблемы
Модель формирования наблюдаемого изображения в системе радиовидения математически может быть записана в следующем общем виде:
(1)
или в более кратких обозначениях
Эта модель учитывает аддитивный шум n, аддитивное общее смещение уровня b, коэффициент пропорциональности k и воздействие аппаратной функции h.
Параметры k и b определяют, как напряжение на выходе радиометра (или отсчеты на выходе АЦП) соотносятся с радиояркостной температурой излучения на входе радиометра, выраженной в кельвинах. Эти величины выражают общий коэффициент пропорциональности и смещение нуля, вызванные всеми линейными преобразованиями сигнала внутри системы. Для упрощения последующих формул будем использовать также следующее сокращенное выражение:
(2)
которое получается из (1) при k=1, b=0. Вместе с тем, надо иметь в виду, что неправильная оценка (измерение) b имеет очень сильное влияние на характеристики нелинейных методов сверхразрешения [4].
Аддитивный шум n является хорошей моделью для шума в радиометрических системах. Более того, в большинстве случаев он может считаться аддитивным белым гауссовским шумом. «Белизна» шума здесь должна пониматься в пространственной области, а не во временной. Заметим, однако, что предположение об аддитивности шума не всегда корректно, и иногда, например, в случае очень слабого сигнала на квантовом пороге чувствительности радиометра необходимо рассматривать более сложные модели, такие как пуассоновский шум.
Если аппаратная функция h является трансляционно-инвариантной, то интеграл общего вида преобразуется в свертку и выражение записывается следующим образом:
В таком виде модель можно записать в области пространственных частот, перейдя к Фурье-образам всех величин
В таком представлении воздействие аппаратной функции H сводится к фильтрации низких пространственных частот, при которой низкочастотные спектральные компоненты слабо изменяются, а высокочастотные сильно ослабляется. Начиная с определенной частоты, называемой частотой среза, все более высокочастотные компоненты становятся пренебрежимо малыми. В общем случае трансляционно-вариантной аппаратной функции, она сохраняет свойства ФНЧ, но теперь конкретный вид фильтра не постоянен, а зависит от координат.
Ниже мы рассмотрим некоторые методы восстановления изображений. Задачей таких методов является компенсация размывания изображения, вызванного конечным разрешением системы. Эти методы позволяют восстанавливать пространственные частоты, ослабленные в процессе измерения, и даже те из них, которые находятся за пределами частоты среза. Таким образом, в результате обработки изображения можно получить систему радиовидения с эффективной разрешающей способностью выше, чем у систем, не использующих такую обработку.
Математически проблема формулируется следующим образом:
найти такое решение 
наиболее
близкое к 
,
основываясь на измеренных данных 
и знании аппаратной функции h. Значения k и b предполагаются
известными, в некоторых методах необходимо знание статистики шума n. Уравнение (2) является уравнением Фредгольма первого рода
с функцией f в качестве
неизвестного. Это уравнение представляет собой некорректно поставленную задачу [5].
Это означает, что не существует точного устойчивого обратного решения, особенно
при наличии шумов. Таким образом, может быть получено только приблизительное решение,
оптимальное в том или ином смысле.
3.2 Линейные методы
Заметим сразу, что, строго говоря, линейные методы не могут быть отнесены к методам сверхразрешения, так как они не позволяют восстановить пространственные частоты за частотой среза. С помощью этих методов можно восстановить частоты, не слишком сильно ослабленные по отношению к уровню шума.
Для простоты будем рассматривать трансляционно-инвариантный
случай. Тогда уравнение (2) можно переписать в области пространственных частот 
в виде
Заглавные буквы отражают Фурье-образы соответствующих функций пространственных координат. В таком случае общий вид линейного решения обратной задачи может быть записан следующим образом:
где 
- конкретный обращающий оператор.
3.2.1 Неитерационные методы
Неитерационные методы получаются в результате аналитического решения задачи минимизации того или иного функционала.
3.2.1.1 Псевдообращение
Результатом применения метода наименьших квадратов является широкоизвестная формула псевдообращения, которая в данном случае записывается как
(3)
Решение 
минимизирует функционал 
и, как видно
непосредственно из формулы, не определено в областях, где 
. Это происходит из-за наличия
шума 
в этих
областях. Таким образом, необходим некий регуляризатор, который бы не давал
шуму неограниченно расти в этих областях.
3.2.1.2 Оптимальная фильтрация
Один из вариантов оператора регуляризации является оптимальный (винеровский) фильтр [6]. Он задается выражением
.
Тогда регуляризованное решение 
запишется следующим образом:
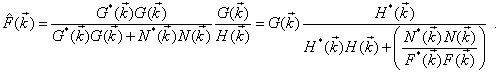
Это решение минимизирует функционал 
при дополнительном предположении,
что и линейно связаны.
Рассмотренный винеровский фильтр является частным случаем метода регуляризации
Тихонова [5] и вытекает из него в предположении, что сигнал и шум являются
стационарными гауссовскими случайными процессами с известными статистическими
свойствами. Его недостатком является то, что он требует знания спектральных
характеристик сигнала и шума, а они могут быть получены из результатов измерения
только приближенными эмпирическими методами.
3.2.2 Итерационные методы
Рассмотрим задачу минимизации функционала
.
Его вариация равна
.
Применение метода наискорейшего
спуска приводит к следующей итерационной схеме, минимизирующей 
:
(4)
Этот алгоритм также известен под названием метода последовательных приближений. Если этот метод сходится, то он сходится к решению (3). Естественным регуляризатором в данном случае выступает число итераций.
3.3 Нелинейные методы
Нелинейные методы, как следует из названия, содержат нелинейные операции, позволяющие восстановить пространственные частоты даже за частотой среза. Из всех нелинейных методов рассмотрим итеративные алгоритмы семейства Люси-Ричардсона. Эти алгоритмы названы по имени авторов, впервые предложивших их [7]. Они сходятся к максимально правдоподобному решению уравнения (2) с дополнительным условием неотрицательности решения.
В используемых обозначениях оригинальный алгоритм Люси-Ричардсона записывается следующим образом:
(5)
Здесь и далее запись вида 
означает интегрирование
со сменой переменной интегрирования, в трансляционно-инвариантном случае это
соответствует транспонированию h, отсюда и
происходит такое обозначение. Этот алгоритм, однако, подразумевает пуассоновскую
статистику шума, что не всегда применимо в радиометрии. Более корректной формой
для случая гауссовского шума является
(6)
описывающей алгоритм ISRA (Image Space Reconstruction Algorithm – алгоритм восстановления
пространства изображений) [8]. На практике же различие между решениями, которые получаются с использованием алгоритмов (5) и (6), весьма мало, хотя и существует. Различие
между решениями (4) и (5), (6) заметно в областях, где близка к нулю.
Основные свойства алгоритмов:
- они сходятся к максимально правдоподобному решению уравнения (2);
- сохраняют неотрицательность
функции ;
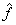- не используют дополнительных предположений относительно аппаратной функции (таких как трансляционная инвариантность, зеркальная симметрия).
Алгоритм ISRA вычислительно ресурсоемок по сравнению с другими алгоритмами, он показывает хорошую устойчивость и приводит к существенному повышению разрешения [9].
3.4 Дискретизация в условиях сверхразрешения
Все приведенные выше уравнения написаны для непрерывных
пространственных координат 
и 
. На практике измерения проводятся в конечном
числе точек, так что координата является дискретной. Более того,
получаемое решение также является функцией дискретной пространственной
переменной. При переходе от непрерывных координат необходимо принимать в расчет
возможный эффект наложения частот и теорему Котельникова.
На практике это означает, что частота Найквиста должна быть выше, чем частота среза аппаратной функции при измерении данных и выше, чем максимальная частота в восстановленном изображении при применении алгоритмов сверхразрешения. Часто встречается ситуация, когда в процессе измерения интервал дискретизации выбран правильно, но при последующей обработке методами сверхразрешения возникают более высокие частоты. При использовании итерационных методов может возникнуть момент, когда исходной частоты дискретизации перестает хватать для корректного представления всех частот – возникает эффект наложения частот. В таких ситуациях можно использовать метод субпиксельного разбиения.
Субпиксельное разбиение - это метод, при котором обработка данных проводится с таким интервалом дискретизации отличным от исходного, который заведомо достаточен для представления всех пространственных частот результирующего изображения. Эффективным и относительно простым подходом является передискретизация в целое число раз, т.е. интерполяция [10]. Для увеличения частоты дискретизации исходного изображения в N раз берется сетка с количеством узлов по каждой из координат в N раз больше чем у исходной. Пикселы исходного изображения копируются на новую сетку с шагом N, а промежуточные пикселы заполняются нулевыми значениями. После этого производится НЧ фильтрация для приведения спектра в соответствие с исходным. При этом используется прямоугольный ФНЧ с частотой среза, равной частоте Найквиста для исходного изображения. Указанные операции проделываются и над изображением, которое будет подвергаться обработке, и над аппаратной функцией, после чего все численное интегрирование в соответствии с конкретным алгоритмом сверхразрешения проводится уже по новой сетке. На практике вполне достаточно выбрать N=2, т.к. изменение спектра в области высоких пространственных частот достаточно слабо.
3.5 Полученные результаты
В данном разделе представлены полученные результаты, которые демонстрируют возможности методов сверхразрешения при применении их к реальным и модельным данным.
3.5.1 Модельные данные
Рассмотрим результаты симуляции процесса сверхразрешения. В качестве начальных данных были взяты распределения яркости, показанные слева на рис.3. Затем, численно была произведена операция свертки (2) и добавлен белый гауссовский шум (отношение сигнал/шум составляло 5·102) – т.е. была решена прямая задача. Описанные операции моделируют процедуры преобразования сигнала в системе радиовидения. Полученные данные были обработаны по алгоритму сверхразрешения в соответствии с итерационной схемой (5). Представленные изображения соответствуют номерам итераций 500 и 2000.
|
|
|
|
|
|
|
|
|
|
Рисунок 3. Восстановление кольцевидного изображения.
3.5.2 Экспериментальные данные
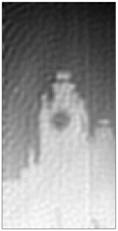
Рис.4 демонстрирует возможности рассматриваемого алгоритма сверхразрешения (6) при применении его к реальным данным, полученным с помощью системы пассивного радиовидения 3-мм диапазона. Объекты на изображениях – это части главного здания Московского государственного университета на Воробьевых горах (верхние изображения) и боковой башенки ГЗ МГУ (нижние). Участкам с более высокой радиояркостной температурой соответствуют более светлые тона, а более «холодным» - темные. Слева представлены исходные изображения, справа – соответствующие результаты после 100 итераций.
|
|
|
|
|
|
Рисунок 4. Сверхразрешение при обработке входных данных данных 3-мм системы радиовидения.
Численной характеристикой для оценки результатов
сверхразрешения может являться норма . Она характеризует, насколько близок
результат реальных измерений g к предсказанному
результату измерений 
.
При обработке данных эта норма после 100 итераций уменьшилась на 19 дБ по сравнению
с начальным приближением. В качестве начального приближения 
использовались необработанные
экспериментальные данные g. Вышесказанное
поясняется выражением
.
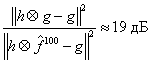При этом, наибольший выигрыш достигается на первых 30-40 итерациях, а далее рассматриваемая величина меняется слабо. Однако именно на последующих итерациях происходит восстановление наиболее мелких деталей изображения.
Преимущества использования субпикселинга при сверхразрешении демонстрирует рис.5. На нем сравниваются результаты действия алгоритма сверхразрешения после 300 итераций с использованием субпикселинга и без него. Различие хорошо заметно даже на глаз. Сверхразрешение с использованием субпикселинга позволяет получить более устойчивое решение с меньшим количеством ложных деталей («звона») при достижении того же разрешения. Иными словами, удается при приблизительно фиксированном уровне «звона» провести большее количество итераций и достичь лучшего разрешения.
|
|
|
Рисунок 5. Иллюстрация метода субпиксельного разбиения.
4 Заключение
В статье была рассмотрена задача повышения разрешения систем радиовидения математическими методами. Приведенные результаты убедительно доказывают перспективность использования алгоритмов сверхразрешения для обработки экспериментальных данных. В то же время необходимо учитывать побочные эффекты, например наложение частот при недостаточной частоте дискретизации. В работе предложен метод борьбы с указанным нежелательным явлением и доказана его эффективность при использовании реальных экспериментальных данных.
В дальнейшем планируется применить описанные методы сверхразрешения для обработки данных, полученных с помощью многоканальных систем радиовидения.
5 Список литературы
[1] Есепкина Е.А., Корольков Д.В., Парийский Ю.Н. Радиотелескопы и радиометры.- М.: Наука, 1973.
[3] Радиотехнические системы, под ред. Казаринова Ю. М., М.: «Высшая школа», 1990.
[5] Тихонов А.Н. Арсенин В.Я. Методы решения некорректных задач.- М.: Наука, 1986.
[6] Press W. H., Teukolsky S. A., Vetterling W. T., Flannery B. P., Numerical recipes in C. The Art of Scientific Computing. Second Edition, Cambridge University Press, New York, 1997.
[10] Сергиенко А.Б. Цифровая обработка сигналов, Санкт-Петербург, «Питер Принт», 2002.
