УДК 621.396 : 681.2

Операция умножения распределений случайных сигналов в пространстве идентификационных чисел

В. Ю. Кобенко

Омский государственный технический университет

Получена 20 марта 2012 г.

 

Аннотация. Представлены результаты моделирования операции умножения двух распределений случайных сигналов в пространстве идентификационных чисел. Дается описание и технология выполнения данной операции умножения. Под идентификационными понимаются числа порядковой шкалы, количественно характеризующие форму сигналов.

Ключевые слова: идентификация, идентификационная алгебра распределений, идентификационные измерения, классификация, случайный сигнал, порядковая шкала.

Abstract. Results of modeling of multiplication operation of two random signals distributions in identification numbers space are presented. The description and performance technology of the given multiplication operation is given. The identification numbers are understood as the numbers of a order scale quantitatively characterizing the signals form.

Keywords: identification, identification algebra of distributions, identification measurements, classification, random signal, order scale.

 

Введение

При анализе сигналов часто возникает проблема, связанная с формальным описанием их взаимодействия, например, в результате перемножения. Технология выполнения операции перемножения известна, если известны математические модели сигналов, но чаще всего, модель взаимодействующих сигналов неизвестна, поскольку сами сигналы носят случайный характер [1]. В таком случае возникает вопрос – как получить подобную модель? Как, аналитическим путем, описать результат взаимодействия случайных сигналов, имеющих минимальное количество известных параметров? Данному вопросу посвящена настоящая работа.

В работе [2] рассмотрены основные понятия и определения идентификационных измерений (ИИ) сигналов. Под идентификационными измерениями понимаются такие измерения, которые позволяют количественно оценивать форму сигналов. Основным инструментом ИИ являются порядковые идентификационные шкалы. Результатом ИИ являются идентификационные числа, удовлетворяющие требованиям масштабной инвариантности, эквивалентности и согласованной упорядоченности [3]. Таким образом, технология ИИ позволяет представлять сигналы любой формы (в том числе случайные) в системе порядковых измерительных шкал в виде идентификационных чисел (параметров).

 

Методика исследований

Пусть даны реализации двух сигналов X(t) и Y(t) в виде распределения мгновенных значений (рис. 1) одинакового объема N. Средние значения сигналов равны нулю. Известны значения их идентификационных параметров NF_x и NF_y, найденных в соответствии с алгоритмом, описанным в [4, 5].

Задача сводится к тому, чтобы, не проводя никаких экспериментов над исходными реализациями X(t) и Y(t), идентифицировать сигнал Z(t) по шкале NF, т.е. найти отображение сигнала произведения  Z(t) = X(t) • Y(t) в пространстве NF аналитически по формуле:

NF_mul = f(NF_x, NF_y).                                             (1)

Определение данной математической модели и ее коэффициентов позволит  формально представить операцию произведения двух распределений сигналов в пространстве идентификационного параметра NF.

 

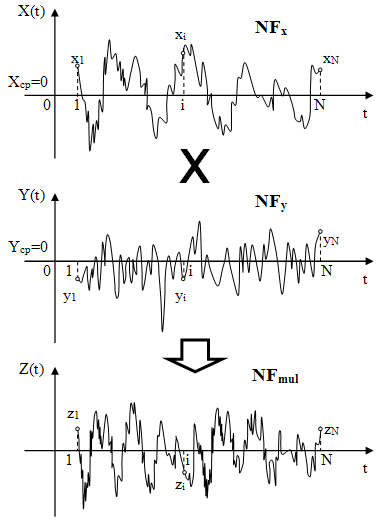
Рис. 1. Технология умножения реализаций двух сигналов X(t) и Y(t) объема N  во временной области. Z(t) – результат произведения.

 

Методика проведения исследований.

1)       Реализации перемножаемых сигналов X(t) и Y(t) получены с помощью генератора случайных стационарных сигналов с заданным законом распределения [6].

2)       Определяются значения NF_x  и NF_y..

3)       Формируется реализация сигнала произведения Z(t) = X(t) • Y(t). На рис. 1 показан алгоритм нахождения мгновенных значений  z_i = x_i • y_i, 1≤i≤N.

4)       Находится значения идентификационного параметра NF_mul сигнала Z(t).

5)       Закон распределения одного из сигналов фиксируется, например Y(t), следовательно, фиксируется NF_y. Для формирования статистического ряда    п.п. 1 – 4 повторяются для произведения Y(t) с другими сигналами. Затем фиксируется другой закон распределения Y(t) и п.п. 1 – 4 вновь повторяются и т.д.

6)       Полученная зависимость описывается математической моделью:

NF_mul (NF_y) = f(NF_x, A, B, C),                                       (2)

где A, B, C – коэффициенты модели.

7)       Для каждого коэффициента модели (2) A=f(NF_y), B=f(NF_y), C=f(NF_y) находится своя математическая модель, как функция от NF_y.

8)       Таким образом, общая формула для вычисления NF_sum будет иметь вид:

NF_mul = f(NF_x, A(NF_y), B(NF_y), C(NF_y)).                                (3)

 

Результаты исследований

Для проведения исследований операции умножения распределений был разработан программный продукт «Система статистического анализа идентификационного умножения сигналов в пространстве NF» [7].

Для большей достоверности и статистической устойчивости результатов исследований в качестве тестовых сигналов были взяты случайные стационарные сигналы с симметричными законами распределения: двумодальный (2МОД), арксинусный (АРКС), равномерный (РАВН), треугольный (СИМП), нормальный (НОРМ) и Лапласа (ЛАПЛ). Объем каждой реализации N = 10000, количество усреднений по каждой паре сигналов – 2000.

Чтобы определить математическую модель (2), найдем произведение  реализации сигналов в различном сочетании и представим результат на одном графике. На рис. 2 – 5 показаны экспериментальные зависимости NF_mul = f(NF_x) при различных фиксированных законах распределения одного из множителей Y(t) (NF_y фиксировано).

 

 

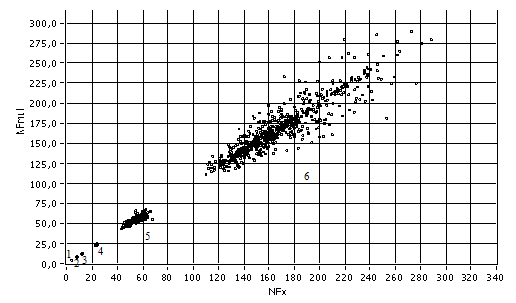
Рис. 2. Экспериментальные значения NF_mul, полученные в результате произведения 2МОД распределения на 2МОД(1), АРКС(2), РАВН(3), СИМП(4), НОРМ(5),  ЛАПЛ(6) распределения.

 

 

 

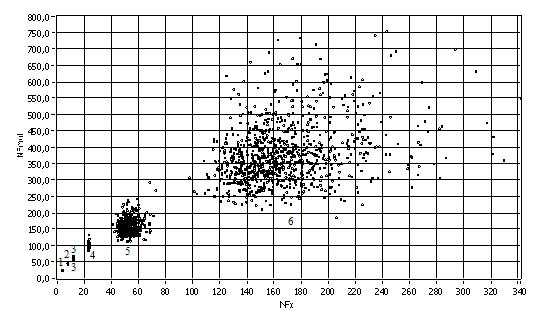
Рис. 3. Экспериментальные значения NF_mul, полученные в результате произведения СИМП распределения на 2МОД(1), АРКС(2), РАВН(3), СИМП(4), НОРМ(5),  ЛАПЛ(6) распределения.

 

 

 

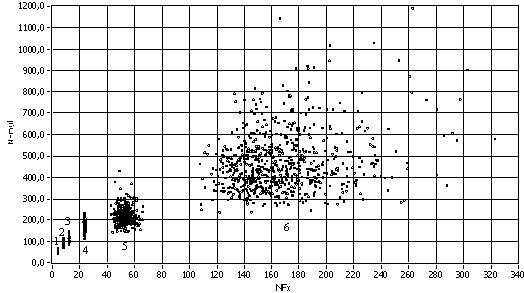
  Рис. 4. Экспериментальные значения NF_mul, полученные в результате произведения НОРМ распределения на 2МОД(1), АРКС(2), РАВН(3), СИМП(4), НОРМ(5), ЛАПЛ(6) распределения.

 

 

 

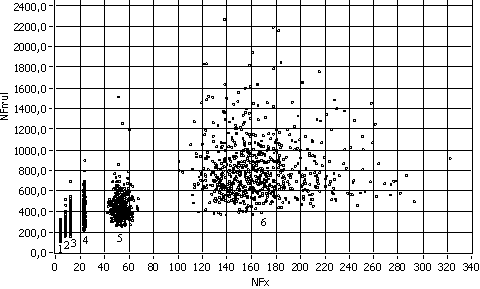
 Рис. 5. Экспериментальные значения NF_mul, полученные в результате произведения ЛАПЛ распределения на 2МОД(1), АРКС(2), РАВН(3), СИМП(4), НОРМ(5), ЛАПЛ(6) распределения.

 

В первом приближении была найдена математическая модель, хорошо описывающая вышеприведенные зависимости:

,                                            (4)

где A, B, C – коэффициенты модели.

В табл. 1 представлены значения коэффициентов модели (4) для произведений с 2МОД, АРКС, РАВН, СИМП, НОРМ, ЛАПЛ распределениями.

 

Таблица 1

Коэффициенты модели (4)

Распределение Y(t)	NFy	A	B	C
2МОД	4	-0,155	1,13	0,976
АРКС	8	-3,07	3,53	0,830
РАВН	12	-4,486	5,86	0,764
СИМП	23,4	-13,4	15,5	0,629
НОРМ	53,3	-24,1	43,1	0,506
ЛАПЛ	167	-32,6	122	0,377

 

Для каждого коэффициента A, B, C находится математическая модель, описывающая его изменение в зависимости от NF_y. В первом приближении были выбраны модели с минимальными среднеквадратическими отклонениями:

 

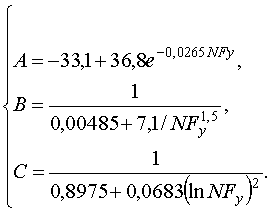                                              (5)

 

Таким образом, вычислив значения коэффициентов  A, B, C по формуле (5), и подставив их в формулу (4), находится значение NF_mul.

Чем меньше значение NF_y, тем кучнее располагаются точки на графиках рис. 2 – 5,  тем точнее будет модель, характеризуемая  коэффициентами  A, B, C в формуле (5). Поэтому для повышения точности расчета  NF_mul необходимо, чтобы  выполнялось условие NF_x > NF_y.

 

Метрологические характеристики операции умножения распределений

Чтобы проверить правильность выполнения операции умножения распределений двух реализаций сигналов X(t) и Y(t) в пространстве параметра NF, найдем погрешность аналитического вычисления NF_mul, при этом за истинное значение примем значение параметра NF_o, найденное для реализации Z(t), полученной экспериментальным образом (см. рис. 1). Определим случайную δ_сл и систематическую δ_с относительные погрешности выполнения операции умножения распределений, а также среднеквадратическое отклонение (СКО) этой погрешности σ [8]. Объем каждой реализации N = 10000, количество усреднений результатов  вычислений – 1000. В табл. 2 представлены данные о распределении относительной погрешности выполнения операции умножения распределений для 2МОД, АРКС, РАВН, СИМП,  НОРМ и ЛАПЛ распределений (ячейки с повторяющимися данными затушированы).

 

Таблица 2

Систематическая (δ_с) и  случайная (δ_сл) относительные погрешности выполнения операции умножения распределений с доверительным

интервалом 2σ (доверительная вероятность 0,95)

		ЛАПЛ	НОРМ	СИМП	РАВН	АРКС	2МОД
2МОД	δс, %	-2,47	0,31	1,63	2,58	3,52	4,9
	δсл, %	0,25	0,14	0,04	0,03	0,04	0,04
	2σ, %	15,8	9,0	2,52	2,18	2,20	2,44
АРКС	δс, %	-5,4	-2,21	-8,2	-9,1	-10,0
	δсл, %	0,58	0,32	0,08	0,03	0,03
	2σ, %	36,8	20,0	4,8	2,04	1,76
РАВН	δс, %	-4,9	-0,64	-9,4	-10,9
	δсл, %	0,64	0,40	0,12	0,05
	2σ, %	40,4	25	7,8	3,06
СИМП	δс, %	0,07	8,9	-4,7
	δсл, %	0,76	0,51	0,22
	2σ, %	48,2	32	13,8
НОРМ	δс, %	25,0	39,2
	δсл, %	1,07	0,85
	2σ, %	67,6	53,8
ЛАПЛ	δс, %	7,7
	δсл, %	1,08
	2σ, %	68,6

 

В табл. 2 жирной линией обведена область, в которой ширина доверительного интервала (2σ) для систематической относительной погрешности не превосходит 20% при доверительной вероятности 0,95. 

 

Выводы

На основании проведенных исследований можно сделать следующие выводы.

1)  Определена операция умножения распределений случайных сигналов с нулевым средним в пространстве идентификационного параметра NF. Формально данную операцию можно записать как:

,

где символом (х) обозначена сама операция умножения.

2)  Систематическая относительная погрешность выполнения операции умножения распределений в пространстве идентификационного параметра NF не превосходит 11%, за исключением нормального закона распределения – 40% (табл. 2).

3)  Случайная относительная погрешность выполнения операции идентификационного умножения не превосходит 1,1% при количестве усреднений 1000.

Исследования проведены в рамках выполнения государственных заданий Министерства образования и науки Российской Федерации высшим учебным заведениям на 2012 и на плановый период 2013 и 2014 годов в части проведения научно-исследовательских работ по теме № 7.3785.2011 «Разработка теоретических основ и прикладных аспектов идентификационной алгебры сигналов».

 

Литература

1.       Хан, Г. Статистические модели в инженерных задачах / Г. Хан, С. Шапиро. – М. : Мир, 1969. – 395 с.

2.        Кликушин, Ю. Н. Основы идентификационных измерений / Ю. Н. Кликушин, В. Ю. Кобенко // Журнал Радиоэлектроники [электронный журнал] / М. : Изд-во ИРЭ РАН. – 2006. – № 5. – Режим доступа: http://jre.cplire.ru/jre/nov06/2/text.html

3.       Гуменюк, А. С. Алгоритмы анализа структуры сигналов и данных: монография / А.С. Гуменюк, Ю.Н. Кликушин, В.Ю. Кобенко, В.Н. Цыганенко. – Омск : Изд-во ОмГТУ, 2010. – 272 с.

4.        Кликушин, Ю. Н. Классификационные шкалы для распределений вероятности / Ю. Н. Кликушин // Журнал Радиоэлектроники [электронный журнал]  / М. : Изд-во ИРЭ РАН. – 2000. – № 11. – Режим доступа: http://jre.cplire.ru/ jre/nov00/4/text.html

5.        Кликушин, Ю. Н. Фрактальная шкала для измерения распределений вероятности / Ю. Н. Кликушин // Журнал Радиоэлектроники [электронный журнал]   / М. : Изд-во ИРЭ РАН. – 2000. – № 3. – Режим доступа: http://jre.cplire.ru/ jre/mar00/2/text.html.

6.       Генератор случайных сигналов с заданным законом распределения / Ю. Н. Кликушин, В. Ю. Кобенко. – М. : ИНИМ РАО ОФЭРНиО, св-во № 17515 от 25.10.2011, ВНТИЦ № 50201151369.

7.       Система статистического анализа идентификационного произведения сигналов в пространстве NF / Ю. Н. Кликушин, В. Ю. Кобенко. – М. : ИНИМ РАО ОФЭРНиО, св-во № 17723 от 22.12.2011, ВНТИЦ № 50201151577.

8.       Новицкий, П. В. Оценка погрешностей результатов измерения / П. В. Новицкий, И. А. Зограф. – Л. : Энергоатомиздат, 1985. – 248 с.