УДК 535.37:523.42
МОДЕЛИРОВАНИЕ РАДИОЗАТМЕННОГО ЭКСПЕРИМЕНТА МЕТОДОМ ЧИСЛЕННОГО РЕШЕНИЯ ПАРАБОЛИЧЕСКОГО УРАВНЕНИЯ ДИФРАКЦИИ
Я. А. Илюшин 1, А. Л. Гаврик 2, Ю. А. Гаврик 2, Т. Ф. Копнина 2
1 МГУ им.
М.В. Ломоносова
2 ФИРЭ им. В.А. Котельникова РАН
Получена 13 марта 2012 г.
Аннотация. На основе прямого моделирования поля радиоволн, зондирующих ионосферу, методом численного решения параболического уравнения дифракции исследованы вариации интенсивности и фазы сигнала вдоль траектории спутника Венеры. Доказана линейная связь между вариациями частоты и интенсивностью сигнала, деформированного при распространении через сферически-симметричную регулярную ионосферу. Показано, что совпадение энергетического и неэнергетического параметров радиоволны свидетельствует о достоверности результатов решения обратной задачи радиопросвечивания.
Ключевые слова: радиопросвечивание, распространение радиоволн, ионосферы и атмосферы планет.
Abstract. We have used direct simulation of occultation signal using a numerical calculation of the parabolic diffraction equation to analyze variations of signal intensity and phase along the line of trajectory of Venus satellite during an occultation experiment. As a result we have proved the liner relationship between variations of phase and intensity of the signal deformed by regular spherically symmetric ionosphere. It is shown that a coincidence between energy and non-energy parameters of a sounding radio wave proves reliability of the result obtained from inverse radio occultation problem.
Keywords: occultation, radio wave propagation, ionosphere and atmosphere of planets.
Введение
Исследование атмосфер и ионосфер планет методом радиозатмений началось в 1965 г. во время полета космического аппарата (КА) MARINER-4 к Марсу [1] и стимулировало развитие теоретических исследований распространения радиоволн в газовых оболочках планет. Анализ условий радиопросвечивания позволил обосновать применение геометрической оптики и локальной сферической симметрии газовой оболочки для вывода обобщенных соотношений, позволяющих определять параметры зондируемой среды [1-5]. Высокая эффективность метода, доказанная при радиопросвечиваниях оболочек планет [6-8], и возможность его внедрения для мониторинга околоземного пространства на трассах радиосвязи спутник-спутник [9,10] выявили необходимость детального теоретического анализа вариаций параметров поля зондирующих сигналов. Разработка новых более совершенных методов, позволяющих изучать тонкую структуру ионосферы и атмосферы [11-16], показала необходимость обеспечения высокого соотношения между исследуемыми эффектами и аппаратурными погрешностями [16]. Уменьшение инструментальных флуктуаций фазы сигнала, связанных с ограниченной стабильностью бортового опорного осциллятора, и увеличение вариаций параметров сигнала, распространяющегося в плазменной оболочке планеты, достигается понижением частоты зондирующего сигнала [16-18]. Однако слишком сильная трансформация низкочастотного сигнала под влиянием плазмы может привести к нарушению условий применимости методов геометрической оптики, на которых основана интерпретация результатов радиозатмений.
Целями работы являются: прямое моделирование поля радиоволны, трансформированного ионосферой планеты, методом численного решения параболического уравнения дифракции; анализ вариаций интенсивности и фазы радиосигнала в процессе радиопросвечивания ионосферы Венеры; сравнение результатов с экспериментальными данными КА ВЕНЕРА-15,-16 и оценка применимости геометрической оптики при интерпретации радиозатменных данных.
1. Методика моделирования радиопросвечивания ионосферы планеты
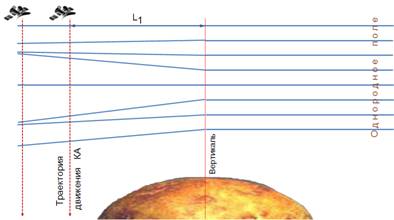
Для увеличения потенциала радиолинии в экспериментах радиопросвечивания целесообразно обеспечить излучение мощных радиосигналов с наземного пункта и определение параметров сигналов на борту спутника планеты [16]. Поэтому рассмотрим радиозатменный эксперимент, в котором наземная антенна излучает монохроматический сигнал высокой мощности в направлении планеты (рис.1). Расстояние до ближайшей к Земле планеты превышает 50 млн. км и можно считать, что область диаметром 0.5 млн. км вблизи планеты облучается однородной плоской монохроматической высокочастотной волной. Ионосфера планеты считается сферически-симметричной средой, её свойства не зависят от времени и вертикальное распределение концентрации электронов меняется плавно.
|
|
|
Рис. 1. Схема эксперимента радиопросвечивания |
При движении приемника сигнала перпендикулярно направлению излучения плоской волны, возмущенной неоднородной средой на пути ее распространения, приемник регистрирует вариации интенсивности и фазы принятого сигнала, обусловленные трансформацией поля в процессе распространения радиоволны в ионосфере планеты (рис.1). Деформация поля нарастает с увеличением расстояния от ионосферы до траектории движения КА. При большой дистанции между КА и ионосферой возникают условия для размножения мод сигнала, образования каустик и заметного влияния эффектов дифракции излучения на мелкомасштабных ионосферных структурах, что усложняет метод интерпретации радиозатменных данных.
Крупномасштабные неоднородности ионосферы вызывают значительные вариации амплитуды и фазы зондирующей монохроматической волны, поэтому для расчетов распределения поля целесообразно использовать прямое численное решение параболического уравнения [19-21]:
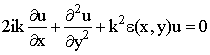 .
.
Здесь координата x выделена направлением распространения первичной волны с волновым числом k, ортогональная координата y определена в плоскости, проходящей через центр планеты, проницаемость ионосферы ε(х,у) входит множителем при искомой комплексной амплитуде поля u, влияние атмосферы и поверхности планеты не учитывается.
Для параболического уравнения дифракции решалась краевая задача в прямоугольной полосе (рис.1), ориентированной параллельно направлению падения зондирующей волны, при численном решении уравнения [20,21] использовалась неявная разностная схема Кранка-Николсона [22]. Наш подход полностью аналогичен типичной постановке краевой задачи для уравнения Шредингера [23]. На боковых границах полосы ставится условие идеального согласования с открытым пространством [23], обеспечивающее отсутствие отражения от границ. Отражения от боковых границ не достигают области локализации информативной части поля волны при достаточно протяженной ширине полосы. В таком случае на боковых границах можно приблизительно поставить второе граничное условие, согласованное с распространением невозмущенной зондирующей волны вдоль боковых границ в свободном пространстве: равенство нулю нормальной к границе производной решения.
Принятая модель позволяет рассчитать квадратурные компоненты радиополя, формирующегося в результате прохождения плоской волны через ионосферу планеты. Реальная и мнимая компоненты поля сигнала с разными длинами волн в диапазоне 0.25...1.5 м вычислялись с шагом по высоте 0.25...1 м вдоль вертикальной линии, расположенной на расстояниях 103...104 км от вертикали, проходящей через центр планеты (рис. 1).
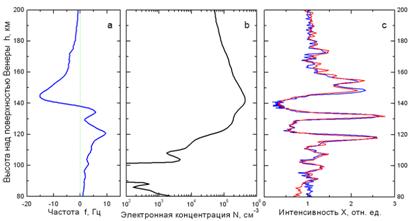
При расчетах применялась сферически-симметричная двумерная модель ионосферы Венеры. В качестве вертикального профиля концентрации электронов (рис.2b) был взят профиль N(h), полученный в эксперименте радиопросвечивания ионосферы Венеры 14.10.1983 г. [24,25] по вариациям частоты радиосигнала с длиной волны 32 см (рис.2а).
|
|
|
Рис. 2. а) Изменение частоты f(h) сигнала λ=32 см в процессе зондирования ионосферы Венеры. b) Профиль электронной концентрации N(h). с) рефракционное изменение интенсивности сигнала в эксперименте (красная кривая) и вычисленное из частоты сигнала (синяя кривая). |
КА Венера-15 находился на расстоянии 104 км от ионосферы, скорость погружения радиолуча в ионосферу составляла 6 км/с. Профиль N(h) рассчитывался по известной методике решения обратной задачи радиопросвечивания, предполагающей справедливость геометрической оптики [26,27]. Однако, экспериментально полученное рефракционное изменение интенсивности сигнала X(h) (красная кривая рис.2с) демонстрирует наличие областей фокусировки волны с увеличением ее интенсивности в 3 раза, что свидетельствует о близости траектории КА к области многомодового распространения радиоволн, где традиционный метод расчета N(h) может оказаться некорректным.
Критерием корректности метода определения N(h) путем решения обратной задачи радиопросвечивания может являться совпадение экспериментальной функции X(h) (красная кривая рис.2с) c рассчитанным из частоты рефракционным ослаблением Xf(h) (синяя кривая рис.2с). Такой вывод следует из результатов работ [27-30], где на основе соотношений геометрической оптики аналитически получена линейная связь энергетического параметра X(t) с неэнергетическим параметром (изменением частоты f(t) сигнала) при зондировании сферически-симметричной среды:
X(t) = 1 + [λ∙L1∙V–2] ∙ df(t)/dt.
Здесь λ – длина излучаемой волны, L1 – расстояние от КА до вертикали к поверхности планеты, V=dh/dt – скорость движения КА, f(t) – изменение частоты сигнала, обусловленное ионосферой. Представленное соотношение позволяет определить прогнозируемое рефракционное ослабление Xf(h), используя неэнергетический параметр сигнала f(h). Совпадение Xf(h) с экспериментальной функцией X(h) наблюдалось во многих сеансах радиопросвечивания [27-29], но представляется целесообразным выявить условия, при которых равенство X(h) = Xf(h) нарушается из-за искажений, обусловленных появлением эффектов размножения мод и дифракции сигнала.
2. Результаты моделирования
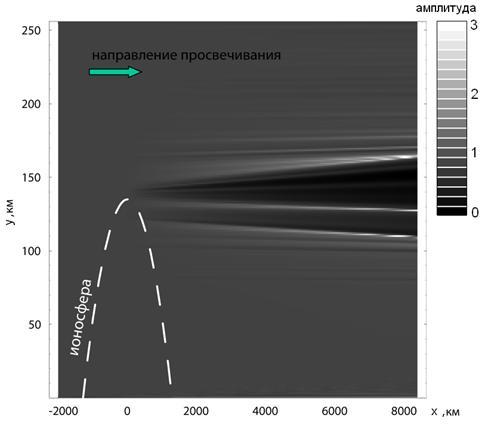
На рис. 3 представлен пример распределения амплитуды радиополя, возмущенного зондируемой ионосферой. При отсутствии возмущений радиополе однородное, его амплитуда, нормированная к 1, соответствует серому цвету. Уменьшению амплитуды поля соответствуют градации серого цвета вплоть до 0 (черный цвет). Увеличению амплитуды поля соответствуют градации серого цвета вплоть до максимальной амплитуды в области размножения мод сигнала и образования каустик (белый цвет). Каустики появляются только на определенном расстоянии от КА до вертикали к поверхности планеты, это расстояние зависит от параметров зондируемой среды и от длины волны излучения. При нахождении КА вблизи или за пределами областей фокусировок, соответствующих геометрооптическим каустикам, интерпретация радиозатменных данных становится затруднительной.
|
|
|
Рис. 3. Распределение амплитуды радиополя, возмущенного зондируемой ионосферой. |
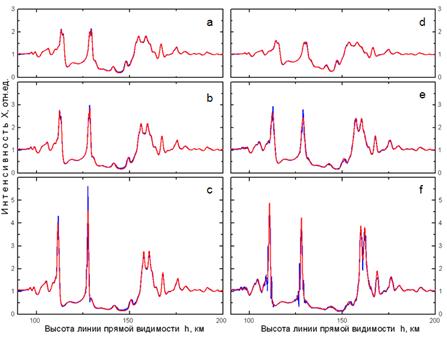
Рассмотрим вариации параметров поля X(h) и f(h) при приближении области каустик к трассе КА из-за увеличения длины волны излучения. На рис. 4a,b представлены результаты расчетов частоты (рис. 4a) и интенсивности (рис. 4b) принятых на расстоянии 1000 км радиосигналов с разной длиной волны λ=80, 100, 120 см. С приближением области каустик к трассе КА (красные кривые) увеличиваются градиент частоты и интенсивность сигнала на высотах 110 км и 127 км. Использование сигнала с длиной волны, превышающей 130 см, приведет к появлению флуктуаций частоты и интенсивности, обусловленных многомодовым распространением радиоволн и дифракционными эффектами. Такие флуктуации сначала появятся только вблизи высот 110 км и 127 км для λ=130 см, а с увеличением λ флуктуации X(h) и f(h) будут проявляться в широком диапазоне высот. Отсутствие дифракционных флуктуаций X(h) и f(h) на рис. 4b позволяет сделать вывод, что при четырехкратном увеличении интенсивности сигнала в области фокусировки применимость лучевых приближений геометрической оптики еще сохраняется.
|
|
|
Рис. 4. Изменение частоты f(h) сигнала (а) и его интенсивности X(h) (b) при зондировании сигналом λ= 80, 100, 120 см при L1=1000 км. Изменение частоты сигнала λ= 50 см (с) и его интенсивности (d) при L1 = 3000, 5000, 6500 км. |
На рис. 4c,d представлены результаты расчетов частоты (рис. 4c) и интенсивности (рис. 4d) радиосигнала с длиной волны излучения 50 см, принятого на разных расстояниях (3000, 5000, 6500 км) от КА до вертикали к поверхности планеты. О приближении трассы КА к области каустик свидетельствует (красные кривые) увеличение градиента частоты на высотах 110 км и 127 км, а также увеличение интенсивности сигнала. При расстояниях меньше 7000 км многомодовость распространения радиоволн и дифракционные эффекты можно не учитывать, т.к. флуктуации X(h) вблизи высот 110 км и 127 км отсутствуют. Отсутствие дифракционных флуктуаций X(h) и f(h) на рис. 4d подтверждает вывод о том, что четырехкратное увеличение интенсивности сигнала в области фокусировки не является признаком нарушения лучевых приближений геометрической оптики.
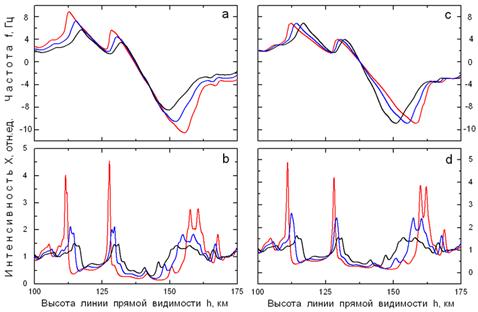
В приближении геометрической оптики вариации интенсивности поля X(h) связаны линейной зависимостью с изменением частоты сигнала, поэтому совпадение вариаций X(h) с вариациями Xf(h) может служить критерием применимости геометрической оптики [27-29], а расхождения между X(h) и Xf(h) могут указывать на влияние эффектов многомодовости и дифракции. На рис. 5a,b,c представлены результаты сравнения вариаций X(h) с вариациями Xf(h) при λ = 80, 100, 120 см. Изменение длины волны излучения, принимаемого приемником КА на расстоянии 1000 км, изменяет величину деформации поля. Полное совпадение X(h) с Xf(h) на рис. 5a,b подтверждает линейную связь X(h) с Xf(h) при разных λ. Однако на рис. 5c максимальные значения X(h) и Xf(h) различаются, что указывает на приближение области каустик к трассе КА, вызывающее небольшое нарушение лучевых приближений геометрической оптики.
|
|
|
Рис. 5. Сравнение вариаций X(h) (красная кривая) с вариациями Xf(h) (синяя кривая) при λ = 80, 100, 120 см (a,b,c) и при приеме сигнала λ = 50 см на расстояниях L1=3000, 5000, 6500 км (d,e,f). |
На рис. 5d,e,f представлены результаты сравнения вариаций X(h) с вариациями Xf(h) при приеме сигнала с длиной волны 50 см на расстояниях 3000, 5000, 6500 км. На рис. 5d,e наблюдается полное совпадение X(h) с Xf(h), подтверждающее линейную связь X(h) с Xf(h), а на рис. 5f вблизи высот 110 км и 127 км появляются флуктуации Xf(h), свидетельствующие о нарастающем влиянии многомодового распространения радиоволн и дифракции. Появление флуктуаций Xf(h) вблизи высот 110 км и 127 км при отсутствии заметных искажений X(h) и f(h) свидетельствует о том, что вариации Xf(h) являются наиболее чувствительным индикатором, указывающим на необходимость учета многомодового распространения радиоволн и дифракции при интерпретации радиозатменных данных.
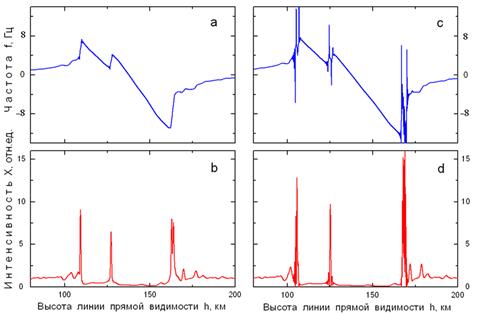
На рис. 6a,b представлены вариации частоты и интенсивности сигнала с длиной волны 50 см, полученные при L1=8000 км.
|
|
|
Рис. 6. Вариации частоты и интенсивности сигнала λ=50 см (a,b) и сигнала λ=60 см (c,d), полученные при L1=8000 км. |
На частоте сигнала (рис. 6a) появляются слабозаметные искажения на высотах 110 км и 127 км вблизи границ области сильной фокусировки сигнала. Но даже при такой сильной фокусировке сигнала флуктуации X(h), обусловленные дифракцией, еще незаметны (рис. 6b). На основании этих результатов можно было бы предположить, что приближения геометрической оптики еще выполняются, но рассчитанная функция Xf(h) оказалась очень сильно искаженной дифракционными эффектами, что однозначно указывает на возможность использования равенства Xf(h) = X(h) в качестве критерия применимости геометрической оптики при интерпретации данных радиопросвечивания.
В качестве примера на рис. 6c,d показаны сильные искажения функций f(h) и X(h) при λ=60 см и L1=8000 км. Осцилляции частоты и интенсивности сигналов на высотах 110, 127, 165 км обусловлены многомодовым распространением радиоволн и дифракционными эффектами, при таких условиях определение функции Xf(h) становится невозможным и нецелесообразным, т.к. функции f(h) и X(h) прямо указывают на неприменимость методов геометрической оптики.
3. Обсуждение результатов
Результаты моделирования подтвердили линейную связь между измеренной интенсивностью сигнала и изменением его частоты при зондировании сферически-симметричной ионосферы монохроматической высокочастотной радиоволной. Численные расчеты показали, что достоверное определение функции Xf(h) возможно только при отсутствии многомодового распространения радиоволн и дифракционных эффектов, а флуктуации Xf(h) из-за влияния таких факторов появляются раньше, чем появляются искажения функций X(h) и f(h). Следовательно, совпадение X(h) с Xf(h) при обработке данных реального эксперимента радиопросвечивания можно считать критерием применимости метода геометрической оптики и предположения о локальной сферической симметрии зондируемой ионосферы. Такой критерий позволяет оценивать достоверность результатов решения обратной задачи радиопросвечивания.
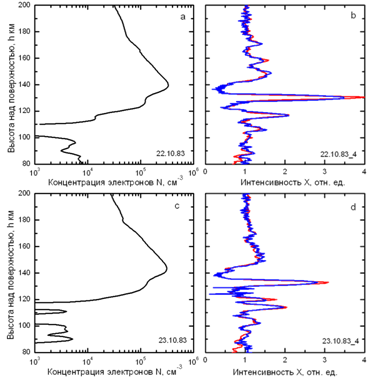
На рис.7a,c показаны профили концентрации электронов N(h), полученные по известной методике путем решения обратной задачи радиопросвечивания в приближении геометрической оптики [17].
На интенсивности сигнала (красные кривые рис.7b,d) наблюдаются области фокусировки с увеличением интенсивности в 4 раза, что ставит вопрос о справедливости использования геометрической оптики. Представленные результаты анализа дифракционных эффектов доказывают, что совпадение Xf(h) с X(h) является надежным критерием допустимости приближений геометрической оптики. На рис. 7b,d видно, что различия функций Xf(h) (синяя кривая) и X(h) (красная кривая) не превышают погрешностей измерений, следовательно, в данных сеансах радиозатмений соотношения геометрической оптики должны быть справедливы и рассчитанные профили N(h) не искажаются дифракционными эффектами.
|
|
|
Рис. 7. Высотные профили концентрации электронов в ионосфере Венеры (а,с) и сравнение функций Xf(t) и X(h) (синяя и красная кривые), совпадение которых одтверждает достоверность полученных результатов. |
Выводы
Проведена валидация результатов обработки данных экспериментов радиопросвечивания ионосферы Венеры, выполненных ранее с помощью КА Венера-15,-16. Прямым численным моделированием с учетом дифракционных эффектов показана справедливость приближения геометрической оптики в областях фокусировок при превышениях уровня интенсивности сигнала порядка 4х кратного, реально имевшего место в эксперименте.
Авторы благодарят администрацию НИВЦ МГУ за предоставленный доступ к вычислительным ресурсам суперкомпьютерного комплекса СКИФ-ГРИД "Чебышев".
Работа выполнена при частичной поддержке программы № 22 Президиума РАН "Фундаментальные проблемы исследований и освоения Солнечной системы".
Литература
1. Kliore A., Gain D.L., Levy S. et al. Occultation experiments results of the first direct measurements of Mars atmosphere and ionosphere // Science. 1965. V. 149. № 3689. P. 1243-1250.
2. Fjeldbo G., Eshleman V.R. The bistatic radar-occultation method for the study of planetary atmospheres //J. Geophys. Res. 1965. V. 70. N 13. P. 3217.
3. Fjeldbo G., Eshleman V.R., Carriott O.K., Smith F.L. The two-frequency bistatic radar-occultation method for the study of planetary ionosphere //J. Geophys. Res. 1965. V. 70. N 15. P. 3701.
4. Phinney R.A., Anderson D.L. On the radio occultation method for a studying planetary atmosphere // J. Geophys. Res. 1968. V. 73. № 5. P. 1819-1827.
5. Lusignan B., Modrell G., Morrison A. et al. Sensing the Earth’s atmosphere with occultation satellites //Proc. IEEE. 1969. V. 57. N 4. P. 458.
6. Tyler. G. L. Radio propagation experiments in the outer solar system with Voyager // Proc. IEEE. 1987. V. 75. P. 1404-1431.
7. Brace L.H., Kliore A.J. The structure of the Venus ionosphere // Space Science Reviews. 1991. V. 55. Jan.-Feb. P. 81-163.
8. Арманд Н.А., Гуляев Ю.В., Гаврик А.Л., Ефимов А.И., Матюгов С.С., Павельев А.Г., Савич Н.А., Самознаев Л.Н., Смирнов В.М., Яковлев О.И. Результаты исследований солнечного ветра и ионосфер планет радиофизическими методами // Успехи физических наук. 2010. Т. 180. № 5. С. 34-40. URL: http://ufn.ru/ufn10/ufn10_5/Russian/r105j.pdf
9. Rangaswamy S. Recovery of atmospheric parameters from the Apollo/Soyuz-ATS-F radio occultation data // Geophys. Res. Letters. 1976. V. 3. N. 8. P. 483.
10. Liu A.S. On the determination and investigation of the terrestrial ionospheric refractive indices using Geos-3 / ATS-6 satellite-to-satellite traking data //Radio Sci. 1978. V. 13. N 4. P. 709.
11. Yunck T.P., Lindal G.F., Liu C.H. The role of GPS in precise earth observation, paper presented at the IEEE Position, Location and Navigation Symposium / 1988. Orlando, Fl., Nov. 29-Dec. 2.
12. Гурвич А.С., Красильникова Т.Г. Об использовании навигационных спутников для радиопросвечивания атмосферы Земли // Космические исследования. 1987. № 6. С. 89.
13. Kursinski E.R., Hajj G.A., Schofield J.T., Linfield R.P., Hardy K.R. Observing Earth’s atmosphere with radio occultation measurements using the global positioning system // Journal of Geophysical Research. 1997. V. 102. D19. P. 23429-23465. doi:10.1029/97JD01569.
14. Gorbunov M.E., Gurvich A.S., Kornblueh L. Comparative analysis of radioholographic methods of processing radio occultation data // Radio Science. 2000. V. 35(4). P. 1025-1034.
15. Liou Y.A., Pavelyev A.G. Simultaneous observations of radio wave phase and intensity variations for locating the plasma layers in the ionosphere // Geophys. Res. Lett. 2006. V. 33(23). P. L23102 1-5.
16. Гаврик А.Л., Гаврик Ю.А., Копнина Т.Ф. О возможности увеличения чувствительности метода радиопросвечивания // Журнал радиоэлектроники [электронный журнал].- 2011. - № 5. - С. 1-18. URL: http://jre.cplire.ru/jre/may11/3/text.pdf
17. Гаврик А.Л. Использование радиосигнала L диапазона в экспериментах двухчастотного радиопросвечивания // Журнал радиоэлектроники [электронный журнал]. - 2011. - № 8. - С. 1-19. URL: http://jre.cplire.ru/jre/aug11/1/text.pdf
18. Гаврик А.Л., Гаврик Ю.А., Копнина Т.Ф., Самознаев Л.Н. Вариации амплитуд и частот когерентных радиосигналов при просвечивании дневной ионосферы Венеры // Радиотехника и электроника. 2010. Т. 55. № 3. С. 277-284.
URL: http://www.maikonline.com/maik/showArticle.do?auid=VAG762MEP3&lang=ru
19. Рытов С.М., Кравцов Ю.А., Татарский В.И. Введение в статистическую радиофизику. - М.: Наука. 1978.
20. Ilyushin Ya.A., Fluctuations of the GPS signals on the tangential paths in the lower terrestrial atmosphere: influence of the small-scale structure // Journal of Atmospheric and Solar-Terrestrial Physics. 2008. V. 70. P. 1863-1869.
doi:10.1016/j.jastp.2008.05.020.
21. Илюшин Я.А., Захаров В.И. Влияние нерегулярных структур нижней атмосферы на распространение сигналов глобальных спутниковых радионавигационных систем // Радиотехника. 2009. № 3. С.84-91.
22. Рихтмайер Р., Мортон К. Разностные методы решения краевых задач. - М.: Мир, 1972. - 418 c.
23. Baskakov V.A., Popov A.V. Implementation of transparent boundaries for numerical solution of the Schroedinger equation. // Wave Motion. 1991. 14. P. 123-128
24. Савич Н.А., Андреев В.Е., Вышлов А.С., Гаврик А.Л., Конофалов В.П., Лаптев Н.В., Мармулев В.А., Местэртон А.П., Набатов А.С., Орлов Ю.Н., Осмоловский И.К., Самознаев Л.Н., Штерн Д.Я. Дневная ионосфера Венеры по данным радиозатмений спутников "Венера-15,16" в 1983 г. // Радиотехника и электроника. 1986. Т. 31. № 11. С. 2113-2120.
25. Гаврик А.Л., Самознаев Л.Н. Особенности дневной ионосферы Венеры в годы низкой и высокой активности Солнца // Космические исследования. 1987. Т. 25. № 2. С. 285-291.
26. Гаврик А.Л., Самознаев Л.Н. Анализ ошибок результатов радиопросвечивания дневной ионосферы Венеры, обусловленных ее несферичностью // Космические исследования. 1985. Т. 23. № 1. С. 148-157.
27. Гаврик А.Л., Гаврик Ю.А., Самознаев Л.Н., Копнина Т.Ф. О возможности радиовидения слоистых структур в экспериментах радиопросвечивания ионосфер планет // Журнал радиоэлектроники [электронный журнал]. - 2010. -№ 5.- С. 1-14.
UPL: http://jre.cplire.ru/jre/may10/1/text.pdf
28. Гаврик А.Л., Гаврик Ю.А., Самознаев Л.Н. Неоднородная структура дневной ионосферы Венеры по данным радиопросвечивания при помощи станций Венера-15,-16 // Радиотехника и электроника. 2008. Т. 53. № 9. С. 1104-1111.
URL: http://www.maikonline.com/maik/download.do?uid=VAFKCB4Y1V&ptype=401&dtype=pdf
29. Гаврик А.Л., Павельев А.Г., Гаврик Ю.А. Обнаружение ионосферных слоев в дневной ионосфере Венеры на высотах 80-120 км по результатам двухчастотного радиопросвечивания КА Венера-15,-16 // Солнечно-земная физика. 2008. № 12. Т. 2. С. 203-205.
URL: http://ru.iszf.irk.ru/images/b/bc/203-205.pdf
30. Pavelyev A.G., Liou Y.A., Wickert J., Gavrik A.L., and Lee C.C. Eikonal acceleration technique for studying of the Earth and planetary atmospheres by radio occultation method // Geophys. Res. Lett. 2009. V. 36. P. L21807.
DOI:10.1029/2009GL040979. URL: http://hrsl.csrsr.ncu.edu.tw/DOCUMENTS/Paper/2009GL040979.pdf