УДК 621.396.96
Повышение вычислительной эффективности методов сверхрэлеевского разрешения сигналов
С. А. Климов
лаборатория проблем обработки радиолокационной информации военной академии войсковой ПВО
имени маршала Советского Союза А. М. Василевского, Смоленск
Получена 15 марта 2012 г.
Аннотация. Рассматривается способ снижения вычислительных затрат одного из достаточно распространенных этапов расчетов, используемых в методах сверхрэлеевского разрешения сигналов при их цифровой обработке, а именно этапа вычисления значений квадратичной целевой функции. Способ основан на свойствах матрицы квадратичной формы, позволяющей осуществить ее факторизацию по методу разложения Холецкого. Представлены оценки вычислительной эффективности стандартного и предложенного алгоритмов.
Ключевые слова: сверхрэлеевское разрешение, вычислительная сложность, разложение Холецкого.
Abstract. Values calculation of a quadratic goal function – is one of the widespread stage of calculations that are used while digital processing of signals. The article discusses the method of reduction in the aforecited expenditure. The method is founded on a quadratic matrix property that allows to factor it out after the fashion of Holecky. The article presents performance evaluations of the standard and offered methods.
Keywords: superreleevsky resolution, computing complexity, decomposition Holetsky.
В настоящее время бурное развитие цифровой обработки сигналов послужило сильным толчком к разработке эффективных методов их сверхрэлеевского разрешения, в том числе и многомерных. Возможность практической реализации любого метода сверхрэлеевского разрешения напрямую связана с вычислительной мощностью используемых аппаратных средств, эффективностью математических методов и реализующих их вычислительных алгоритмов и программ, с потребным объемом вычислений и располагаемыми вычислительными ресурсами [1]. Одна из серьезных задач, с которой сталкиваются в ходе практической реализации методов сверхрэлеевского разрешения, - резкий рост объема вычислений при увеличении количества разрешаемых сигналов. Алгоритмы сверхрэлеевского разрешения, основанные на методах цифрового спектрального оценивания [1, 2], многоканального анализа [3], а также различных модификациях методов статистических решений [4–6], с ростом гипотезы о количестве разрешаемых сигналов требуют значительных вычислительных затрат, что предъявляет очень жесткие требования к программным и временным ресурсам для их реализации. Проблема обеспечения требуемых вычислительных ресурсов для алгоритмов сверхрэлеевского разрешения становится еще более острой, если одновременно с увеличением количества разрешаемых сигналов повышается и число параметров, по которым они разрешаются. Последнее связано с тем, что при росте количества разрешаемых сигналов и, как следствие, повышении размерности пространства сигналов, методы сверхрэлеевского разрешения требуют в сравнении с классическими методами обработки сигналов существенно более мелкого шага при вычислении целевой функции и, соответственно, характеризуются повышенной относительной сложностью вычислений, что ограничивает их применение на практике. В связи с этим задача повышения вычислительной эффективности методов сверхрэлеевского разрешения является актуальной.
Ряд подходов к снижению вычислительных затрат при практической реализации различных методов сверхрэлеевского разрешения изложен в работах [7, 8]. В работе [7] рассматриваются вопросы повышения вычислительной эффективности методов оценки двумерного углового спектра, обладающих повышенной разрешающей способностью, в антенных решетках кольцевой и пространственной конфигурации. В частности, для расчета пространственной корреляционной матрицы (КМ) предложено использовать ее спектральное разложение в сочетании с алгоритмом коротких сверток для вычислительной схемы классического формирования луча решетки. В работе [8] изложены подходы к сокращению вычислительных затрат при реализации алгоритмов сверхрэлеевского разрешения по угловым координатам в антенных решетках с адаптивной обработкой. Показано, что все эти алгоритмы так или иначе связаны с получением оценки прямой или обратной КМ входных сигналов, что требует большого объема вычислений. Для практического применения алгоритмов сверхрэлеевского разрешения, основанных на использовании оценки КМ входных сигналов, предлагается применять семейство способов, основанных на методах ортогонализации и ортогональных преобразований (Грама-Шмидта, Хаусхолдера, Гивенса и адаптивной решетчатой фильтрации). Данное направление сокращения вычислительных операций связано с факторизацией оценки КМ входных сигналов, т. е. представлением ее в виде произведения сомножителей с большим числом нулевых элементов. Таким образом, работы [7, 8] в основном касаются подходов к повышению вычислительной эффективности методов сверхрэлеевского разрешения по угловым координатам, основанных на спектральном анализе. Кроме того, в них не рассматриваются вопросы влияния на вычислительную эффективность алгоритмов сверхрэлеевского разрешения размерности вектора параметров целевой функции, зависящей от количества разрешаемых сигналов М и числа разрешаемых параметров I сигналов.
Цель статьи − разработка экономичной, с точки зрения операций умножения − сложения, процедуры вычисления квадратичной целевой функции, часто используемой в методах сверхрэлеевского разрешения сигналов, а также проведение оценки ее вычислительной эффективности по числу операций умножения − сложения в зависимости от дискретности N вычисления целевой функции, количества разрешаемых сигналов М и числа разрешаемых параметров I сигналов.
Многие методы сверхрэлеевского разрешения сигналов [1−6] частично или полностью основываются на достаточно общей вычислительной схеме, определяемой выражением
где Ψ(·) – целевая функция, подлежащая оптимизации; Z(·) – векторный корреляционный интеграл; G(·) – матрица значений функции рассогласования сигналов; α – вектор параметров целевой функции, зависящий от количества разрешаемых сигналов М и числа разрешаемых параметров I сигналов; “H” - символ комплексно-сопряженного транспонирования.
При организации матричных вычислений (1) особый интерес вызывает количество операций умножения − сложения для достижения требуемой точности результата. Возможный путь сокращения потребного числа данных операций связан с факторизацией матриц, т. е. представлением ее в виде произведения сомножителей при условии, что сомножители имеют большое число нулевых элементов [9]. Факторизация используется для получения достаточных статистик без явного формирования самих матриц. За счет этого повышается численная устойчивость алгоритмов обработки; экономятся элементы запоминающих устройств; обеспечивается конвейеризация систем обработки сигналов [9].
Один из возможных подходов по сокращению числа операций комплексного умножения – сложения (1) основан на использовании свойств матрицы рассогласования сигналов G. Рассмотрим структуру матрицы G квадратичной формы (1) более подробно. Например, при разрешении М сигналов по двум параметрам она может быть записана в виде
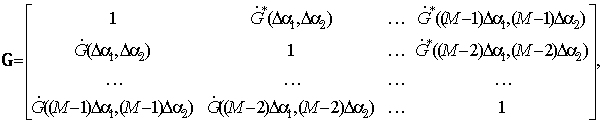 (2)
(2)
где ![]() – функция рассогласования сигнала;
– функция рассогласования сигнала; ![]() – разница по параметру
– разница по параметру ![]() между m-м и (m −
1)-м сигналом;
между m-м и (m −
1)-м сигналом; ![]() – разница по параметру
– разница по параметру ![]() между m-м и (m − 1)-м сигналом; (
между m-м и (m − 1)-м сигналом; (![]() ) – символ комплексно-сопряженного числа. Анализ
(2) позволяет заключить, что G является положительно
определенной эрмитовой матрицей. Следовательно, к ней можно применить
специальные способы факторизации, в значительной степени сокращающие объем
вычислительных затрат. В наиболее эффективных алгоритмах сверхрэлеевского
разрешения [3 − 6] матрица рассчитывается и
записывается в память вычислителя заранее. Тем не менее, квадратичная форма (1)
должна вычисляться в реальном масштабе времени для всех возможных сочетаний параметров
всей совокупности разрешаемых сигналов. Если дискретность параметра
) – символ комплексно-сопряженного числа. Анализ
(2) позволяет заключить, что G является положительно
определенной эрмитовой матрицей. Следовательно, к ней можно применить
специальные способы факторизации, в значительной степени сокращающие объем
вычислительных затрат. В наиболее эффективных алгоритмах сверхрэлеевского
разрешения [3 − 6] матрица рассчитывается и
записывается в память вычислителя заранее. Тем не менее, квадратичная форма (1)
должна вычисляться в реальном масштабе времени для всех возможных сочетаний параметров
всей совокупности разрешаемых сигналов. Если дискретность параметра ![]() составляет N1, а дискретность
параметра
составляет N1, а дискретность
параметра ![]() − N2, то общее количество
матриц G, используемых при вычислении (1) составляет N = N1N2, причем каждая
размерностью M×M. Следовательно, для оценки вычислительной сложности
алгоритма (1) требуется введение еще одного параметра – дискретности N вычисления целевой
функции
− N2, то общее количество
матриц G, используемых при вычислении (1) составляет N = N1N2, причем каждая
размерностью M×M. Следовательно, для оценки вычислительной сложности
алгоритма (1) требуется введение еще одного параметра – дискретности N вычисления целевой
функции ![]() . Очевидно, что при достаточно больших M, N и I расчет (1) требует
значительного количества вычислительных операций, что создает серьезные
трудности в практической реализации методов сверхрэлеевского разрешения.
. Очевидно, что при достаточно больших M, N и I расчет (1) требует
значительного количества вычислительных операций, что создает серьезные
трудности в практической реализации методов сверхрэлеевского разрешения.
С целью сокращения вычислительных затрат положительно определенную матрицу G сведем к произведению треугольных по методу разложения Холецкого [2]
![]() , (3)
, (3)
где ![]() - нижнетреугольная матрица
с ненулевыми действительными элементами на главной диагонали. Обращая матрицу
- нижнетреугольная матрица
с ненулевыми действительными элементами на главной диагонали. Обращая матрицу![]() , найдем обратную матрицу
, найдем обратную матрицу ![]() . Тогда матрица
. Тогда матрица ![]() равна
равна
G-1=(R-1)HR-1. (4)
Подставляя выражение (4) в (1) получим
Ψ(α)=ZH(α)G-1(α)Z(α)=ZH(α)[R-1(α)]H[R-1(α)]Z(α)=
[R-1(α)Z(α)]H[R-1(α)Z(α)]=YH(α)Y(α), (5)
где Y(α)=R-1(α)Z(α).
Рассмотрим пример. Пусть число разрешаемых сигналов M = 3, число параметров I = 1 и требуется вычислить одно значение N = 1 целевой функции Ψ. Тогда величина Ψ по формуле (1) будет равна (параметр α опущен для компактности записи)
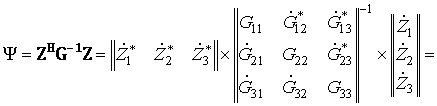
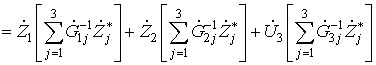 ,
,
т. е. для вычисления требуется 12 операций комплексного умножения и 8 комплексного сложения. Теперь определим количество операций для вычисления скаляра Ψ по формуле (5)
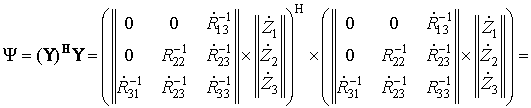
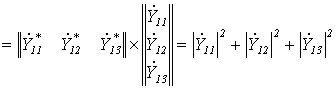 ,
,
где ![]() ;
; ![]() ;
; ![]() .
.
Анализ последнего выражения показывает, что в этом случае требуется 9 операций умножения и 5 сложения. Таким образом, выигрыш составил 25% и 37,5% по числу умножений и сложений соответственно.
В общем случае вычислительная сложность OΣ алгоритма (1) по количеству операций умножения Ox и сложения Os равна
![]() ;
; ![]() ;
; ![]() . (6)
. (6)
Вычислительная сложность ÕΣ алгоритма с использованием факторизации матрицы G методу разложения Холецкого (5) по количеству операций умножения Õx и сложения Õs определяется выражениями
![]() ;
; ![]() ;
;
(7)
![]() ;
; ![]() ;
; ![]() ;
; ![]() ,
,
где ![]() и
и ![]() определяются рекуррентно:
определяются рекуррентно:
![]() ,
, ![]() ;
; ![]() ,
, ![]() ;
;
![]() ,
, ![]() ;
; ![]() ,
, ![]() .
.
Сравнительный анализ вычислительной эффективности алгоритмов (1) и (5) в зависимости от числа разрешаемых сигналов М, дискретности вычисления целевой функции N и числа разрешаемых параметров сигналов I, выполненный по формулам (6), (7), представлен графически на рис. 1.
Анализ рис. 1 позволяет заключить, что вычислительная сложность рассматриваемых алгоритмов существенно зависит, прежде всего, от числа параметров I, по которым разрешаются сигналы. Затем решающим фактором является число разрешаемых сигналов М и уже в последнюю очередь − дискретность вычисления целевой функции N. Вместе с тем видно, что вычислительный алгоритм, основанный на разложении Холецкого (5), требует для своей реализации существенно меньшего количества операций умножения − сложения по сравнению с алгоритмом (1).
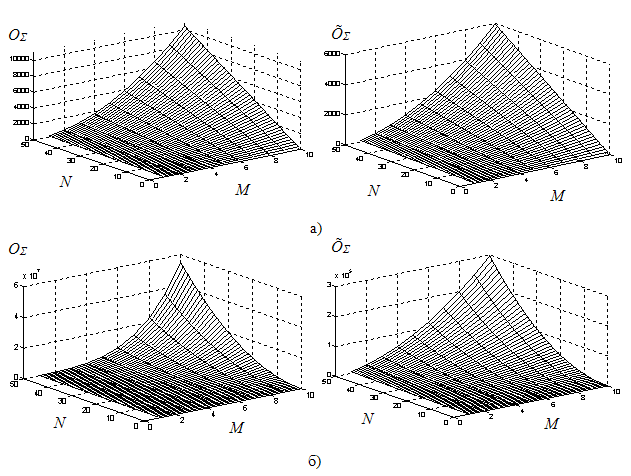
Рис. 1. Зависимость вычислительных затрат (операций комплексного умножения и сложения) от числа разрешаемых сигналов M, дискретности вычисления N и числа разрешаемых параметров сигналов I
а) число разрешаемых параметров сигналов I = 1;
б) число разрешаемых параметров сигналов I = 2
Относительный выигрыш эффективности ΔOΣ алгоритма (5) по сравнению с (1) по количеству операций умножения − сложения показан на рис. 2, из которого следует, что снижение вычислительных затрат также зависит от числа разрешаемых сигналов М, дискретности вычисления целевой функции N и числа разрешаемых параметров сигналов I.
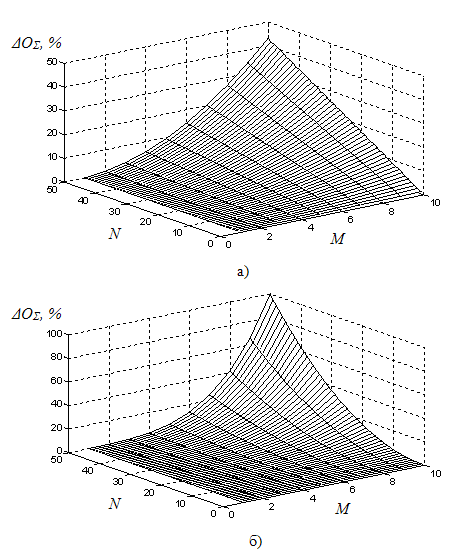
Рис. 2. Относительный выигрыш в вычислительных затратах ΔOΣ
(операций комплексного умножения и сложения) от числа разрешаемых сигналов M, дискретности вычисления N и числа разрешаемых параметров сигналов I
а) число разрешаемых параметров сигналов I = 1;
б) число разрешаемых параметров сигналов I = 2
Из рис. 2 видно, что при малом количестве разрешаемых сигналов (М ≤ 4) и дискретности вычисления (N ≤ 20) снижение вычислительных затрат не столь значительно. Однако с ростом М, N и особенно числа разрешаемых параметров сигналов I выигрыш становится существенным и может достигать 100% и более по сравнению с алгоритмом (1).
Таким образом, вычислительная процедура (5) открывает возможности для практического использования методов многомерного (I>1) сверхрэлеевского разрешения сигналов. Последние позволяют обеспечить более высокие показатели разрешающей способности по сравнению с одномерными [4].
Литература
1. Алгоритмы оценивания угловых координат источников излучений, основанные на методах спектрального анализа: Научно-технические серии/В. В. Дрогалин, В. И. Меркулов, В. А. Родзивилов, И. Б. Федоров, М. В. Чернов. 1999. №1. Вып. 1. С. 52-68.
2. Марпл-мл. С. Л. Цифровой спектральный анализ и его приложения: Пер. с англ. М., Мир, 1990. 584 с.
3. Варюхин В. А. Основы теории многоканального анализа. Киев, ВА ПВО СВ, 1993.
4. Чижов А. А. Сверхрэлеевское разрешение. Т. 2. Преодоление фактора некорректности обратной задачи рассеяния и проекционная радиолокация. М., Красанд, 2010. 104 с.
5. Слюсар В. И. Синтез алгоритмов измерения дальности М источников при дополнительном стробировании отсчетов АЦП//Радиоэлектроника, 1996. №5. С. 55-62.
6. Абраменков В. В., Климов С. А., Савинов Ю. И. Способ и устройство измерения дальностей до М источников вторичного излучения, сигналы которых перекрываются во времени//Радиотехника, 2002. № 1. С. 32-38.
7. Иванов Н. М., Шевченко В. Н. Повышение вычислительной эффективности методов высокого разрешения в задачах двумерного апертурного синтеза//Электромагнитные волны и электронные системы, 2009. № 7. С. 18-22.
8. Ратынский М. В. Адаптация и сверхразрешение в антенных решетках. М., Радио и связь, 2003. 200 с.
9. Ширман Я. Д., Манжос В. Н. Теория и техника радиолокационной информации на фоне помех. М., Радио и связь, 1981. 416 с.