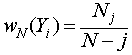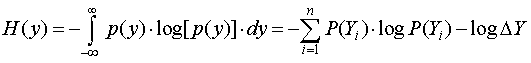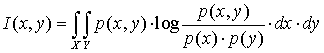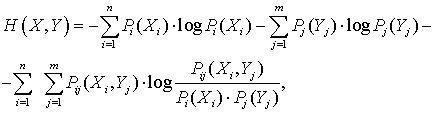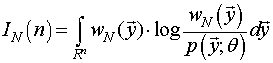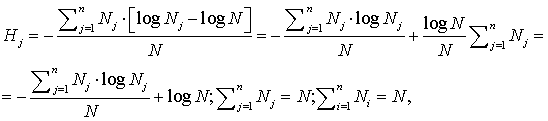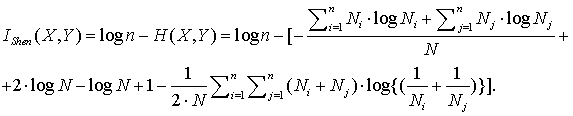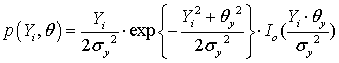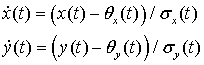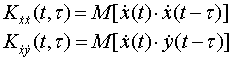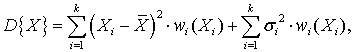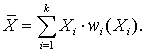ОБРАБОТКА СИГНАЛОВ М-, ДМ- ДИАПАЗОНОВ ДЛИН ВОЛН ПРИ ЭЛЕКТРОМАГНИТНОМ ИМПУЛЬСНОМ СВЕРХШИРОКОПОЛОСНОМ ЗОНДИРОВАНИИ ПОДСТИЛАЮЩЕЙ СРЕДЫ
В. Б. Болтинцев
ЗАО НПФ «Геодизонд»
Получена 5 марта 2013 г.
Аннотация. Подстилающая среда представлена макросистемой. Для неё предполагается значительная дисперсия диэлектрической проницаемости в м-, дм- диапазонах длин волн. Использован вариационный принцип описания динамики макросистемы с введением энтропии для двух электромагнитных импульсных (ЭМИ) сверхширокополосных (СШП) сигналов. Показано, что порядок построения эмпирических плотностей вероятностей (ЭПВ) определяется методом формирования числа интервалов группирования экспериментальных данных. Построение ЭПВ есть построение волнового спектра отражённого сигнала. Путём введения сингулярности в ЭПВ ЭМИ СШП сигналов проведено построение энтропийных критериев оценивания объёмов выборки для сдвиг – масштабного преобразования сигналов с последующим нахождением авто -, взаимокорреляционной функций (АКФ, ВКФ) и волатильностей для АКФ и ВКФ. Показано, что центрировано-нормированные ЭМИ СШП сигналы идентифицируемы по Тейчеру. На примере плотины Бурейской ГЭС, зоны «Размыва» в г. Санкт-Петербурге и месторождения сланцев в Мьянме показана работоспособность предложенных критериев.
Ключевые слова: волновой спектр; сингулярность; эмпирическая плотность вероятности; информационная мера Кульбака; производная Радона – Никодима, идентифицируемость по Тейчеру, волатильность, суффозия, сланцы.
За последние сорок лет изучение свойств объектов с помощью СШП сигналов превратилось из экзотического в один из самых перспективных путей развития современных технологий, в частности, в целое направление по изучению свойств подстилающей среды.
Подстилающая среда – это большой, постоянно увеличивающийся класс учитываемых соединений (от фракталов[1] до молекул). Сегодня главный акцент исследований перемещается в область более глубокого изучения молекулярных механизмов многоатомных молекул, имеющих большое число степеней свободы вращательных и трансляционных движений, которые определяют форму и физические свойства среды.
Известно [1], что попытка учёта вращательных и трансляционных движений на уровне моделей приводит к «размытию» частотных диэлектрических спектров, что существенно затрудняет анализ и установление связи между измеряемыми макроскопическими свойствами мезофаз и такими микроскопическими характеристиками, как времена диэлектрической релаксации молекул.
«Размытые» диэлектрические спектры хорошо описываются с помощью функции непрерывного распределения времен релаксации [2], но построить модель сложных молекулярных релаксационных движений удается лишь в исключительных случаях. Поэтому в мировой практике особую важность приобретают разрабатываемые численные методы восстановления распределения времен релаксации непосредственно из экспериментально измеряемых спектров, чтобы обеспечить их более совершенный анализ и лучшее понимание. Разработка новых программных методов их диагностики является важной и актуальной задачей.
Традиционный подход к решению данной проблемы – объявить подстилающую среду макросистемой [3], и уже для неё посредством измеряемых макропараметров отражать состояние системы[2], что предполагает использование статистического формализма Э. Т. Джейнса, предложившего вариационный принцип описания динамики системы.
Методы описания СШП сигналов
Точные непериодические и нестационарные решения уравнений Максвелла применительно к СШП сигналам предложены:
- Х. Ф. Хармутом (1980) - метод решения нестационарного волнового уравнения с заданными начальными и граничными условиями является одним из наиболее универсальных, однако плата за это - значительная сложность и трудоёмкость, что наглядно иллюстрируется его использованием для решения задачи об излучении СШП сигналов простейшей антенной - вибратором Герца. Большинство получаемых выражений настолько громоздки, что подавляющее число интегралов не может быть вычислено точно;
- А. Б. Шварцбургом (1993) - метод развивает точно решаемые модели импульсной оптики диспергирующих сред во временном представлении на основании полиномов Лагерра. Эти модели описывают взаимодействие ультракоротких видеоимпульсов с диэлектриками и проводниками. Поля, возбуждаемые видеоимпульсами в этих средах, представляются аналитически благодаря новым точным непериодическим и нестационарным решениям уравнений Максвелла (уравнений типа свёртки)[3];
- О. А.Третьяковым
(1998) - метод модового базиса,
который опирается на теорию нестационарных операторных уравнений
и общие
результаты применения этой теории для уравнений Максвелла. Спектральное
разложение искомого поля по модовому базису основано на ортогональных
разбиениях Вейля гильбертова функционального пространства ![]() и приводит к
отщеплению от пространственно – временного дифференциального оператора,
в
уравнениях Максвелла - оператора пространственного дифференцирования. В
результате получают дифференциальные уравнения с соответствующим
набором
начальных условий, именуемых эволюционными, поскольку в качестве
независимой
переменной в них входит время. Решая их, определяют скалярные функции
времени,
которые являются коэффициентами разложения искомого поля по модовому
базису.
Недостатком является сложность построения модового базиса в условиях конкретной задачи[4];
и приводит к
отщеплению от пространственно – временного дифференциального оператора,
в
уравнениях Максвелла - оператора пространственного дифференцирования. В
результате получают дифференциальные уравнения с соответствующим
набором
начальных условий, именуемых эволюционными, поскольку в качестве
независимой
переменной в них входит время. Решая их, определяют скалярные функции
времени,
которые являются коэффициентами разложения искомого поля по модовому
базису.
Недостатком является сложность построения модового базиса в условиях конкретной задачи[4];
- Л. Ю. Астаниным, А. А. Костылевым (1989) - метод обобщенной фазовой плоскости как альтернатива использованию любых интегральных преобразований при описании СШП сигналов. К сожалению, метод не применим при рассмотрении задач распространения СШП сигналов в различных средах.
Также следует отметить метод функций Уолша – метод замены разложения в гармонический ряд исследуемых при решении уравнений Максвелла функций на разложение по ортогональной системе функций Уолша (ряд Фурье - Уолша); метод мгновенного спектра (А. А. Харкевич, 1986), который заключается в описании СШП сигнала текущим и мгновенным спектрами; метод атомарных функций (В. Ф. Кравченко, 2007), который даёт хорошую сопоставимость модели распространяющегося СШП сигнала с экспериментальными данными.
Широко распространены следующие виды описания СШП сигналов.
Временное описание СШП сигналов является наиболее удобным для анализа задач распространения во временной области, когда вид сигнала в данной точке пространства определяется с использованием вида сигнала на границе раздела сред как интеграл свёртки, и распространено при описании решения задач излучения СШП сигналов[5].
Частотное описание СШП сигналов требуется для получения импульсных характеристик, которые позволяют получать аналитические решения для более широкого класса задач, так как основным их достоинством является возможность использовать в негармоническом анализе хорошо известные результаты классической теории.
Вейвлет (wavelet) анализ (Гроссманн, Морле, 1984)[6] с зависящей от времени частотой мало похож на реальные излучаемые импульсы ЭМИ СШП зондирования, отличающиеся отсутствием несущей частоты и асимметрией переднего и заднего фронтов.
Деформация импульсов в
диспергирующей
среде описывается, как известно [4] в частотной
области методом разложения фазы
в ряд по степеням отношения спектральной ширины импульса ![]() к
несущей частоте
к
несущей частоте ![]() [5].
Однако для коротких СШП импульсов, излучаемых как полтора колебания
поля,
отношение
[5].
Однако для коротких СШП импульсов, излучаемых как полтора колебания
поля,
отношение ![]() не
является малым параметром; при этом
количество спектральных компонент, требуемое для синтеза поля импульса
в
глубине среды, становится непомерно большим [6]. В
разложении фазы все
слагаемые содержат в знаменателе показатель преломления среды
не
является малым параметром; при этом
количество спектральных компонент, требуемое для синтеза поля импульса
в
глубине среды, становится непомерно большим [6]. В
разложении фазы все
слагаемые содержат в знаменателе показатель преломления среды ![]() . Если в
спектре содержится частота
отсечки диспергирующей прозрачной среды
. Если в
спектре содержится частота
отсечки диспергирующей прозрачной среды ![]() , то
, то ![]() и
ряд, представляющий собой разложение
фазы, расходится [4].
и
ряд, представляющий собой разложение
фазы, расходится [4].
Отмеченные трудности связаны не с уравнениями Максвелла, а с традиционными методами их решения с помощью разделения переменных и преобразований Фурье как способа решения, удобного для описания квазимонохроматических волн с медленно меняющейся амплитудой и фазой.
Одна из проблем, с которыми сталкиваются исследователи диэлектрических свойств веществ, - это наличие «неудобных» участков[7] частотного диапазона на стыке м- и дм- диапазонов длин волн (10−1000 МГц), обусловленных существованием в среде низкочастотной дисперсии диэлектрической проницаемости. Экспериментальная модель отклика многослойной среды на ЭМИ СШП сигнал, подтверждающая выводы Шварцбурга А. Б. (2000 г.), в этом частотном диапазоне представляет собой временную последовательность узкополосных, почти гармонических сигналов. Как правило, значения частот лежат в диапазоне 1-100 МГц и на каждом временном интервале определяются геометрией и материалом (внутренним строением и, как правило, количеством «связанной» воды) слоя среды, находящегося на соответствующей глубине.
Однако вывод о резонансной модели отклика многослойной среды на ЭМИ СШП сигнал был бы не полным без анализа волновых свойств отражённого сигнала и непоставленного вопроса о предельном поглощении сигнала определённых частот подстилающей средой, поскольку оснований для этого достаточно [7].
Представление волнового спектра отражённого сигнала его эмпирическим распределением
Поскольку затухания сигналов в основном[8] привязаны к длине волны и имеют размерность дБ/м, автоматически возникает вопрос о длинах волн в отражённом сигнале[9]. Ниже предлагается представление волнового спектра отражённого сигнала его эмпирическим распределением[10].
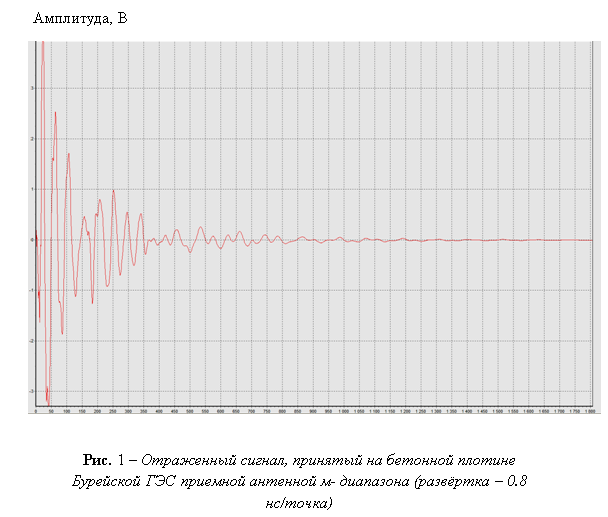
Представим
отраженный сигнал ЭМИ СШП зондирования
м – диапазона (рис. 1), записанный как временной
ряд ![]() , вектором наблюдений
, вектором наблюдений ![]() .
.
Определим
эмпирические плотности вероятности (ЭПВ) для ![]() в
каждый момент
в
каждый момент ![]()
![]() размерностью
размерностью
![]() для
сколь угодно больших
для
сколь угодно больших ![]() (на рис. 1
(на рис. 1 ![]() ) и
всевозможных
) и
всевозможных ![]() как вероятность
для i-го интервала группирования экспериментальных данных
как вероятность
для i-го интервала группирования экспериментальных данных
где
![]() частота
попаданий значений
частота
попаданий значений ![]() в
интервал
в
интервал ![]() ;
;![]() -
вариационный ряд, построенный из амплитудных значений
-
вариационный ряд, построенный из амплитудных значений![]() :
:
![]() . Здесь
. Здесь ![]() –
неизвестное собственное число степеней свободы
–
неизвестное собственное число степеней свободы ![]() ,
которое оценивается по
формуле
,
которое оценивается по
формуле
где ![]() –
максимальное значение
–
максимальное значение ![]() ;
; ![]() –
минимальное значение
–
минимальное значение ![]() ;
; ![]() -
вариационный интервал (далее –«ширина
ящика»).
-
вариационный интервал (далее –«ширина
ящика»).
Погрешность по определению, задаваемому (2), равна
![]() - знак
математического ожидания[11].
- знак
математического ожидания[11].
В
настоящее время отсутствует метод определения оптимального числа
интервалов
группирования экспериментальных данных ![]() (далее
«ящиков»). Так, для решения этой задачи в [8]
приведено более 30 способов
построения эмпирического распределения, устанавливающих связь между
объёмом
выборки
(далее
«ящиков»). Так, для решения этой задачи в [8]
приведено более 30 способов
построения эмпирического распределения, устанавливающих связь между
объёмом
выборки ![]() и
числом ящиков
и
числом ящиков ![]() ,
наиболее используемые из них приведены в [9-13].
,
наиболее используемые из них приведены в [9-13].
Первая публикация по
этому вопросу относится к 1730 г[12]. В неизвестное число ящиков ![]() бросают
бросают
![]() шаров
так, что в любой ящик каждый шар
попадает с вероятностью
шаров
так, что в любой ящик каждый шар
попадает с вероятностью ![]() . В [14] показано, что единственной
несмещенной оценкой с равномерно-минимальной дисперсией для параметра
. В [14] показано, что единственной
несмещенной оценкой с равномерно-минимальной дисперсией для параметра ![]() будет
будет
где
![]() –
число Стирлинга II рода:
–
число Стирлинга II рода:
![]() ;
;![]() достаточная
статистика для неизвестного
достаточная
статистика для неизвестного
![]() ;
; ![]()
![]() при
при ![]()
![]()
![]() [15].
[15].
Возникает вопрос: «Что будет, если в ящик ничего не попадёт?». Действительно, достаточно в задаче о подбрасывании монеты заменить твёрдую поверхность стола песочницей с влажным рыхлым песком и число степеней свободы у подброшенной монеты станет равным трём («решка», «орёл», «ребро»), а у монеты с идеальными геометрическими формами и таким же центрированием число степеней свободы в песочнице выродится в одно – «ребро», два ящика («решка» и «орёл») будут пустыми, но появится новая степень свободы – угол наклона, под которым монета застрянет в песке.
Вырождение
степеней свободы ![]() математически
сформулировано в виде «концентрации энтропии» Э. Т. Джейнсом.
«…Без
использования логарифмических форм, которые мы сейчас называем
«энтропия», Якоб
Бернулли и Пьер Симон Лаплас предложили обоснование, рассчитав
множества
следующим образом:
математически
сформулировано в виде «концентрации энтропии» Э. Т. Джейнсом.
«…Без
использования логарифмических форм, которые мы сейчас называем
«энтропия», Якоб
Бернулли и Пьер Симон Лаплас предложили обоснование, рассчитав
множества
следующим образом:
но сегодня мы предпочитаем использовать приближение Стирлинга для вывода формы энтропии Шеннона
![]() »[13].
»[13].
Э.
Т. Джейнс установил базис, сейчас более известный как «МЕ
формализм» или
«формализм Джейнса», и нашёл его место в Байесовской статистике. По К.
Шеннону энтропия
непрерывного распределения с плотностью ![]() (К.
Шеннон, 1948; Э. Т. Джейнс, 1957, 1982) имеет вид
(К.
Шеннон, 1948; Э. Т. Джейнс, 1957, 1982) имеет вид
Непрерывное распределение с максимальной энтропией характеризуется собственными моментами
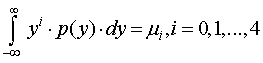 .
.
Лагранжиан (Zellner, Highfield, 1988) выглядит как
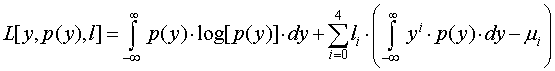 ,
,
где
![]() множители
Лагранжа. Тогда (Hildebrand, 1972)
множители
Лагранжа. Тогда (Hildebrand, 1972)
![]() ,
,
отсюда следует, что плотность непрерывного распределения с максимальной энтропией имеет вид
![]() .
.
Решение задач на функционалах (множителях) Лагранжа строится как решение с учетом ограничений на средние значения [16] [14].
На больших временах
используется эргодическая теорема, далее - законы больших чисел, или
явление
концентрации инвариантной (стационарной) меры:
«хорошие» (липшицевы, т. е. удовлетворяющие соотношению ![]() )
функции на «хороших» (гладких, с ненулевой кривизной) компактных
пространствах
с мерой большого числа измерений[15]. Для случая стационарных цепей Маркова, как
показано А.
Хинчиным (1953), достаточно длинные траектории всегда можно разбить на
два
класса. Все траектории первого класса обладают равными вероятностями
вида
)
функции на «хороших» (гладких, с ненулевой кривизной) компактных
пространствах
с мерой большого числа измерений[15]. Для случая стационарных цепей Маркова, как
показано А.
Хинчиным (1953), достаточно длинные траектории всегда можно разбить на
два
класса. Все траектории первого класса обладают равными вероятностями
вида
![]() ,
,
где ![]() длина
Марковской цепи (число шагов);
длина
Марковской цепи (число шагов); ![]() так
называемая энтропия эволюции на один
шаг (траекторная энтропия)
так
называемая энтропия эволюции на один
шаг (траекторная энтропия)
![]() .
.
Число таких
траекторий есть
величина ![]() . Про
второй класс траекторий известно,
что на основании эргодической теоремы для конечных марковских цепей
сумму
вероятностей этих траекторий при достаточно большом
. Про
второй класс траекторий известно,
что на основании эргодической теоремы для конечных марковских цепей
сумму
вероятностей этих траекторий при достаточно большом ![]() можно
сделать произвольно малой.
можно
сделать произвольно малой.
В случае ЭМИ
СШП сигналов [19, 20] за
определением ![]() с
точки зрения
физических процессов стоит волна - такая временная последовательность yj, которая
образуется
тогда, когда имеется хотя
бы два значения в i-ом ящике, таких, что время
для этих
значений не совпадает (tj1 ≠ tj2). В нашем
случае построение эмпирического
распределения есть построение волнового спектра. Непрерывное изменение
эмпирического распределения (волнового спектра) обусловлено наличием
сильной
частотной дисперсии диэлектрической проницаемости подстилающей среды
для м-,
дм- диапазонов длин волн.
с
точки зрения
физических процессов стоит волна - такая временная последовательность yj, которая
образуется
тогда, когда имеется хотя
бы два значения в i-ом ящике, таких, что время
для этих
значений не совпадает (tj1 ≠ tj2). В нашем
случае построение эмпирического
распределения есть построение волнового спектра. Непрерывное изменение
эмпирического распределения (волнового спектра) обусловлено наличием
сильной
частотной дисперсии диэлектрической проницаемости подстилающей среды
для м-,
дм- диапазонов длин волн.
Определение. Моменты времени заполнения конкретного ящика в эмпирическом распределении суть длина конкретной волны.
Введение энтропии двух процессов обусловлено, в первую очередь, необходимостью оценки дисперсии диэлектрической проницаемости, а также невозможностью отказа от учёта логарифма ширины «ящика» в одномерной энтропии и ограниченностью применения множителей Лагранжа для max энтропии[16].
Аналогично
введённому
выше представлению отраженного сигнала ЭМИ СШП зондирования м-
диапазона
временным рядом ![]() представим временной
ряд дм- диапазона
представим временной
ряд дм- диапазона ![]() вектором
наблюдений
вектором
наблюдений ![]()
![]() ,
который будет полностью определен, если заданы его
,
который будет полностью определен, если заданы его ![]() -мерные
плотности вероятности
-мерные
плотности вероятности ![]() для сколь угодно
больших
для сколь угодно
больших ![]() и
всевозможных
и
всевозможных ![]() .
.
Поскольку энтропия для двух процессов определяется как
логарифмы
ширины «ящика»
по ![]() и
и ![]() в (6) сокращаются
с логарифмами ширины ящиков взаимной информации, но появляется «третий
игрок» в
виде взаимной информации, чьё интегральное представление имеет вид
в (6) сокращаются
с логарифмами ширины ящиков взаимной информации, но появляется «третий
игрок» в
виде взаимной информации, чьё интегральное представление имеет вид
В общем случае выражение для энтропии для двух процессов выглядит как
где ![]() двумерное
распределение векторов
наблюдений
двумерное
распределение векторов
наблюдений ![]() ;
; ![]() количество
ящиков для
количество
ящиков для ![]() и
и ![]() ;
двойная сумма – выражение для
;
двойная сумма – выражение для ![]() ;
;![]() и
и![]() соответствуют
(2) и (3). Очевидно, что
соответствуют
(2) и (3). Очевидно, что ![]() ,
поскольку для каждой из
одномерных энтропий
,
поскольку для каждой из
одномерных энтропий ![]() и
и ![]() ищутся
свои
ищутся
свои ![]() и
и ![]() соответственно.
соответственно.
![]() представляет
собой матрицу размером
представляет
собой матрицу размером ![]() [17].
Предполагается
«перекладка» ящиков, из меньшего числа ящиков в большее.
[17].
Предполагается
«перекладка» ящиков, из меньшего числа ящиков в большее.
Таким образом, переход к энтропии двух процессов подразумевает появление третьего игрока - взаимной информации. Его роль состоит в обнулении логарифма от ширины ящика в (6), однако платой за это является переход к матричному счислению, или использованию на этом этапе наисложнейших моделей диэлектрической проницаемости для связи значений сигналов в м- и дм- диапазонах длин волн.
Шахматная доска как способ построения двумерного эмпирического распределения
Идея шахматной доски
принадлежит С. Кульбаку [21]:
предположим, что
эмпирическое распределение ![]() расклассифицировано (раскассировано) в
строку длиною n и определено по
критерию max
энтропии,
а гипотетическое распределение
расклассифицировано (раскассировано) в
строку длиною n и определено по
критерию max
энтропии,
а гипотетическое распределение ![]() в
столбец такой же длины
n, тогда
может быть
введена мера (информационная мера Кульбака, или мера Кульбака –
Лейблера -
Санова[18], далее ИМК)
в
столбец такой же длины
n, тогда
может быть
введена мера (информационная мера Кульбака, или мера Кульбака –
Лейблера -
Санова[18], далее ИМК)
как мера приближения
условной
энтропии к безусловной (свойства: строго выпукла вниз; всегда ≥0;
относительно равномерного ![]() с точностью до замены знака и сдвига
начала отсчёта совпадает с
энтропией).
с точностью до замены знака и сдвига
начала отсчёта совпадает с
энтропией).
А. Таглиани (2003) показал, что [19]
где ![]() -
мера изменения эмпирического и
модельного распределений. Очевидно, что
-
мера изменения эмпирического и
модельного распределений. Очевидно, что ![]() [20].
[20].
Для построения из
эмпирических плотностей вероятностей двух независимых процессов ![]() эмпирического
аналога величины
эмпирического
аналога величины ![]() из (8) используется 3D модель: по
z откладываются
эмпирические плотности
вероятности
из (8) используется 3D модель: по
z откладываются
эмпирические плотности
вероятности ![]() и
и ![]() ,
по вертикали – вариационный ряд
,
по вертикали – вариационный ряд ![]() , по
горизонтали – вариационный ряд
, по
горизонтали – вариационный ряд ![]() , в плоскости
, в плоскости ![]() образуется
«логическая» сумма
событий
образуется
«логическая» сумма
событий ![]() .
.
Возникает
задача по перераспределению данных –
«перекладыванию» данных из ![]() ящиков в
ящиков в ![]() , и
наоборот. Математически: поиск такого
значения аргументов, при котором по двум независимым векторам
, и
наоборот. Математически: поиск такого
значения аргументов, при котором по двум независимым векторам ![]() с
помощью величин интервалов вариации
с
помощью величин интервалов вариации![]() и
и
![]() максимизируется
функционал вида [22]
максимизируется
функционал вида [22]
по которому, уже полагая,
что ![]() , находятся
значения
, находятся
значения ![]() и
и ![]() .
Введение
пустого ящика, показанное как
.
Введение
пустого ящика, показанное как ![]() либо
либо
![]() , в эмпирическое
распределение (Приложение 1) обусловлено необходимостью трансформации
матрицы
взаимной информации
, в эмпирическое
распределение (Приложение 1) обусловлено необходимостью трансформации
матрицы
взаимной информации ![]() в
определитель[21]. Такая трансформация в значительной
степени
унифицирует форму записи
в
определитель[21]. Такая трансформация в значительной
степени
унифицирует форму записи ![]() и
и ![]() , делая их
идеально алгоритмическими
, делая их
идеально алгоритмическими
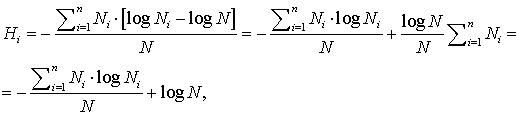
здесь ![]()
![]() объём выборки;
объём выборки; ![]() число
ящиков.
число
ящиков.
Тогда
выражение для взаимной
информации ![]() из (7) выглядит как
из (7) выглядит как
Основным
ограничением в (14) является сингулярность типа ![]() , или
вопрос о существовании ящиков с нулевым заполнением. Если ввести их
существование, это заметно ослабит ограничение о равномерном
распределении для
величины
, или
вопрос о существовании ящиков с нулевым заполнением. Если ввести их
существование, это заметно ослабит ограничение о равномерном
распределении для
величины ![]() .
.
Нахождение ![]() в
(9) представляет собой решение первой вариационной
задачи теории информации. Разложив
выражение под логарифмом в (14), получим формулу для выражения
информации по
Шеннону[22]
как разность информационной меры Хартли и энтропии
в
(9) представляет собой решение первой вариационной
задачи теории информации. Разложив
выражение под логарифмом в (14), получим формулу для выражения
информации по
Шеннону[22]
как разность информационной меры Хартли и энтропии
Очевидно,
что в (15)
Шеннон использовал разность между мерой Хартли и энтропией (мера Хартли
получила свою известность как энтропия алфавита с равномерным
распределением
вероятности ![]() для
букв – полностью аналогична
для
букв – полностью аналогична ![]() в ИМК для равномерного распределения
в ИМК для равномерного распределения![]() ).
).
Поиск
значения аргумента, при котором по двум независимым векторам ![]() с
помощью варьирования по ширине ящиков
с
помощью варьирования по ширине ящиков![]() и
и
![]() минимизируется функционал
вида
минимизируется функционал
вида
по которому (уже полагая,
что ![]() ) находятся
значения
) находятся
значения![]()
![]() и
и ![]()
![]() представляет
собой вторую вариационную задачу теории информации.
представляет
собой вторую вариационную задачу теории информации.
Характер поведения ![]() как функции
объёма выборки
как функции
объёма выборки ![]() позволяет
найти точку, в
которой скорость изменения информации по Шеннону как
позволяет
найти точку, в
которой скорость изменения информации по Шеннону как ![]() будет
минимальна [24][23]. Порядок вычисления этой точки сводится к
следующей
процедуре: для определения кривизны в точке
будет
минимальна [24][23]. Порядок вычисления этой точки сводится к
следующей
процедуре: для определения кривизны в точке
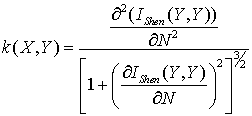 ,
,
где ![]() объём
выборки, находятся первая и вторая
производные для
объём
выборки, находятся первая и вторая
производные для ![]() :
:
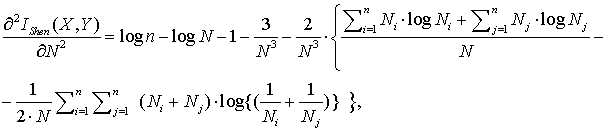
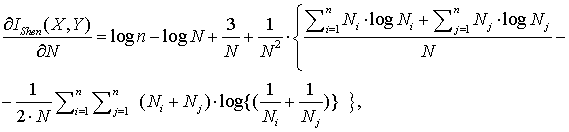
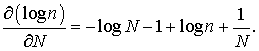
Поиск
значения объёма
данных, при котором по двум независимым векторам ![]() с
помощью варьирования по ширине ящиков
с
помощью варьирования по ширине ящиков ![]() и
и ![]() находится функционал вида
находится функционал вида
по которому (уже полагая,
что ![]() ) находятся
значения
) находятся
значения ![]()
![]() и
и ![]()
![]() , представляет
собой третью вариационную задачу теории информации.
, представляет
собой третью вариационную задачу теории информации.
Результаты построения эмпирических распределений
Ниже приведены некоторые
результаты построения эмпирических распределений отраженных сигналов
м-, дм-
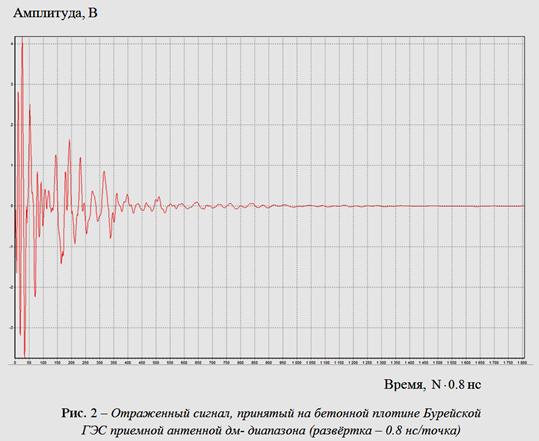
диапазонов [19]. На рис.
1, 2 представлены
сигналы, принятые на бетонной плотине Бурейской ГЭС приёмными
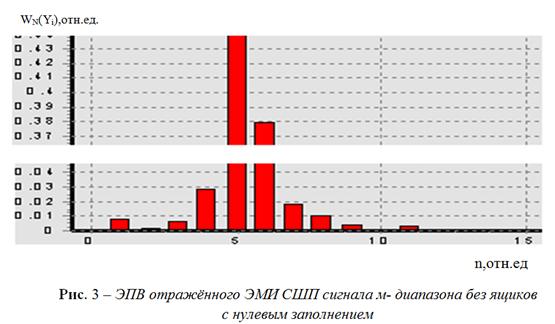
антеннами [20]. На рис.
3 представлена ЭПВ отраженного
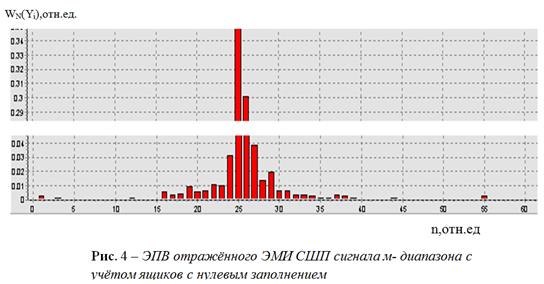
сигнала м- диапазона без ящиков с нулевым заполнением, на рис. 4
- с
учётом ящиков с нулевым заполнением. ЭПВ на рис. 3,4 построены
по
критерию (9), в котором ![]() определена с учётом «третьего игрока»
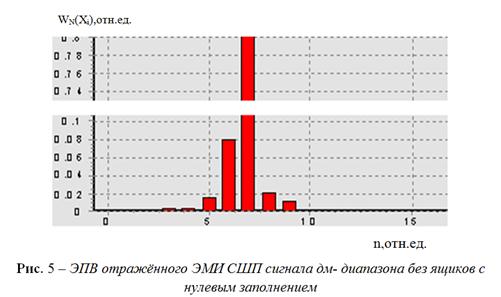
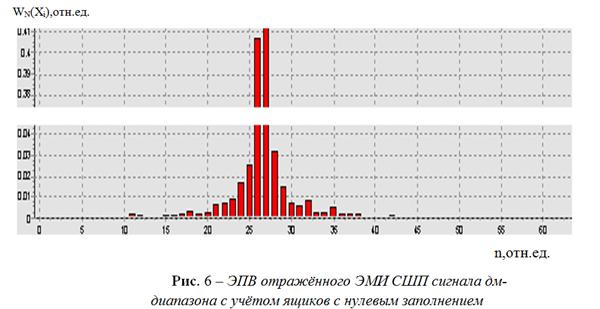
выражениями (10÷12). На рис.
5, 6 представлены аналогичные ЭПВ сигнала дм- диапазона.
определена с учётом «третьего игрока»
выражениями (10÷12). На рис.
5, 6 представлены аналогичные ЭПВ сигнала дм- диапазона.
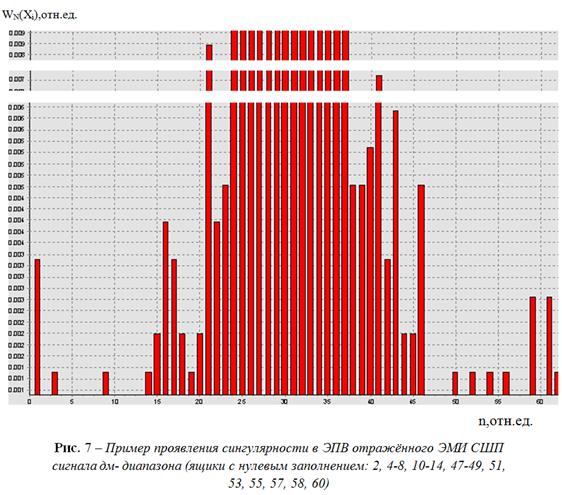
На рис. 7 приведён
пример проявления сингулярности в ЭПВ сигнала дм - диапазона. Очевидно,
что величина
![]() как оценка
собственного числа степеней
свободы входного процесса весьма различается для случаев учёта или не
учёта сингулярности
в ЭПВ.
как оценка
собственного числа степеней
свободы входного процесса весьма различается для случаев учёта или не
учёта сингулярности
в ЭПВ.
Приведенная на рис.
8 (в плане - рис. 8а) 3D ЭПВ двух
независимых процессов ![]() имеет
явно выраженные особенности разложения по ящикам: максимум ЭПВ по
имеет
явно выраженные особенности разложения по ящикам: максимум ЭПВ по
![]() существует
в пределах
существует
в пределах ![]() ящиков,
по
ящиков,
по ![]() - в
пределах
- в
пределах![]() ящиков.
ящиков.
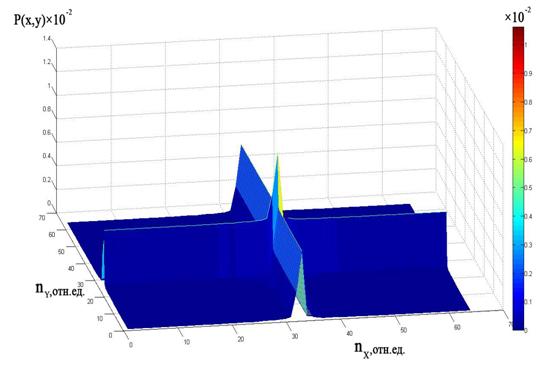
Рис. 8 – Поведение ЭПВ отражённых ЭМИ СШП сигналов м-, дм- диапазонов,
построенной по принципу «шахматной доски». Амплитуды сигналов X, Y (рис. 1,2) представлены номерами ящиков
Очевидно,
что
при варьировании величинами ![]() ,
, ![]()
![]() из (9) является
сильным «игроком» рядом с «игроками»
из (9) является
сильным «игроком» рядом с «игроками» ![]() и
и ![]() , участвующими в поиске max (12) между
, участвующими в поиске max (12) между ![]() , и соответствующим ему значением
, и соответствующим ему значением ![]() ,
и
,
и ![]() с
с ![]() . Ситуация
с третьим «игроком» аналогична для второй и третьей вариационных
задач.
. Ситуация
с третьим «игроком» аналогична для второй и третьей вариационных
задач.
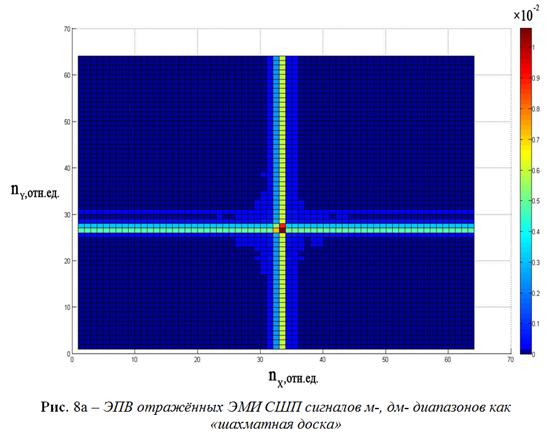
Величина ![]() более
известна как производная Радона –
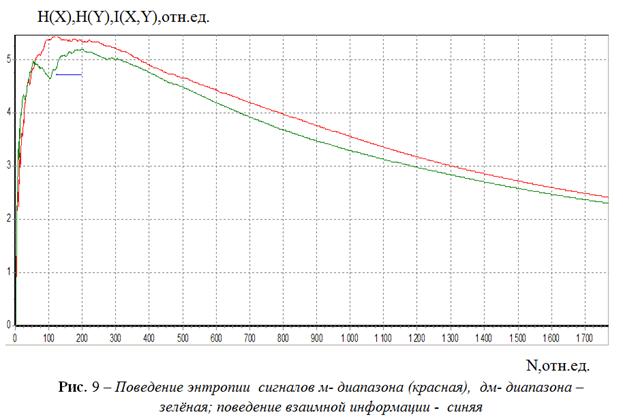
Никодима (рис. 8а). Поведение трёх составляющих
энтропии двух
процессов (9) как функций
от объёма выборки
более
известна как производная Радона –
Никодима (рис. 8а). Поведение трёх составляющих
энтропии двух
процессов (9) как функций
от объёма выборки ![]() показано
на рис. 9. Зависимость величины информации по Шеннону от объёма выборки
показано
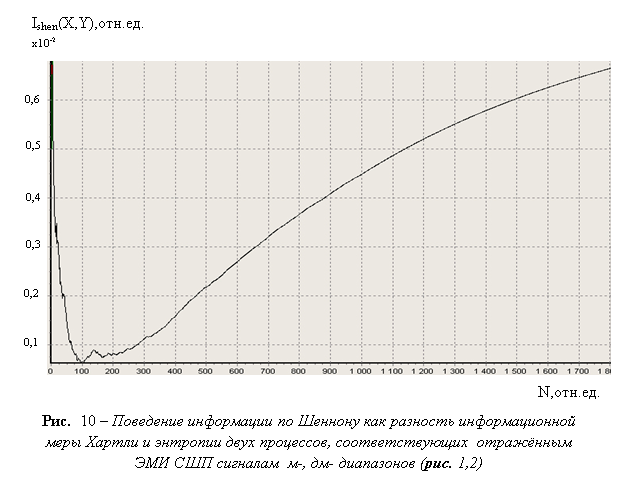
на рис. 9. Зависимость величины информации по Шеннону от объёма выборки ![]() как
разности информационной меры Хартли и энтропии двух процессов, или ИМК при равномерном
как
разности информационной меры Хартли и энтропии двух процессов, или ИМК при равномерном ![]() , показана
на рис. 10.
Данный график соответствует отражённым ЭМИ СШП
сигналам м-, дм-
диапазонов длин волн, приведенным на рис. 1,2.
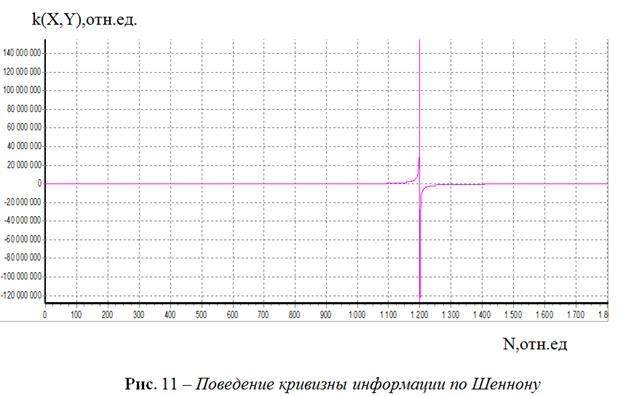
На рис. 11 показано поведение кривизны информации по Шеннону
для этих же
сигналов.
, показана
на рис. 10.
Данный график соответствует отражённым ЭМИ СШП
сигналам м-, дм-
диапазонов длин волн, приведенным на рис. 1,2.
На рис. 11 показано поведение кривизны информации по Шеннону
для этих же
сигналов.
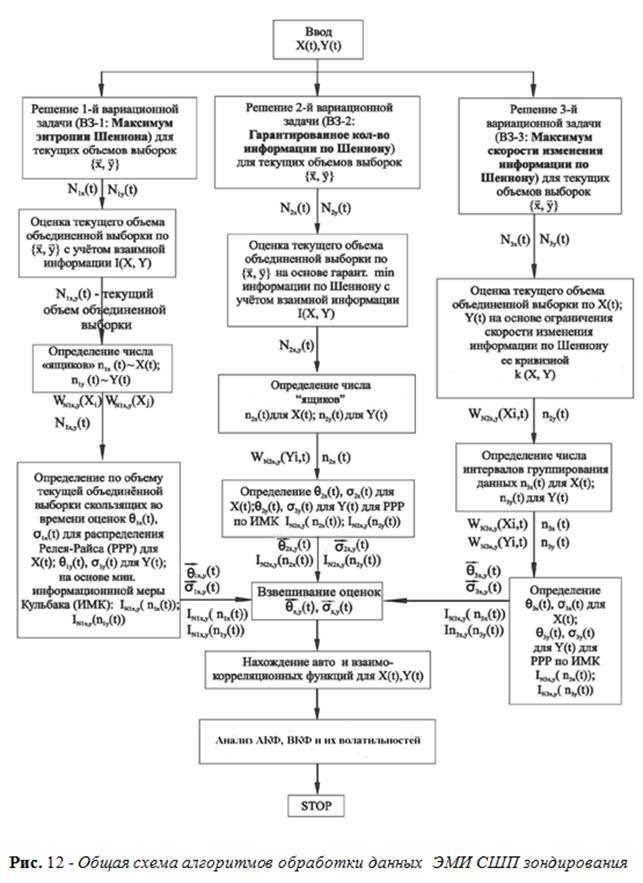
Алгоритмы обработки данных ЭМИ СШП зондирования
Схема алгоритмов
обработки данных ЭМИ СШП зондирования представлена на рис.
12. Общая
идея алгоритма обработки состоит в предположении «эллиптичности» [24]
уравнений связи оценок в модельном распределении (идея заимствована у
Г.
Крамера, который ввёл понятие «эллипс рассеяния» в 1946 г.
(«Математические
методы статистики». – М.: Мир, 1975. – 648 с.). Если описывать
эмпирическое
распределение данных ЭМИ СШП зондирования семейством вероятностных
плотностей
Релея-Райса, то ![]() - оценка
моды основной волны,
- оценка
моды основной волны, ![]() - оценка
её затухания, а их связь выглядит
как
- оценка
её затухания, а их связь выглядит
как 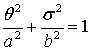 ,
, ![]() полуоси
эллипса рассеяния.
полуоси
эллипса рассеяния.
Примеры исходных сигналов
представлены на рис. 1, 2. Для входных сигналов,
представленных на рис.
12 как ![]() и
и
![]() ,
в каждый момент времени
,
в каждый момент времени ![]() (
(![]()
![]() объем
записанного сигнала) по критериям, в качестве которых выступают решения
[19,22]
трех вариационных задач, определяются три пары объемов выборки
объем
записанного сигнала) по критериям, в качестве которых выступают решения
[19,22]
трех вариационных задач, определяются три пары объемов выборки ![]() ,
, ![]() ,
,![]() .
Следующий этап – определение
текущих объёмов трёх объединенных выборок:
.
Следующий этап – определение
текущих объёмов трёх объединенных выборок: ![]() ,
,![]() ,
,![]() .
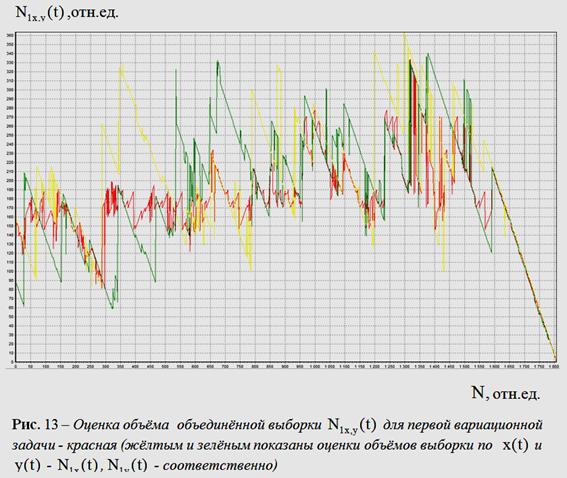
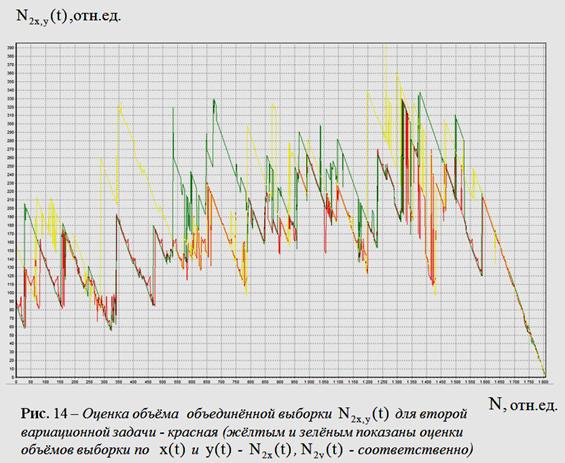
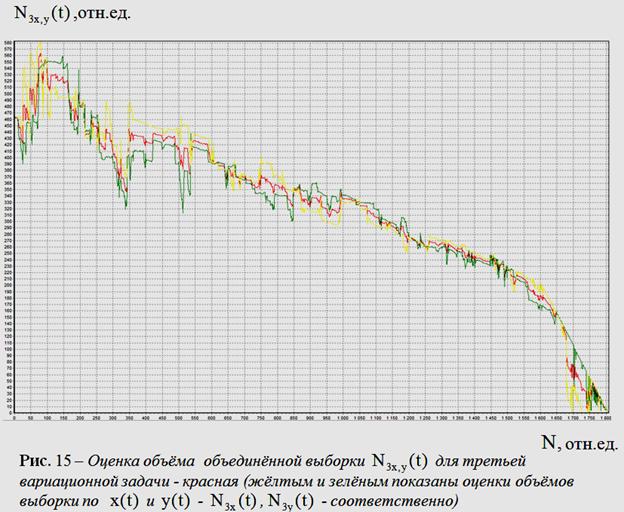
Графики оценок объемов объединенных выборок
.
Графики оценок объемов объединенных выборок ![]() ,
,![]() ,
,![]() приведены
на рис. 13-15. На каждом из рисунков приведены пары текущих
(собственных) объёмов выборок
приведены
на рис. 13-15. На каждом из рисунков приведены пары текущих
(собственных) объёмов выборок![]() ,
, ![]() ,
,![]() , характерные
для первой, второй и третьей
вариационных задач.
, характерные
для первой, второй и третьей
вариационных задач.
Для каждой из объёмов
выборок ![]() ,
,![]() ,
,![]() в
каждой из трёх вариационных задач определяется число «ящиков» -
количество интервалов
группирования экспериментальных данных {
в
каждой из трёх вариационных задач определяется число «ящиков» -
количество интервалов
группирования экспериментальных данных {![]() ,
, ![]() ,
, ![]() } как
для
} как
для
![]() ,
так и для
,
так и для ![]() - {
- {![]() ,
, ![]() ,
, ![]() }. В
случае
несовпадения числа ящиков для
}. В
случае
несовпадения числа ящиков для ![]() с
числом ящиков для
с
числом ящиков для ![]() производится
переукладка данных из
меньшего числа ящиков в большее, например
производится
переукладка данных из
меньшего числа ящиков в большее, например ![]() ,
если
,
если ![]() .
.
Для каждого из этих
эмпирических распределений, например для ![]() ,
, ![]() ;
; ![]() ;
; ![]() из
семейства вероятностных плотностей
Релея - Райса
из
семейства вероятностных плотностей
Релея - Райса
выбирается та, которая с
помощью
параметров ![]() минимизирует
информационную меру Кульбака (10)[25].
минимизирует
информационную меру Кульбака (10)[25].
Доказательство
«эллиптичности» связи
оценок ![]() выглядит
следующим образом. Вариация от
выглядит
следующим образом. Вариация от ![]() :
:
![]() ,
,
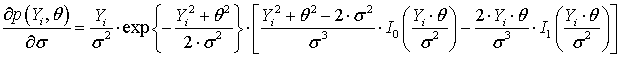
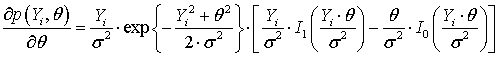
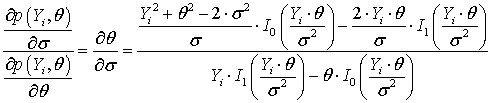 .
.
Приведя последнее выражение к эллиптическому уравнению, получим
Здесь слева – уравнение
эллипса в
частных производных, справа ![]() размеры полуосей эллипса рассеяния ( Г. Крамер,
1975)[26]:
размеры полуосей эллипса рассеяния ( Г. Крамер,
1975)[26]:
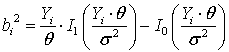 .
(21)
.
(21)
Зависимости вида (20,21)
определяют
порядок последовательного приближения к оценкам первого и второго
моментов
распределения Релея - Райса. Решением первой вариационной задачи
(блок ВЗ-1 на
рис. 12) являются оценки первого и
второго моментов ![]() и их вес
(достоверность), определяемый мерой Кульбака как {
и их вес
(достоверность), определяемый мерой Кульбака как {![]() };
решением второй вариационной задачи (блок ВЗ-2 на рис. 12) являются
оценки
};
решением второй вариационной задачи (блок ВЗ-2 на рис. 12) являются
оценки ![]() и их вес – {
и их вес – {![]() };
решением третьей вариационной задачи (блок ВЗ-3 на рис.
12)
являются оценки
};
решением третьей вариационной задачи (блок ВЗ-3 на рис.
12)
являются оценки ![]() и их вес – {
и их вес – {![]() }.
Параметры
}.
Параметры ![]() определяются
как скользящие во
времени взвешенные оценки трех вариационных задач (блок
«Взвешивание оценок» на рис.
12)
определяются
как скользящие во
времени взвешенные оценки трех вариационных задач (блок
«Взвешивание оценок» на рис.
12)
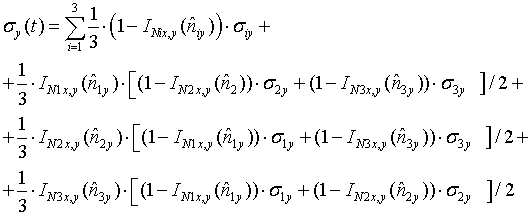 . (23)
. (23)
Точность вычисления пары ![]() определяется
углом (рис. 16) между нормалью к плоскости,
образованной тремя парами
оценок
определяется
углом (рис. 16) между нормалью к плоскости,
образованной тремя парами
оценок ![]() с учётом
их веса, и ортом ИМК:
с учётом
их веса, и ортом ИМК: ![]() При
недостижении требований по точности
цикл по вычислению
При
недостижении требований по точности
цикл по вычислению ![]() повторяется,
но с входными
данными из (22) и (23).
повторяется,
но с входными
данными из (22) и (23).
Для проверки
статистической устойчивости
оценок, полученных по критерию ![]() ИМК для трёх вариационных задач, использован
критерий Колмогорова -
Смирнова. Сравнивались различные методы формирования оценок по
ЭМИ СШП
измерениям, а характеристикой сравнения выбрана вероятность
ИМК для трёх вариационных задач, использован
критерий Колмогорова -
Смирнова. Сравнивались различные методы формирования оценок по
ЭМИ СШП
измерениям, а характеристикой сравнения выбрана вероятность
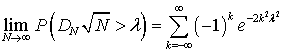 ,
,
где ![]() ,
,
![]() –
эмпирическая функция распределения
результатов ЭМИ СШП измерений; F(
–
эмпирическая функция распределения
результатов ЭМИ СШП измерений; F(![]() ,q) – гипотетическая функция
распределения Релея - Райса
с оценкой
,q) – гипотетическая функция
распределения Релея - Райса
с оценкой ![]() ,
сформированной по имеющейся выборке
объёмом N различными методами при
трёх e - загрязняющего
распределения и без
него; DN – статистика
Колмогорова-Смирнова.
,
сформированной по имеющейся выборке
объёмом N различными методами при
трёх e - загрязняющего
распределения и без
него; DN – статистика
Колмогорова-Смирнова.
При определении
устойчивости данного алгоритма рассмотрены частные случаи e-загрязняющих ЭПВ
в
соответствии с моделью
Тьюки [25]. Положим, что величина ![]() является мерой подобия
гипотетического
распределения
является мерой подобия
гипотетического
распределения ![]() и апостериорного
распределения
и апостериорного
распределения![]() , тогда
вместо
, тогда
вместо ![]() можно
использовать выражение
можно
использовать выражение
![]() ,
(24)
,
(24)
где
![]() - величина ИМК,
характеризующая выбранный
метод статистического оценивания;
- величина ИМК,
характеризующая выбранный
метод статистического оценивания; ![]() загрязняющее распределение;
загрязняющее распределение; ![]() его
параметры;
его
параметры; ![]() – переменная распределения
– переменная распределения
![]() .
.
Результаты сравнения гипотез приведены в табл. 1.
Таблица 1
|
Метод формирования оценки |
Вероятность гипотезы по критерию Колмогорова-Смирнова |
|||
|
Гипотеза Н0:
|
Гипотеза Н1:
|
Гипотеза Н2:
|
Гипотеза Н3:
|
|
|
МНК |
0.79348 |
0.48273 |
0.48334 |
0.20360 |
|
МНМ |
0.79373 |
0.85074 |
0.88574 |
0.90723 |
|
Метод с min ИМК |
0.79365 |
0.85448 |
0.88453 |
0.91106 |
|
Метод |
0.79371 |
0.85421 |
0.88591 |
0.90981 |
Здесь МНК - метод наименьших квадратов; МНМ - метод наименьших модулей.
Очевидно
(табл. 1), что по критерию
Колмогорова -
Смирнова метод с min
ИМК сопоставим с методом ![]() правдоподобия,
а в ряде случаев
превосходит его. Следует обратить внимание на эффективность применения
МНМ при
лапласовском загрязняющем распределении. Это ещё раз подтверждает тот
факт, что
лапласовское распределение стоит особняком [18].
правдоподобия,
а в ряде случаев
превосходит его. Следует обратить внимание на эффективность применения
МНМ при
лапласовском загрязняющем распределении. Это ещё раз подтверждает тот
факт, что
лапласовское распределение стоит особняком [18].
Применение корреляционо-дисперсионного анализа данных ЭМИ СШП зондирования для литологического разделения подстилающей среды
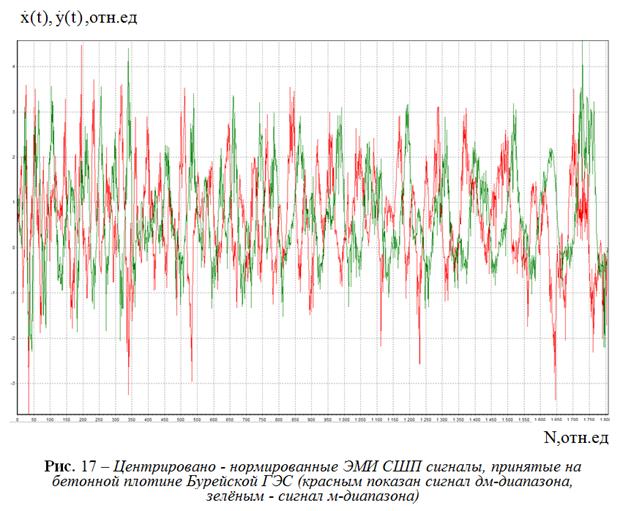
После получения взвешенных по (22, 23) оценок по формулам:
производится центрирование
относительно ![]() и
нормирование относительно
и
нормирование относительно ![]() сигналов,
или сдвиг – масштабное
преобразование сигнала[27].
сигналов,
или сдвиг – масштабное
преобразование сигнала[27].
Литологическое разделение подстилающей среды по данным ЭМИ СШП зондирования предполагает идентифицируемость[28]. Г. Тейчер (Teicher H., 1961) получил следующие результаты: сдвиг – масштабные смеси функций распределений идентифицируемы, если
(i) для функции, обратной масштабу, существует Фурье преобразование, нигде не обращающееся в нуль;
(ii) характеристическая функция, соответствующая функции распределения сигнала, нигде не обращается в нуль.
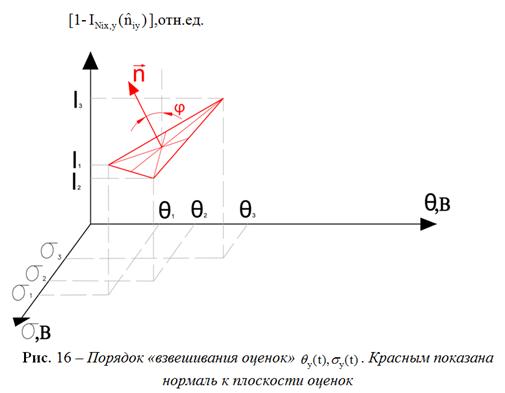
На рис. 17 зелёным
показан отражённый сигнал м – диапазона (рис. 1),
центрированный по (22)
относительно ![]() и
нормированный по (23)
относительно
и
нормированный по (23)
относительно ![]() ,
полученных по (19-20), для семейства
вероятностных плотностей
Релея-Райса; красным показан сигнал дм – диапазона (рис.
2), центрировано-нормированный
относительно оценок, полученных по (19-20),
того же семейства распределений.
,
полученных по (19-20), для семейства
вероятностных плотностей
Релея-Райса; красным показан сигнал дм – диапазона (рис.
2), центрировано-нормированный
относительно оценок, полученных по (19-20),
того же семейства распределений.
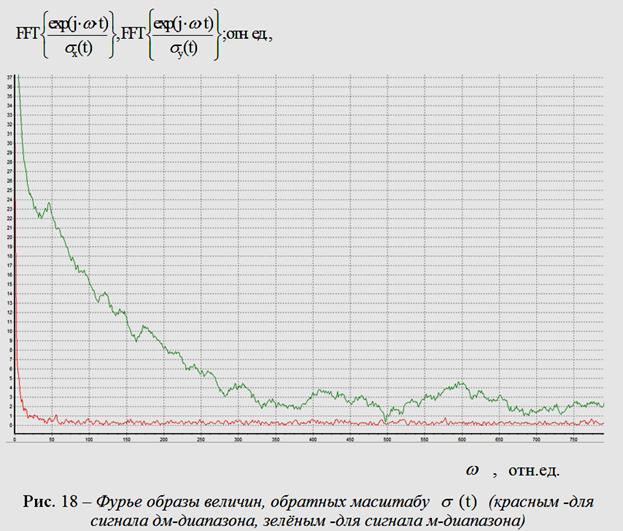
Для (i) на рис. 18
зелёным показано
Фурье преобразование (![]() ) величины,
обратной масштабу
) величины,
обратной масштабу ![]() для сигнала м – диапазона (рис.
1);
красным - для сигнала дм – диапазона (рис.
2).
для сигнала м – диапазона (рис.
1);
красным - для сигнала дм – диапазона (рис.
2).
Для (ii) допуск на ящик с
нулевым
заполнением в ЭПВ, заданный «шахматной доской» как способом построения
двумерной ЭПВ, означает, что двумерная ЭПВ является «не![]() функцией» (число ящиков ≥3), что однозначно
определяет существование преобразования Фурье от одномерных ЭПВ, а
следовательно, существование ненулевых
значений их характеристической функции [23].
Следует отметить, что теорема 4.3
(Королёв В. Ю., 2007) соответствует сдвигу в (25)
относительно первого момента
распределения Релея – Райса, которое может быть разложено на два
распределения
Лапласа, имеющие однозначные характеристические функции [29].
функцией» (число ящиков ≥3), что однозначно
определяет существование преобразования Фурье от одномерных ЭПВ, а
следовательно, существование ненулевых
значений их характеристической функции [23].
Следует отметить, что теорема 4.3
(Королёв В. Ю., 2007) соответствует сдвигу в (25)
относительно первого момента
распределения Релея – Райса, которое может быть разложено на два
распределения
Лапласа, имеющие однозначные характеристические функции [29].
Исследование корреляционных зависимостей центрировано - нормированных сигналов вида
является одной из задач, тесно примыкающих к задачам оценивания корреляционных функций[30], и называется задачей оценивания нормированной корреляционной функции[31].
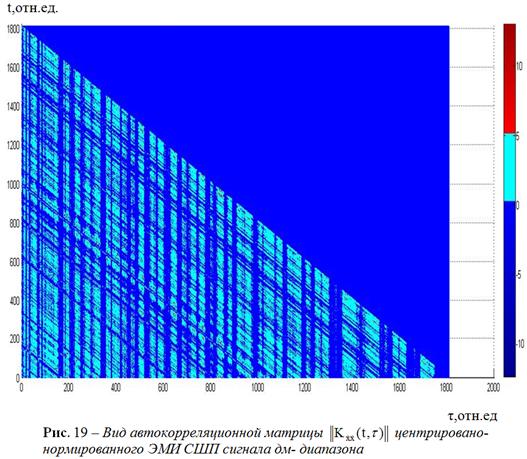
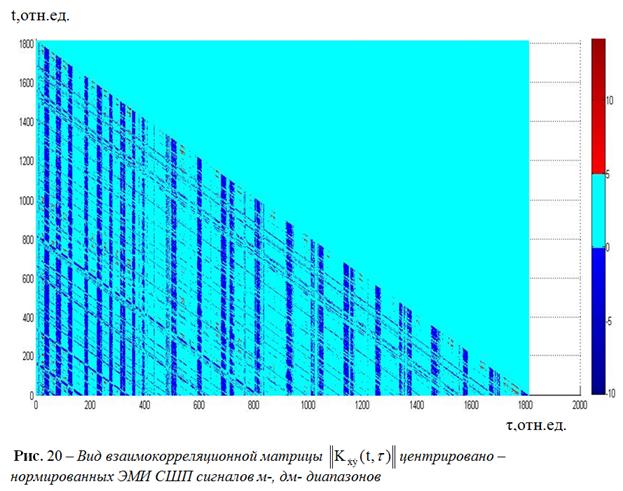
На рис.
19-20 представлен
общий вид треугольных матриц ![]() и
и ![]() центрировано
- нормированных сигналов (рис.
17), принятых
на бетонной плотине Бурейской ГЭС.
центрировано
- нормированных сигналов (рис.
17), принятых
на бетонной плотине Бурейской ГЭС.
На рис. 21 представлены первые строки
треугольных
матриц ![]() и
и
![]() ЭМИ
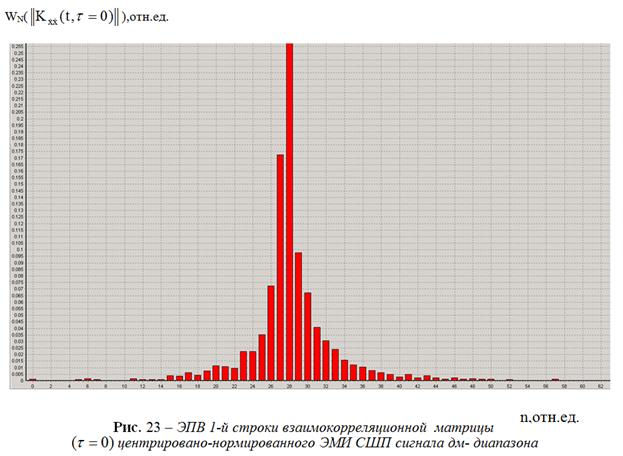
СШП сигналов м-, дм- диапазонов. Для каждой строки из (26)
строятся ЭПВ величин
ЭМИ
СШП сигналов м-, дм- диапазонов. Для каждой строки из (26)
строятся ЭПВ величин ![]() и
и
![]() (рис. 22,
23).
(рис. 22,
23).
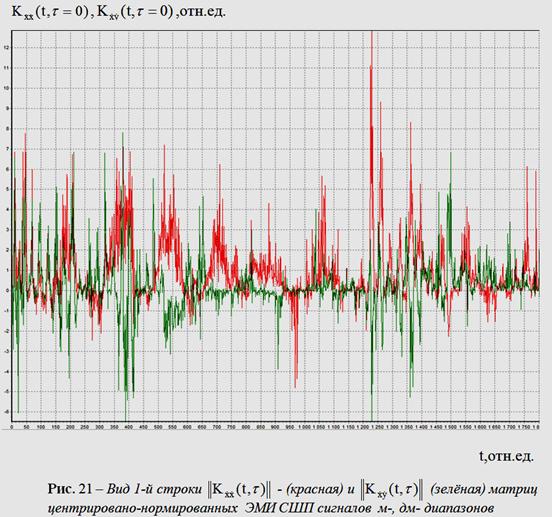
ЭПВ самих центрировано – нормированных величин,
стоящих под
знаком мат. ожидания в (26), имеют ярко выраженные
особенности (рис.
21, 22), для строки взаимокорреляционной матрицы ![]() она
более «размазана», чем для автокорреляционной
она
более «размазана», чем для автокорреляционной![]() . Попытка
объяснить заострённость таких распределений была предпринята Б.
Мандельбротом [32].
. Попытка
объяснить заострённость таких распределений была предпринята Б.
Мандельбротом [32].

Порядок работы со
значениями матриц ![]() и
и ![]() следующий:
следующий:
![]() номер
строки, задающей значения строк
матриц (рис. 21); для каждой из строк строятся ЭПВ и по ним
находится мат. ожидания
(26) как значение для строки с номером
номер
строки, задающей значения строк
матриц (рис. 21); для каждой из строк строятся ЭПВ и по ним
находится мат. ожидания
(26) как значение для строки с номером ![]() ;
последовательность этих значений образуют авто- и взаимокорреляционные
функции функции
от
;
последовательность этих значений образуют авто- и взаимокорреляционные
функции функции
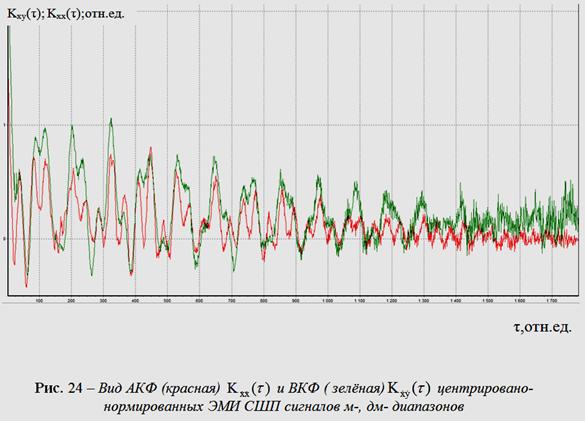
от ![]() . Вид АКФ
и ВКФ центрировано-нормированных
ЭМИ СШП сигналов м-, дм- диапазонов показан на рис. 24,
для
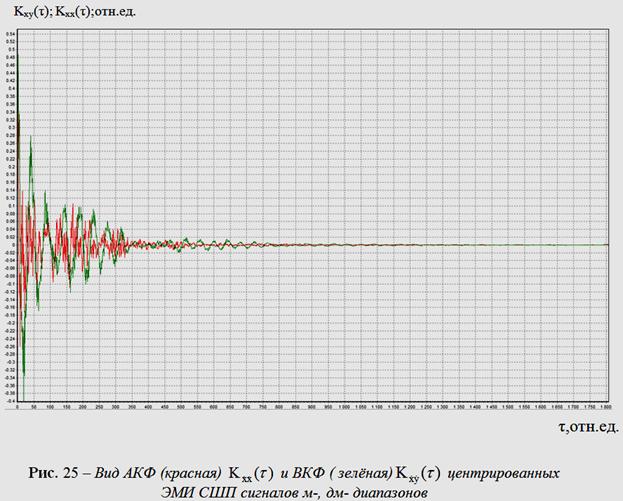
сравнения на рис. 25 приведены АКФ и ВКФ центрированных
ЭМИ СШП
сигналов м-, дм- диапазонов.
. Вид АКФ
и ВКФ центрировано-нормированных
ЭМИ СШП сигналов м-, дм- диапазонов показан на рис. 24,
для
сравнения на рис. 25 приведены АКФ и ВКФ центрированных
ЭМИ СШП
сигналов м-, дм- диапазонов.
При изучении
тонкой стохастической структуры корреляционных матриц наибольший
интерес представляет
скорость изменения процесса (его волатильность) [33]. Дисперсия
случайной величины ![]() может
быть представлена в виде суммы двух
слагаемых
может
быть представлена в виде суммы двух
слагаемых
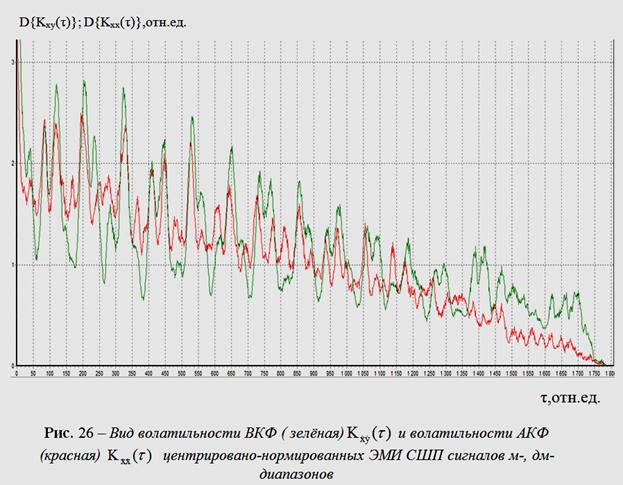
На рис. 26 зелёным показана волатильность - та часть дисперсии, которая обусловлена наличием ненулевых сдвигов, или динамическая составляющая дисперсии (27) для ВКФ сигналов м-, дм - диапазонов (рис. 1,2), центрировано-нормированных по (22, 23) относительно оценок первого и второго моментов, полученных по (19-20), для семейства вероятностных плотностей Релея-Райса; красным показана волатильность для АКФ сигнала дм – диапазона.
Первое выражение в (27) характеризует ту часть дисперсии которая обусловлена наличием ненулевых сдвигов, то есть динамическую составляющую дисперсии (волатильность), тогда как второе выражение характеризует чисто диффузионную составляющую дисперсии[34]. Их свойства анализируются с помощью критерия отношения правдоподобия (Королёв В. Ю., 2011).
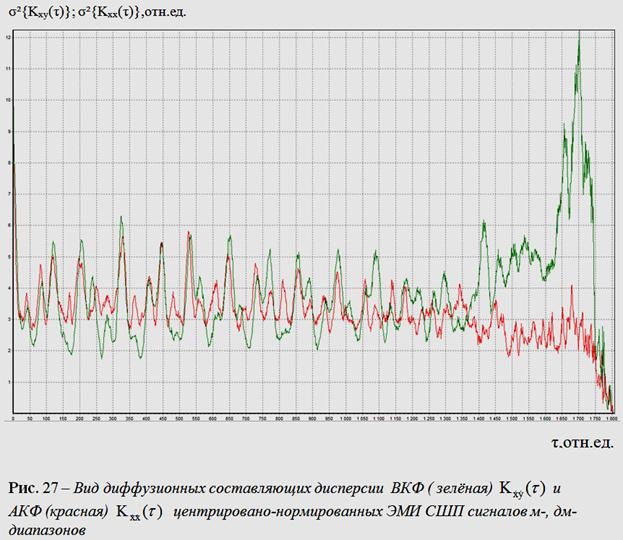
На рис. 27 показана диффузионная составляющая дисперсии.
Особый интерес вызывает
логарифм от отношения спектральных составляющих[35].
Поскольку центрировано–нормированное (сдвиг – масштабное)
преобразование
сигналов (25) осуществляется относительно объёмов
объединённых выборок ![]() ,
, ![]() ,
, ![]() , очевидно, что Фурье преобразования,
например, для
ВКФ, её волатильности и диффузионной составляющей дисперсии ВКФ будут
выглядеть
как
, очевидно, что Фурье преобразования,
например, для
ВКФ, её волатильности и диффузионной составляющей дисперсии ВКФ будут
выглядеть
как
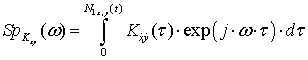 ,
,
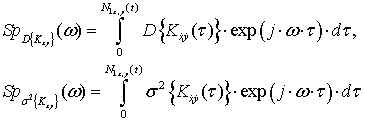 ,
(27)
,
(27)
Поскольку формула Йовица – Джексона не требует существования обратного преобразования Фурье, возможно создание (путём комбинирования) до 30 минимаксных критериев:
- дифференциального
(различающего волатильности
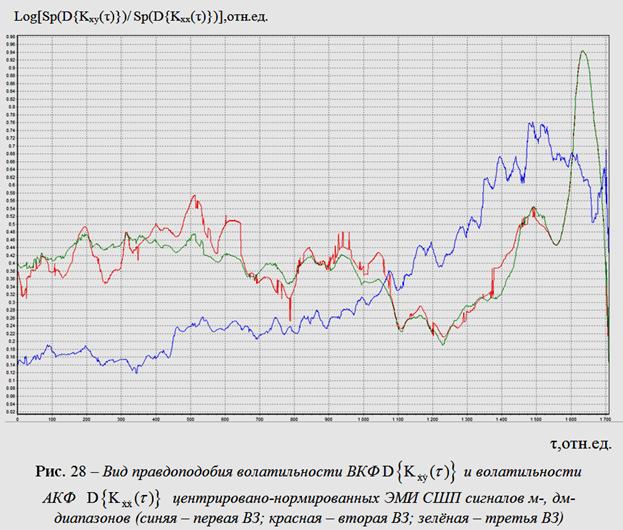
ВКФ и АКФ разных вариационных задач). Например, на рис. 28
представлены
отношения правдоподобия спектров волатильностей для ![]() и
и ![]() для трёх
вариационных задач. Уровень подобия между
спектрами волатильностей для
для трёх
вариационных задач. Уровень подобия между
спектрами волатильностей для ![]() и
и ![]() для
второй (красная, рис. 28) и третьей (зелёная, рис. 28)
вариационных задач очевиден;
для
второй (красная, рис. 28) и третьей (зелёная, рис. 28)
вариационных задач очевиден;
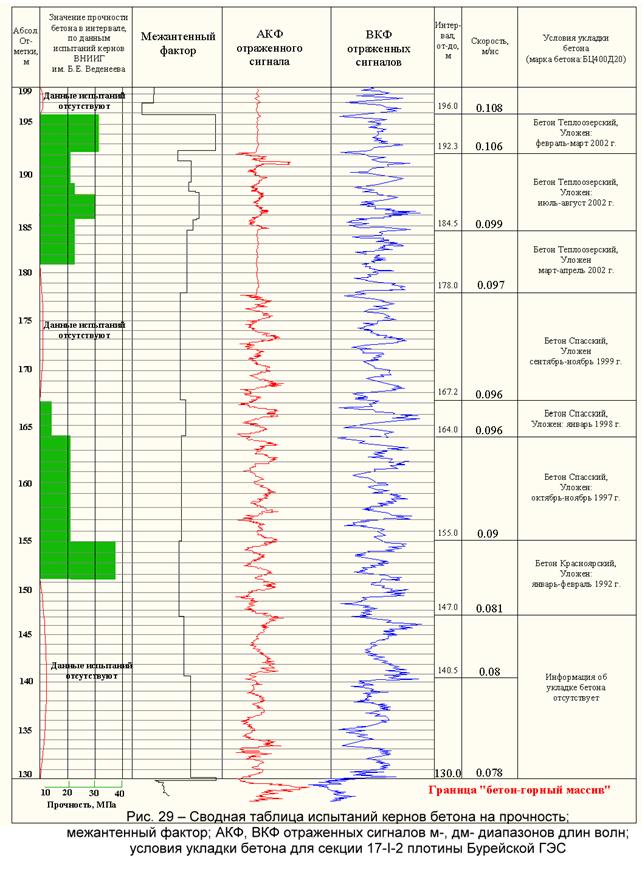
- интегрального (объединяющего МСКО ВКФ и АКФ с МСКО их волатильностей и МСКО диффузионной составляющей дисперсии корреляционных функций) для ТРЁХ вариационных задач – межантенный фактор (рис. 29).
Ниже приведены результаты приведенной выше обработки для данных, полученных методом ЭМИ СШП зондирования.
Примеры практического применения энтропийно – комбинаторных критериев. Результаты обработки данных ЭМИ СШП зондирования секции 17-I-2 плотины Бурейской ГЭС
Целью данных работ являлось обследование качества бетонной кладки плотины и выявление в ней трещин, пустот и неоднородностей[36].
В результате геофизического обследования и последующей интерпретации данных ЭМИ СШП зондирования были выделены, в первую очередь, границы между бетоном тела плотины и ниже залегающими горными породами. После математической обработки измеренных СШП сигналов были получены АКФ и ВКФ отраженных центрировано-нормированных сигналов в точках зондирования. На основании вида правдоподобия волатильности АКФ и ВКФ (рис. 28) тело плотины в точках измерений было дифференцировано на определенные интервалы, в которых бетон обладает различными физико-механическими свойствами. Основными геофизическими критериями для характеристики изучаемой среды (бетона плотины) являются рассчитанные значения относительной диэлектрической проницаемости, периода колебаний электромагнитного сигнала и амплитуды АКФ и ВКФ отраженных центрировано-нормированных сигналов.
Рассчитанные значения относительной диэлектрической проницаемости бетона колеблются от 4.8 до 8.8.
По периоду колебаний электромагнитного сигнала выделяются интервалы с малым (абсолютные значения до 25 наносекунд), средним (абсолютные значения 25 - 40 наносекунд) и большим (абсолютные значения > 40 наносекунд) периодом.
Амплитуды АКФ и ВКФ центрировано-нормированных ЭМИ СШП сигналов подразделяются на три относительные категории: низкую, среднюю и высокую. Кроме этого, в отдельных интервалах графиков АКФ и ВКФ наблюдается неустойчивое поведение амплитуды, выражающееся в частой смене фаз. Такое поведение амплитуды условно названо «высокой изломанностью» сигнала.
Из литературных данных известно, что рост значений относительной диэлектрической проницаемости связан с увеличением влажности в породах. Из опыта исследований геологических объектов методом ЭМИ СШП зондирования установлено, что малый период колебаний электромагнитной волны характерен для песчанистых (рыхлых) литологических разностей, а большой период колебаний присущ плотным разностям. Тот же самый признак использовался и при обследовании ряда более мелких бетонных сооружений – опоры мостов, фундаменты зданий, сваи-оболочки и буронабивные сваи, когда внутри плотного бетона выделялись пористые его разности или включения грунта.
Высокие значения амплитуды СШП сигнала связаны с повышением электропроводных свойств среды, что в свою очередь может свидетельствовать о наличии влаги в порах породы. «Высокая изломанность» АКФ и ВКФ указывает, как правило, на локальное нахождение (локализацию) в грунтах большого количества гравийно-галечникового материала.
На рис. 29 в качестве примера приводится результат геофизического обследования секции 17-I-2, которое осуществлялось посредством вертикального зондирования в точке измерения №3.
В соответствии с рабочей документацией в точке измерения №3 поверхность плотины имеет абсолютную отметку +199.0 м, подошва тела плотины в этой секции, находится на абсолютной отметке +130.0 м. Мощность бетона плотины в точке зондирования на момент измерения составляла 69.0 м. Бетон вибрированный (метод укладки).
В результате геофизического обследования секции 17-I-2 установлено положение подошвы плотины на отметке +130.0 м. Бетон плотины был разбит на отдельные интервалы, в пределах которых рассчитывались значения относительной диэлектрической проницаемости, величина периода колебаний электромагнитной волны и даны особенности амплитудных характеристик ЭМИ СШП сигнала.
Анализ геофизических данных в разрезе точки зондирования №3 выявил следующие особенности бетона секции:
- в интервалах 195.8 – 192.2 м, 136.5 – 130.0 бетон плотный с малым содержанием поровой влаги;
- в интервалах 192.2 – 186.5 м, 180.0 – 167.2 м, 148.5 – 140.0 м преобладает песчанистая составляющая бетонной смеси;
- в интервалах 186.5 – 180.0 м, 167.2 – 148.5м и 140.0 – 136.5м преобладает гравийно-галечниковый заполнитель бетона.
На графиках АКФ и ВКФ центрировано-нормированных сигналов видно, что период и амплитуда изменяются в зависимости от типа бетона, различающегося временем укладки и поставщиком. График межантенного фактора (сумма: МСКО ВКФ и АКФ, МСКО их волатильностей, МСКО диффузионной составляющей дисперсии ВКФ и АКФ для ТРЁХ вариационных задач) указывает точное положение границ интервалов с однородными свойствами в среде, что подтверждается различными значениями прочности по данным испытаний кернов ВНИИГ им. Б.Е. Веденеева и внутри одного типа бетона, и между его разными типами[37].
По результатам обработки (алгоритмы представлены на рис. 12) данных ЭМИ СШП зондирования, проведенных на плотине Бурейской ГЭС, можно говорить о том, что бетонная кладка плотины по своим электрофизическим свойствам существенно неоднородна. Обследование методом ЭМИ СШП зондирования позволило установить следующее:
- в точках зондирования определены границы между бетоном тела плотины и ниже залегающими породами горного массива, а также между бетоном и воздушной средой – при горизонтальных измерениях в сторону верхнего и нижнего бьефов плотины;
- в точках измерений определено местоположение инженерных внутриплотинных коммуникаций: галерей, водопропускной трубы и насосных станций;
- выделены три основные группы геоэлектрических характеристик электромагнитного сигнала, отраженного от слагающих плотину бетонных элементов. Первая группа представлена разновеликими значениями относительной диэлектрической проницаемости, вторая группа - различными величинами периода электромагнитной волны, в третьей группе отмечены амплитудные особенности ЭМИ СШП сигнала.
На основе различных геоэлектрических характеристик выделены группы неоднородностей в бетоне: I - по значениям относительной диэлектрической проницаемости, изменяющейся как в зависимости от плотности, так и от влажности инженерно-геологического материала; II - песчанистые (рыхлые) и плотные разности; III – участки с повышенной поровой влажностью, участки высокопрочного бетона и интервалы высокопористого материала.
На примере плотины
Бурейской
ГЭС (рис. 29) показана эффективность
обработки данных ЭМИ СШП
зондирования при построении разреза на глубину до 69.0 м даже в
пределах одной
инженерной разности – бетона, отличающегося временем укладки и
изготовителем.
Следует отметить границу на отметке +167 м, она соответствует границе ![]() на рис. 28,
и границу на отметке + 155 м она соответствует границе
на рис. 28,
и границу на отметке + 155 м она соответствует границе ![]() (разница
в сроках укладки бетона 5 лет). Еще контрастнее на графиках отражаются
границы
между инженерно-геологическими разностями – граница «бетон – горный
массив».
(разница
в сроках укладки бетона 5 лет). Еще контрастнее на графиках отражаются
границы
между инженерно-геологическими разностями – граница «бетон – горный
массив».
Результаты обработки данных ЭМИ СШП зондирования при геотехническом мониторинге зоны «Размыва»
Из-за неустойчивого состояния грунтов в районе площади Мужества между станциями метро “Лесная” - ”Площадь Мужества” в г. Санкт-Петербурге 8 апреля 1974 г. и 15 марта 1995 г. произошли аварии в тоннелях, вызвавшие проседания дневной поверхности и серьёзные повреждения зданий: в первом случае – на Политехнической улице и на территории НПО «Аврора», во втором – на территории ОАО «Красный Октябрь».
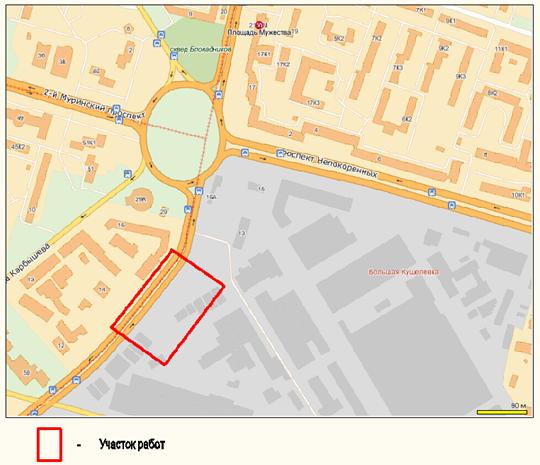
Рис. 30 – Территория между станциями метро “Лесная” - ”Площадь Мужества”,
на которой проводились исследования методом ЭМИ СШП зондирования в период с 2005 по 2011 гг.
Основной общепринятой версией причины аварий до сих пор является наличие плывунов в том месте, где тоннели метрополитена пересекают русло палеореки (зона “Размыва”). Чтобы упредить тяжелейшие последствия, связанные с провалами грунта на дневной поверхности, где находятся жилые дома и здания предприятия оборонного комплекса, в аварийные тоннели под давлением закачали воду, одновременно закупорив затопленные участки бетонными пробками. В настоящее время затопленные тоннели находятся под наблюдением специалистов.
ЗАО НПФ “Геодизонд”, участвовавшее в геотехническом мониторинге за состоянием грунтов около тоннелей по трассе Кировско-Выборгской линии Петербургского метрополитена в период с лета 2005г. по осень 2011 г., провело 14 этапов геофизических исследований методом ЭМИ СШП зондирования на территории ОАО «Красный Октябрь» и ул. Политехнической (рис. 30).
Задачами геофизических исследований являлись: выявление в разрезах по линиям профилей, составленным на основе пунктов геофизического зондирования, участков разуплотненных грунтов различной степени интенсивности; определение масштабов их развития и количественные изменения за период проведения наблюдений (рис. 31) [38].
В ходе наблюдений околотоннельного пространства по результатам ЭМИ СШП исследований в разрезах участка были выявлены и оконтурены зоны разуплотненных грунтов и зоны суффозии[39].
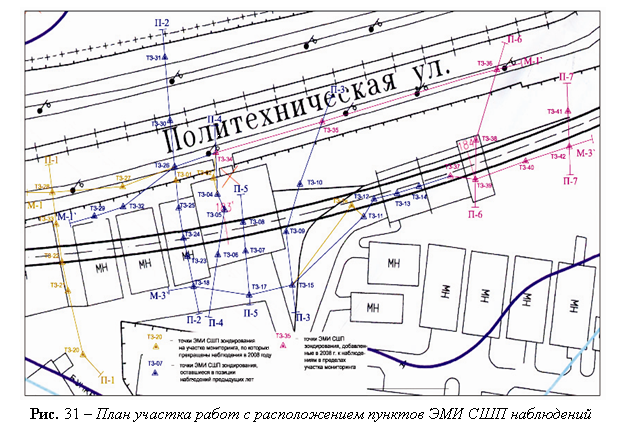
Для прослеживания динамики и характера развития физико-механических нарушений в горном массиве на инженерно-геологические разрезы, составленные по многолетним данным ЭМИ СШП исследований, были вынесены все зоны разуплотнения грунтов и зоны суффозий, наблюдавшиеся в период с 2005 по 2011 гг. На рис. 32 приведено обобщение результатов наблюдений на разрезе по линии П-6 (пересечение заводской территории и ул. Политехническая, рис. 31).
Далее для общей оценки состояния грунтового массива были оконтурены области наибольшего скопления фрагментов физико-механической нарушенности геологических разностей. По количеству выявленных за весь период мониторинга зон разуплотнения и суффозии внутри оконтуренных областей были выделены участки различной степени возможного влияния на образование просадок дневной поверхности.
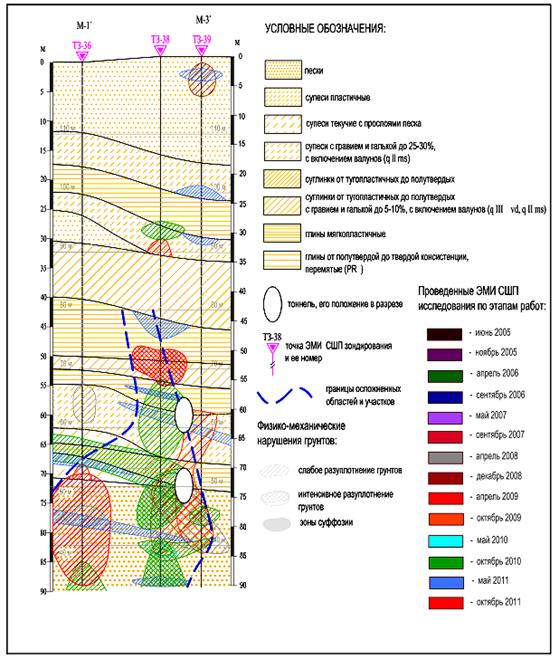
Рис. 32 – Оценка состояния грунтов около тоннелей по трассе Кировско-Выборгской линии Петербургского метрополитена. Разрез по линии П-6
Участки I степени влияния характеризуются наличием суффозионных зон и разуплотненных грунтов различной степени интенсивности. Нарушения в сплошности грунтов в пределах участка наблюдались на протяжении всего периода наблюдений.
Участки II степени влияния характеризуются единичными проявлениями суффозионных зон на фоне разуплотнений в грунтах, при этом зоны слабо разуплотненных разностей преобладают над зонами интенсивного разуплотнения. Изредка отмечается отсутствие нарушений в сплошности грунтов.
Участки III степени влияния характеризуются отсутствием суффозионных зон и наличием единичных проявлений зон интенсивного разуплотнения на преобладающем фоне слабо разуплотненных грунтов. Нарушения в сплошности грунтов проявляются периодически на отдельных этапах мониторинга.
На рис. 33 приведен разрез по линии П-2 с участками I, II и III степеней влияния.
Анализ результатов геофизических исследований, периодически проводимых в период с июня 2005 г. по октябрь 2011 г., позволяет выделить следующие аспекты в динамике развития осложняющих процессов, происходящих в грунтовой толще объекта:
- в горном массиве до глубины 100 м от уровня дневной поверхности были выявлены многочисленные фрагменты грунтовой толщи, характеризующиеся деструктивными нарушениями - разуплотнениями геологических разностей и суффозионными процессами, которые преимущественно наблюдаются либо в непосредственной близости с тоннелями метрополитена, либо на удалении до 30 м от них. Большая часть указанных зон разуплотненного грунта в разрезах объекта выражена локально, некоторые из них формируют протяженные структуры;
- установлено, что в околотоннельном пространстве сосредоточены преимущественно участки I степени влияния на образование просадок дневной поверхности (рис. 34).
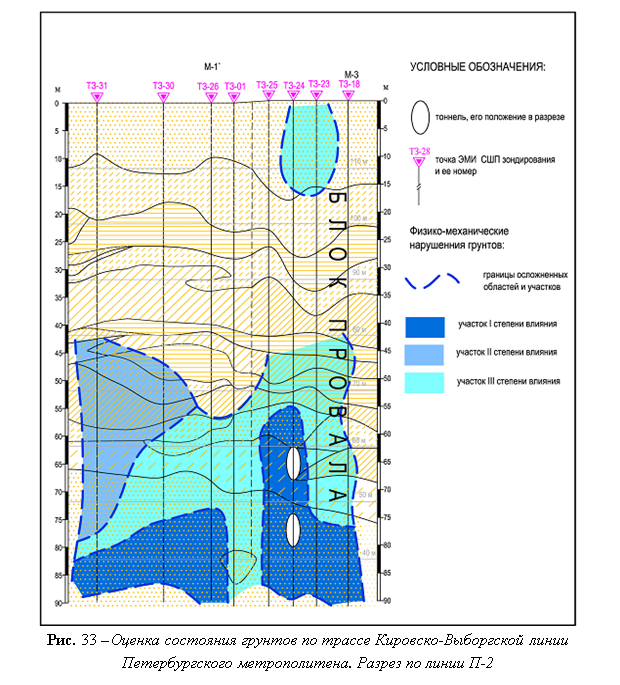
На рис. 34 видно, что участки I степени влияния, характеризующиеся наличием зон суффозии и разуплотненных грунтов различной степени интенсивности, наблюдаются: над сводом верхнего тоннеля в интервалах между ПК[40] 182+75 – ПК 183+12 и ПК 183+32 – ПК 183+84; в целике между тоннелями в интервале между ПК 182+56 – ПК 183+88.5, за исключением района ПК 182+98 и ПК 183+20; в подошве нижнего тоннеля в интервалах между ПК 182+46 – ПК 182+92 и ПК 183+02 – ПК 183+54. Верхняя граница залегания участков I степени влияния над сводом верхнего тоннеля отмечается в районе ПК 182+98 на глубине 43.8 м, а нижняя граница опускается ниже глубины измерений (90.0 м).
Оценка динамики процессов, происходящих в системе «затопленные тоннели – массив», проведена по характеру проявления нарушений грунтов за период мониторинга в общем контуре участков I степени. Для этого было подсчитано суммарное количество нарушений сплошности грунтов на разрезах на каждом этапе наблюдений.
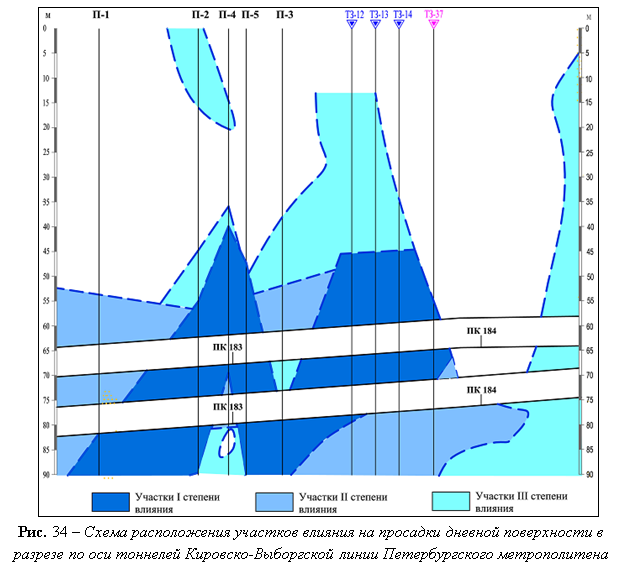
На рис. 35 приведены графики суммарного количества выявленных зон с нарушениями сплошности в грунтах в объединенном контуре участков I степени влияния в околотоннельном пространстве. Анализ графиков свидетельствует о “волнообразном” процессе происходящих изменений в строении грунтов в околотоннельном пространстве в период с 2005 по 2011 гг.: во время осеннего этапа измерений 2006 г. и весенних 2009 и 2011гг. количество наблюдаемых нарушений в грунтах было минимальным, а осенью 2007 г. – максимальным за весь период мониторинга. В период с весны 2007 г. по весну 2008 г. отмечалась активизация суффозионных процессов.
Для стабилизации горного массива в так называемой зоне «Размыва» рекомендовано, в первую очередь, закреплять грунты на участках в зависимости от степени их влияния на образование просадок дневной поверхности, а также решить вопрос о замещении водного заполнения затопленных тоннелей метрополитена твердеющими растворами или реагентами.
Результаты обработки данных ЭМИ СШП зондирования, полученных на стадии разведки месторождения горючих сланцев в Мьянме
ЗАО НПФ «Геодизонд» (г. Санкт-Петербург) в период с ноября 2011 г. по май 2012 г. выполнило обследование методом ЭМИ СШП зондирования месторождения горючих сланцев[41] в юго-восточной части Союза Мьянмы.
Основными задачами являлось определение перспективных участков в пределах трёх предполагаемых бассейнов горючих сланцев (Mepale, Melamat and Phalu basins) [42], с целью дальнейших разведочных работ, а также дифференциация толщи горючих сланцев на богатые и бедные разности по содержанию в них сланцевого масла.
Участок, условно названный блок R (рис. 36 а, 36 б), площадью около 10 кв. км, представляет собой древнюю долину реки (озера), сложенную осадочными породами, сформированными в третичном периоде около 50-52 млн. лет назад. Обследуемая территория окружена горными поднятиями триасового периода (≈250 млн. лет назад), которые на протяжении многих миллионов лет изолировали среду от внешнего воздействия и сохраняли оседавший на дне озера биоматериал, послуживший генезису горючих сланцев[43]. В настоящее время породы прикрыты чехлом четвертичных отложений.
Исходя из материалов 24, пробуренных на участке разведочных скважин (рис. 33 в), ниже четвертичных отложений геологический разрез слагает толща горючих сланцев с прослоями «пустых» пород (песчаников, аргиллитов, глинистых сланцев и мергелей). Для калибровки электромагнитного сигнала по данным скважин часть пунктов зондирования находилась в непосредственной близости от них (рис. 36 г).
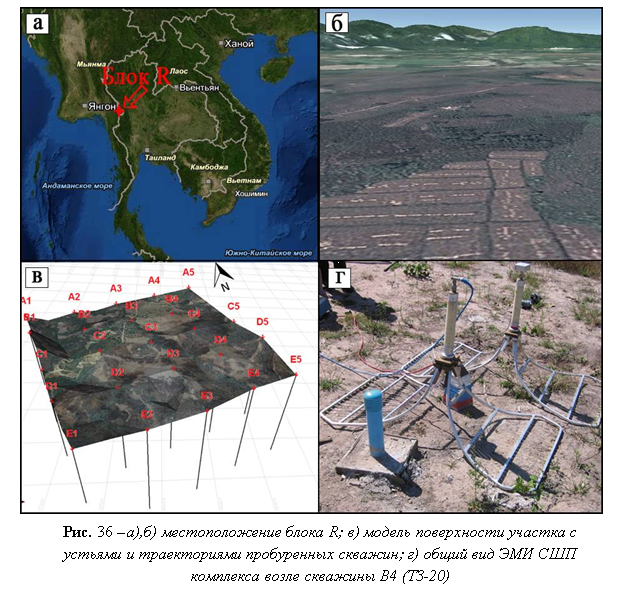
Работы методом ЭМИ СШП зондирования проводились в два этапа. На первом этапе пункты геофизических измерений располагались таким образом, чтобы шаг исследований вкупе с разведочными скважинами составлял квадрат ~ 400м х 400м. На втором этапе с целью сгущения разведочной сети были выполнены измерения в Западной и Центральной части блока R. Топопривязка точек к плану блока R согласовывалась с представителем Заказчика и выполнялась прибором GPSMAP 60CSx. Геофизические измерения на площади были выполнены в 66 точках зондирования (ТЗ) с глубиной исследования ≈ 170 м (рис. 37, обозначение 20\B4 – означает, что ТЗ № 20 выполнена на скважине B4), отношение масштабов поверхности (X,Y = М 1:1000) к глубине (Z= М 1:100) составляет 1:10.
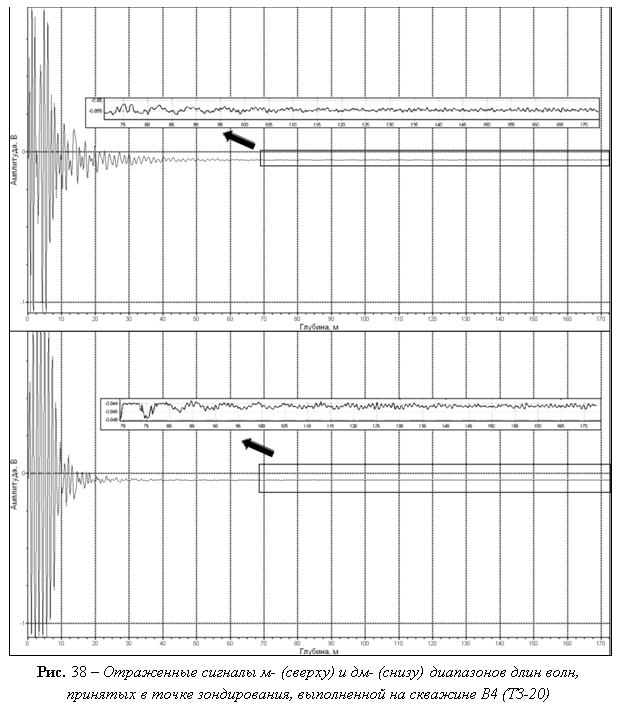
В каждой точке зондирования излучался ЭМИ сигнал, и здесь же регистрировался отраженный сигнал на две антенны м-, дм- диапазонов (рис. 38).

В результате решения обратной задачи для проведенных измерений были получены АКФ и ВКФ центрировано-нормированных ЭМИ СШП сигналов для каждой ТЗ, которые отображают корреляционные связи сигналов в пределах различных геологических элементов и характеризуют изменения электродинамических и электрофизических свойств среды в радиочастотном диапазоне. Для калибровки результатов измерений комплекса были использованы данные по кернам разведочных скважин №№ A-1 ÷ E-5, пробуренных на участке в апреле 2011 г. компанией Заказчика.
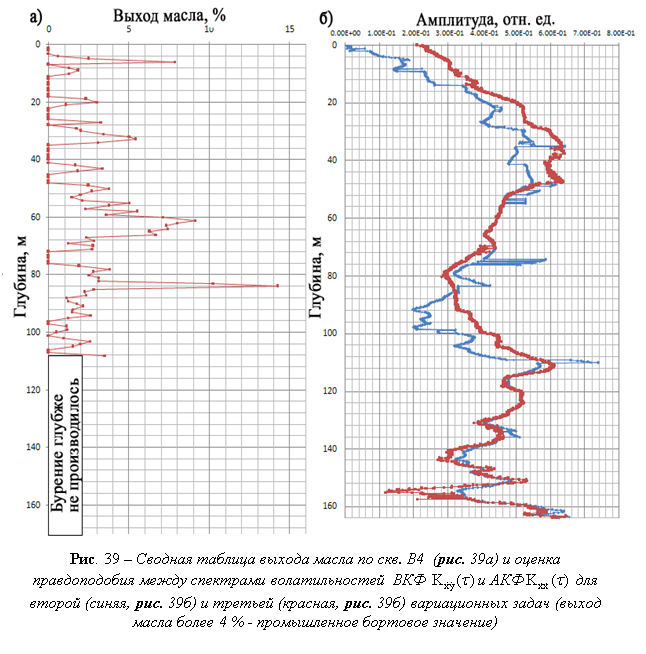
На основании материалов разведочного бурения на блоке R и калибровочных измерений на скважинах A1-E5 (рис. 36в) были определены геофизические критерии для выявления и прослеживания в разрезах горного массива богатых по содержанию сланцевого масла слоев и разработана методика расчета количества масла в породе по данным ЭМИ СШП зондирования. Пример соотношения результатов обработки данных ЭМИ СШП зондирования со значениями выхода сланцевого масла по глубине, полученными по скважине В4, представлен на рис. 39.
Из оценки правдоподобия между спектрами волатильностей
ВКФ ![]() и АКФ
и АКФ ![]() для
второй (синяя, рис. 39 б) и третьей (красная, рис. 39
б)
вариационных задач следует, что значения их подобия пропорциональны
процентному
содержанию сланцевого масла в породе.
для
второй (синяя, рис. 39 б) и третьей (красная, рис. 39
б)
вариационных задач следует, что значения их подобия пропорциональны
процентному
содержанию сланцевого масла в породе.
При сравнении расчетного содержания масла по данным ЭМИ СШП зондирования и фактического содержания по данным технологического опробования скважин было установлено, что систематическая погрешность расчетного содержания масла составляет «минус» 0.95%[44].
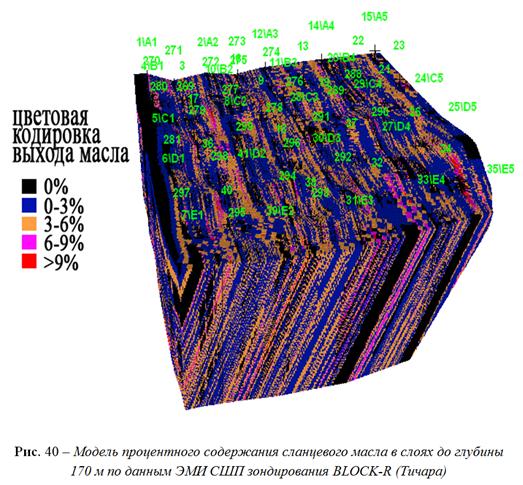
Результатом обработки данных ЭМИ СШП зондирования, полученных на стадии разведки месторождения горючих сланцев на участке BLOCK-R (Тичара), является база данных, включающая в себя информацию о прогнозируемом выходе сланцевого масла в %-ом отношении по каждому метру подповерхностного пространства в точках стояния антенн до глубины 170 м. Для визуализации базы данных в программе MICROMINE по 3D координатам была построена модель с окраской значений выхода масла (рис. 40).
Заключение
1. Рассматриваемый подход представляется наиболее простым и удобным способом построения классической статистической идентификации подповерхностных структур при зондировании в одной точке. Способ основан, по сути, на одной гипотезе и лишён ряда сложностей (эргодическая гипотеза и т.д.).
2. Задача выбора числа интервалов группирования экспериментальных данных для их статистической обработки есть задача многокритериальной оптимизации. Оптимальные оценки числа интервалов существуют. Их нахождение сведено к задачам линейного программирования.
3. Практическая реализуемость рассмотренных вариационных задач позволяет упростить процедуру определения эллипса рассеяния, существующего для любой несмещённой оценки. Существенным достоинством формализма Джейнса является возможность его обобщения для описания релаксационных процессов в подповерхностной среде.
4. Показано, что центрировано – нормированные ЭМИ СШП сигналы (сдвиг – масштабные преобразования) идентифицируемы по Г. Тейчеру. Для этого использованы гладкие (дифференцируемые по оценке) распределения, обеспечивающие сходимость оценки к локальному max правдоподобия.
5. Применение корреляционо-дисперсионного анализа данных ЭМИ СШП зондирования позволяет расширить круг минимаксных задач: от дифференциальных (правдоподобие спектров волатильностей ВКФ и АКФ) до интегральных (наиболее мощных), таких, как межантенный фактор.
6. Существование трендов волатильностей ВКФ и АКФ позволяет использовать спектры правдоподобия – один из самых мощных инструментов статистики. Решён вопрос о ширине окна Фурье преобразования.
7. Примеры проведенных работ подчёркивают эффективность предложенного подхода. Проведенные исследования указывают также на перспективность разработанной методики для анализа состава и характеристик подповерхностных слоев геологических субстратов, а также оценок искусственных сооружений и прогнозирования их поведения в сложных природных средах.
Приложение 1
Сингулярность данных ЭМИ СШП зондирования как связь
волнового спектра отражённого сигнала с его эмпирическим распределением
Задача зондирования подстилающей среды во многом схожа с вопросом усреднения задач с частым чередованием граничных условий, которым посвящено достаточно много работ [26, 27]. Как правило, основным результатом является определение вида предельных (усреднённых) задач и, по возможности, получение оценок скорости сходимости.
В [28] предполагается трехмерная краевая задача с частой сменой типа граничных условий, решения которой сходятся к решениям задач с классическими краевыми условиями, чей тип определяется соотношением мер частей границы с различными условиями в исходной задаче.
Данная задача относится к сингулярно возмущенным краевым задачам на собственные значения лапласиана в цилиндре с краевым условием Дирихле на верхнем основании и условием Неймана на нижнем основании с частой сменой типа граничного условия на боковой поверхности [28].
Смена граничных условий задается путем разбиения боковой поверхности на большое число узких полос, на которых поочередно задаются условия Дирихле и Неймана.
Поскольку уравнения электродинамики, описывающие ЭМИ СШП зондирование многослойной трехмерной среды, принадлежат уравнениям Пуассона, условия Дирихле и Неймана выполняются по определению (по типу используемого сигнала). Как худший из вариантов – цилиндр, расходящийся вниз[45]. Это решение справедливо для потенциала объемных масс, потенциала простого слоя и, самое главное, потенциала двойного слоя.
Такое разложение стало возможным после исследований усреднения уравнения Пуассона с граничными условиями
![]() =0,
=0,
![]() .
.
Здесь υ –
внешняя нормаль к границе ![]() Ω, а
множество Г
Ω, а
множество Г![]() определяется
как дополнение
определяется
как дополнение ![]()
![]()
![]() до
боковой поверхности
до
боковой поверхности ![]() .
Установлено, что при
выполнении равенства
.
Установлено, что при
выполнении равенства
![]()
![]() ,
,
решение такой задачи сходится в норме H(Ω) к решению того же уравнения Пуассона с прежними граничными условиями на основаниях и граничным условиям Дирихле на боковой поверхности[46], что говорит о возможности существования граничных условий не производящих энтропию.
Литература
1. Дрокин Н.А., Тимашов В.А. Измерения диэлектрических свойств жидких кристаллов на высоких частотах // Известия ВУЗов. Физика.−2006.−№ 9.− С. 78−81.
2. Фролов А. Д. Электрические и упругие свойства мёрзлых пород и льдов. Пущино: ОНТИ ПНЦ РАН, 2005. -607 с.
3. Коломенский Е. H., Королёв В. А. Об информационно-энтропийном анализе структурообразования глинистых грунтов.— Инженерная геология, 1982, № 5, с. 34—35.
4. Шварцбург А. Б. Дисперсия электромагнитных волн в слоистых и нестационарных средах (точно решаемые модели) // УФН. - дек. 2000, т. 170, № 12, с. 1297 – 1324.
5. Ландау Л.А., Лифшиц Е.М. Электродинамика сплошных сред. -М.: Наука,1982. – 625с.
6. Sun E., Rusch W. IEEE Trans. Ant. Propag. 42 (1) 9 (1994).
7. Болтинцев В. Б. Расширение возможностей мониторинга подземного пространства методом ЭМИ СШП зондирования // Жилищное строительство. -2012, № 9. – С.34-37.
8. Новицкий П.В., Зограф И.А. Оценка погрешностей результатов измерений. -М.: Энергоатомиздат, 1985. – 248 с.
9. Бендат Дж., Пирсон. А. Измерение и анализ случайных процессов / пер. с англ. – М.: Мир. 1971. - 408 с.
10. Венецкий И.Г., Венецкая В.И. Основные математико – статистические понятия и формулы. – М.: Статистика. 1979. -447с.
11. Кендалл М., Стьюарт А. Статистические выводы и связи. –М.: Наука. 1973. -542 с.
12. Митропольский А.К. Техника статистических вычислений. – М.: Сов. радио. 1976. -576 с.
13. Хальд А. Математическая статистика с техническими приложениями. – М: Изд. иностр. лит. 1956. – 664 с.
14. Справочник по теории вероятности и математической статистике / Под ред. В.С. Королюк. –М.: Наука, 1985. -640 с.
15. Риордан Дж. Введение в комбинаторный анализ. - М.: Физ. мат. лит., 1963. – 380 с.
16. Джейнс Э.Т. О логическом обосновании метода максимальной энтропии // ТИИЭР. -1982. Т.70. -№ 9.- С. 33-51.
17. Мудров В.И., Кушко В.Л. Методы обработки измерений: квазиправдоподобные оценки. - М.: Сов. Радио, 1976. – 192 с.
18. Зорич В. А. Математический анализ задач естествознания. –М.: МЦНМО. 2008, - 136 с.
19. Болтинцев В. Б., Ильяхин В. Н., Безродный К. П. Метод электромагнитного импульсного сверхширокополосного зондирования подстилающей среды // Журнал радиоэлектроники [электронный журнал] . 2012, №1; Режим доступа: http://jre.cplire.ru/jre/jan12/14/text.pdf. - 39 с.
20. Болтинцев В. Б. Оценка реализации свойства сверхширокополосности Т- волн для антенн подповерхностного зондирования с параметрической оптимизацией размеров поперечных сечений токоведущих линий // Журнал радиоэлектроники [электронный журнал] . 2012, №3; Режим доступа: http://jre.cplire.ru/jre/mar12/13/text.pdf. - 42 с.
21. Кульбак С. Теория информации и статистика. -М.: Наука, 1967. – 408 с.
22. Болтинцев В.Б. Применение вариационных задач для компенсации динамической погрешности информационно - измерительного комплекса /В. Б. Болтинцев, И. Ю. Лютынский, А. А. Чапчай // Проблемы машиностроения и автоматизации. -1990, № 6(36). - С.36-40.
23. Малахов А. Н. Кумулянтный анализ случайных негауссовских процессов и их преобразований. –М.: Сов. радио. 1978. -376 с.
24. Гасников А. В., Гасникова Е. В. О возможной динамике в модели расчёта матрицы корреспонденций (А. Дж. Вильсона) // ТРУДЫ МФТИ. – 2010. – Т. 2, № 4. С. 45-54.
25. Мостеллер Ф., Тьюки Дж. Анализ данных и регрессия. –М.: Финансы и статистика. 1982. - 239 с.
26. Lobo M., Perez E. Boundary homogenization of certain elliptic problems for cylindrical bodies// Bull. Soc. Math. Ser. 2. 1992. V. 116. P. 399–426.
27. Чечкин Г. А. Усреднение краевых задач с сингулярным возмущением граничных условий // Математический сборник. 1993. Т. 79. № 6. - С. 99-150.
28. Борисов Д. И. Асимптотика и оценки скорости сходимости в трехмерной краевой задаче с частой сменой граничных условий // Сибирский математический журнал, март – апрель, 2004. Т. 45. № 2. - С. 275 – 294.
[1] Фрактальная геометрия, ее первичные понятия рассмотрены в классических работах Б. Мандельброта, Р. Кроновера, А.А. Потапова, Г.Ю. Иванюка. Отличие искусственных от природных образований в Земле будет определяться фрактальностью их размерности: искусственные должны иметь целочисленную, а естественные – дробную (фрактальную) размерность. Фрактальная структура оказалась присуща многим гетерофазным средам со случайным и периодическим расположением фаз. К таким неоднородным средам мы можем в полной мере отнести земную почву, водонасыщенные среды, лесные и ледовые покровы, представляющие типичные фрактальные объекты. Геоэлектрическая модель тектонических нарушений (разломов) на поверхности кристаллического массива интересна с точки зрения фрактальных антенн - излучателей электромагнитных эмиссий литосферной природы. Проводящий (или диэлектрический) активный разлом можно рассматривать как полосковую (щелевую) антенну-излучатель в высокоомной среде, а всю разбитую системой разломов площадь кристаллического массива как плоскостную фрактальную излучающую систему. Фрактальная размерность тектонических нарушений (разломов) основана на методе встречного масштабирования (В. К. Балханов, Ю. Б. Башкуев, Электрические свойства подстилающей среды с учетом фрактального распределения проводимости // Электромагнитные волны и электронные системы, 2004. № 7. С. 34 -38).
[2] В биологии М. Эйгеном было предложено оценивать скорость микроэволюционных процессов по информации, связанной с перераспределением генных частот, посредством информационной меры Кульбака. Связь меры С. Кульбака и «традиционной» меры Р. Фишера дана в [23] и работе: Болтинцев В.Б. Использование метода максимальной энтропии в системах контроля // Контроль и диагностика общей техники // Сб. научн. тр. –ЧЛ. М.: 1989. - С.13 -15.
[3] Такие неразделяющиеся решения образуют математическую основу оптики несинусоидальных волн [4].
[4] Метод модового базиса основан на неполном разделении переменных, которое применяется к уравнениям Максвелла во временной области. После выделения из уравнений Максвелла оператора дифференцирования по поперечным координатам и доказательства его самосопряженности, получается модовый базис из собственных функций этого оператора, который можно использовать для разложения полей. В результате искомое решение во временной области представляется в виде модового разложения с коэффициентами, зависящими от продольной координаты и времени. Третьяков О. А. Метод модового базиса // Радиотехника и электроника. – 1986. – Т. 31, № 6. – С. 1071-1082. 3. Третьяков О. А., Думин А. Н. Излучение нестационарных электромагнитных полей плоским излучателем // Электромагнитные волны и электронные системы. – 1998. – Т. 3, № 1. – С. 12-22. Nicolson A. M, Ross G. F. The measurement of the intrinsic properties of materials by time-domain techniques // IEEE Trans. Instrum. Meas. - 1970. - Vol. 9.-P. 377-382.
[5]Иммореев И.Я., Синявин А.Н. Излучение сверхширокополосных антенн. –М.: Антенны, вып. 1(4), 2001. –С.8-16.
[6] Grossman A., Morlet J. Decomposition of Hardy functions into square integrable wavelets of constant shape // SIAM J. Math. P.723-736, 1984.
[7] Дрокин Н. А. Микрополосковые резонаторы и их применение для исследования диэлектрических свойств жидких кристаллов. Автореф. докт. ф.-м. н. Красноярск. 2007. – 31 с.
[8] Исключение составляет определение затухания через ширину спектральной моды: Матвеев А. Н. Оптика. –М.: Высш. Школа, 1985.- 351 с.
[9] Обобщение на случай несамосопряжённого и незнакопеременного эллиптического оператора сделано А. Г. Свешниковым. Найденное решение является асимптотическим при стремлении поглощения к нулю.( -К обоснованию метода расчета нерегулярных волноводов. Ж. вычисл. матем. и матем. физ., 1963, 3:1, с. 170–179). Предложен в начале 60-х годов А.Г.Свешниковым (докторская диссертация «Методы исследования колебаний в нерегулярных волноводах», 1963 г.). Нерегулярный участок волновода со сложной боковой поверхностью с помощью введения неортогональной криволинейной системы координат отображается на регулярный цилиндрический волновод постоянного сечения с анизотропным заполнением, которое определяется метрическим тензором преобразования координат: решается вопрос о возможности предотвратить трансформацию мод путем выбора специального анизотропного заполнения волновода. Поле в любом сечении разлагается по системе нормальных волн с коэффициентами разложения, зависящими от продольной координаты. Найденное решение является асимптотическим при стремлении поглощения к нулю. А. Г. Свешниковым сформулирован принцип парциальных условий излучения, в котором на решение для фиктивной границы заданной области накладываются условия в виде функционалов, что позволяет перейти к задаче в ограниченной области. Свешников А.Г. Принцип излучения // ДАН СССР. 1950. Т. 3. № 5. С. 517-520. Morgenrother K., Werner P. On the Instability of Resonances in Parallelplane Waveguides // Mathematical Methods in the Applied Sciences. 1989. V. 11. Р. 279–315.
[10] Пусть y(t1), y(t2), ...y(tN) - результаты наблюдений, которые могут быть представлены вариационным рядом Y1, Y2, ..., Yn, где Y1<Y2< ...<Yn, n<<N. Эмпирическим распределением wN(Yi) такого ряда называется дисткретное распределение , приписывающее каждому результату наблюдения yj попадание в интервал [Yi, Yi+1] вероятность 1/N.
[11] Распределения экстремальных величин могут быть выведены из точного исходного распределения, см.: Галамбош Я. Асимптотическая теория экстремальных порядковых статистик. – М.: Наука, 1984. – 304 с.
[12] Джеймс Стирлинг в работе Metodus differetialis, London, 1730 впервые дал асимптотическое разложение Г-функции (ряд Стирлинга). Формула Стирлинга прекрасно описывает увеличение размерности макросистем (биология, экономика, социальная сфера). Автор статьи использовал следующее разложение ряда Стирлинга

[13] Цитируется по [16], см: Edwin T. Jaynes “On The Rationale of Maximum – Entropy Methods”, proc. of the IEE, vol. 70, № 9, September 1982. Очевидно, что N1+...+Nn=N.
[14] Наиболее известные решения: равномерное распределение p(y) - при ограничении на пиковые значения сигнала; гауссовское распределение p(y) – при ограничении на мощность сигнала (дисперсию). Если предположить, что дисперсия измерений постоянна лишь в среднем, то окажется, что величина энтропии будет максимальна, когда исходная совокупность погрешностей измерений подчинена распределению Лапласа [17], см. также Dewar R.//J..Phys. A: Math. Gen. 2003. V. 36. P. 631.
[16] Golan A., G. Judge and D. Miller (1996) в работе Maximum Entropy Econometrics: Robust Estimation with Limited Data (Wiley, Chichester) приводят решение с применением четырех множителей Лагранжа – соотвественно четырёх ненулевых моментов распределения. Отмечается, что при нулевом эксцессе распределение вырождается в гауссовское. Задача max энтропии для центральных моментов вплоть до четвертого порядка имеет решение только тогда, когда эксцесс находится на отрезке [-2;0].
[17] В теории марковских процессов её принято называть матрицей переходных вероятностей. Она исследуется, как правило, оператором Фробениуса - Перрона - оператором изменения во времени распределений вероятности в отображениях (системах с дискретным временем). Оператор Фробениуса - Перрона (знание его собственных функций и собственных чисел) позволяет исследовать одномерные хаотические модели, предсказывать их поведение во времени, а также изучать их свойства (например, исследовать скорость установления инвариантного распределения - инвариантной плотности; автокорреляционные функции). Однако следует отметить, что дискретное время в такой матрице м.б. представлено как геометрической прогрессией, так и волновой функцией.
[18] Kullback S., Leibler R.A. On information and sufficiency // The Annals of Mathematical Statistics. 1951. V.22. №1. P. 79-86; Санов И. Н. О вероятностях больших отклонений случайных величин. «Матем. сб.», 1957, т. 42, в. 1, с. 11-44. Аджиев С. З., Веденяпин В.В. Временные средние и экстремали Больцмана для марковских цепей, дискретного уравнения Лиувилля и круговой модели Каца //Журнал вычислительной математики и математической физики - том 51, № 11, Ноябрь 2011, С. 2063-2074. Elements of Information Theory, Second Edition. Thomas M. Cover, Joy A. Thomas ISBN: 0-471-24195-4 Hardcover 776 pages July 2006.
[19]Tagliani, A. Note on Proximity of Distributions in Terms of Coinciding Moments //Applied Mathematics and Computation 145 (2003): pp. 195-203.
[20]Использование расстояния Кульбака – Лейблера в качестве штрафной функции обеспечивает алгоритму свойство монотонности, что означает увеличение функции правдоподобия на каждом шаге итерации. Чтобы обеспечить сходимость оценки к локальному max правдоподобия приходится использовать гладкие (дифференцируемые по оценке) распределения. Вопросы сходимости см. в работе M. I. Jordan and L. Xu. On convergence properties of EM algorithm for Gaussian mixtures. – Neural Computation,1996, vol. 8, p. 129-151.
[21] Основным
ограничением на
существование ящиков с нулевым заполнением является сингулярность типа
![]() , поскольку это является
достаточно
принципиальным для построения характеристических функций от
эмпирического
распределения с последующим вычислением по ней кумулянтов высшего
порядка [22].
, поскольку это является
достаточно
принципиальным для построения характеристических функций от
эмпирического
распределения с последующим вычислением по ней кумулянтов высшего
порядка [22].
[22]
Причиной введения Клодом Шенноном новой информационной меры
является наличие
систематического смещения максимума энтропии, определяемого как
![]() мат.
ожидание. Буйнявичус В.-А.В. в работе
«Статистические методы в радиоизмерениях. - М.: Радио и связь, 1985.
-240 с.»
показал, что
мат.
ожидание. Буйнявичус В.-А.В. в работе
«Статистические методы в радиоизмерениях. - М.: Радио и связь, 1985.
-240 с.»
показал, что
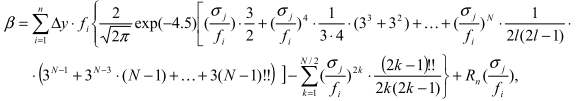
где Rn (σj / fi ) – остаточный член; σj - дисперсия дискретных значений dj ; ∆ у - интервал дискретизации.
[23] Вильсон А. Дж. в работе «Энтропийные методы моделирования сложных систем. –М.: Наука, 1978. -248 с.» впервые показал порядок применения первой и второй производных по ящикам для энтропийно – подобных критериев.
[24]
Такой подход позволяет спускаться к идеальным (в рамках ИМК) оценкам
![]() σ
по
спирали, а не в плоскости
σ
по
спирали, а не в плоскости
![]() σ, варьируя по
σ, варьируя по![]() при
σ=Const и наоборот.
при
σ=Const и наоборот.
[25]
Практикуется название меры Кульбака – Лейблера – негэнтропия
(отрицательная
энтропия) распределения
![]() относительно модельного
относительно модельного
![]() -
предложен Хиротогу Акаике в 1971 г. как информационный критерий «An Information Criterion», сейчас
известен как «Akaike Information
Criterion».
-
предложен Хиротогу Акаике в 1971 г. как информационный критерий «An Information Criterion», сейчас
известен как «Akaike Information
Criterion».
[26] Здесь и выше I0(...), I1(...) - модифицированные функции Бесселя мнимого аргумента (Е. Янке, Ф. Эмде, Ф. Лёш. СПЕЦИАЛЬНЫЕ ФУНКЦИИ Формулы, графики, таблицы –М.: Наука, 1977. - 344 с.):
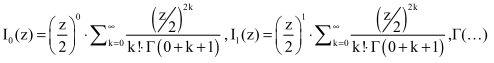
,– гамма функция (определена выше);
![]() оценка
количества ящиков в i-ой вариационной задаче.
оценка
количества ящиков в i-ой вариационной задаче.
[27] Королёв В. Ю. ЕМ-алгоритм, его модификации и их применение к задаче разделения смесей вероятностных распределений — М.:, изд-во ИПИ РАН, 2007. -94 с.
[28] Понятие идентифицируемой смеси интенсивно используют в прикладных задачах, связанных с декомпозицией (разделением, разложением, расщеплением). Библиография обширна, например, Teicher H. Identifiability of finite mixtures // The Annals of Statistics, 1963. Vol. 34. No. 4. P. 1265–1269; Исаенко О. К., Урбах. В. Ю. Разделение смесей распределений вероятностей на их составляющие. - в сб.: Итоги науки и техники. Теория вероятностей, мат. статистика и теор. кибернетика. Изд. ВИНИТИ, -М.:, 1976. с. 37-58; Круглов В. М. Смеси распределений вероятностей. - Вестник МГУ. Серия 15. ВМК, 1991, №2, с. 3-15; Titterington D. M., Smith A. F. and Makov U. E. Statistical Analysis of Finite Mixture Distributions. John Wiley and Sons, Chichester-New York-Brisbane Toronto-Singapore, 1987; Prakasa Rao B. L. S. Identifiability in Stochastic. Models. Academic Press, Boston-San Diego-New York-London Sydney-Tokyo-Toronto, 1992, 253 p.
[29] В. Е. Бенинг, В. Ю. Королёв в работе «Некоторые статистические задачи, связанные с распределением Лапласа - Информатика и её применение, 2008, т. 2, вып. 2, с. 19-34» показывают, что распределение Лапласа является масштабной смесью симметризованного распределения Релея – Райса.
[30] Дуб Дж. Л. Вероятностные процессы. -М., Изд-во иностр. лит. 1956, -605 с.; Бартлетт М. С. Введение в теорию случайных процессов. –М.: Изд-во иностр. лит., 1958. - 384 с.; Андерсон Т. Статистический анализ временных рядов, М.: "Мир", 1976 г. , 756 с.; Яглом А. М. Корреляционная теория стационарных случайных процессов. Л., Гидрометеоиздат, 1981. -280 с.
[31] ГОСТ 16465-70. Сигналы радиотехнические. Термины и определения. Более узко нормированная корреляционная функция понимается как коэффициент корреляции (Гихман И. И., Скороход А. В. Введение в теорию случайных процессов. М.,«Наука», 1977. - 568 с.)
[32] B. B. Mandelbrot. The variation of some other speculative prices. –J. Business, 1967, vol. 40, p. 393 – 413. E. Fama. The behavior of stock market prices. –J. Business, 1965, vol. 38, p. 34 – 105. Основная идея: отклонение распределений приращений от нормального означает, что классическая центральная теорема здесь не применима, так как нарушаются её условия – отсутствие конечных дисперсий у приращений за бесконечно малые промежутки времени. Поэтому вместо центральной предельной теоремы в качестве основы для построения моделей приращения Б. Мандельброт и Э. Фама предложили использовать предельные теоремы, описывающие сходимость сумм независимых слагаемых с бесконечными дисперсиями. Однако для устойчивых законов, описывающих предельные распределения, не нашлось явных выражений устойчивой плотности в терминах элементарных функций (лишь недавно доказано, что все устойчивые плотности допускают представление в терминах так называемых функций Фокса или в терминах обобщённых J – функций Мейера [Прудников А.П., Брычков Ю.А., Маричев О.И. Интегралы и ряды. Том 3. Специальные функции. Дополнительные главы. 2-е изд. - М.: Физматлит, 2003. - 688 с.]). Bownik M., Speegle D. Meyer Type Wavelet Bases in R2 // J. of Approx. Theory. 2002. V. 116. P. 49–75.
[33]Королёв В. Ю. в работе « Вероятностно – статистические методы декомпозиции волатильности хаотических процессов. – М.: изд-во Моск. Ун-та, 2011. – 512 с.» для статистического анализа хаотических случайных процессов предложил метод скользящего разделения смесей (СРС-метод), который позволяет спонтанно разложить волатильность рассматриваемого процесса на динамическую и диффузионную компоненты.
[34]В теории марковских процессов эти понятию соответствуют коэффициентам сноса и диффузии. Отличие в квадратичной форме волатильности.
[35] В оригинальной работе «M. C. Yovits and J. L. Jackson. “Linear filter optimization with game theory considerations,” in IRE National Convention Record, Pt.4, pp. 193-199, 1955» путем решения уравнения Винера – Хопфа выведена формула Йовица – Джексона для минимальной среднеквадратической ошибки (МСКО)
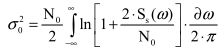
![]() - спектральные
плотности сигнала и шума.
- спектральные
плотности сигнала и шума.
[36]На данный пример распространяются все рис. 1-28.
[37]Болтинцев В.Б. Применение метода сверхширокополосного зондирования при обследовании инженерных сооружений / В. М. Власов, В. Н. Ильяхин, В. Б. Болтинцев, П. В. Кондратенко // Научно - технич. и произв. сб. статей «Безопасность энергетических сооружений», вып. 14. –М.: 2004. - С.129-138.
[38]Основная часть аномальных зон, характеризующихся описанными нарушениями во вмещающих грунтах, находится в «блоке провала» - вертикальном грунтовом «столбе», в пределах которого вследствие постоянного процесса миграции микрочастиц породы находятся в неустойчивом состоянии (оконтурен по данным ЭМИ СШП зондирования в 1998 г.). Бурение подтвердило отсутствие каких либо физико-механических связей грунтов в пределах данного «блока». Просадка грунтов поднимается до самой поверхности, что подтверждено сравнением топографических измерений до и после аварии.
[39] Разуплотнение грунтов - физико-механические нарушения сплошности грунтов, в результате которых увеличивается их пористость. Определяющим признаком при этом являлся высокий уровень затухания сигнала (резкое уменьшение значений амплитуды АКФ и ВКФ центрировано-нормированного ЭМИ СШП сигнала) в той части разреза, где присутствует нарушение сплошности геологической среды. В зависимости от степени нарушенности выделялись слабо и интенсивно разуплотненные грунты.
Суффозия - физический процесс, способствующий выносу из определенных участков разреза мелких минеральных частиц подземными водами, фильтрующимися в грунтах. В результате анализа отраженных сигналов в пределах некоторых интервалов разреза отмечалось одновременное присутствие геофизических признаков, выраженных высоким уровнем затухания АКФ и ВКФ центрировано-нормированного сигнала, что свидетельствует о высокой пористости среды, и нулевыми значениями разности фаз Фурье - преобразований для АКФ и ВКФ, что соотносится с водонасыщенностью грунтов. Совпадение этих признаков было отнесено ведущими специалистами проектных организаций, в том числе «Ленметрогипротранса», к проявлению суффозии.
[40] ПК – пикет, его длина 100 м.
[41] Горючий сланец (oil shale) - полезное ископаемое из группы твёрдых каустобиолитов, дающее при сухой перегонке значительное количество смолы (близкой по составу к нефти).
[42]Пример аналогичной работы см: Применение метода электромагнитного импульсного сверхширокополосного (ЭМИ СШП) зондирования на стадии разведки месторождения горючих сланцев в Иордании / В. Б. Болтинцев, В. Н. Ильяхин, Р. М. Салихов // Записки Горного института. 2011, т. 194. - С.138-145.
[43] Cook, A.C. and N.R. Sherwood, 1981, Classification of Oil Shale, Centres de recherches Exploration-Production Elf-AlfAquitane, 5, p.353-381. Near the Myanmar (Burma) border. It contains an estimated 18.7 billion tons of oil shale, which is estimated to yield 6.4 billion barrels(916 million tons) of shale oil. The gross heating value ranges from 287 to 3700 kcal/kg (количество тепла, которое выделяется при полном сгорании единицы массы твердого топлива в калориметрической бомбе в среде кислорода, ГОСТ 147-95), the moisture content ranges from 1 to 13 percent, and the sulfur content is about 1 percent. The deposit at Li is probably also a lamosite but the reservesare small—estimated at 15 million tons of oil shale yielding 12–41 gallons of shale oil per ton of rock (50–171 l/t) (Vanichseni and others, 1988, p. 515–516)
[44] Тичара (Бирма-Мьянма) SNOG |
|
Сингапурская компания SNOG Pte. заключила соглашение о разделе продукции с правительством Мьянмы на поиск, разведку и разработку горючих сланцев в блоке R - Тичара. В течение 2011-2012 гг. выполнены поисково-разведочные работы с применением метода ЭМИ СШП зондирования. В процессе геологоразведочных работ выполнено зондирование 300 точек на глубину до 200 м. на площади . Подсчитаны запасы в выделенном блоке R- Тичара до глубины 170 метров, предварительная технико - экономическая оценка добычи и переработки сланца при проектной мощности 4 млн. тонн в год с производством 4300 баррелей сланцевого масла в день и 52 МВт электроэнергии. Средний выход масла 69 литров с тонны сланца. |
.
[45]
Хотя задача Дирихле не всегда
разрешима для
пространственных областей, гомеоморфных шару (при наличии достаточно
острого
входящего в область острия границы - острие Лебега), т.е. существуют
такие
непрерывные функции
![]() для
которых задача Дирихле неразрешима никаким способом, Винер в
рамках
решения задачи Дирихле для уравнений Лапласа показал, что задача
разрешима,
поскольку ему удалось свести краевые задачи для эллиптических уравнений
к
интегральным уравнениям.
для
которых задача Дирихле неразрешима никаким способом, Винер в
рамках
решения задачи Дирихле для уравнений Лапласа показал, что задача
разрешима,
поскольку ему удалось свести краевые задачи для эллиптических уравнений
к
интегральным уравнениям.
[46] Решение задачи через вычеты дано А. Г. Свешниковым.