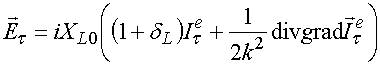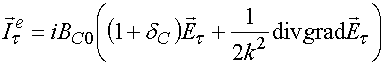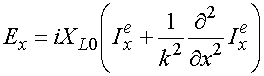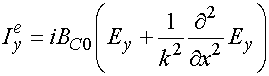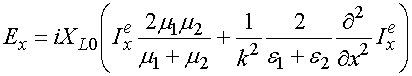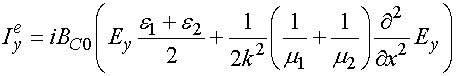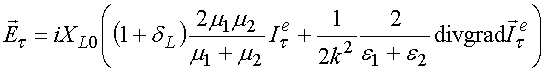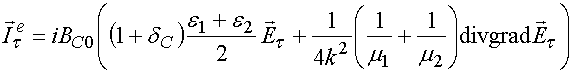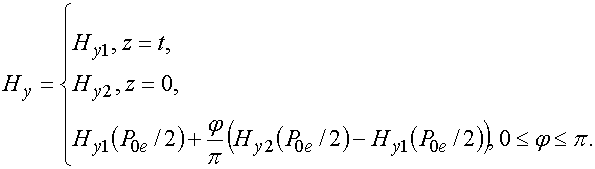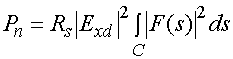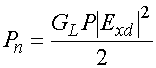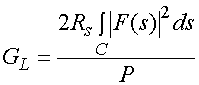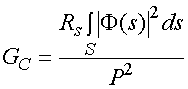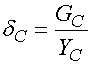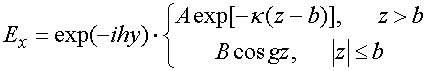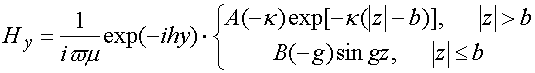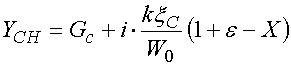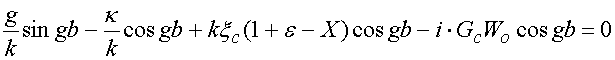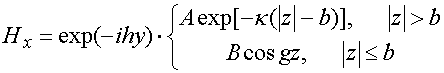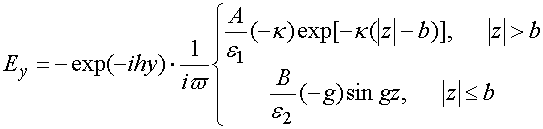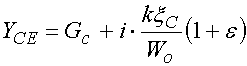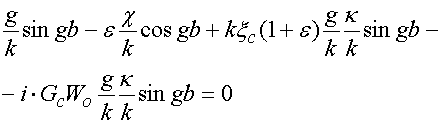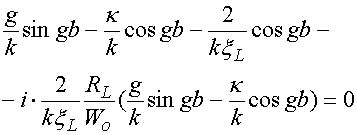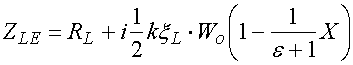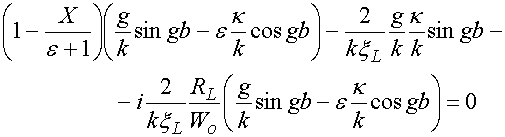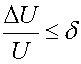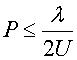УДК 621.396.67
ДВУМЕРНЫЕ СРЕДЫ НА ОСНОВЕ ДИЭЛЕКТРИЧЕСКОЙ ПЛАСТИНЫ С ИЗОТРОПНЫМИ ЛЕНТОЧНЫМИ ЧАСТОПЕРИОДИЧЕСКИМИ РЕШЕТКАМИ
С. Е. Банков, Е. В. Фролова
ИРЭ им. В.А. Котельникова РАН
Получена 26 марта 2013 г.
Аннотация. Рассматриваются вопросы математического моделирования, оценки по совокупности показателей качества и оптимизации двумерных искусственных сред – метаматериалов в виде диэлектрической пластины с нанесенными на ее поверхности частопериодическими изотропными решетками. Вводятся приближенные эквивалентные граничные условия импедансного типа, описывающие изотропную частопериодическую решетку, расположенную на границе раздела двух сред. Предложена методика учета тепловых потерь в решетках емкостного и индуктивного типа. Получены дисперсионные уравнения для определения постоянных распространения собственных волн пластины с решетками. Вводятся показатели качества искусственных сред, позволяющие оценивать эффективность их применения в устройствах интегральной СВЧ оптики. Проводится цикл численных исследований, направленных на оптимизацию метаматериалов по совокупности показателей качества.
Ключевые слова: метаматериал, частопериодическая решетка, собственная волна, СВЧ оптика.
Abstract. Problems of mathematical modeling and multi-criteria optimization of two-dimensional artificial medias on the base of dielectric slab with isotropic metal strip grids on its surfaces are considered. Approximate equivalent impedance boundary conditions are introduced for description of the grid located between two medias. A model that takes into account dissipative loss in the grid is proposed. Dispersion equations relatively propagation constants of eigen modes of dielectric slab with grids are obtained. Quality factors of artificial medias are introduced. These factors allow one to evaluate efficiency of artificial medias application in devices of microwave integral optics. Results of numerical experiments oriented to optimization of artificial medias are presented.
Keywords: metamaterial, frequently periodical array, eigen mode, microwave optics.
1. Постановка задачи
Техническое освоение коротковолновой части миллиметрового и субмиллиметрового диапазонов (ММД и СММД) достаточно давно признано актуальной научно – технической задачей [1]. Ее решение невозможно без создания технологичных СВЧ устройств и антенн. Общепризнанным способом повышения технологичности СВЧ устройств является применение технологии интегральных схем [2]. Поэтому, можно утверждать, что разработка интегральных схем для коротковолновой части ММД и СММД также является актуальной задачей, которая в настоящее время не имеет полноценного решения.
Освоение новых диапазонов частот всегда было связано с использованием новых принципов пространственной обработки и формирования полей. В случае ММД и СММД важной тенденцией является отказ от волноводного принципа и переход к квазиоптическим методам формирования полей.
Такой переход является закономерным этапом развития техники СВЧ, которое сопровождается постоянным продвижением в область коротковолновых диапазонов. Ранее, переход из сантиметрового диапазона в ММД сопровождался отказом от «проводного» способа передачи электромагнитной энергии, который реализуется в полосковых схемах и переходом к волноводному механизму, который реализуется с помощью металлических, диэлектрических и других волноводов [3]. Дальнейшее повышение частоты делает актуальным переход от направляемых волн к волновым пучкам.
Синтез отмеченной тенденции с технологией интегральных схем может быть достигнут в устройствах планарной или интегральной СВЧ оптики, которые допустимо рассматривать в качестве аналогов интегральных устройств оптического диапазона [4].
Пример устройства интегральной
СВЧ оптики показан на рис. 1. На рис. 1 изображена планарная линза, которая
выполнена путем нанесения на поверхности диэлектрической пластины тонких
пленок. Известно, что волны диэлектрической пластины, распространяющиеся в
плоскости XOY могут быть описаны как волны двумерной
среды с эффективной диэлектрической проницаемостью ![]() ,
которая равна квадрату коэффициента замедления волны пластины
,
которая равна квадрату коэффициента замедления волны пластины ![]() [5]. Пленки в области линзы меняют
свойства волны и, следовательно, эффективную проницаемость
[5]. Пленки в области линзы меняют
свойства волны и, следовательно, эффективную проницаемость ![]() . За счет этого создается в плоскости XOY неоднородная область, которая используется для преобразования
двумерного волнового пучка, распространяющегося в пластине. В случае линзы это
может быть преобразованием пучка с цилиндрическим фазовым фронтом в пучок с
плоским фронтом.
. За счет этого создается в плоскости XOY неоднородная область, которая используется для преобразования
двумерного волнового пучка, распространяющегося в пластине. В случае линзы это
может быть преобразованием пучка с цилиндрическим фазовым фронтом в пучок с
плоским фронтом.
Пленки могут быть выполнены разными способами, например, в виде тонкого слоя диэлектрика с высокой проницаемостью. Большими возможностями обладают пленки в виде периодических решеток из плоских металлических проводников, в том числе, в виде лент, щелей и т.д. С их помощью можно создавать двумерные среды, свойства которых существенно отличаются от свойств естественных сред. Отметим анизотропные среды и среды с принудительным преломлением [6].
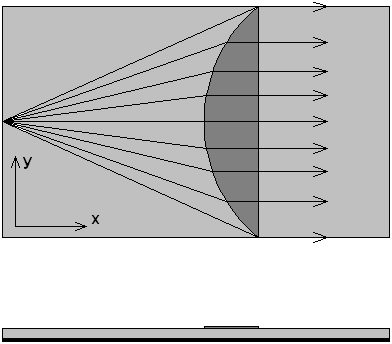
Рис. 1. Планарная линза
Диэлектрическая пластина не является единственно возможной средой для распространения двумерных волн. К их числу можно отнести также плоские волноводы, различные планарные диэлектрические волноводы и т.д. Вместе они формируют широкий класс планарных волноводов, на основе которых создаются разнообразные двумерные или планарные среды. Такие среды в силу необычности их электродинамических свойств можно назвать планарными метаматериалами по аналогии с трехмерными метаматериалами [7].
Наряду с относительно простыми однофокальными линзами (см. рис. 1), в интегральной СВЧ оптике могут использоваться более сложные градиентные линзы Люнеберга, представляющие собой двумерную осесимметричную искусственную среду с радиальным градиентом эффективной диэлектрической проницаемости.
Нетрудно увидеть, что одной из ключевых задач проектирования устройств интегральной СВЧ оптики является исследование свойств их базовых элементов – однородных искусственных сред. В нашей работе представлены результаты исследования искусственных сред на основе изотропных частопериодических ленточных решеток, расположенных на поверхностях диэлектрической пластины.
Следует отметить, что структуры такого типа рассматривались с разных точек зрения во многих работах. Например, в книге [8] дано обобщение результатов анализа планарных волноводов с периодическими решетками как элементов антенн бегущей волны. В работе [9] исследовались, волны диэлектрической пластины с импедансными пленками на ее поверхностях. В работе [10] рассмотрены волны диэлектрической пластины с анизотропными ленточными решетками.
Подход, который использовался в нашей работе, имеет следующие важные особенности. Мы рассматриваем регулярную диэлектрическую пластину с частопериодическими решетками как изотропную двумерную среду, в которой невозможно в отличие от работы [8] излучение в свободное пространство. Отсутствие излучения достигается при достаточно малом периоде решетки, при котором эффекты, связанные с ее периодичностью становятся несущественными. В этом случае для описания решетки можно использовать аппарат эквивалентных граничных условий (ЭГУ).
В нашей работе предложены приближенные ЭГУ для изотропных ленточных решеток, расположенных на границе раздела двух сред. Отметим, что достаточно строгий учет влияния параметров сред, окружающих решетку выполнен в работе [11] только для анизотропных решеток. Изотропные решетки, расположенные в однородной среде рассмотрены в работе [12]. Таким образом, строгие ЭГУ для изотропной решетки, находящейся на границе двух магнито – диэлектриков неизвестны. В нашей работе представлена приближенная методика учета влияния границы раздела сред на ЭГУ для изотропной решетки.
Отличие нашего подхода от работы [9] состоит в том, что мы исследуем структуру, содержащую не абстрактные импедансные пленки, а частопериодические ленточные решетки, которые описываются конкретной совокупностью геометрических и материальных параметров. Конкретизация типа импедансной пленки позволяет нам ставить принципиальный для КЧ ММД и СММД вопрос о тепловых потерях в решетках, которые существенно влияют на суммарное затухание собственных волн пластины. Нами предложена приближенная методика учета тепловых потерь в решетках, основанная на использовании выражений для электрических токов на металлических лентах, которые получены в ходе анализа анизотропных ленточных решеток [11].
Важной особенностью нашего подхода является его практическая направленность на применение искусственных сред в устройствах СВЧ интегральной оптики. Она выражается в том, что исследуемые объекты оцениваются по совокупности показателей качества, которые формулируются с учетом требований, которые предъявляются к ним со стороны указанных устройств. Одним из таких требований является условие минимизации тепловых потерь, которое особенно актуально для ММД и СММД. Для оценки данного показателя качества в работе построена модель исследуемой структуры, позволяющая определять затухание ее собственных волн, обусловленное тепловыми потерями.
Перечисленные выше особенности определяют актуальность проведенного исследования и новизну результатов, которые будут представлены ниже.
2. ЭГУ для решетки, расположенной на границе раздела двух сред
В разделах 2 и 3 обсуждаются вопросы, связанные с построением адекватной модели изотропной ленточной решетки, расположенной на границе раздела двух сред. К числу таких вопросов относятся: вид ЭГУ и учет тепловых потерь в них. Первый из них рассматривается во втором разделе.
Следует отметить, что частопериодические решетки, то есть решетки с периодом много меньшим длины волны относятся к числу классических объектов электродинамики, которые неоднократно рассматривались в разных работах. Среди них можно отметить уже упоминавшуюся работу [12], в которой обобщаются результаты анализа изотропных и анизотропных металлических сеток. В книге [13] представлена теория анизотропных решеток, расположенных в свободном пространстве. В работе [12] эта теория обобщается на случай анизотропной решетки расположенной на границе двух сред.
Общим выводом из всех упомянутых работ является вывод о возможности описания всех видов частопериодических решеток с помощью ЭГУ. При таком подходе решетка представляется в виде бесконечно тонкой однородной пленки, на поверхности которой компоненты электромагнитного поля имеют разрывы. Связь между компонентами полей на поверхностях пленки устанавливается с помощью ЭГУ.
Отметим, что в работах [12] и [13] рассматривается вопрос о решетке, находящейся на границе двух сред. Однако, его решение не является удовлетворительным, так как влияние границы учитывается только для равномерной части поля. Ближнее поле, которое сосредоточено вблизи решетки считается таким же как в однородной среде. Учет изменения ближнего поля, обусловленного скачком параметров среды, представлен в работе [11] для анизотропной решетки. Результаты анализа показывают, что строгие ЭГУ существенно отличаются от полученных в работах [12] и [13]. Таким образом, для достижения целей нашего исследования нам необходимо получить ЭГУ для изотропной решетки на границе раздела сред.
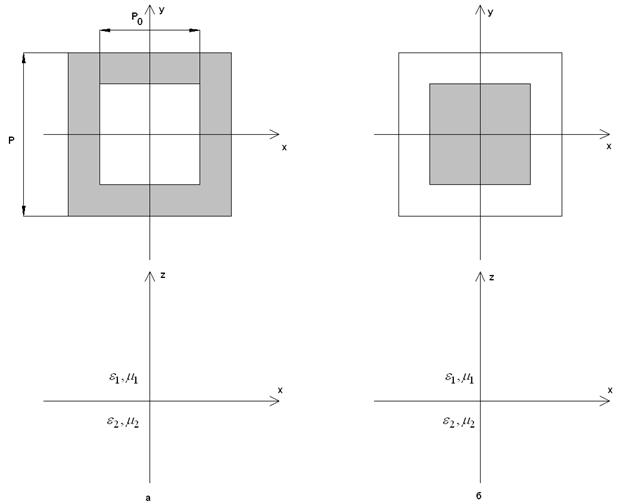
На рис. 1 а,b показаны периоды изотропных решеток. Рис. 1 а соответствует индуктивной, а рис. 1 b емкостной решетке.
Рис. 1. Период индуктивной (а) и емкостной (b) решеток
Рассмотрим ЭГУ для таких решеток, расположенных в свободном пространстве [12]:
где ![]() - вектор
электрического поля тангенциальный к плоскости XOY,
- вектор
электрического поля тангенциальный к плоскости XOY, ![]() - вектор поверхностных электрических,
текущих в плоскости XOY, этот вектор связан с разрывами
тангенциальных компонент магнитного полей известным образом [14],
- вектор поверхностных электрических,
текущих в плоскости XOY, этот вектор связан с разрывами
тангенциальных компонент магнитного полей известным образом [14], ![]() - волновое число свободного пространства,
- волновое число свободного пространства,
![]() - реактивное сопротивление индуктивной
решетки,
- реактивное сопротивление индуктивной
решетки, ![]() - проводимость емкостной решетки,
- проводимость емкостной решетки, ![]() - параметры, учитывающие тепловые потери
в решетках. ЭГУ (1) относится к индуктивной, а ЭГУ (2) к емкостной решетке.
Отметим, что параметры
- параметры, учитывающие тепловые потери
в решетках. ЭГУ (1) относится к индуктивной, а ЭГУ (2) к емкостной решетке.
Отметим, что параметры ![]() были найдены в работе [12] для
решеток из проводников с круглым поперечным сечением, тогда как нас интересуют
проводники ленточного типа. Также отметим, что полный набор граничных условий,
описывающих решетки включает также пару условий, устанавливающих непрерывность
тангенциальных компонент электрического поля по обе стороны от решетки. Далее,
говоря об ЭГУ мы будем их иметь ввиду, но для сокращения записи приводить в
явном виде не будем.
были найдены в работе [12] для
решеток из проводников с круглым поперечным сечением, тогда как нас интересуют
проводники ленточного типа. Также отметим, что полный набор граничных условий,
описывающих решетки включает также пару условий, устанавливающих непрерывность
тангенциальных компонент электрического поля по обе стороны от решетки. Далее,
говоря об ЭГУ мы будем их иметь ввиду, но для сокращения записи приводить в
явном виде не будем.
Рис. 2. Анизотропная ленточная решетка
Рассмотрим далее ЭГУ для анизотропных решеток (см. рис. 2) в свободном пространстве:
 ,
,
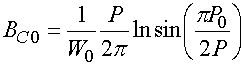 ,
,
где ![]() - волновое
сопротивление свободного пространства.
- волновое
сопротивление свободного пространства.
Учет материальных параметров сред приводит к следующим ЭГУ [11]:
где ![]() и
и ![]() - материальные параметры сред (см. рис. 1
а,б).
- материальные параметры сред (см. рис. 1
а,б).
В ЭГУ (3) – (6) отсутствуют параметры ![]() , поскольку в работах, в которых они были
получены, потери не учитывались. ЭГУ для анизотропных решеток записать в
компактной векторной форме аналогично ЭГУ (1), (2) невозможно по причине
анизотропии структуры. Ленточная решетка (см. рис. 2) является индуктивной
структурой для компонент
, поскольку в работах, в которых они были
получены, потери не учитывались. ЭГУ для анизотропных решеток записать в
компактной векторной форме аналогично ЭГУ (1), (2) невозможно по причине
анизотропии структуры. Ленточная решетка (см. рис. 2) является индуктивной
структурой для компонент ![]() ,
,![]() и емкостной для
и емкостной для ![]() ,
,![]() . В силу анизотропии в ЭГУ (3) – (6) в них
вместо векторных операторов из (1),(2) присутствуют вторые производные по
координате
. В силу анизотропии в ЭГУ (3) – (6) в них
вместо векторных операторов из (1),(2) присутствуют вторые производные по
координате ![]() .
.
Из формул (3) – (6) видно, что
учет влияния границы раздела сред приводит к появлению дополнительных
множителей перед обоими слагаемыми, стоящими в скобках. Первое слагаемое
описывает сопротивление или проводимость решетки для поля постоянного в
плоскости XOY, а второе слагаемое, содержащее
дифференциальный оператор, учитывает влияние вариаций поля в указанной
плоскости. Отметим, что дополнительные множители обращаются в единицу при ![]() ,
, ![]() . При
этом ЭГУ (5),(6) переходят в ЭГУ (3),(4).
. При
этом ЭГУ (5),(6) переходят в ЭГУ (3),(4).
Для описания изотропных решеток, лежащих на границе раздела сред мы использовали следующие ЭГУ:
Из соотношений (7) и (8) видно, что мы предположили, что наличие границы раздела сред проявится появлением в ЭГУ множителей аналогичным множителям из (5),(6).
Для слагаемых без дифференциальных операторов
данное предположение обосновывается тем, что эти слагаемые можно получить для
случая ![]() . Однако в этом случае, который
соответствует возбуждению решетки плоской волной, падающей на нее вдоль оси 0z, то есть по нормали, изотропные и анизотропные решетки
имеют весьма близкие свойства. Например, если изотропная индуктивная решетка
возбуждается полем с компонентами
. Однако в этом случае, который
соответствует возбуждению решетки плоской волной, падающей на нее вдоль оси 0z, то есть по нормали, изотропные и анизотропные решетки
имеют весьма близкие свойства. Например, если изотропная индуктивная решетка
возбуждается полем с компонентами ![]() , то токи на
вертикальных лентах (см. рис. 1 а) возбуждаются весьма слабо, по крайней мере,
когда мы имеем дело с узкими лентами. Поэтому их влияние можно не учитывать.
Таким образом, мы приходим к анизотропной решетке с индуктивным сопротивлением,
которое определяется из условия (5). Аналогично для изотропной емкостной
решетки первое слагаемое можно взять из условия (6).
, то токи на
вертикальных лентах (см. рис. 1 а) возбуждаются весьма слабо, по крайней мере,
когда мы имеем дело с узкими лентами. Поэтому их влияние можно не учитывать.
Таким образом, мы приходим к анизотропной решетке с индуктивным сопротивлением,
которое определяется из условия (5). Аналогично для изотропной емкостной
решетки первое слагаемое можно взять из условия (6).
Отметим, что дифференциальные операторы в ЭГУ
для изотропных и анизотропных решеток в ряде частных случаев совпадают. Если
ленты анизотропной решетки ориентированы вдоль оси 0х, как показано на рис. 2,
то такой частный случай соответствует условию ![]() .
Аналогично при
.
Аналогично при ![]() свойства изотропной решетки
будут совпадать со свойствами анизотропной решетки, ориентированной вдоль оси
0у.
свойства изотропной решетки
будут совпадать со свойствами анизотропной решетки, ориентированной вдоль оси
0у.
Совпадение дифференциальных операторов позволяет ожидать совпадение множителей учитывающих влияние границы раздела сред в ЭГУ (5),(6) и (7),(8). В самом общем случае, когда ни один из дифференциальных операторов не равен нулю, множители в ЭГУ могут отличаться, но это отличие не должно быть существенным в силу высокой степени однородности свойств решеток с прямоугольной сеткой в плоскости XOY.
3. Учет тепловых потерь в решетках
При определении потерь в
решетках мы исходили из вида ЭГУ (1) и (2), в которых параметры ![]() входят только в слагаемые, не имеющие
дифференциальных операторов. Мы исходили из того, что изменение формы сечения
проводника не изменит вида ЭГУ. Поэтому для ленточной решетки можно найти
поправки, обусловленные тепловыми потерями для частного случая:
входят только в слагаемые, не имеющие
дифференциальных операторов. Мы исходили из того, что изменение формы сечения
проводника не изменит вида ЭГУ. Поэтому для ленточной решетки можно найти
поправки, обусловленные тепловыми потерями для частного случая:
который, как было сказано выше, соответствует возбуждению решетки нормально падающей плоской волной.
Для определения потерь нам потребуются выражения для электрических токов, текущих по проводникам. Будем в качестве исходной информации использовать соотношения для токов на бесконечно тонких металлических лентах анизотропной решетки при условии (9). Далее мы скорректируем их с учетом отличий между двумя типами решеток.
Использовать выражения для токов на бесконечно тонких проводниках для вычисления потерь непосредственно невозможно, так как интегралы от квадратов токов расходятся [15]. Поэтому мы предварительно должны провести коррекцию соотношений для токов с учетом конечной толщины проводников. Такая коррекция устранит всплески токов, стремящихся к бесконечности, и позволит осуществить интегрирование.
Далее мы найдем мощность
потерь в решетке, которая связана с действительной частью сопротивления или
проводимости решетки и определяет искомые параметры ![]() .
.
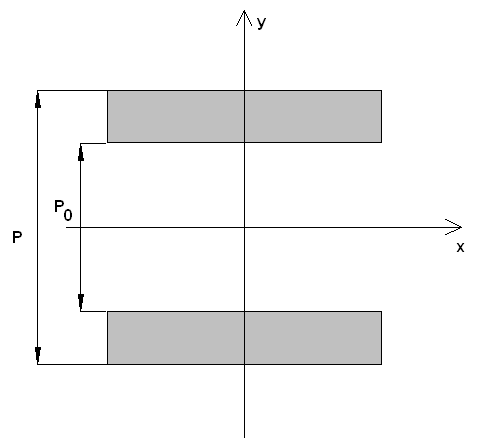
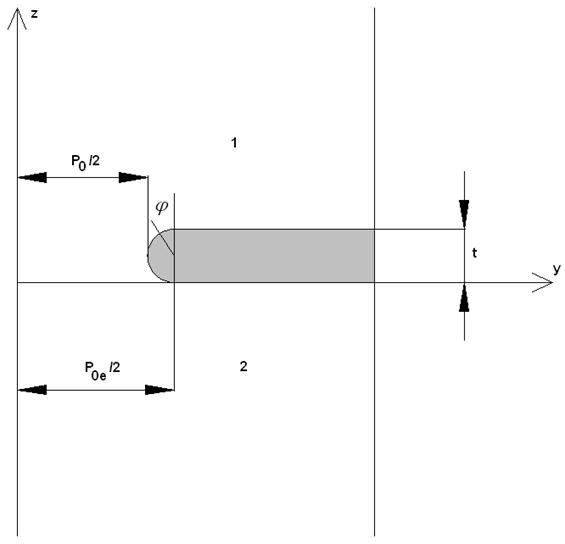
Начнем с более простого случая индуктивной решетки. Рассмотрим анизотропную ленточную решетку в режиме возбуждения плоской волной по нормали к плоскости XOY (см. рис. 3).
Рис. 3. Период анизотропной ленточной решетки
Решетка возбуждается волной с компонентами ![]() . Подход, развитый в работе [11],
позволяет найти выражения для компонент магнитного поля на поверхностях
металлических проводников. Прежде чем записать эти выражения отметим следующие
важные обстоятельства. В подходе, связанном с ЭГУ полное электромагнитное поле
разделяется на две части: дальнее поле и ближнее поле. Вместе они составляют
полное поле решетки. Известно, что поле в периодической структуре, которой
является решетка, может быть представлено в виде ряда по пространственным
гармоникам Флоке [13]. В частопериодической решетке все гармоники Флоке, кроме
нулевой являются запредельными. Их поля экспоненциально затухают вдоль оси 0z. Эти гармоники формируют ближнее поле. Дальнее поле – это
поле нулевой гармоники. Оно определяет взаимодействие решетки с внешними по
отношению к ней структурами. ЭГУ записываются относительно дальнего поля. Они
позволяют находить дальнее поле из решения отдельной электродинамической
задачи. Считаем его на данном этапе известным. Будем использовать индекс
. Подход, развитый в работе [11],
позволяет найти выражения для компонент магнитного поля на поверхностях
металлических проводников. Прежде чем записать эти выражения отметим следующие
важные обстоятельства. В подходе, связанном с ЭГУ полное электромагнитное поле
разделяется на две части: дальнее поле и ближнее поле. Вместе они составляют
полное поле решетки. Известно, что поле в периодической структуре, которой
является решетка, может быть представлено в виде ряда по пространственным
гармоникам Флоке [13]. В частопериодической решетке все гармоники Флоке, кроме
нулевой являются запредельными. Их поля экспоненциально затухают вдоль оси 0z. Эти гармоники формируют ближнее поле. Дальнее поле – это
поле нулевой гармоники. Оно определяет взаимодействие решетки с внешними по
отношению к ней структурами. ЭГУ записываются относительно дальнего поля. Они
позволяют находить дальнее поле из решения отдельной электродинамической
задачи. Считаем его на данном этапе известным. Будем использовать индекс ![]() для обозначения дальнего поля.
для обозначения дальнего поля.
Полное магнитное поле на поверхностях лент записывается следующим образом:
![]() ,
,
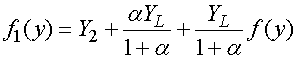 ,
,
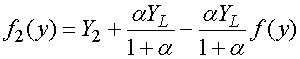
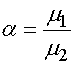 ,
, 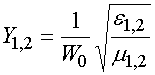 ,
,
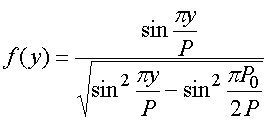 ,
,
![]() ,
,
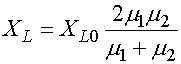 ,
, 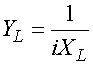 .
.
Из формул (10) видно, что магнитное поле при ![]() стремится к бесконечности пропорционально
стремится к бесконечности пропорционально
![]() . Мощность потерь в металле
пропорциональна интегралу от квадрата магнитного поля. Таким образом,
непосредственное использования выражений (10) для определения мощности потерь
невозможно, так как интеграл будет расходящимся. Расходимость интеграла
является следствием приближения, принятого при описании решетки, в частности,
допущения о бесконечно тонких проводниках.
. Мощность потерь в металле
пропорциональна интегралу от квадрата магнитного поля. Таким образом,
непосредственное использования выражений (10) для определения мощности потерь
невозможно, так как интеграл будет расходящимся. Расходимость интеграла
является следствием приближения, принятого при описании решетки, в частности,
допущения о бесконечно тонких проводниках.
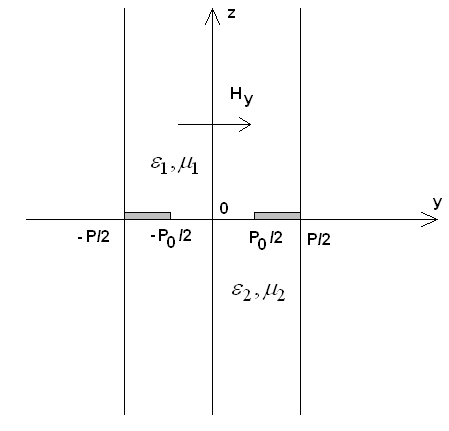
Рис. 4. Проводник конечной толщины
Скорректируем выражения (10), вводя малую, но
конечную толщину проводников ![]() . Проводник конечной
толщины показан на рис. 4. Из рис. 4 видно, что проводник конечной толщины на
участке
. Проводник конечной
толщины показан на рис. 4. Из рис. 4 видно, что проводник конечной толщины на
участке ![]() ,
, ![]() имеет
плоские поверхности, а при
имеет
плоские поверхности, а при ![]() у него появилось
скругление радиуса
у него появилось
скругление радиуса ![]() . Определим магнитное поле на
поверхности проводника следующим образом:
. Определим магнитное поле на
поверхности проводника следующим образом:
В формуле (11) поля ![]() описываются
выражениями (10). Учтем, что поля
описываются
выражениями (10). Учтем, что поля ![]() пропорциональны
пропорциональны ![]() и запишем выражение для
и запишем выражение для ![]() следующим образом:
следующим образом:
где ![]() - известная функция,
которую можно определить из формул (10) и (11), координата
- известная функция,
которую можно определить из формул (10) и (11), координата ![]() определяет положение точки на поверхности
проводника.
определяет положение точки на поверхности
проводника.
Найдем мощность потерь ![]() в
проводниках решетки на одном ее периоде:
в
проводниках решетки на одном ее периоде:
Интегрирование в (13) ведется по всей
поверхности проводника, ![]() - поверхностное
сопротивление металла, обусловленное его конечной проводимостью. Отметим, что
на периоде мы имеем два таких проводника.
- поверхностное
сопротивление металла, обусловленное его конечной проводимостью. Отметим, что
на периоде мы имеем два таких проводника.
С другой стороны, в рамках приближения ЭГУ
мощность потерь можно найти как мощность, рассеиваемую в пленке, имеющую
активную проводимость ![]() :
:
Приравнивая мощности (13) и (14), находим
параметр ![]() :
:
Параметр ![]() ,
входящий в ЭГУ определяется следующим образом:
,
входящий в ЭГУ определяется следующим образом:
Приведенный выше для анизотропной решетки вывод
соотношения, описывающего параметр ![]() остается верным и для
изотропной решетки, так как выше было отмечено, что при нормальном падении
волны на изотропную решетку возбуждается только одна система лент. При этом
изотропная решетка эквивалентна анизотропной.
остается верным и для
изотропной решетки, так как выше было отмечено, что при нормальном падении
волны на изотропную решетку возбуждается только одна система лент. При этом
изотропная решетка эквивалентна анизотропной.
Рассмотрим далее емкостную решетку, используя методику описанную выше. Особенностью емкостной решетки является то, что для описания электрического тока на ней мы не можем непосредственно использовать выражения, полученные в анизотропном случае, как это было для индуктивной решетки.
Емкостная решетка является дуальной по отношению к индуктивной решетке структурой. К ней можно применить принцип Бабине [14]. Согласно этому принципу магнитный ток в щелях емкостной решетки совпадает с электрическим током на лентах индуктивной структуры. Таким образом, эквивалентность емкостных анизотропной и изотропной решеток при нормальном падении волны имеет место, но она справедлива для магнитных токов в щелях, которые для обеих структур можно описать одинаковыми функциями. Однако по отношению к электрическим токам такое утверждение не вполне оправданно.
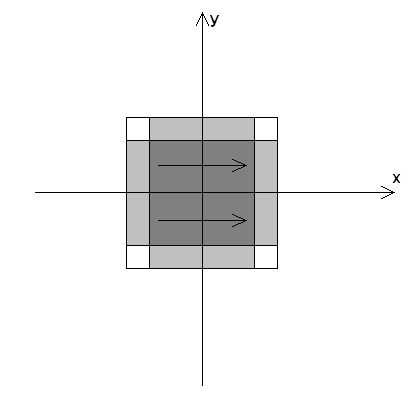
Рассмотрим качественно
поведение электрических токов в емкостной решетке. Оно поясняется рис. 5.
Решетка возбуждается волной с компонентами ![]() .
Поэтому на квадратном металлическом проводнике (выделен на рис. 5 темно – серым
цветом) токи преимущественно текут вдоль оси 0у, а магнитное поле направлено
вдоль оси 0х.
.
Поэтому на квадратном металлическом проводнике (выделен на рис. 5 темно – серым
цветом) токи преимущественно текут вдоль оси 0у, а магнитное поле направлено
вдоль оси 0х.
Рис. 5. Электрические токи в изотропной емкостной решетке
С точки зрения проводимости ![]() изотропная решетка эквивалентна
анизотропной решетке с лентами вытянутыми вдоль оси 0х. Поэтому мы можем
предположить, что электрический ток и магнитное поле в изотропном случае
усредненные по координате
изотропная решетка эквивалентна
анизотропной решетке с лентами вытянутыми вдоль оси 0х. Поэтому мы можем
предположить, что электрический ток и магнитное поле в изотропном случае
усредненные по координате ![]() совпадают с
соответствующими величинами указанной выше анизотропной решетки, в которой поля
однородны вдоль оси 0х. Появление горизонтальных щелей (см. рис. 5),
разрезающих ленту анизотропной решетки приводит к нарушению однородности тока и
поля и появлению их зависимости от координаты
совпадают с
соответствующими величинами указанной выше анизотропной решетки, в которой поля
однородны вдоль оси 0х. Появление горизонтальных щелей (см. рис. 5),
разрезающих ленту анизотропной решетки приводит к нарушению однородности тока и
поля и появлению их зависимости от координаты ![]() .
Считаем, что она такая же, как в анизотропной решетке, но повернутой на
девяносто градусов.
.
Считаем, что она такая же, как в анизотропной решетке, но повернутой на
девяносто градусов.
Суммируя соображения, изложенные выше, мы можем получить с помощью результатов работы [11] следующие соотношения:
![]() ,
,
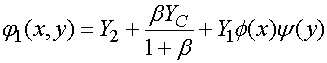 ,
,
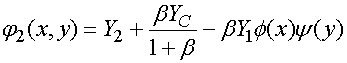 ,
,
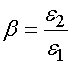 ,
,
![]() ,
,
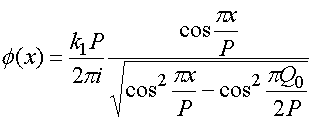 ,
,
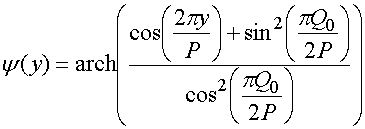 ,
,
![]() ,
,
![]() ,
, ![]() ,
,
где ![]() .
.
Выражения (17) позволяют нам аналогично
рассмотренному ранее случаю представить компоненту поля ![]() :
:
Учет толщины проводника
проводим аналогично индуктивной решетки. В результате получаем выражение для
активной части проводимости емкостной решетки ![]() :
:
где ![]() - поверхность
квадратного проводника. Параметр
- поверхность
квадратного проводника. Параметр ![]() из ЭГУ выражается
через проводимость
из ЭГУ выражается
через проводимость ![]() :
:
5. Дисперсионные уравнения
Получим дисперсионные
уравнения для собственных волн структуры, образованной двухсторонним
симметричным нанесением на диэлектрическую пластину изотропных ленточных
решеток индуктивного и емкостного типа. Подобные задачи рассматривались во
многих работах, например, в [3,9]. В них показано, что поле в пластине с
изотропными пленками разделяется на Е – и Н – волны. В двумерном случае, когда ![]() , они имеют по три компоненты. Е – волны
имеют компоненты
, они имеют по три компоненты. Е – волны
имеют компоненты ![]() , Н – волны компоненты
, Н – волны компоненты ![]() . Кроме того, отметим, что в силу
симметрии структуры относительно плоскости
. Кроме того, отметим, что в силу
симметрии структуры относительно плоскости ![]() , волны
в ней разделяются на четные и нечетные. Поперченные компоненты четных волн
описываются четными по переменной
, волны
в ней разделяются на четные и нечетные. Поперченные компоненты четных волн
описываются четными по переменной ![]() функциями,
соответственно, компоненты нечетных волн нечетными функциями. Ограничимся
анализом четных типов волн, к числу которых относится наиболее интересная
основная волна.
функциями,
соответственно, компоненты нечетных волн нечетными функциями. Ограничимся
анализом четных типов волн, к числу которых относится наиболее интересная
основная волна.
Для пластины,
изображенной на рис. 3, компоненты поля E – и H – волн
выражаются через функцию поперечного сечения ![]() следующим
образом:
следующим
образом:
для H–волн
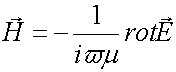 ,
,
для E-волн
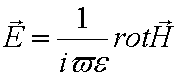 ,
,
Где h – продольное волновое число, ![]() –
относительные диэлектрическая и магнитная проницаемости пластины. Поля (21) и
(22) взяты в виде волн, бегущих вдоль оси 0у. Функция
–
относительные диэлектрическая и магнитная проницаемости пластины. Поля (21) и
(22) взяты в виде волн, бегущих вдоль оси 0у. Функция ![]() для
четных волн симметричной структуры должна быть четной и стремиться к нулю при
для
четных волн симметричной структуры должна быть четной и стремиться к нулю при ![]() .
.
Емкостная решетка, H- волны. Получим далее дисперсионное уравнение для Н – волн пластины с емкостными решетками.
Тангенциальные к поверхностям пластины компоненты электрического и магнитного поля вне и внутри диэлектрика записываются в следующем виде
![]() ,
,
![]() ,
,
где A и B – неизвестные коэффициенты. Из соотношений (23), (24) видно, что функция поперечного сечения взята таким образом, что поля удовлетворяют однородному волновому уравнению вне пластины и внутри нее. Неизвестные коэффициенты, входящие в выражения (23),(24) находим, подставляя указанные выражения в ЭГУ.
ЭГУ (8) для рассматриваемого частного случая можно записать в виде:
![]() ,
,
где ![]() –
комплексная проводимость емкостной решетки:
–
комплексная проводимость емкостной решетки:
где
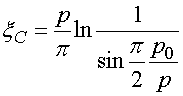 ,
,
![]() ,
,
![]() -
определяется выражением (19).
-
определяется выражением (19).
Подставляя выражения
(23), (24) в условия (25), получаем однородную систему линейных алгебраических
уравнений относительно неизвестных коэффициентов A и B.
Приравнивая ее определитель нулю, получаем искомое дисперсионное уравнение
относительно неизвестной постоянной распространения ![]() :
:
где ![]() ,
, ![]() .
.
Емкостная решетка, E- волны. Аналогично получим дисперсионное уравнение для Е – волн.
В этом случае компоненты электрического и магнитного поля имеют вид:
ЭГУ (8) преобразуются к виду:
![]() ,
,
где
Дисперсионное уравнение имеет вид:
Индуктивная решетка, H- волны. Выполнив для индуктивной решетки преобразования, аналогичные описанным выше, получим следующие соотношения:
![]() ,
,
где ![]() –
комплексный импеданс индуктивной решетки для Н - волн:
–
комплексный импеданс индуктивной решетки для Н - волн:
 ,
,
![]() .
.
Дисперсионное уравнение имеет следующий вид:
Индуктивная решетка, E-волны
![]() ,
,
где ![]() –комплексный
импеданс индуктивной решетки для Е - волн:
–комплексный
импеданс индуктивной решетки для Е - волн:
Дисперсионное уравнение имеет вид:
6. Решения дисперсионных уравнений
Дисперсионные уравнения
решались численными методами на комплексной плоскости продольного волнового
числа h. Поиск
действительных корней уравнений (27), (32), (35), (38) осуществлялся при
фиксированных значениях геометрических и материальных параметров: относительной
диэлектрической проницаемости ![]() , толщины слоя
диэлектрика 2b, периода решетки P и частоты заполнения
, толщины слоя
диэлектрика 2b, периода решетки P и частоты заполнения ![]() .
.
Потери в пластине связаны с потерями в металле и в диэлектрике, соответственно, суммарные потери можно определить из следующего приближенного соотношения [3]:
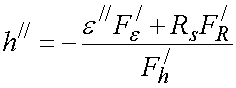 , (39)
, (39)
где ![]() -
мнимая часть комплексной диэлектрической проницаемости диэлектрика
-
мнимая часть комплексной диэлектрической проницаемости диэлектрика ![]() , Rs – поверхностное сопротивление металла,
, Rs – поверхностное сопротивление металла, ![]() - производные функций F, стоящих в левой части
дисперсионных уравнений (27), (32), (35), (38), которые можно получить, разлагая
эти функции в ряд Тейлора по степеням малых величин
- производные функций F, стоящих в левой части
дисперсионных уравнений (27), (32), (35), (38), которые можно получить, разлагая
эти функции в ряд Тейлора по степеням малых величин ![]() и
и ![]() .
.
В результате расчетов
были получены частотные зависимости замедления ![]() и
затухания
и
затухания ![]() для четных E– и H–волн
в структурах с емкостными и индуктивными решетками.
для четных E– и H–волн
в структурах с емкостными и индуктивными решетками.
Исследуем решения дисперсионных уравнений (27), (32), (35), (38).
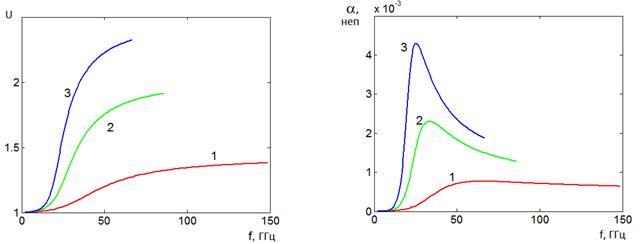
Емкостная решетка, H–волны. На рис.6 приведены частотные
зависимости замедления ![]() (рис.6а) и затухания на длине
волны
(рис.6а) и затухания на длине
волны ![]() (рис.6b), полученные на основе решения уравнения (27) для значений
2b=2мм, P=1мм,
(рис.6b), полученные на основе решения уравнения (27) для значений
2b=2мм, P=1мм, ![]() =0.2 при изменении
относительной диэлектрической проницаемости
=0.2 при изменении
относительной диэлектрической проницаемости ![]() =2,4,6
(кривые 1,2,3, соответственно). Для каждой кривой частота ограничена
критической частотой ближайшего высшего типа волны.
=2,4,6
(кривые 1,2,3, соответственно). Для каждой кривой частота ограничена
критической частотой ближайшего высшего типа волны.
a) замедление b) затухание
Рис. 6. Дисперсионные характеристики Н-волн в пластине с емкостными решетками
Емкостная решетка, Е–волны. Для Е–волн частотные зависимости
замедления ![]() и затухания на длине волны
и затухания на длине волны ![]() , полученные на основе решения уравнения
(32) для тех же значений, что и для Н–волн (2b=2мм, P=1мм,
, полученные на основе решения уравнения
(32) для тех же значений, что и для Н–волн (2b=2мм, P=1мм, ![]() =0.2,
=0.2, ![]() =2,4,6
, кривые 1,2,3), изображены на рисунках 7 a,b.
=2,4,6
, кривые 1,2,3), изображены на рисунках 7 a,b.
a) замедление b) затухание
Рис. 7. Дисперсионные характеристики Е-волн в пластине с емкостными решетками
Для анализа эффективности
управления свойствами волн в диэлектрической пластине с помощью решеток введем
показатель преломления n,
равный относительному замедлению ![]() , где
, где ![]() – замедление в диэлектрическом слое без
решеток.
– замедление в диэлектрическом слое без
решеток.
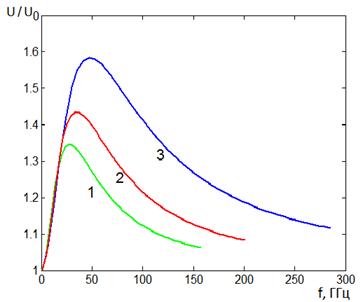
Зависимости показателя
преломления n=![]() от
частоты f для H–волн в емкостной решетке с параметрами P=0.5мм,
от
частоты f для H–волн в емкостной решетке с параметрами P=0.5мм, ![]() =0.2,
=0.2, ![]() =10 при изменении толщины диэлектрической
подложки 2b=0.4мм, 0.3мм, 0.2мм (кривые 1,2,3,
соответственно) приведены на рис.8. Как видно из рисунка, эти зависимости имеет
максимумы. Частота максимума и уровень относительного замедления на этой
частоте зависят от параметров решетки P,
=10 при изменении толщины диэлектрической
подложки 2b=0.4мм, 0.3мм, 0.2мм (кривые 1,2,3,
соответственно) приведены на рис.8. Как видно из рисунка, эти зависимости имеет
максимумы. Частота максимума и уровень относительного замедления на этой
частоте зависят от параметров решетки P, ![]() и параметров
диэлектрической подложки
и параметров
диэлектрической подложки ![]() , 2b.
, 2b.
Рис.8 Зависимости показателя преломления ![]() пластины с емкостными решетками от частоты
пластины с емкостными решетками от частоты
Для Е–волн частотные зависимости показателя преломления имеют такой же вид, как и кривые на рис 8. Положение максимума относительного замедления и его уровень также зависят от параметров пластины. Следует заметить, что частоты максимумов для Е–волн при одинаковых параметрах выше, чем для H–волн.
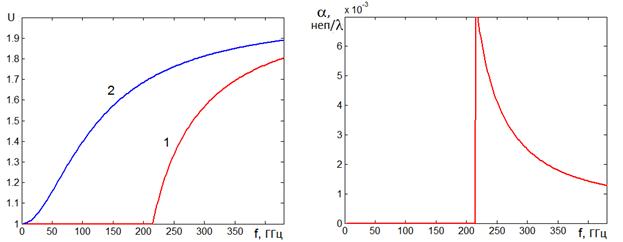
Индуктивная решетка, H–волны. Решение дисперсионного уравнения (35)
для замедления и затухания при значениях параметров ![]() ,
2b=0.4мм, P=0.2мм,
,
2b=0.4мм, P=0.2мм, ![]() =0.2 представлено на
рисунках 9 a,b. Кривые красного цвета соответствуют основному типу волны в
пластине с решетками, кривая синего цвета - волнам в открытом диэлектрическом
слое.
=0.2 представлено на
рисунках 9 a,b. Кривые красного цвета соответствуют основному типу волны в
пластине с решетками, кривая синего цвета - волнам в открытом диэлектрическом
слое.
a) замедление b) затухание
Рис.9 Дисперсионные характеристики Н-волн в пластине с индуктивными решетками
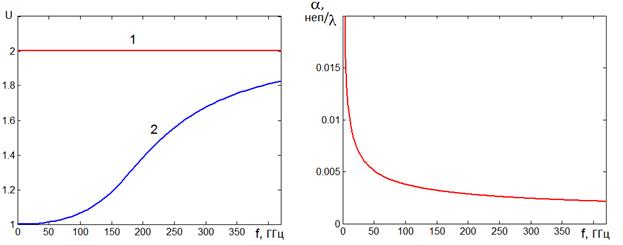
Индуктивная решетка, Е–волны. Частотные зависимости замедления и затухания на длине, полученные для Е-волн при решении уравнения (38) для тех же параметров, что и для Н-волн, представлены на рис. 10 a,b. Обозначения и цвет кривых аналогичны рис. 9.
a) замедление b) затухание
Рис. 10. Дисперсионные характеристики E-волн в пластине с индуктивными решетками
Приведенные выше характеристики различных волн пластины с индуктивными и емкостными решетками позволяют сделать ряд важных выводов относительно эффективности управления параметрами волн диэлектрического слоя с помощью решеток разных типов.
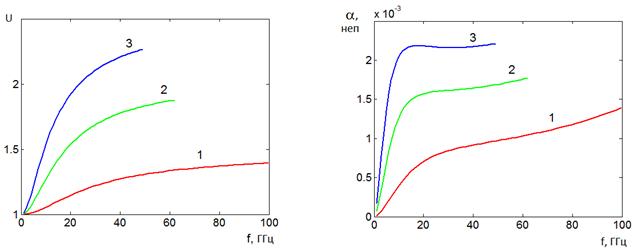
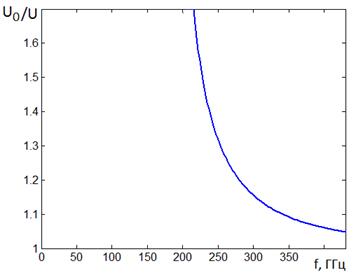
Проанализируем полученные дисперсионные характеристики пластины с индуктивными решетками. Рассмотрим зависимость относительного замедления или показателя преломления для Н-волн от частоты, приведенную на рис. 11.
Рис. 11. Частотная зависимость показателя преломления Н-волны в пластине с индуктивными решетками
Как видно из рис. 11, кривая не имеет локального максимума в отличие от кривых, соответствующих емкостным решеткам (см. рис. 8) и при значениях показателя преломления n>1.2 обладает значительной крутизной. Поэтому использование индуктивных решеток для управления Н – волнами оказывается менее эффективным, чем емкостных решеток в силу того, что они явно уступают им по полосе рабочих частот, в которой реализуемый коэффициент преломления близок к требуемому значению. Кроме того, как следует из рис. 9b и рис. 6b затухание этого типа волны в структуре с индуктивными решетками также заметно превосходит затухание в пластине с емкостными решетками. Суммируя сказанное выше, мы можем сделать вывод о том, что емкостные решетки являются более эффективным инструментом управления параметрами Н – волн, чем индуктивные.
Рассмотрим далее
возможность управления Е-волнами с помощью индуктивных решеток (см.
рис. 10
а). Оказалось, что замедление Е – волны практически не зависит от параметров
решетки ![]() и очень близко к
и очень близко к ![]() .
Однако, такое замедление можно получить без помощи решеток, просто полностью
металлизируя поверхности пластины. В этом случае мы получаем плоский волновод с
основной Т – волной, имеющей коэффициент замедления равный
.
Однако, такое замедление можно получить без помощи решеток, просто полностью
металлизируя поверхности пластины. В этом случае мы получаем плоский волновод с
основной Т – волной, имеющей коэффициент замедления равный ![]() .
.
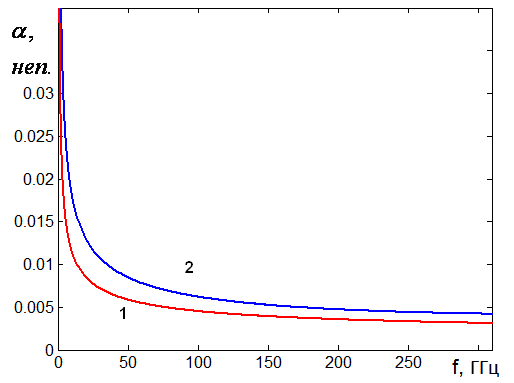
Рис. 12. Частотная зависимость затухания в плоском волноводе и в пластине с решетками
Следует отметить, что с точки зрения затухания плоский волновод предпочтительнее пластины с решетками. Данный вывод можно сделать, анализируя кривые, показанные на рис. 12. Кривые 1 и 2 соответствуют затуханию на длину волны Т - волны плоского волновода и Е – волны пластины с индуктивными решетками. Видно, что затухание в плоском волноводе меньше, чем в исследуемой структуре.
Наконец, реализация решетки с малым периодом часто представляет достаточно сложную с технологической точки зрения задачу. Поэтому полная металлизация поверхности, дающая тот же результат, представляется лучшим техническим решением.
Таким образом, проведенный анализ решений дисперсионных уравнений для Н – и Е – волн в пластинах с емкостными и индуктивными решетками показал, что емкостные решетки обладают большими возможностями с точки зрения реализации структур с заданным коэффициентом замедления и поэтому далее мы будем рассматривать только емкостные решетки.
7. Постановка задачи оптимизация двумерных сред
На следующем этапе выполним оптимизацию анализируемых структур с помощью описанных выше математических моделей. При выполнении этапа будем следовать методике, которая изложена в работах [16,17]. В соответствии с ней нам необходимо сформулировать ряд характеристик оптимизируемых структур. Среди них важнейшее место занимают показатели качества. Показатель качества является количественной характеристикой, которая монотонно меняется при изменении качества рассматриваемого объекта.
Для формулировки
показателей качества нам необходимо предварительно сформулировать функцию,
которую выполняют анализируемые структуры. Как отмечалось в первом разделе,
основной решаемой с их помощью задачей, является создание областей
диэлектрической пластины, в которых свойства волн отличаются от свойств волн в
исходной, то есть свободной от решеток пластине. При этом мы может отметить,
что чем сильнее указанное отличие, тем больше мы имеем возможностей по
управлению свойствами волн. Выше для описания различия свойств волн мы
использовали коэффициент преломления ![]() . Будем рассматривать
его, как показатель качества, описывающий эффективность управления параметрами
волн пластины с помощью периодических решеток.
. Будем рассматривать
его, как показатель качества, описывающий эффективность управления параметрами
волн пластины с помощью периодических решеток.
Из результатов разд. 6
видно, что коэффициент преломления достаточно сильно зависит от частоты.
Поэтому очевидным показателем качества является полоса частот ![]() , в пределах которой он остается близким к
некоторому заданному значению. Для удобства будем использовать также
относительную полосу рабочих частот, равную отношению
, в пределах которой он остается близким к
некоторому заданному значению. Для удобства будем использовать также
относительную полосу рабочих частот, равную отношению ![]() к
центральной частоте полосы
к
центральной частоте полосы ![]() .
.
Также показателем
качества можно считать параметр, характеризующий тепловые потери в структуре.
Таким параметром может служить затухание ![]() .
Однако, непосредственно использовать его неудобно, так как введенные выше
показатели увеличиваются при улучшении качества, а затухание уменьшается.
Поэтому будем использовать далее добротность структуры
.
Однако, непосредственно использовать его неудобно, так как введенные выше
показатели увеличиваются при улучшении качества, а затухание уменьшается.
Поэтому будем использовать далее добротность структуры ![]() :
:
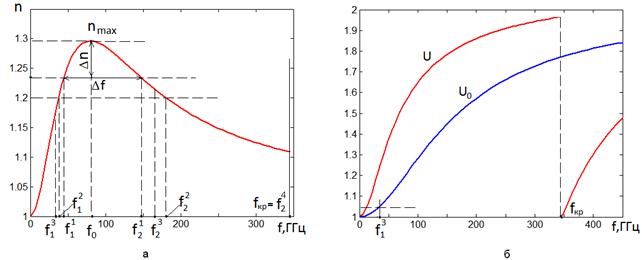
Рассмотрим далее процедуру определения введенных показателей качества с помощью представленных выше моделей. На рис. 13 а показана типичная частотная зависимость коэффициента преломления. Качественно она одинакова для Н – и Е – волн в пластине с емкостными решетками.
Рис. 13. Выбор центральной частоты и полосы рабочих частот
С точки зрения расширения
полосы рабочих частот и увеличения коэффициента преломления ![]() целесообразно работать в окрестности его
максимума, который достигается на частоте
целесообразно работать в окрестности его
максимума, который достигается на частоте ![]() (см.
рис. 13 а). Для оптимизации будем использовать как показатель качества
(см.
рис. 13 а). Для оптимизации будем использовать как показатель качества ![]() , описывающий эффективность управления
свойствами волны значение коэффициента преломления на указанной частоте:
, описывающий эффективность управления
свойствами волны значение коэффициента преломления на указанной частоте:
![]() .
.
Аналогично, будем
использовать как показатель качества ![]() , описывающий тепловые
потери в структуре значение добротности на частоте
, описывающий тепловые
потери в структуре значение добротности на частоте ![]() :
:
![]() .
.
Определим далее
показатель качества ![]() , характеризующий диапазонные
свойства рассматриваемых структур. Для этого потребуем выполнения ряда условий,
ограничивающих полосу рабочих частот.
, характеризующий диапазонные
свойства рассматриваемых структур. Для этого потребуем выполнения ряда условий,
ограничивающих полосу рабочих частот.
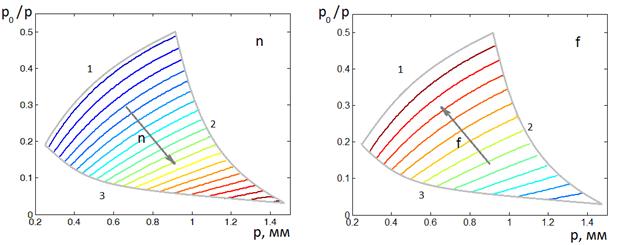
Первым из них является
ограничение на относительное изменение коэффициента замедления ![]() в полосе рабочих частот, которое не
должно превышать некоторой малой величины
в полосе рабочих частот, которое не
должно превышать некоторой малой величины ![]() :
:
Можно показать, что при ![]() максимальное отклонение фазы на краю
простейшей однофокальной линзы, выполненной из двумерных метаматериалов, в
полосе частот не превысит величины
максимальное отклонение фазы на краю
простейшей однофокальной линзы, выполненной из двумерных метаматериалов, в
полосе частот не превысит величины ![]() .
.
Из рис. 13 видно, что
условие (41) задает границы полосы рабочих частот ![]() и
и ![]() . Нижние индексы здесь и далее
соответствуют нижней и верхней граничным частотам. Верхний индекс соответствует
разным факторам, определяющим полосу частот.
. Нижние индексы здесь и далее
соответствуют нижней и верхней граничным частотам. Верхний индекс соответствует
разным факторам, определяющим полосу частот.
Наряду с неравенством (41) существуют другие причины, ограничивающие полосу рабочих частот. К их числу относится следующее неравенство:
где ![]() - минимально
допустимое значение коэффициента преломления. Структуры, имеющие коэффициент
преломления меньший
- минимально
допустимое значение коэффициента преломления. Структуры, имеющие коэффициент
преломления меньший ![]() не представляют практического
интереса. Выполнение неравенства (42) приводит к появлению граничных частот
не представляют практического
интереса. Выполнение неравенства (42) приводит к появлению граничных частот ![]() и
и ![]() .
.
Также мы должны удалить из рассмотрения структуры с очень малым замедлением. В первую очередь, это относится к замедлению волн пластины без решеток, которое всегда меньше замедления волны в структуре с решетками (см. рис. 13 б). Структуры с малым замедлением основной волны неустойчивы, так как такая волна легко связывается на нерегулярностях с волнами свободного пространства и излучается. Поэтому потребуем:
Неравенство (43) порождает
нижнюю граничную частоту ![]() (см. рис. 13 а и б).
(см. рис. 13 а и б).
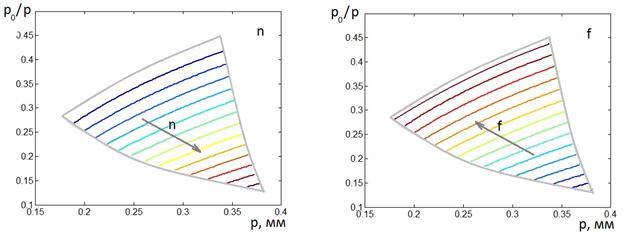
Далее необходимо отметить,
что применение периодических решеток для создания двумерных сред допустимо не
при всех сочетаниях параметров и частот. Мы должны использовать только решетки
с периодом ![]() меньшим половины длины
меньшим половины длины ![]() волны:
волны:
Только при выполнении
условия (44) пластину с решетками можно рассматривать как однородную среду.
Если неравенство (44) нарушается, то в структуре начинают сказываться эффекты,
связанные с ее периодичность: полосы запирание, излучение и т.д. Выполнение
неравенства (44) дает нам верхнюю граничную частоту ![]() .
.
Естественным требованием
к исследуемым структурам является требование одноволнового режима, в котором в
них существует одна распространяющаяся волна Н или Е – типа. Пусть ближайший
высший тип волны имеет критическую частоту ![]() (см.
рис. 13 б), Будем использовать ее в качестве еще одной верхней граничной
частоты
(см.
рис. 13 б), Будем использовать ее в качестве еще одной верхней граничной
частоты ![]() .
.
Теперь мы можем
определить нижнюю и верхнюю граничные частоты ![]() :
:
![]() .
.
С учетом соотношений (45)
определяем полосу рабочих частот ![]()
![]()
и относительную полосу рабочих частот
![]()
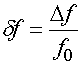 ,
,
которую будем использовать далее как
показатель качества ![]() :
:
Корректная постановка задачи
оптимизации [16] предусматривает формулировку свободных параметров структуры,
варьируя которые мы будем добиваться максимально возможного увеличения всех
показателей качества. К их числу относятся: P- период решетки, ![]() -
коэффициент заполнения, 2b
- толщина подложки,
-
коэффициент заполнения, 2b
- толщина подложки, ![]() - диэлектрическая проницаемость
диэлектрика.
- диэлектрическая проницаемость
диэлектрика.
Оптимизация будет
выполняться при условии фиксированной центральной частоты рабочего диапазона ![]() . Будем также считать постоянными
величинами: толщину металлической пленки
. Будем также считать постоянными
величинами: толщину металлической пленки ![]() =10мкм и
тангенс угла потерь в диэлектрике
=10мкм и
тангенс угла потерь в диэлектрике ![]() .
.
Ограничения на параметры структуры зададим из технологических соображений:
![]() ,
,
![]() ,
,
Введенная выше
совокупность показателей качества позволяет сравнивать разные варианты
выполнения двумерных сред. Для сравнения используется критерий Парето или
безусловный критерий предпочтения (БКП). Его формулировка приводится ниже.
Пусть мы сравниваем два объекта (технических решения, устройства и т.д.),
которые характеризуются показателями качества: ![]() и
и ![]() . Верхний индекс соответствует номеру
сравниваемого технического решения. Техническое решение 1 считается лучшим по
сравнению с решением 2 если все его показатели качества больше показателей
качества решения 2. Аналогично техническое решение 1 хуже, если все его
показатели качества меньше. Наконец, технические решения 1 и 2 называются
несравнимыми, если часть показателей качества одного из них больше, а другая
часть меньше показателей качества другого.
. Верхний индекс соответствует номеру
сравниваемого технического решения. Техническое решение 1 считается лучшим по
сравнению с решением 2 если все его показатели качества больше показателей
качества решения 2. Аналогично техническое решение 1 хуже, если все его
показатели качества меньше. Наконец, технические решения 1 и 2 называются
несравнимыми, если часть показателей качества одного из них больше, а другая
часть меньше показателей качества другого.
Целью оптимизационной задачи в постановке описанной выше является применение БКП к полному множеству возможных технических решений и выделение из него части, состоящей из несравнимых решений. Такая процедура получила название векторной оптимизации [16]. Часто ее также называют оптимизацией Парето по имени выдающегося итальянского математика, исследовавшего ее с точки зрения теории множеств.
Векторная оптимизация, в отличие от скалярной, использующей одну целевую функцию, дает в качестве результата не одно наилучшее решение, а множество решений, которое принято называть множеством нехудших решений (МНХ) или множеством Парето. Указанное множество состоит из несравнимых технических решений. Решения, которые не входят в МНХ безусловно хуже решений входящих в него. Ценность МНХ состоит в том, что оно дает наиболее объективную картину противоречия между показателями качества, когда улучшение одного из них приводит к ухудшению других. Скалярная оптимизация в принципе не дает такой возможности.
8. Методика построения МНХ
Рассмотрим методику
построения МНХ для исследуемой структуры. На первом этапе осуществляется расчет
множества вариантов, удовлетворяющих ограничениям на параметры (44), (47). При
этом одновременно осуществляется его дискретизация, вследствие того, что
расчеты проводятся для набора фиксированных значений параметров ![]() . Получаемое в результате множество
принято (см. [16]) называть множеством строго допустимых решений (МСД). На
следующем этапе из МСД по критерию Парето удаляются худшие решения. Оставшаяся
часть составляет искомое МНХ.
. Получаемое в результате множество
принято (см. [16]) называть множеством строго допустимых решений (МСД). На
следующем этапе из МСД по критерию Парето удаляются худшие решения. Оставшаяся
часть составляет искомое МНХ.
Расчет МСД должен проводиться в конечном диапазоне изменения параметров структуры. Неравенства (44) и (47) не позволяют ограничить все свободные параметры с двух сторон. Их необходимо дополнить ограничениями, которые не имеют принципиального характера, в отличие от соотношений (44) и (47), но необходимы для выполнения численных расчетов:
![]() ,
, ![]() .
.
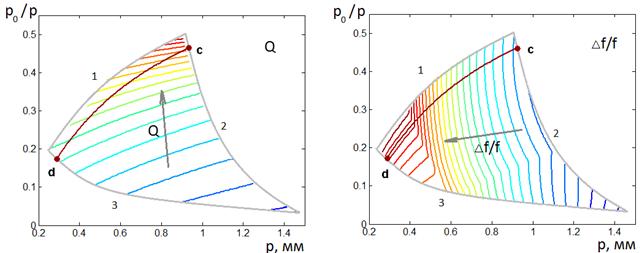
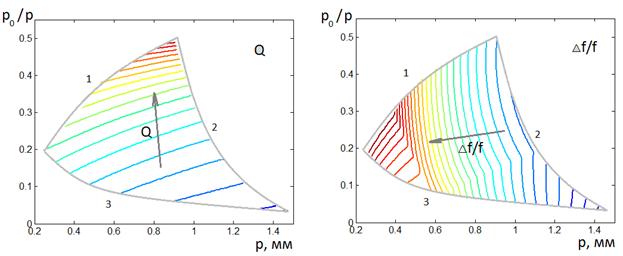
На рис. 14 в представлены
результаты расчета показателей качества для Н – волн в виде линий уровня n, Q, ![]() на плоскости двух
переменных параметров: периода решетки P и коэффициента заполнения
на плоскости двух
переменных параметров: периода решетки P и коэффициента заполнения ![]() , при
фиксированных значениях параметров подложки (
, при
фиксированных значениях параметров подложки (![]() =4 и 2b=0.1 мм). На рис. 14 a изображены линии уровня показателя
преломления n , на рис. 14
b –линии уровня рабочей частоты
=4 и 2b=0.1 мм). На рис. 14 a изображены линии уровня показателя
преломления n , на рис. 14
b –линии уровня рабочей частоты ![]() , на рис. 14 c - добротности Q , на рис. 14 d – относительной
полосы частот
, на рис. 14 c - добротности Q , на рис. 14 d – относительной
полосы частот ![]() . Красный цвет линий
соответствует максимальным значениям уровня величин, синий цвет – минимальным.
. Красный цвет линий
соответствует максимальным значениям уровня величин, синий цвет – минимальным.
Как видно из рисунка 14, область решений ограничена кривыми 1,2,3. Границе 1 соответствует минимальное значение показателя преломления n=1.2, граница 2 определяется ограничениями (43), (44), граница 3 обусловлена минимальными значениями P и P0.
a) b)
c) d)
Рис. 14.
Линии уровня показателей качества n, Q,
![]() и рабочей
и рабочей ![]() ,
Н-волны
,
Н-волны
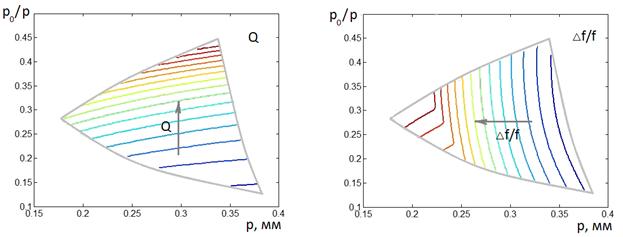
Аналогичные линии уровня
для Е-волн представлены на рис. 15 a–d для тех же значений параметров
подложки 2b=0.1 мм, ![]() =4.
=4.
a) b)
c) d)
Рис. 15. Линии уровня показателей
качества n, Q, ![]() и рабочей частоты
и рабочей частоты ![]() , Е-волны
, Е-волны
Из рис. 14 а,b можно сделать интересный вывод,
который позволил нам существенно упростить процедуру поиска МНХ. Оказалось, что
на плоскости параметров P
и ![]() линии постоянного уровня частоты
линии постоянного уровня частоты ![]() совпадают с линиями постоянного уровня
показателя преломления n.
Таким образом, фиксируя частоту
совпадают с линиями постоянного уровня
показателя преломления n.
Таким образом, фиксируя частоту ![]() , мы можем получить
зависимости одного показателя качества, например, Q от другого
, мы можем получить
зависимости одного показателя качества, например, Q от другого ![]() при постоянной
величине третьего n.
при постоянной
величине третьего n.
На рис. 16 поясняется
методика построения зависимости ![]() путем наложения линии
уровня постоянных
путем наложения линии
уровня постоянных ![]() и
и ![]() (кривые
(кривые
![]() ) на семейство линий уровня
) на семейство линий уровня ![]() и
и ![]() .
.
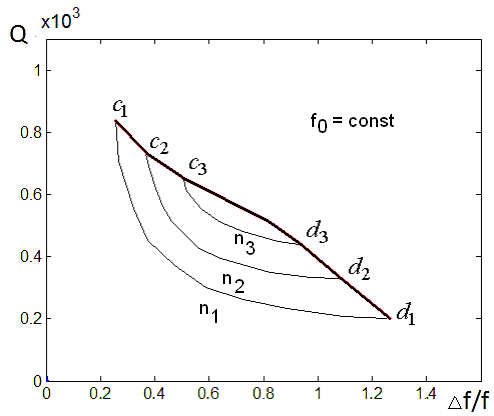
На рис. 17 качественно
показаны получаемые при этом кривые. На каждой кривой значения показателей
качества меняются от крайней точки ![]() до крайней точки
до крайней точки ![]() .
.
Рис. 16. Построение зависимостей ![]() от
от ![]() при
постоянных
при
постоянных ![]() и
и ![]()
Рис. 17.
Построение части МНХ при постоянном параметре ![]()
Кривые, соответствующие
разным номерам ![]() , получены для разных
фиксированных значений
, получены для разных
фиксированных значений ![]() и
и ![]() , а
также фиксированного значения
, а
также фиксированного значения ![]() и разных значений
и разных значений ![]() . Следует отметить, что на практике
диэлектрическую проницаемость менять непрерывно весьма сложно в силу
ограниченного набора приемлемых материалов с достаточно малыми потерями. В
миллиметровом диапазоне, например, тангенс угла диэлектрических потерь близкий
к
. Следует отметить, что на практике
диэлектрическую проницаемость менять непрерывно весьма сложно в силу
ограниченного набора приемлемых материалов с достаточно малыми потерями. В
миллиметровом диапазоне, например, тангенс угла диэлектрических потерь близкий
к ![]() имеют такие материалы как поликор и кварц
с диэлектрической проницаемостью
имеют такие материалы как поликор и кварц
с диэлектрической проницаемостью ![]() и
и ![]() соответственно. Поэтому имеет смысл
проводить поиск МНХ для определенных значений
соответственно. Поэтому имеет смысл
проводить поиск МНХ для определенных значений ![]() ,
например, 4 и 10. При этом толщину подложки
,
например, 4 и 10. При этом толщину подложки ![]() допустимо
изменять непрерывно. Поэтому мы можем считать, что каждой кривой на рис. 17
соответствует заданное значение толщины подложки
допустимо
изменять непрерывно. Поэтому мы можем считать, что каждой кривой на рис. 17
соответствует заданное значение толщины подложки ![]() .
.
Множество, показанное на
рис. 17, соответствует фиксированной центральной частоте ![]() .
Из этого множества нам необходимо выбрать нехудшие решения с помощью БКП.
Нетрудно увидеть, что за исключением ряда специальных случаев все решения
оказываются нехудшими, так как большим значениям показателя качества
.
Из этого множества нам необходимо выбрать нехудшие решения с помощью БКП.
Нетрудно увидеть, что за исключением ряда специальных случаев все решения
оказываются нехудшими, так как большим значениям показателя качества ![]() соответствуют кривые, располагающиеся
ближе к началу координат. Специальным случаям, о которых говорилось выше,
соответствуют изломы линий уровня на рис. 14,15 д. Они рассматриваются с
помощью БКП, который позволяет устранить из МСД худшие варианты.
соответствуют кривые, располагающиеся
ближе к началу координат. Специальным случаям, о которых говорилось выше,
соответствуют изломы линий уровня на рис. 14,15 д. Они рассматриваются с
помощью БКП, который позволяет устранить из МСД худшие варианты.
9. Анализ МНХ
Отметим, что диапазон
изменения центральной частоты ![]() ограничен с двух
сторон (см. рис. 14 б, рис. 15 б). Поэтому мы можем записать следующее
неравенство:
ограничен с двух
сторон (см. рис. 14 б, рис. 15 б). Поэтому мы можем записать следующее
неравенство:
![]() ,
,
где fmax, , fmin - граничные значения, зависящие от
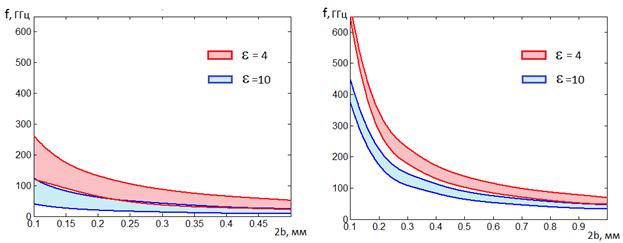
параметров подложки ![]() и 2b. На рисунках 18 a,б представлены области изменения центральных частот рабочих
диапазонов для Н– и Е–волн, соответственно, в зависимости от толщины подложки 2b для двух значений диэлектрической
проницаемости
и 2b. На рисунках 18 a,б представлены области изменения центральных частот рабочих
диапазонов для Н– и Е–волн, соответственно, в зависимости от толщины подложки 2b для двух значений диэлектрической
проницаемости ![]() и
и ![]() .
.
a) H-волны b) Е-волны
Рис. 18. Зависимости граничных значений частоты от толщины подложки
Из рис. 18 видно, что Е –
волны позволяют продвинуться в область высоких частот сильнее, чем Н – волны
при тех же значениях толщины подложки ![]() .
.
Приведем результаты
расчетов МНХ для двух значений диэлектрической проницаемости ![]() и
и ![]() .
Выберем фиксированные значения частоты
.
Выберем фиксированные значения частоты ![]() . Для
Н-волн представим результаты на двух частотах:
. Для
Н-волн представим результаты на двух частотах: ![]() =50 ГГц
и 100ГГц, для Е-волн – на трех частотах: 50 ГГц, 100 ГГц и 200 ГГц.
=50 ГГц
и 100ГГц, для Е-волн – на трех частотах: 50 ГГц, 100 ГГц и 200 ГГц.
Область решений для
показателей качества изобразим в виде линий постоянного уровня показателя
преломления n на плоскости
переменных: добротности Q
и относительной полосы рабочих частот ![]() , где
каждому постоянному значению n
соответствует фиксированное значение толщины подложки 2b.
, где
каждому постоянному значению n
соответствует фиксированное значение толщины подложки 2b.
a) b)
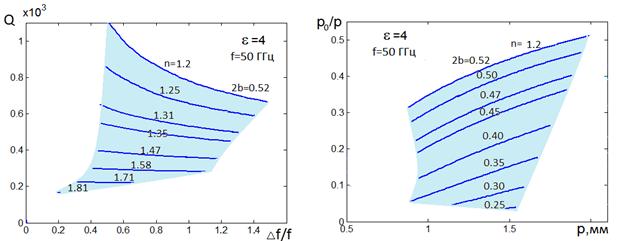
Рис. 19. Н-волны, ![]() =4, f= 50ГГц
=4, f= 50ГГц
a) b)
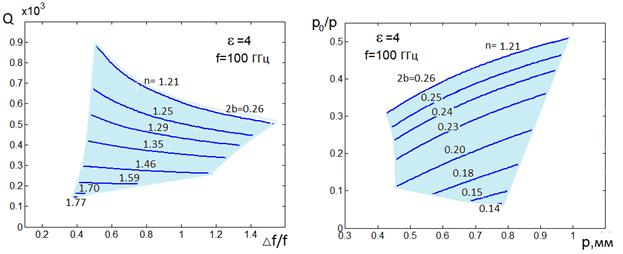
Рис. 20. Н-волны, ![]() =4, f= 100ГГц
=4, f= 100ГГц
a) b)
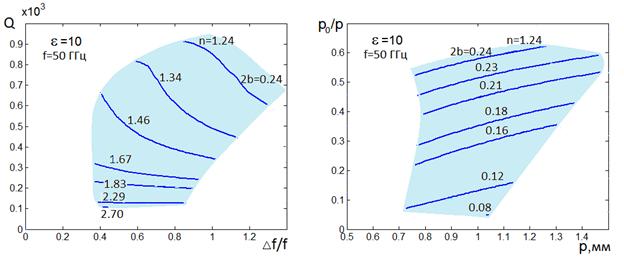
Рис. 21. Н-волны, ![]() =10, f=50 ГГц
=10, f=50 ГГц
Результаты оптимизации по
критерию Парето для Н-волн приведены на рис. 19-21. На рис.
19-21 a изображены МНХ в пространстве
показателей качества, а на рис. 19-21 b – области изменения соответствующих геометрических параметров P, ![]() , 2b. Для Е-волн результаты оптимизации
приведены на рис. 22 – 27.
, 2b. Для Е-волн результаты оптимизации
приведены на рис. 22 – 27.
Анализ МНХ показывает,
что все три показателя качества как для Е – волн, так и для Н – волн находятся
в состоянии технического противоречия, так как улучшение одного из них приводит
к ухудшению, по крайней мере, одного из двух оставшихся. При больших
коэффициентах преломления указанное противоречие не является глубоким,
поскольку увеличение ![]() может происходить при
постоянном
может происходить при
постоянном ![]() почти без уменьшения добротности
почти без уменьшения добротности ![]() . При уменьшении
. При уменьшении ![]() увеличение
увеличение
![]() возможно в существенно больших пределах,
но уже за счет заметного снижения добротности.
возможно в существенно больших пределах,
но уже за счет заметного снижения добротности.
Кривые на рис.
19 – 27 б
решают задачу параметрического синтеза исследуемых структур, поскольку с их
помощью можно находить параметры структуры, которые реализуют заданную
совокупность показателей качества. Например, если мы с помощью рис.
19 а
выбираем приемлемые значения показателей качества, то с помощью рис. 19 б мы
можем определить значения ![]() и
и ![]() , при которых выбранная совокупность
показателей качества будет реализована.
, при которых выбранная совокупность
показателей качества будет реализована.
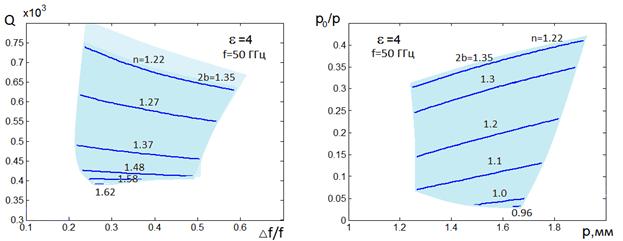
a) b)
Рис. 22. Е-волны, ![]() =4, f=50ГГц
=4, f=50ГГц
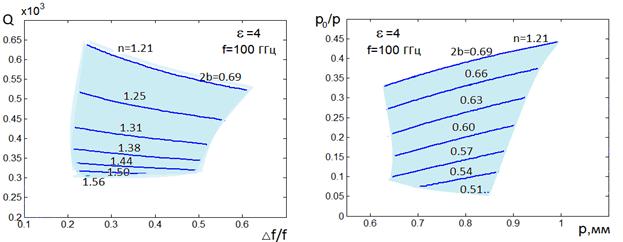
a) b)
Рис. 23. Е-волны, ![]() =4, f=100ГГц
=4, f=100ГГц
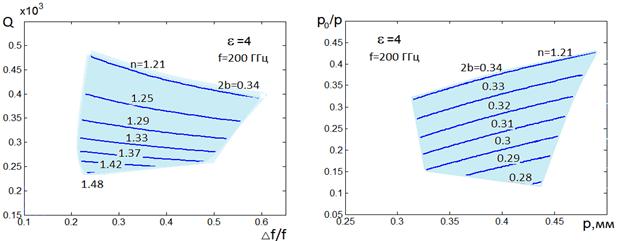
a) b)
Рис. 24. Е-волны, ![]() =4, f=200ГГц
=4, f=200ГГц
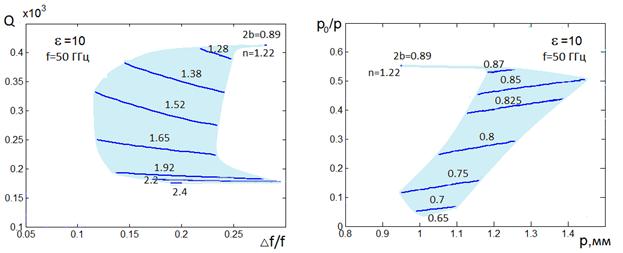
a) b)
Рис. 25. Е-волны, ![]() =10, f=50ГГц
=10, f=50ГГц
a) b)
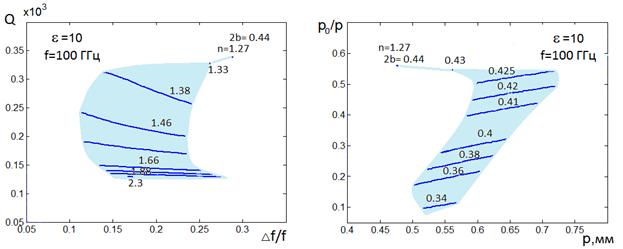
Рис.26 Е-волны, ![]() =10, f=100ГГц
=10, f=100ГГц
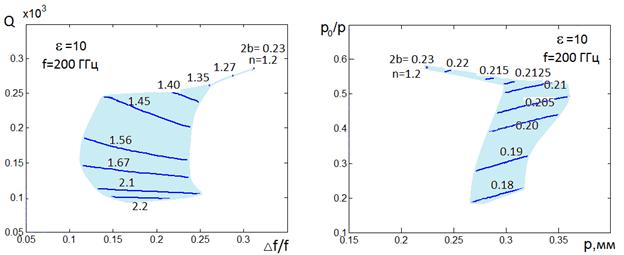
a) b)
Рис. 27. Е-волны, ![]() =10, f=200ГГц
=10, f=200ГГц
Приведем пример сравнения
характеристик пластин с емкостными решетками с диэлектрическими проницаемостями
подложки ![]() =4 и
=4 и ![]() =10,
реализующих показатель преломления n=1.5 на частоте f=50ГГц
.
=10,
реализующих показатель преломления n=1.5 на частоте f=50ГГц
.
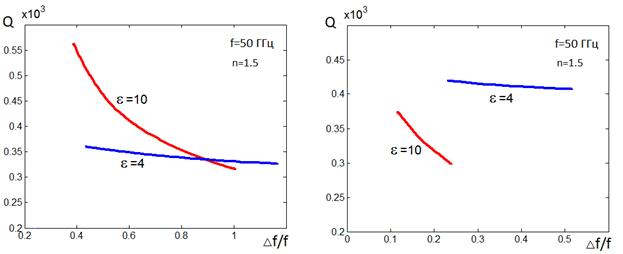
a) H –волны b) Е-волны
Рис. 28. Паретооптимальные решения для показателей качества пластин с емкостными решетками
Как видно из рисунка, при
использовании Н-волн на заданной частоте лучшие показатели качества реализуются
при ![]() =10 до значений
относительной полосы частот
=10 до значений
относительной полосы частот ![]() <0.9. При
использовании Е-волн при заданных параметрах лучшими показателями качества
обладает пластина с
<0.9. При
использовании Е-волн при заданных параметрах лучшими показателями качества
обладает пластина с ![]() =4.
=4.
Работа выполнена при поддержке Российского фонда фундаментальных исследований, проект №12-08-12003-офи_м.
1. Взятышев В.Ф., Нарытник Т.Н., Рябов Б.А., Емельяненков Б.Н., Банков С.Е. // Обзоры по электронной технике. - М.: ЦНИИ “Электроника”, 1985, Вып. 13, 62 с.
2. Нефедов Е.И., Фиалковский А.Т. Полосковые линии передачи. М.: Наука. 1980.
3. Взятышев В.Ф. Диэлектрические волноводы. М.: Сов. Радио. 1970.
4. Унгер Г.Г. Планарные и волоконные оптические волноводы. М.: Мир, 1980.
5. Маркузе Д. Оптические волноводы. М: Мир. 1974.
6. Банков С.Е. Бугрова Т.И. // РЭ. 1993. Т. 38. №1. С. 73.
7. Sihvola A. // Metamaterials. 2007. V.1. N1. P.2.
8. Уолтер К. Антенны бегущей волны. М.: Энергия. 1970.
9. Банков С.Е. Электродинамические особенности металлического волновода с продольной импедансной вставкой // В кн.: Доклады V Московской городской конференции молодых ученых и специалистов.- М.: МЭИ. 1983. С. 27.
10. Банков С.Е. Бугрова Т.И. Собственные волны планарной металло - диэлектрической решетки // РЭ. 1993. №1. С. 73-80.
11. Банков С.Е., Левченко И.В. Эквивалентные граничные условия для ленточной частопериодической решетки на границе раздела двух сред // РЭ. 1988. Т. 33. №10. С. 2045-2050.
12. Конторович М.И., Астрахан М.И., Акимов В.П., Ферсман Г.А. Электродинамика сетчатых структур. М.: Радио и связь. 1987.
13. Нефедов Б.И., Сивов А.Н Электродинамика периодических структур. М.: Наука. 1977.
14. Марков Г.Т., Чаплин А.Ф. Возбуждение электромагнитных волн. М.: Радио и связь. 1983.
15. Нобл Б. Метод Винера-Хопфа. // М.: Изд-во иностр. лит. 1962.
16. Гуткин Л.С. Оптимизация радиоэлектронных устройств по совокупности показателей качества. М.: Сов. радио, 1975.
17. Ногин В.Д. Принятие решений в многокритериальной среде: количественный подход. – М.: ФИЗМАТЛИТ, 2002. – 144 с.