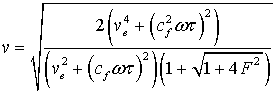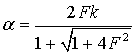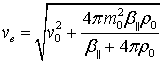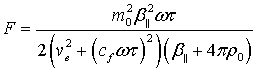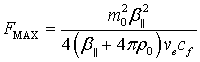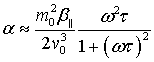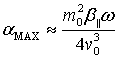Ultrasonic absorption in magnetic nanofluids with magnetic field relaxation
I. E. Ovchinnikov
Moscow State University of Information Technologies, Radioengineering and Electronics
The paper is received on March 4, 2015
Abstract: Analysis has been provided for the experimental data on ultrasonic absorption in magnetic nanofluids. It was shown for magnetic nanofluids that experimental data for peaks of ultrasonic absorption coefficient can be explained using the process of magnetic field relaxation to its equilibrium value in the model of magnetic fluid with frozen-in magnetization.
Key words: magnetic field relaxation, magnetic nanofluid, ultrasonic absorption.
1. Introduction
Magnetic fluids are used in various branches of science and technology [1, 2]. In the first half of the twentieth century an unstable magnetic suspensions were in use for investigation of ferromagnetism, and in these suspensions the particle size was about one micron [3-5]. With development of technology the magnetic nanoparticles were obtained and applied in magnetic fluids [6]. So the magnetic nanofluid consists of a carrier liquid (water, dodecane, kerosene, etc.), magnetic nanoparticles and small auxiliary surfactant (often, oleic acid) [2, 7, 8]. At present, magnetic nanoparticles of magnetite are in use in general. Magnetic nanoparticles are coated by molecules of surfactant, which prevents adhesion of them. Because of this, the magnetic nanofluids are stable and there is no coagulation. The exposure of the magnetic field strongly influences the motion of magnetic nanoparticles, but the magnetic nanofluid is stable and it is a continuous medium for the propagation of small-amplitude ultrasound. Hence, magnetic field can affect the elasticity of the magnetic nanofluids, which changes the ultrasonic velocity in experiments [2, 7, 8]. Also, magnetic field may affect the ultrasonic absorption coefficient. With the rate of magnetic field from 0 to 90 kA/m a peak ultrasonic absorption coefficient shows an increase of 0.75 cm-1, which is quite a lot. These results were obtained at ultrasonic frequency 3.6 MHz [7]. At a close frequency 4.37 MHz ultrasonic absorption coefficient equals 0.185 cm-1 under 6 kA/m and 0.17 cm-1 under 160 kA/m in parallel propagation to static magnetic field [8]. So, the peak absorption coefficient value is larger than the absorption coefficient under static magnetic field. The purpose of this article is to explain the significant increase in the ultrasonic absorption coefficient using the relaxation process of the magnetic field to its equilibrium value.
2. Analysis of experimental data on ultrasonic absorption in magnetic nanofluids
In [9,
10] the
system of equations was obtained for a non-conducting magnetic fluid with frozen-in magnetization with
taking into account the relaxation process of the magnetic field
to its equilibrium value. In [11] for this model of magnetic fluid the sound propagation was
considered in
parallel to external homogeneous static magnetic field. There are expressions for the sound velocity
and the absorption coefficient 
[11]:
|
|
(1) |
|
|
(2) |
where
|
|
(3) |
|
|
(4) |
|
|
|
,
– relaxation time of the
magnetic field to its equilibrium value in a magnetic fluid, 
– magnetoelastic parameter, 
– unperturbed specific magnetization value, 
– unperturbed magnetization value, 
– unperturbed magnetic fluid density, 
– sound velocity in magnetic
fluid without exposure of external magnetic field, 
– sound cyclic frequency, 
– sound wave number.
The unitless
parameter 
(5) depends on the and 
resonantly, so in the cases
of 
and 
, 
and 
it tends to zero, and when 
in the maximum it takes
the form [11]:
|
|
(6) |
In the case of 
the sound velocity
(1) 
equals the sound wave velocity (3) in an ideal
magnetic fluid with equilibrium magnetization in the propagation parallel to the
magnetic field [12]. In the case of 
the sound velocity (1) 
equals the fast magnetoacoustic
wave velocity (4) in an ideal magnetic fluid with frozen-in magnetization under
parallel propagation to the magnetic field [2, 12].
For the magnetic nanofluid
EMG – 605 [2, 7, 8,
12] 
g/cm3 and the parameter maximum 
(6) numerical value
approximately equals 
. Here, inequality 
was used, which is confirmed by
comparing the theoretical calculations with experimental data [2,
11, 12], so
in linear approximation the sound absorption coefficient (2) is
|
|
(7) |
With constant cyclic frequency
investigating the dependence
on for (7), so with 
the maximum value of
the absorption coefficient is approximately equal to [11]:
|
|
(8) |
In the case of the absorption coefficient
is a small quantity relative to 
, i. e. 
.
In the case of the absorption coefficient
is also a small quantity relative to , i. e. 
.
In [13] it was shown for
the magnetic nanofluid EMG – 605 that in the interval for the magnetic field
of 30 kA/m to 120 kA/m the theoretical dependence 
was confirmed with good
accuracy. So this theory [9, 10] can be used to explain ultrasonic absorption
peaks in [7]. In [13] 
increased approximately 100 times, and 
increased approximately 6 times on the mentioned
above interval. In [13] analytical functions were used to approximate the
experimental data on the change in the ultrasound velocity in the magnetic nanofluids with dependence on the exposure time of the static magnetic field. It was shown that relaxation time tends to zero then the
exposure time is small, and the relaxation product 
can be approximated
by this exponential dependence 
then the exposure time 
is sufficiently large,
where the characteristic times 
and 
are approximately about hour
[11]. So, according to technique of mathematical estimation [14], this
relaxation time is a fast function in formula (7), and the composition
is a slow function then the factor 
depends on the relaxation time resonantly. In experiments [7] the cyclic frequency is constant and the magnetic field
is increased slowly from time to time. Therefore in Fig. the peak theoretical
values (circles) were calculated by the formula (8). The sound velocity in
magnetic fluid without exposure of external magnetic field 
cm/s, the numerical values of magnetoelastic parameter and specific
magnetization 
were taken from [13]. In Fig. 1 the experimental data (triangles) are the numerical values of
ultrasonic absorption maxima from Fig. 2 in [7] for sweep times 20, 40, 60, 120 and 200 minutes. The theoretical values are a little more than the experimental data. It is
good, because the theoretical calculations
were made under condition . Moreover, for 90 kA/m theoretical value (8) 
cm-1 is larger than the
maximum experimental value, which is
approximately equal to 0.8 cm-1
in Fig. 2 of
[7].
In Fig. 1 experimental datum is very
close to theoretical
value under magnetic field 39 kA/m. So, using the condition and ultrasonic frequency 3.6 MHz [7], relaxation time is
approximately equal to 
s. Parameter 
g/cm3 was taken from
[13]. In [11] also water-based magnetic nanofluid W – 40 was considered, but
with other concentration of magnetic nanoparticles and magnetic
field was static with value 100 mT. However, according to the formula
(20) in [11] relaxation time is 
s at the maximum absorption
coefficient, which is very close to mentioned above relaxation time.
In experiment [15] the
absorption peak is smooth in magnetic nanofluid APG-832 on the exposure of the
static magnetic field. Also in theoretical calculations [11] the absorption
peaks are smooth for magnetic nanofluids W – 40 and HC-50 on the exposure
of the static magnetic field. In experiments [7] the absorption peaks are sharp
for the magnetic nanofluid EMG – 605, which may be due to the fact that the magnetic
field increased on the time, so the relaxation time can increase faster than on
the exposure of the static magnetic field.
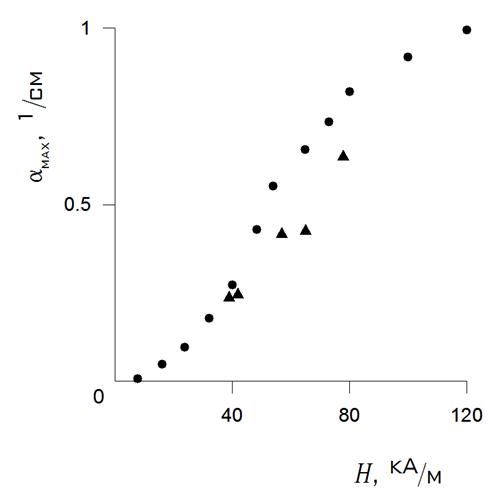
Fig. 1. The maxima of ultrasonic absorption coefficient: circles – the theoretical values by the formula (8) and triangles – the experimental data [7], with dependence on magnetic field strength.
3. Conclusion
The magnetic nanofluid is a complex system, so in it the magneto-mechanical properties may depend on the conditions of the experiment [2, 7, 8]. Big peaks of ultrasonic absorption coefficient were observed under the rate of magnetic field in experiments [7], which is connected with irreversible process of formation of chain-like clusters. In this article these peaks can be explained by the fact that there is a relaxation process of magnetic field to its equilibrium value in magnetic nanofluid [9, 10]. Thus, formation of chain-like clusters is connected with a relaxation process of magnetic field to its equilibrium value.
References
[1] R. E. Rosensweig. Ferrohydrodynamics, Cambridge Univ. Press, New York, 1985. 368p.
[2] A. Józefczak, T. Hornowski, V. Závišová, A. Skumiel, M. Kubovčíková, M. Timko. Acoustic Wave in a Suspension of Magnetic Nanoparticle with Sodium Oleate Coating // J. Nanopart. Res. 2014, Vol. 16, p. 2271. DOI: 10.1007/s11051-014-2271-z
[3] C.G. Montgomery. The Magnetization of Colloidal Suspensions // Phys. Rev. 1931. Vol. 38. No. 9. p. 1782.
[4] W.C. Elmore. Ferromagnetic Colloid for Studying Magnetic Structures // Phys. Rev. 1938. Vol. 54. No. 4. p. 309-310.
[5] W.C. Elmore. The Magnetization of Ferromagnetic Colloids // Phys. Rev. 1938. Vol. 54, No. 12. p. 1092-1095.
[6] S.S. Papell. Low Viscosity Magnetic Fluid Obtained by the Colloidal Suspension of Magnetic Particles, US Patent No 3215572, 1965.
[7] A. Józefczak, M. Łabowski, A. Skumiel. Hysteresis of Changes of Ultrasonic Wave Absorption Coefficient in a Magnetic Fluid Caused by the Magnetic Field // J. Magn. Magn. Mat. 2002, Vol. 252, p. 356–359.
[8] T. Hornowski. Ultrasonic Properties of EMG-605 Magnetic Liquid // Proc. SPIE. 2005. Vol. 5828. p. 205-212. http://dx.doi.org/10.1117/12.612810
[9] V.V. Sokolov, V.V. Tolmachev. Propagation of Shear Waves in a Magnetic Liquid with Frozen-In Magnetization // Tech. Phys. Lett. 1997. Vol. 23, No. 1 p.5-6. DOI: 10.1134/1.1261628
[10] B.U. Felderhof, V.V. Sokolov, P.A. Eminov. Ferrofluid Dynamics, Magnetic Relaxation and Irreversible Thermodynamics // J. Chem. Phys. 2010. Vol. 132. No. 18. p. 184907. http://dx.doi.org/10.1063/1.3430726
[11] I.E. Ovchinnikov. Effect of a Static Magnetic Field on the Ultrasonic Propagation in Magnetic Fluids // J. Radio Electronics. 2013. N1. URL: http://jre.cplire.ru/jre/jan13/12/text.pdf [in Russian with abstract in English]
[12] I.E. Ovchinnikov, V.V. Sokolov. Waves in Magnetic Fluids with Equilibrium
and Frozen-In Magnetizations // Acoust. Phys., 2013. Vol. 59, No. 1, p. 51-
55. DOI: 10.1134/S1063771012060115
[13] I.E. Ovchinnikov. Effect of a Magnetic Field Relaxation on the Splash of Ultrasonic Absorption Coefficient in Magnetic Nanofluid EMG – 605 // J. Radio Electronics. 2014. N1. URL: http://jre.cplire.ru/jre/jan14/17/text.pdf [in Russian with abstract in English]
[14] A. B. Migdal. Qualitative Methods in Quantum Theory, W.A. Benjamin, Inc. London. 1977. 437p.
[15] K. Charaziak, M. Marecki, T. Hornowski, A. Józefczak, A. Skumiel. Resonance Attenuation of Ultrasonic Waves in a High Viscosity Magnetic Liquid // Arch. Acoust. 2008, Vol. 33 (4, Suppl.), p. 105–110.