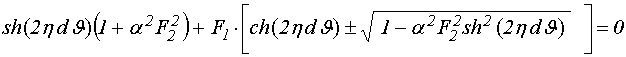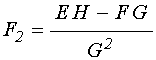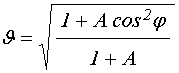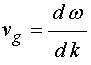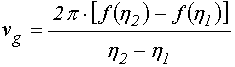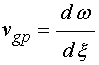"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 3, 2016

оглавление

УДК 537.874; 537.624

ПОВЕРХНОСТНЫЕ МАГНИТОСТАТИЧЕСКИЕ ВОЛНЫ В ПЛАСТИНЕ ФЕРРИТА С ДИССИПАЦИЕЙ.

ЧАСТЬ 2. РАСПРОСТРАНЕНИЕ ВОЛНЫ ПЕРПЕНДИКУЛЯРНО НАПРАВЛЕНИЮ ПОЛЯ

 

Ю. И. Келлер1, П. А. Макаров1, В. Г. Шавров2, В. И. Щеглов2

1Сыктывкарский государственный университет

2Институт радиотехники и электроники им. В.А.Котельникова РАН

 

Статья поступила в редакцию 14 февраля 2016 г.

 

Аннотация. На основе последовательного решения уравнения движения для намагниченности проведен учет затухания поверхностных магнитостатических волн (ПМСВ) в касательно намагниченной ферритовой пластине. Выявлено существование диссипативной ветви обратных ПМСВ, лежащей выше по частоте относительно основного спектра прямых ПМСВ, а также ограничение сверху предельных значений волнового числа для обеих ветвей спектра. Рассмотрена роль диссипации в формировании дисперсионных свойств действительной и мнимой частей волнового числа. Проведено сопоставление со свойствами электромагнитных волн в области аномальной дисперсии.  

Ключевые слова: феррит, магнитостатические волны, диссипация. 

Abstract. By means of consistent solution of motion equation for magnetization the consideration of dissipation for magnetostatic surface waves (MSSW) propagating on in-plane magnetized ferrite plate is considered. It is revealed the existence of dissipative branch backward MSSW laying higher on frequency relative to the main spectrum of forward MSSW and also the limitation on top of wave number maximum values for both spectrum branches. The role of dissipation in the forming of dispersion properties of real and imaginary wave number parts is investigated. The comparison with properties of electromagnetic waves in anomalous dispersion region is carried out. 

Key words: ferrite, magnetostatic waves, dissipation.

 

Введение

Поверхностные магнитостатические волны (ПМСВ) в пленках железоиттриевого граната (ЖИГ) [1], составляют основу широкого класса устройств аналоговой обработки информации в диапазоне СВЧ [2-5]. Типичное устройство содержит пленку ЖИГ с расположенными на ее поверхности излучающей и приемной антеннами из тонкой проволоки. Диапазон частот таких устройств – , подмагничивающее поле в плоскости пленки – . Обычные параметры пленки ЖИГ: толщина , намагниченность насыщения . Длина ПМСВ составляет от  до , ослабление волны за счет диссипации может достигать десятков децибел.

Работы по распространению ПМСВ в пленках ЖИГ, в том числе в неоднородных полях [6-11] и сложных структурах [12-17], как правило, ограничиваются случаем бездиссипативной среды. Однако в работах [18,19] показано, что наличие диссипации приводит к появлению в спектре ПМСВ обратных «диссипативных» волн, по частоте примыкающих к верхней границе спектра обычных прямых ПМСВ типа Дэймона-Эшбаха [1]. Отмечено обусловленное диссипацией ограничение спектра ПМСВ по волновому числу.

В работах [20,21] распространение ПМСВ в среде с затуханием рассмотрено более подробно. Для частного случая распространения волны перпендикулярно направлению магнитного поля получены дисперсионные соотношения для действительной и мнимой частей волнового числа, выявлены некоторые особенности спектров прямых и обратных ПМСВ, в частности ограничение по волновому числу.  

В работах [22,23] для случая диссипативной среды рассмотрено распространение ПМСВ в произвольном направлении относительно поля. Построены индикатрисы (изочастотные кривые) прямых ПМСВ и исследовано направление групповой скорости волны при изменении ориентации ее волнового вектора, однако ограничение по волновому числу не отмечено и дисперсионное соотношение в достаточной мере не исследовано.  

В работе [24] показано, что распространение ПМСВ в среде с диссипацией может быть описано на основе введения комплексного волнового числа. Получены дисперсионные соотношения как для действительной, так и для мнимой частей волнового числа в случае произвольного направления распространения волны относительно магнитного поля.

Настоящая работа является продолжением [24] и посвящена исследованию свойств прямых и обратных ПМСВ на основе полученных в [24] дисперсионных соотношений. На данном этапе рассматривается случай распространения волны перпендикулярно направлению поля. Произвольному направлению распространения предполагается посвятить следующую часть работы.

 

1. Геометрия задачи

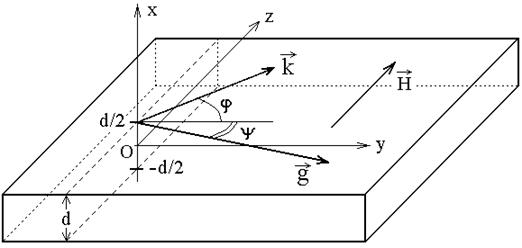
Общая геометрия задачи, совпадающая с принятой в работах [20,21,24], показана на рис.1.

 

 

Рис.1. Общая геометрия задачи.

 

Ферритовая пластина толщины  намагничена в плоскости полем . Декартова система координат выбрана таким образом, что ее начало, точка , находится на середине толщины пластины, плоскость  параллельна плоскости пластины, а ось  ей перпендикулярна. При этом координаты плоскостей пластины по оси  равны . Ось  ориентирована вдоль поля . Далее рассматриваются поверхностные магнитостатические волны (ПМСВ), распространяющиеся вдоль верхней поверхности пластины при . Волновой вектор  лежит в плоскости и  составляет угол  с осью , вектор групповой скорости  лежит в той же плоскости и составляет угол  с осью .

 

2. Параметры задачи

Основные параметры задачи совпадают с принятыми в работах [20,21,24]. Намагниченность материала пластины была выбрана типичной для монокристалла ЖИГ: . Толщина пластины  равнялась . Постоянное поле  в плоскости пластины составляло . Величина угла  менялась в пределах от  до (при максимальном угле отсечки на низшей частоте спектра ПМСВ равном ). Параметр затухания  менялся в пределах от  до . При этом время релаксации (то есть спада амплитуды свободных колебаний в  раз) составляло порядка . Остальные значения параметров, используемые для построения кривых, указаны в подписях к рисункам и в тексте.

 

3. Волновое число и дисперсионные соотношения

Следуя работе [24] будем считать волновое число ПМСВ комплексным:

,                                                                                             (1)

где  и  – действительные постоянные ( и ).

Приведем без вывода полученные в работе [24] дисперсионные соотношения.

Так дисперсионное соотношение для действительной части волнового числа имеет вид [24, формула (115)]:

                      (2)

Дисперсионное соотношение для мнимой части волнового числа имеет вид [24, формула (137)]: 

 

 

,   (3)

 

Входящие в эти формулы вспомогательные обозначения  и  определяются формулами [24, формулы (98),(99)]:

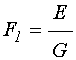;                                                                                                 (4)

,                                                                                 (5)

 

где [24, формулы (92)-(95)]:

;                                                                                      (6)

;                                                                                              (7)

;                                                         (8)

,                                                      (9)

 

в которых [24, формула (70)]:

,                                                                            (10)

 

при вспомогательных обозначениях [24, формулы (14)-(18)]:

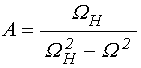;                                                                                    (11)

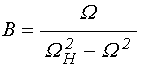;                                                                                    (12)

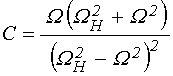;                                                                             (13)

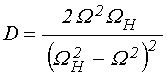.                                                                              (14)

 

содержащих нормированные частоты  и  в виде [24, формулы (11)-(12)]:

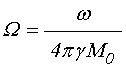;                                                                                       (15)

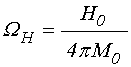.                                                                                      (16)

 

В двух последних формулах  означает частоту возбуждения,  – постоянное магнитное поле в плоскости пластины,  – намагниченность насыщения материала пластины. 

Замечание. Напомним, что эти соотношения получены в приближении малого затухания, то есть диссипативный параметр Гильберта  [25-28] полагается значительно меньшим единицы. В соответствии с этим, в процессе вывода слагаемые, содержащие  наравне с , были опущены, однако оставлены там, где сопутствующие слагаемые, пропорциональные , отсутствовали.

Отметим еще важные для дальнейшего рассмотрения характерные частотные границы областей существования прямых и обратных ПМСВ [24, формулы (34)-(39)]:

;                                                                                         (17)

;                                                                                         (18)

,                                                                                         (19)

соответствующие линейным частотам:

;                                                                                 (20)

;                                                                                 (21)

.                                                                                 (22)

Согласно показанному в [24], прямые ПМСВ существуют в интервале частот между  и , а обратные – в интервале частот между  и , то есть  является разграничительной линией между областями прямых и обратных волн. Явные выражения для этих частот через значения намагниченности и поля имеют вид [24, формулы (23),(25),(27)]:

;                                                               (23)

;                                                                        (24)

,                                           (25)

где  – гиромагнитная постоянная, для линейной частоты равная . 

 

4. Основные алгоритмы расчета

Дисперсионные кривые в настоящей работе рассчитывались в соответствии с приведенными выше формулами (2) и (3). При заданном значении действительной  или мнимой  части волнового числа определялась частота  при помощи алгоритма поиска нуля. Шаг по волновому числу составлял , заданная точность определения частоты равнялась .

Кроме законов дисперсии исследовалась групповая скорость ПМСВ, которая в соответствии с классическим определением [29,30] имеет вид:

.                                                                                              (26)

При численном расчете групповая скорость определялась как касательная к дисперсионной кривой для действительной части волнового числа, построенная по формуле:

,                                                                 (27)

где  и  – два последовательных значения волнового числа, расположенные на расстоянии одного шага.   

Кроме классической групповой скорости волны , определенной относительно действительной части волнового числа , в настоящей работе исследовался также аналогичный параметр , определяемый как производная по  от дисперсионных кривых для  мнимой части волнового числа, то есть по формуле:

,                                                                                            (28)

или при численном расчете по формуле:

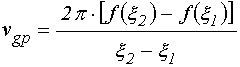,                                                                (29)

где  и  – два последовательных значения мнимой части волнового числа, расположенные на расстоянии одного шага.

Очевидно, эти формулы являются аналогом (26) и (27) для действительной части волнового числа, поэтому по аналогии с , являющейся групповой скоростью распространения волны, величину  можно назвать «групповой скоростью роста затухания волны».

Замечание. Благодаря гиротропным свойствам ферритовой среды, при углах вектора фазовой скорости , отличных от нуля, направление вектора групповой скорости определяется углом , в общем случае не равном  (рис.1). То есть вместо формул (26) и (28 ) следует использовать формулы:

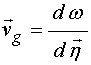;                                                                                              (30)

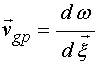.                                                                                            (31)

В среде с диссипацией необходимо учитывать комплексный характер волнового числа, вследствие чего угол  по отношению к бездиссипативному случаю несколько изменяется. Частично этот вопрос рассмотрен в работах [31,32], а применительно к магнитным средам – в [22,23]. В двух последних работах показано, что при принятых там параметрах (близких к принятым здесь) зависимость угла  от угла  по мере увеличения  от нуля до спадает от нуля до . При малом затухании зависимость  от    идет ниже кривой, соответствующей большому затуханию, при большом – выше. Различие максимально при  и меняется при переходе от малого затухания к большому с  до . При  различие имеет обратный знак и при переходе от малого затухания к большому меняется с до . К сожалению, конкретизация понятий «малого» и «большого» затухания в цитированных работах отсутствует, что не позволяет использовать приведенные там данные для более точных численных оценок, однако можно видеть, что роль диссипации сказывается в основном при углах   в окрестности , тогда как при  влияние диссипации полностью отсутствует, а при удалении от  составляет не более . Предметом рассмотрения настоящей работы является не направление вектора групповой скорости, а его абсолютная величина, поэтому для ее расчета здесь используется классическая формула (26). Для расчета групповой скорости роста затухания соответственно используется формула (28). Более точно вопрос о роли направления вектора групповой скорости предполагается рассмотреть в следующей части настоящей работы.   

 

5. Схема определения времени установления

Для интерпретации свойств дисперсии ПМСВ далее в качестве вспомогательного параметра будет использоваться время релаксации колебаний намагниченности, затухающих благодаря диссипативным свойствам среды. Рассмотрим схему определения этого параметра.  

 

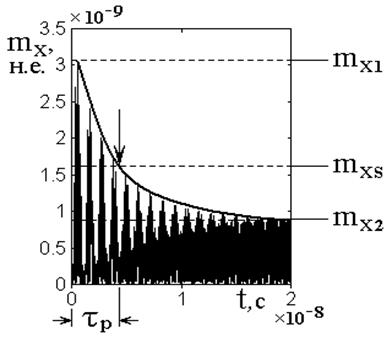
Рис.2. Схема определения времени установления вынужденных колебаний намагниченности.

Амплитуда переменного поля . Остальные параметры совпадают с приведенными в разделе №2.

 

Время релаксации намагниченности  определялось как время установления стационарной амплитуды вынужденных колебаний при линейном возбуждении переменным полем небольшой амплитуды () в геометрии, представленной на рис.1. Рассматривалась развертка колебаний во времени для одной из компонент намагниченности (в данном варианте – , колебания  аналогичны с несколько меньшей амплитудой). Общий расчет развертки колебаний производился с помощью метода, предложенного в работе [33], многократно использовавшегося в статьях [34-40] и обобщенного в монографии [41], поэтому здесь подробно не рассматривается.

Схема определения времени установления стационарной амплитуды представлена на рис.2. Показано развитие колебаний во времени для положительного полупериода компоненты , происходящее после включения возбуждения. Постоянная затухания  установлена равной . Частота возбуждения соответствовала минимуму зависимости групповой скорости от волнового числа, представленной далее на рис.4 кривой 1, то есть равнялась .  

Установление колебаний происходило путем биений между частотой возбуждения и частотой ферромагнитного резонанса в заданной геометрии при поле . Огибающая биений имела характер спадающей экспоненты, показанной на рис.2 утолщенной линией. На развертке колебаний регистрировались два уровня амплитуды намагниченности: , соответствующий началу возбуждения и , соответствующий установлению стационарного режима. Уровень  определялся по времени спада амплитуды биений в  раз, то есть по формуле:

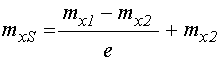.                                                                    (32)

Время установления  определялось как промежуток между началом возбуждения и моментом спада амплитуды биений до уровня   (точка пересечения этого уровня с огибающей показана стрелкой).

 

6. Роль диссипации в формировании дисперсии действительной части волнового числа для прямых ПМСВ

Рассмотрим теперь роль диссипации в формировании дисперсионных свойств действительной и мнимой частей волнового числа. В рамках данной (второй) части настоящей работы ограничимся случаем распространения волны перпендикулярно направлению поля, то есть будем полагать угол  (рис.1) равным нулю. В настоящем разделе рассмотрим действительную часть волнового числа, для чего обратимся к рис.3.

 

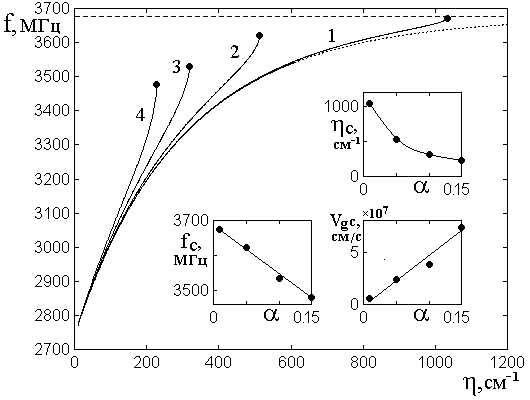
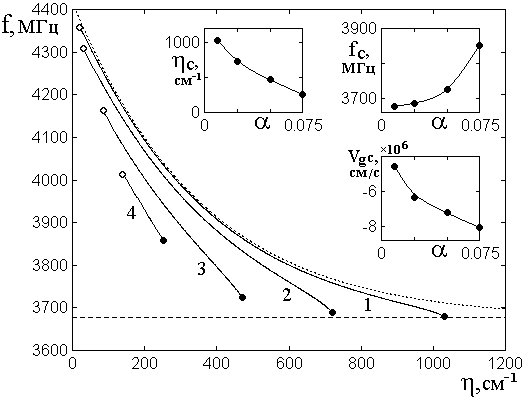
Рис.3. Дисперсия действительной части волнового числа прямых ПМСВ в случае  при различных уровнях диссипации.

Параметр затухания :  1 – ;  2 – ;  3 – ;  4 – .

Точечная кривая соответствует .

Остальные параметры указаны в разделе №2.

На врезках показаны зависимости предельных значений ,  и  от параметра .

На этом рисунке показаны дисперсионные кривые для действительной части волнового числа прямых ПМСВ, построенные в соответствии с формулой (2) со знаком «плюс» в случае  при различных уровнях диссипации. Горизонтальная пунктирная линия соответствует верхней частотной границе области существования прямых ПМСВ (согласно (21), при принятых параметрах равной ).

Можно видеть, что по мере увеличения диссипации дисперсионные кривые отклоняются вверх по частоте относительно бездиссипативной кривой, причем такое отклонение проявляется тем сильнее, чем диссипация выше. Однако кривые с диссипацией, в отличие от бездиссипативной кривой (точечная линия), обрываются при критическом значении волнового числа , которому соответствует критическая частота. На рис.3 обрыв дисперсионных кривых при различных значениях диссипации показан укрупненными точками. Видно, что предельные волновое число и частота становятся тем меньше, чем величина диссипации больше.

Из общего хода дисперсионных кривых видно, что вблизи предельного значения волнового числа все они изгибаются вверх, подходя к граничной частоте почти с вертикальной касательной. Такое их поведение соответствует увеличению групповой скорости ПМСВ, определяемой по формуле (27).

На врезках показаны зависимости ,  и  от параметра  в предельных точках кривых .

Замечание. При построении использовались значения этих параметров, полученные из окончания кривых, рассчитанных с шагом по  равным  (раздел №2). Уменьшение этого шага до  привело к незначительному (доли процента) уточнению предельных значений ,  и , однако время расчета существенно (на два порядка) увеличилось, поэтому, с учетом приближенного характера аналитической формулы (2), в рамках настоящей работы такое уточнение было признано нецелесообразным. 

Из первой врезки на рис.3 можно видеть, что зависимость  от  близка к обратной пропорциональности. Действительно, при  ограничение зависимостей  пропадает, то есть . В то же время при  величина , так что приближение зависимости  обратной пропорциональностью является вполне правдоподобным. Из двух других врезок видно, что зависимости  и  от параметра  довольно точно приближаются прямыми линиями.

Следует отметить, что наблюдаемое из общего хода кривых 1-4, а также из последней врезки с зависимостью  от параметра , возрастание групповой скорости волны при увеличении затухания, с точки зрения классической электродинамики, является определенным парадоксом. Так в классике принято считать, что при фиксированной частоте групповая скорость с увеличением диссипации уменьшается. Такое положение, например, имеет место при распространении электромагнитных волн в передающих линиях с потерями [42, стр.254, формула (51.16)].

Заметим однако, что классическое рассмотрение предполагает бездисперсионный либо слабо дисперсионный характер распространения волн, когда фазовая скорость при изменении частоты остается постоянной или меняется в незначительной степени.

Предметом же рассмотрения настоящей работы являются поверхностные магнитостатические волны, дисперсионная зависимость которых вблизи верхней границы области существования (горизонтальная пунктирная линия на рис.3) имеет весьма сильную особенность При приближении частоты волны к этой границе снизу, как фазовая, так и групповая скорости ПМСВ стремятся к нулю, то есть волна по мере увеличения частоты как бы «зацепляется» за прецессию намагниченности, в результате чего почти останавливается. Вообще говоря, магнитостатические волны являются частным случаем электромагнитных волн, для которых дисперсионная зависимость имеет вид прямой линии, причем наклон этой линии значительно превышает наклон ПМСВ во всем интервале их существования, то есть такая прямая располагается значительно левее кривых 1-4, приведенных на рис.3 (в принятом на рис.3 масштабе эта прямая практически совпадает с вертикальной осью: так при частоте  волновое число равно всего , поэтому упомянутая прямая отдельно не отмечена). В отсутствие затухания дисперсионная кривая для ПМСВ (точечная линия на рис.3) располагается значительно правее упомянутой прямой, что обусловлено именно «зацеплением» электромагнитной волны за прецессию намагниченности. В случае увеличения затухания взаимодействие магнитного поля ПМСВ с прецессирующей намагниченностью уменьшается, то есть электромагнитная волна в какой-то степени высвобождается от «зацепления», в результате чего бездиссипативная кривая (точечная линия на рис.3) отклоняется в сторону дисперсионной кривой для электромагнитных волн, то есть по рисунку налево. При этом групповая скорость волны, определяемая по углу касательной к кривой дисперсии, соответственно увеличивается, что и является причиной разрешения упомянутого парадокса с классикой.

Рассмотрим теперь групповую скорость прямых ПМСВ несколько более подробно. Поскольку ограничение зависимостей  (кривых 1-4 на рис.3) сопровождается изгибом их вверх, то есть ростом групповой скорости, обратимся теперь к рис.4, где показано, как меняется групповая скорость ПМСВ при изменении действительной части волнового числа  для различных уровней диссипации (параметра ). 

Можно видеть, что все кривые по мере увеличения  сначала спадают, после чего, проходя через минимум (обозначенный открытыми точками), нарастают до значительных величин. Как и на рис.3 все кривые обрываются при тех же, что и там значениях , однако здесь обрыв сопровождается значительным ростом , тем более выраженным, чем параметр затухания  больше. При увеличении параметра  положение минимума смещается к меньшим значениям , причем абсолютная  глубина его повышается.

 

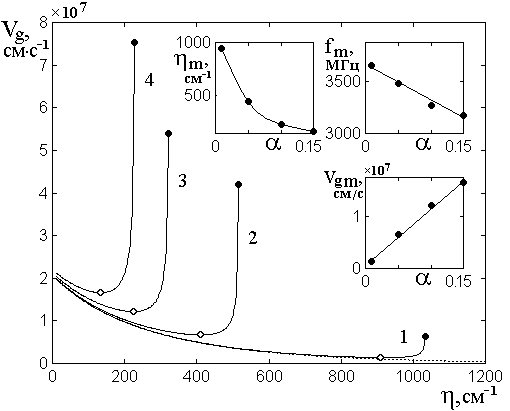
Рис.4. Зависимости групповой скорости прямых ПМСВ от действительной части волнового числа в случае  при различных уровнях диссипации.

Параметр затухания : 1 – ;  2 – ;  3 – ;  4 – .

Точечная кривая соответствует .

Остальные параметры указаны в разделе №2.

На врезках показаны соответствующие минимумам кривых зависимости значений ,  и  от параметра .

 

   На врезках показаны зависимости ,  и  от параметра  в точках минимумов кривых . Можно видеть, что эти зависимости ведут себя подобно таковым на врезках рис.3, то есть зависимость  соответствует обратной пропорциональности, а зависимости  и  приближаются прямыми. Здесь однако эти зависимости располагаются значительно ниже зависимостей на рис.3, что определяется тем, что кривые на рис.3 соответствуют предельным значениям действительной части волнового числа, тогда как кривые на рис.4 – промежуточным значениям тех же зависимостей.

Таким образом, главным результатом настоящего раздела можно считать определяемое диссипацией ограничение дисперсионных кривых при критическом значении действительной части волнового числа, сопровождающееся прохождением групповой скорости через минимум с последующим ее возрастанием.

 

7. Механизм ограничения дисперсионных кривых 

Рассмотрим теперь возможные механизмы ограничения дисперсионных кривых за счет диссипации.

С математической стороны, обрыв дисперсионных кривых соответствует изменению знака подкоренного выражения в дисперсионном соотношении (2) с положительного на отрицательный. При этом в диапазоне частот существования ПМСВ оба сомножителя перед , благодаря своей квадратичности, остаются положительными, так что второе слагаемое при увеличении  возрастает, а когда оно становится равным единице, дисперсионные кривые обрываются. Таким образом, расчет предельного значения действительной части волнового числа сводится к решению уравнения:

,                                                                   (33)  

где параметры  и  зависят только от частоты и определяются соответственно формулами (5) и (10), с учетом входящих в эти формулы промежуточных обозначений.

Замечание. Это уравнение при заданном значении параметра  связывает предельную частоту  с предельным волновым числом , то есть содержит две независимых переменных, вследствие чего не может быть однозначно разрешено в отсутствие зависимости  от . То есть для того, чтобы найти зависимость  и  от , надо сначала определить зависимость  от , которая в свою очередь может быть получена только из решения полного уравнения (2). Таким образом, решение уравнения (33) сводится к «порочному кругу» и не может быть осуществлено независимо от решения полного уравнения (2). В этом случае алгоритм нахождения зависимости  и  от  можно свести к последовательному вычислению с определенным шагом по  предельных значений  и  по уравнению (33) с учетом (2), после чего по полученным значениям  и  построить их зависимости от , как это и было сделано при построении первых двух врезок на рис.3. В первом же приближении для решения уравнения (33) можно воспользоваться зависимостью  от  для бездиссипативной среды [24, формула (116) со знаком «плюс»], сохраняя однако зависимость от диссипации в виде коэффициента перед вторым слагаемым в (2). Такое решение, хотя и возможно, но является чрезвычайно громоздким, поэтому в рамках настоящей работы не проводилось.

Рассмотрим теперь качественную физическую причину ограничения дисперсионных кривых. Вспомогательный расчет времени релаксации (или установления постоянного уровня) вынужденных колебаний намагниченности , выполненный по методике, описанной в разделе №5, показывает, что при неизменном параметре  по мере увеличения частоты время релаксации уменьшается. То есть, чем выше частота возбуждаемой волны, тем на меньшем расстоянии она затухает. Можно полагать, что при увеличении , сопровождающемся увеличением , когда расстояние затухания волны сравнивается с ее длиной, волна переходит к апериодическому режиму и дальше не распространяется.

В подтверждение такого предположения рассмотрим таблицу №1, в первом столбце которой приведены значения параметра , а в следующих – параметры распространяющейся волны.  

 

Таблица №1.

 

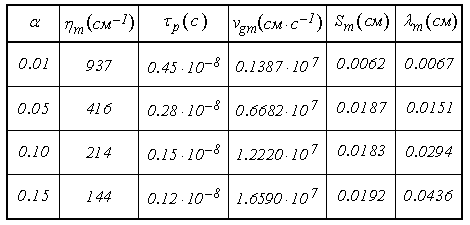
При построении таблицы во втором и четвертом столбцах использованы значения волнового числа  и групповой скорости , соответствующие минимумам кривых 1-4 на рис.4. В третьем столбце приведено время релаксации , рассчитанное по алгоритму, описанному в разделе №5.

В пятом столбце приведена величина пути, проходимого волной за время своей релаксации, определяемого как:

.                                                                                       (34)

В последнем шестом столбце приведена длина волны, рассчитываемая из значения действительной части волнового числа по формуле: 

.                                                                                        (35)

Можно видеть, что значения пробега волны за время релаксации  и ее длины , приведенные в двух последних столбцах таблицы, довольно близки между собой. Для  совпадение можно считать хорошим (около ), хотя по мере увеличения  различие постепенно увеличивается, достигая при  примерно двух раз. Однако, учитывая невысокую точность определения времени релаксации (раздел №5), падающую при увеличении частоты за счет того, что колебания до полного затухания успевают пройти всего несколько периодов (при  не более 5-7), можно полагать, что соответствие данных, приведенных в пятом и шестом столбцах таблицы, является вполне приемлемым.

Такое их совпадение подтверждает высказанное предположение о том, что рост волнового числа приводит к затуханию волны на расстоянии своей длины, то есть к апериодическому режиму, дальнейшему распространению волны препятствующему. 

Переход к такому режиму происходит в области минимумов кривых 1-4 на рис.4, для чего в таблице №1 и были использованы значения параметров волны, соответствующие этим минимумам. После установления апериодического режима колебания волны как таковые прекращаются, то есть намагниченность своего нулевого значения не переходит, а плавно стремится к нулю на расстоянии, могущем значительно превышать длину волны. Такое плавное стремление уже не ограничивается переколебаниями намагниченности с изменением знака, происходящими при периодическом волновом процессе, что и приводит в результате к кажущемуся увеличению групповой скорости до больших значений, отражаемых ростом кривых 1-4 на рис.4. 

 

8. Роль диссипации в формировании дисперсии  волнового числа для обратных ПМСВ

Рассмотрим теперь роль диссипации в формировании дисперсии  волнового числа в случае обратных (диссипативных) ПМСВ, для чего обратимся к рис.5. 

 

Рис.5. Дисперсия действительной части волнового числа обратных ПМСВ в случае  при различных уровнях диссипации.

Параметр затухания : 1 – ;  2 – ;  3 – ;  4 – .  Точечная кривая соответствует .

Остальные параметры указаны в разделе №2.

На врезках показаны зависимости предельных значений ,  и  от параметра .

 

На этом рисунке показаны дисперсионные кривые для действительной части волнового числа обратных ПМСВ, построенные в соответствии с формулой (2) со знаком «минус» в случае  при различных уровнях диссипации. Горизонтальная пунктирная линия соответствует нижней частотной границе области существования обратных ПМСВ, совпадающей с верхней границей для прямых ПМСВ (согласно (21), при принятых параметрах равной ).

В отличие от подобных зависимостей для прямых волн (рис.3), здесь при увеличении волнового числа кривые спадают, что соответствует отрицательной групповой скорости, то есть отражает обратный характер распространяющихся волн.  

Можно видеть, что по мере увеличения диссипации дисперсионные кривые отклоняются вниз по частоте относительно бездиссипативной кривой, причем такое отклонение проявляется тем сильнее, чем диссипация выше.

Кривые с диссипацией, в отличие от бездиссипативной кривой (точечная линия), обрываются по волновому числу как снизу, так и сверху. Верхний обрыв (при больших ) является аналогом такового для прямых волн, тогда как нижний обрыв (при меньших ) для прямых волн отсутствует.

Нижнее критическое значение волнового числа  по мере увеличения затухания увеличивается, соответствующие ему частота  и групповая скорость  уменьшаются. Так при  (кривая 3) эти величины составляют: ,  ,  ,  а при увеличении  до  (кривая 4) равны соответственно:  ,  ,  . 

Верхнее критическое значение , являющееся аналогом такового для прямых волн, при увеличении затухания также уменьшается, а соответствующие ему частота  и групповая скорость  увеличиваются. Так при  (кривая 3) эти величины составляют: ,  ,  ,  а при увеличении  до  (кривая 4) равны соответственно:  ,  ,  . 

Причина обрыва дисперсионных кривых сверху для обратных волн – та же, что и для прямых и состоит в приближении пути, проходимого волной за время релаксации к длине самой волны, в результате чего волны приобретают апериодический характер.  Более подробно этот вопрос рассмотрен в разделе №7, так что здесь его обсуждение является излишним.  

Обрыв снизу для прямых волн отсутствует и связан, по-видимому, с обратным характером волн. Возможной причиной нижнего обрыва является следующая. Из обратного характера волн следует, что при уменьшении волнового числа частота волны увеличивается, так что время ее релаксации уменьшается и путь, проходимый волной за это время, также уменьшается. С другой стороны, уменьшение волнового числа соответствует увеличению длины волны, то есть тенденции уменьшения пути и увеличения длины волны действуют навстречу друг другу, поэтому волна приходит в апериодическое состояние даже быстрее, чем в случае прямых волн. Так для прямой волны время релаксации вынуждено «догонять» длину волны, для обратной же волны они «стремятся навстречу» друг другу. Таким образом, причина обрыва для обратных волн – та же самая, что для прямых, однако здесь она проявляется не только для коротких волн, но и для длинных. Заметим однако, что этот вопрос требует более подробного количественного рассмотрения, в данный момент за рамки настоящей работы выходящего.

Таким образом, в результате совместного действия обоих упомянутых ограничений, рассматриваемые здесь обратные диссипативные волны по параметру затухания существуют только в области, ограниченной сверху предельным значением . На существование такого ограничения указывалось ранее в работах [20,21], однако природа его не была рассмотрена.

Можно полагать, что причина ограничении кроется в сужении области существования обратных ПМСВ по мере увеличения , происходящем как сверху, так и снизу благодаря механизму перехода к апериодическому состоянию. Такое сужение в конце концов приводит к смыканию обеих встречных тенденций, что и определяет предельное значение . Получающиеся при этом границы областей существования ПМСВ рассматриваются далее в разделе №9.  

На рис.5 верхний обрыв дисперсионных кривых при различных значениях диссипации показан укрупненными точками. Видно, что с увеличением диссипации предельное волновое число уменьшается, а частота, ему соответствующая, увеличивается. Подобный обрыв по волновому числу наблюдался и в случае прямых волн (рис.3), однако здесь при тех же значениях параметра затухания критическое волновое число  насколько меньше, причем это различие по мере увеличения параметра затухания также увеличивается.

Так например, при  критическое волновое число  для прямых волн равно , а для обратных – , так что различие составляет всего , тогда как при  соответствующие значения равны  и , то есть различие достигает .

Замечание. При сравнении приведенных здесь данных с кривыми на рис.3 следует обращать внимание на то, что здесь шаг по параметру  между следующими друг за другом кривыми вдвое меньше, чем на рис.3. Это сделано из стремления уместить на рисунке большее число кривых в ограниченной по  области.

Можно видеть, что вблизи предельного значения волнового числа дисперсионные кривые слегка изгибаются вниз, что соответствует увеличению групповой скорости ПМСВ, подобно случаю прямых волн, однако здесь эта скорость является отрицательной.

На врезках показаны зависимости ,  и  от параметра  в предельных точках кривых . Можно видеть, что приведенная на первой врезке зависимость  от   близка к подобной зависимости на рис.3 и также близка к обратной пропорциональности. Однако приведенные на двух других врезках зависимости  и  от , будучи несколько отличными от прямых, имеют наклон, обратный таковому на рис.3. Можно полагать, что такое изменение наклона определяется именно обратным характером рассматриваемых здесь волн. 

 

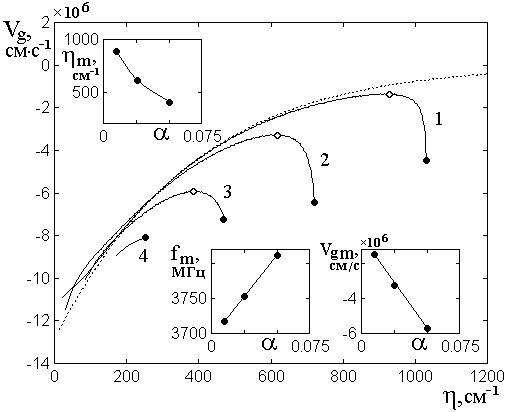
Рис.6. Зависимости групповой скорости обратных ПМСВ от действительной части волнового числа в случае  при различных уровнях диссипации.

Параметр затухания : 1 – ;  2 – ;  3 – ;  4 – .

Точечная кривая соответствует .

Остальные параметры указаны в разделе №2.

 

Поскольку ограничение зависимостей  (кривых 1-4 на рис.5) сопровождается изгибом их вниз, то есть ростом групповой скорости, обратимся теперь к рис.6, где показано, как меняется групповая скорость обратных ПМСВ при изменении действительной части волнового числа  для различных уровней диссипации (параметра ).  

Можно видеть, что все кривые с качественной стороны по структуре представляют собой как бы «зеркальное» отражение подобных кривых, приведенных на рис.4, то есть по мере увеличения  сначала возрастают, после чего, проходя через максимум (обозначенный открытыми точками), спадают до величин, однако меньших, чем начальные точки, соответствующие стремлению  к нулю.

Как и на рис.5 все кривые обрываются при тех же, что и там значениях , причем здесь обрыв сопровождается ростом , однако тем менее выраженным, чем параметр затухания  больше. Для кривой 4 максимум и следующий за ним спадающий участок вообще отсутствует.

На врезках показаны зависимости ,  и  от параметра  в точках максимумов кривых . Можно видеть, что зависимость  ведет себя подобно таковой, приведенной на первой врезке на рис.5, однако здесь, как и в случае прямых волн, она проходит несколько ниже. Зависимости  и  имеют ход, подобный таковым на рис.5, причем в этом случае уже довольно близко  приближаются прямыми. Здесь эти зависимости располагаются также ниже зависимостей на рис.5, что определяется тем, что кривые на рис.5 соответствуют предельным значениям действительной части волнового числа, а кривые на рис.6 – промежуточным значениям тех же зависимостей.

Таким образом, главным результатом настоящего раздела, как и для случая прямых волн, можно считать определяемое диссипацией ограничение дисперсионных кривых при критическом значении действительной части волнового числа, сопровождающееся прохождением групповой скорости через максимум с последующим ее убыванием. Главное отличие от прямых волн состоит в качественной симметрии всех зависимостей относительно горизонтальной оси, соответствующей предельному значению частоты или групповой скорости, однако количественные характеристики прямых и обратных волн в этих случаях различаются. Дополнительное отличие состоит в ограничении сверху области допустимых значений параметра затухания.  

 

9. Области существования прямых и обратных волн по параметру затухания 

Из рис.3 и 5 можно видеть, что в диссипативной среде как прямые, так и обратные ПМСВ существуют только в ограниченных областях как по частоте, так и по параметру затухания. Причина ограничения по , состоящая в сближении времени релаксации волны с ее периодом, рассмотрена в разделе №7. Здесь же приведем общий вид областей существования в непрерывных пределах изменения параметра затухания, для чего обратимся к рис.7.    

 

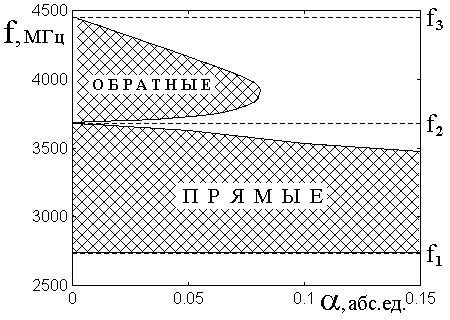
Рис.7. Области существования прямых и обратных ПМСВ.

Параметры соответствуют приведенным на рис.3-6.

 

На этом рисунке штриховкой показаны области, где возможно существование прямых и обратных ПМСВ. Вне этих областей ПМСВ отсутствуют. Пунктирные горизонтальные линии соответствуют граничным частотам спектра ПМСВ, определяемым формулами (20)-(22), и равным соответственно: ,  ,  .

Можно видеть, что при стремлении  к нулю прямые ПМСВ существуют во всей области частот от  до , тогда как область существования обратных ПМСВ при этом, хотя и расширяется, стремясь в пределе к интервалу между  и , однако до вертикальной оси, соответствующей , не доходит (как это для наглядности отмечено свободным от штриховки промежутком), что обусловлено их исключительно диссипативной природой.

Область прямых ПМСВ при увеличении  сужается сверху, тогда как область обратных сужается сверху и снизу, ограничиваясь при значении  на частоте . Такое сужение соответствует верхнему и нижнему ограничениям по частоте кривых 1-4 на рис.5, а также границам пунктирных участков кривых 1-4 на приведенных в следующем разделе рис.8 и 9. 

 

10. Роль диссипации в формировании дисперсии  мнимой части волнового числа

Рассмотрим теперь роль диссипации в формировании дисперсионных свойств мнимой части волнового числа, для чего обратимся к рис.8. 

На рис.8 показаны дисперсионные кривые для мнимой части волнового числа ПМСВ в случае  при различных уровнях диссипации. Кривые построены путем полного решения уравнения (3) без каких-либо ограничений, заключенных в самом этом уравнении. Однако из рис.3 и 5 можно видеть, что области существования как прямых, так и обратных ПМСВ по частоте ограничиваются, не доходя до граничных частот, определяемых формулами (20)-(22). Поэтому на рис.8 участки кривых, выходящие за пределы таких частотных ограничений, хотя и получаются из решения уравнения (3), но в силу условности их существования отмечены пунктиром. Более подробно области ограничения рассмотрены в разделах №8 и №9, здесь же для сохранения общности обсудим полные кривые, получаемые непосредственно из решения уравнения (3).  

 

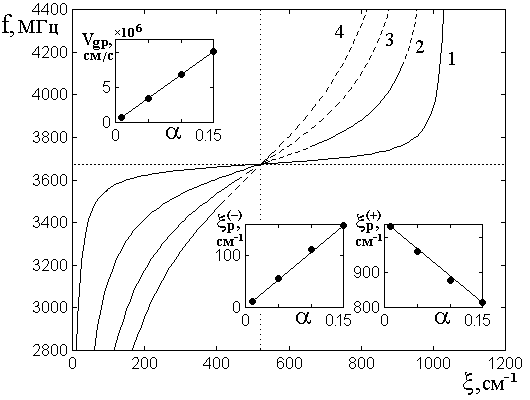
Рис.8. Дисперсия мнимой части волнового числа ПМСВ в случае  при различных уровнях диссипации.

Параметр затухания : 1 – ;  2 – ;  3 – ;  4 – .

Горизонтальная точечная кривая соответствует .

Остальные параметры указаны в разделе №2.

На врезках показаны зависимости предельных значений  и  от параметра .

 

Из рис.8 можно видеть, что по мере увеличения частоты мнимая часть волнового числа всегда монотонно возрастает, то есть затухание волн при этом увеличивается. Вблизи среднего участка кривые имеют перегиб, соответствующий резкому росту затухания при переходе от прямых волн к обратным. По мере увеличения параметра  перегиб становится более плавным, причем его сглаживание проявляется тем сильнее, чем параметр затухания больше. Так для кривой 1, соответствующей , по краям области существования ПМСВ дисперсионные кривые идут почти вертикально, а вблизи середины этой области близки к горизонтали, тогда как для кривой 4, соответствующей , наклон дисперсионной зависимости по всей области ПМСВ значительно превышает таковой для кривой 1 и сохраняется почти постоянным.  

Все кривые начинаются вблизи нижней границы существования прямых ПМСВ  и заканчиваются вблизи верхней границы существования обратных (диссипативных) ПМСВ , частоты которых определяются формулами (20) и (22) соответственно. Перегиб кривых происходит на частоте, соответствующей границе между областями существования прямых и обратных ПМСВ, равной  и определяемой формулой (21). При этом мнимая часть волнового числа единая для всех кривых равна .

Наименьшее значение мнимой части волнового числа при  на частоте  (кривая 1) составляет , а наибольшее значение для той же кривой на частоте  равно . Такие же числа для кривой 4, то есть при  равны соответственно  и .

В правой нижней части рис.8 на врезках показаны зависимости низшего и высшего  значений волнового числа от параметра . Можно видеть, что обе зависимости близки к прямым линиям. Общий их ход отражает сужение области существования ПМСВ по мнимому волновому числу, происходящее по мере увеличения затухания. .

Из врезки в левом верхнем углу рис.8 можно видеть, что по мере увеличения параметра  групповая скорость роста затухания в общей точке пересечения кривых возрастает, то есть волна затухает тем быстрее, чем параметр  больше, причем зависимость  от  является практически линейной.

Обратимся теперь к рис.9, где показаны зависимости групповой скорости роста затухания ПМСВ от мнимой части волнового числа в случае  при различных уровнях диссипации. Пунктирный характер отдельных участков кривых имеет то же значение, что на рис.8.

 

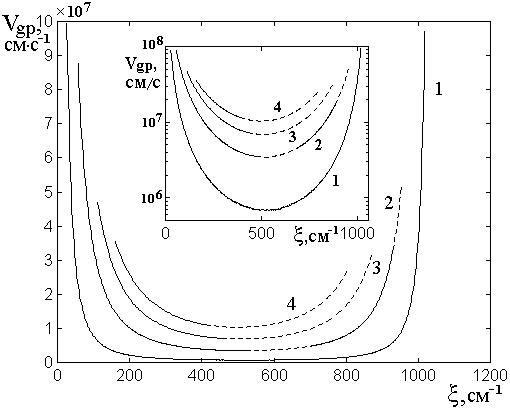
Рис.9. Зависимости групповой скорости затухания ПМСВ от мнимой части волнового числа в случае  при различных уровнях диссипации.

Параметр затухания : 1 – ;  2 – ;  3 – ;  4 – .

Остальные параметры указаны в разделе №2.

На врезках показаны те же кривые в логарифмическом масштабе.

 

Можно видеть, что все кривые по мере приближения к краям области существования ПМСВ возрастают тем более резко, чем параметр затухания  меньше. Минимум кривых приходится на общую точку перегиба кривых на рис.8, соответствующую  и . Рост противоположных ветвей кривых заканчивается при тех значениях , при которых кривые на рис.8 выходят на верхний и нижний пределы по частоте.

На врезке показаны те же зависимости в логарифмическом масштабе, несколько более наглядно иллюстрирующие ход кривых  в области минимумов.

Таким образом, основным результатом настоящего раздела можно считать монотонный рост дисперсионной кривой для мнимой части волнового числа, быстрый вблизи нижней и верхней границ объединенной области существования прямых и обратных ПМСВ и медленный в окрестности частотной границы между этими областями. При этом групповая скорость роста затухания на противоположных границах области существования ПМСВ велика, а вблизи границы, разделяющей области прямых и обратных волн – минимальна.

 

11. Аналогия со случаем электромагнитных волн

Магнитостатические волны являются частным случаем электромагнитных волн (ЭМВ), распространяющихся в магнитной среде в условиях настолько большой магнитной проницаемости, что электрическое поле волны по сравнению с магнитным становится исчезающе малым. В волне любой природы волновой процесс обеспечивается задержанным во времени взаимодействием локальных элементов волны, расположенных в пространственно отстоящих друг от друга точках. В электромагнитной волне такое взаимодействие обеспечивается за счет превращения друг в друга электрического и магнитного полей. В магнитостатической волне, благодаря условиям ферромагнитного резонанса, главную роль играют дипольные поля, создаваемые отдельными намагниченными участками магнитной среды.

Для электромагнитной волны сильное взаимодействие со средой при ферромагнитном резонансе имеет характер известной в оптике  аномальной дисперсии [30], при которой волна испытывает значительное затухание. 

Сравним с качественной стороны дисперсионные свойства прямых и обратных ПМСВ со свойствами ЭМВ в условиях аномальной дисперсии, для чего обратимся к рис.10, где показаны дисперсионные кривые для магнитостатических (а) и электромагнитных (б) волн. 

 

Рис.10. Иллюстрация аналогии между магнитостатическими (а) и  электромагнитными (б) волнами.

Параметры построения аналогичны принятым для рис.3 и 5 при .

Частоты:  ,  ,  .

 

На рис.10а участок дисперсионной кривой  соответствует кривой 1 на рис.3, а участок  – кривой 1 на рис.5. Характерные частоты, показанные горизонтальными точечными линиями, соответствуют границам областей существования прямых и обратных ПМСВ, определяемым формулами (20)-(22).

На рис.10б показана дисперсионная кривая для электромагнитных волн в области аномальной дисперсии между частотами  и . Точки ,  и  соответствуют пересечению дисперсионной кривой с горизонтальными линиями характерных частот. Наклонная пунктирная линия – закон дисперсии ЭМВ в отсутствие взаимодействия волны со средой.

Из сравнения рис.10а с рис.10б можно видеть, что дисперсионная кривая для прямых ПМСВ на участке  подобна таковой для ЭМВ на участке , то есть на подходе снизу по частоте к области аномальной дисперсии.

Дисперсионная кривая для обратных ПМСВ на участке  подобна таковой для ЭМВ на участке , то есть внутри области аномальной дисперсии. Именно в этой области ПМСВ испытывают значительное затухание (раздел №10), что характерно и для ЭМВ в области аномальной дисперсии.

Ниже частоты  и выше частоты  ПМСВ отсутствуют, хотя ЭМВ имеют место. Такое различие обусловлено тем, что вне области между частотами  и  магнитная проницаемость падает и условия существования дипольных волн, каковыми являются ПМСВ, не реализуются.

Таким образом, можно полагать, что дисперсионные свойства ПМСВ в общем случае аналогичны подобным свойствам ЭМВ в среде со значительной магнитной проницаемостью, за счет чего дисперсия ЭМВ становится аномальной. 

 

Заключение

В геометрии плоскопараллельной намагниченной в плоскости ферритовой пластины с использованием дисперсионных соотношений для действительной и мнимой частей волнового числа, полученных в первой части настоящей работы [24], исследованы законы дисперсии для прямых и обратных ПМСВ при параметрах, близких к реальному эксперименту.

Приведены основные алгоритмы численного  расчета обеих компонент волнового числа, групповой скорости и времени установления стационарной амплитуды колебаний намагниченности.

Рассмотрена роль диссипации в формировании дисперсионных свойств действительной и мнимой частей волнового числа. Показано, что в среде с диссипацией дисперсионные кривые ограничены со стороны максимального значения действительной части волнового числа.

Выявлена математическая природа такого ограничения, получено соотношение, являющееся условием существования обеих ветвей поверхностных магнитостатических волн, включающее в себя кроме частоты и волнового числа также параметр затухания и толщину магнитной пластины.

Рассмотрена качественная физическая причина ограничения дисперсионных кривых. На основе анализа соотношения между временем релаксации колебаний намагниченности и периодом распространяющейся волны показано, что рост волнового числа приводит к затуханию волны на расстоянии своей длины, то есть к апериодическому режиму, что и является препятствием для дальнейшего распространения волны.

Выявлены две ветви дисперсионных кривых, соответствующие прямым и обратным волнам.

Для прямых волн выявлен возрастающий характер дисперсионных кривых по мере увеличения действительной части волнового числа. Показано, что по мере увеличения диссипации дисперсионные кривые отклоняются вверх по частоте относительно бездиссипативной кривой, причем такое отклонение проявляется тем сильнее, чем диссипация выше. Отмечено, что вблизи предельного значения волнового числа дисперсионные кривые изгибаются вверх, подходя к граничной частоте с близкой к вертикали касательной.

Определена групповая скорость распространяющейся волны. Показано, что по мере увеличения действительной части волнового числа групповая скорость сначала убывает, а после прохождения через минимум переходит к возрастанию.

Для обратных волн выявлен убывающий характер дисперсионных кривых по мере увеличения действительной части волнового числа. Показано, что по мере увеличения диссипации дисперсионные кривые отклоняются вниз по частоте относительно бездиссипативной кривой, причем такое отклонение проявляется тем сильнее, чем диссипация выше. Отмечено, что вблизи предельного значения волнового числа дисперсионные кривые изгибаются вниз, подходя к граничной частоте с близкой к вертикали касательной.

Определена групповая скорость распространяющейся волны. Показано, что по мере увеличения действительной части волнового числа групповая скорость сначала возрастает, а после прохождения через максимум убывает.

Отмечена качественная симметрия дисперсионных зависимостей для обратных волн таковым для прямых волн относительно горизонтальной оси, соответствующей граничному значению частоты между ними, однако количественные характеристики прямых и обратных волн в этих случаях различаются. Дополнительное отличие состоит в ограничении сверху по частоте области допустимых значений параметра затухания, эквивалентное  ограничению снизу допустимых значений волновых чисел.

В качестве предполагаемой причины такого ограничения отмечен тот же механизм сближения времени релаксации с периодом волны, что и для прямых волн, однако здесь действующий в обратном порядке, что обусловлено встречным направлением фазовой и групповой скоростей для обратных волн.

Определены частотные границы областей существования прямых и обратных волн в зависимости от параметра затухания. Показано, что эти области при увеличении затухания сужаются, причем для обратных волн сужение выражено значительно сильнее, чем для прямых. Для обратных волн выявлено предельное значение параметра затухания, выше которого их существование полностью прекращается. 

При тех же параметрах, близких к эксперименту, построены дисперсионные кривые для мнимой части волнового числа. По мере увеличения мнимой части выявлен монотонный рост дисперсионной кривой, быстрый вблизи нижней и верхней границ объединенной области существования прямых и обратных ПМСВ и медленный в окрестности частотной границы между этими областями, причем скорость роста дисперсионной кривой с увеличением затухания увеличивается.

Выполнен анализ групповой скорости роста затухания, показано, что эта скорость на противоположных границах области существования ПМСВ велика, а вблизи границы, разделяющей области прямых и обратных волн – минимальна.

Проведено качественное сравнение законов дисперсии для магнитостатических волн с таковыми для электромагнитных волн. Показано, что дисперсионные свойства магнитостатических волн в общем случае аналогичны подобным свойствам электромагнитных волн, распространяющихся в среде со значительной магнитной проницаемостью, за счет чего дисперсия электромагнитных волн приобретает аномальный характер.  

 

Благодарность

Авторы признательны сотрудникам ИРЭ им. В.А.Котельникова РАН (Фрязинского филиала): д.ф.-м.н. В.И.Зубкову, д.ф.-м.н. Э.Г.Локку и д.ф.-м.н. А.В.Вашковскому за консультации на начальном этапе работы, а также д.ф.-м.н. С.В. Герусу и к.ф.-м.н. А.Ю.Анненкову за ознакомление с материалами работ  [22,23]. Отдельная благодарность к.ф.-м.н. В.С.Власову (СыктГУ) за внимание к работе и многочисленные стимулирующие замечания.

 

Работа выполнена при финансовой поддержке за счет гранта Российского Научного Фонда (проект № 14-22-00279).

 

Литература

1. Damon R.W., Eshbach J.R. // J. Phys. Chem. Solids. 1961. V.19 №3/4. P.308.

2. Адам Дж.Д. // ТИИЭР. 1988. Т.76. №2. С.73.

3. Исхак В.С. // ТИИЭР. 1988. Т.76. №2. С.86.

4. Шлеман Э.Ф. // ТИИЭР. 1988. Т.76. №2. С.105.

5. Adam J., Davis L., Dionne G., Schloemann E., Stitzer S. // IEEE Trans. on MTT. 2002. V.50. №3. P.721.

6. Вашковский А.В., Зубков В.И., Локк Э.Г., Щеглов В.И. // ПЖТФ. 1989. Т.15. №4. С.1.

7. Вашковский А.В., Зубков В.И., Локк Э.Г., Щеглов В.И. // ПЖТФ. 1989. Т.15. №4. С.5.

8. Вашковский А.В., Зубков В.И., Локк Э.Г., Щеглов В.И. // ЖТФ. 1990. Т.60. №7. С.138.

9. Зубков В.И., Локк Э.Г., Щеглов В.И. // РЭ. 1990. Т.35. №8. С.1617.

10. Vashkovsky A.V., Lock E.H., Shcheglov V.I., Zubkov V.I. // IEEE Trans. on Magn. 1990. V. Mag-26. №5. P.1480.

11. Вашковский А.В., Зубков В.И., Локк Э.Г., Щеглов В.И. // РЭ. 1991. Т.36. №1. С.18.

12. Зубков В.И., Щеглов В.И. // РЭ. 2000. Т.45. №4. С.471.

13. Зубков В.И., Щеглов В.И. // РЭ. 2001. Т.46. №4. С.433.

14. Зубков В.И., Щеглов В.И. // РЭ. 2006. Т.51. №3. С.328.

15. Зубков В.И., Щеглов В.И. // РЭ. 2007. Т.52. №6. С.701.

16. Зубков В.И., Щеглов В.И. // РЭ. 2009. Т.54. №9. С.1064.

17. Зубков В.И., Щеглов В.И. // РЭ. 2012. Т.57. №5. С.565.

18. Вызулин С.А., Розенсон А.Э., Шех С.А. // РЭ. 1991. Т.36. №1. С.164-168.

19. Вызулин С.А. Обобщенные плоские волны в задачах электродинамики магнитогиротропных сред. Диссертация. на соискание уч. ст. д.ф.-м.н. Краснодар. 2000.

20. Макаров П.А., Шавров В.Г., Щеглов В.И. // Электронный "Журнал радиоэлектроники". 2014. №7. С.1-31. http://jre.cplire.ru/jre/jul14/8/text.html,

http://jre.cplire.ru/jre/jul14/8/text.pdf.

21. Макаров П.А., Шавров В.Г., Щеглов В.И. // Сборник трудов XXII Международной конференции «Электромагнитное поле и материалы». Москва: НИУ МЭИ. 2014. С.221-236.

22. Annenkov A.Yu., Gerus S.V. // Book of Abstracts of Moscow International Symposium on Magnetism (MISM). 2014. Published by “Изд-во Физ.фак. МГУ". Moscow. P.863.

23. Анненков А.Ю., Герус С.В. // Сборник трудов XXII Международной конференции «Электромагнитное поле и материалы». Москва: НИУ МЭИ. 2014. С.99-102.

24. Келлер Ю.И., Макаров П.А., Шавров В.Г., Щеглов В.И. // Электронный "Журнал радиоэлектроники". 2016. №2. С.1-32. http://jre.cplire.ru/jre/feb16/2/text.html; http://jre.cplire.ru/jre/feb16/2/text.pdf

25. Гуревич А.Г. Ферриты на сверхвысоких частотах. М.: Гос.Изд.физ.-мат.лит. 1960. 

26. Гуревич А.Г. Магнитный резонанс в ферритах и антиферромагнетиках. М.: Наука. 1973.

27. Гуревич А.Г., Мелков Г.А. Магнитные колебания и волны. М.: Физматлит. 1994.

28. Gilbert T.L. // IEEE Trans. on Magn. 2004. V.40. №6. P.3443.

29. Рэлей Дж.У. Теория звука. Т.1,2. М.: ИЛ. 1955.

30. Ландсберг Г.С. Оптика. М.: Наука. 1976.

31. Вайнштейн Л.А. Групповая скорость затухающих волн. // ЖТФ. 1957. Т.27. №11. С.2606.

32. Гинзбург В.Л. Распространение электромагнитных волн в плазме. М.: Наука. 1967.

33. Власов В.С., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2009. Т.54. №7. С.863.

34. Власов В.С., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2010. Т.55. №6. С.689.

35. Власов В.С., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2011. Т.56. №1. С.84.

36. Власов В.С., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2011. Т.56. №6. С.719.

37. Власов В.С., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2011. Т.56. №9. С.1120.

38. Власов В.С., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2012. Т.57. №5. С.501.

39. Власов В.С., Кирушев М.С., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2013. Т.58. №8. С.806.

40. Власов В.С., Кирушев М.С., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2013. Т.58. №9. С.857.

41. Власов В.С., Котов Л.Н., Щеглов В.И.  Нелинейная прецессия вектора намагниченности в условиях ориентационного перехода (монография). Сыктывкар: ИПО СыктГУ. 2013.

42. Вайнштейн Л.А. Электромагнитные волны. М.: Сов. радио. 1957.