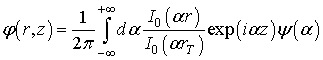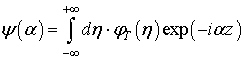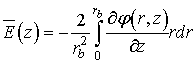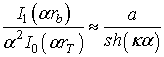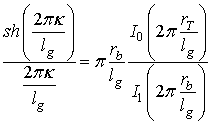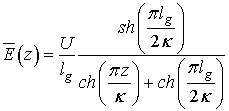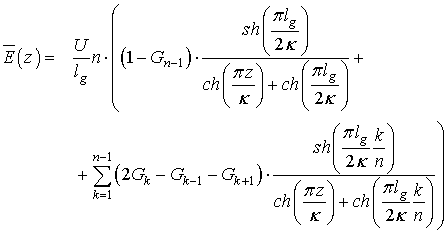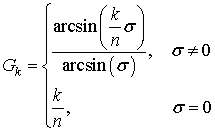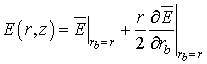УДК 621.385, 537.533.9, 519.688

Модель распределения СВЧ поля в бессеточном зазоре резонатора

 

А. Ю. Байков ²,  О. А. Байкова ¹,  О. А. Перевозчикова ¹

¹Национальный исследовательский ядерный университет (МИФИ)

²Московский финансово-юридический университет (МФЮА)

 

Статья поступила в редакцию 20 марта 2016 г.

 

Аннотация. Предложена математическая модель распределения продольной составляющей электрической компоненты СВЧ поля в эффективном зазоре резонатора. Распределение получено в виде аналитической формулы с одним управляющим параметром. На основе численного моделирования получена зависимость управляющего параметра от геометрических параметров зазора. Показано, что погрешность полученного аналитического решения  по сравнению с результатами численного моделирования не превышает 5%, а влияние этой погрешности на погрешность вычисления КПД клистрона не превышает 0.5%.

Ключевые слова: клистрон, СВЧ резонатор, распределение СВЧ поля, математическое моделирование.

Abstract. The mathematical model of the longitudinal distribution of the microwave electric component in the effective RF cavity gap is proposed. The distribution is obtained in the form of the analytical formula with one control parameter.  The dependence of the control parameter on the geometric parameters of the gap is obtained by the numerical simulation. It is shown that the error of the analytical solutions obtained in comparison with the results of numerical simulation does not exceed 5%, and the effect of this error on the error in calculating the klystron efficiency does not exceed 0.5%

Key words: klystron, microwave cavity, microwave field distribution, mathematical simulation.

 

Введение

В настоящее время актуальной является проблема увеличения КПД мощных клистронов и других резонаторных СВЧ приборов о-типа до предельно возможных значений [1]-[5]. Решение этой проблемы связано, в первую очередь, с возможностью проведения многопараметрической оптимизации [6]-[7] на этапе компьютерного моделирования приборов. Для этого требуется компьютерная модель, сочетающая в себе высокую точность с высокой скоростью расчетов.

Следует отметить, что двумерные и трехмерные эффекты типа радиального расслоения могут только понижать КПД, поэтому необходимым условием достижения высокого КПД клистрона является высокая степень «одномерности» электронных пучков, которая может быть достигнута специальными конструктивными мерами. В этой связи использование одномерных программ для оптимизации клистронов с высоким КПД является вполне оправданным.

Достаточно адекватной и эффективной одномерной моделью клистрона является дискретно-аналитическая модель [8]-[12], на основе которой разработан комплекс программ KlypWin [6],[7],[13]. Соответствующая модель группирования подробно описана в [8], а результаты оптимизации клистронов по этой модели представлены в [1].

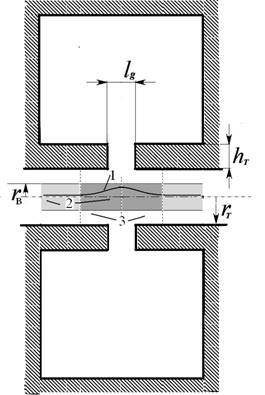
Адекватность модели подразумевает корректное математическое описание всех процессов, происходящих в приборе, в том числе, процессов группирования электронного пучка и отбора энергии. При этом следует учесть, что группирование происходит не только в тех частях труб дрейфа, где отсутствует СВЧ поле, но и в области "эффективного зазора резонатора", т.е. в самом зазоре и в прилегающих к нему частях труб дрейфа, в которых СВЧ поле нельзя считать нулевым (рис. 1).

 

Рис.1.Схема резонатора с бессеточным зазором.  1 – зависимость продольной электрической составляющей СВЧ поля резонатора от координаты; 2 – область электронного пучка; 3 – область эффективного зазора.

 

Распределение СВЧ поля в эффективном зазоре может быть найдено с помощью численного моделирования на основе метода конечного элемента по таким программам, как HFSS, SuperFish и т.д. Однако расчет по этим программам занимает значительное время, а результаты каждого расчета справедливы только для одной конструкции резонатора с конкретными значениями его геометрических характеристик. При оптимизации прибора эти характеристики необходимо все время изменять, поэтому для проведения оптимизации требуется более эффективная  (желательно аналитическая) модель распределения поля в зазоре.

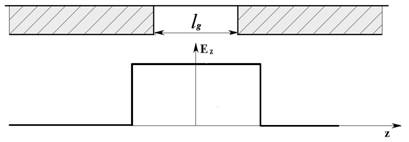
Наиболее простая из известных в настоящее время аналитических моделей предполагает плоское ([14], рис. 2-a) распределение поля в эффективном зазоре.  Такая модель позволяет качественно правильно описать процессы группирования и отбора энергии, однако при моделировании клистронов с высоким КПД (более 70%) ее точность оказывается недостаточной.

 

a)
b)
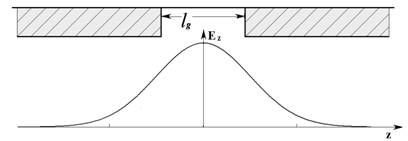
Рис. 2. Приближения a)- плоского  и b)- гауссова распределений поля в зазоре.

 

Другая известная аналитическая модель, использованная в программе AJDISK [15], предполагает гауссово распределение поля  ( рис.2-b) . Эта модель точнее, чем модель плоского распределения, но и она дает неверную асимптотику при удалении от центра зазора, т.к. поле в запредельном волноводе должно спадать как . Это, в свою очередь, приводит, кроме  неточности распределения поля,  к неверной оценке минимально допустимой длины трубы дрейфа, обеспечивающей разделение полей соседних резонаторов.

Настоящая работа посвящена построению аналитической модели распределения СВЧ поля в зазоре резонатора, настраиваемой с помощью численного моделирования по программе HFSS и обеспечивающей правильную асимптотику и хорошее совпадение с результатами численных расчетов.

Модель  реализована в комплексе программ KlypWin.

1. Постановка задачи

В дискретно-аналитической модели, использованной в программе KlypWin, для описания взаимодействия электронного пучка с электромагнитными полями используется процедура усреднения по сечению пучка, соответственно, СВЧ поле также должно быть усреднено по сечению пучка. При этом усреднения радиальной и азимутальной составляющих дает ноль, поэтому задача состоит в нахождении усредненной по пучку продольной составляющей электрической компоненты СВЧ поля как функции координаты .

В [16] решена задача для распределения магнитостатического потенциала, который найден в приближении азимутальной симметрии как функция координат и  с помощью разложения в интеграл Фурье. СВЧ потенциал в зазоре резонатора является квазистатическим [17], в приближении одного вида колебаний его можно представить в виде , где  - СВЧ частота. Далее будем рассматривать только пространственную компоненту СВЧ потенциала, называя ее для краткости СВЧ потенциалом. Соответственно, под "электрическим полем" будем понимать пространственную компоненту напряженности электрического поля.

Учитывая приведенные соображения, можно распространить подход, использованный в [16],  на распределение СВЧ поля в эффективном зазоре.

Следуя [16], будем считать, что СВЧ потенциал  как функция продольной координаты  и радиальной координаты  определяется выражением

,                                 (1)

 

где  - модифицированная функция Бесселя нулевого порядка, - внутренний радиус трубы, - переменная интегрирования, имеющая смысл пространственной Фурье-гармоники, а

.                                                 (2)

 

В выражении (2) функция  - это заданное распределение СВЧ потенциала на внутренней границе трубы и на ее продолжении в область зазора, аргумент  имеет смысл координаты вдоль внутренней поверхности трубы.

Функция  является управляющей функцией, задавая ее, можно получить любое возможное распределение СВЧ потенциала в трубе.

Продольная составляющая СВЧ поля связана с СВЧ потенциалом выражением , поэтому усредненное по области пучка распределение поля  запишется как

,                                                             (3)

 

где  - радиус пучка.

Выражения (1)-(3) решили бы поставленную задачу, если управляющая функция  была бы известна для любого заданного резонатора. Но эта функция неизвестна. Кроме того, для поточечно заданной функции  вычисление распределения поля по выражениям (1)-(3) является очень затратным, т.к. требует тройного вложенного  численного интегрирования несобственных интегралов. Соответствующий вычислительный алгоритм эффективным назвать нельзя. Рассмотрим возможности получения из выражений (1)-(3) более простой аналитической зависимости.

2. Вывод аналитических зависимостей

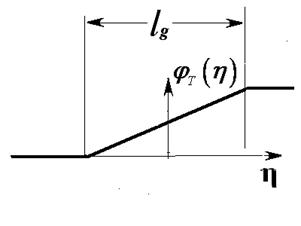
В [16] получено выражение для распределения потенциала при линейной  в области зазора управляющей функции вида (рис.3-a):

 

 

 

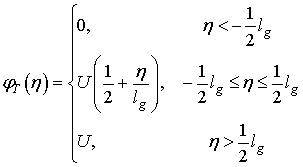
,                                   (4)  

 

 

где - протяженность зазора, - амплитуда напряжения на зазоре.

 

a)		b)
Рис. 3. Аппроксимации управляющей функции a)-линейная, b)-кусочно-линейная

 

В выражении (4) координата  отсчитывается от центра зазора. Такой вид управляющей функции соответствует предположению о неограниченной толщине торца трубы  (рис.1-а), поэтому задание функции  в виде (4) можно назвать приближением "толстого торца трубы". Распределение потенциала (1) при управляющей функции вида (4) будет иметь вид

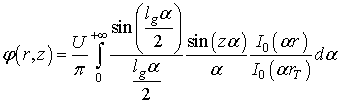.                         (5)

При этом усредненное по сечению пучка электрическое поле (3) можно вычислить аналитически

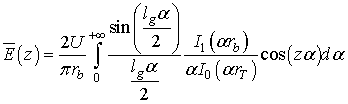,                    (6)

где  - модифицированная функция Бесселя первого порядка.

Выражение (6) существенно проще, чем система (1)-(3), однако оно все равно представляет некоторую вычислительную сложность, т.к. требует численного взятия интеграла с бесконечным пределом.

Для упрощения выражение (6) воспользуемся следующей аппроксимацией.

,                                                          (7)

где  и  - параметры аппроксимации, которые необходимо определить  из условия наименьшей разницы между левой и правой частями выражения (7).

Потребуем точного равенства в выражении (7) при  (для нулевой пространственной Фурье-гармоники) и при  (для Фурье-гармоники с периодом ). Из равенства при  получаем . С учетом этого условие равенства при  приводит к трансцендентному уравнению

 ,                                               (8)

из которого находится параметр.

После этого усредненное по сечению пучка поле получается  в виде следующей аналитической зависимости

.                                           (9)

Выражения (8) и (9) дают решение задачи о распределении усредненной по сечению пучка продольной составляющей электрической компоненты СВЧ поля в эффективном зазоре в приближении толстого торца трубы.

Не всегда торец трубы  можно считать бесконечно толстым, иногда необходимо учитывать его конечную толщину. При этом решение, определяемое выражениями (8), (9), становится неприменимым.

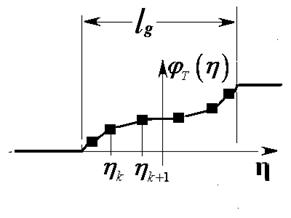
Рассмотрим более общий случай задания управляющей функции  в виде кусочно-линейной зависимости (рис.3-b). Пусть

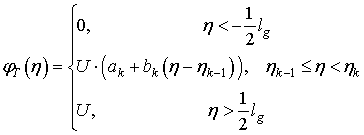,                   (10)

где ,  - количество сегментов кусочно-линейной функции,  - координаты узлов.

Далее для простоты будем считать, что все сегменты кусочно-линейной функции имеют одинаковую длину, т.е. , .

Для управляющей функции вида (10) интеграл в выражении (2) берется, и функция  получается в виде

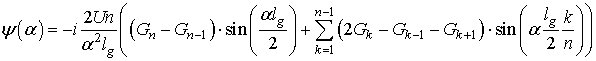   (11)

где  - узловые значения управляющей функции, причем , , , .

После подстановки выражения (11) в выражения (1) и (3) и использования аппроксимации (7) получим следующее выражение для поля в зазоре, усредненного по сечению пучка.

,         (12)

где параметр  находится из уравнения (8).

Для вычисления напряженности поля с помощью выражения (12) необходимо задать все узловые коэффициенты , кроме фиксированных  и , поэтому выражение (12) задает семейство функций с управляющими параметрами , количество которых равно .

Поставим задачу минимизировать количество управляющих параметров.

Построим для  аппроксимирующую формулу, зависящую от одного управляющего параметра. Качественным соображениям удовлетворяет следующая зависимость.

               ,                             (13)

где  - управляющий параметр, .

Изменение параметра  от 0 до 1 соответствует уменьшению толщины торца трубы от  до 0. При  выражение (12) переходит в выражение (9).

Отметим, что зная среднее по сечению пучка поле, можно легко получить и значение поля на конкретном радиусе по формуле

,                                             (14)

где производная 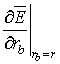 может быть вычислена численно.

 

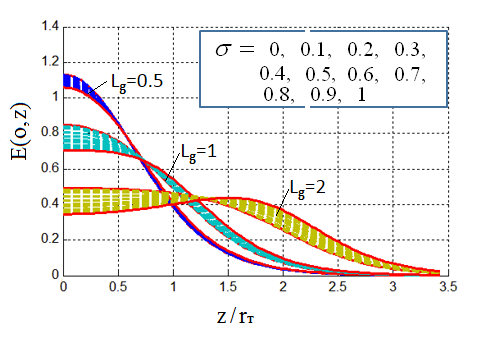
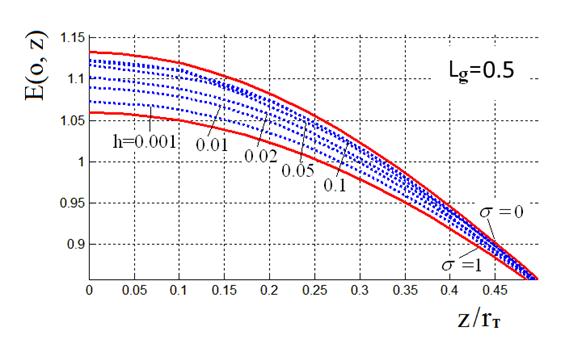
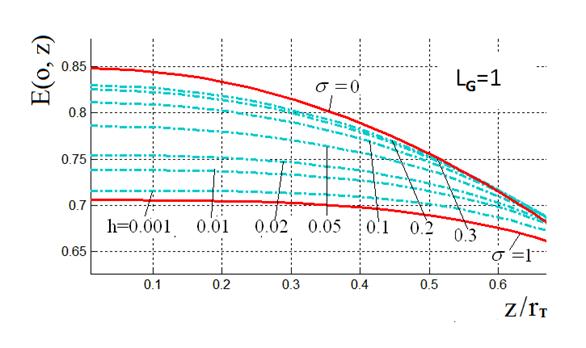
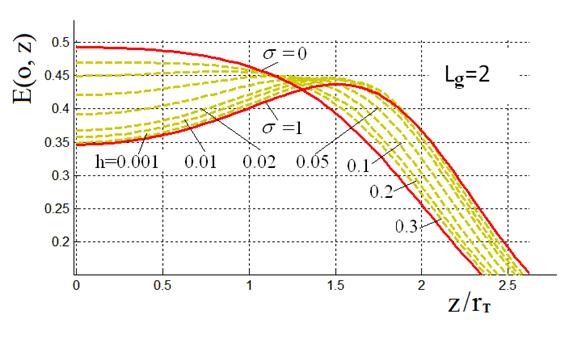
На рис.4 приведены семейства зависимостей  при трех различных значениях отношения . Эти зависимости используются далее для настройки модели с помощью результатов численного моделирования по программе HFSS.

 

Рис.4. Распределение поля на оси по аналитической модели. В каждой из 3-х серий графиков, соответствующих значениям  , , и , управляющий параметр  пробегает  диапазон значений от   (бесконечно толстый торец) до  (бесконечно тонкий торец).

 

3.Настройка аналитической зависимости с помощью численного моделирования

Параметр  в выражении (13) зависит от геометрических параметров эффективного зазора резонатора ,  и . Так как распределение поля инвариантно относительно геометрического масштабирования, можно сократить количество параметров до двух, нормировав все длины на один из них. Нормируем длины на радиус трубы , введя безразмерные параметры , .

Рассмотрим  задачу нахождения зависимости  на основе обеспечения соответствия между результатами расчета поля по полученным аналитическим зависимостям и результатами численного 3D-моделирования по программе HFSS [18].

На первом этапе решения этой задачи была проведена настройка программы HFSS с целью достижения максимальной точности.

Экспериментальным путем было установлено, что для моделирования резонаторов достаточная точность обеспечивается при следующих параметрах численной модели: конечно-разностный элемент сетки имеет тетраэдрическую форму; общее количество элементов сетки от 200000 до 450000; аппроксимация цилиндрической поверхности 5 градусов; допустимая относительная погрешность итераций по частоте 0.0001.

Оптимальная настройка параметров численной модели позволила достичь погрешности по пространственному распределению поля и по итерациям около . После этого по программе HFSS были проведены 3 серии расчетов для значений , ,. В каждой серии расчетов параметр  менялся от значения  до таких значений, при которых дальнейшее увеличение  не приводило к изменению результата. Экспериментальным путем установлено, что это значение . 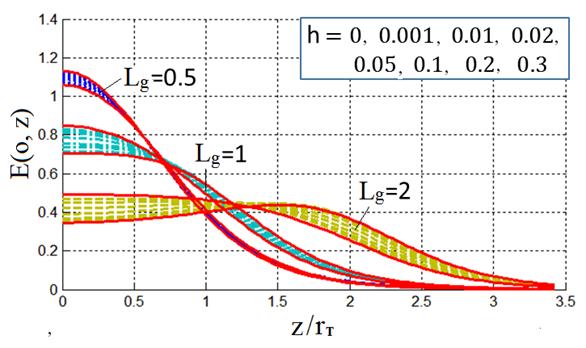В результате каждого расчета распределение поля получалось на различных радиусах, но для настройки аналитической модели были выбраны распределения поля на оси. На рис.5-a  приведены эти распределения, а на рис.5-b - 5-d они  показаны отдельно в увеличенном масштабе. На этих же рисунках сплошными линиями показаны аналитические зависимости для бесконечно толстого торца () и для бесконечно тонкого торца ().  Как видно из приведенных рисунков, аналитические зависимости для толстого и тонкого торцов являются границами семейств численных зависимостей и почти совпадают с соответствующими численными зависимостями для минимального и максимального значений .

 

a)
b)
c)
d)
Рис.5. Распределение поля на оси, рассчитанное по нрограмме HFSS (штриховые линии) для различных значений   вместе с аналитическими зависимостями (сплошные линии) для бесконечно тонкого ()  и бесконечно толстого ()  торцов трубы:  a)- общий вид,  b)-d)- фрагменты в увеличенном масштабе при различных .

 

Далее решалась задача нахождения оптимального значения величины  как функции величин . С этой целью рассматривалась норма разности ,   где  - распределение поля на оси, рассчитанное по программе HFSS, а  - распределение поля на оси, рассчитанное по аналитической модели (12), (13), (8).

Норма  вычислялась как норма в  пространстве , т.е.

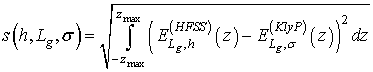,                                        (15)

где  - полуширина эффективного зазора.

Рассмотрим задачу нахождения минимума функции  по аргументу  при фиксированных значениях аргументов  . 

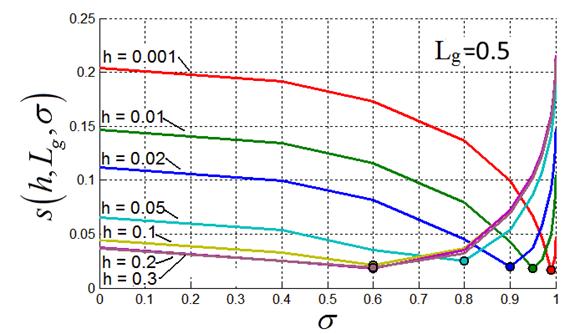
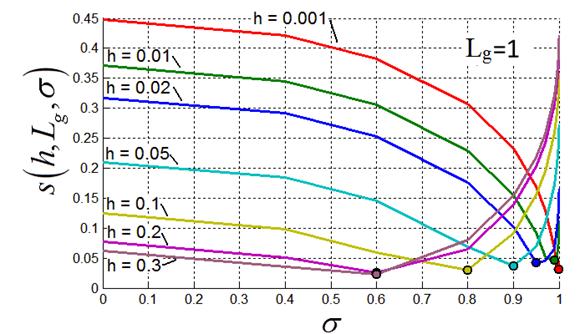
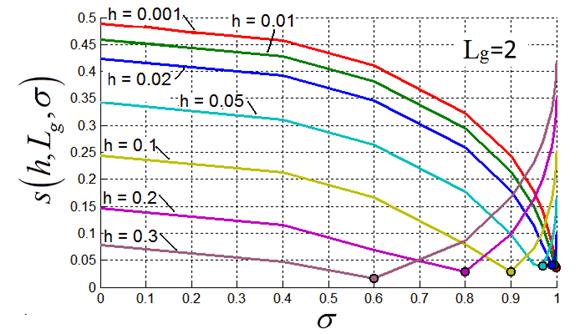
На рис. 6 приведены семейства графиков  при различных значениях . У каждой кривой  есть единственный минимум,  т.е. оптимальная величина  управляющего параметра  определяется однозначно для каждой кривой и может быть найдена в процессе оптимизации как функция величины .

 

a)
b)
c)
Рис. 6. Норма невязки (15)  при различных значениях a)- для  ,   b)- для  ,  c)- для  .

 

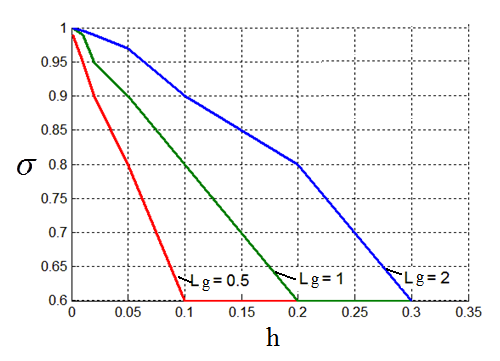
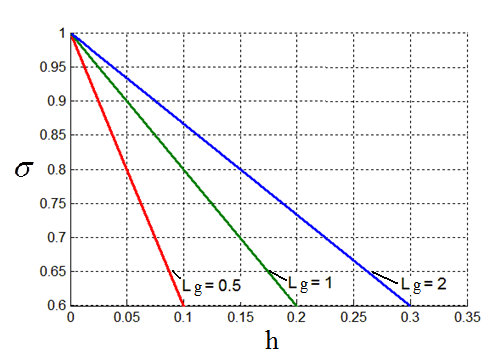
Найденные таким образом зависимости  для различных значений  (рис.7-a) хорошо аппроксимируются пучком прямых (рис.7-b), который можно описать общей линейной зависимостью

,                                                      (16)

где  - некоторая функция. Аппроксимируя эту функцию полиномом второй степени с учетом полученных значений, находим окончательную аппроксимирующую формулу для функции  :

,                     (17)

причем, если по формуле (17) получается отрицательное выражение, то необходимо считать, что .

 

a)
b)
Рис. 7. Зависимость a)- полученная в результате численного моделирования, b)- аппроксимированная по формуле (17).

 

Дополнение соотношений  (12), (13), (8) выражением (17)  полностью решает поставленную задачу. Расчет распределения поля по этим выражениям занимает менее 0.01 с. на стандартном персональном компьютере, т.е. происходит примерно на 4-5 порядков быстрее, чем расчет распределения поля по программе HFSS и по другим аналогичным численным программам. 

Величина , имеющая смысл расхождения между аналитической и численной зависимостями, не превышает 5% (рис.6), причем для большинства точек оказывается еще значительно меньше, т.е. полученные решения обеспечивают погрешность менее 5%.

4. Результаты расчетов клистронов с использованием построенной аналитической модели распределения СВЧ поля

Полученные аналитические зависимости распределения СВЧ поля в зазоре встроены в комплекс программ KlypWin и использованы для моделирования реальных (разрабатываемых) клистронов.

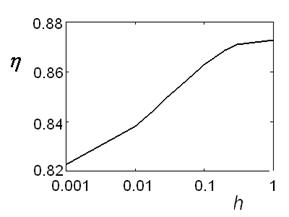
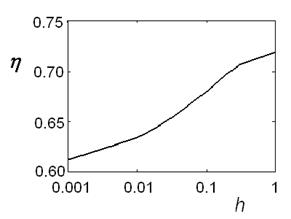
Рассмотрим зависимости КПД от нормированной толщины торца  для перспективного сверхмощного многолучевого клистрона L-диапазона (рис.8-a) и для однолучевого прибора X-диапазона (рис.8-b) в логарифмическом масштабе по оси абсцисс. Входная мощность в обоих случаях соответствует оптимуму для прибора с толстым торцом. Кривые имеют аналогичный вид, они монотонно возрастают при увеличении  и выходят на насыщение примерно при  .  Для первого прибора разница между максимальным и минимальным значениями КПД составляет чуть больше 5%, для второго прибора – около 10% .

 

a)	b)
Рис. 8. Зависимость КПД клистрона от нормированной толщины торца трубы (предполагается одинаковой для  всех зазоров):  а)-перспективный сверхмощный многолучевой клистрон L-диапазона, b)-однолучевой клистрон X –диапазона с выходной мощностью 3 kW.

 

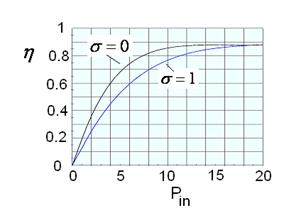
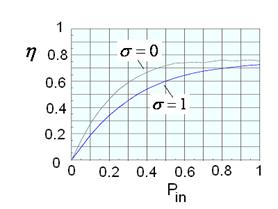
Амплитудные характеристики рассмотренных клистронов (рис. 9) для бесконечно тонкого  ( или )  и для бесконечно толстого ( или  )  торцов трубы показывают, что максимальный КПД почти не зависит от толщины торца трубы,  но при утоньшении трубы насыщение возникает при большей величине входной мощности.  

 

a)	b)
Рис. 9. Амплитудные характеристики для клистронов  в приближении  бесконечно тонкого торца трубы () и в приближении бесконечно толстого торца трубы () : а)- перспективный сверхмощный многолучевой клистрон L-диапазона,  b)-однолучевой клистрон X –диапазона с выходной мощностью 3 kW.

 

 Расчеты  клистронов с другими параметрами приводит к аналогичным результатам, что позволяет сделать следующие выводы.

1. Эффект пространственного распределения СВЧ-поля в зазорах клистронных резонаторов оказывают влияние на КПД клистрона в пределах от 0 до 10%. Это означает, что погрешность (5%) выведенных аналитических формул вносит вклад в погрешность расчета КПД-клистрона не более, чем 0.5%.

2. При  торец трубы можно считать бесконечно толстым и не учитывать его толщину при расчетах взаимодействия электронного пучка с СВЧ полем . В частности, для всех многолучевых клистронов (MBK) можно пользоваться приближением толстого торца и, соответственно, вместо формул (12), (13) использовать более простую формулу (9).

В целом, полученные результаты показывают, что построенная модель может успешно использоваться для моделирования клистронов, причем, ее использование возможно не только в программе KlypWin, но и в любых других одномерных программах моделирования клистронов. 

Заключение

Таким образом, построена аналитическая модель распределения продольной составляющей электрической компоненты СВЧ-поля в системе "зазор резонатора + прилегающие части трубы дрейфа" в виде семейства функций, зависящих от одного управляющего параметра.

Такие же зависимости получены с помощью численного моделирования на основе конечноэлементной программы HFSS. Математическая обработка массива результатов численных и аналитических вычислений позволила найти аппроксимирующую зависимость управляющего параметра от геометрических параметров резонатора - относительной протяженности зазора и относительной величины толщины трубы. В результате получена аналитическая модель, обеспечивающая погрешность вычислений менее 5%  при увеличении быстродействия (по сравнению с численным расчетом) на 4-5 порядков.

Построенная модель реализована в комплексе программ KlypWin. Показано, что при изменении толщины торца трубы при прочих фиксированных параметрах КПД клистрона может изменяться на несколько процентов, причем, влияние толщины торца на КПД является заметным только при нормированной толщине торца .

При этом влияние погрешности выведенных формул на погрешность вычисления КПД клистрона не превышает 0.5%.

 

Литература

1.     Байков А.Ю., Грушина О.А., Стриханов М.Н. Моделирование условий достижения максимального КПД в клистронах дециметрового диапазона. // ЖТФ. 2014. Т. 84. Вып.3. C. 113-119.

2.      Байков А.Ю., Грушина О.А., Колунтаев И.В., Стриханов М.Н. Поэтапная оптимизация клистрона с высоким КПД и с мощностью пучка 8.5МВт. // Тр. конф. Математика, информатика, естествознание в экономике и обществе. М.: МФЮА, 2014. С.117-124.

3.     Байков А.Ю., Байкова О.А., Мулярик Е.И., Стриханов М.Н. Синтез клистронов с максимальным КПД на основе приведенной длины.// Тр. конф. Математика, информатика, естествознание в экономике и обществе. М.: МФЮА, 2015. С.131-135.

4.     Байков А.Ю., Грушина О.А., Стриханов М.Н. Моделирование зависимости максимального КПД от коэффициента усиления в трехрезонаторном клистроне дециметрового диапазона. //Вестник МФЮА. 2013. № 1. С.116-125.

5.     Байков А.Ю., Грушина О.А., Стриханов М.Н. Исследование зависимости максимального КПД от коэффициента усиления в двухрезонаторных клистронах. // ЖТФ, 2013. Т. 83. Вып.4. C.127-133.

6.     Антонова Г.М., Байков А.Ю. Использование ЛПτ -поиска с усреднением для выбора параметров при синтезе мощных вакуумных резонаторных СВЧ-приборов О-типа //Тр. 5-межд. конф. Идентификация систем и задачи управления. М.: ИПУ, 2006. С.823-837.

7.     Байков А.Ю., Грушина О.А. Дискретно-аналитическая модель клистрона и многопараметрическая оптимизация. //Тр. конф. Проблемы СВЧ-электроники. М.: МИЭМ НИУ ВШЭ, 2013. С.34.

8.     Байков А.Ю., Грушина О.А., Стриханов М.Н., Тищенко А.А. Математическая модель трансформации электронного пучка в узкой трубе.//ЖТФ. 2012. №6. С. 90 – 100.

9.     Байков А.Ю. Компьютерное моделирование мощных и сверхмощных резонаторных СВЧ приборов О-типа //Информационно-измерительные и управляющие системы. 2010. Т.8. №4. С.36-46.

10. Байков А.Ю., Байкова О.А. К вопросу об оптимальном торможении d - сгустка в СВЧ поле.// Тр. конф. Математика, информатика, естествознание в экономике и обществе. М.: МФЮА, 2015. Т.1. С.136-145.

11.  Байков А.Ю., Грушина О.А., Стриханов М.Н., Тищенко А.А. . Влияние пространственного заряда на процесс группирования в клистроне в рамках "приближения замороженного пучка". //Вестник МФЮА. 2012. № 1. С.68-77.

12.  Байков А.Ю., Грушина О.А., Стриханов М.Н. Решение уравнения группирования интенсивного электронного пучка в узкой трубе методом кинематического шага. //Вестник МФЮА. 2013. № 1. С.32-40.

13.     Байков А.Ю., Ежиков В.Б. Редактируемый интерфейс ввода-вывода данных для вычислительной модели, включающей многопараметрическую оптимизацию. /Вестник МФЮА. 2011. №1. С.173-182.

14.   Гайдук В.И., Палатов К.И., Петров Д.М. Физические основы электроники СВЧ.  М.: Сов. радио, 1971. 600с.

15. A. J. Jensen, G. Caryotakis, D. Scheitrum, D. Sprehn, and B. Steele. “Sheet beam klystron simulations using AJDISK,”//Proc. IEEE 7th. IVEC Conf. Monterey, CA, USA, Apr. 2006. PP. 489-490.

16.    Глазер В. Основы электронной оптики, пер. с нем. М.: Гос. изд. техн.-теор. лит., 1957. §77 и 89.

17. Лебедев И.В. Техника и приборы СВЧ. М.: Высш. Шк., 1972. Т.2. 376с.

18.Банков С.Е., Курушин А.А. Разевиг В.Д. Анализ и оптимизация трехмерных СВЧ структур с помощью HFSS. М.: СОЛОН-Пресс, 2004. 208с.