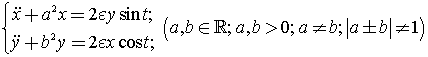УДК 517.437, 531, 534, 621.37
СПЕКТРАЛЬНО-АНАЛИТИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ ОТДЕЛЬНЫХ КЛАССОВ НЕАВТОНОМНЫХ МОДЕЛЬНЫХ СИСТЕМ С ПЕРИОДИЧЕСКОЙ МАТРИЦЕЙ
А. А. Егоров1, Ю. А. Коняев2, Nguyen Viet Khoa3
1 Институт общей физики им. А.М. Прохорова РАН
2 НИУ Московский энергетический институт
3 Kien Giang Teacher Training College, Vietnam
Статья поступила в редакцию 18 января 2016 г., после доработки – 17 февраля 2016 г.
Аннотация. Представленная работа посвящена развитию известных математических методов, а также разработке новых спектрально-аналитических методов и конструктивных алгоритмов, необходимых при анализе различных теоретических линейных и квазилинейных динамических моделей, реализуемых в виде систем обыкновенных дифференциальных уравнений с периодической, полиномиальной и полиномиально периодической матрицей. Такие модели имеют большое значение при изучении ряда реальных физических явлений и процессов. Основное внимание в работе уделено рассмотрению спектрального варианта метода усреднения при анализе неавтономных систем дифференциальных уравнений с периодической матрицей, описывающих регулярно возмущенные системы. В статье также приведены некоторые результаты использования указанных методов для исследования отдельных реальных физических явлений, представляющих несомненный практический интерес. В частности проанализировано взаимодействие двух связанных линейных осцилляторов в отсутствие резонансных явлений.
Ключевые слова: неавтономные системы, уравнение Матье, параметрический резонанс, спектральный метод, дифференциальные уравнения с периодической матрицей, исследование устойчивости, линейный осциллятор.
Abstract. The presented work is devoted to the development of known mathematical methods, and also working out of new spectral analytical methods and constructive algorithms necessary at the analysis of various theoretical linear and quasi-linear dynamic models, realized in the form of systems of ordinary differential equations with periodic, polynomial and polynomially periodic matrix. Such models are of great importance at studying of some real physical phenomena and processes. The basic attention in work is given to consideration of a spectral variant of the averaging method at the analysis of non-autonomous systems of differential equations with the periodic matrix, describing regularly perturbed systems. Some results of use of the specified methods for research of the specific real physical phenomena representing doubtless practical interest also are resulted in the paper. In particular the interaction of two coupled linear oscillator in the absence of resonance phenomena is analyzed.
Key words: non-autonomous systems, Mathieu equation, parametric resonance, spectral method, differential equations with periodic matrix, study of stability, linear oscillator.
Введение
Значительная часть физических, биологических, социальных, экономических и других процессов может быть записана (для дальнейшего анализа и исследования) в виде модельных неавтономных линейных и квазилинейных систем обыкновенных дифференциальных уравнений [1-24].
Напомним, что автономная система
дифференциальных уравнений (иногда: стационарная система
дифференциальных уравнений) – частный случай системы дифференциальных
уравнений, когда время (аргумент) ![]() не входит явным
образом в функции, описывающие данную систему.
не входит явным
образом в функции, описывающие данную систему.
Первоначально указанные системы изучались с помощью как аналитических, так и асимптотических (приближенных качественных) методов. Численные методы были слабо развиты и использовались мало. Но очень быстро известные аналитические методы себя исчерпали и, по мере развития ЭВМ и вычислительных методов, на следующем этапе развития численные и компьютерные методы исследования вышли на первое место.
Линеаризация задач теории (в общем случае – нелинейных) колебаний приводит к отсутствию устойчивых состояний движения в зонах (областях) резонанса и близких к нему, что означает, по сути, потерю таких решений.
Более того: идеи линеаризации малоприменимы для решения многих проблем, с которыми физика и техника постоянно сталкивались и продолжают сталкиваться [8-22].
Вместе с тем данная проблема периодически возникает при решении различных прикладных задач в различных областях не только физики и техники, но и электроники, механики, биологии, экологии и медицины (см., например, [4-22]).
Отметим для примера только некоторые из таких задач:
а) бесконтактное ориентирование, удержание и управление микродеталями при сборке различных устройств и приборов (роботизация);
б) селективное разделение различных порошков (магнитных, ферромагнитных);
в) сверхчувствительные датчики полей (электрических, магнитных, оптических, тепловых, акустических и др.);
г) взвешивание, удержание и перемещение различных объектов (одиночных молекул, гироскопов, транспорта на магнитном подвесе);
д) создание ловушек частиц различного типа с широким диапазоном размеров (от нано до макро, включая клетки, электроны, ионы, атомы и молекулы) и изучение свойств и динамики отдельных частиц в таких ловушках, электродинамическое удержание плазмы;
e) получение автономных, устойчивых, осциллирующих систем, в частности: самоустойчивой плазмы, устойчивых треков волноводных и квазиволноводных мод в нестационарных тонкопленочных и жидкостных волноводах.
Известно, что решение таких задач даже в первом приближении наталкивается на серьезные математические и физические проблемы.
Так физическая проблема заключается в том, что в области взвешивания частиц при отсутствии источников поля (электрического, магнитного или гравитационного) могут существовать единственно особые точки – седловые [4-6, 12, 14]. В этих точках частица в одном направлении будет втягиваться в область взвешивания, а в другом выталкиваться. Более того, согласно теореме Ирншоу (1842) в статике устойчивое удержание частицы просто невозможно. А в динамике нестабильное равновесие может стать устойчивым (Браунбек, 1939). В динамике же исследование подобных задач наталкивается с одной стороны на серьезные проблемы физической интерпретации, а с другой – на математические трудности их решения.
Основная математическая проблема связана с тем, что до настоящего времени нет общей теории колебаний сильно нелинейных систем (при отсутствии малого параметра) и в появлении различных особенностей [14].
В настоящее время для дальнейшего успешного развития качественной теории обыкновенных дифференциальных уравнений (ОДУ), включая вопросы устойчивости, необходимо хорошо обоснованное сочетание аналитических и численных методов. Преобладание одного из этих методов исследования будет только тормозить развитие теории ОДУ.
В данной работе уделено особое внимание разработке новых аналитических спектральных методов, которые могут быть полезны при исследовании неавтономных систем ОДУ с периодической, полиномиальной и полиномиально периодической матрицей с учетом одного из вариантов метода расщепления (см., например, [11]).
Напомним, что в традиционном спектральном методе
приближенное решение ![]() различных радиофизических,
радиотехнических, электрических и механических задач, описываемых ОДУ, ищется в
следующем виде (см., например, [23, 24]):
различных радиофизических,
радиотехнических, электрических и механических задач, описываемых ОДУ, ищется в
следующем виде (см., например, [23, 24]):
где коэффициенты ![]() –
собственные значения, а
–
собственные значения, а ![]() –
собственные функции (собственные формы колебаний).
–
собственные функции (собственные формы колебаний).
Можно показать (см., например, [24]), что решение дифференциального уравнения
описывающего сложную
электрическую цепь, можно искать в виде (1), т.е. по сути, необходимо решить
задачу на собственные значения (частоты) и собственные (базисные) функции, т.е.
собственные формы колебаний. В уравнении (2): ![]() – ток
(в общем случае N-мерный вектор токов системы;
– ток
(в общем случае N-мерный вектор токов системы; ![]() – число контуров);
– число контуров); ![]() – индуктивность (в общем случае это
матрица индуктивностей);
– индуктивность (в общем случае это
матрица индуктивностей); ![]() – активное
сопротивление (в общем случае это матрица сопротивлений);
– активное
сопротивление (в общем случае это матрица сопротивлений); ![]() – коэффициент емкостного сопротивления (в
общем случае это матрица коэффициентов емкостных сопротивлений);
– коэффициент емкостного сопротивления (в
общем случае это матрица коэффициентов емкостных сопротивлений); ![]() – N-мерный вектор
напряжений, действующих в контурах системы (см. Рис. 1).
– N-мерный вектор
напряжений, действующих в контурах системы (см. Рис. 1).
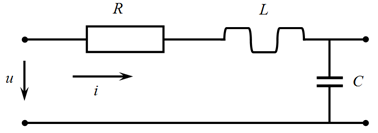
Рис. 1. Один из контуров сложной электрической цепи.
На схеме обозначены: R – активное сопротивление, L – индуктивность, С – емкость, i – ток, u – напряжение.
Неизвестные величины ![]() могут
быть найдены, например, из условия равенства нулю нормы невязки, введённой в
пространстве
могут
быть найдены, например, из условия равенства нулю нормы невязки, введённой в
пространстве ![]() (пространство функций, интегрируемых с
квадратом). В качестве ортогональных базисных функций (собственных векторов)
(пространство функций, интегрируемых с
квадратом). В качестве ортогональных базисных функций (собственных векторов) ![]() могут использоваться, например, интерполяционные
многочлены.
могут использоваться, например, интерполяционные
многочлены.
Используя спектральное разложение (1), можно
получить для достаточно гладких функций экспоненциальную скорость сходимости
приближенного решения к точному. Это основное преимущество спектрального
метода: очень точные приближенные решения могут быть получены при небольшом
числе слагаемых, причём ошибка аппроксимации будет уменьшаться экспоненциально
с ростом ![]() .
.
Важно подчеркнуть, что известен только ряд теорем
[12] об исследовании систем вида ![]() с почти постоянной матрицей, где возможно применение спектрального
метода. Здесь необходимо отметить, например, хорошо известную в физике теорему Флоке-Ляпунова
(теорема Блоха, Флоке-Блоха) [12], в которой говорится о возможности
преобразования линейной периодической системы
с почти постоянной матрицей, где возможно применение спектрального
метода. Здесь необходимо отметить, например, хорошо известную в физике теорему Флоке-Ляпунова
(теорема Блоха, Флоке-Блоха) [12], в которой говорится о возможности
преобразования линейной периодической системы ![]() с помощью невырожденной замены
с помощью невырожденной замены ![]() к
эквивалентной системе с постоянной матрицей вида
к
эквивалентной системе с постоянной матрицей вида ![]() , что позволяет судить о характере поведения её
решения с учетом структуры спектра матрицы С, однако данная терема не
является конструктивной, так как до настоящего времени не разработан алгоритм
построения нужной замены.
, что позволяет судить о характере поведения её
решения с учетом структуры спектра матрицы С, однако данная терема не
является конструктивной, так как до настоящего времени не разработан алгоритм
построения нужной замены.
Так при рассмотрении неавтономной системы, описываемой уравнением Матьё [4-6, 12-16]
где ![]() – параметры системы, обнаруживаются
области стабильности, в которых величина
– параметры системы, обнаруживаются
области стабильности, в которых величина ![]() ограничена
и меняется апериодически, и, в соответствии с теоремой Флоке-Ляпунова (теорема
Блоха), величина
ограничена
и меняется апериодически, и, в соответствии с теоремой Флоке-Ляпунова (теорема
Блоха), величина ![]() является двухпериодической
функцией.
является двухпериодической
функцией.
В этой связи особую важность
приобретает исследование параметрического резонанса – явления раскачки
колебаний при периодическом изменении некоторых параметров исследуемой
колебательной системы. При этом изменяются параметры элементов, в которых
сосредотачивается энергия колебаний (реактивные или энергоемкие параметры).
Явление параметрического резонанса возможно в колебательных системах различной
природы, например, в электрическом колебательном контуре. В последнем
реактивными параметрами являются емкость ![]() индуктивность
индуктивность
![]() , в которых собственно и запасены
электрическая
, в которых собственно и запасены
электрическая ![]() (
(![]() –
величина заряда на обкладках конденсатора) и магнитная
–
величина заряда на обкладках конденсатора) и магнитная ![]() энергии
(
энергии
(![]() – величина тока в катушке индуктивности).
– величина тока в катушке индуктивности).
Собственные колебания в
электрическом контуре (без потерь) с постоянными параметрами ![]() и
и ![]() происходят
с частотой
происходят
с частотой ![]() . А полная энергия
. А полная энергия ![]() ,
запасенная в контуре, сохраняется неизменной. При этом происходит ее
периодическая трансформация из электрической в магнитную и обратно с частотой
,
запасенная в контуре, сохраняется неизменной. При этом происходит ее
периодическая трансформация из электрической в магнитную и обратно с частотой ![]() . При действии на электрический контур
внешней накачки (работа внешних сил) происходит изменение параметров
. При действии на электрический контур
внешней накачки (работа внешних сил) происходит изменение параметров ![]() и
и ![]() ,
которое ведет к изменению полной энергии системы. Например, если изменять
емкость
,
которое ведет к изменению полной энергии системы. Например, если изменять
емкость ![]() периодически в такт изменениям полной
энергии, уменьшая ее в моменты, когда
периодически в такт изменениям полной
энергии, уменьшая ее в моменты, когда ![]() и
и ![]() максимальны, и увеличивая в обратном
случае (
максимальны, и увеличивая в обратном
случае (![]() и
и ![]()
![]() 0), то в среднем за период над системой
будет совершаться положительная работа, следовательно, полная энергия и
амплитуда колебаний будут монотонно нарастать.
0), то в среднем за период над системой
будет совершаться положительная работа, следовательно, полная энергия и
амплитуда колебаний будут монотонно нарастать.
Если изменять параметры
колебательной системы (например, электрического колебательного контура или
гироскопического устройства) с
периодом ![]() (кратным полупериоду собственных колебаний
(кратным полупериоду собственных колебаний
![]() ), то параметрический резонанс проявится
наиболее эффективно:
), то параметрический резонанс проявится
наиболее эффективно:
где ![]() – целое число,
– целое число, ![]() – частота внешней накачки.
– частота внешней накачки.
Как известно, математически колебания в
таких системах описываются обыкновенными дифференциальными уравнениями с
переменными коэффициентами (неавтономные
системы). Так в случае электрического колебательного контура с
переменной емкостью ![]() (омическое сопротивление
контура
(омическое сопротивление
контура ![]() ) дифференциальное уравнение второго
порядка относительно электрического заряда
) дифференциальное уравнение второго
порядка относительно электрического заряда ![]() имеет
следующий вид:
имеет
следующий вид:
где ![]() . Уравнение (5)
известно как уравнение Хилла.
Согласно теореме Флоке, общее решение уравнения (5) можно записать в следующем
виде:
. Уравнение (5)
известно как уравнение Хилла.
Согласно теореме Флоке, общее решение уравнения (5) можно записать в следующем
виде:
где ![]() – коэффициенты, определяемые из начальных
условий;
– коэффициенты, определяемые из начальных
условий; ![]() – некоторый коэффициент, зависящий от параметров системы;
– некоторый коэффициент, зависящий от параметров системы; ![]() –
периодическая функция с периодом
–
периодическая функция с периодом ![]() .
.
Если выполнено условие (4), то ![]() и
один из членов выражения (3) дает нарастающие во времени колебания в системе.
При
и
один из членов выражения (3) дает нарастающие во времени колебания в системе.
При ![]() , когда частота накачки
, когда частота накачки ![]() равна частоте колебаний
равна частоте колебаний ![]() в системе (у величин
в системе (у величин ![]() и
и ![]() ),
наблюдается наиболее быстрая раскачка колебаний. Однако рост амплитуды
колебаний возможен не только при точном выполнении соотношений (4), но и в
некоторых конечных интервалах значений
),
наблюдается наиболее быстрая раскачка колебаний. Однако рост амплитуды
колебаний возможен не только при точном выполнении соотношений (4), но и в
некоторых конечных интервалах значений ![]() вблизи
вблизи
![]() в так называемых зонах неустойчивости.
Эти зоны имеют тем большую ширину, чем сильнее изменяются параметры системы
в так называемых зонах неустойчивости.
Эти зоны имеют тем большую ширину, чем сильнее изменяются параметры системы ![]() и
и ![]() .
Заметим, что в частном случае при синусоидальном изменении величины
.
Заметим, что в частном случае при синусоидальном изменении величины ![]() уравнение (5) называется уравнением
Матьё.
уравнение (5) называется уравнением
Матьё.
Известно, что параметрический
резонанс приводит к неустойчивости колебательной системы, при которой
наблюдается нарастание первоначальных малых флуктуаций в системе, среди которых
(в силу статистического характера таких процессов) всегда есть составляющая
колебаний с подходящей фазой по отношению к фазе изменения параметров системы
(синфазность процессов). Если потерь в системе нет или они достаточно малы,
неустойчивость наступает при достаточно малой глубине изменения параметров. При
наличии потерь (система с затуханием, например, электрический контур с ![]() или механический маятник с переменной
длиной подвеса с трением) неустойчивость возникает только при больших изменениях
параметров системы
или механический маятник с переменной
длиной подвеса с трением) неустойчивость возникает только при больших изменениях
параметров системы ![]() и/или
и/или ![]() ,
когда параметрическая накачка внешней энергии в систему превосходит потери. Существующие зоны неустойчивости при этом
уменьшаются или могут даже исчезнуть.
,
когда параметрическая накачка внешней энергии в систему превосходит потери. Существующие зоны неустойчивости при этом
уменьшаются или могут даже исчезнуть.
Важно подчеркнуть, что в
условиях параметрического резонанса нет бесконечного роста амплитуды колебаний,
поскольку при достаточно больших амплитудах этот рост ограничен различными
нелинейными эффектами. Так в электрическом контуре, например, емкость ![]() зависит от напряжения на ней, а это
приводит к изменению периода собственных колебаний
зависит от напряжения на ней, а это
приводит к изменению периода собственных колебаний ![]() и, как
следствие, к увеличению расстройки между значениями частоты внешней накачки
и, как
следствие, к увеличению расстройки между значениями частоты внешней накачки ![]() и
и ![]() .
Равновесие может наступить, только если параметрическая накачка внешней энергии
в среднем за период компенсируется потерями.
.
Равновесие может наступить, только если параметрическая накачка внешней энергии
в среднем за период компенсируется потерями.
В колебательных системах с
несколькими степенями свободы (связанные контура и др.) возможны нормальные
колебания (моды) с различными частотами: ![]() . Как
следствие, колебания энергии (в реактивных элементах) содержат составляющие,
как с частотами
. Как
следствие, колебания энергии (в реактивных элементах) содержат составляющие,
как с частотами ![]() , так и с частотами равными
суммам и разностям различных нормальных частот. Поэтому здесь нарастание колебаний
возможно как при выполнении условия (4) для любой пары нормальных частот, так и
изменении параметра системы (в электрическом контуре это
, так и с частотами равными
суммам и разностям различных нормальных частот. Поэтому здесь нарастание колебаний
возможно как при выполнении условия (4) для любой пары нормальных частот, так и
изменении параметра системы (в электрическом контуре это ![]() или
или ![]() ) с
суммарной частотой:
) с
суммарной частотой: ![]() , и т.д. В колебательных
системах с несколькими степенями свободы параметрический резонанс приводит к
самовозбуждению обоих нормальных колебаний с определенными соотношениями их
фаз. При этом резонансная связь возможна также и для разностных частот:
, и т.д. В колебательных
системах с несколькими степенями свободы параметрический резонанс приводит к
самовозбуждению обоих нормальных колебаний с определенными соотношениями их
фаз. При этом резонансная связь возможна также и для разностных частот: ![]() , и т.д. Однако в этом случае вместо
самовозбуждения происходит только периодическая перекачка энергии между данными
модами. Можно сказать, что в соответствии с законом сохранения энергии «квант
накачки» (с энергией
, и т.д. Однако в этом случае вместо
самовозбуждения происходит только периодическая перекачка энергии между данными
модами. Можно сказать, что в соответствии с законом сохранения энергии «квант
накачки» (с энергией ![]() ) распадается на два кванта (с
энергиями:
) распадается на два кванта (с
энергиями: ![]() и
и ![]() ). Как
следствие, выполняется соотношение пропорциональности между мощностями и
соответствующими частотами, т.е. между мощностью накачки
). Как
следствие, выполняется соотношение пропорциональности между мощностями и
соответствующими частотами, т.е. между мощностью накачки ![]() на частоте
на частоте ![]() ,
поступающей в колебательную систему, и мощностями данных мод
,
поступающей в колебательную систему, и мощностями данных мод ![]() и
и ![]() на
частотах
на
частотах ![]() и
и ![]() (соотношение
Мэнли-Роу):
(соотношение
Мэнли-Роу):
Параметрический резонанс в волновых
системах (т.е. системах или средах с распределенными параметрами) имеет
важную особенность: его эффективность зависит от соотношения между законом
изменения параметров системы в пространстве и пространственной структурой волн,
существующих в данной системе. Так, если накачка, меняющая параметры среды,
является бегущей волной с частотой ![]() и волновым вектором
и волновым вектором ![]() , то возбуждение пары нормальных волн
(мод) с частотами
, то возбуждение пары нормальных волн
(мод) с частотами ![]() ,
, ![]() и
волновыми векторами
и
волновыми векторами ![]() ,
, ![]() происходит,
если одновременно выполнено условие параметрического резонанса во времени и
пространстве:
происходит,
если одновременно выполнено условие параметрического резонанса во времени и
пространстве:
Как видно из соотношении (8),
возможны два предельных случая: 1) случай бесконечно большой фазовой скорости ![]() волны накачки:
волны накачки: ![]() ,
где
,
где ![]() , но
, но ![]() остается
конечным; здесь из (8) следует, что
остается
конечным; здесь из (8) следует, что ![]() , а
, а ![]() , т.е. в структуре может нарастать стоячая
волна на половинной частоте накачки; 2) случай резонансного (Брэгговского)
отражения падающей волны (волны накачки) от неподвижной периодической
неоднородности среды:
, т.е. в структуре может нарастать стоячая
волна на половинной частоте накачки; 2) случай резонансного (Брэгговского)
отражения падающей волны (волны накачки) от неподвижной периодической
неоднородности среды: ![]() , при конечном
, при конечном ![]() , а
, а ![]() . В
данном случае полная энергия падающей волны остается постоянной (нет потерь на
рассеяние и поглощение) и происходит ее отражение от периодической структуры
(неоднородности) среды.
. В
данном случае полная энергия падающей волны остается постоянной (нет потерь на
рассеяние и поглощение) и происходит ее отражение от периодической структуры
(неоднородности) среды.
В заключение отметим, что различные параметрические и нелинейные резонансные взаимодействия волн могут происходить в разнообразных средах и структурах, в том числе в различных волноводных структурах, для которых наиболее типично проявление волновых явлений.
Всякий метод численного решения системы ОДУ для непрерывных функций непрерывного аргумента с помощью некоторой процедуры дискретизации ставит ей в соответствие систему алгебраических разностных уравнений для сеточных функций дискретного аргумента. В этой связи можно напомнить некоторые распространенные методы решения волновых задач физики, радиофизики и радиоэлектроники: метод разложения по плоским волнам (PWEM – Plane Wave Expansion Method), метод матриц перехода (TMM – Transfer-Matrix Method), метод разложения по собственным модам (EME – Eigenmode Expansion Method), метод матриц рассеяния (SMM – Scattering Matrix Method), метод конечных элементов.
Следует отметить, что даже анализ
простейшей линейной системы ![]() с периодической
матрицей
с периодической
матрицей ![]() , описывающей многие циклические процессы,
например (при некоторых допущениях) движение Луны (уравнение Матье или
уравнение Хилла:
, описывающей многие циклические процессы,
например (при некоторых допущениях) движение Луны (уравнение Матье или
уравнение Хилла: ![]() ), а также различных
гироскопических устройств вызывает заметные трудности. Поэтому важнейшим моментом качественного анализа неавтономных динамических линейных и квазилинейных
систем дифференциальных уравнений являются вопросы устойчивости их решения.
Несмотря на заметное число классических и современных работ по теории
устойчивости, основы которой изложены в трудах А. Пуанкаре, А.М. Ляпунова, Н.Г.
Четаева, И.Г. Красовского, Д.Р. Меркина и ряда других авторов, в настоящее
время есть определенный дефицит достаточно эффективных и конструктивных
аналитических методов исследования устойчивости.
), а также различных
гироскопических устройств вызывает заметные трудности. Поэтому важнейшим моментом качественного анализа неавтономных динамических линейных и квазилинейных
систем дифференциальных уравнений являются вопросы устойчивости их решения.
Несмотря на заметное число классических и современных работ по теории
устойчивости, основы которой изложены в трудах А. Пуанкаре, А.М. Ляпунова, Н.Г.
Четаева, И.Г. Красовского, Д.Р. Меркина и ряда других авторов, в настоящее
время есть определенный дефицит достаточно эффективных и конструктивных
аналитических методов исследования устойчивости.
Настоящая работа посвящена
развитию известных математических методов, а также разработке новых
аналитических спектральных методов и конструктивных алгоритмов, необходимых при
анализе, например, устойчивости решения различных линейных и квазилинейных
неавтономных систем вида: ![]() ,
, ![]() . С этой целью основное внимание будет
уделено рассмотрению спектрального варианта метода усреднения при анализе
неавтономных систем дифференциальных уравнений с периодической матрицей,
описывающих регулярно (т.е. систематически) возмущенные системы. В статье также
приведены некоторые результаты использования указанных методов для исследования
некоторых физических явлений, представляющих несомненный практический интерес.
. С этой целью основное внимание будет
уделено рассмотрению спектрального варианта метода усреднения при анализе
неавтономных систем дифференциальных уравнений с периодической матрицей,
описывающих регулярно (т.е. систематически) возмущенные системы. В статье также
приведены некоторые результаты использования указанных методов для исследования
некоторых физических явлений, представляющих несомненный практический интерес.
Спектральный вариант метода усреднения при анализе неавтономных систем дифференциальных уравнений с периодической матрицей
Буден проведено исследование
модельных неавтономных систем дифференциальных уравнений с периодической
матрицей (регулярно зависящей от малого параметра ![]() ) и
выполнен их теоретический анализ с доказательством важных теорем об
асимптотической приводимости этих уравнений к более простым эквивалентным
системам с почти постоянной диагональной матрицей (с учетом последних вариантов
метода расщепления).
) и
выполнен их теоретический анализ с доказательством важных теорем об
асимптотической приводимости этих уравнений к более простым эквивалентным
системам с почти постоянной диагональной матрицей (с учетом последних вариантов
метода расщепления).
Структура полученных в результате более простых эквивалентных систем дифференциальных уравнений позволит конструктивно проводить не только качественный, но и более точный численный анализ, включая исследование вопросов устойчивости.
С помощью предложенных методов анализа регулярно возмущенных неавтономных систем дифференциальных уравнений могут быть изучены, например, некоторые типы колебательных систем, в частности электрические колебательные контура или гироскопические устройства [4-17].
1.
О почти приводимости отдельных классов неавтономных систематически
возмущенных неавтономных систем дифференциальных уравнений с периодической
матрицей при наличии предельной матрицы ![]() простой
структуры
простой
структуры
Исследование линейных систем с периодической матрицей является нетривиальной задачей. Здесь наиболее известна теорема Флоке-Ляпунова о приводимости таких систем:
к системе с постоянной матрицей ![]() с помощью Т-периодической замены
с помощью Т-периодической замены ![]() , алгоритм построения которой до сих пор
не разработан.
, алгоритм построения которой до сих пор
не разработан.
К изучению периодических систем вида (1.1) можно подойти с учетом того,
что любая Т-периодическая матрица ![]() представима в виде:
представима в виде:
![]() ,
(1.2)
,
(1.2)
где постоянная матрица ![]() ,
являющаяся средним значением
,
являющаяся средним значением ![]() , а Т-периодическая
матрица
, а Т-периодическая
матрица ![]() имеет нулевое среднее значение,
имеет нулевое среднее значение, ![]() – период (интервал усреднения),
– период (интервал усреднения), ![]() – некоторый параметр.
– некоторый параметр.
При анализе большинства
конкретных прикладных модельных задач наибольший интерес представляет случай,
когда параметр ![]() может быть малым (
может быть малым (![]() ), который может быть изучен с помощью
доказанных в данной работе теорем и различных вариантов метода расщепления.
), который может быть изучен с помощью
доказанных в данной работе теорем и различных вариантов метода расщепления.
Напомним отдельные положения теории дифференциальных уравнений, которые мы используем в нашей работе (см., например, [1-3]).
Теорема существования и единственности решения
Пусть функция ![]() (
(![]() )
удовлетворяет в
)
удовлетворяет в ![]() условиям Липшица, то есть
существует
условиям Липшица, то есть
существует ![]() такое, что для любых точек
такое, что для любых точек ![]() и
и ![]() в
в ![]() имеет место неравенство
имеет место неравенство ![]() (это условия всегда имеет место если
(это условия всегда имеет место если 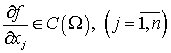 ).
).
Тогда для любой точки ![]() в некоторой
окрестности
в некоторой
окрестности ![]() всегда существует единственное решение
всегда существует единственное решение ![]() задачи Коши:
задачи Коши:
![]() ;
;
![]() ; (
; (![]() ;
; ![]() ). (1.2a)
). (1.2a)
Если решение ![]() ограничено на своем максимальном
промежутке существования
ограничено на своем максимальном
промежутке существования ![]() , то оно бесконечно
продолжаемо вправо, то есть
, то оно бесконечно
продолжаемо вправо, то есть ![]() (
(![]() ).
).
Определение
1. Решение ![]() задачи (1.2a) называется устойчивым по
Ляпунову, если для любого
задачи (1.2a) называется устойчивым по
Ляпунову, если для любого ![]() существует
существует ![]() такое, что все решения
такое, что все решения ![]() и
и ![]() задачи
(1.2a), удовлетворяющие условию
задачи
(1.2a), удовлетворяющие условию ![]() , определены при
, определены при ![]() и при этом
и при этом ![]()
![]() .
.
2. При дополнительном условии ![]() , решение
, решение ![]() называется
асимптотически устойчивым.
называется
асимптотически устойчивым.
Следуя методу расщепления для
удобства изложения для произвольной квадратной матрицы ![]() введём
специальные обозначения:
введём
специальные обозначения:
![]() ,
,
![]() и
и ![]() ,
, ![]() ,
,![]() .
.
Здесь мы рассмотрим подробнее линейные и квазилинейные системы дифференциальных уравнений с периодической (регулярно возмущенной) матрицей, которая может быть представлена в общем случае в виде сходящегося ряда:
![]()
из достаточно гладких Т-периодических матриц ![]() ,
, ![]() .
.
Теорема 1. Рассмотрим неавтономную систему:
![]() ;
(1.3)
;
(1.3)
![]()
в случае если постоянная матрица ![]() имеет простой спектр
имеет простой спектр ![]() , удовлетворяющий условиям:
, удовлетворяющий условиям:
![]() .
(1.4)
.
(1.4)
При этом в (1.3) матричный ряд ![]() из Т-периодических
достаточно гладких матриц
из Т-периодических
достаточно гладких матриц ![]() сходится абсолютно и
равномерно по некоторой норме при достаточно малых
сходится абсолютно и
равномерно по некоторой норме при достаточно малых ![]() (
(![]() ) и при
) и при ![]() . А
функция
. А
функция ![]() является достаточно гладкой в области
является достаточно гладкой в области ![]() .
.
Тогда система (1.3) при
достаточно малых ![]() может быть с помощью
невырожденной Т-периодической замены
может быть с помощью
невырожденной Т-периодической замены
![]() ,
(1.5)
,
(1.5)
![]()
приведена к эквивалентной системе с почти диагональной постоянной матрицей вида:
![]() ;
(1.6)
;
(1.6)
(![]() ;
; ![]() ;
;
![]() ;
; ![]() ),
),
где постоянные диагональные матрицы ![]() и Т-периодические матрицы
и Т-периодические матрицы ![]() однозначно определяются с помощью простого
итерационного алгоритма.
однозначно определяются с помощью простого
итерационного алгоритма.
Замечание. Метод Ляпунова в рассматриваемом случае неавтономной системы
(1.3) не подходит, поэтому мы предлагаем свой метод, позволяющий решить эту
проблему. С этой целью, развивая идеи Ляпунова об устойчивости, мы выделяем в
(1.3) линейную часть и малую нелинейную добавку ![]() . Затем, анализируя спектр матрицы
линейной части, мы судим об устойчивости системы. А вопрос об асимптотической
устойчивости тривиального решения системы (1.3) рассматриваем в Теореме 2.
. Затем, анализируя спектр матрицы
линейной части, мы судим об устойчивости системы. А вопрос об асимптотической
устойчивости тривиального решения системы (1.3) рассматриваем в Теореме 2.
Доказательство. В условиях теоремы
1 всегда существует невырожденная замена ![]() ,
приводящая систему (1.3) к более простому виду:
,
приводящая систему (1.3) к более простому виду:
![]() ;
;
![]() . (1.7)
. (1.7)
Последующее невырожденное при
достаточно малых ![]() Т-периодическое преобразование
Т-периодическое преобразование ![]() приводит к нужному результату (1.6), если
матрицы
приводит к нужному результату (1.6), если
матрицы ![]() ,
, ![]() и
и ![]() удовлетворяют дифференциальному
матричному уравнению:
удовлетворяют дифференциальному
матричному уравнению:
![]() .
(1.8)
.
(1.8)
Приравнивая в (1.8) коэффициенты
при одинаковых степенях ![]() , получим для
последовательного и однозначного определения всех матриц
, получим для
последовательного и однозначного определения всех матриц ![]() и
и ![]() однотипные
дифференциальные матричные уравнения:
однотипные
дифференциальные матричные уравнения:
![]() ;
(1.9)
;
(1.9)
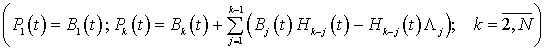 ,
,
которые распадаются на «диагональные» матричные уравнения:
![]() (1.10)
(1.10)
и «бездиагональные» матричные уравнения:
![]() ;
(1.11)
;
(1.11)
![]() .
.
При этом каждое из уравнений (1.10) имеет в классе Т-периодических функций единственное решение:
![]() , если
, если ![]() .
.
Далее отметим, что каждая из уравнений (1.11) распадается на ![]() скалярных дифференциальных уравнений
первого порядка вида:
скалярных дифференциальных уравнений
первого порядка вида:
![]() ,
(1.12)
,
(1.12)
имеющих в условиях теоремы 1 единственное Т-периодическое решение вида:
![]() .
(1.13)
.
(1.13)
Оценка ![]() при достаточно малых
при достаточно малых ![]() следует из конкретного представления этой
матричной функции:
следует из конкретного представления этой
матричной функции:
![]() .
.
Итак, Теорема 1 доказана.
Теорема 2. Если в условиях теоремы 1 спектр ![]() вспомогательной
матрицы
вспомогательной
матрицы ![]() в системе (1.6) удовлетворяет
неравенствам:
в системе (1.6) удовлетворяет
неравенствам:
![]()
и для достаточно гладкой функции ![]() справедлива оценка:
справедлива оценка:
![]() ,
,
то тривиальное решение системы (1.6) и эквивалентной ей системы (1.3) асимптотически устойчиво.
Перед доказательством теоремы 2 предварительно сформулируем вспомогательную лемму.
Лемма. Квадрат евклидовой нормы
решения линейной неавтономной системы ![]() удовлетворяет
дифференциальному уравнению:
удовлетворяет
дифференциальному уравнению:
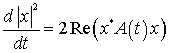 .
(1.14)
.
(1.14)
Доказательство леммы. С учетом
соотношений (![]() ;
; ![]() ) для квадрата евклидовой нормы
решения исходной системы можно записать дифференциальное уравнение:
) для квадрата евклидовой нормы
решения исходной системы можно записать дифференциальное уравнение:
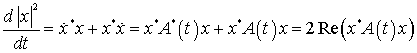 ,
,
что и требовалось доказать.
Доказательство теоремы 2. Запишем (с учетом соотношения (1.14)) дифференциальное неравенство для квадрата евклидовой нормы для системы (1.6):
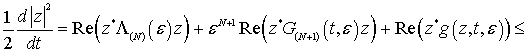
![]()
![]()
![]()
откуда следует оценка ![]() ,
гарантирующая асимптотическую устойчивость тривиального решения квазилинейной
системы вида (1.6), эквивалентной системе (1.3), что и требовалось доказать.
,
гарантирующая асимптотическую устойчивость тривиального решения квазилинейной
системы вида (1.6), эквивалентной системе (1.3), что и требовалось доказать.
Доказанные теоремы позволяют с новой точки зрения исследовать ряд нетривиальных конкретных прикладных модельных физических задач.
Теорема 3. В
условиях теоремы 1. асимптотика
решения ![]() линейной задачи Коши:
линейной задачи Коши:
![]() ;
;
![]() , (1.15)
, (1.15)
(где ![]() достаточно гладкая
Т-периодическая функция) в случае, если спектр
достаточно гладкая
Т-периодическая функция) в случае, если спектр ![]() вспомогательной
матрицы
вспомогательной
матрицы ![]() удовлетворяет условиям:
удовлетворяет условиям:
![]()
может быть представлена в форме:
![]() ;
(1.16)
;
(1.16)
(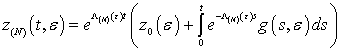 ;
; ![]() ),
),
где функции ![]() и
и ![]() определяются методами теоремы 1.
определяются методами теоремы 1.
Доказательство. После преобразования вида (1.5) ![]() система
(1.15) приводится к виду:
система
(1.15) приводится к виду:
![]() .
(1.17)
.
(1.17)
Её решение представим в виде:
![]() ;
(1.18)
;
(1.18)
(![]() ).
).
При этом векторная функции ![]() удовлетворяет задаче Коши:
удовлетворяет задаче Коши:
![]() ;
(1.19)
;
(1.19)
![]() .
.
Докажем ограниченность ![]() (при
(при ![]()
![]() 0). С учетом леммы оценим квадрат евклидовой нормы решения
задачи (1.19):
0). С учетом леммы оценим квадрат евклидовой нормы решения
задачи (1.19):
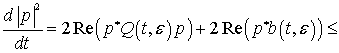
![]()
![]() ;
; ![]() .
.
После обозначения ![]() изучим дифференциальное неравенство
Бернулли:
изучим дифференциальное неравенство
Бернулли:
![]() .
.
После стандартных замен (![]() (
(![]() ),
получим:
),
получим:
![]() ;
; 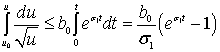 ;
; 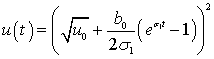 .
.
Это позволяет в итоге получить оценку:
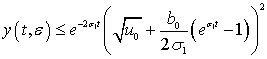 ,
,
что и доказывает ограниченность нормы:
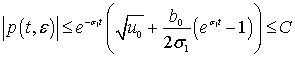
при ![]() и
и ![]() , и справедливость асимптотического
представления (1.16). Теорема 3 доказана.
, и справедливость асимптотического
представления (1.16). Теорема 3 доказана.
2. Примеры использования указанных методов для исследования отдельных реальных физических явлений, представляющих несомненный практический интерес
2.1. Взаимодействие двух связанных линейных (гармонических) осцилляторов в отсутствие резонансных явлений (вдали от резонансов).
Гармонический осциллятор в классической механике – система, которая при
смещении из положения равновесия испытывает действие возвращающей силы F, пропорциональной смещению,
например, по координате x
(согласно закону Гука: ![]() , где
, где ![]() –
коэффициент жёсткости данной системы,
–
коэффициент жёсткости данной системы, ![]() – величина смещения).
Механические примеры гармонического осциллятора: математический маятник (с
малыми углами отклонения), груз на пружине и др. Электрический гармонический
осциллятор – электрический контур (LC-цепь).
– величина смещения).
Механические примеры гармонического осциллятора: математический маятник (с
малыми углами отклонения), груз на пружине и др. Электрический гармонический
осциллятор – электрический контур (LC-цепь).
Гармонический осциллятор в квантовой механике представляет собой квантовый
аналог гармонического осциллятора, при этом рассматривают не силы, действующие
на частицу, а гамильтониан, то есть полную энергию ![]() (
(![]() , где
, где ![]() и
и ![]() – кинетическая и потенциальная
энергии соответственно) гармонического осциллятора, причём потенциальная
энергия
– кинетическая и потенциальная
энергии соответственно) гармонического осциллятора, причём потенциальная
энергия ![]() предполагается квадратично зависящей от
координат. При этом, учёт следующих слагаемых в разложении потенциальной
энергии
предполагается квадратично зависящей от
координат. При этом, учёт следующих слагаемых в разложении потенциальной
энергии ![]() по координате ведёт к понятию ангармонического
осциллятора, т.е. осциллятора с не квадратичной зависимостью потенциальной
энергии от координаты.
по координате ведёт к понятию ангармонического
осциллятора, т.е. осциллятора с не квадратичной зависимостью потенциальной
энергии от координаты.
Рассматриваемая система двух связанных линейных (гармонических) осцилляторов [12] может быть описана следующей системой линейных дифференциальных уравнений:
которая, после замены: ![]() ,
преобразуется к виду (1.1):
,
преобразуется к виду (1.1):
![]() ,
(2.2)
,
(2.2)
где
![]() ;
;
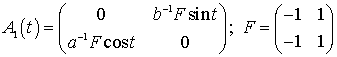 .
.
В отличие от известного [12] с помощью теоремы 1. и преобразования:
![]()
получим эквивалентную систему с почти диагональной и постоянной матрицей:
![]() ,
,
![]() ,
(2.3)
,
(2.3)
где матрицы ![]() ,
, ![]() и
и ![]() удовлетворяют
дифференциальному матричному уравнению:
удовлетворяют
дифференциальному матричному уравнению: ![]() .
.
Приравнивая коэффициенты при
одинаковых степенях ![]() , на первом шаге получим
дифференциальное матричное уравнение:
, на первом шаге получим
дифференциальное матричное уравнение:
![]() ,
,
распадающееся на «диагональную» систему ![]() , откуда однозначно определяются матрицы
, откуда однозначно определяются матрицы ![]() :
:
![]()
и «бездиагональное» дифференциальное матричное уравнение:
![]() ,
,
которое распадается на скалярные дифференциальные уравнения вида:
![]() .
.
Далее, с помощью рядов Фурье
однозначно определяются скалярные функции ![]() :
:
![]() ,
,
а другие периодические функции ![]() равны:
равны:
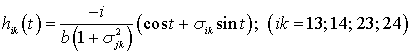 .
.
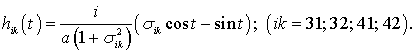
После этого по аналогичному алгоритму определяется диагональная матрица:
![]() ,
,
имеющая спектр:
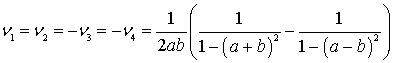 .
.
Заметим, что диагональная матрица ![]() имеет
чисто мнимый спектр, матрица
имеет
чисто мнимый спектр, матрица ![]() , а спектр диагональной
матрицы
, а спектр диагональной
матрицы ![]() имеет действительные собственные значения
разного знака.
имеет действительные собственные значения
разного знака.
Это позволяет сделать вывод, что тривиальное решение системы (2.3) и эквивалентной ей системы (2.1) будет в этом случае (т.е. при отсутствии резонансов, точнее – вдали от них) неустойчивым.
Численно получены графики нормы решения ![]() системы
(2.1) для двух случаев: 1)
системы
(2.1) для двух случаев: 1) ![]() ,
, ![]() ,
, ![]() (рис.
2); и 2)
(рис.
2); и 2) ![]() ,
, ![]() ,
, ![]() (рис. 3) отражающие неустойчивый характер
решения, что собственно и подтверждает справедливость теоремы 1.
(рис. 3) отражающие неустойчивый характер
решения, что собственно и подтверждает справедливость теоремы 1.
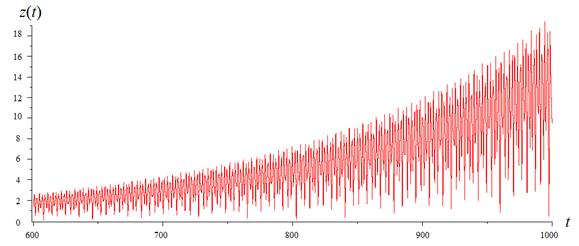
Рис. 2. Взаимодействие двух связанных
линейных осцилляторов при отсутствии резонансов.
График нормы решения ![]() системы (2.1) при заданных параметрах:
системы (2.1) при заданных параметрах: ![]() ,
, ![]() ,
, ![]() .
.
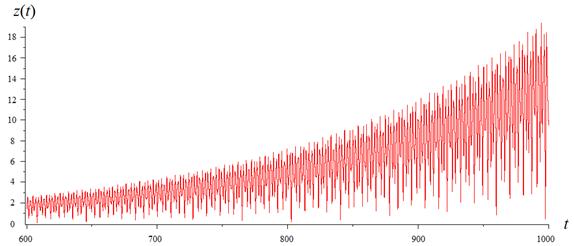
Рис. 3. Взаимодействие двух связанных
линейных осцилляторов при отсутствии резонансов.
График нормы решения ![]() системы (2.1) при заданных параметрах:
системы (2.1) при заданных параметрах: ![]() ,
, ![]() ,
, ![]() .
.
2.2. Стационарное вращение бесконтактного гироскопа в переменном магнитном поле.
Рассматриваемый процесс [16] может быть описан с помощью линеаризованной системы дифференциальных уравнений первого порядка:
![]() (2.4)
(2.4)
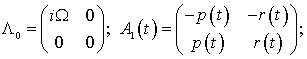
![]() ;
;
![]() ,
,
где ![]() – частота магнитного
поля,
– частота магнитного
поля, ![]() – амплитуда колебаний магнитного поля,
– амплитуда колебаний магнитного поля, ![]() – частота нутационных колебаний тела,
– частота нутационных колебаний тела, ![]() – моменты инерции тела относительно его
осей
– моменты инерции тела относительно его
осей ![]() ,
, ![]() –
величина, определяемая поляризуемостью тела относительно его осей,
–
величина, определяемая поляризуемостью тела относительно его осей, ![]() – безразмерный малый параметр. Полезно
напомнить некоторые определения. Поляризуемость – физическое свойство
веществ приобретать электрический или магнитный дипольный момент (поляризацию)
во внешнем электромагнитном поле. Нутация (от лат. nūtāre – колебаться) –
слабое нерегулярное движение вращающегося (твёрдого) тела, совершающего
прецессию. Оно напоминает «подрагивание» оси вращения и заключается в слабом
изменении так называемого угла нутации между осями собственного и
прецессионного вращения тела. Прецессия гироскопа наблюдается спустя
некоторое время после его запуска, когда его вращение начнёт замедляться.
Первоначально ось вращения гироскопа вертикальна. Затем его верхняя точка
постепенно опускается и движется по расходящейся спирали. Это и есть прецессия
оси гироскопа. Для ее наблюдения можно также слегка толкнуть ось вращающегося
гироскопа – начнётся прецессия. В однородном силовом поле возможно
вращение гироскопа, совершающееся без нутаций, которое называется регулярной
прецессией. Особым случаем регулярной прецессии является вращение гироскопа
вокруг неподвижной оси. Если центр масс гироскопа совпадает с неподвижной
точкой, то возможно долговременное (постоянное) вращение тела вокруг некоторой
произвольной оси при заданной начальной угловой скорости.
– безразмерный малый параметр. Полезно
напомнить некоторые определения. Поляризуемость – физическое свойство
веществ приобретать электрический или магнитный дипольный момент (поляризацию)
во внешнем электромагнитном поле. Нутация (от лат. nūtāre – колебаться) –
слабое нерегулярное движение вращающегося (твёрдого) тела, совершающего
прецессию. Оно напоминает «подрагивание» оси вращения и заключается в слабом
изменении так называемого угла нутации между осями собственного и
прецессионного вращения тела. Прецессия гироскопа наблюдается спустя
некоторое время после его запуска, когда его вращение начнёт замедляться.
Первоначально ось вращения гироскопа вертикальна. Затем его верхняя точка
постепенно опускается и движется по расходящейся спирали. Это и есть прецессия
оси гироскопа. Для ее наблюдения можно также слегка толкнуть ось вращающегося
гироскопа – начнётся прецессия. В однородном силовом поле возможно
вращение гироскопа, совершающееся без нутаций, которое называется регулярной
прецессией. Особым случаем регулярной прецессии является вращение гироскопа
вокруг неподвижной оси. Если центр масс гироскопа совпадает с неподвижной
точкой, то возможно долговременное (постоянное) вращение тела вокруг некоторой
произвольной оси при заданной начальной угловой скорости.
В нерезонансном случае при ![]() с учетом теоремы 1 после Т-периодической
замены (
с учетом теоремы 1 после Т-периодической
замены (![]() )
)
![]()
система (1.23) приводится к виду:
![]() ,
,
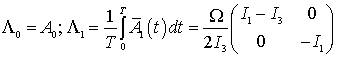 . (2.5)
. (2.5)
Структура спектра матрицы ![]()
![]() и матрицы
и матрицы ![]()
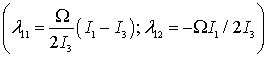 позволяет сделать вывод о том, что
стационарное движение будет асимптотически устойчивым (в силу следствия к
теореме 1.), если тело гироскопа является сплюснутым эллипсоидом инерции (
позволяет сделать вывод о том, что
стационарное движение будет асимптотически устойчивым (в силу следствия к
теореме 1.), если тело гироскопа является сплюснутым эллипсоидом инерции (![]()
![]()
![]() ), что следует из теоремы Ляпунова об асимптотической устойчивости по
первому приближению [12].
), что следует из теоремы Ляпунова об асимптотической устойчивости по
первому приближению [12].
В окрестности резонанса существенно изменяется характер стационарных вращений бесконтактного гироскопа.
Введем расстройку ![]() , обозначив
, обозначив ![]() (
(![]() –
малый параметр). В этом случае после замены
–
малый параметр). В этом случае после замены ![]() система
(2.1) преобразуется к системе
система
(2.1) преобразуется к системе ![]() , где
, где
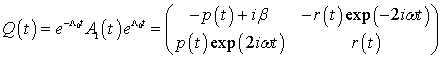 ,
,
которая после замены вида ![]() приводится
с учетом обобщённого варианта теоремы 1. к почти автономной системе:
приводится
с учетом обобщённого варианта теоремы 1. к почти автономной системе:
![]() ;
;
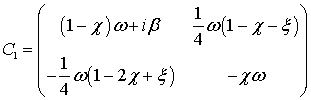 .
.
Следует отметить, что корни характеристического
уравнения для матрицы ![]() :
:
![]() ;
;
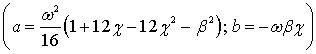 ;
;
лежат в левой полуплоскости ![]() при
выполнении следующего неравенства:
при
выполнении следующего неравенства:
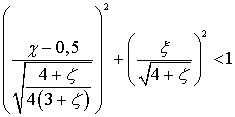 ;
;
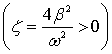 .
.
Это позволяет сделать вывод,
что стационарное движение гироскопа будет асимптотически устойчивым (вблизи
резонанса) для немного вытянутого эллипсоида инерции (![]() )
при нулевой расстройке (
)
при нулевой расстройке (![]() = 0). При увеличении
расстройки (
= 0). При увеличении
расстройки (![]() > 0) мы имеем асимптотически
устойчивое движение при (
> 0) мы имеем асимптотически
устойчивое движение при (![]() ) [16].
) [16].
1. Якубович В.А., Старжинский В.М. Линейные дифференциальные уравнения с периодическими коэффициентами и их приложения. – М.: Наука, 1972.
2. Коддингтон Э.А., Левинсон Н. Теория обыкновенных дифференциальных уравнений. – М.: ИЛ, 1958.
3. Федорюк М.В. Асимптотические методы для линейных обыкновенных дифференциальных уравнений. – М.: Наука, 1983.
4. Андронов А.А., Витт А.А., Хайкин С.Э. Теория колебаний. 2-е изд. – M.: Физматгиз, 1959.
5. Горелик Г.С. Колебания и волны. Введение в акустику, радиофизику и оптику. 2-е изд. – М.: Физматлит, 1959.
6. Алешкевич В.А., Деденко Л.Г., Караваев В.А. Колебания и волны. – М.: Физфак МГУ, 2001.
7. Абаренков И.В., Загуляев С.Н. Простейшие модели в квантовой механике. – СПб.: Издат. С.-Петерб. ун-та, 2004.
8. Николаи Е.Л. Теория гироскопов. – Л., М.: ОГИЗ. Гос. Издат. Технико-теоретической литературы, 1948.
9. Ишлинский А.Ю. Ориентация, гироскопы и инерциальная навигация. – М.: Наука, 1976.
10. Меркурьев И.В., Подалков В.В. Динамика микромеханического и волнового твердотельного гироскопов. – М.: Физматлит, 2009.
11. Коняев Ю.А. Асимптотические и аналитические методы решения некоторых классов прикладных модельных задач. – М.: Изд-во РУДН, 2005.
12. Розо М. Нелинейные колебания и теория устойчивости. – М.: Наука, 1971.
13. Рид М., Саймон Б. Методы современной математической физики. – М.: Мир, Т. 4, 1982.
14. Широносов В.Г. Резонанс в физике, химии и биологии. – Ижевск: Издательский дом “Удмуртский университет”, 2000/01.
15. Волосов В.М., Моргунов Б.К. Метод усреднения в теории нелинейных колебательных систем. – М.: МГУ, 1971.
16. Коняев Ю.А., Мартыненко Ю.Г. Об устойчивости стационарных вращений симметричного твердого тела в переменном магнитном поле // Прикладная математика и механика. 1987. Т.51. №3. С. 375-381.
17. Коняев Ю.А., Безяев В.И., Филиппова О.Н. Асимптотический анализ регулярно и сингулярно возмущенных задач и их приложения в биологии // «Современная математика. Фундаментальные направления». 2010. Т. 37. С. 16-28.
18. Нгуен Вьет Хоа. Спектральной вариант метода усреднения для линейных систем обыкновенных дифференциальных уравнений с периодической матрицей // Тез. докл. Всероссийской конф. с междунар. участием «Информационно – телекоммуникационные технологии и математическое моделирование высокотехнологичных систем». – М.: РУДН. 2012. С. 356-358.
19. Егоров А.А. Систематика, принцип работы и области применения датчиков // Журнал Радиоэлектроники. 2009. № 3. http://jre.cplire.ru/jre/mar09/3/text.pdf
20. Егоров А.А. Исследование бифуркационных процессов в многомодовом оптическом волноводе со статистическими нерегулярностями // Квантовая Электроника. 2011. Т. 41. № 10. С. 911-916.
21. Egorov A.A. Introduction to the analysis of the bifurcation phenomena in an optical waveguide with statistic irregularities // Журнал Радиоэлектроники. 2013. N. 9. http://jre.cplire.ru/jre/sep13/13/text.pdf
22. Егоров А.А. Основы теоретического анализа нерегулярных интегрально-оптических волноводов как нелинейных динамических диссипативных систем // Научная Сессия НИЯУ МИФИ-2013, г. Москва, 1 – 6 февраля 2013 г., Конференция «Методы математической физики и математическое моделирование физических процессов». – М.: НИЯУ МИФИ, 2013. Т. 3. С. 129.
23. Попонин В.С. Метод спектральных элементов на неструктурированной сетке в вычислительной механике. – Томск: Томский госуниверситет, 2009.
24. Санкин Ю.Н., Пирожков С.Л. Спектральные методы исследования электромеханических систем, включающих звенья с распределенными параметрами. – Ульяновск: УлГТУ, 2009.