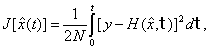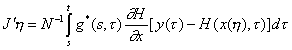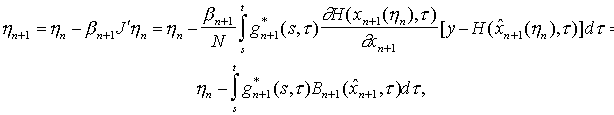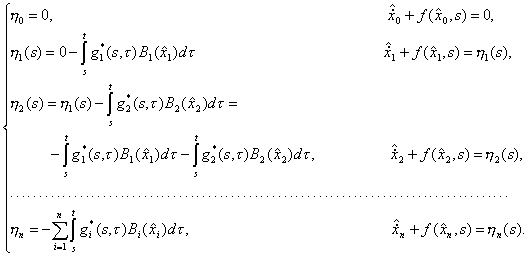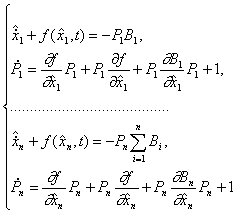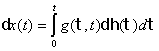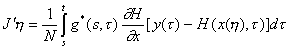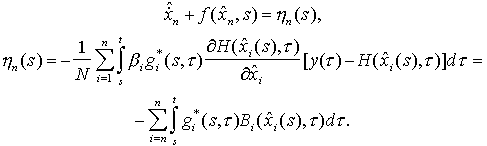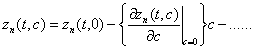|
|
"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 5, 2002 |
|
МЕТОД СИНТЕЗА АЛГОРИТМОВ АДАПТИВНОЙ ФИЛЬТРАЦИИ НА БАЗЕ ПРИНЦИПА РЕГУЛЯРИЗАЦИИ А.Н. ТИХОНОВА
А. А. Костоглотов, e-mail: kostoglotov@aaanet.ru
Ростовский военный институт.
Получена 15 апреля 2002 г.
Работа посвящена одному из методов решения проблемы синтеза алгоритмов адаптивной оценки параметров динамических систем. Математически задача фильтрации представлена как обратная некорректно поставленная по А.Н. Тихонову. Получены уравнения фильтра, реализующего итеративный принцип получения уточнённой оценки. При этом точность исходных данных согласуется с точностью оценок соответствующим выбором параметра регуляризации. Рассмотрен пример синтеза алгоритма фильтрации и показаны преимущества предложенного подхода в сравнении с классическим на основе численного моделирования.
1. Введение
Проблема синтеза алгоритмов оценки параметров динамических систем, подверженных априорно неизвестным воздействиям, имеет исключительно большое значение для различных областей знаний и ей посвящены многочисленные опубликованные работы, содержащие как различные частные задачи, так и теоретические обобщения.
Исторически сложилось так, что на первый план при решении такого рода задач выступает теория статистических решений, дающая общую методологию статистического синтеза. Для ее осуществления необходимы исходные сведения, которые в наилучшем случае полной априорной определенности сводятся к заданию законов распределения вероятностей для всех величин, процессов, относящихся к синтезируемой системе. К этому наилучшему случаю относится большая часть результатов, известных из литературы и соответствующих положений теории статистических решений.
Однако, как известно [1, 2], полная априорная определенность не является типичной для практических задач. Априорные сведения сводятся, как правило, к частичному знанию законов распределения и ограниченного числа их параметров. Это послужило причиной появления эмпирических методов, связанных с обучением [3], адаптацией систем [1,2,4], подверженных неизвестным воздействиям. Эти методы являются до настоящего времени довольно разобщенными, причем их возможности достаточно сложно сопоставить и оценить с каких-либо единых теоретических позиций. Данный факт затрудняет их правильный выбор при решении задач, имеющих практическое значение и относящихся к таким конкретным проблемам, как оценка параметров, фильтрация, управление объектами и наблюдениями.
Достаточно отметить, что даже выбор модели неизвестного входного воздействия в рамках единого подхода к синтезу алгоритмов фильтрации приводит к существенно отличающимся решениям, как по структуре, так и по качеству функционирования [4,5,6].
Необходимость задания совокупности исходных статистических характеристик является, вообще говоря, недостатком статистических методов синтеза. И причина этого заключается в степени обоснованности байесовской методологии применительно к вероятностным задачам вообще [7], поскольку в практических задачах чаще всего не имеется достаточного объема предварительных экспериментов по выяснению вероятностного характера неизвестных параметров. Более того, во многих практически важных случаях нет даже возможности получения такого рода информации.
В такой ситуации основой решения задачи синтеза систем, функционирующих в условиях неопределенности относительно параметров входных воздействий, с успехом могут служить методы регуляризации. Особенности применения метода А.Н.Тихонова, как наиболее строгого и эффективного квазидетерминистского метода при решении задач восстановления достаточно подробно исследованы [8]. Применительно к задачам фильтрации данный метод за исключением некоторых тривиальных вариантов [9] практически не использовался.
Однако положительный опыт использования квазидетерминистских методов при решении задач динамической оценки параметров и состояния систем имеется [10,11]. Результат работы [10] показывает, что эффективность субоптимальных алгоритмов фильтрации по таким параметрам как устойчивость к априорно неизвестным внешним возмущениям выше в сравнении с традиционными, что с другой стороны приводит к увеличению ошибки фильтрации исследуемых параметров. Один из возможных способов повышения точности оценок квазидетерминистских методов базируется на использовании итерационных алгоритмов получения оценки, минимизирующей заданный функционал ошибки с учетом согласования величины невязки с погрешностью исходных данных. Это дает основание для постановки задачи синтеза алгоритма фильтрации с последовательным уточнением оценок на основе итерационных методов.
Целью настоящей работы является разработка метода оптимальной адаптивной фильтрации на основе принципов регуляризации А.Н.Тихонова. При этом оптимальность решения понимается в смысле критерия невязки, величина которой должна быть согласована с погрешностью исходных данных.
2. Постановка задачи
Пусть динамическая система описывает физический процесс, представленный дифференциальным уравнением первого порядка
Для наглядности и простоты преобразований ограничимся одномерным случаем,
поскольку обобщение на многомерный случай не вызывает принципиальных
затруднений. В уравнении (1)
![]() параметр,
характеризующий состояние динамической системы,
параметр,
характеризующий состояние динамической системы,
![]() неизвестное
внешнее возмущение, которое характеризуется функцией, удовлетворяющей
требованиям физической реализуемости. Пусть
неизвестное
внешнее возмущение, которое характеризуется функцией, удовлетворяющей
требованиям физической реализуемости. Пусть
![]() при
этом
при
этом
![]() характеризует
точность априорных знаний о переходной функции системы (1)
характеризует
точность априорных знаний о переходной функции системы (1)
![]() Предположим,
что
Предположим,
что
![]() непрерывна
вместе со своими производными по совокупности переменных.
непрерывна
вместе со своими производными по совокупности переменных.
Информация о состоянии системы (1) поступает в виде
Сигнальная
функция
![]() также
полагается непрерывной по совокупности переменных, а шум
также
полагается непрерывной по совокупности переменных, а шум
![]() является
белым гауссовским с известными локальными характеристиками
является
белым гауссовским с известными локальными характеристиками
![]()
![]() ,
,
где
![]() односторонняя
спектральная плотность шума наблюдения,
односторонняя
спектральная плотность шума наблюдения,
![]() дельта-функция.
дельта-функция.
Поставим
задачу построения рекуррентного во времени алгоритма оценки
![]() процесса
(1), (2), доставляющей минимум
неотрицательному функционалу ошибки
процесса
(1), (2), доставляющей минимум
неотрицательному функционалу ошибки
при условии, что
![]() увеличивается.
увеличивается.
Очевидно,
что решение уравнения (1) непрерывно зависит от внешнего
возмущения
![]() в
силу теоремы о его непрерывной зависимости от параметров и исходных данных
[12]. Поэтому значение функционала
в
силу теоремы о его непрерывной зависимости от параметров и исходных данных
[12]. Поэтому значение функционала
![]() на
каждом решении системы (1) будет непрерывным функционалом от
на
каждом решении системы (1) будет непрерывным функционалом от
![]() определенном
на множестве
определенном
на множестве
![]() то
есть
то
есть
![]() .
.
Это
позволяет заключить, что задача нахождения оценки
![]() минимизирующей
(3) адекватна задаче определения
минимизирующей
(3) адекватна задаче определения
Представим (1), (2) в более удобной для дальнейшего рассмотрения операторной форме
где A – оператор, являющийся композицией отображений (1), (2).
Задачу (4), (5) можно отнести согласно принятой терминологии [13], [14] к обратным задачам типа синтеза оптимального управления.
Теорема 1. Задача (4), (5) является обратной некорректно поставленной по Адамару.
На
практике исходные данные
![]() в
уравнении (5) известны обычно лишь приближенно: оператор
A при решении задачи на ЭВМ должен быть
аппроксимирован некоторым конечномерным оператором, правая часть
в
уравнении (5) известны обычно лишь приближенно: оператор
A при решении задачи на ЭВМ должен быть
аппроксимирован некоторым конечномерным оператором, правая часть
![]() также
известна с погрешностью, которая не в полной мере соответствует математической
модели (2), поскольку определяется в ходе эксперимента.
также
известна с погрешностью, которая не в полной мере соответствует математической
модели (2), поскольку определяется в ходе эксперимента.
Поэтому вместо точного уравнения (5) рассмотрим уравнение с приближенными исходными данными
где
![]() некоторые
линейные нормированные пространства,
некоторые
линейные нормированные пространства,
![]() оператор
из семейства аппроксимирующих операторов с условием аппроксимации
оператор
из семейства аппроксимирующих операторов с условием аппроксимации
![]()
Использование градиентных методов для решения задачи (4), (6)
может привести к расходящейся последовательности приближений. Но даже если они
сходятся к некоторым решениям
![]() то
и это не гарантирует успеха, так как
то
и это не гарантирует успеха, так как
![]() могут
значительно отличаться от точных решений задачи (4), (5)
при
могут
значительно отличаться от точных решений задачи (4), (5)
при
![]()
Поэтому применение любого итерационного метода для решения задачи (4), (6) требует определения регуляризирующего семейства операторов, в котором параметром регуляризации является номер итерации [14]. Необходимым для этого условием (но не достаточным) является, очевидно, сходимость метода при точных исходных данных.
3. Итерационная регуляризация
В соответствии с общим определением регуляризирующего семейства операторов по А.Н.Тихонову [13] будем говорить, что итерационный метод
порождает регуляризирующее
семейство операторов, в котором параметром является номер итерации, если для
любого начального приближения
![]() и
для любого
и
для любого
![]() ,
удовлетворяющего условию
,
удовлетворяющего условию
![]() ,
существует номер
,
существует номер
![]() такой,
что
такой,
что
![]()
то есть полученные
приближения сходятся к точному решению в норме пространства
![]() при
стремлении погрешности исходных данных к нулю.
при
стремлении погрешности исходных данных к нулю.
Из совокупности итерационных методов рассмотрим метод простой итерации, когда
отображение
![]() имеет
вид [14]
имеет
вид [14]
где
![]() градиент
функционала J, а
b - выбирается
из условия
градиент
функционала J, а
b - выбирается
из условия
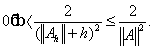
При этом
параметром регуляризации служит номер итерации, а регуляризованные приближения
сходятся к нормальному относительно начального приближения
![]() решению
решению
![]() задачи
(4), (6).
задачи
(4), (6).
Один из
возможных подходов к выбору параметра регуляризации
![]() при
использовании алгоритма простой итерации заключается в использовании критерия
невязки, т.е. в выборе
при
использовании алгоритма простой итерации заключается в использовании критерия
невязки, т.е. в выборе
![]() из
условий согласования величины невязки
из
условий согласования величины невязки
![]()
![]()
с величиной
![]()
Таким образом, в качестве приближенного решения будем выбирать элемент
итерационной последовательности с номером
![]() удовлетворяющим
условию [14]
удовлетворяющим
условию [14]
![]() где
где
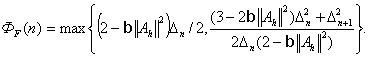
Градиент функционала
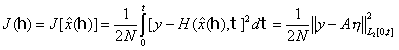
определяется следующим образом.
Рассмотрим
приращение функционала
![]() в
точке
в
точке
![]() вызванное
приращением
вызванное
приращением
![]()
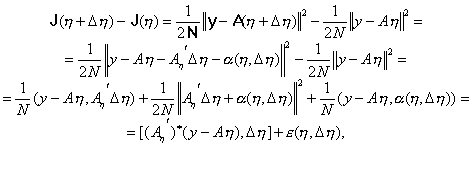
где
![]() линейный,
ограниченный оператор, производная Фреше оператора
линейный,
ограниченный оператор, производная Фреше оператора
![]() в
точке
в
точке
![]() ,
,
![]() удовлетворяет
условию
удовлетворяет
условию
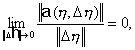 т.е.
т.е.
![]() при
при
![]() ,
,
![]() удовлетворяет
условию
удовлетворяет
условию
![]()
![]() обозначает
оператор, сопряженный
обозначает
оператор, сопряженный
![]() .
.
Из последнего равенства следует, что
При выводе
данного выражения сделано предположение, что непрерывный нелинейный оператор
![]() может
быть линеаризован
может
быть линеаризован
![]()
Для
использования выражения (9) в итеративной процедуре (8)
необходимо определить структуру линейного оператора
![]()
Теорема 2. Структура линейного оператора
![]() определяется
выражением
определяется
выражением
4. Алгоритм фильтрации
В соответствии с выражением для регуляризирующего семейства операторов (8) и структуры градиента (10) итерационный алгоритм (7) можно представить в следующем виде
где обозначение
![]() вводится
для сокращения записи.
вводится
для сокращения записи.
Как
показано выше задача нахождения оценки
![]() ,
минимизирующей (3) при ограничениях (1), (2)
адекватна задаче (4), что дает основание записать уравнение
для оценки
,
минимизирующей (3) при ограничениях (1), (2)
адекватна задаче (4), что дает основание записать уравнение
для оценки
![]() по
аналогии с [10] в виде
по
аналогии с [10] в виде
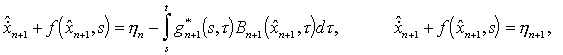
где
![]() приближение
к элементу
приближение
к элементу
![]() ,
доставляющему минимум (3) при условии согласования невязки с
величиной погрешности исходных данных,
,
доставляющему минимум (3) при условии согласования невязки с
величиной погрешности исходных данных,
![]() -
соответствующие оценки состояния процесса (1), (2).
-
соответствующие оценки состояния процесса (1), (2).
Приняв за нулевое приближение h0=0, запишем итерационную последовательность в развернутой форме
Здесь уравнения для
![]() представляют
собой уравнения для последовательности приближений интервальной оценки
состояния процесса (1), (2) в смысле
функционала (3).
представляют
собой уравнения для последовательности приближений интервальной оценки
состояния процесса (1), (2) в смысле
функционала (3).
Теорема 3. Система уравнений точечной рекуррентной итеративной оценки имеет вид
где,
![]() ,
P0 – некоторая постоянная.
,
P0 – некоторая постоянная.
Анализ системы уравнений фильтрации (13) позволяет
заключить, что каждое последующее уравнение оценки при n³1
использует в качестве входных параметров функции y
и
![]() ,
причем по форме все уравнения идентичны, поскольку для их решения может быть
использован один и тот же алгоритм расчета. Это дает возможность использовать
при организации процесса фильтрации рекурсивные функции, которые используют в
своем теле вызов самой себя. При этом критерием выхода из рекурсивного расчета
может быть использован, например, описанный выше критерий невязки.
,
причем по форме все уравнения идентичны, поскольку для их решения может быть
использован один и тот же алгоритм расчета. Это дает возможность использовать
при организации процесса фильтрации рекурсивные функции, которые используют в
своем теле вызов самой себя. При этом критерием выхода из рекурсивного расчета
может быть использован, например, описанный выше критерий невязки.
Обобщение полученного результата на многомерные системы не вызывает принципиальных затруднений и демонстрируется на следующем примере.
5. Пример
Рассмотрим задачу определения неизвестного параметра k0 в динамической системе
![]()
при наблюдении выходного сигнала
y=x+n,
где n- белый гауссовский шум измерений с известными локальными характеристиками. Точка обозначает производную по времени.
Расширение
пространства состояний приводит к задаче оценки вектора
![]()
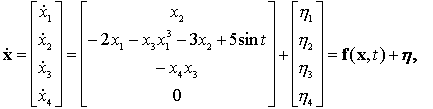
![]() -
вектор неизвестных возмущений, а вектор наблюдений имеет вид
-
вектор неизвестных возмущений, а вектор наблюдений имеет вид
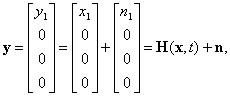
где
![]() .
.
Согласно уравнениям системы (13) уравнения для оценки
![]() запишутся
как
запишутся
как
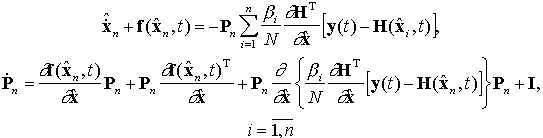
где
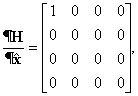
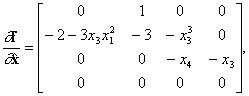
а
![]() назначаются
согласно [10]
назначаются
согласно [10]
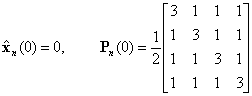 .
.
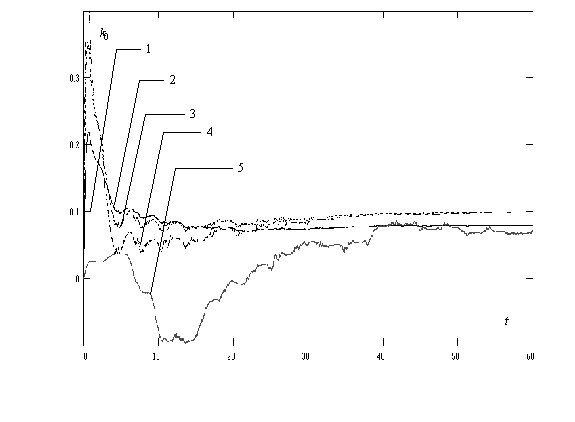
Результаты численного моделирования процесса итеративной оценки параметра
k0 представлены на
рисунке, где для сравнения представлено также решение, полученное с помощью
обобщенного фильтра Калмана. Параметры вычислительного алгоритма выбраны
экспериментально и имеют следующие значения:
![]() .
.
Рисунок 1.
Оценка параметра k0 динамической системы:
1 – истинное значение параметра k0, 2 – оценка первой итерации,
3 – оценка второй итерации, 4 – оценка третьей итерации,
5 –. оценка обобщенного фильтра Калмана.
Сравнительный визуальный анализ полученных решений показывает, что точность оценок параметра k0 в установившемся режиме повышается с увеличением номера итерации от 1 до 3. Оценки итераций от 4 и далее не показаны, поскольку их точностные характеристики с увеличением номера итерации ухудшаются. Наилучшей оценкой параметра k0 по критерию точности для данного примера следует считать оценку итерации 3, по критерию минимума времени переходного процесса – оценку 1, а по критерию максимума точности и запаса устойчивости оценки при минимуме вычислительных затрат – оценку итерации 2. Таким образом, можно утверждать, что полученный алгоритм является универсальным в плане практического применения в зависимости от поставленной цели. Следует отметить, что сравнение полученных результатов с результатами моделирования фильтра Калмана дает основание говорить о преимуществах предлагаемого подхода по отношению к классическому решению.
6. Заключение
Предложенный в данной работе подход к оценке параметров динамических систем позволяет получить решение, выгодно отличающееся от классического. Данный алгоритм, несмотря на увеличение вычислительных затрат, является более предпочтительным в условиях априорной неопределенности относительно параметров модели исследуемого объекта в плане обеспечения точности и устойчивости процесса оценивания.
Доказательство теоремы 1.
Задачу (4), (5) можно сформулировать как
задачу отыскания
![]() в
некотором классе функций
в
некотором классе функций
![]() пространства
пространства
![]() когда
функционал
когда
функционал
![]() достигает
минимума.
достигает
минимума.
Для корректности задачи (4) (5) необходимо выполнение условий существования решения, его единственности и устойчивости [13].
Покажем, что рассматриваемая задача не удовлетворяет, по крайней мере, требованию устойчивости.
Рассмотрим случай, когда класс допустимых внешних воздействий
![]() есть
пространство функций одной переменной
есть
пространство функций одной переменной
![]() с
равномерной метрикой.
с
равномерной метрикой.
Поскольку
функционал
![]() непрерывно
зависит от
непрерывно
зависит от
![]() то,
каково бы ни было
то,
каково бы ни было
![]() можно
найти такое
можно
найти такое
![]() что
что
1)
![]()
2)
![]() можно
принимать как угодно большие значения, допустимые принадлежностью функций
можно
принимать как угодно большие значения, допустимые принадлежностью функций
![]() и
и
![]() классу
классу
![]() .
.
Рассмотрим
функцию
![]() совпадающую
с
совпадающую
с
![]() всюду,
кроме интервала
всюду,
кроме интервала
![]() в
котором
в
котором
![]()
где
![]() некоторое
число, определяемое принадлежностью функций
некоторое
число, определяемое принадлежностью функций
![]() и
и
![]() классу
классу
![]()
В силу
непрерывной зависимости решения
![]() уравнения
(1) от
уравнения
(1) от
![]() [12]
для любого числа
[12]
для любого числа
![]() можно
указать такое
можно
указать такое
![]() чтобы
для решений
чтобы
для решений
![]() и
и
![]() уравнения
(1) выполнялось неравенство
уравнения
(1) выполнялось неравенство
![]()
Выбирая
![]() и
соответственно
и
соответственно
![]() достаточно
малым, будем иметь
достаточно
малым, будем иметь
![]()
и при этом
![]()
Таким образом, малые изменения исходных данных задачи (1),(2),(4) могут привести к как угодно большим изменениям ее решения, и, следовательно, условие устойчивости Адамара не выполняется. Теорема доказана.
Доказательство теоремы 2.
Воспользуемся локальным представлением оператора
![]() заданного
уравнениями (1), (2).
заданного
уравнениями (1), (2).
При входном воздействии h0 реакцию системы обозначим x0:
Рассмотрим
вариацию возмущения
![]() ,
ограниченную по норме
,
ограниченную по норме
![]() ,
и, принимая во внимание ограниченность линейного оператора
,
и, принимая во внимание ограниченность линейного оператора
![]() ,
запишем уравнение в отклонениях для dx(t)
,
запишем уравнение в отклонениях для dx(t)
из которого следует, что
где g - фундаментальное решение для (П.2), которое удовлетворяет линейному однородному уравнению
![]() .
.
Предположение об ограниченности оператора
![]() выполняется
за счет ограниченности по норме производной
выполняется
за счет ограниченности по норме производной
![]() ,
что следует из требования ее непрерывности, и непрерывности функции
,
что следует из требования ее непрерывности, и непрерывности функции
![]() в
постановке задачи.
в
постановке задачи.
Выражение (П.3) в совокупности с (2) и (9) определяет структуру градиента функционала (3) следующим образом
где знак * обозначает сопряженную функцию.
Теорема доказана.
Доказательство теоремы 3.
Уравнение для интервальной
оценки
![]() в
системе (12) с учетом (11) модифицируем
к виду двухточечной краевой задачи следующим образом
в
системе (12) с учетом (11) модифицируем
к виду двухточечной краевой задачи следующим образом
Граничные условия задачи (П. 5) согласно [10] имеют вид
Предположим, что
![]() есть
результат последовательного решения уравнений системы (12)
и для уравнений задачи (П. 5) являются известными функциями
времени, также как и y(t).
есть
результат последовательного решения уравнений системы (12)
и для уравнений задачи (П. 5) являются известными функциями
времени, также как и y(t).
Выполним
процедуру инвариантного погружения задачи (П. 5), (П.
6). Для этого предположим, что
![]() .
Это условие требует определения функций
.
Это условие требует определения функций
![]() ,
зависящих от s,t,c и удовлетворяющих уравнениям (П.
5) и (П. 6)
,
зависящих от s,t,c и удовлетворяющих уравнениям (П.
5) и (П. 6)
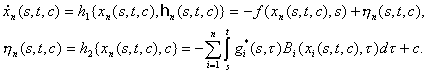
Граничные условия (П. 6) трансформируются следующим образом
![]()
Отметим,
что
![]() ,
и введем обозначения
,
и введем обозначения
![]() .
.
Пусть изменение интервала наблюдения [0,t] определяется малым приращением Dt, тогда
![]() ,
,
и с учетом
![]() ,
соотношения (12) и правила Лейбница
,
соотношения (12) и правила Лейбница
![]()
и, принимая во внимание (П.5)
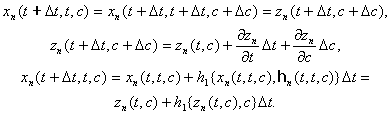
Используя
последние выражения и переходя при
![]() к
пределу, запишем уравнение погружения в виде, поскольку
к
пределу, запишем уравнение погружения в виде, поскольку
![]()
и его
решение при
![]() представляет
собой уравнение оценки
представляет
собой уравнение оценки
![]() процесса
(1), (2) в смысле функционала (3).
процесса
(1), (2) в смысле функционала (3).
Традиционное решение уравнения (П.7) может быть
представлено в виде разложения в ряд Тейлора по параметру с в
окрестности оценки
![]()
Принимая
обозначение
![]() и
подставляя (П.8) в (П.7) с точностью до
бесконечно малых второго порядка получим уравнения точечной рекуррентной
оценки
и
подставляя (П.8) в (П.7) с точностью до
бесконечно малых второго порядка получим уравнения точечной рекуррентной
оценки
![]() процесса
(1), (2)
процесса
(1), (2)
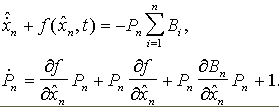
При выводе
данных уравнений учтено, что
![]() .
.
Теорема доказана.
8. ЛИТЕРАТУРА
1. Репин В.Г., Тартаковский Г.П. Статистический синтез при априорной неопределенности и адаптация информационных систем. М.: Сов. Радио, 1977.
2. Фарина А., Студер Ф. Цифровая обработка радиолокационной информации. Сопровождение целей: Перевод с англ. М.: Радио и связь, 1993.
3. Цыпкин Я.З. Основы теории обучающихся систем. М.: Наука, 1970.
4. Bar-Shalom Y., Chang K.C., Tracking a maneuvering target using input estimation versus the interacting multiple model algorithm // IEEE Trans.- 1989.- Vol. AES 25, № 2.
5. Farooq M., Bruder S. Comments on tracking a maneuvering target using input estimation // IEEE Trans. - 1989.- Vol. AES 25, № 2.
6. Berg R.F., Estimation and prediction for maneuvering target trajectories // IEEE Trans. - 1983.- Vol. AES 28, № 3.
7. Тихонов В.И., Харисов В.Н. Статистический анализ и синтез радиотехнических устройств и систем. М.: Радио и связь, 1991.
8. Фалькович С.Е., Пономарев В.И., Шкварко Ю.В. Оптимальный прием пространственно-временных сигналов в радиоканалах с рассеянием. М.: Радио и связь, 1989.
9. Справочник по теории автоматического управления / Под. ред. Красовского А.А. М.: Наука, 1987.
10. Костоглотов А.А., Таран В.Н. Субоптимальная оценка параметров динамических систем // А и Т. 1997. № 4. С. 83-94.
11. Евстратов И.Ю., Кабанов С.А. Управление процессом стабилизации с использованием оптимального адаптивного регулятора// А и Т. 1997. №6, С. 135 – 143.
12. Карташев А.П., Рождественский Б.Л. Обыкновенные дифференциальные уравнения и основы вариационного исчисления. М.: Наука, 1986.
13. Тихонов А.Н., Арсенин В.Я. Методы решения некорректных задач. М.: Наука, 1986.
14. Алифанов О.М., Артюхин Е.А., Румянцев С.В. Экстремальные методы решения некорректных задач. М.: Наука, 1988.
|
|
|