Метод импедансного аналога электромагнитного пространства для двумерных задач электродинамики
С.А. Иванов*, Б.В. Сестрорецкий**
*Физический ф-т МГУ им. М.В. Ломономова, **ФГУП НПО им. С.А. Лавочкина.
Получена 4 мая 2007 г.
Рассмотрены основные положения метода импедансного аналога электромагнитного пространства, предназначенного для компьютерного моделирования сложных двух- и трехмерных электродинамических систем во временной и частотной областях. Подробно изложены основы метода, наиболее важные теоретические результаты и практические приложения для двумерных задач.
Введение
В настоящее время при расчете устройств СВЧ широко применяются методы конечных элементов и конечных разностей. К ним близко примыкает метод импедансного аналога электромагнитного пространства (ИАЭП) [1-3], а также его западный аналог – метод матриц линий передач (Transmission Line Matrix Method, TLM) [4, 5], краткий обзор которого дан в [6].
Метод ИАЭП является логическим продолжением метода электрических сеток, основателем которого является советский математик С.А. Гершгорин, разработавший в 1927 г. основы построения сеточных моделей [7]. В своей пионерской работе С.А. Гершгорин предложил использовать электрическую сетку для экспериментального исследования уравнения Лапласа. Эта сетка была радиотехническим аналогом конечноразностной схемы для дифференциального уравнения в частных производных. Серия работ С.А. Гершгорина привела к возникновению нового класса аналоговых вычислительных машин (АВМ) – электроинтеграторов сеточного типа [8], которые весьма продуктивно использовались вплоть 70-х годов 20-го века [8-15].
Первые попытки создания сеточных радиотехнических моделей для уравнений Максвелла были предприняты в 40-е годы прошлого столетия Габриэлем Кроном [16-18]. Для двумерных задач модели были правильные, однако полная трехмерная сеточная модель Г. Крона [16] была ошибочна, т.к. была энергетически неэквивалентна уравнениям Максвелла. Метод Крона оценивался как слишком сложный для инженеров и слишком нестрогий и неточный для математиков (см., например, предисловие к [17]), поэтому он не получил широкого распространения даже для двумерных задач.
Вторая волна исследований по данной тематике возникла в
начале 70-х годов благодаря работам П. Джонса на западе и Б.В. Сестрорецкого в
СССР. Метод, развиваемый Б.В. Сестрорецким, получил название импедансного
аналога электромагнитного пространства. В основе метода ИАЭП лежит идея о
сведении краевой задачи к задаче анализа сеточной электрической цепи. Процедура
составления радиотехнической сетки состоит из двух этапов. На первом этапе
вакуум, в котором размещается устройство, разбивается на элементарные объемы с
малыми по сравнению с длиной волны размерами и каждому элементарному объему
сопоставляется электрическая схема с сосредоточенными (RLC) или
распределенными (![]() )
элементами. Далее схемы элементарных объемов объединяются в единую сетку –
эквивалентную схему замещения вакуума с параметрами
)
элементами. Далее схемы элементарных объемов объединяются в единую сетку –
эквивалентную схему замещения вакуума с параметрами ![]() ,
, ![]() (
(![]() вакуума). При формировании
вакуума). При формировании ![]() сетки минимизируется
сеточная дисперсионная ошибка (как основная погрешность метода), т.е. отклонение
скорости плоских волн в сетке (плоских сеточных волн) от скорости света
сетки минимизируется
сеточная дисперсионная ошибка (как основная погрешность метода), т.е. отклонение
скорости плоских волн в сетке (плоских сеточных волн) от скорости света ![]() .
.
Свойства вещества, “погруженного” в сетку ![]() вакуума, учитываются
дополнительными реактивными двухполюсниками, которые “навешиваются” на пары
клемм вакуумной сетки. Пары клемм на границах элементарных объемов определяют
взаимодействие объемов по правилу: “каждый влияет только на соседа”. Подобная
концепция, названная в ИАЭП методом информационной матрицы Z,
отличается от концепции “каждый влияет на всех”, характерной для методов
решения краевых задач электродинамики Максвелла. Эти задачи решаются путем
поиска самосогласованного решения, например, задается предполагаемое
распределение токов на металлических электродах и с помощью уравнений Максвелла
находится распределение полей; эти поля требуют корректировки распределения
токов и т.д. В методе ИАЭП поиск самосогласованного решения производить не
требуется. RLC (
вакуума, учитываются
дополнительными реактивными двухполюсниками, которые “навешиваются” на пары
клемм вакуумной сетки. Пары клемм на границах элементарных объемов определяют
взаимодействие объемов по правилу: “каждый влияет только на соседа”. Подобная
концепция, названная в ИАЭП методом информационной матрицы Z,
отличается от концепции “каждый влияет на всех”, характерной для методов
решения краевых задач электродинамики Максвелла. Эти задачи решаются путем
поиска самосогласованного решения, например, задается предполагаемое
распределение токов на металлических электродах и с помощью уравнений Максвелла
находится распределение полей; эти поля требуют корректировки распределения
токов и т.д. В методе ИАЭП поиск самосогласованного решения производить не
требуется. RLC (![]() ) сетка всегда консервативна (как радиотехническая
схема) и сводит краевую задачу к прямым методам решения системы линейных
уравнений с известными коэффициентами.
) сетка всегда консервативна (как радиотехническая
схема) и сводит краевую задачу к прямым методам решения системы линейных
уравнений с известными коэффициентами.
Если вводимое вещество поглощает или генерирует СВЧ энергию,
то в “навешиваемые” двухполюсники вводятся сопротивления и источники ЭДС.
Границы исследуемого объема и границы, где задаются возбуждающие поля,
описываются аналогичным образом RLC-схемами и ЭДС. Деление краевой
задачи на внутреннюю и внешнюю задачи, а также деление устройств на блоки и
сшиваемые “базовые элементы”, использовать в общем случае не требуется. Анализ RLC-
и ![]() -сеток может
производиться на ЭВМ автоматизированно, при этом могут производиться операции
по сгущению и изменению формы элементарных объемов сетки для устройств со
сложной геометрией.
-сеток может
производиться на ЭВМ автоматизированно, при этом могут производиться операции
по сгущению и изменению формы элементарных объемов сетки для устройств со
сложной геометрией.
Достигнутый к настоящему времени уровень освоения метода ИАЭП позволяет проектировать сложные волноводные комплексы без макетирования и настройки образцов, с передачей чертежей с “экрана ЭВМ” прямо на серийный завод [19, 20], поскольку точность программ зачастую превышает возможности измерительной аппаратуры. Получен опыт разработки как единого целого многолучевой полосковой антенны с числом излучателей около 1000 с машинной корректировкой производственного разброса диэлектрической постоянной материала печатной платы.
В теоретическом плане метод ИАЭП находится в стадии развития, осваивая такие сложные объекты, как подмагниченная плазма в термоядерных установках ТОКАМАК и ITER [21-24], исследование взаимодействия антенны в крупногабаритных системах (радарные полигоны, антенны на многоступенчатых спутниковых антеннах). Начаты исследования релятивистских эффектов в различных средах [25].
Первые теоретические и практические исследования метода ИАЭП
относятся к 1967-74 гг. В частности, исследовалось поверхностное сопротивление ![]() ионно-легированных распределенных
кремниевых pin-структур (для коммутаторов в радиометрах
миллиметрового диапазона 0.2¸2
см) при учете закона изменения проводимости
ионно-легированных распределенных
кремниевых pin-структур (для коммутаторов в радиометрах
миллиметрового диапазона 0.2¸2
см) при учете закона изменения проводимости ![]() по толщине слоя (прямоугольный, гауссовый,
экспоненциальный). В моделирующую лестничную LC-схему вводились
параметры
по толщине слоя (прямоугольный, гауссовый,
экспоненциальный). В моделирующую лестничную LC-схему вводились
параметры ![]() и
и ![]() . Величина
. Величина ![]() , как входное
сопротивление лестничной LC-схемы, определялась численными методами
(редукция LC-схемы, приближенные интегральные соотношения) [1,
2].
, как входное
сопротивление лестничной LC-схемы, определялась численными методами
(редукция LC-схемы, приближенные интегральные соотношения) [1,
2].
Замена RLC-схемы генератора Ганна на ![]() -схему, содержащую
замкнутые и разомкнутые шлейфы с временем задержки, кратным
-схему, содержащую
замкнутые и разомкнутые шлейфы с временем задержки, кратным ![]() (
(![]() – время пролета домена в диоде Ганна),
позволила исследовать и устранить неустойчивость генератора, работающего в
новом “ключевом” режиме [26, 27].
– время пролета домена в диоде Ганна),
позволила исследовать и устранить неустойчивость генератора, работающего в
новом “ключевом” режиме [26, 27].
В 1977 и 1983 годах были предложены два типа импедансных
операторов в дискретном пространстве-времени (12-входовых операторов роторного
(рис. 1а) [28] и потокового типов (рис. 1б) [29]). Для варианта “а”
входы (пары клемм) располагаются на ребрах элементарного объема ![]() с ориентацией
напряжения по линии ребер при некотором удалении от вершин
с ориентацией
напряжения по линии ребер при некотором удалении от вершин ![]() (круг обозначает пару клемм,
черта, пересекающая круг – ориентацию электрического поля). Для варианта “б”
входы (по две пары клемм с ортогональными поляризациями электрического поля)
размещаются в центрах каждой грани куба.
(круг обозначает пару клемм,
черта, пересекающая круг – ориентацию электрического поля). Для варианта “б”
входы (по две пары клемм с ортогональными поляризациями электрического поля)
размещаются в центрах каждой грани куба.
Рис. 1. Размещение пар клемм на ребрах
оператора роторного типа (а) и ортогональных пар клемм в центрах граней
оператора потокового типа (б) для элементарного объема кубической формы ![]() .
.
На рис. 2а,б показаны LC-схемы для двух
вариантов операторов, где незачерненными кружками обозначены конденсаторы, а
зачерненными – индуктивности (![]() ,
, ![]() , где
, где ![]() ,
, ![]() – постоянные вакуума); параллельными
линиями на схемах обозначены симметрирующие трансформаторы Т (1:1). В схеме
рис. 2б внутренние обмотки трансформаторов пересекаются в 6 точках (кружки
увеличенного диаметра).
– постоянные вакуума); параллельными
линиями на схемах обозначены симметрирующие трансформаторы Т (1:1). В схеме
рис. 2б внутренние обмотки трансформаторов пересекаются в 6 точках (кружки
увеличенного диаметра).
Рис. 2. Эквивалентные LC-схемы
для оператора роторного (а) и потокового типа (б).
LC-схемы рис 2а,б преобразуются в ![]() -схемы рис. 3.а,б на основе
эквивалентности LC-схемы рис. 4а и короткого отрезка идеальной
двухпроводной линии рис. 4б с волновым сопротивлением
-схемы рис. 3.а,б на основе
эквивалентности LC-схемы рис. 4а и короткого отрезка идеальной
двухпроводной линии рис. 4б с волновым сопротивлением ![]() и временем задержки сигнала
и временем задержки сигнала ![]() , где L и C
подставляются по величинам индуктивностей и емкостей во входных цепях
рис. 2а,б. LC-схема рис. 4а отличается от общепринятой наличием
единичных трансформаторов, основное назначение которых заключается в выравнивании
токов в клеммах. Для двумерных задач эти трансформаторы, как правило, могут
быть опущены, однако для трехмерных векторных задач их учет необходим.
, где L и C
подставляются по величинам индуктивностей и емкостей во входных цепях
рис. 2а,б. LC-схема рис. 4а отличается от общепринятой наличием
единичных трансформаторов, основное назначение которых заключается в выравнивании
токов в клеммах. Для двумерных задач эти трансформаторы, как правило, могут
быть опущены, однако для трехмерных векторных задач их учет необходим.
Рис. 3. Эквивалентные ![]() -схемы для оператора
роторного (а) и потокового типа (б).
-схемы для оператора
роторного (а) и потокового типа (б).
Рис. 4. Преобразование LC-схемы
(а) в отрезок линии передач (б) с волновым сопротивлением ![]() и временем задержки
и временем задержки ![]() .
.
Схемы рис. 2а,
3а являются сеточным радиотехническим
аналогом роторных уравнений Максвелла и описываются уравнениями Кирхгофа.
Отрезки линий в схемах рис. 3а,б имеют электрическую длину ![]() при геометрической
длине
при геометрической
длине ![]() , что
можно интерпретировать как локальное движение энергии с двойной скоростью
света. Это связано с тем, что импульсы в сетке вынуждены перемещаться по
ломаной траектории, проходя некоторые участки пути дважды.
, что
можно интерпретировать как локальное движение энергии с двойной скоростью
света. Это связано с тем, что импульсы в сетке вынуждены перемещаться по
ломаной траектории, проходя некоторые участки пути дважды.
Подчеркнем, что локальное движение энергии с двойной скоростью света – исключительно сеточный эффект, вызванный дискретностью модели. Аналогичную ситуацию можно наблюдать и в других временных сеточных методах: в методе TLM [4, 30, 31], FDTD [32] и т.д. Если разделить процессы в сетке на микроскопические (распространение отдельных импульсов в сетке) и макроскопические (перемещение больших сгустков энергии), то окажется, что для широкого класса сеток микроскопические процессы протекают со скоростью большей, чем скорость света. При этом макроскопические процессы – как переходные, так и стационарные, – описываются достаточно точно. Более того, корректно промоделировать переходные процессы в сетке можно только при условии превышения микроскопической скорости над скоростью света.
Отметим, что роторная схема
рис. 2а является
исправленным вариантом схемы Крона [16]. Консервативность схемы достигнута
введением идеальных трансформаторов на каждой грани ![]() , что обеспечивает равенство
токов в четырех парах клемм на одной грани
, что обеспечивает равенство
токов в четырех парах клемм на одной грани ![]() в соответствии с уравнениями Кирхгофа и
схемной реализацией роторных уравнений Максвелла.
в соответствии с уравнениями Кирхгофа и
схемной реализацией роторных уравнений Максвелла. ![]() -схема рис. 3а, элементарно получаемая
из рис. 2а на основе преобразований рис. 4, может интерпретироваться
как радиотехническая модель консервативного варианта конечно-разностной схемы метода
FDTD [32].
-схема рис. 3а, элементарно получаемая
из рис. 2а на основе преобразований рис. 4, может интерпретироваться
как радиотехническая модель консервативного варианта конечно-разностной схемы метода
FDTD [32].
Существенным недостатком конечно-разностного анализа
является то, что схемы роторного типа рис 2а, и
рис. 3а имеют вдвое
большую сеточную дисперсионную погрешность (точность описания плоских волн) и
требуют вдвое большее время анализа, чем схемы ИАЭП рис. 2б и
рис. 3б
потокового типа. Оператор рис. 1б (и схемы вида
рис. 3б) начали
использовать в методе TLM существенно позднее, чем в методе ИАЭП. Метод TLM
характеризуется нечеткой физической обоснованностью потокового оператора,
названного в [30] симметричным конденсированным узлом (symmetrical condensed node, SCN). При выводе SCN двойная скорость света в длинных
линиях постулируется, а не доказывается. Несмотря на то, что потоковый оператор
и SCN имеют идентичные S-матрицы
и базовые алгоритмы расчета, в эквивалентной схеме SCN
отсутствует система центральных трансформаторов (вместо нее введен “черный
ящик” с такой же S-матрицей). Таким образом,
эквивалентная схема SCN является неполной. На западе
неоднократно высказывалось сомнение в том, что полную эквивалентную схему SCN удастся придумать. Отсутствие системы идеальных трансформаторов
затрудняет преобразования ![]() -сетки, возможные для ускорения
вычислительного процесса. В методе ИАЭП наглядность схем с трансформаторами
позволила выявить “избыточность”
-сетки, возможные для ускорения
вычислительного процесса. В методе ИАЭП наглядность схем с трансформаторами
позволила выявить “избыточность” ![]() -процесса (при вычислениях можно
использовать только половину подводимых волн или только половину
трансформаторных узлов в сетке), а также формировать более сложные
-процесса (при вычислениях можно
использовать только половину подводимых волн или только половину
трансформаторных узлов в сетке), а также формировать более сложные ![]() -схемы для уменьшения
сеточных дисперсионных погрешностей.
-схемы для уменьшения
сеточных дисперсионных погрешностей.
В данном обзоре возможности метода ИАЭП анализируются для
двумерных (2D) RLC- и ![]() -сеток. Длительный опыт
использования программ на основе RLC- и
-сеток. Длительный опыт
использования программ на основе RLC- и ![]() -сеток показал эффективность двумерных
сеток для анализа широкого класса СВЧ устройств. Если краевую задачу удается
свести к анализу двумерных сеток, то достигается лучшая точность, уменьшается
время анализа и увеличивается исследуемый электродинамический объем.
Существенно упрощаются алгоритмы анализа 2D сеток по
сравнению с 3D сетками. В
большей мере оказывается возможным использовать конечно-разностную трактовку
процессов, особенно ориентируясь на аппарат телеграфных уравнений.
-сеток показал эффективность двумерных
сеток для анализа широкого класса СВЧ устройств. Если краевую задачу удается
свести к анализу двумерных сеток, то достигается лучшая точность, уменьшается
время анализа и увеличивается исследуемый электродинамический объем.
Существенно упрощаются алгоритмы анализа 2D сеток по
сравнению с 3D сетками. В
большей мере оказывается возможным использовать конечно-разностную трактовку
процессов, особенно ориентируясь на аппарат телеграфных уравнений.
Основы метода ИАЭП для двумерных задач в частотной области (RLC-сетки)
Центральным понятием метода ИАЭП является понятие сеточного вакуума.
Сеточный вакуум – это эквивалентная RLC- или ![]() -схема пустого пространства. Для
двумерных задач (для H-волн вида
-схема пустого пространства. Для
двумерных задач (для H-волн вида ![]() ,
, ![]() и при отсутствии сторонних источников тока
и зарядов) сеточный вакуум должен моделировать процессы, описываемые
стационарными уравнениями Максвелла следующего вида:
и при отсутствии сторонних источников тока
и зарядов) сеточный вакуум должен моделировать процессы, описываемые
стационарными уравнениями Максвелла следующего вида:
где ![]() – циклическая частота,
– циклическая частота, ![]() – диэлектрическая проницаемость
вакуума,
– диэлектрическая проницаемость
вакуума, ![]() – магнитная
проницаемость вакуума, здесь и далее временная зависимость для RLC-сеток
принимается равной
– магнитная
проницаемость вакуума, здесь и далее временная зависимость для RLC-сеток
принимается равной ![]() .
Систему уравнений (1) можно записать в конечных разностях:
.
Систему уравнений (1) можно записать в конечных разностях:
Как показано в [3,
4, 18], системе (2) можно поставить в
соответствие RLC-схему замещения элемента пространства, эквивалентную
двумерному телеграфному уравнению (см. рис. 5).
Рис. 5. Эквивалентная RLC-схема элемента пространства:
а) четырехугольник, б) четырехлучевая звезда
При таком сопоставлении напряжение U
на конденсаторах определяется напряженностью электрического поля ![]() , а токи
, а токи ![]() и
и ![]() через катушки индуктивности определяются
значениями напряженностей магнитного поля
через катушки индуктивности определяются
значениями напряженностей магнитного поля ![]() и
и ![]() соответственно:
соответственно:
где ![]() ,
, ![]() ,
, ![]() – геометрические размеры элемента
пространства (прямоугольного параллелепипеда) вдоль осей x,
y, z
соответственно. Номиналы элементов эквивалентной схемы [19, 33-35] определяются
параметрами элемента пространства:
– геометрические размеры элемента
пространства (прямоугольного параллелепипеда) вдоль осей x,
y, z
соответственно. Номиналы элементов эквивалентной схемы [19, 33-35] определяются
параметрами элемента пространства:
Схема сеточного вакуума собирается из элементарных объемов
путем объединения эквивалентных схем элементов пространства. При этом
уравнения, описывающие сетку, задаются системой (2) (первые два уравнения –
закон Ома для индуктивностей, третье – закон Кирхгофа). Таким образом,
топология сеточного вакуума задает взаимооднозначное соответствие между
конечно-разностной моделью (поля ![]() ,
, ![]() ,
, ![]() ) и сеточной RLC-схемой (напряжение U и токи
) и сеточной RLC-схемой (напряжение U и токи ![]() ,
, ![]() ).
).
Вещество моделируется подключением к эквивалентной схеме
вакуума рис. 5а,б двухполюсников. То есть влияние вещества – локально, и
все взаимодействие осуществляется через сеточный вакуум. Такую модель называют
моделью информационного многополюсника [36]. Вещество с параметрами ![]() ,
, ![]() моделируется подключением
дополнительных емкостей и индуктивностей. При этом вещество увеличивает емкость
элемента пространства
моделируется подключением
дополнительных емкостей и индуктивностей. При этом вещество увеличивает емкость
элемента пространства ![]() на
на
![]() и
индуктивности элемента пространства
и
индуктивности элемента пространства ![]() и
и ![]() на
на ![]() и на
и на ![]() соответственно. Эквивалентная схема
элемента пространства рис. 5а преобразуется в схему рис. 6.
соответственно. Эквивалентная схема
элемента пространства рис. 5а преобразуется в схему рис. 6.
Рис. 6. Моделирование в RLC-схеме элемента пространства
диэлектрического и магнитного заполнения для вещества с ![]() и
и ![]() .
.
Емкости и индуктивности, вносимые веществом, описываются формулами
При наличии в веществе потерь к эквивалентной схеме
рис. 6 подключаются дополнительные сопротивления – параллельно к емкостям
и последовательно к индуктивностям.
Рис. 7. Объединение эквивалентных RLC-схем элементарных
объемов “четырехугольник” и формирование эквивалентной схемы всей анализируемой
геометрии.
Эквивалентная RLC-схема устройства собирается из элементарных объемов путем объединения эквивалентных схем элементов пространства [21, 37] (см. рис. 7). Т.е. сначала мы произвели декомпозицию сложной анализируемой области на простые однотипные узлы (рис. 5а или рис. 6), а затем проводим процедуру рекомпозиции устройства из элементарных узлов [17]. Таким образом, мы получаем вместо электродинамической задачи задачу нахождения параметров сетки многополюсников [19, 37, 38], эквивалентной всей анализируемой области – задачу теории цепей. Граничные условия задаются путем подключения к клеммам получаемого многополюсника различных нагрузок: условие короткого замыкания для металла и холостого хода для магнитной стенки.
Подобную процедуру можно назвать построением импедансной модели исходной электродинамической задачи. Это позволяет перейти от языка дифференциальных уравнений (формально-математического) к наглядному описанию задачи на языке импедансных сеток (схемному).
Для регулярной сетки, составленной из элементарных схем рис. 5, 6 можно ввести понятие пространственной, или угловой, сеточной дисперсии плоских волн [3, 19, 35], заключающейся в зависимости скорости распространения плоской электромагнитной волны в сетке от ориентации фронта относительно координатных осей.
Плоская сеточная волна – это собственное решение вида
где ![]() – радиус-вектор емкости (узла) с индексами
– радиус-вектор емкости (узла) с индексами
![]() ,
, ![]() – комплексное
напряжение на емкости с индексами
– комплексное
напряжение на емкости с индексами ![]() ,
, ![]() – комплексная амплитуда волны,
– комплексная амплитуда волны, ![]() – сеточный волновой
вектор,
– сеточный волновой
вектор, ![]() –
направление распространения волны. В [19] выведено уравнение сеточной дисперсии
для плоской волны:
–
направление распространения волны. В [19] выведено уравнение сеточной дисперсии
для плоской волны:
где
![]() – волновой вектор в среде с
диэлектрическим заполнением
– волновой вектор в среде с
диэлектрическим заполнением ![]() ,
, ![]() . Там же приведена приближенная формула для
длины волны в сетке:
. Там же приведена приближенная формула для
длины волны в сетке:
где ![]() – длина волны в среде с диэлектрическим
заполнением
– длина волны в среде с диэлектрическим
заполнением ![]() ,
, ![]() ,
, ![]() – длина волны в сетке.
– длина волны в сетке.
В [35,
39] получены выражения для расчета длины волны ![]() , распространяющейся в
сетке, моделирующей регулярный полый металлический волновод с поперечным
сечением прямоугольной формой. Для определения длины волны
, распространяющейся в
сетке, моделирующей регулярный полый металлический волновод с поперечным
сечением прямоугольной формой. Для определения длины волны ![]() принимается допущение о том, что
в продольном направлении, то есть вдоль оси y,
распределение напряжений имеет характер бегущей волны, а в поперечном
направлении напряжение распределено по синусоидальному закону. Полученное
выражение имеет вид
принимается допущение о том, что
в продольном направлении, то есть вдоль оси y,
распределение напряжений имеет характер бегущей волны, а в поперечном
направлении напряжение распределено по синусоидальному закону. Полученное
выражение имеет вид
где N
– число элементарных ячеек вдоль широкой стенки волновода. Это выражение
совпадает в пределе при ![]() с классической формулой для длины волны
с классической формулой для длины волны ![]() .
.
Погрешность вычислений параметров СВЧ устройства вызывается
также отличием характеристического сопротивления волны, распространяющейся в
сетке, от аналогичного сопротивления для регулярного волновода. Для вычисления
сеточного характеристического сопротивления волны ![]() в [19, 35,
39] использован следующий
прием. Регулярный сеточный волновод, составленный из эквивалентных схем
рис. 5а, условно рассекается поперечной плоскостью, проходящей через
емкости и индуктивности
в [19, 35,
39] использован следующий
прием. Регулярный сеточный волновод, составленный из эквивалентных схем
рис. 5а, условно рассекается поперечной плоскостью, проходящей через
емкости и индуктивности ![]() (см. рис. 8а). Каждый узел с клеммами
2, 4, 5, находящимися в этой плоскости (см. рис. 8б), разделяется на две
части (см. рис. 8в). Между клеммами 5 и 5¢
появляется ток.
(см. рис. 8а). Каждый узел с клеммами
2, 4, 5, находящимися в этой плоскости (см. рис. 8б), разделяется на две
части (см. рис. 8в). Между клеммами 5 и 5¢
появляется ток.
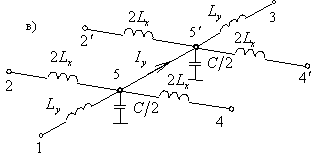
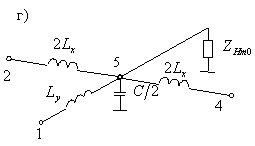
Рис. 8. Определение
характеристического сопротивления сеточной волны: а) разделение регулярного
волновода поперечной плоскостью, б) отдельный узел в поперечной плоскости, в)
разделение узла поперечной плоскостью на две части, г) замена правой части
схемы характеристическим сопротивлением
Теперь, если вместо правой подсхемы подключить к клемме 5 и
“земле” сопротивление ![]() (см.
рис. 8г), то распределение токов и напряжений в левой подсхеме не
изменится. Величина сеточного характеристического сопротивления определяется
формулой [35]
(см.
рис. 8г), то распределение токов и напряжений в левой подсхеме не
изменится. Величина сеточного характеристического сопротивления определяется
формулой [35]
где ![]() – волновое сопротивление среды.
– волновое сопротивление среды.
В работах [19,
40] описана простейшая электрическая схема
для возбуждения RLC-сетки, называемая одномодовым трансформатором (ОТ).
ОТ корректно работает на регулярных участках волноводов, достаточно далеко
удаленных от ближайших неоднородностей – так, что на этих участках
распространяются только прямые и обратные волны основного типа. Для перехода от
сетки с большим числом пар клемм в сечении волновода к одной паре клемм,
определяющей поведение одного энергетического канала с прямой и обратной волнами,
к схеме замещения рис. 9а необходимо добавить трансформирующее устройство
на входе и выходе (см. рис. 9б). Схема замещения в виде сетки вместе с
трансформаторами ![]() и
и
![]() образует цепь
из трех последовательно включенных многополюсников (см. рис. 9в). Каждый
ОТ обеспечивает полное согласование некоторого внешнего активного сопротивления
(сопротивление генератора и нагрузки) с сеткой при возбуждении в ней волны,
эквивалентной волне
образует цепь
из трех последовательно включенных многополюсников (см. рис. 9в). Каждый
ОТ обеспечивает полное согласование некоторого внешнего активного сопротивления
(сопротивление генератора и нагрузки) с сеткой при возбуждении в ней волны,
эквивалентной волне ![]() в
регулярном волноводе. Кроме того, ОТ спроектированы таким образом, что они не
вносят затухания при передаче через них энергии и имеют эффективную
электрическую длину (фазовые углы
в
регулярном волноводе. Кроме того, ОТ спроектированы таким образом, что они не
вносят затухания при передаче через них энергии и имеют эффективную
электрическую длину (фазовые углы ![]() и
и ![]() на рис. 9в), равную
на рис. 9в), равную ![]() или
или ![]() . При этом нормированная S-матрица схемы замещения с трансформаторами полностью
совпадает с нормированной матрицей рассеяния устройства для выбранных отсчетных
сечений волноводов, к которым подключены трансформаторы.
. При этом нормированная S-матрица схемы замещения с трансформаторами полностью
совпадает с нормированной матрицей рассеяния устройства для выбранных отсчетных
сечений волноводов, к которым подключены трансформаторы.
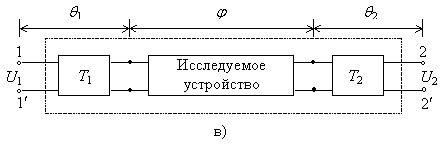
Рис. 9. Схема возбуждения планарной сетки волной ![]() с помощью одномодового
трансформатора: а) схема замещения (эквивалентная схема устройства), б) схема
замещения с трансформаторами, в) блок-схема устройства с трнсформаторами.
с помощью одномодового
трансформатора: а) схема замещения (эквивалентная схема устройства), б) схема
замещения с трансформаторами, в) блок-схема устройства с трнсформаторами.
Возбуждение волны ![]() эквивалентно требованию, чтобы при подаче
на вход напряжения
эквивалентно требованию, чтобы при подаче
на вход напряжения ![]() выходное
напряжение на всех выходных клеммах трансформатора было синфазным с синусным
амплитудным распределением в поперечном сечении. Если волновод имеет сложное
диэлектрическое заполнение, то напряжение на выходных клеммах для основной
волны будет описываться некоторой функцией
выходное
напряжение на всех выходных клеммах трансформатора было синфазным с синусным
амплитудным распределением в поперечном сечении. Если волновод имеет сложное
диэлектрическое заполнение, то напряжение на выходных клеммах для основной
волны будет описываться некоторой функцией ![]() , отличной от синусоиды.
, отличной от синусоиды.
Рис. 10. Схема входного согласующего одномодового
трансформатора: а) полная схема, б) схема отдельного делителя напряжения.
ОТ образуется из ![]() однотипных цепей, входы
которых соединены между собой и выведены в виде пары входных клемм
(рис. 10а), а выходы подключены к соответствующим клеммам схемы замещения.
Каждая такая схема состоит из четырех реактивных сопротивлений (рис. 10б)
и представляет собой делитель напряжений, подобранный так, чтобы для волны
однотипных цепей, входы
которых соединены между собой и выведены в виде пары входных клемм
(рис. 10а), а выходы подключены к соответствующим клеммам схемы замещения.
Каждая такая схема состоит из четырех реактивных сопротивлений (рис. 10б)
и представляет собой делитель напряжений, подобранный так, чтобы для волны ![]() выполнялось условие
выполнялось условие ![]() . При однородном
заполнении внутреннего объема амплитудная функция
. При однородном
заполнении внутреннего объема амплитудная функция ![]() имеет вид:
имеет вид:
![]() ,
, ![]() (13)
(13)
Анализ итоговой RLC-схемы в методе ИАЭП проводится на основе эквивалентных преобразований электрических схем [19, 33]. Рис. 11 поясняет преобразование “треугольник-звезда”.
Рис. 11. Эквивалентное преобразование “треугольник-звезда”: а)
4-звезда, б) 4-треугольник (тетраэдр).
Рис. 12 иллюстрирует один из алгоритмов свертывания плоской RLC-схемы – алгоритм свертывания угловой ячейки сетки. Исходная схема изображена на рис. 12а. На первом этапе с помощью преобразования “3-звезда-треугольник” уничтожается угловая вершина схемы и получается схема рис. 12б. В этой схеме объединяются две пары параллельно соединенных сопротивлений. Таким образом, от исходной угловой ячейки остается только диагонально подключенное сопротивление (см. рис 12в).
Далее последовательно повторяется процесс перемещения
данного сопротивления вдоль диагонали сетки. Вначале к угловому треугольнику
применяется эквивалентное преобразование “треугольник-3-звезда” (см.
рис. 12г). К звезде с центральной вершиной, помеченной черным кружком,
применяется преобразование “4-звезда-тетраэдр” (см. рис. 12д). На место
исчезнувшей вершины помещается вершина, появившаяся при предыдущем
преобразовании (помечена белым кружком на рис. 12г), после чего объединяются
две пары параллельно соединенных сопротивлений на рис 12д. Получившаяся
схема изображена на рис. 12е. На рис. 12ж-12и изображена следующая
итерация. При достижении противоположной границы сетки диагональное
сопротивление исчезает, не изменяя структуру RLC-схемы. Время анализа
плоской RLC-схемы пропорционально ![]() , где N –
число элементов сетки.
, где N –
число элементов сетки.
Рис. 12. Алгоритм свертывания RLC-схемы.
В методе ИАЭП разработаны различные варианты эквивалентных преобразований RLC-схем [19, 33, 37], являющихся, по существу, радиотехническими аналогами фронтальных методов для решения больших разреженных систем линейных уравнений. Фронтальные методы, формально введенные в вычислительную математику только в 70-е годы, и на сегодня являются наиболее эффективными прямыми методами решения разреженных систем линейных уравнений [41, 42].
Исключительно быстродействующие и гибкие процедуры анализа планарных RLC-сеток, моделирующих Е- и Н-плоскостные волноводные СВЧ-устройства, позволили создать высокоэффективные программные комплексы TAMIC-E, TAMIC-Н и TAMIC-W [33, 38, 43, 44]. Алгоритм расчета содержит следующие операции:
– декомпозиция устройства на независимо анализируемые подобласти (решение принимается пользователем, см. рис. 13);
– выбор метода анализа каждой из частичных областей (метода прямых для регулярных участков устройства или метода редукции RLC-сеток [33], решение принимается пользователем);
– определение параметров частичных областей (автоматически);
–
определение параметров устройства (автоматически).
Рис. 13. Декомпозиция устройства на частичные подобласти.
Пусть необходимо определить многомодовую матрицу рассеяния устройства, изображенного на рис. 13а. Для этого:
–
Внутренняя область ![]() анализируемого устройства разбивается на
подобласти
анализируемого устройства разбивается на
подобласти ![]() ,
, ![]() (см. рис. 13б).
(см. рис. 13б).
– В областях сшива задается шаг сетки, определяющий количество учитываемых мод.
–
Для каждой подобласти определяется алгоритм расчета (метод редукции минимальной
степени [38] для областей ![]() и
и ![]() , для остальных – метод прямых), проводится
разбиение на конечные элементы, каждому элементу сопоставляется ячейка
импедансной сетки [44] (см. рис. 14), полученные ячейки объединяются в
единую RLC-сетку.
, для остальных – метод прямых), проводится
разбиение на конечные элементы, каждому элементу сопоставляется ячейка
импедансной сетки [44] (см. рис. 14), полученные ячейки объединяются в
единую RLC-сетку.
–
Проводится анализ подобластей, в результате которого определяются импедансные
Y-матрицы ![]() (рис. 13б),
связывающие токи и напряжения на узлах сетки, находящихся на границе разбиения.
Порядок импедансной матрицы
(рис. 13б),
связывающие токи и напряжения на узлах сетки, находящихся на границе разбиения.
Порядок импедансной матрицы ![]() равен количеству узлов, попавших на
границы разбиения k-й подобласти.
равен количеству узлов, попавших на
границы разбиения k-й подобласти.
– Производится сшив Y-матриц и находится Y-матрица всего устройства.
–
Y-матрица устройства преобразуется в
многомодовую S-матрицу.
Рис. 14. Сопоставление конечного элемента и ячейки RLC-сетки.
Отметим, описанный алгоритм является упрощенным и не дает возможности произвольно задавать размеры устройства, поэтому в действительности для регулярных участков волноводов применяется версия метода прямых, позволяющая обойти данное ограничение.
Точность расчетов E- и H-плоскостных устройств, как правило, превышает возможности современной измерительной аппаратуры, в результате чего полностью исключается этап настройки и доводки разработанных элементов. Это позволяет исключить настроечные элементы из конструкции и разрабатывать устройство с учетом применяемых технологий изготовления устройств.
Программа TAMIC-W позволяет объединять в едином расчете E- и H-плоскостные устройства. Сшив E- и H-областей происходит в одномодовом режиме, что несколько ухудшает точность расчетов. В настоящее время ведется разработка пакета программ, в котором данное ограничение снято.
Комплексное применение пакета позволяет рассчитывать как отдельные элементы (фильтры, поляризаторы, тройники, диплексоры, мосты и т.п., см. рис. 15-17), так и тракты целиком [45, 46].
Таким образом, в [33,
38, 43] разработан комбинированный
алгоритм, сочетающий применение нескольких электродинамических методов. Это и
определяет превосходство в эффективности разработанного на его основе семейства
программных продуктов TAMIC перед всеми другими
известными на сегодняшний день программами данного класса, включая и зарубежные.
Рис. 15. Поляризационный тройник (а), КВС для различных
каналов (б).
Рис. 16. Фильтр (а), его КСВ в полосе пропускания (б) и
затухание в полосе запирания (в).
Рис. 17. Поляризатор, реализованный на изгибе волновода (а),
сдвиг фаз между каналами (б).
Основы метода ИАЭП для двумерных задач во временной области (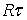 -сетки)
-сетки)
Эквивалентные ![]() -схемы элементарного объема пространства
состоят из отрезков линий передачи без потерь (и сопротивлений при наличии
потерь в веществе). Если схему предполагается анализировать во временной
области, то временные задержки в линиях передачи должны быть одинаковы.
Эквивалентная
-схемы элементарного объема пространства
состоят из отрезков линий передачи без потерь (и сопротивлений при наличии
потерь в веществе). Если схему предполагается анализировать во временной
области, то временные задержки в линиях передачи должны быть одинаковы.
Эквивалентная ![]() -схема
формируется на основе соответствующей RLC-схемы и базируется на
соответствии отрезка линии передачи с временной задержкой
-схема
формируется на основе соответствующей RLC-схемы и базируется на
соответствии отрезка линии передачи с временной задержкой ![]() и характеристическим импедансом
и характеристическим импедансом ![]() (см. рис 18а) и ее LC-аналога (см. рис. 18б).
(см. рис 18а) и ее LC-аналога (см. рис. 18б).
Рис. 18. Линия передачи (а) и ее
эквивалентный четырехполюсник (б).
На рис. 19 [21,
22] изображено преобразование RLC-схемы
(рис. 5а) в ![]() -схему
для случая квадратной сетки (
-схему
для случая квадратной сетки (![]() и
и ![]() ). Все длинные линии на схеме рис. 19
имеют время задержки сигнала
). Все длинные линии на схеме рис. 19
имеют время задержки сигнала ![]() и волновой адмитанс
и волновой адмитанс ![]() .
.
Рис. 19. Преобразование эквивалентной RLC-схемы “четырехугольник”
в эквивалентную ![]() -схему
для элемента пространства, незаполненного веществом.
-схему
для элемента пространства, незаполненного веществом.
На рис. 20 [4] изображена ![]() -схема, полученная из схемы рис. 5б.
На схеме рис. 20 символами
-схема, полученная из схемы рис. 5б.
На схеме рис. 20 символами ![]() и
и ![]() обозначены соответственно падающие и
отраженные волны с ориентацией электрического поля вдоль оси Z.
Волны
обозначены соответственно падающие и
отраженные волны с ориентацией электрического поля вдоль оси Z.
Волны ![]() и
и ![]() с индексами
с индексами ![]() (
(![]() ) распространяются вдоль оси X (Y). Время задержки сигнала в длинных
линиях равно
) распространяются вдоль оси X (Y). Время задержки сигнала в длинных
линиях равно ![]() ,
волновой адмитанс линий –
,
волновой адмитанс линий – ![]() . Параметры
. Параметры ![]() и
и ![]() удовлетворяют соотношениям [35]:
удовлетворяют соотношениям [35]:
Рис. 20. ![]() -схема, соответствующая RLC-схеме “четырехлучевая
звезда”.
-схема, соответствующая RLC-схеме “четырехлучевая
звезда”.
Как видно из (14), для планарной (двумерной) задачи, время
задержки сигнала в линиях ![]() соответствует локальной скорости
распространения сигналов между двумя соседними узлами сетки (микроскопической
скорости), в
соответствует локальной скорости
распространения сигналов между двумя соседними узлами сетки (микроскопической
скорости), в ![]() раз
большей скорости света
раз
большей скорости света ![]() . Данный факт легко объясняется
дискретностью модели: плоская волна, распространяющаяся под углом
. Данный факт легко объясняется
дискретностью модели: плоская волна, распространяющаяся под углом ![]() к осям координат,
распространяется без отражений на узлах
к осям координат,
распространяется без отражений на узлах ![]() -сетки по ломаной траектории длиной в
-сетки по ломаной траектории длиной в ![]() раз большей реального
расстояния, пройденного волной. Отметим, что это означает отсутствие какой-либо
сеточной дисперсии в данном направлении.
раз большей реального
расстояния, пройденного волной. Отметим, что это означает отсутствие какой-либо
сеточной дисперсии в данном направлении.
Вещество моделируется также, как и в RLC-схеме – подключением
дополнительных емкостей (разомкнутые шлейфы) и индуктивностей (короткозамкнутые
шлейфы). Задержки шлейфов могут различаться, но всегда должны быть кратны ![]() . На рис. 21 [21,
22] показана
. На рис. 21 [21,
22] показана ![]() -схема
элемента пространства с параметрами
-схема
элемента пространства с параметрами ![]() ,
, ![]() , соответствующая RLC-схеме “четырехугольник”,
со шлейфами длиной
, соответствующая RLC-схеме “четырехугольник”,
со шлейфами длиной ![]() ,
характеристической проводимостью
,
характеристической проводимостью ![]() для разомкнутого шлейфа и характеристическим
сопротивлением
для разомкнутого шлейфа и характеристическим
сопротивлением ![]() для
короткозамкнутого шлейфа.
для
короткозамкнутого шлейфа.
Рис. 21. Моделирование в ![]() -схеме элемента пространства
диэлектрического и магнитного заполнения для вещества с
-схеме элемента пространства
диэлектрического и магнитного заполнения для вещества с ![]() и
и ![]() .
.
Рис. 22. Бесконечная ![]() -сетка, образованная из элементов рис. 20.
-сетка, образованная из элементов рис. 20.
Рассмотрим вычислительный алгоритм для сетки, составленной из элементов рис. 20 (см. рис. 22). S-матрица центрального узла элемента рис. 20 (т.е. S-матрица пересечения линий передачи) задается следующей формулой [4, 19]:
Данная S-матрица не зависит от частоты. Этот факт позволяет использовать элемент рис. 20 при вычислениях как в частотной, так и во временной области. В частотной области падающие и отраженные волны будут связаны следующим образом:
где ![]() – вектор падающих волн,
– вектор падающих волн, ![]() – вектор отраженных
волн. Во временной области данная S-матрица связывает
вектор прямоугольных импульсов
– вектор отраженных
волн. Во временной области данная S-матрица связывает
вектор прямоугольных импульсов ![]() длительностью
длительностью ![]() , падающих на входы элемента в
промежуток времени
, падающих на входы элемента в
промежуток времени ![]() ,
где
,
где ![]() , с
вектором прямоугольных импульсов
, с
вектором прямоугольных импульсов ![]() , отражаемых от входов элемента в промежуток
времени
, отражаемых от входов элемента в промежуток
времени ![]() :
:
В данном случае импульс с амплитудой U соответствует элементарному потоку Гюйгенса с энергией ![]() .
.
Пронумеруем в сетке
рис. 22 каждый элемент
индексами ![]() соответственно
по оси X и Y. Координаты
центрального узла элемента с индексами
соответственно
по оси X и Y. Координаты
центрального узла элемента с индексами ![]() положим равными
положим равными ![]() . Обозначим через
. Обозначим через ![]() (
(![]() ) вектор импульсов, падающих на
входы (отражаемых от входов) элемента с индексами
) вектор импульсов, падающих на
входы (отражаемых от входов) элемента с индексами ![]() в промежуток времени
в промежуток времени ![]() . Тогда согласно (17) падающие и
отраженные импульсы будут связаны следующим образом:
. Тогда согласно (17) падающие и
отраженные импульсы будут связаны следующим образом:
Импульсы ![]() ,
, ![]() , отраженные от входов элемента с индексами
, отраженные от входов элемента с индексами
![]() являются падающими
для соседних элементов:
являются падающими
для соседних элементов:
Вычислительный процесс для сетки
рис. 22 состоит в
циклическом повторении двух этапов: в момент времени ![]() на входах исследуемой системы
задаются падающие импульсы
на входах исследуемой системы
задаются падающие импульсы ![]() , производится операция “рассеяния”
согласно формулам (15, 18) и определяются отраженные импульсы
, производится операция “рассеяния”
согласно формулам (15, 18) и определяются отраженные импульсы ![]() . Затем производится
операция “переброса” импульсов согласно формулам связи (19). После чего
вычислительный процесс повторяется до достижения необходимой точности анализа
системы. Таким образом, для проведения вычислений по данному алгоритму
требуется хранить
. Затем производится
операция “переброса” импульсов согласно формулам связи (19). После чего
вычислительный процесс повторяется до достижения необходимой точности анализа
системы. Таким образом, для проведения вычислений по данному алгоритму
требуется хранить ![]() переменных,
где N – количество элементов, и использовать 8
операций на один временной шаг для одного элемента [19,
47].
переменных,
где N – количество элементов, и использовать 8
операций на один временной шаг для одного элемента [19,
47].
Критерий прекращения вычислений зависит от возбуждающего сигнала и числа элементов сетки. При возбуждении сигналом конечной длительности легко выбрать количественный критерий: например, вычисления останавливаются, когда в сетке остается достаточно малый уровень энергии, значительно меньший энергии возбуждающего сигнала. При возбуждении полубесконечным сигналом (например, синусоидой) вычисления останавливаются при стабилизации ключевых параметров системы (S-матрицы и т.п.) в заданных пределах на протяжении заданного промежутка времени. Несмотря на нестрогость, такого критерия вполне достаточно для большинства практических задач.
Граничные условия для описанного алгоритма вводятся на гранях элементов. Идеальный металл моделируется коротким замыканием клемм на грани, идеальный магнетик (магнитная стенка) – холостым ходом. Алгоритмически это соответствует изменению операции “переброса” импульсов. Например, при введении металла на грани со входом 1 (см. рис. 20) соответствующее уравнение связи в (19) изменится на следующее:
При моделировании внешних задач применяются различные поглощающие граничные условия [48-50]. В простейшем случае ко входам элементов подключаются резисторы с сопротивлением, равным волновому сопротивлению вакуума.
Для данного алгоритма поля могут определяться как в центре элемента, так и на его гранях. Приведем связь импульсов-потоков и полей на грани элемента [51]:
Описанный выше алгоритм называется
четырехпараметрическим (по количеству хранимых параметров). Более эффективным в
вычислительном отношении является двухпараметрический алгоритм. Данный алгоритм
применяется для сетки, составленной из элементов рис. 19 (см.
рис. 23) и оперирует импульсами напряжений на узлах сетки.
Рис. 23. Бесконечная ![]() -сетка, образованная из элементов
рис. 11.
-сетка, образованная из элементов
рис. 11.
Анализ схемы элемента
рис. 19 показывает [19],
что импульс напряжения ![]() в центральном узле элемента с индексами
в центральном узле элемента с индексами ![]() в промежуток времени
в промежуток времени ![]() связан с импульсами-потоками
на входах элемента:
связан с импульсами-потоками
на входах элемента:
Анализ S-матрицы (15) дает еще одну связь между импульсами-потоками и импульсами напряжения:
откуда получаем, что импульсы напряжения соседних узлов связаны следующим образом:
Таким образом, для расчета напряжений в момент
времени ![]() необходимо
знать напряжения в моменты времени
необходимо
знать напряжения в моменты времени ![]() и
и ![]() .
.
Нетрудно заметить, что формула (24) совпадает с
конечно-разностной схемой 2-го порядка для волнового уравн ения. Поэтому
алгоритм анализа сетки рис. 23 во многом совпадает с конечно-разностным
алгоритмом анализа данного уравнения. В методе ИАЭП принято использовать т.н.
“шахматный” алгоритм расчета, основанный на понятии четности узла [52,
53].
Каждому узлу с индексами ![]() присваивается четность
присваивается четность
Тогда согласно (24) можно вести
расчет для четных узлов (белые кружки на рис. 23) только в четные моменты
времени ![]() , а для
нечетных узлов (черные кружки на рис. 23) – только в нечетные моменты
времени
, а для
нечетных узлов (черные кружки на рис. 23) – только в нечетные моменты
времени ![]() , что
позволяет вдвое уменьшить количество хранимых параметров. Данный алгоритм
является однопараметрическим и требует в среднем 2.5 операции на один временной
шаг для одного узла [21].
, что
позволяет вдвое уменьшить количество хранимых параметров. Данный алгоритм
является однопараметрическим и требует в среднем 2.5 операции на один временной
шаг для одного узла [21].
Рис. 24. Введение граничных условий в сетку рис. 23.
Граничные условия для сетки рис. 23 вводятся на гранях элементов рис. 19. Электрическая стенка соответствует подключению к узлам нагрузки с нулевым сопротивлением, магнитная – подключению нагрузки с нулевой проводимостью. Поэтому эквивалентные схемы электрической и магнитной стенок существенно различны: электрическая стенка закорачивает граничные узлы и удаляет линии передач между ними, магнитная стенка сохраняет линии передачи между граничными узлами, но удваивает их характеристическое сопротивление (см. рис. 24). Изменение схемы узла на границе анализируемой области влечет изменение формулы (22) для напряжения и формулы рассеяния (24). Например, если узел лежит на электрической стенке, то полагают
Отметим, что такой способ введения граничных условий сохраняет возможность расчета по “шахматному” алгоритму.
Дисперсные свойства ![]() -сеток, как правило, существенно лучше
дисперсных свойств их RLC-аналогов. Например,
для данной сетки уравнение сеточной дисперсии для плоской волны описывается
формулой [35, 54]:
-сеток, как правило, существенно лучше
дисперсных свойств их RLC-аналогов. Например,
для данной сетки уравнение сеточной дисперсии для плоской волны описывается
формулой [35, 54]:
где ![]() – сеточный волновой вектор,
– сеточный волновой вектор, ![]() – направление распространения
волны. Непосредственный анализ формулы (27) показывает, что при
– направление распространения
волны. Непосредственный анализ формулы (27) показывает, что при ![]() фазовая скорость
сеточной волны совпадает со скоростью света в вакууме для любого дискрета
фазовая скорость
сеточной волны совпадает со скоростью света в вакууме для любого дискрета ![]() . Приближенный анализ
дает следующую формулу для длины волны в сетке:
. Приближенный анализ
дает следующую формулу для длины волны в сетке:
где ![]() – длина волны в свободном пространстве,
– длина волны в свободном пространстве, ![]() – длина волны в сетке.
Сравнивая эту формулу с приближенной формулой (10) для RLC-сетки,
получаем, что сеточная дисперсия в
– длина волны в сетке.
Сравнивая эту формулу с приближенной формулой (10) для RLC-сетки,
получаем, что сеточная дисперсия в ![]() -сетке меньше в среднем 3 раза. Более
подробное сравнение дисперсии RLC- и
-сетке меньше в среднем 3 раза. Более
подробное сравнение дисперсии RLC- и ![]() -сеток приведено на
рис. 25, где изображены дисперсионные кривые, полученные для точных
уравнений (8) и (27).
-сеток приведено на
рис. 25, где изображены дисперсионные кривые, полученные для точных
уравнений (8) и (27).
Рис. 25. Зависимость ![]() от угла
от угла ![]() для планарных RLC-
и
для планарных RLC-
и ![]() -сеток при
различных отношениях
-сеток при
различных отношениях ![]() .
.
Свойства сеточных волн типа ![]() исследуются по той же схеме, что и для RLC-сеток.
Приведем выражение для длины волны
исследуются по той же схеме, что и для RLC-сеток.
Приведем выражение для длины волны ![]() [21, 23]:
[21, 23]:
Это выражение совпадает в пределе
при ![]() с
классической формулой для длины волны
с
классической формулой для длины волны ![]() .
.
Рис. 26. Определение характеристического сопротивления
сеточной волны ![]() .
.
Схема, используемая для определения характеристического
сопротивления сеточной волны ![]() , показана на рис. 26. Величина
, показана на рис. 26. Величина ![]() , вычисленная для схемы
рис. 26, определяется формулой [23]
, вычисленная для схемы
рис. 26, определяется формулой [23]
где ![]() .
.
Для возбуждения ![]() -сеток можно использовать классические
приемы, разработанные для конечно-разностных методов (возбуждение
дельта-импульсом, функцией Хевисайда, “оконной” функцией (windowing function) и т.п. [5]). Однако
наибольшее распространение получили возбуждающие схемы, подобные описанным
выше, т.е. с согласующими трансформаторами. Для
-сеток можно использовать классические
приемы, разработанные для конечно-разностных методов (возбуждение
дельта-импульсом, функцией Хевисайда, “оконной” функцией (windowing function) и т.п. [5]). Однако
наибольшее распространение получили возбуждающие схемы, подобные описанным
выше, т.е. с согласующими трансформаторами. Для ![]() -сеток разработано несколько типов трансформаторов:
одно- и многомодовые (т.е. возбуждающие и поглощающие одну или несколько мод),
одно- и многочастотные (т.е. одновременно возбуждающие и поглощающие одну или
несколько частот), а также их комбинации [55].
-сеток разработано несколько типов трансформаторов:
одно- и многомодовые (т.е. возбуждающие и поглощающие одну или несколько мод),
одно- и многочастотные (т.е. одновременно возбуждающие и поглощающие одну или
несколько частот), а также их комбинации [55].
На рис. 27 изображен одночастотный одномодовый
трансформатор [21, 56] для волновода шириной ![]() . Трансформатор состоит из
. Трансформатор состоит из ![]() генератора напряжения с
внутренней проводимостью
генератора напряжения с
внутренней проводимостью ![]() . В момент времени
. В момент времени ![]() генераторы начинают излучать с
тактом
генераторы начинают излучать с
тактом ![]() падающую
волну (эквидистантный пакет прямоугольных импульсов с синусоидальной
огибающей):
падающую
волну (эквидистантный пакет прямоугольных импульсов с синусоидальной
огибающей):
Рис. 27. Одномодовый трансформатор.
Эти импульсы излучаются в линии
передач с характеристической проводимостью ![]() , непосредственно подключенные к
генераторам. Энергия каждого импульса-потока равна
, непосредственно подключенные к
генераторам. Энергия каждого импульса-потока равна ![]() .
.
Алгоритм расчета на узлах, непосредственно прилегающих к генератору (более крупные кружки на рис. 28), изменяется: напряжения определяются по формуле
Рис. 28. Схема отдельного узла одномодового трансформатора
рис. 19.
Отраженные обратно в генератор импульсы-потоки определяются по формуле (23). Поскольку в начальный момент времени напряжения на всех узлах и потоки во всех линиях равны нулю, то указанных формул достаточно для определения напряжения на всех узлах и отраженных импульсов-потоков на всех входах исследуемой системы. Параметры отраженной волны определяются на основе Фурье-анализа отраженных импульсов. Точный учет сеточного волнового сопротивления позволяет добиться для данного трансформатора идеального согласования (с точностью до машинного шума) возбуждающего устройства и волноводной системы [21, 56].
Моделирование частотно-зависимых диэлектриков
Как было сказано выше, моделирование диэлектриков
производится с помощью двухполюсников – емкостей или разомкнутых шлейфов для
изменения диэлектрической проницаемости, индуктивностей или короткозамкнутых
шлейфов для изменения магнитной проницаемости. Такой способ хорошо работает для
частотно-независимых диэлектриков с ![]() и
и ![]() . Для сред с параметрами
. Для сред с параметрами ![]() и/или
и/или ![]() этот способ требует
добавления отрицательных емкостей и индуктивностей в RLC-сетку и шлейфов
с отрицательными характеристическими сопротивлениями в
этот способ требует
добавления отрицательных емкостей и индуктивностей в RLC-сетку и шлейфов
с отрицательными характеристическими сопротивлениями в ![]() -сетку. Отметим, что если
-сетку. Отметим, что если ![]() и/или
и/или ![]() и предполагается, что
и предполагается, что ![]() и
и ![]() частотнонезависимы, то сама
система является физически неустойчивой, т.е. такая система не имеет
стационарного режима. Поэтому исследовать подобную систему в частотной области
нельзя. Решение во временной области имеется, но является расходящимся. Если
для физически устойчивой системы известна частотная зависимость тензора диэлектрической
(магнитной) проницаемости, то может быть получена соответствующая ей
импедансная схема, которая будет устойчива как в частотной, так и во временной
области. Методика построения импедансных схем описана в [57].
частотнонезависимы, то сама
система является физически неустойчивой, т.е. такая система не имеет
стационарного режима. Поэтому исследовать подобную систему в частотной области
нельзя. Решение во временной области имеется, но является расходящимся. Если
для физически устойчивой системы известна частотная зависимость тензора диэлектрической
(магнитной) проницаемости, то может быть получена соответствующая ей
импедансная схема, которая будет устойчива как в частотной, так и во временной
области. Методика построения импедансных схем описана в [57].
В [22] предложено простейшее и вместе с тем исключительно
эффективное решение данной проблемы: при расчете на некоторой частоте ![]() отрицательная емкость/индуктивность
(разомкнутый/короткозамкнутый шлейф с отрицательным характеристическим
сопротивлением) заменяется положительной индуктивностью/емкостью
(короткозамкнутым/разомкнутым шлейфом с положительным
характеристическим сопротивлением) – так, чтобы реактивности, вносимые в
отрицательная емкость/индуктивность
(разомкнутый/короткозамкнутый шлейф с отрицательным характеристическим
сопротивлением) заменяется положительной индуктивностью/емкостью
(короткозамкнутым/разомкнутым шлейфом с положительным
характеристическим сопротивлением) – так, чтобы реактивности, вносимые в ![]() -схему, были одинаковы у
старого и нового шлейфов. Линии передач, ответственные за передачу энергии
между узлами (линии “сеточного вакуума”, см. рис. 19, 29б)
оставляются неизменными.
-схему, были одинаковы у
старого и нового шлейфов. Линии передач, ответственные за передачу энергии
между узлами (линии “сеточного вакуума”, см. рис. 19, 29б)
оставляются неизменными.
Рис. 29. RLC- и ![]() -схемы элемента пространства для вещества с
диэлектрическим
-схемы элемента пространства для вещества с
диэлектрическим ![]() и
магнитным заполнением
и
магнитным заполнением ![]() .
.
На рис. 29а показаны схемы для высокотемпературной
плазмы с параметрами ![]() и
и
![]() . Емкости и
индуктивности, вносимые веществом, описываются формулами
. Емкости и
индуктивности, вносимые веществом, описываются формулами
где пара ![]() принимает значения
принимает значения ![]() или
или ![]() . Таким образом, если
. Таким образом, если ![]() , то дополнительная
положительная емкость
, то дополнительная
положительная емкость ![]() увеличивает
емкость ячейки, если
увеличивает
емкость ячейки, если ![]() (включая
(включая
![]() ), то
дополнительная положительная индуктивность
), то
дополнительная положительная индуктивность ![]() , моделирующая на некоторой частоте
отрицательную емкость
, моделирующая на некоторой частоте
отрицательную емкость ![]() ,
уменьшает емкость ячейки. При этом схемы для случаев
,
уменьшает емкость ячейки. При этом схемы для случаев ![]() ,
, ![]() и
и ![]() не отличаются друг от друга. Аналогичная
ситуация возникает и при
не отличаются друг от друга. Аналогичная
ситуация возникает и при ![]() .
.
Достаточно интересным следствием данного подхода является
обязательная частотная зависимость диэлектрической и/или магнитной
проницаемости от частоты в случаях ![]() и/или
и/или ![]() для консервативных
для консервативных ![]() -сеток. Причем такая зависимость
от частоты диэлектрической и магнитной проницаемости не может иметь произвольный
вид (в теории цепей аналогичное утверждение носит название теоремы Фостера).
Это согласуется с физическими представлениями о невозможности превысить фазовую
скорость плоской электромагнитной волны в вакууме – скорость света.
-сеток. Причем такая зависимость
от частоты диэлектрической и магнитной проницаемости не может иметь произвольный
вид (в теории цепей аналогичное утверждение носит название теоремы Фостера).
Это согласуется с физическими представлениями о невозможности превысить фазовую
скорость плоской электромагнитной волны в вакууме – скорость света.
Еще более удивительно то, что ![]() -сетки вида рис. 29 очень хорошо
описывают поведение реальных веществ с частотно-зависимыми параметрами
(например, плазмы) в достаточно широкой полосе частот. Таким образом, элементы
вида рис. 29 пригодны для расчета как стационарных, так и переходных
процессов в данных веществах.
-сетки вида рис. 29 очень хорошо
описывают поведение реальных веществ с частотно-зависимыми параметрами
(например, плазмы) в достаточно широкой полосе частот. Таким образом, элементы
вида рис. 29 пригодны для расчета как стационарных, так и переходных
процессов в данных веществах.
Рис. 30. Геометрия Е-плоскостного устройства на основе
прямоугольного волновода.
Аналогичные схемы получаются для E-плоскостных волноводных систем (см. рис. 30), описываемых следующей системой уравнений:
где ![]() – критическая частота для волны
– критическая частота для волны ![]() . Данные схемы показаны
на рис. 31.
. Данные схемы показаны
на рис. 31.
Рис. 31. RLC- и ![]() -схемы элемента
пространства для Е-плоскостных устройств.
-схемы элемента
пространства для Е-плоскостных устройств.
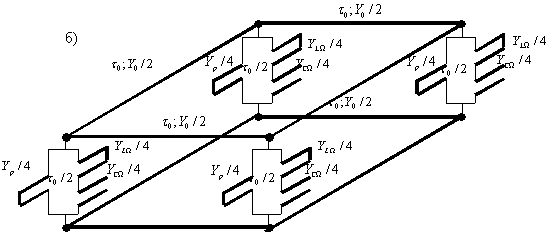
Рис. 32. RLC- и ![]() -схемы элемента пространства, содержащего
подмагниченную плазму.
-схемы элемента пространства, содержащего
подмагниченную плазму.
Более сложные схемы получаются для подмагниченной плазмы
[24] (см. рис. 32). Данные схемы получены для системы уравнений,
описывающей волны E-поляризации (![]() ,
, ![]() ):
):
где ![]() ,
, ![]() – плазменная частота,
– плазменная частота, ![]() – циклическая циклотронная
частота. Формулы для параметров
– циклическая циклотронная
частота. Формулы для параметров ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() приведены в [21,
24].
приведены в [21,
24].
На базе вышеописанных схем создан пакет прикладных программ TAMIC-Rt-H для расчета планарных СВЧ-устройств и анализа плазмы в системах типа ТОКАМАК. Данный пакет используется в РНЦ “Курчатовский институт” для оптимизации волноводной системы рефлектометрической диагностики проектируемой термоядерной установки ITER, а также для сравнения результатов расчета параметров плазмы с экспериментальными данными, полученными на установке ТОКАМАК-10. В настоящее время это единственный пакет, применяемый для диагностики плазмы в установке ТОКАМАК-10.
Пример типичной задачи для ТОКАМАК-10 приведен на
рис. 33. В данной задаче требовалось рассчитать отражение от неоднородного
(по радиусу) цилиндра с гауссовым возмущением диэлектрической проницаемости
вблизи границы, где ![]() .
.
Рис. 33. Геометрия задачи рассеяния на цилиндре с гауссовым
возмущением вблизи радиуса с диэлектрической проницаемостью ![]() , равной нулю.
, равной нулю.
Распределения поля ![]() в различные моменты времени показано на
рис. 34.
в различные моменты времени показано на
рис. 34.
0.5 ns 1.5 ns 4.0 ns
Рис. 34. Распределение амплитуды ![]() в различные моменты времени.
в различные моменты времени.
Подробно вопросы моделирования методом ![]() -сеток сред с частотно-зависимыми
параметрами изложены в недавно изданной монографии [21].
-сеток сред с частотно-зависимыми
параметрами изложены в недавно изданной монографии [21].
Импедансно-сеточная функция Грина
Метод ИАЭП позволяет также решать задачи дифракции в открытых областях. Для этого был разработан метод импедансно-сеточной функции Грина, сочетающий в себе преимущества универсальности и простоты традиционного конечно-разностного метода с преимуществами метода интегральных уравнений при учете условий излучения [58, 59].
Импедансно-сеточная функция Грина – это Z-матрица, описывающая связь токов и напряжений на клеммах некоторой бесконечной однородной радиотехнической сетки. Для LC-сетки вида рис. 7 данная матрица записывается следующим образом [59]:
где ![]() – комплексные параметры, характеризующие
величину наведенного напряжения на клеммах сетки i,
j при подведении внешнего возбуждающего тока к
клеммам k, l (см.
рис. 35).
– комплексные параметры, характеризующие
величину наведенного напряжения на клеммах сетки i,
j при подведении внешнего возбуждающего тока к
клеммам k, l (см.
рис. 35).
Рис. 35. Бесконечная однородная ненагруженная LC-сетка.
Построение импедансно-сеточной функции Грина для решения двумерных задач дифракции происходит следующим образом:
- Бесконечная однородная LC-сетка вида рис. 7 разбивается произвольным образом на прямоугольные блоки больших размеров, на границах которых накладываются условия периодичности и энергетической изоляции. Так поступают всегда при анализе бесконечных периодических структур [60], конечный результат, при устремлении размеров блока к бесконечности, не зависит от способа разбиения.
- Если находить Z-матрицу бесконечной сетки, устремляя размеры блока к бесконечности и переходя к пределу, то мы получим расходящийся ряд, поскольку не учтены условия излучения.
- Для моделирования условий излучения применяется принцип предельного поглощения: в сетку вводятся малые потери и находится Z-матрица отдельного блока в виде конечного ряда по полной системе собственных функций, описывающих резонансные колебания данного блока. Затем размеры блока устремляются к бесконечности и одновременно потери устремляются к нулю – таким образом, чтобы при увеличении размеров блоков влияние стенок уменьшалось (т.е. увеличивалось затухание плоских волн при пробеге от одной стенки до другой).
- В результате предыдущей процедуры искомая функция Грина бесконечной LC-сетки представляется как предельное значение некоторой последовательности рядов. Отметим, что именно введение потерь обеспечивает сходимость
- Производится переход от представления Z-матрицы в виде рядов к интегральному представлению.
Приведем окончательное выражение для сеточной функции Грина [59]:
где
При стремлении шага сетки к нулю сеточная функция Грина переходит в классическую функцию Грина непрерывного пространства.
Формула (38) неудобна для вычисления. Поэтому в [58]
предложен эффективный способ определения элементов Z-матрицы
для случая квадратной сетки (![]() ). В этом случае аналитическое
представление для
). В этом случае аналитическое
представление для ![]() может
быть сведено к интегралу специального вида, удобного для численных расчетов:
может
быть сведено к интегралу специального вида, удобного для численных расчетов:
где
где
Интеграл (40) приближенно вычисляется с помощью рядов:
где
Для случая ![]() формула (43) упрощается:
формула (43) упрощается:
где ![]() и
и ![]() – функции Лежандра первого и второго рода
соответственно. Кроме того, из анализа LC-сетки получаются следующие
рекуррентные соотношения:
– функции Лежандра первого и второго рода
соответственно. Кроме того, из анализа LC-сетки получаются следующие
рекуррентные соотношения:
Последовательность расчета блока из ![]() ячеек (
ячеек (![]() ) следующая: вначале
рассчитываются диагональные элементы:
) следующая: вначале
рассчитываются диагональные элементы: ![]() и
и ![]() (помечены белыми кружками на рис. 36)
– по формуле (45), остальные (помечены черными кружками на
рис. 36) – по
рекуррентной формуле (46); затем рассчитываются недиагональные элементы:
(помечены белыми кружками на рис. 36)
– по формуле (45), остальные (помечены черными кружками на
рис. 36) – по
рекуррентной формуле (46); затем рассчитываются недиагональные элементы: ![]() ,
, ![]() (помечены крестиками на
рис. 36) – с помощью интегральных формул (41)-(43), остальные – по
рекуррентным формулам (47) и (48). Последовательность вычислений недиагональных
элементов показана стрелками. Вначале вычисляется ветвь, помеченная цифрой 1,
затем – ветвь, помеченная цифрой 2 и т.д. Отметим, что вычисления по формулам
(47), (48) в сторону увеличения индексов
(помечены крестиками на
рис. 36) – с помощью интегральных формул (41)-(43), остальные – по
рекуррентным формулам (47) и (48). Последовательность вычислений недиагональных
элементов показана стрелками. Вначале вычисляется ветвь, помеченная цифрой 1,
затем – ветвь, помеченная цифрой 2 и т.д. Отметим, что вычисления по формулам
(47), (48) в сторону увеличения индексов ![]() неустойчивы.
неустойчивы.
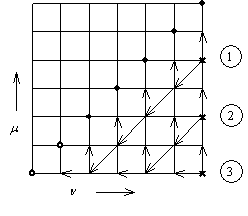
Рис. 36. Последовательность вычисления коэффицинентов Z-матрицы.
Полученные результаты позволяют решить задачу возбуждения ненагруженной сетки точечным источником: падающая волна полностью определяется функцией Грина. При возбуждении плоской волной напряжение падающей волны определяется с помощью формул (7)-(9).
Вещество моделируется стандартным для RLC-сеток образом – введением соответствующих двухполюсников в узлы сетки (параллельно к емкостям). В свою очередь двухполюсники моделируются методом вспомогательных источников.
Задача дифракции плоской волны на металлическом теле решается следующим образом. Металлическое тело моделируется введением вспомогательных источников тока в узлах сетки, аппроксимирующих границу G. Амплитуды источников подбираются таким образом, чтобы напряжение на границе равнялось нулю. В итоге получается следующая задача для определения амплитуд источников:
где ![]() – вектор напряжений падающей волны на
границе, определяемый по формулам (7)-(9),
– вектор напряжений падающей волны на
границе, определяемый по формулам (7)-(9), ![]() – вектор амплитуд токов вспомогательных
источников,
– вектор амплитуд токов вспомогательных
источников, ![]() –
сеточная функция Грина, вычисленная в соответствии с заданной топологией.
–
сеточная функция Грина, вычисленная в соответствии с заданной топологией.
Аналогичным образом решаются задачи дифракции на
диэлектрических телах, в том числе имеющих потери, и на комбинированных
металло-диэлектрических структурах. Во всех случаях задача дифракции сводится к
непосредственному обращению матрицы ![]() , вычисленной заранее и не зависящей от
геометрии и состава исследуемых тел. Матрица возникающей при этом системы
уравнений является произведением блочно-тёплицевой и диагональной матрицы, что
позволяет применить ускоренные процедуры их решения с помощью быстрого
преобразования Фурье и метода сопряженных градиентов. Представленные выше
алгоритмы стали основой для пакета программ DIGRID,
ориентированного на решение двумерных задач дифракции.
, вычисленной заранее и не зависящей от
геометрии и состава исследуемых тел. Матрица возникающей при этом системы
уравнений является произведением блочно-тёплицевой и диагональной матрицы, что
позволяет применить ускоренные процедуры их решения с помощью быстрого
преобразования Фурье и метода сопряженных градиентов. Представленные выше
алгоритмы стали основой для пакета программ DIGRID,
ориентированного на решение двумерных задач дифракции.
Данный метод легко обобщается на трехмерный случай и на случай слоистых сред [58], причем для слоистых сред метод сеточной функции Грина имеет преимущество перед традиционным методом интегральных уравнений, в котором использование смешанной потенциальной формулировки для слоистой среды встречает трудности.
Заключение
Изложенные концепции метода ИАЭП (импедансных RLC- и
![]() -сеток) предполагают
использование интуитивно понятной радиотехнической модели изучаемой системы и
относительно простого математического аппарата, присущего теории цепей. Одной
их основных задач исследователя является синтез удачной эквивалентной схемы,
позволяющей создавать эффективные вычислительные алгоритмы. Достигнутые на этом
пути результаты не хуже, а зачастую и превосходят результаты, достигнутые с
помощью других методов.
-сеток) предполагают
использование интуитивно понятной радиотехнической модели изучаемой системы и
относительно простого математического аппарата, присущего теории цепей. Одной
их основных задач исследователя является синтез удачной эквивалентной схемы,
позволяющей создавать эффективные вычислительные алгоритмы. Достигнутые на этом
пути результаты не хуже, а зачастую и превосходят результаты, достигнутые с
помощью других методов.
Все изложенные идеи переносятся и на трехмерный случай, для
которого характерны более сложные эквивалентные RLC- и ![]() -схемы элемента пространства
и более сложные алгоритмы анализа [28-31,
61].
-схемы элемента пространства
и более сложные алгоритмы анализа [28-31,
61].
Укажем перспективные двумерные задачи метода ИАЭП:
- Разработка сеток с уменьшенной сеточной дисперсией.
- Моделирование процессов распространения электромагнитных волн в подмагниченной плазме.
-
Создание эффективных алгоритмов для многочастотного анализа импедансных ![]() -сеток во временной
области.
-сеток во временной
области.
- Разработка треугольных элементов для уточнения границ.
- Разработка эквивалентных схем для киральных и бианизотронпных сред.
- Решение практических задач проектирования планарных СВЧ устройств и систем любого требуемого уровня сложности.
- Расширение метода для решения смежных физико-математических и технических задач: акустики, термодинамики, механики, гидродинамики [62].
- Уточнение схем элементов, учитывающих концентрацию поля на ребрах.
Работа выполнена при поддержке РФФИ, проект №06-01-00146.
Литература
1. Сестрорецкий Б.В. Полупроводниковые коммуникаторы для высокочастотных трактов. // В сб. “Современные проблемы антенно-волноводной техники”. –М.: Наука, 1967, стр. 126-144.
2. Сестрорецкий Б.В. Полупроводниковые регулирующие устройства СВЧ. // Раздел III монографии “СВЧ устройства на полупроводниковых диодах. Проектирование и расчет. –М.: Сов. радио, 1969, стр. 414-572.
3. Сестрорецкий Б.В. Возможности прямого численного решения краевых задач на основе метода импедансного аналога электромагнитного пространства (ИАЭП). // Вопросы радиоэлектроники, сер. “Общетехническая”, 1976, вып. 2, стр. 113-128.
4. Johns P.B., Beurle R.L. Numerical solution of 2-dimensional scattering problems using a transmission-line matrix. // Proc. Inst. Elec. Eng. Sept. 1971, vol. 118, pp. 1203-1208.
5. Christopoulos С. The Transmission-Line Modelling (TLM) Method. Series on Electromagnetic Wave Theory. // IEEE/Oxford University Press, 1995, 232 pp.
6. Петров А.С., Иванов С.А, Королев С.А., Фастович С.В. Метод матриц линий передачи в вычислительной электродинамике. // Зарубежная радиоэлектроника. Успехи современной радиоэлектроники. 2002, №1, стр. 3-38.
7. Гершгорин С.А. Об электрических сетках для приближенного решения дифференциального уравнения Лапласа. // Журнал прикладной физики. 1929, т. 6, вып. 3-4, стр. 3-29.
8. Гутенмахер Л.И. Электрическое моделирование (электроинтегратор). // –М.-Л.: Изд-во АН СССР, 1943, 128 стр.
9. Тетельбаум И.М. Электрическое моделирование. // –М.: Физматгиз, 1959, 319 стр.
10. Веников В.А. Физическое моделирование электрических систем. // –М.-Л.: Госэнергоиздат, 1956, 359 стр.
11. Штейн Н.И. Методы электрического моделирования волноводов. // В Сб. “Электрическое моделирование”. Изд-во АН СССР, 1952.
12. Пухов В.В., Сазонов В.П. Модели с сосредоточенными параметрами для изучения электромагнитных полей. // Вопросы радиоэлектроники. Сер. 1 Электроника. 1961, вып. 12.
13. Филатова Е.А. // Диссертация на соискание степени кандидата технических наук. –М.: МЭИ, 1969.
14. Федоров Н.Н. Решение двумерных задач электродинамики в неоднородных средах методом моделирования. // –М.: Труды МЭИ. Радиотехника. 1969, вып. 65.
15. Федоров Н.Н. Решение некоторых задач электродинамики в неоднородных средах методами конечно разностных сеток. // Диссертация на соискание степени кандидата технических наук. –М.: МЭИ, 1969, 472 стр.
16. Kron G. Equivalent circuits of the field equations of Maxwell. // Proc. of I.R.E. May 1944. pp. 289-299.
17. Крон Г. Тензорный анализ сетей. // –М.: Сов. радио, 1978, 719 стр.
18. Крон Г. Исследования сложных систем по частям (диакоптика). // –М.: Наука, 1972, 542 стр.
19. Кухаркин Е.С., Сестрорецкий Б.В. Диалоговая оптимизация топологии устройств в электродинамических САПР. // –М.: МЭИ, 1987, 96 стр.
20. Рученков В.А., Камышев Т.В., Климов К.Н., Сестрорецкий Б.В., Белостоцкая К.К. Проектирование режекторных волноводных фильтров для диплексера станций “Индия”. // –М.: ОКБ МЭИ, “Радиотехнические тетради”, 2004, №30, стр. 20-23.
21. Климов К.Н., Сестрорецкий Б.В., Вершков В.А., Солдатов С.В., Камышев Т.В., Рученков В.А. Электродинамический анализ двумерных неоднородных сред и плазмы. // –М.: МАКС Пресс, 2005, 322 стр.
22. Климов К.Н., Сестрорецкий Б.В. Построение консервативных сеток для решения двумерных задач электродинамического анализа систем с произвольным распределением диэлектрической и магнитной проницаемостей. // Радиотехника и электроника. 2001, т. 46, №1, стр. 30-39.
23. Климов К.Н., Сестрорецкий Б.В. Анализ во временной области планарных структур с произвольным распределением диэлектрической проницаемости. // Радиотехника и электроника. 2001, т. 46, №3, стр. 271-276.
24. Климов К.Н., Сестрорецкий Б.В. Построение эквивалентной схемы элементарного объема пространства для подмагниченной плазмы // Радиотехника и электроника. 2005, т. 50, №6, стр. 647-658.
25. Рученков В.А. Развитие методики импедансного аналога электромагнитного пространства. // Диссертация на соискание степени кандидата технических наук. –М.: МГИЭМ, 2006, 255 стр.
26. Сестрорецкий Б.В., Владимиров Ю.К. О некоторых задачах машинного проектирования сложных СВЧ систем. // В сб. “Машинное проектирование устройств и систем СВЧ”. Общество “Знание” Украинской ССР, Киев, 1974, вып. 1, стр. 14-15.
27. Рыков В.В., Сестрорецкий Б.В. Машинное моделирование нестационарных процессов в твердотельных СВЧ генераторах. // Межвузовский сборник научных трудов “Машинное проектирование устройств и систем СВЧ”. –М.: МИРЭА, 1978, вып. 2, стр. 110-132.
28. Сестрорецкий Б.В. RLC
и ![]() -аналоги
электромагнитного пространства. // Межвузовский сборник научных трудов
“Машинное проектирование устройств и систем СВЧ”, МИРЭА, 1977,
стр. 127-158.
-аналоги
электромагнитного пространства. // Межвузовский сборник научных трудов
“Машинное проектирование устройств и систем СВЧ”, МИРЭА, 1977,
стр. 127-158.
29. Сестрорецкий Б.В. Балансные RLC
и ![]() схемы
элементарного объема пространства. // Вопросы радиоэлектроники, сер.
“Общие вопросы радиоэлектроники”, 1983, вып. 5, стр. 56-85.
схемы
элементарного объема пространства. // Вопросы радиоэлектроники, сер.
“Общие вопросы радиоэлектроники”, 1983, вып. 5, стр. 56-85.
30. Johns P.B. A Symmetrical Condensed Node for the TLM Method. // IEEE Transactions on Microwave Theory and Techniques. Apr. 1987, pp. 370-377.
31. Akhtarzad S., Johns P.B. Solution of Maxwell’s equations in three space dimensions and time by the TLM method of analysis. // Proc. Inst. Elec. Eng. 1975, vol. 122, pp. 1344-1348.
32. Yee K.S. Numerical solution of initial boundary value problems involving Maxwell’s equations in isotropic media. // IEEE Trans. on Antennas and Propagation. May 1966, vol. AP-14, pp. 302-307.
33. Кухаркин Е.С., Сестрорецкий Б.В. Машинные методы расчета в инженерной электрофизике. // –М.: МЭИ, 1986, 68 стр.
34. Сестрорецкий Б.В., Климов К.Н., Королев С.А., Петров А.С. Моделирование волноводных устройств с помощью метода импедансных сеток. // –М.: МГИЭМ, 1999, 38 стр.
35. Сестрорецкий Б.В., Петров
А.С., Иванов С.А., Климов К.Н., Королев С.А., Фастович С.В. Анализ
электромагнитных процессов на основе RLC и ![]() сеток. // –М.: МГИЭМ, 2000, 149 стр.
сеток. // –М.: МГИЭМ, 2000, 149 стр.
36. Сестрорецкий Б.В., Кустов В.Ю., Шлепнев Ю.О. Анализ СВЧ-микросборок методом информационного многополюсника. // Вопросы радиоэлектроники. Сер. Общие вопросы радиоэлектроники. 1988, вып. 12, стр. 26-42.
37. Голиус А.Б., Вешникова И.Е., Сестрорецкий Б.В., Чернов И.В. Расчет волнового сопротивления полосковой линии методом импедансного аналога электромагнитного пространства. // Вопросы радиоэлектроники, сер. “Общетехническая”, 1976. вып. 3, стр. 38-47.
38. Сестрорецкий Б.В., Кустов В.Ю. Эффективный алгоритм анализа плоских волноводных устройств. // Вопросы радиоэлектроники. Сер. Общие вопросы радиоэлектроники. 1988, вып. 2, стр. 3-16.
39. Голиус А.Б., Сестрорецкий Б.В. Оценка методических ошибок при расчете плоских волноводных устройств методом ИАЭП. // Вопросы радиоэлектроники. Сер. Общетехническая. 1979, вып. 3, стр. 43–57.
40. Голиус А.Б., Сестрорецкий Б.В. Алгоритмы вычисления параметров плоских волноводных систем методом ИАЭП. // Межвузовский сборник научных трудов “Машинное проектирование устройств и систем СВЧ”. –М.: МИРЭА, 1978, вып. 2, стр. 133-146.
41. Бахрах Л.Д., Ильинский А.С. и др. К 80-летию со дня рождения Бориса Васильевича Сестрорецкого. // Радиотехника и электроника. 2004, т. 49, №3, стр. 380-382.
42. Писсанецки С. Технология разреженных матриц. // –М.: 1988, 411 стр.
43. Сестрорецкий Б.В., Зиновьев А.В. Электродинамический анализ и оптимизация геометрии Е плоскостных волноводных устройств. // Вопросы радиоэлектроники. Сер. Общие вопросы радиоэлектроники. 1988, вып. 12, стр. 43.
44. Кустов В.Ю. Импедансная интерпретация метода конечных элементов для электродинамического анализа планарных волноводных устройств. // Диссертация на соискание степени кандидата физико-математических наук. –М.: МФТИ, 1988, 210 стр.
45. Сестрорецкий Б.В., Дризе М.А., Иванов С.А., Климов К.Н. Тракты наземных антенн Ku и C диапазонов для перспективных спутников связи. // III Международная конференция “Антенная теория и техника”, Севастополь, Украина, 8-11 сентября, 1999, стр. 528-533.
46. Иванов С.А., Сестрорецкий Б.В., Дризе М.А. Синтез поляризатора, реализованного на изгибе волновода. // Крымская микроволновая конференция “СВЧ техника и телекоммуникационные технологии”. Севастополь, Украина, 8-12 сентября, 2003, стр. 55-56.
47. Hoefer W. The transmission-line matrix method – theory and applications. // IEEE Trans., Oct. 1985, pp. 882-893.
48. Berenger J.P. A perfectly matched layer for the absorption of electromagnetic waves // J. Comput. Phys. 1994, vol. 114, pp. 185-200.
49. Berenger J.P. An Effective PML for the Absorption of Evanescent Waves in Waveguides // IEEE Microwave and Guided Wave Letters. May 1998, vol. 8, №5, pp. 188-190.
50. Fang J. and Wu Z. Generalized perfectly matched layer for the absorption of propagating and evanescent waves in lossless and lossy media. // IEEE Trans. MTT. Dec. 1996, pp. 2216-2222.
51. Johns P.B. A new mathematical model to describe the physics of propagation. // The Radio and Electronic Engineer. 1974, №44(12), pp. 657-665.
52. P. Russer. The Alternating Rotating Transmission Line Matrix ARTLM Scheme. // Electromagnetics. October 1996, №16(1), pp. 537-551.
53. B.V. Sestoretsky, S.A. Ivanov. A new 6-parametrical three-dimensional algorithm for 12-port symmetrical condensed node. // TLM-99. III International Workshop on TLM, Modelling theory and applications. Nitza, France, October 27-29, 1999, pp. 197-200.
54. Brewitt-Taylor C.R., Johns P.B. On the construction and numerical solution of transmission-line and lumped network models of Maxwell’s equations. // International journal for numerical methods in engineering. 1980, vol. 19, pp. 13-30.
55. Сестрорецкий Б.В., Иванов С.А., Климов К.Н. Теория и точность аппарата потоковых сеток во временной области при одночастотном и многочастотном трехмерном электродинамическом анализе. // Сборник трудов IV международной научно-технической конференции “Антенно-фидерные устройства, системы и средства радиосвязи (ICARSM-99)”, Воронеж, 1999.
56. Климов К.Н., Сестрорецкий
Б.В. Граничные условия поглощения и возбуждения плоских и собственных волн
прямоугольного волновода в планарной ![]() -сетке. // Радиотехника и электроника.
2001, т. 46, №9, стр. 1048-1058.
-сетке. // Радиотехника и электроника.
2001, т. 46, №9, стр. 1048-1058.
57. Климов К.Н., Сестрорецкий Б.В. Дифференциальные уравнения электромагнитных волн во временной области в средах с частотной дисперсией. // Радиотехника и электроника. 2001, т. 46, №10, стр. 1223-1225.
58. Карцев И.Ю. Метод импедансно-сеточной функции Грина для решения двумерных задач дифракции // Диссертация на соискание степени кандидата технических наук. –М. МЭИ, 1991, 138 стр.
59. Сестрорецкий Б.В., Карцев И.Ю. Метод импедансно-сеточной функции Грина для решения двумерных задач дифракции. // Вопросы радиоэлектроники. Сер. Общие вопросы радиоэлектроники. 1991, вып. 1, стр. 18-26.
60. Марадудин А., Монтролл Э., Вейс Дж. Динамическая теория кристаллической решетки в гармоническом приближении. // –М.: Мир, 1965, 383 стр.
61. Сестрорецкий Б.В., Иванов
С.А., Середов В.М., Климов К.Н. Новые эффективные 3D алгоритмы
электродинамического анализа на основе потоковых ![]() -сеток. // VII Всероссийская
школа-семинар “Волновые явления в неоднородных средах”. Красновидово,
Московская обл., 22-27 мая 2000 г., т. 2, стр. 101-103.
-сеток. // VII Всероссийская
школа-семинар “Волновые явления в неоднородных средах”. Красновидово,
Московская обл., 22-27 мая 2000 г., т. 2, стр. 101-103.
62. Digest of the Third international workshop on transmission line matrix (TLM). // University of Nice-Sophia Antipolis, France, October 27–29, 1999, 325 рр.
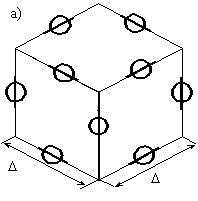

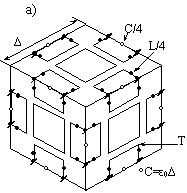
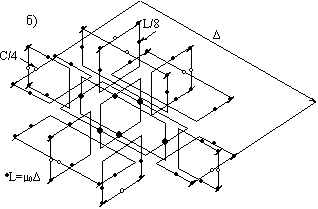
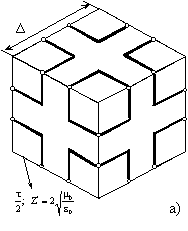
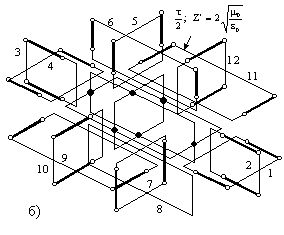
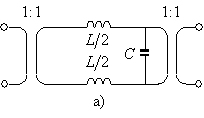
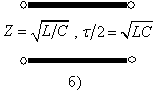
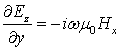 ,
,
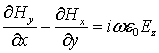 (1)
(1)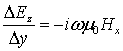 ,
,
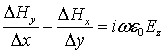 (2)
(2)
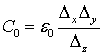 ,
,
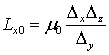 ,
,
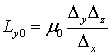 (4)
(4)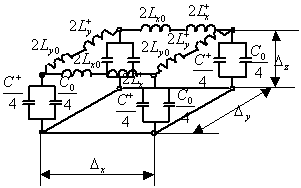
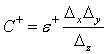
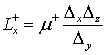 ,
,
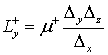
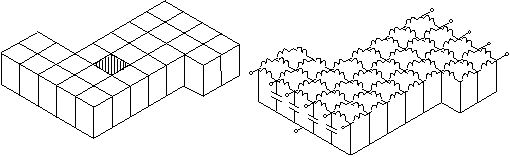
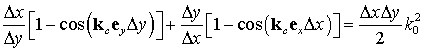 (8)
(8)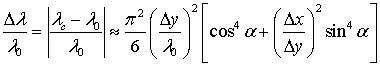 (10)
(10)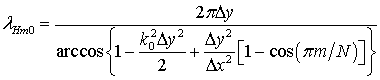 (11)
(11)

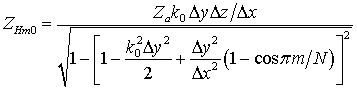 (12)
(12)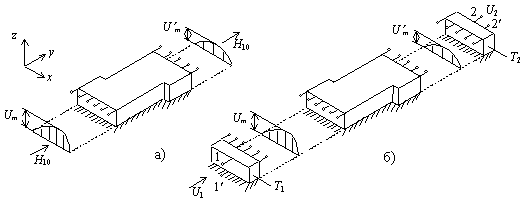
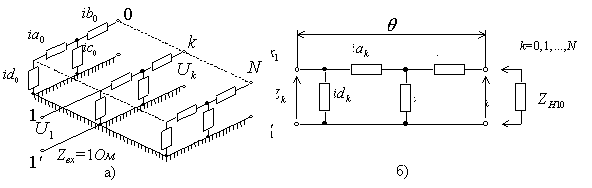
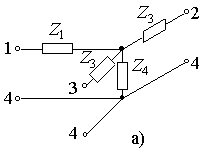
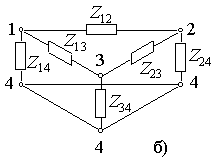
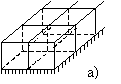
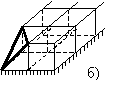
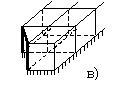
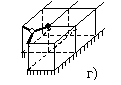
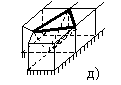
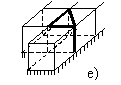
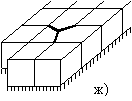
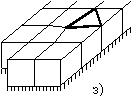
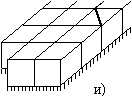


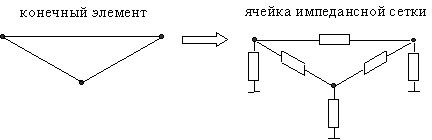
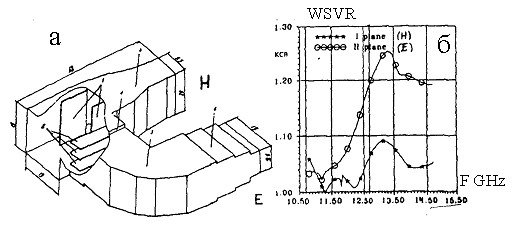
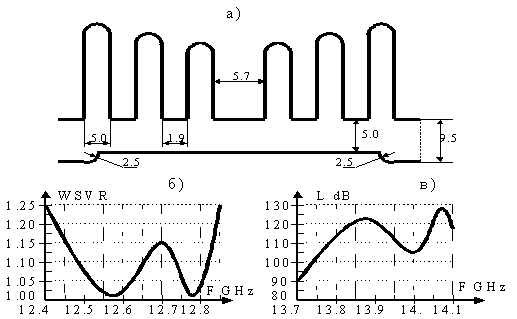
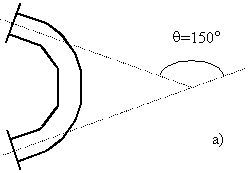

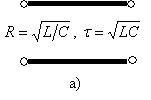
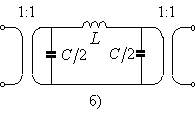
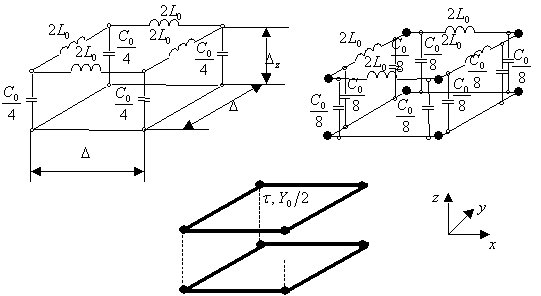
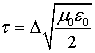 ,
,
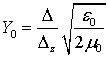 (14)
(14)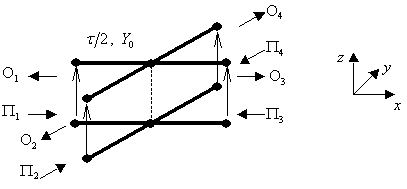

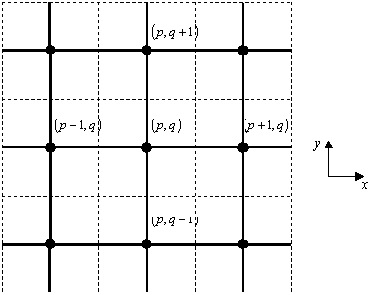
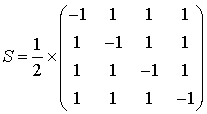 (15)
(15)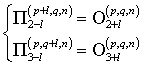 ,
,
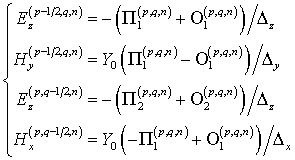 (21)
(21)
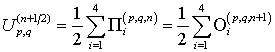 (22)
(22)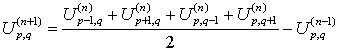 (24)
(24)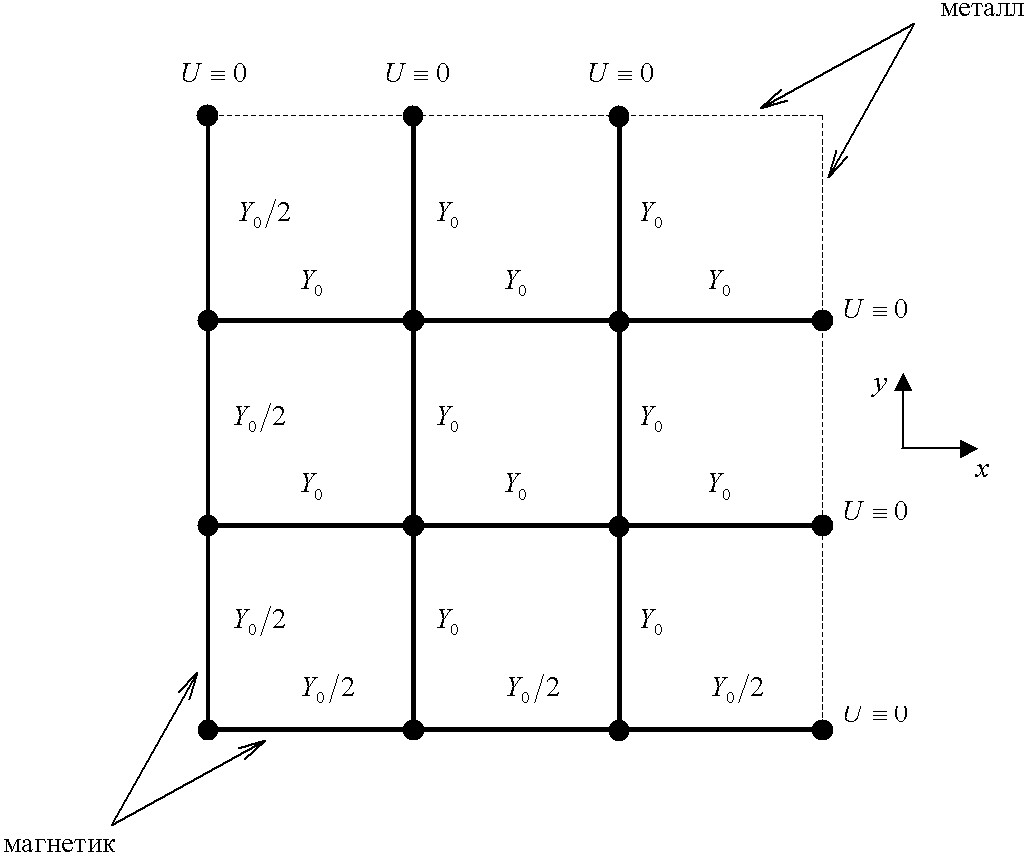
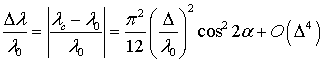 (28)
(28)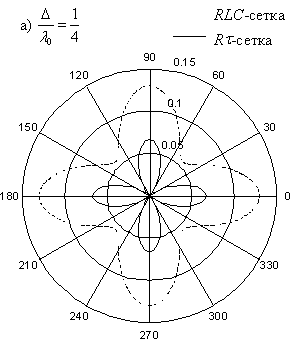
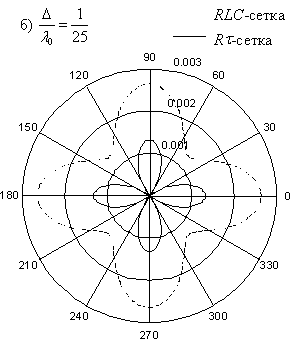
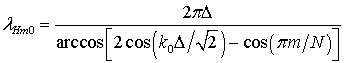 (29)
(29)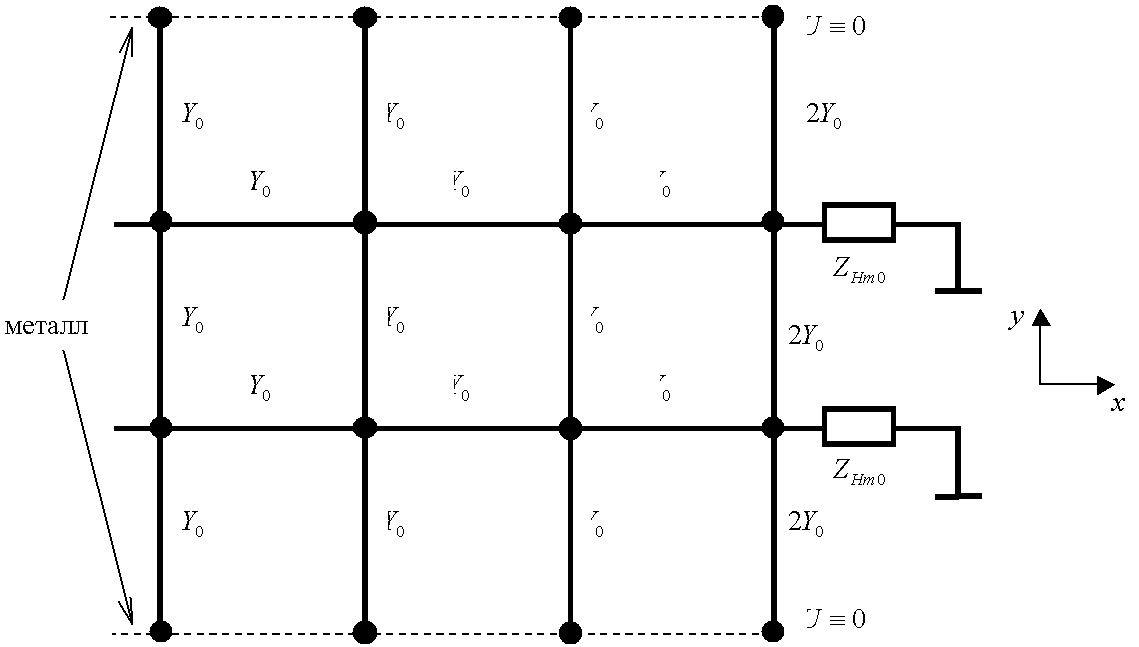
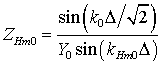 (30)
(30)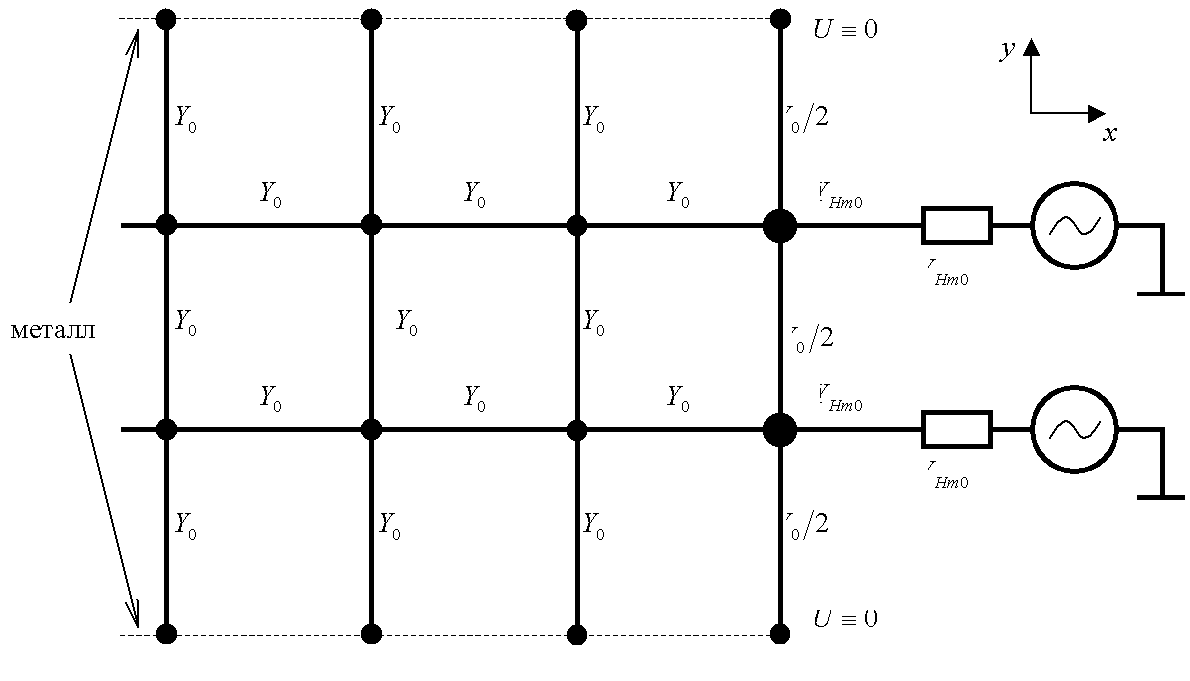
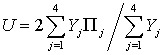 , (32)
, (32)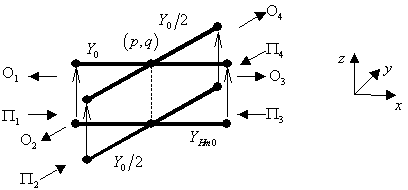

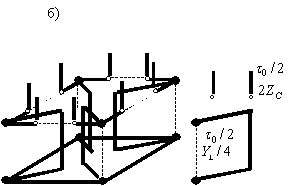
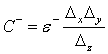 ,
,
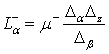 ,
,
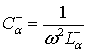
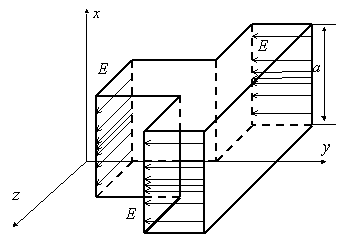
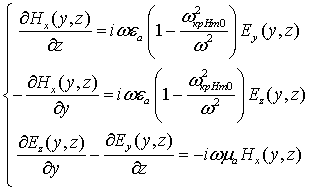 (35)
(35)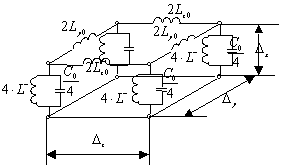
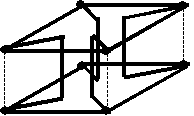
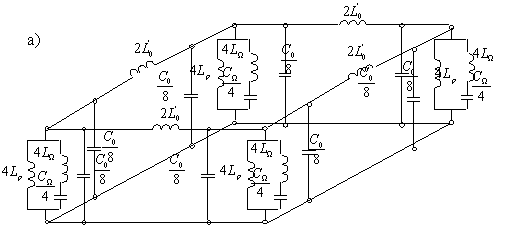
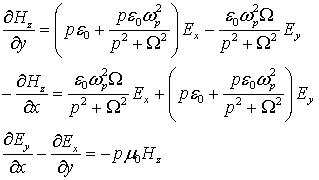 (36)
(36)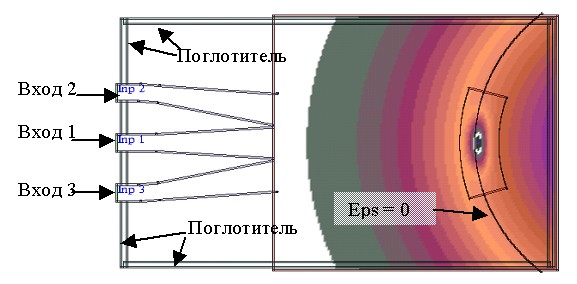
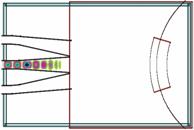
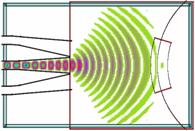
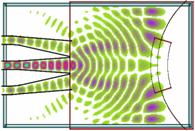

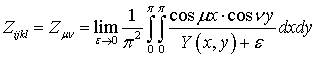 ,
,
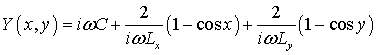 (39)
(39)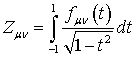 (40)
(40)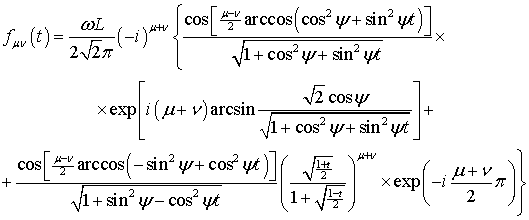 (41)
(41)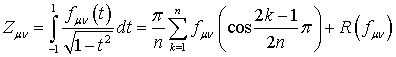 (43)
(43)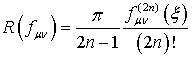 ,
,
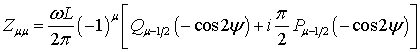 (45)
(45)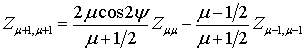 (46)
(46)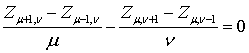 ,
,