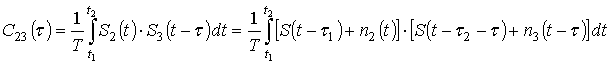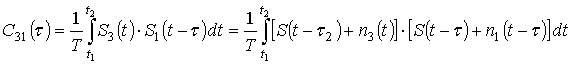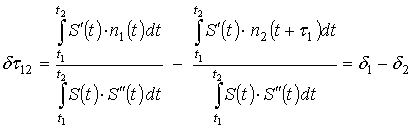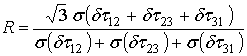УДК 47.05.17
О влиянии ошибок измерения задержек сигналов в многопозиционных приемных системах
Ю. А. Земский
Учреждение Российской академии наук Институт динамики геосфер РАН
Получена 16 мая 2011 г.
Аннотация. Описано влияние когерентных и некогерентных ошибок при измерении задержек сигналов одного источника несколькими приемными устройствами многопозиционных систем. Приводятся теоретические описания возможных ошибок при измерении задержек сигналов и результаты математического моделирования, показывающие зависимость случайных и когерентных составляющих этих ошибок. Эти ошибки могут быть учтены при разработке и конструировании приемных многопозиционных систем.
Ключевые слова: дисперсия, время задержки, многопозиционный приемный модуль, отношение сигнал/шум.
Abstract. The influence of coherent and incoherent faults of measurement of the signal delays of one source by several receiving devices of multiposition systems is described in the article. The theoretical descriptions of possible faults in measurement of signal delays and the results of the mathematical simulation, which show the dependence of random and coherent components of these errors are also given in the article. These errors can be taken into account in development and construction of receiving multiposition systems.
Keywords: the dispersion, delay time, multiposition, the receiving module, ratio signal-to-noise.
При измерении задержек сигналов одного источника несколькими приемными устройствами многопозиционных систем могут возникать различные ошибки, которые необходимо учитывать при разработке и конструировании этих систем.
Рассмотрим приемную
систему, состоящую из трех приемных модулей, взаимное положение которых
определено векторами ![]() ,
, ![]() и
и ![]() (рис. 1). При этом предполагается, что фронт распространения
принимаемой электромагнитной волны плоский [1].
(рис. 1). При этом предполагается, что фронт распространения
принимаемой электромагнитной волны плоский [1].
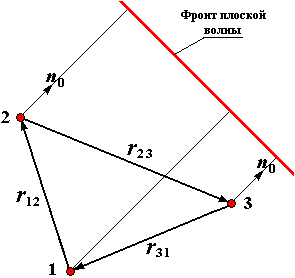
Рис.1. Схема расположения трех приемных модулей.
Задержка
прихода волнового сигнала в точку 1 по отношению к точке 2 будет равна: ![]() , где
, где ![]() – единичный вектор направления прихода
плоского фронта волны,
– единичный вектор направления прихода
плоского фронта волны, ![]() – скалярное произведение векторов, с
– скорость распространения волнового сигнала.
– скалярное произведение векторов, с
– скорость распространения волнового сигнала.
Аналогично
определяются задержки: ![]() и
и ![]() .
.
Как видно из рис. 1, направления векторов, определяющих геометрию приемной системы, выбраны так, что:
Подставляя значения времени задержки, получим очевидное соотношение:
С выхода приемных модулей
на систему обработки информации поступают три сигнала: ![]() ,
, ![]() и
и ![]() , имеющих следующий вид:
, имеющих следующий вид:
![]() ,
, ![]() ,
, ![]() , (3)
, (3)
где: ![]() – сигнал удаленного источника;
– сигнал удаленного источника; ![]() и
и ![]() – задержки этого сигнала;
– задержки этого сигнала; ![]() ,
, ![]() и
и ![]() – помехи.
– помехи.
Далее, для различных пар
сигналов на временном интервале ![]() производится вычисление трех
корреляционных интегралов [2]
производится вычисление трех
корреляционных интегралов [2] ![]()
![]() и
и ![]() :
:
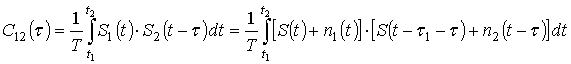 , (4)
, (4)
Исходя из полученных
соотношений, поиск времени задержек между сигналами заключается в определении ![]() соответствующих максимальным значениям
соответствующих максимальным значениям ![]() , т.е. фактически в решении уравнений
, т.е. фактически в решении уравнений 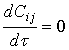 .
.
Все дальнейшие вычисления построены при следующих допущениях:
1.
Дисперсии помех
гораздо меньше дисперсии сигнала: ![]() .
.
2.
Функции сигнала (![]() ) и помех (
) и помех (![]() ,
, ![]() и
и ![]() ) дифференцируемы на временном интервале
) дифференцируемы на временном интервале ![]() .
.
3.
Величина сигнала
равна нулю на границах временного интервала интегрирования ![]() , т.е. фактически рассматривается
импульсный сигнал неопределенной длительности.
, т.е. фактически рассматривается
импульсный сигнал неопределенной длительности.
4. Величины задержек между сигналами гораздо меньше временного интервала интегрирования T.
Произведя перемножение
под интегралами (4) - 6) и используя допущение о том, что дисперсии помех
гораздо меньше дисперсии сигнала, каждый корреляционный интеграл (![]() ) можно приближенно представить в виде трех функций,
например:
) можно приближенно представить в виде трех функций,
например:
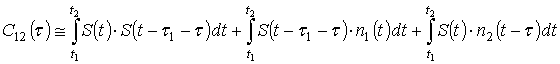 (7)
(7)
Чтобы не загромождать
выкладок, здесь и далее перед интегралами опущены множители ![]() .
.
Максимального значения ![]() достигает при
достигает при ![]() , где
, где ![]() - истинная величина задержки, а,
ввиду малости помехи,
- истинная величина задержки, а,
ввиду малости помехи, ![]() будет соответственно малой ошибкой
измерения. Сделав в (7) замену переменной
будет соответственно малой ошибкой
измерения. Сделав в (7) замену переменной ![]() получим:
получим:
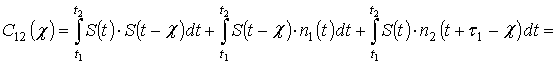
![]() (8)
(8)
где 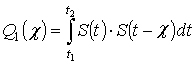 ,
, 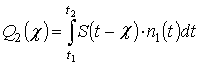 и
и 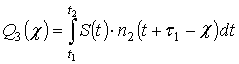 .
.
Если разложить ![]() в ряд Тейлора по малым значениям
в ряд Тейлора по малым значениям ![]() и решить уравнение по поиску
τ12, соответствующих максимальным значениям С12, т.е.
и решить уравнение по поиску
τ12, соответствующих максимальным значениям С12, т.е.
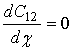 , то можно в явном виде получить
выражение для ошибки нахождения задержки
, то можно в явном виде получить
выражение для ошибки нахождения задержки ![]() . Для
. Для ![]() это разложение имеет вид:
это разложение имеет вид:
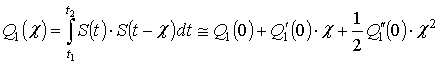 , (9)
, (9)
где: 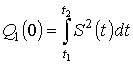 ;
; 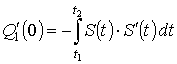 ;
; 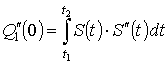 .
.
Можно показать, что
значение первой производной 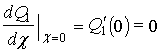 :
:
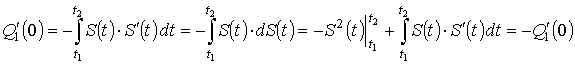 ,
,
т.е. ![]() .
.
Здесь применяются
следующие математические операции: сначала ![]() заносится под знак дифференциала, а затем производится
интегрирование по частям и используется допущение 3 (
заносится под знак дифференциала, а затем производится
интегрирование по частям и используется допущение 3 (![]() ). Таким образом, для
). Таким образом, для ![]() имеем приближенное выражение:
имеем приближенное выражение:
![]() (10)
(10)
Аналогично получаются
разложения в ряд по малым ![]() для
для ![]() и
и ![]() :
:
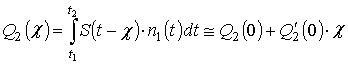 , (11)
, (11)
где: 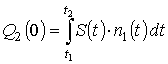 и
и 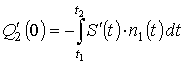 .
.
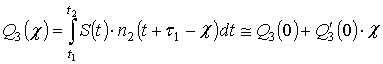 , (12)
, (12)
где: 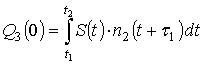 и
и 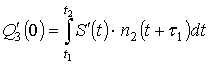 .
.
Объединив полученные
выражения (10) - (12) для разложения ![]() по малым
по малым ![]() имеем:
имеем:
![]() (13)
(13)
Приравняв нулю
производную по ![]() (13)
и решив получившееся уравнение, получим значение ошибки измерения задержки
(13)
и решив получившееся уравнение, получим значение ошибки измерения задержки ![]() :
:
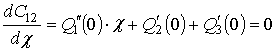 , откуда:
, откуда: 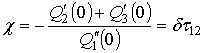 .
.
Таким образом, выражение
для ![]() имеет вид:
имеет вид:
Аналогичным образом, из
корреляционного интеграла (5) для ![]() , можно найти выражение для определения ошибки измерения
задержки
, можно найти выражение для определения ошибки измерения
задержки ![]() . Для этого сначала также необходимо
ввести новую переменную
. Для этого сначала также необходимо
ввести новую переменную ![]() , использовав преобразование:
, использовав преобразование: ![]() , и привести
, и привести ![]() к виду:
к виду:
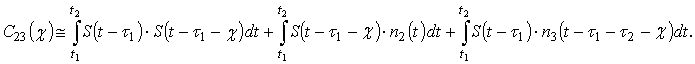 (15)
(15)
Затем, используя
допущение 4, в (15) производим замену переменной интегрирования ![]() :
:
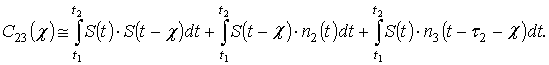
Проделав все необходимые
вычисления, для ![]() получим выражение:
получим выражение:
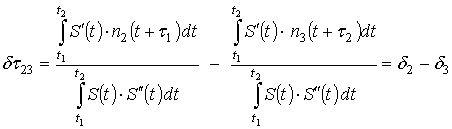 (16)
(16)
И, наконец, приведем
выражение для определения ошибки измерения задержки ![]() , которое можно получить из корреляционного интеграла (6) для
, которое можно получить из корреляционного интеграла (6) для
![]() :
:
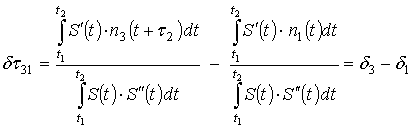 (17)
(17)
Таким образом, используя (1), (2), а также сравнивая выражения (14), (16) и (17), для приемной системы из трех приемных модулей получаем три простых соотношения:
1. Для суммы векторов,
соединяющих точки размещения модулей: ![]() .
.
2. Для алгебраической
суммы задержек сигналов: ![]() .
.
3. Для ошибок измерения
задержек сигналов при малых отношениях шум/сигнал: ![]() , где:
, где: ![]() ;
; ![]() ;
; ![]() .
.
Далее проведем статистическое моделирование корреляционного метода измерения задержек прихода сигнала при помехах, сравнимых с сигналом по дисперсии.
В качестве сигналов и
помех использовались подвергнутые полосовой фильтрации псевдослучайные
последовательности с нормальным распределением размером 16384 выборок. При
отношениях шум/сигнал (![]() ) в интервале от 0,1 до 1,5 были получены
оценки задержек
) в интервале от 0,1 до 1,5 были получены
оценки задержек ![]() , где
, где ![]() – истинная величина задержек и
– истинная величина задержек и ![]() – ошибка измерения. Ансамбль испытаний составлял 1000
измерений, что обеспечило не хуже чем 3% точность получаемых оценок [4].
– ошибка измерения. Ансамбль испытаний составлял 1000
измерений, что обеспечило не хуже чем 3% точность получаемых оценок [4].
В процессе моделирования вычислялись:
1. Коэффициенты
корреляции ошибок измерения задержек между сигналами: ![]() ,
, ![]() и
и ![]() .
.
2. Дисперсия суммы ошибок
измерения задержек: ![]() , в виде безразмерной величины:
, в виде безразмерной величины:
Такой вид коэффициента R
выбран из следующего: если ![]() ,
, ![]() и
и ![]() будут независимыми случайными величинами с
дисперсиями равными
будут независимыми случайными величинами с
дисперсиями равными ![]() ,
то в этом случае величина R должна быть порядка
единицы.
,
то в этом случае величина R должна быть порядка
единицы.
Полученные результаты моделирования приведены на графиках (рис. 2, рис. 3).
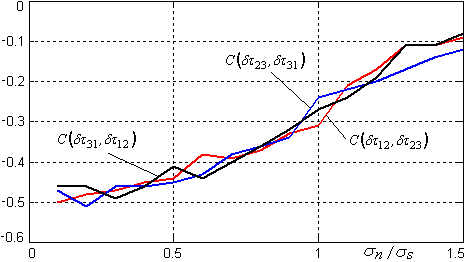
Рис. 2. Коэффициенты корреляции между ошибками измерения задержек сигналов.
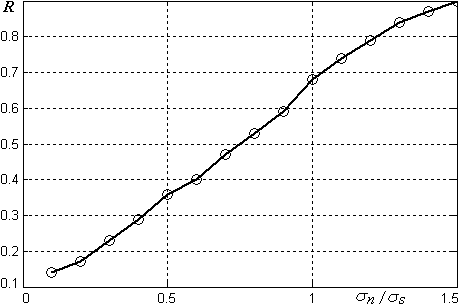
Рис. 3. Зависимость безразмерного коэффициента R от отношения шум/сигнал.
Анализируя полученные
результаты, следует отметить значительный уровень отрицательной корреляции
между ошибками измерения задержек ![]() в диапазоне отношений
в диапазоне отношений ![]() от 0,1 до 1,0, что говорит о существенной статистической
связи между этими величинами в указанном диапазоне.
от 0,1 до 1,0, что говорит о существенной статистической
связи между этими величинами в указанном диапазоне.
Кроме этого, если бы ![]() ,
, ![]() и
и ![]() были независимы, то коэффициент R, как отмечалось выше, должен быть
равен порядка единицы, а фактически в этом диапазоне
были независимы, то коэффициент R, как отмечалось выше, должен быть
равен порядка единицы, а фактически в этом диапазоне ![]() величина R не
превышала 0,7.
величина R не
превышала 0,7.
Необходимо отметить, что приведенные выше результаты моделирования практически не зависят (в пределах точности проведенных расчетов) от величин относительных задержек между сигналами.
Полученные данные подтверждают соотношения для ошибок, возникающих при измерении задержек корреляционным способом, и позволяют предложить следующие формулы для этих ошибок:
![]() ,
, ![]() ,
, ![]() (19)
(19)
где ![]() и
и ![]() являются независимыми случайными
величинами, причем
являются независимыми случайными
величинами, причем ![]() можно назвать “когерентной”, а
можно назвать “когерентной”, а ![]() случайной компонентой ошибок измерения задержек.
случайной компонентой ошибок измерения задержек.
Дисперсии ![]() и
и ![]() можно определить из значений
коэффициента R.
Действительно, если подставить формулы (19) в выражение (18) для R, то получим:
можно определить из значений
коэффициента R.
Действительно, если подставить формулы (19) в выражение (18) для R, то получим:
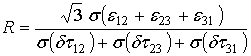 . (20)
. (20)
Считая, что ![]() =
=![]() =
=![]() =
=![]() и
и ![]() =
=![]() =
=![]() =
=![]() , из (20) несложно получить следующее
простое соотношение:
, из (20) несложно получить следующее
простое соотношение:
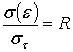 . (21)
. (21)
Напомним, что ![]() является дисперсией
полной ошибки измерения задержек между сигналами. Значения
является дисперсией
полной ошибки измерения задержек между сигналами. Значения ![]() представлены на графике (рис. 4)
в виде кривой синего цвета.
представлены на графике (рис. 4)
в виде кривой синего цвета.
Теперь, используя любую
из формул (19), например первую, запишем: ![]() . Положив
. Положив ![]() =
=![]() =
=![]() и
и ![]() , будем иметь:
, будем иметь: ![]() . Подставив в это выражение значение
для
. Подставив в это выражение значение
для ![]() (21), получим:
(21), получим:
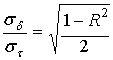 . (22)
. (22)
Значения ![]() представлены в виде кривой красного цвета на рис. 4.
Здесь же приведена пунктиром кривая
представлены в виде кривой красного цвета на рис. 4.
Здесь же приведена пунктиром кривая ![]() , т.е. сигма величин
, т.е. сигма величин ![]() (
(![]() ). Из этих графиков видно, что
практически до значений шум/сигнал равных единице, дисперсии “когерентных”
компонент ошибки превалируют над случайными. При этом, чем меньше соотношение
уровня помехи к уровню сигнала, тем больше влияние когерентных компонент ошибки
измерения сигнала.
). Из этих графиков видно, что
практически до значений шум/сигнал равных единице, дисперсии “когерентных”
компонент ошибки превалируют над случайными. При этом, чем меньше соотношение
уровня помехи к уровню сигнала, тем больше влияние когерентных компонент ошибки
измерения сигнала.
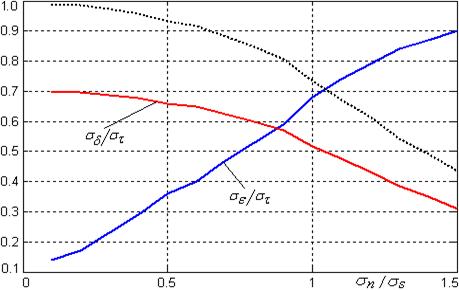
Рис. 4. Зависимости дисперсий
случайной (![]() ) и “когерентной” (
) и “когерентной” (![]() )
)
составляющих ошибки измерения задержки между сигналами.
Таким образом,
проведенные расчеты по ошибкам измерения задержек между сигналами в
многопозиционных приемных системах показали, что ошибки измерений не являются
случайными величинами. Отмечен значительный уровень отрицательной корреляции
между ошибками измерения задержек ![]() в диапазоне отношений
в диапазоне отношений ![]() от 0,1 до 1,0, что говорит о существенной статистической
связи между этими величинами в указанном диапазоне. Коэффициенты корреляции
между ошибками измерения задержек сигналов находятся в диапазоне от 0,1 до 0,7
и зависят от отношения дисперсии помех к дисперсии сигнала. Чем больше это
отношение, тем меньше коэффициент корреляции.
от 0,1 до 1,0, что говорит о существенной статистической
связи между этими величинами в указанном диапазоне. Коэффициенты корреляции
между ошибками измерения задержек сигналов находятся в диапазоне от 0,1 до 0,7
и зависят от отношения дисперсии помех к дисперсии сигнала. Чем больше это
отношение, тем меньше коэффициент корреляции.
Кроме того, при
отношениях шум/сигнал (![]() ) в интервале от 0,1 до 0,8 когерентная
составляющая ошибки измерения задержки между сигналами выше случайной
составляющей.
) в интервале от 0,1 до 0,8 когерентная
составляющая ошибки измерения задержки между сигналами выше случайной
составляющей.
Приведенные выше результаты моделирования практически не зависят (в пределах точности проведенных расчетов) от величин относительных задержек между сигналами.
Полученные результаты могут оказаться полезными при расчетах приемных систем, например многопозиционных интерферометрических систем с числом приемных модулей N > 3.
ЛИТЕРАТУРА
1. Фалькович С.Е. Оценка параметров сигнала. – М.: Советское радио, 1970.
2. Левин Б.Р. Теоретические основы статистической радиотехники. В трех книгах. Книга вторая. - М.: Советское радио, 1975.
3. Вологдин Э.И. Повышение точности преобразования временных интервалов в цифровой код методом корреляционного усреднения. // Автометрия. - СО АН СССР, 1969, № 2.
4. Соболь И.М. Численные методы Монте-Карло. - М.: Наука, 1973.