УДК 621.371, 537.86
Моделирование управляемой частотно-избирательной поверхности
В. Н. Кисель
Институт теоретической и прикладной электродинамики РАН
Статья поступила в редакцию 16 апреля 2016 г.
Аннотация. Разработана электродинамическая модель частотно-селективного управляемого или неуправляемого экрана. Соответствующая граничная задача дифракции решена методом интегральных уравнений. Модель позволяет оптимизировать геометрические параметры плоских частотно-избирательных поверхностей (ЧИП) с учетом наличия управляющих элементов или пленок, ее можно использовать для расчета свойств экранов различной формы на основе таких ЧИП. Приведены результаты численных расчетов частотных и угловых характеристик ЧИП с управляющими элементами и пленками.
Ключевые слова: частотно-избирательная поверхность, управляемая прозрачность, экран, антенна, интегральное уравнение.
Abstract. Electromagnetic model of a controllable or non-controllable frequency-selective screen is developed. Corresponding boundary problem of diffraction is solved by integral equation method. The model can be used to optimize geometrical dimensions of the flat frequency-selective surfaces (FSS) taking into account the presence of control devices or films, it can be useful when calculating properties of different screens based on such FSS. The results of numerical calculations of the frequency and angular performance of FSS with control devices and films are discussed.
Key words: frequency selective surfaces, controllable transparency, screen, antenna, integral equation.
Введение
Для улучшения некоторых параметров излучающих систем (например, показателей электромагнитной совместимости), а также в целях снижения радиолокационной заметности антенн могут применяться экраны, степень радиопрозрачности которых зависит от частоты или от управляющего воздействия. Рассмотрим особенности использования и моделирования экранов, предназначенных для укрытия (маскировки) антенн бортовых РЛС (БРЛС) летательных аппаратов.
Демаскирование антенного отсека происходит за счет рассеяния падающей волны на металлических элементах оборудования, установленного в отсеке, и рассеяния на антенне БРЛС. Основной вклад в рассеянное поле определяется зеркальным отражением волны от металлической поверхности диска (в направлениях, близким к нормали к его плоскости), а также дифракцией на системе щелевых излучателей антенной решетки (рис. 1).
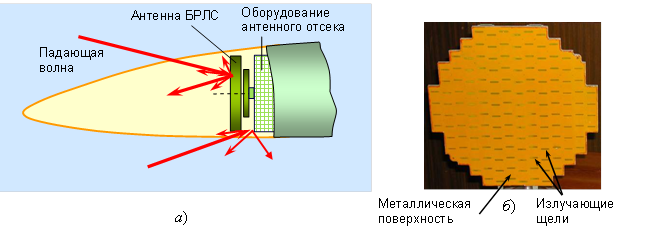
Рис. 1. Рассеяние падающей волны на
элементах антенного отсека (а) и
типовая конструкция антенны БРЛС (плоская
волноводно-щелевая антенная решетка) (б)
Снижение отражения зондирующего сигнала от антенны может быть достигнуто за счет того, что защищаемый объект (антенна) помещается в оболочку (экран), специальная форма которого обеспечивает меньшее рассеяние в обратном направлении по сравнению с незащищенной антенной, причем в частном случае экран может быть совмещен с обтекателем (рис. 2).
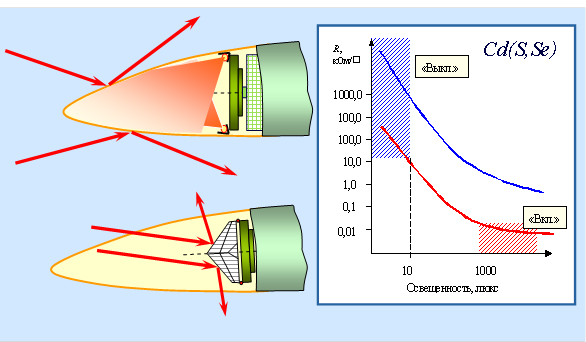
Рис. 2. Варианты экранирования антенного отсека
Экраны могут быть как управляемыми, так и неуправляемыми. При использовании неуправляемых экранов возможность работы антенны в штатном режиме сохраняется, если экран имеет частотную полосу прозрачности, соответствующую рабочему диапазону, и согласован с антенной по поляризационным характеристикам. При этом защита антенны обеспечивается лишь вне полосы пропускания экрана. Отметим, однако, что можно рассчитывать на некоторое снижение ЭПР и в пределах полосы прозрачности экрана, если поляризация облучения внешним источником не соответствует его настройке (например, когда рассматривается равновероятное облучение с различной поляризацией, а экран настроен на прохождение линейно поляризованного поля антенны). К достоинствам неуправляемых экранов можно отнести дешевизну, простоту, отсутствие каких-либо управляющих элементов (УЭ) и схем управления, минимальные вес и толщину стенок экрана, высокую стойкость к механическим и электрическим перегрузкам.
Управляемые экраны могут обеспечить выполнение очень широкого спектра функций. Возможности экрана во многом определяются физическим принципом управления и типом УЭ. Так, возможно использование механической, электронной, фотоэлектронной и других управляющих систем. Соответственно, УЭ представляют собой механические коммутаторы или шторки, электронные (полупроводниковые или газоразрядные) и пьезоэлектрические приборы, фоточувствительные полупроводниковые элементы и пленки. Уточнение предельно достижимых параметров экрана на основе перечисленных УЭ требует проведения обширных исследований.
Пример технического решения такого рода [1] ‑ нанесение на внутреннюю поверхность обтекателя антенны управляемой (например, фоточувствительной) пленки, поверхностное сопротивление которой изменялось бы под воздействием управляющего (например, оптического) облучения для обеспечения возможности работы БРЛС. К сожалению, существуют пока еще не преодоленные технологические трудности по созданию пленки с требуемым диапазоном изменения поверхностного сопротивления. В идеальном случае пленка должна переводиться из практически проводящего состояния (режим экранирования) в состояние с очень высоким сопротивлением (режим «отсутствия» экрана, работа БРЛС). Реальный диапазон изменения параметров должен составлять (по порядку величины) от 10 Ом до 100 кОм на квадрат поверхности (см. рис. 2, где красной кривой показана желаемая, а синей – реально достигнутая на настоящий момент зависимость поверхностного сопротивления пленки от уровня ее освещенности, а также рис. 3 с типичными зависимостями для существующих материалов на основе соединений CdS, CdSe).
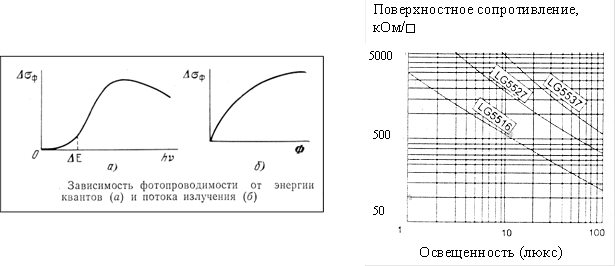
Рис. 3. Типичные свойства фоточувствительных пленок
Существуют и другие приемы создания поверхности с изменяемым эффективным сопротивлением, например, путем использования низкотемпературной столкновительной плазмы. Этот подход активно разрабатывался в ИТПЭ РАН [2].
Альтернативным техническим решением может служить экран, основой которого является на частотно-избирательная поверхность (ЧИП) с системой периодических отверстий определенной формы (рис. 4), настроенных так, чтобы пропускать электромагнитные волны в узкой полосе собственных частот локатора; для электромагнитных волн других частот такой экран работает как отражающий. Введя в эти отверстия (открытые резонаторы) управляющие элементы (УЭ), можно по желанию делать его непрозрачным и в диапазоне рабочих частот локатора.
Исследованию, расчетам свойств и применению частотно-селективных поверхностей посвящена обширная литература (в частности, рис. 4 воспроизведен из [3]), однако практически нигде не рассматриваются управляемые ЧИП с учетом свойств существующих УЭ, а также ограничений, вызванных реальными условиями эксплуатации. В доступной литературе отсутствуют практические рекомендации по выбору типов управляющих элементов и их параметров, влиянию паразитных емкостей и индуктивностей УЭ и т.п.
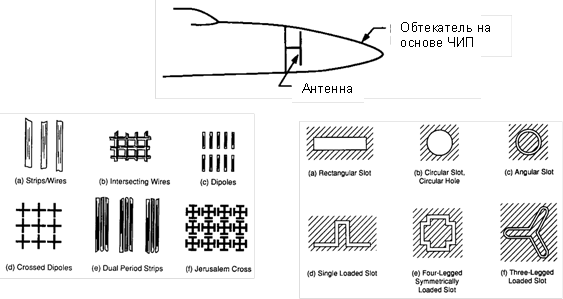
Рис. 4. Маскировка антенного отсека с помощью частотно-селективного обтекателя-экрана и типовые частотно-избирательные поверхности [3]
Более того, большинство известных моделей не позволяет учесть, например, потери в фоточувствительной пленке или материале экрана, поскольку основаны на использовании принципа эквивалентности и «металлизации» поверхности экрана с заменой перфорированных щелей эквивалентными магнитными токами (такая замена справедлива в случае идеально проводящих ЧИП). Ниже рассмотрен способ построения электродинамической модели управляемой ЧИП без указанного недостатка.
2. Модель экрана на основе частотно-избирательной поверхности с управляемой прозрачностью
Все характерные размеры реальных экранов антенны обычно гораздо больше длины волны, и, исходя из назначения экрана, конструкция его поверхности выбирается таким образом, чтобы исключить возможность возникновения незатухающих поверхностных волн. Поэтому можно рассчитывать прохождение волны через экран, используя приближение физической оптики и соответствующие коэффициенты прохождения и отражения для отдельных зон (точек) экрана. Согласно положениям физической оптики, эти коэффициенты можно найти из решения граничной задачи возбуждения бесконечной плоской ЧИП, на которую падает волна под теми же углами и с той же поляризацией, что и на плоскость, касательную к экрану в данной точке.
Подходящей структурой для модели управляемой ЧИП является бесконечная плоскость с двумерно-периодическим распределением комплексного поверхностного сопротивления R, Ом/□, которое может изменяться на заданных участках при переключении режима работы устройства (рис. 5).
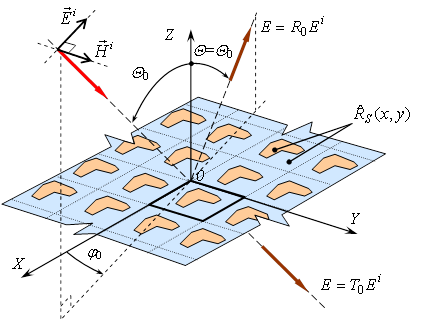
Рис. 5. Постановка задачи дифракции на периодической поверхности с переменным сопротивлением (случай вертикальной поляризации)
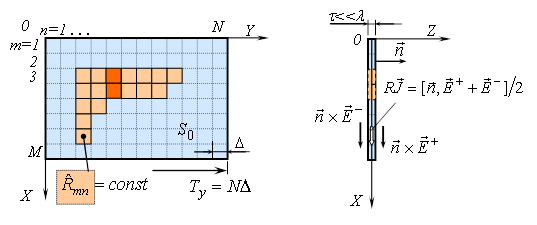
Рис. 6. Период структуры и формулировка граничного условия
В пределах периода решетки распределение R(x,y) задается в виде кусочно-постоянной функции на сетке с малыми ячейками квадратной формы (рис. 6). На эту плоскость из верхнего полупространства падает плоская электромагнитная волна. Требуется найти характеристики прошедшей и отраженной волны (коэффициенты прохождения и отражения).
3. Решение задачи возбуждения плоскости с двумерно-периодическим распределением поверхностного сопротивления
Отметим, что в литературе (например, [4]) для решения задач возбуждения ЧИП обычно используется принцип эквивалентности, и ИУ составляется относительно эквивалентного магнитного тока на щелях в идеально проводящем экране. При этом достигается экономия вычислительных ресурсов и упрощение модели (снимается, например, вопрос о расчете токов, пересекающих границу периода), но значительно снижается общность постановки задачи (например, не удается учесть потери в материале экрана и элементах управления).
В настоящей работе применяются ИУ, составленные относительно компонентов
поверхностной плотности электрического тока 
, 
во всем объеме структуры, состоящей из
несущей перфорированной поверхности и УЭ (возможно, пленочного типа). При этом
использованы резистивные граничные условия [5] (рис. 6).
В частном случае нулевого поверхностного сопротивления они правильно описывают
и идеально проводящую поверхность, что позволило рассмотреть ЧИП с УЭ в рамках
единой методики. При этом УЭ могут быть как пленочными, так и сосредоточенными,
в последнем случае УЭ задается элементом поверхности в форме квадрата с
поверхностным сопротивлением, равным импедансу элемента на данной частоте. Еще
одной особенностью решения является возможность учета реактивных свойств УЭ
(например, собственных емкости и индуктивности выводов фоточувствительного
элемента или переключательного диода, наличия диэлектрической подложки).
Соответствующие свойства УЭ описываются мнимой частью комплексного
поверхностного сопротивления.
Из приведенного граничного условия с учетом связи между компонентами поверхностных токов на смежных периодах
,
где 
, 
, k – коэффициент распространения волны
в свободном пространстве, 
, 
- периоды структуры по x и y, lx, ly - номера периодов по x и y
соответственно, можно получить систему ИУ вида
, 
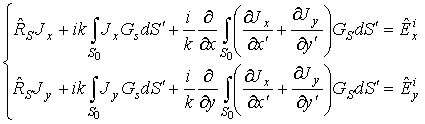, (1)
где
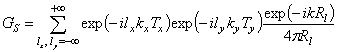, (2)
,
‑ нормированное к 
Ом удельное поверхностное сопротивление;
ИУ записываются для одного («нулевого») периода ЧИП S0.
Эта система уравнений решается численно, путем сведения к системе линейных алгебраических уравнений (СЛАУ) методом Галеркина с крышеобразными базисными и весовыми функциями. Главная особенность при этом заключается в использовании периодической функции Грина GS вместо обыкновенной функции Грина свободного пространства. Как видно из (1), функция GS и соответствующие ядра ИУ и коэффициенты СЛАУ содержат медленно сходящиеся ряды. При вычислении коэффициентов матрицы СЛАУ сходимость рядов ускоряется аналогично методике [6] с использованием асимптотических выражений и спектрального представления периодической функции Грина (2), т.е. формулы Пуассона
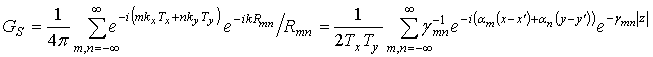
где
,
.
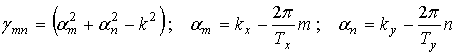По найденным из решения СЛАУ распределениям токов рассчитывается рассеянное поле
,
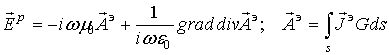при этом используется запись функции Грина с учетом условий дальней зоны
,
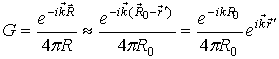где 
‑ расстояние от начала
координат до точки наблюдения; 
‑ расстояние от начала координат до точки
интегрирования, расположенной в плоскости 
; кроме
того,
; 
.
На практике интересен, в первую очередь, расчет коэффициентов прохождения и отражения поля по 0-й пространственной гармонике (т.е. в направлениях прямого прохождения и зеркального отражения). При этом единичные орты падающей и, например, прошедшей волны можно записать в виде
Записывая дифференциальные операторы (с учетом условий дальней зоны), получим
;
.
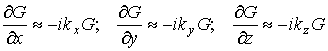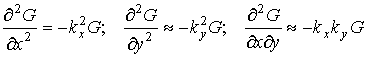Тогда выражения для вклада в 0-ю пространственную гармонику компонентов вектора вторичного электрического поля от тока на элементе с индексами n, m принимают вид
.
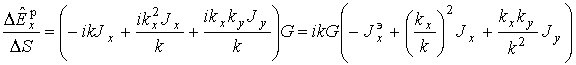
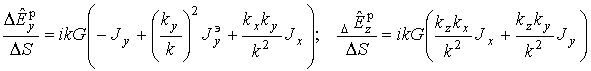После применения формулы Пуассона и
нормировки к 
получим следующие выражения для вклада
поверхностных токов одного элемента 
в рассеянное поле 00-й
гармоники (m=n=0) периодической системы 
,
,
,
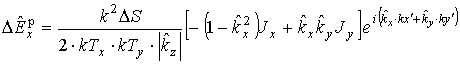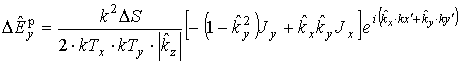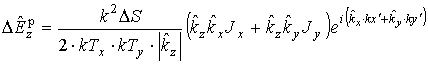где
,
После суммирования этих вкладов для всех (
) компонент рассеянное поле, как обычно [4],
характеризуется коэффициентами отражения 
и
прохождения 
на согласованной и кросс-поляризациях (по
отношению к вертикально или горизонтально поляризованной падающей волне).
При расчете прохождения для различных случаев
поляризации волны определим соответствующие единичные орты направлений (при 
):
,
коэффициент прохождения определим как
отношение амплитуд падающей и прошедшей волн 
для
соответствующей поляризации поля.
4. Результаты численных исследований
На основе разработанной модели составлены вычислительные программы, позволяющие оптимизировать геометрические параметры плоских ЧИП с учетом наличия УЭ, а также рассчитать свойства экранов с такими ЧИП. Расчеты проводились с целью поиска наилучшей конфигурации резонансных элементов периодической решетки, которые обеспечили бы эффективную управляемость, хорошие угловые и поляризационные характеристики, заданные частотные свойства, а также с целью определения требований, предъявляемых к управляющим элементам. При этом рассмотрены характеристики частотно-избирательных поверхностей с щелевыми элементами различной формы (линейная щель, кольцо, крест, «мальтийский» крест). Общей закономерностью является то, что при увеличении собственной добротности элемента (за счет выбора его формы или увеличения периода структуры) снижаются требования к управляющим элементам, но, как правило, ухудшаются угловые характеристики. Заметим, что добиться улучшения угловых характеристик и снижения уровня кроссполяризации, по-видимому, можно, применив хаотическое размещение элементов или повернув их на случайный угол вокруг нормали.
Управление коэффициентом прохождения
волны может быть реализовано за счет изменения поверхностного сопротивления
фоточувстствительной пленки, нанесенной на структуру. Оказалось, что для
эффективного уменьшения коэффициента пропускания (на величину около 10 дБ при
нормальном падении волны) поверхностное сопротивление управляемого тонкого
покрытия в составе щелей типа «мальтийского креста» (рис. 7а) не должно
превышать 1 кОм/□, при использовании низкодобротных элементов (типа
кольца) – в несколько раз ниже, например, 300 Ом/□. Интересно отметить,
что при отсутствии резонансных элементов (т.е. для управляемой поверхности на
основе резистивной пленки) это же значение коэффициента прохождения
обеспечивается только при 
Ом/□.
Учитывая технологические трудности изготовления сплошных низкоомных фотоуправляемых пленок (даже с сопротивлением около 1 кОм/□), была рассмотрена возможность применения иных управляющих элементов и структур. Расчеты показали, что аналогичный результат дает использование сосредоточенных УЭ (рис. 7б) с сопротивлением в освещенном состоянии около 700 Ом. Их можно изготовить в виде объемных элементов (сформированных, например, из порошков, паст) и установить по отработанной технологии гибридных интегральных схем. Для обеспечения минимальной поляризационной зависимости потребуется применение 4-х УЭ на один период.
Технологические преимущества этих подходов, вероятно, можно объединить, если использовать схемы частичного нанесения фотоуправляемых пленок или композиционных материалов. Так, при использовании «мальтийского» креста эффективное управление обеспечивается нанесением пленки с R ≈ 1 кОм/□ на его центральную область, причем УЭ в форме, например, диска (пленки или «таблетки», рис. 7б) может иметь диаметр всего 25-30% периода. Определенный эффект может дать и установка УЭ с обеих сторон экрана-подложки, что позволит использовать более технологичные УЭ с повышенным удельным сопротивлением.
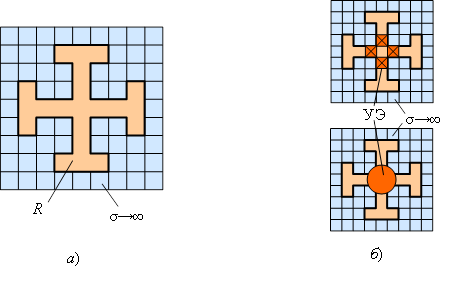
Рис. 7. Структура периода ЧИП в форме
«мальтийского креста» с распределенным (а)
и сосредоточенными (б)
управляющими элементами
Максимальное («темновое») сопротивление УЭ должно быть не ниже величин порядка 300 кОм (или кОм/□ - для пленок), в противном случае увеличиваются потери в режиме пропускания.
С увеличением угла падения, отсчитываемого от нормали, эффективность управления (как правило, на вертикальной поляризации) снижается, например, ухудшается на несколько дБ при угле падения Θ ≈ 40°…50°.
Следует отметить, что приведенные выше результаты получены для случая, когда управляющий элемент обладает чисто активным сопротивлением. На практике это обеспечивается при использовании резистивных пленок на тонкой диэлектрической подложке или же когда, например, небольшая собственная емкость сосредоточенных УЭ компенсируется индуктивностью подводящих проводников или индуктивным импедансом щели. Ниже отдельно будут обсуждены характеристики ЧИП, которые можно обеспечить за счет использования емкостных свойств УЭ.
Расчетами и экспериментами подтверждено, что улучшение основных свойств структуры (в первую очередь, угловых характеристик, которые получаются более равномерными) достигается за счет уменьшения ее периода. Именно этот фактор (уменьшенный размер резонансного элемента и, соответственно, периода структуры) определяет преимущество «мальтийского» креста перед крестом обычной формы. Аналогичный результат достигается и применением диэлектрического заполнения щелевого элемента, например, путем погружения ЧИП в слой диэлектрика. Разработанная модель позволяет приближенно учесть наличие тонкого диэлектрического слоя путем перехода к комплексным значениям эквивалентного поверхностного сопротивления структуры.
В связи с тем, что экранируемое оборудование может работать на различных частотах в пределах определенного диапазона, интерес представляют результаты исследования способов перестройки рабочей частоты управляемого экрана.
Механический способ такой перестройки, как правило, связан с использованием сложной кинематики и не обеспечивает высокого быстродействия, оптоэлектронный ‑ пригоден для бинарного управления («включен» - «выключен»), но плавную перестройку рабочей частоты с его помощью осуществить практически невозможно из-за ряда технологических ограничений. Наиболее практичным способом электронной перестройки является, вероятно, управление реактивной (емкостной) составляющей сопротивления УЭ. При этом в качестве УЭ могут быть использованы полупроводниковые структуры (смещенный в обратном направлении p-n переход) или управляемые конденсаторы на основе сегнетоэлектриков (в зарубежной литературе – ферроэлектриков), диэлектрическая проницаемость которых зависит от напряжения смещения.
Преимущества полупроводниковых приборов проявляются в том, что с их помощью можно электрически замыкать щели, подавая прямое напряжение на переход и тем самым делая экран непрозрачным, кроме того, для них характерен широкий диапазон изменения барьерной емкости (возможность в широких переделах менять рабочую частоту). Недостатки – разброс параметров от экземпляра к экземпляру, выраженная температурная зависимость. Большая плотность размещения УЭ (десятки на квадрат длины волны) делает рациональным только такой путь изготовления структуры, когда все p-n-переходы некоторого фрагмента экрана формируются в одном технологическом процессе.
Что касается использования сегнетоэлектриков,
то известны запатентованные в США конструкции сканирующих антенн, где
сканирование осуществляется именно изменением постоянного напряжения смещения
(до 19 кВ/см), прикладываемого к подложке или управляемым фазовращателям.
Устройства управления этих антенн выполнены на основе керамики BST 
,
которая, по данным из литературы, может применяться на частотах вплоть до
миллиметрового диапазона волн, позволяет реализовать 
при
малых потерях и обеспечить диапазон изменения диэлектрической проницаемости (в
зависимости от состава керамики и значения ε) от 30% до 54%,
например, в диапазоне ММВ получено изменение ε от 14 до 21. В
заявках ряда компаний на выполнение поисковых и опытно-конструкторских работ,
направленных на рассмотрение агентства DARPA (США), предлагается развернуть
работы по конструированию сканирующих антенн на основе уже разработанной
технологии нанесения пленок 
, а также 
и 
.
Учитывая, что ожидаемая и
подтвержденная расчетами зависимость резонансной частоты от диэлектрической
проницаемости УЭ близка к закону 
, можно предположить,
что уже сейчас возможна реализация электронной перестройки управляемого экрана
в диапазоне частот, по крайней мере, от 9 до 11 ГГц, что является практически
значимым результатом. Расширение доступного диапазона изменения ε
позволило бы даже перейти на такой способ управления, когда «запирание» экрана
происходит просто за счет перестройки полосы пропускания до ее выхода за
пределы рабочего диапазона. Отметим, что этот способ осуществим уже сейчас, если
использовать в качестве УЭ обратно смещенный p-n-переход с более широкими пределами изменения емкости
(существуют отечественные серийно выпускаемые настроечные СВЧ диоды с
изменением емкости более чем в 2 раза). Можно также рассматривать
комбинированный способ управления (например, оптоэлектронное «запирание» и
электронная подстройка изменением емкости). С учетом малых потерь материала
керамики напряжение смещения может подаваться высокоомными пленочными
проводниками, которые не повлияют на прохождение СВЧ сигнала. Отметим, что даже
простое ограничение полосы пропускания экрана с возможностью оперативной
перестройки окна прозрачности может способствовать существенному улучшению
параметров электромагнитной совместимости и расширению возможностей использования
экранируемого оборудования.
Для оценки возможностей практической реализации этих предположений были проведены расчеты. В частности, расчет характеристик рассеяния экрана на основе прямолинейных щелей (рис. 8а) показал, что введение УЭ с эквивалентной емкостью С=0,2 пф (что характерно для недорогих бескорпусных p-i-n диодов) приводит к увеличению добротности системы (сужению полосы пропускания) и понижению резонансной частоты. Для восстановления прежней резонансной частоты следует уменьшить все размеры элемента ЧИП приблизительно в 3,4 раза. Уменьшение размеров позволяет повысить плотность элементов ЧИП и получить хорошие угловые характеристики (рис. 8б).
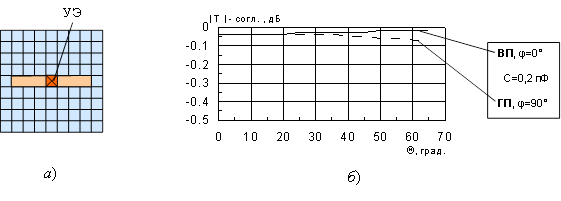
Рис. 8. Один период ЧИП с простыми
линейными щелями и переключательным диодом в качестве УЭ (а)
и угловые
характеристики такой ЧИП с учетом собственной емкости диода в двух
ортогональных плоскостях (б)
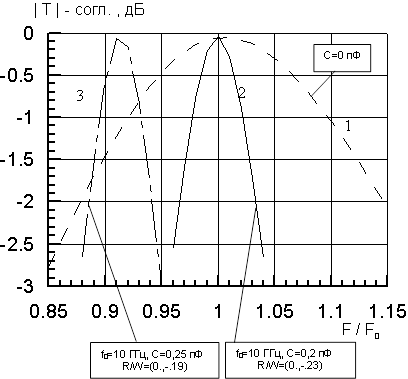
Рис. 9. Частотные характеристики коэффициента прохождения ЧИП с учетом собственной емкости УЭ
Увеличение емкости на 25% (с 0,2 до 0,25 пФ) приводит к понижению резонансной частоты (например, с 10 ГГц до 9,1 ГГц, рис. 9, кривая 1 - частотная характеристика щели без УЭ, кривая 2 – та же структура с УЭ, С=0,2 пФ, размеры уменьшены в 3,4 раза для приведения к той же нормированной центральной частоте, см. комментарии к рис. 8, кривая 3 – случай с С=0,25 пФ без дополнительной нормировки размеров).
Однако увеличение добротности линейных или крестообразных щелей может оказаться чрезмерным, что проявится в слишком узкой полосе пропускания экрана, трудностях настройки всех элементов ЧИП на одну и ту же частоту, потерях из-за неизбежного рассогласования, сильному влиянию тепловых потерь в УЭ или пленке. В этом случае есть смысл применить щели кольцевой формы, которые при наличии емкостной нагрузки способны обеспечить хорошие резонансные свойства и угловые характеристики (без такой нагрузки угловые характеристики кольцевых щелей слишком неравномерны). Это иллюстрируется рис. 10б и рис. 11 (обозначения – те же, что и для случая линейной щели, рис. 8).
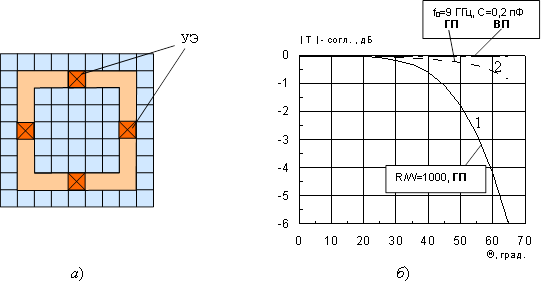
Рис. 10.
Структура периода ЧИП с кольцевыми щелями и УЭ (а) и
угловые
характеристики такой ЧИП при двух поляризациях (б) при азимутальном угле
падения φ=30˚
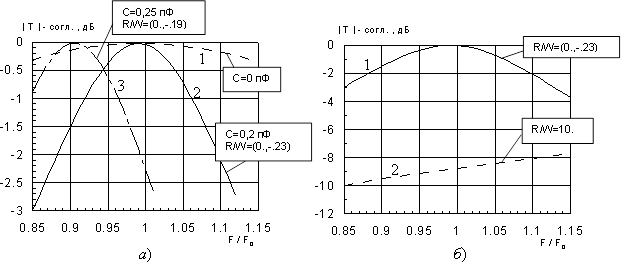
Рис. 11. Частотные характеристики коэффициента прохождения ЧИП с кольцевыми щелями с учетом собственной емкости УЭ
Дополнительно на рис. 11б (кривая 2) изображена частотная характеристика такой же ЧИП на основе кольцевых структур, УЭ которых имеют активное сопротивление R~3,8 кОм. Видно, что за счет совместного действия двух факторов (введения потерь и сдвига по частоте) обеспечивается эффективное управление коэффициентом прохождения ЧИП.
5. Выводы
Подробно описана электродинамическая модель частотно-селективного управляемого или неуправляемого экрана. Решение задачи о падении плоской волны на плоскость, характеризуемую двухмерно-периодическим неоднородным поверхностным сопротивлением, получено методом интегральных уравнений. Модель позволяет оптимизировать геометрические параметры плоских частотно-избирательных поверхностей с учетом наличия управляющих элементов или пленок. В рамках применимости метода физической оптики эта модель может быть использована для расчета свойств электрически больших экранов различной формы посредством определения коэффициентов прохождения и отражения для отдельных зон экрана. Результаты демонстрационных численных расчетов дают представление о степени влияния активных и реактивных компонентов собственного импеданса упраляющих устройств или пленок на угловые и частотные характеристики экрана и о возможности достижения требуемых показателей.
Литература
1. Martin M.T., Duhl M.L. Method and apparatus using photoresistive materials as switchable EMI barriers and shielding. US Patent No.5278562, Jan.11,1994. H01Q 17/00.
2. Лагарьков А.Н., Погосян М.А. Фундаментальные и прикладные проблемы стелс-технологий// Вестник РАН. 2003. Т.73. №9. С. 779-787.
3. Radar cross section/ E.F. Knott, J.F. Shaeffer, M.T. Tuley. – 2nd ed. Artech House, Inc., Boston-London. – 1993.
4. Computational methods in electromagnetics// A.F. Peterson, S.L. Ray, R. Mittra. – New York, NY. IEEE, Inc. – 1998.
5. Senior T.B.A. Scattering by resistive strips// Radio Science. 1979. V.14. №5. P.911-924.
6. Lampe R., Klock P., Mayes P. Integral transforms useful for the accelerated summation of periodic, freespace Green's functions// IEEE Trans. 1985. V. MTT-33. No. 8. P.734-736.