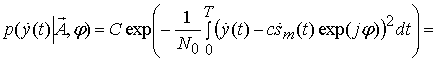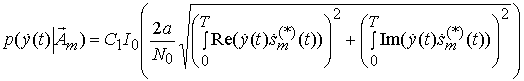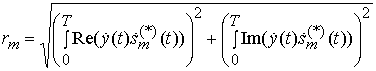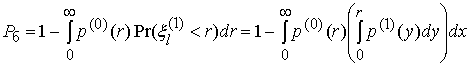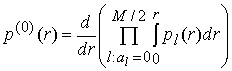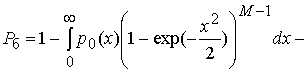УДК 621.391.01

ВЫЧИСЛЕНИЕ ВЕРОЯТНОСТНЫХ ХАРАКТЕРИСТИК ПОСИМВОЛЬНОГО НЕКОГЕРЕНТНОГО ПРИЕМА ОРТОГОНАЛЬНЫХ СИГНАЛОВ

 

Л. Е. Назаров ¹, П. В. Шишкин ²

¹Фрязинский филиал Института радиотехники и электроники им. В.А.Котельникова РАН, г. Фрязино

²АО «Информационные спутниковые системы» им. академика  М.Ф.Решетнева, г. Железногорск

 

Статья поступила в редакцию 26 апреля 2016 г.

 

Аннотация. Приведен модифицированный алгоритм посимвольного некогерентного приема ортогональных в усиленном смысле сигналов, более простой по реализации, чем алгоритм оптимального посимвольного некогерентного приема. Приведено аналитическое выражение для вероятности ошибки на информационный бит при использовании этого алгоритма приема. Показано, что доказанное выражение тождественно выражению для вероятности ошибки на бит при использовании правила некогерентного приема, реализующего статистический критерий максимального правдоподобия.

Ключевые слова: ортогональные сигналы, посимвольный прием, некогерентный прием, вероятность ошибки.

Abstract. The suboptimal algorithm of symbol-by-symbol noncoherent decoding for orthogonal signals and error-performances of that are presented in the article. The error-performances for orthogonal signal symbol-by-symbol decoding are evaluated by means of utilizing analytical expression.

Key words: orthogonal signals, symbol-by-symbol decoding, noncoherent decoding, error performance.

 

Введение

Теоретическое исследование вероятностных характеристик ансамблей сигналов, определяемых применяемыми правилами их приема, составляет один из основных этапов создания систем передачи информации [1]. Это определяет актуальность проблемы разработки и развития математического аппарата для теоретического оценивания или вычисления вероятностей ошибочных решений (вероятностей ошибки на сообщение , вероятность ошибки на бит (символ) ) при приеме сигналов для различных видов канальных помех. Базовой моделью является помеха в виде аддитивного белого гауссовского шума (АБГШ) [1,2].

Наиболее полно эта проблема решена для когерентного приема, реализующего статистический критерий максимального правдоподобия [2]. При его применении минимизируется вероятность ошибочного приема . Для этого случая известен ряд аналитических соотношений, определяющих вычисление точных значений  [1-4] либо их границ [3-7].

Значительно более сложной является проблема оценивания вероятностных характеристик для правила посимвольного приема сигналов, реализующего статистический критерий максимальной посимвольной апостериорной вероятности [8,9]. При применении этого правила минимизируется вероятность ошибки .

Интерес к данному правилу приема объясняется тем, что алгоритмы посимвольного приема составляют основу процедур приема класса ансамблей сигналов, соответствующих наиболее эффективным помехоустойчивым кодам с итеративными алгоритмами декодирования (турбо-коды [10], низкоплотностные коды [10], турбо-подобные коды [10,11]).

Известны аналитические выражения для оценки вероятностных характеристик  при применении когерентного посимвольного приема для ограниченного ряда ансамблей сигналов, например, для ансамблей симплексных сигналов [12,13]. В данной работе приведено аналитическое выражение для вычисления вероятности ошибки  при некогерентном посимвольном приеме сигналов, ортогональных в усиленном смысле.

 

1. Постановка задачи

Пусть (, ) - множество дискретных сообщений объемом , каждому сообщению сопоставляется сигнал с комплексной огибающей  длительностью , . Сигналы  являются ортогональными в усиленном смысле [2,3], т.е. 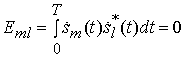 для , иначе ;  - операция комплексного сопряжения. Примером рассматриваемых сигналов являются сигналы, соответствующие базисным функциям Уолша-Адамара [2].

Вектор  с двоичными компонентами  рассматривается как двоичное представление его номера , .

Обозначим  реализацию на входе приемного устройства при передаче сигнала . Здесь  - амплитуда сигнала;  - начальная фаза сигнала, полагаемая случайной величиной с равномерным законом распределения ;  - помеховая составляющая АБГШ с односторонней спектральной плотностью .

Правило оптимального посимвольного приема сигналов заключается в вычислении апостериорных вероятностей  и принятии решения , если  и  в противном случае [8].

Апостериорная вероятность  () задается выражением

.                                  (1)

С учетом правила Байеса имеем 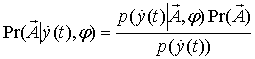. Здесь  - плотность вероятности реализации  и

               (2)

.

 

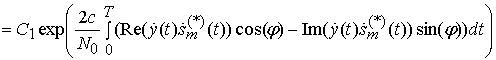Здесь  - нормирующие множители, не зависящие от .

После усреднения (2) по  имеем результирующее выражение [2-4]

.       (3)

 

 

Здесь  - модифицированная функция Бесселя 1-го рода 0-го порядка.

Таким образом, алгоритм оптимального некогерентного посимвольного приема заключается в вычислении корреляционных соотношений в составе выражения (3), их нелинейном преобразовании (3) и суммировании (1) для вычисления апостериорных вероятностей .

Модифицированный (подоптимальный) и более простой алгоритм посимвольного приема заключается в замене суммирования (1) вычислением и сравнением величин  [10, 11]

,                                           (4)

.                                            (5)

Принимается решение , если , иначе .

Так как функция  монотонно возрастающая, выражения (4), (5) могут быть записаны в следующем виде

,                                             (6)

.                                               (7)

.                              (8)

 

Здесь  - значения отсчетов с выходов детекторов огибающих сигналов .

Вычисление множества  может быть осуществлено с помощью согласованных фильтров или корреляторов для сигналов  [2].

Суть задачи - доказать аналитическое выражение для оценки вероятности ошибки на бит  при использовании алгоритма посимвольного некогерентного приема (6)-(8) для ансамблей сигналов, ортогональных в усиленном смысле.

 

2. Вероятность ошибки при посимвольном некогерентном приеме

В работах [7,9] показано, что вероятность ошибки  для фиксированного значения  при посимвольном приеме не зависит от номера  передаваемого сообщения  (от передаваемого сигнала ). Для ортогональных в усиленном смысле сигналов в виде базисных функций Уолша-Адамара вероятность  при посимвольном приеме не зависит от номера символа  (в общем случае произвольных ансамблей сигналов вероятности  при посимвольном приеме зависят от номера  [9]). В этом случае без потери общности полагаем передачу сигнала . Ниже докажем аналитическое выражение для вероятности ошибки на бит (символ)  при применении алгоритма посимвольного приема (6)-(8).

Вероятность ошибки  задается соотношением [3]

.                 (9)

 

Здесь  - плотности распределения величин  и .

Случайные величины  (8) статистически независимые, поэтому плотности распределения  для  и  имеют вид

,                                     (10)

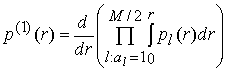.                                      (11)

Случайные нормированные величины 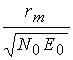 распределены по закону Релея для  и по закону Релея-Райса для  [3,14], поэтому имеем

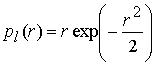. .                                (12)

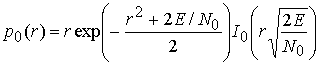.                   (13)

 

Здесь  - энергия сигналов при приеме.

Интегрируя соотношение (9) и используя (10)-(13), получаем выражение

                               (14)

.

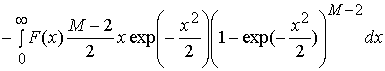Здесь 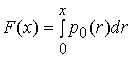 - интегральная функция распределения Релея-Райса.

Отметим, что два первых слагаемых в (14) задают вероятность ошибочного приема 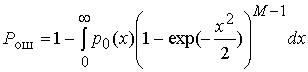 ортогональных в усиленном смысле сигналов при использовании правила максимального правдоподобия [1,2]. В этом случае вероятность ошибки на бит  связана с  соотношением [3]

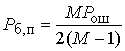.                                                 (15)

 

Выражение для  может быть приведено к виду [3]

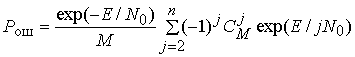.                      (16)

Для  справедливо соотношение 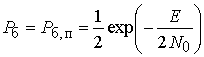 [3].

 

Покажем, что справедливо общее соотношение

.                                                 (17)

Для доказательства (17) приведем соответствующие выкладки. Запишем выражение (14) в виде

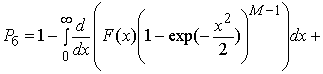
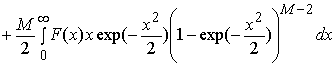.                (18)

Учитывая условие 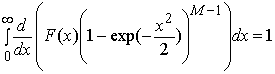, запишем (18) в виде 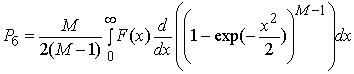. Интегрируя это выражение по частям, имеем

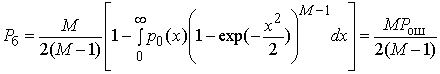.     (19)

Выражение (19) совпадает с доказываемым выражением (17).

При вычислении  в (19) можно использовать выражение (16).

При наличии лишь помехи (энергия сигналов ) справедливо соотношение  и , что согласуется с физическим смыслом посимвольного приема сигналов.

 

3. Результаты вычислений

На рисунке 1 приведены вероятности ошибки на бит  посимвольного некогерентного приема ортогональных в усиленном смысле сигналов Уолша-Адамара для канала АБГШ, вычисленные с использованием выражения (19). Вероятностные кривые 1, 2, 3 соответствуют объему ансамблей сигналов,  и . По оси абсцисс отложены значения отношения сигнал/помеха , здесь  - энергия сигналов на информационный бит, . Для фиксированного значения  вероятности ошибки  уменьшаются с увеличением объема ансамблей сигналов, например, для 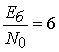 дБ имеем  для  и  для .

 

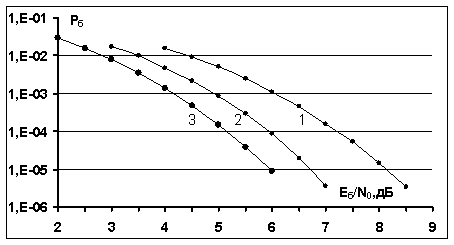
Рис.1. Вероятности ошибки на бит  посимвольного некогерентного приема сигналов Уолша-Адамара для канала АБГШ:
1 - объем ансамбля сигналов 8; 2 - объем ансамбля сигналов 64; 3 - объем ансамбля сигналов 256.

 

Моделирование алгоритма оптимального посимвольного некогерентного приема (1) сигналов Уолша-Адамара показало его эквивалентность рассматриваемому модифицированному (подоптимальному) алгоритму посимвольного некогерентного приема (4), (5) относительно их вероятностных характеристик.

 

Заключение

Доказано аналитическое выражение для вычисления вероятности ошибки на бит при использовании модифицированного алгоритма посимвольного некогерентного приема для ансамблей сигналов, ортогональных в усиленном смысле. Модифицированный алгоритм посимвольного некогерентного приема является более простым по отношению к алгоритму оптимального посимвольного некогерентного приема. Доказанное выражение для вероятности ошибки на бит совпадает с выражением для вероятности ошибки на бит при использовании алгоритма некогерентного приема ортогональных в усиленном смысле сигналов, реализующего правило максимального правдоподобия.

Путем моделирования алгоритма оптимального посимвольного некогерентного приема ортогональных в усиленном смысле сигналов Уолша-Адамара показано, что этот алгоритм эквивалентен рассматриваемому модифицированному (подоптимальному) алгоритму посимвольного некогерентного приема относительно их вероятностных характеристик.

 

Работа выполнена при поддержке РФФИ (№16-07-00746).

 

Литература

1. Коржик В.И., Финк Л.М., Щелкунов Н.Н. Расчет помехоустойчивости систем передачи дискретных сообщений. М.: Радио и связь, 1981.

2. Финк Л.М. Теория передачи дискретных сообщений. М.:Сов.радио. 1970.

3. Витерби Э.Д. Принципы когерентной связи. М.: Сов. Радио. 1970.

4. Возенкрафт Дж., Джекобс И. Теоретические основы техники связи. М.: Мир. 1969.

5. Смольянинов В.М., Назаров Л.Е. Мультипликативная граница вероятности правильного распознавания при когерентном приеме. // Радиотехника и электроника. 1987. Т.32. №2. Стр. 446-449.

6. Herzberg H., Poltyrev G. Techniques of bounding the probability of decoding error for block coded modulation structures. // IEEE Transactions on Information Theory. 1994. Vol. 40, №3. P.903-911.

7. Cheng U., Huth G.K. Bounds on the bit error probability of linear cyclic code over GF() and its extended code. // IEEE Transactions on Information Theory. 1988. Vol. 34, №4. P.776-785.

8. Кларк Дж. мл., Кейн Дж. Кодирование с исправлением ошибок в системах цифровой связи. М.: Радио и связь. 1987.

9. Назаров Л.Е. Вероятностные характеристики при оптимальном посимвольном приеме сигналов, соответствующих двоичным блоковым кодам. // Радиотехника и электроника. 1999. Т. 44. №10. Стр. 1231-1235.

10. Johnson S.J. Iterative Error Correction: Turbо, Low-Density Parity-Check and Repeat-Accumulate Codes. Cambridge. University Press. UK. 2010.

11. Назаров Л.Е., Головкин И.В. Последовательные турбо-коды с пониженной сложностью алгоритмов приема.// Радиотехника и электроника. 2010. Т. 55. №10. Стр. 1193-1199.

12. Назаров Л.Е., Головкин И.В. Оценки вероятностей ошибки при посимвольном приеме ансамблей ортогональных и симплексных сигналов. // Известия вузов. Электроника. 2008. №5. Стр.63-68.

13. Назаров Л.Е., Головкин И.В. Границы ошибки при посимвольном приеме сигналов на основе линейных блоковых кодов.// Известия вузов. Электроника. 2009. №5. Стр.44-49.

14. Левин Б.Р. Теоретические основы статистической радиотехники. Книга 1. М.: Сов. радио. 1969.