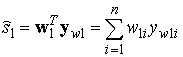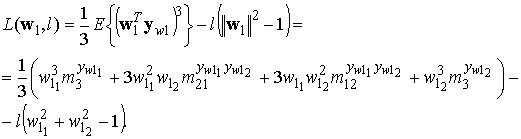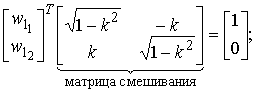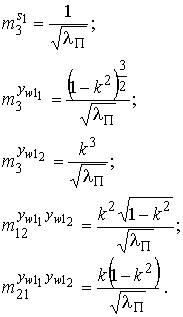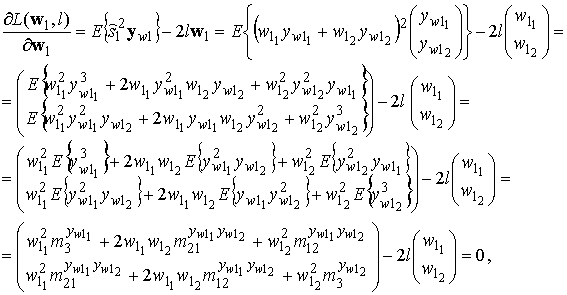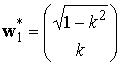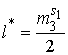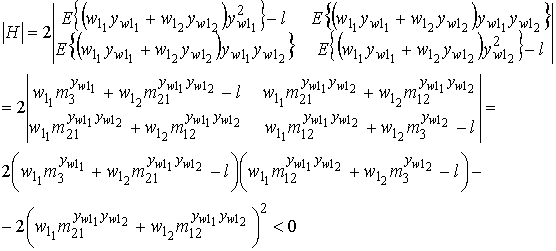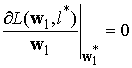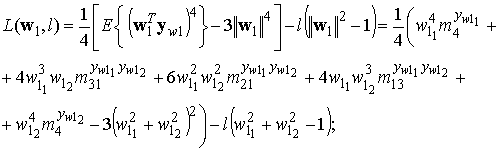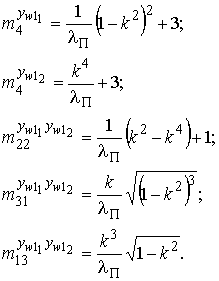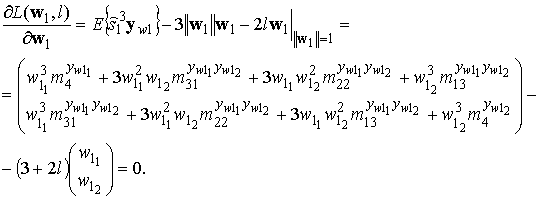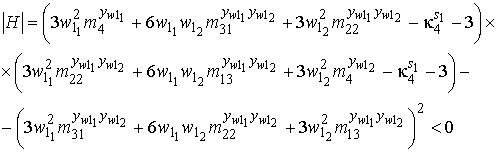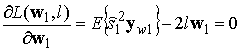О разработке и исследовании эффективности алгоритма слепого выделения импульсного сигнала при наличии белого гауссовского шума

УДК 681.513.6

А. Е. Манохин

Институт радиоэлектроники и информационных технологий-РТФ УрФУ
им. первого Президента РФ Б.Н.Ельцина, кафедра радиоэлектронных и телекоммуникационных систем, Екатеринбург

Статья поступила в редакцию 14 марта 2016 г., поле доработки – 9 мая 2016 г.

Аннотация. В работе решается задача синтеза алгоритма слепого выделения импульсного сигнала из смеси с белым гауссовым шумом, использующего критерий максимизации момента 3 порядка выходного сигнала нейронной сети. В отличие от распространенных алгоритмов слепого выделения на основе максимизации эксцесса, алгоритм, максимизирующий момент 3 порядка, обладает большей скоростью сходимости и не зависит от начальных условий, а также от интенсивности импульсного процесса.

Ключевые слова: слепое выделение сигналов, эксцесс, момент 3 порядка, искусственная нейронная сеть, скорость сходимости.

Abstract. In the work a problem of synthesizing the blind pulse signal extraction algorithm from the mixture with white Gaussian noise based on maximization of neuron network output signal third moment is decided. In contrast to widespread blind algorithms based on maximizing kurtosis, the third moment maximization algorithm possesses higher convergence rate and doesn’t depend on initial conditions and the pulse process intensity.

Key words: blind sources extraction, kurtosis, third moment, artificial neural network, convergence rate.

Введение

Задача слепого выделения сигналов является частным случаем слепого разделения сигналов. Слепое разделение может трактоваться как нахождение линейного преобразования в виде разделяющей матрицы W размерности nxm , полного ранга и такой, чтобы при умножении входного вектора смесей сигналов на эту матрицу выходной вектор содержал максимально статистически независимые компоненты [1].

В отличие от слепого разделения, слепое выделение выражается как оценка одного или нескольких интересующих сигналов с особыми статистическими свойствами, а остальные (помеховые) сигналы должны быть проигнорированы.

По-другому задачу слепого выделения сигналов можно сформулировать как идентификацию соответствующего вектора h_j смешивающей матрицы H и (или) их обращений w_j, которые являются строками разделяющей матрицы W, предполагая только статистическую независимость первичных источников и линейную независимость столбцов матрицы H [1]. Как правило, слепое выделение сигналов происходит последовательно, одно за другим.

Слепое выделение сигналов имеет ряд важных преимуществ.

1) Сигналы могут быть отфильтрованы в определенном порядке в соответствии с их стохастическими особенностями (например, в порядке убывания нормированного эксцесса [2] или с определенным значением эксцесса [3]).

2) Можно применять множество различных критериев, основанных на статистиках 2 и более высоких порядков, для выделения широкого спектра сигналов — статистически независимых, гауссовых окрашенных [4,5], нестационарных [6] и т. п. в зависимости от особенностей сигналов, которые необходимо выделить.

3) Нет необходимости выделять все сигналы, число которых в смеси может быть неизвестно.

4) Алгоритмы выделения более просты по сравнению с алгоритмами слепого разделения сигналов.

Некоторые из подходов слепого выделения сигналов требуют предварительной обработки в форме обеления вектора смеси сигналов с датчиков или ортогонализации смешивающей матрицы.

Существует множество алгоритмов получения обеляющей матрицы: алгоритм градиентного поиска (NGA[1]) [7], процедура ортогонализации Грамма-Шмидта [8], алгоритм стандартного разложения по собственным значениям (EVD^{^[2]}) [9], алгоритм обобщенного разложения по собственным значениям (GEVD^{^[3]}) [10] и т. п.

Процедуру выделения сигналов можно реализовать с помощью каскадной нейронной сети (рис. 1).

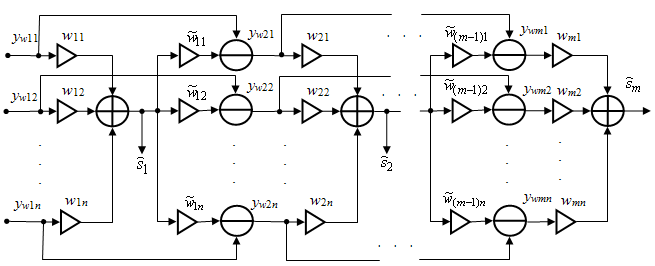
Рис. 1. Структурная схема, иллюстрирующая последовательное слепое выделение сигналов

Если предположить, что все сигналы источников взаимно независимы и имеют особые статистические свойства (например, негауссовость), то в этом случае для выделения сигналов чаще всего используют критерии экстремума эксцесса [1, 11, 12, 13].

После успешного выделения первого сигнала необходимо применить процедуру подавления для того, чтобы повторно не фильтровать сигнал из смеси во втором блоке. Процедура подавления представляет удаление уже выделенного сигнала из смеси, например по критерию минимизации суммарной мощности смеси, подаваемой на второй блок [2].

Однако если на каждом шаге выделения сигнала производится обеление вектора смеси и накладываются ограничения на норму вектора ||w₁||=1, то вектор подавления оценивать не нужно, т.к. он равен вектору выделения w₁[1].

Описать процедуру последовательного выделения можно следующим образом. Смесь полезного сигнала и помех поступает на устройство обеления. После выделения первой помехи происходит ее подавление (компенсация) в смеси с сигналом. Далее процесс повторяется до тех пор, пока все помехи не будут подавлены.

Постановка задачи

Результаты ряда исследований, изложенных в [1,14], показывают, что при слепом выделении случайных процессов, когда один из них импульсный, наблюдается плохая сходимость алгоритмов на основе максимизации эксцесса.

Кроме того, при использовании в слепых алгоритмах в качестве критерия экстремум эксцесса выходного сигнала количество локальных минимумов (максимумов) и седловых точек, к которым может сходиться решение, гораздо больше, чем в случае использования критерия асимметрии или момента 3 порядка случайного процесса, что снижает скорость сходимости таких алгоритмов [15].

Необходимо синтезировать алгоритм, который выделял бы импульсный процесс и доказать, что критерий максимизации момента 3 порядка значительно превосходит критерий максимизации эксцесса по скорости сходимости и эффективности выделения полезного сигнала на фоне белого гауссова шума.

Момент 3 порядка случайного процесса — коэффициент, характеризующий степень асимметрии распределения относительно математического ожидания или моды.

Процедуру последовательного слепого выделения сигналов можно реализовать с помощью каскадной нейронной сети (см. рис. 1). На ее входах действуют аддитивные смеси сигналов с разными коэффициентами смешивания. Один из сигналов источников — негауссов (имеет асимметричное распределение) и не зависим от остальных.

Пусть на вход блока выделения поступает обеленный вектор смеси , где Q — матрица обеления; y — вектор аддитивных смесей. Под обелением смеси сигналов и помех понимается декорреляция смешанных сигналов от приемных датчиков [1].

Первый блок (рис. 1) выделяет оценку :

, (1)

где w₁ — вектор весовых коэффициентов выделения сигнала s₁ первого блока.

Рассмотрим преимущества алгоритма, который максимизирует функционал:

, (2)

где — момент 3 порядка выходного сигнала нейронной сети с нулевым математическим ожиданием.

Во многих случаях для улучшения сходимости максимизация функционала производится под определенными ограничениями [11]:

. (3)

С целью нахождения оптимального решения w₁^* для функционала (2) запишем функцию Лагранжа [16] с ограничением (3):

(4)

где l — множитель Лагранжа, m₃— центральный момент 3 порядка, m₁₂ и m₂₁— смешанные моменты 3 порядка.

Конкретизируем задачу. Допустим, на фоне гауссова процесса s₂(n), у которого моменты высших порядков равны нулю, выделяется случайный процесс Пуассона s₁(n) с интенсивностью λ_П, единичной дисперсией и нулевым математическим ожиданием. Смеси в двух каналах после обеления представим следующим образом:

; (5)

где k и — среднеквадратическое отклонение случайных процессов в каналах (k < 1).

Вектор выделения сигнала w₁ находим через уравнение с матрицей смешивания:

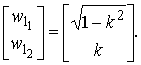(6)

Статистики 3 порядка для обеленных смесей в (5) будут равны:

(7)

Определим стационарные точки функции Лагранжа. Для этого возьмем частные производные выражения (4) по l и w₁с учетом оценки сигнала (1) и приравняем их к нулю:

(8)

(9)

Для положительных множителей Лагранжа стационарная точка [17] единственная и находится из (9) при значениях вектора весовых коэффициентов:

при . (10)

Для определения наличия экстремума функции Лагранжа найдем определитель матрицы Гесса:

(11)

Определитель матрицы Гесса (11) при подстановке значений из (7) и (10) всегда отрицательный, стационарная точка является седловой (рис. 2) или точкой минимакса [17].

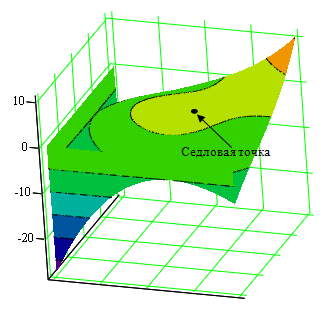
Рис. 2. Поверхность, построенная по формуле (4) при k=0.7 и λ_П=0.15

Обратимся к условиям Куна-Таккера: если существует такой неотрицательный множитель Лагранжа l^*≥ 0, что:

; (12)

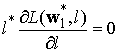, (13)

то седловая точка является точкой глобального максимума функции Лагранжа [18].

При подстановке значений из (10) условия (12) и (13) выполняются. Таким образом, при максимизации момента 3 порядка решение сходится к оптимальному вектору (6).

Аналогичные преобразования сделаем для функционала:

, (14)

где — эксцесс для сигналов с нулевым математическим ожиданием.

Запишем функцию Лагранжа с ограничением (3):

(15)

где m₂₂, m₁₃ и m₃₁ — смешанные моменты 4 порядка, m₄ — центральный момент 4 порядка, вычисляемые как:

(16)

Для определения стационарных точек функции Лагранжа возьмем частные производные выражения (15) по l и w₁с учетом оценки сигнала (1) и приравняем их к нулю:

(17)

Для положительного множителя Лагранжа 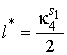обнаруживаются две стационарные точки:

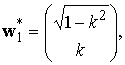
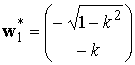. (18)

Обе стационарные точки являются седловыми (рис. 3), поскольку гессиан (определитель матрицы Гесса) при подстановке значений из (16) и (18) отрицательный:

(19)

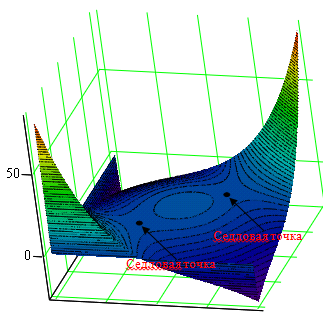
Рис. 3. Поверхность, построенная по формуле (15) при k=0.7 и λ_П=0.15

Обе точки удовлетворяют условиям Куна-Таккера (12) и (13) и являются глобальными максимумами, поэтому, максимизируя эксцесс при выделении процесса Пуассона на фоне гауссовой помехи, можно получить решение, сходящееся к двум значениям векторов w₁ (18) в зависимости от полярности (знака момента 3 порядка) процесса Пуассона.

Таким образом, с одной стороны, алгоритм выделения процесса Пуассона на основе максимизации момента 3 порядка не чувствителен к изменению полярности, тогда как алгоритм на основе максимизации эксцесса этим недостатком не обладает.

С другой сторроны, сходимость алгоритма выделения процесса Пуассона на основе максимизации момента 3 порядка индифферентна к значению интенсивности процесса Пуассона. Сходимость же алгоритма на основе максимизации эксцесса ухудшается и в конечном итоге приводит к невозможности выделения импульсного сигнала при его больших интенсивностях.

Причиной этому является зависимость обусловленности матрицы Гесса от интенсивности λ_П, а, как известно, чем хуже обусловленность, тем труднее осуществлять поиск глобального максимума [19].

Определим обусловленность матрицы Гесса как отношение ее абсолютных максимального и минимального собственных значений [20]:

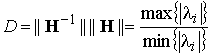. (20)

Подставим оптимальные значения весовых коэффициентов (6) и значения статистик 3 порядка (7) в матрицу Гессе, выраженную по ф. 11, и найдем ее собственные значения:

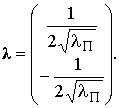(21)

Отношение абсолютных собственных значений из (21) в итоге равно единице, что свидетельствует о наилучшей обусловленности матрицы и ее независимости от интенсивности процесса Пуассона.

При максимизации эксцесса для упрощения расчетов собственных значений матрицы Гессе, выраженной по ф. 19, возьмем предельный случай, когда k=0 (=1 и =0). Тогда:

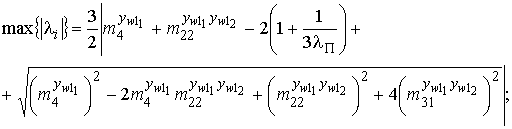(22)

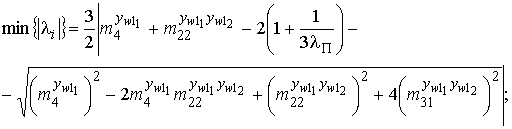(23)

Поставляя значения из ф. 16 в (22) и (23), получаем:

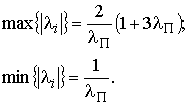(24)

Аналогичный результат получается при другом предельном случае, когда k=1 (=0 и =1). Тогда обусловленность матрицы Гесса определяется:

и находится в прямой пропорции от интенсивности процесса Пуассона.

Можно графически продемонстрировать, что при увеличении интенсивности λ_П происходит ухудшение сходимости, когда максимизируется эксцесс и, наоборот наблюдается постоянство сходимости, когда максимизируется момент 3 порядка. Подставим параметры из (7) в функцию (9) и параметры из (16) в функцию (17) соответственно и построим поверхности (рис. 4–7) для k=0.7. Пересечение этих поверхностей с нулевым уровнем в точках и есть искомое решение:

=0.71;

=0.7.

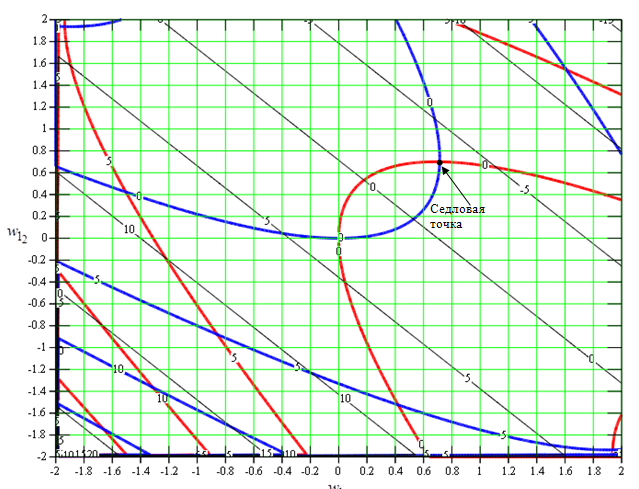
Рис. 4. Линии уровней функций (9) (красные и синие жирные линии) и (11) (черные тонкие линии) при λ_П=0.15

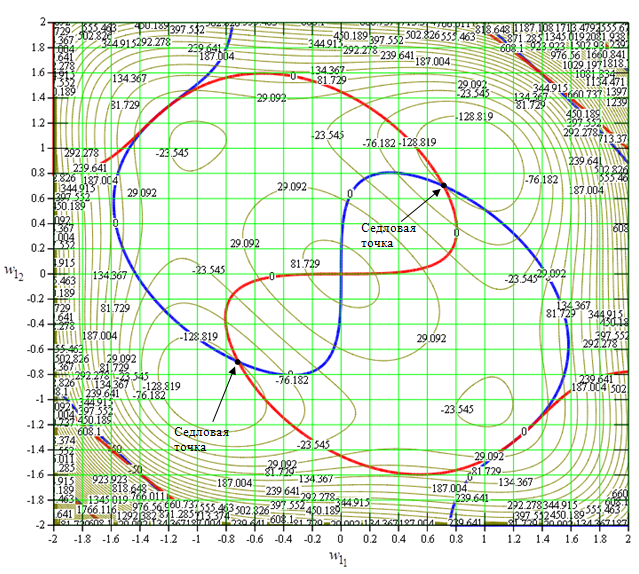
Рис. 5. Линии уровней функций (17) (красные и синие жирные линии) и (19) (коричневые тонкие линии) при λ_П=0.15

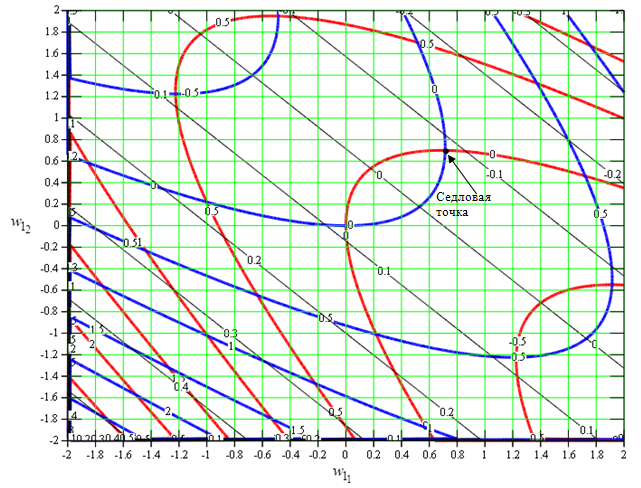
Рис. 6. Линии уровней функций (9) (красные и синие жирные линии) и (11) (черные тонкие линии) при λ_П=6.0

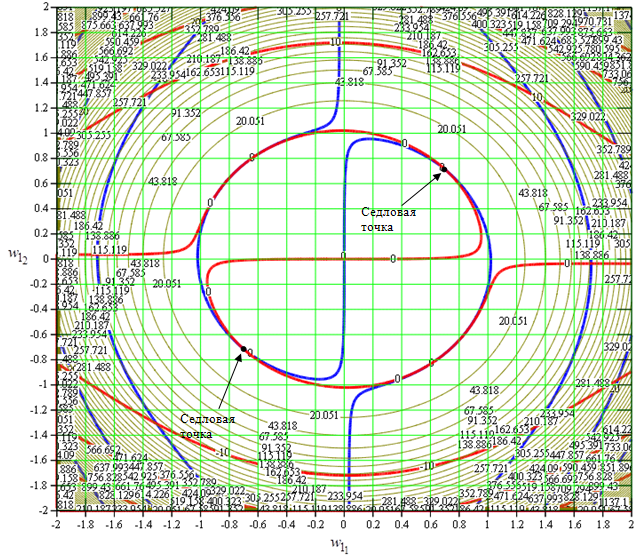
Рис. 7. Линии уровней функций (17) (красные и синие жирные линии) и (19) (коричневые тонкие линии) при λ_П=6.0

Сравнивая рис. 4, 5, 6 и 7, легко можно заметить, что при больших интенсивностях (λ_П=6.0) градиент функционала (2) в стационарной точке гораздо более выпуклый, нежели градиент эксцесса, что увеличивает скорость сходимости к оптимальным значениям весовых коэффициентов. В свою очередь, градиент эксцесса настолько мал, что вызывает медленную сходимость к оптимальным весовым коэффициентам или вообще не позволяет выделять полезный сигнал.

Если необходимо выделить сигнал с моментом 3 порядка, имеющим определенный знак, то необходимо воспользоваться следующим функционалом:

, (25)

где b — параметр, определяющий знак момента 3 порядка выделяемого сигнала (b = –1 для сигналов отрицательной полярности, и b = 1 для сигналов с положительной полярностью).

Синтез алгоритма на основе максимизации момента 3 порядка

Синтезируем алгоритм поиска весовых коэффициентов нейронной сети на основе критерия максимума момента 3 порядка. Как было упомянуто выше, сходимость к оптимальному решению возможна при равенстве нулю производной функции Лагранжа:

. (26)

Выразим вектор w₁ с учетом функционала (25):

где с — скаляр, значение которого с учетом нормировки весовых коэффициентов существенного влияния на них не имеет, поэтому результирующий алгоритм на основе максимизации момента 3 порядка можно записать:

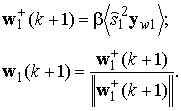(27)

Критерием достижения значения весовых коэффициентов оптимального значения может быть следующее условие:

Структурная схема, реализующая алгоритм на основе максимизации момента 3 порядка, приведена на рис. 8.

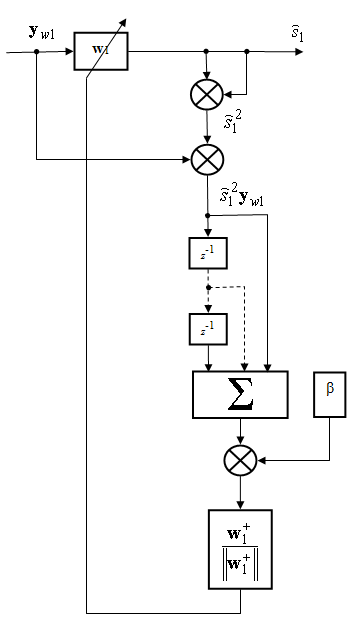
Рис. 8. Структурная схема, иллюстрирующая работу алгоритма (27), основанного на максимизации момента 3 порядка

Компьютерное моделирование алгоритмов слепого выделения сигналов

Компьютерное моделирование синтезированного алгоритма (назовем его Min3Mom) и алгоритма на основе максимизации эксцесса (FastICA [21]) проведено в Simulink (рис. 9 и 10).

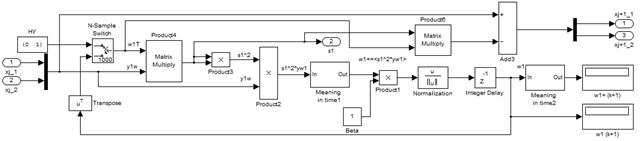
Рис. 9. Алгоритм Min3Mom, основанный на максимизации момента 3 порядка

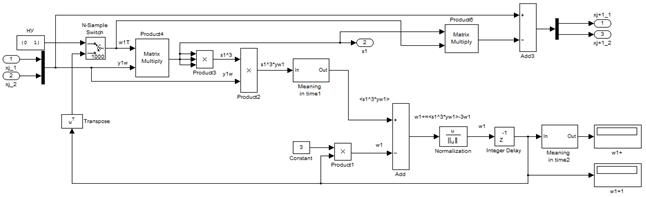
Рис. 10. Алгоритм FastICA, основанный на максимизации эксцесса

В двух приемных датчиках действует сумма помехи и полезного сигнала с разными среднеквадратическими отклонениями, задаваемыми коэффициентом k (см. ф. 5). Результаты экспериментов отображены в таблицах 1, 2 и на рис. 11–13. Эффективность алгоритмов определяется по выигрышу в отношении сигнал–помеха G.

Таблица 1

Зависимости выигрыша G от отношения сигнал-помеха на входе при разных алгоритмах слепого выделения процесса Пуассона на фоне белого гауссова шума (при λ=0.15)

k	0.85	0.8	0.75	0.7	0.65	0.6	0.55	0.5
η_вх, дБ	–3.4	–2.6	–1.2	0.1	1.3	2.4	3.6	4.7
G_Min3Mom,дБ	49.9	49.2	47.9	46.8	45.6	44.5	43.4	42.3
G_FastICA,дБ	40.1	38.7	36.8	35.0	32.9	30.7	–	–

Таблица 2

Зависимости выигрыша G от отношения сигнал-помеха на входе при разных алгоритмах слепого выделения процесса Пуассона на фоне белого гауссова шума (при k=0.7)

λ	0.15	1	6	10
G_Min3Mom,дБ	46.8	42.0	35.2	30.3
G_FastICA,дБ	35.0	–	–	–

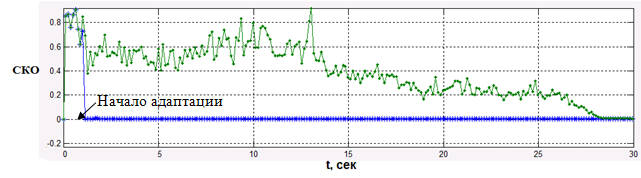
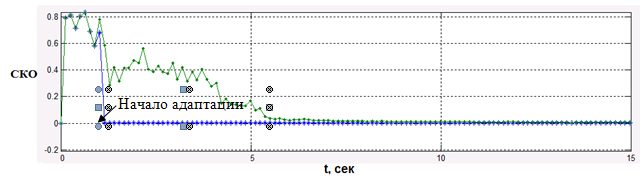
Рис. 11. Средний квадрат ошибки воспроизведения процесса Пуассона,
полученный алгоритмом FastICA (зеленая линия) и Min3Mom (синяя линия) при k=0.57 и λ=0.15

Рис. 12. Средний квадрат ошибки воспроизведения процесса Пуассона,
полученный алгоритмом FastICA (зеленая линия) и Min3Mom (синяя линия) при k=0.6 и λ=0.15

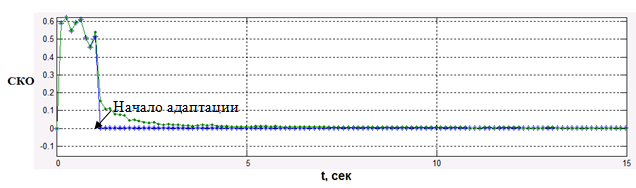
Рис. 13. Средний квадрат ошибки воспроизведения процесса Пуассона,
полученный алгоритмом FastICA (зеленая линия) и Min3Mom (синяя линия) при k=0.7 и λ=0.15

Анализируя изменение среднего квадрата ошибки воспроизведения процесса Пуассона (см. рис. 11, 12, 13), можно оценить выигрыш в скорости сходимости алгоритма Min3Mom, который составляет от 5 до 27 раз. Сходимость алгоритма Min3Mom практически мгновенная (менее 0.1 с) и не зависит от изменяемых параметров (k и λ), в то же время сходимость алгоритма FastICA зависит от длины линии нулевого уровня функции (9), проходящей от точки начальных условий до точки оптимального решения — чем она меньше, тем быстрее сходимость. Необходимо отметить, что нормировка весовых коэффициентов w₁ в алгоритме FastICA (аналогичная в алгоритме Min3Mom) эквивалентна проекции вектора на единичную сферу [11], поэтому градиент вектора проходит по касательной этой сферы в направлении оптимального решения.

Например, при k=0.7 точка оптимального решения находится примерно в центре дуги линии нулевого уровня, соединяющей точки (1,0) и (0,1); при уменьшении k оптимальная точка отдаляется по дуге окружности от начальных условий (0,1), что приводит к снижению скорости сходимости.

Данная особенность подтверждена результатами эксперимента, отраженными в таблице 1. При уменьшении k происходит снижение выигрыша G при использовании алгоритмов Min3Mom и FastICA. Алгоритм FastICA при значениях k менее 0.6 вообще перестает выделять сигнал из-за недостаточной выпуклости градиента функционала (14) и большей отдаленности оптимального решения от начальных условий. В то же время, алгоритм Min3Mom сохраняет свою работоспособность.

Кроме того, анализ результатов в таблице 2 дает основание полагать, что с увеличением интенсивности процесса Пуассона до единичного значения и более алгоритм Min3Mom продолжает выделять импульсы, тогда как алгоритм FastICA вообще перестает функционировать.

Вывод

Если импульсный случайный процесс асимметричен, то применение алгоритма слепого выделения на основе максимизации момента 3 порядка гораздо более эффективно, нежели алгоритма на основе максимизации эксцесса. Эффективность в данном случае определяется более высокой скоростью сходимости, а также сохранением работоспособности в широком диапазоне изменения соотношений среднеквадратического отклонения случайных процессов и при больших (более единицы) значениях интенсивности импульсного процесса.

Литература

1. A.Cichoki and S.Amari, Adaptive Blind Signal and Image Processing: Learning Algorithms and Applications, John Wiley & Sons, 2002.

2. A. Cichocki, R. Thawonmas, and S. Amari, “Sequential blind signal extraction in order specified by stochastic properties” Electron. Lett., vol. 33, № 1, pp. 64–65, Jan. 1997.

3. Zhi-Lin Zhang, Zhang Yi, Extraction of a Source Signal Whose Kurtosis Value Lies in a Specific Range, Neurocomputing, vol. 69, № 7–9, pp. 894–899, 2006.

4. Zhi-Lin Zhang, Zhang Yi, Robust Extraction of Specific Signals with Temporal Structure, Neurocomputing, vol. 69, № 7-9, pp. 888–893, 2006.

5. S. Amari, “ICA of temporally correlated signals - learning algorithm,” in Proceedings of ICA’99: International workshop on blind signal separation and independent component analysis, Aussois, France, Jan. 1999. pp. 13–18.

6. K. Matsuoka, M. Ohya, and M. Kawamoto. A neural net for blind separation of nonstationary signals. Neural Networks, 8(3) : 411–419, 1995.

7. S. Amari. Natural gradient works efficiently in learning. Neural Computation, № 10 : pp. 271–276, 1998.

8. Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры : учеб. Для вузов. – 10-е изд., испр. – ФИЗМАТЛИТ, 2005. – 304 с.

9. L. Tong, V.C. Soon, Y.F. Huang, and R. Liu. AMUSE: a new blind identification algorithm. In Proc. IEEE ISCAS, pp. 1784–1787 vol.3, New Orleans, LA, 1990.

10. S. Choi and A. Cichocki. Blind separation of nonstationary and temporally correlated sources from noisy mixtures. In IEEE Workshop on Neural Networks for Signal Processing, NNSP’2000, pp. 405–414, Sydney, Australia, December 11–13 2000.

11. Hyvarinen, A., Karhunen, J. and Oja, E. Independent component analysis. New York: J. Wiley, 2001.

12. R. Thawonmas, A. Cichocki, and S. Amari. A Cascade neural network for blind signal extraction without spurious equilibria. IEICE Trans. on Fundamentals of Electronics, Communications and Computer Sciences, E81-A(9) : 1833–1846, 1998.

13. S.C. Douglas and S.Y. Kung. Kuicnet algorithms for blind deconvolution. In Proc. IEEE Workshop on Neural Networks for Signal Processing, pp. 3–12, Cambridge, UK, August 1998.

14. Zhi-Lin Zhang, Liqing Zhang. A Two-Stage Based Approach for Extracting Periodic Signals // Independent Component Analysis and Blind Signal Separation, 6th International Conference, ICA 2006, Charleston, SC, USA, March 5–8, 2006, Proceedings. Lecture Notes in Computer Science 3889, Springer 2006, pp. 303-310.

15. Patrik Paajarvi and James P. LeBlanc. Skewness Maximization for Impulsive Sources in Blind Deconvolution // Proceedings of the 6th Nordic Signal Processing Symposium - NORSIG 2004, June 9–11, 2004, Espoo, Finland.

16. Зангвилл У. Нелинейное программирование. Единый подход. 1969 г. Пер. с англ., под ред. Е.Г. Гольштейна, М. : Советское радио, 1973, 312 с.

17. Математический анализ : дифференцирование и интегрирование / И. Г. Араманович [и др.] под общ. ред. : Л. А. Люстерник, А. Р. Янпольский. – М. : Физматгиз, 1961. – 351 с. : ил.

18. Мицель А.А. Методы оптимизации : учебное пособие / А.А. Мицель, А.А. Шелестов. – Томск : ТУСУР, 2004. – 255с.

19. Норенков И.П. Экстремальные задачи при схемотехническом проектировании в электронике / И.П. Норенков, С.Г. Мулярчик, С.Р. Иванов. – Минск : Изд-во БГУ, 1976. – 239 с. : ил.

20. Шарый С.П. Курс вычислительных методов. – Новосибирск : Институт вычислительных технологий СО РАН, 2013. – 497 с.

21. Hyvarinen A., Oja. E. A fast fixed-point algorithm for independent component analysis, Neural Computation., 9, pp. 1483–1492, 1997.

[1] Natural Gradient Algorithm (англ.)

[2] EigenValue Decomposition (англ.)

[3] Generalized EigenValue Decomposition (англ.)