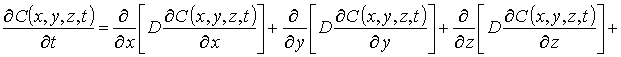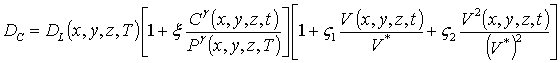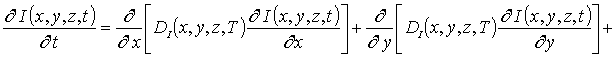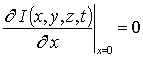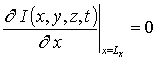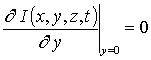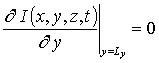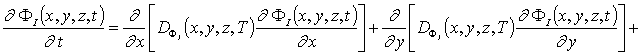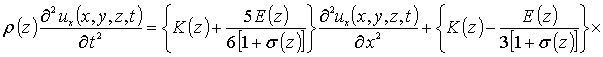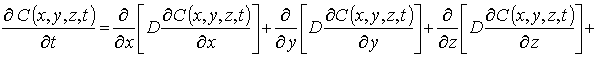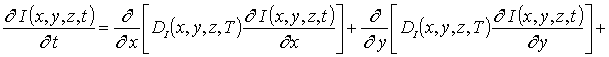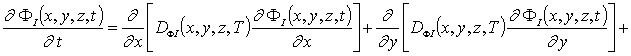Влияние заращивания диффузионно и ионно легированных областей гетероструктуры на распределения в ней концентраций примесей
Е. Л. Панкратов1, Е. А. Булаева1,2
1Нижегородский государственный университет им. Н.И. Лобачевского
2Нижегородский государственный архитектурно-строительный университет
Статья поступила в редакцию 16 апреля 2016 г.
Аннотация. В данной работе рассматривается влияние заращивания диффузионно и ионно легированных областей гетероструктуры на распределения концентраций примесей в ней. Определяются условия увеличения резкости формируемых в данном технологическом процессе p-n-переходов (одиночных и в составе биполярных транзисторов). Одновременно исследуется влияние скорости заращивания областей и механических напряжений в рассматриваемой гетероструктуре на распределения концентраций примесей в ней.
Ключевые слова: p-n-гетеропереходы; механические напряжения; заращивание.
Abstract. In this paper we consider influence of overgrowth of doped by diffusion and ion implantation areas of heterostructures on distributions of concentrations of dopants. Several conditions to increase sharpness of p-n-junctions (single and framework bipolar transistors), which were manufactured during considered technological process, have been determined. At the same time we analyzed influence of speed of overgrowth of doped areas and mechanical stress in the considered heterostructure on distribution of concentrations of dopants in the structure.
Keywords: p-n-heterojunctions; mechanical stress; overgrowth.
Введение
В настоящее время ведутся интенсивные работы по увеличению степени интеграции элементов интегральных схем, уменьшения размеров данных элементов, а также улучшения их параметров [1-10]. Для решения данных целей разработаны и используются различные методы [1-10]. В рамках данной работы рассматривается двухслойная структура, состоящая из подложки с известным типом проводимости (n или p) и эпитаксиального слоя. Эпитаксиальный слой легируется с помощью диффузии или ионной имплантации с целью формирования в нем противоположного типа проводимости (p или n). Далее проводится заращивание эпитаксиального слоя покровным слоем с типом проводимости, совпадающим с типом проводимости подложки (см. рис. 1). Основной целью данной работы является анализ влияния заращивания эпитаксиального слоя на распределения примесей в рассматриваемой гетероструктуре.
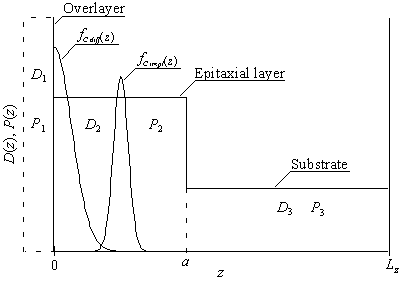
Рис. 1. Гетероструктура, состоящая из подложки, легируемого эпитаксиального слоя и покровного слоя
Методика анализа
Для решения поставленной цели определим пространственно-временное распределение примеси в рассматриваемой гетероструктуре и проведем его анализ. Пространственно- временное распределение концентрации примеси определим путем решения следующей краевой задачи [1,11-13]
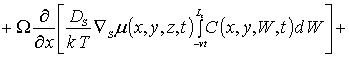 (1)
(1)
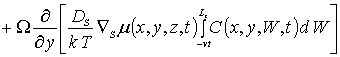
с граничными и начальным условиями
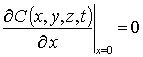 ,
, 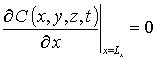 ,
, 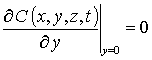 ,
, 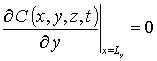 ,
,
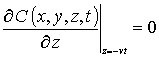 ,
, 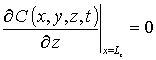 , C (x,y,z,0)=fC (x,y,z).
, C (x,y,z,0)=fC (x,y,z).
В данных соотношениях введены
следующие обозначения: C(x,y,z,t) - пространственно -временное
распределение концентрации примеси; W - атомный вес примеси; символ ![]() обозначает поверхностный градиент;
обозначает поверхностный градиент; ![]() - поверхностная концентрация примеси на границе раздела между слоями (в данном случае считалось, что ось Oz
перпендикулярна границе раздела между слоями гетероструктуры); m (x,y,z,t) - химический потенциал, обусловленный наличием
механических напряжений в гетероструктуру; D и DS – коэффициенты объемной и поверхностной (обусловленной
механическими напряжениями) диффузий, величина которых зависит от свойств
материалов слоев гетероструктуре, скорости прогрева и охлаждения гетероструктуре, а также от пространственно-временных
распределений концентраций примеси и радиационных дефектов. Зависимости коэффициентов диффузии от параметров могут быть аппроксимированы следующими соотношениями [13,14]
- поверхностная концентрация примеси на границе раздела между слоями (в данном случае считалось, что ось Oz
перпендикулярна границе раздела между слоями гетероструктуры); m (x,y,z,t) - химический потенциал, обусловленный наличием
механических напряжений в гетероструктуру; D и DS – коэффициенты объемной и поверхностной (обусловленной
механическими напряжениями) диффузий, величина которых зависит от свойств
материалов слоев гетероструктуре, скорости прогрева и охлаждения гетероструктуре, а также от пространственно-временных
распределений концентраций примеси и радиационных дефектов. Зависимости коэффициентов диффузии от параметров могут быть аппроксимированы следующими соотношениями [13,14]
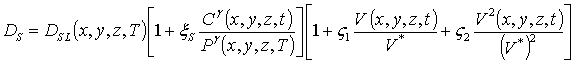 . (2)
. (2)
В данных соотношениях DL (x,y,z,T) и DLS (x,y,z,T) - пространственные (за счет многослойности гетероструктуре) и температурные (в соответствии с законом Аррениуса) зависимости коэффициентов диффузии; T - температура отжига; P (x,y,z,T) - предел растворимости примеси; определяемый свойствами материала параметр g может принимать целые значения в интервале g Î[1,3] [14]; V (x,y,z,t) - пространственно-временное распределение концентрации радиационных вакансий; V* - равновесное распределение концентрации вакансий. Концентрационная зависимость коэффициентов диффузии подробно обсуждается в [14]. Пространственно -временные распределения концентраций радиационных дефектов определим с помощью следующей системы уравнений [1,11-13]
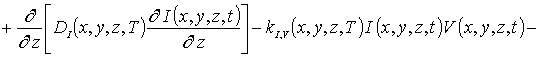
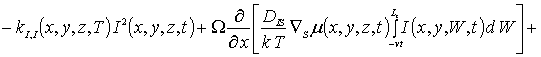
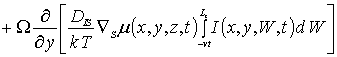 (3)
(3)
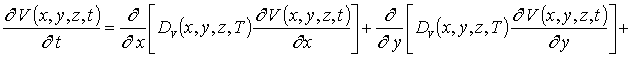
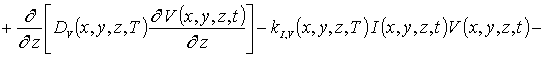
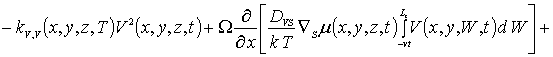
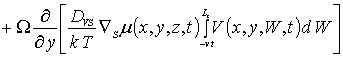
с граничными и начальными условиями
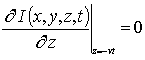 ,
, 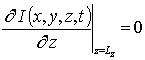 ,
, 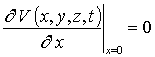 ,
, 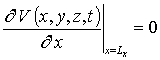 ,
,
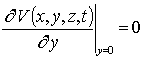 ,
, 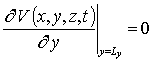 ,
, 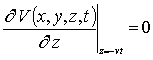 ,
, 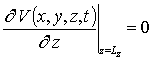 ,
,
I (x,y,z,0)=fI (x,y,z), V (x,y,z,0)=fV (x,y,z). (4)
В соотношениях (3) и (4) I (x,y,z,t) - пространственно-временное распределение концентрации междоузельных атомов; I* - равновесное распределение концентрации междоузельных атомов; DI(x,y,z,T), DV(x,y,z,T), DIS(x,y,z,T), DVS(x,y,z,T) - коэффициенты объемной и поверхностной диффузий междоузельных атомов и вакансий; слагаемые V2(x,y,z,t) и I2(x,y,z,t) соответствуют образованию дивакансий и аналогичных комплексов междоузельных атомов (см., например, [13] и соответствующие ссылки в данной работе); kI,V(x,y,z,T), kI,I(x,y,z,T) и kV,V(x,y,z,T) – соответственно, параметры рекомбинации точечных дефектов и образования комплексов, k – постоянная Больцмана.
Пространственно-временные распределения концентраций дивакансий FV (x, y,z,t) и аналогичных комплексов междоузельных атомов FI (x,y,z,t) определим с помощью следующей системы уравнений [11-13]
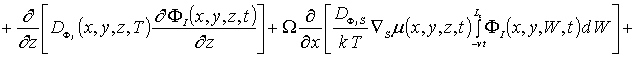
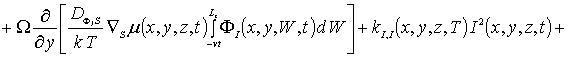
![]() (5)
(5)

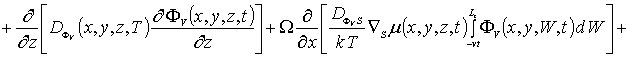
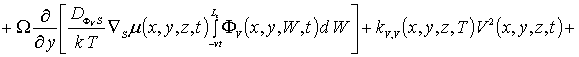
![]()
с граничными и начальными условиями
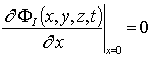 ,
, 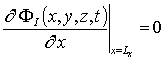 ,
, 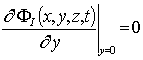 ,
, 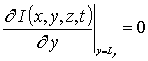 ,
,
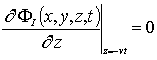 ,
, 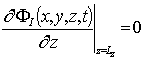 ,
, 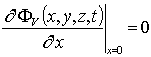 ,
, 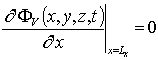 ,
,
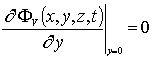 ,
, 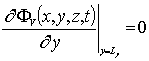 ,
, 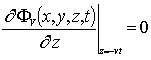 ,
, 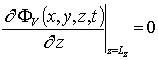 ,
,
FI (x,y,z,0)=fFI (x,y,z), FV (x,y,z,0)=fFV (x,y,z). (6)
В последних соотношениях введены следующие обозначения: DFI(x,y,z,T), DFV(x,y,z,T), DFIS (x,y,z,T) и DFVS(x,y,z,T) - коэффициенты объемной и поверхностной диффузий комплексов точечных дефектов; kI(x,y,z,T) и kV(x,y,z,T) - параметры распада комплексов точечных дефектов.
Химический потенциал m в уравнении (1) может быть определен с помощью следующего соотношения [11]
m =E(z)Wsij [uij(x,y,z,t)+uji(x,y,z,t)]/2, (7)
где E - модуль растяжения (Юнга); sij - тензор напряжений; 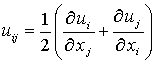 - тензор деформаций; ui, uj - компоненты ux(x,y,z,t), uy(x,y,z,t)
и uz(x,y,z,t) вектора смещений
- тензор деформаций; ui, uj - компоненты ux(x,y,z,t), uy(x,y,z,t)
и uz(x,y,z,t) вектора смещений ![]() ; xi, xj - координаты x, y, z.
Соотношение (3) может быть преобразовано к следующему виду
; xi, xj - координаты x, y, z.
Соотношение (3) может быть преобразовано к следующему виду
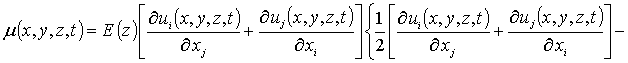
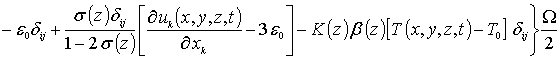 ,
,
где s - коэффициент Пуассона; e0=(as-aEL)/aEL - параметр несоответствия решетки; as, aEL - постоянные решеток подложки и эпитаксиального слоя; K - модуль всестороннего сжатия; b - коэффициент теплового расширения; Tr - совпадающая с комнатной равновесная температура. Компоненты вектора смещений могут быть определены с помощью следующей системы уравнений [15]
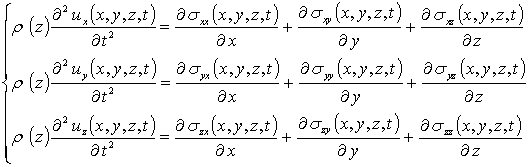
где
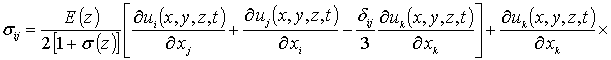
![]() , r (z)
- плотность материалов гетероструктуры, dij - символ Кронекера.
, r (z)
- плотность материалов гетероструктуры, dij - символ Кронекера.
С учетом такого соотношения данная система уравнений имеет вид
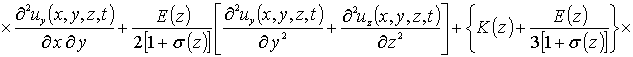
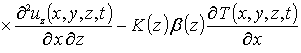
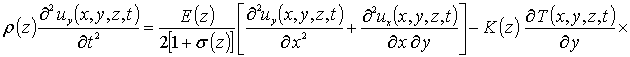
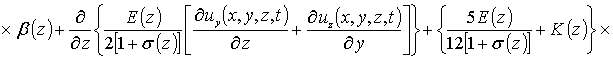
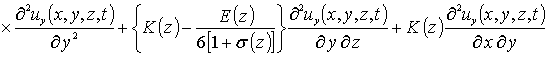 (8)
(8)
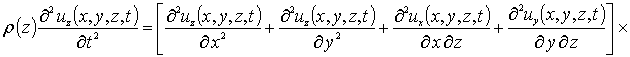
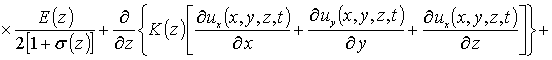
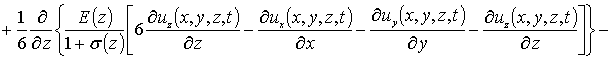
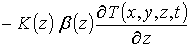 .
.
Система условий для данных уравнений представима в следующей форме
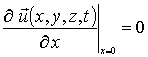 ;
; 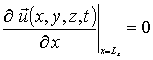 ;
; 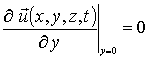 ;
; 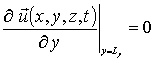 ;
;
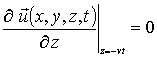 ;
; 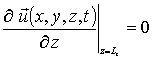 ;
; ![]() ;
; ![]() .
.
Пространственно-временное распределение концентрации примеси определим с помощью метода осреднения функциональных поправок [16-22]. Для применения данного метода запишем уравнения (1), (3) и (5) с учетом начальных распределений рассматриваемых концентраций, т.е.
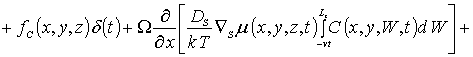
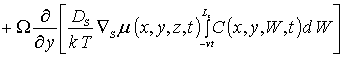
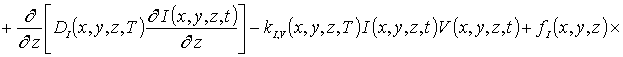
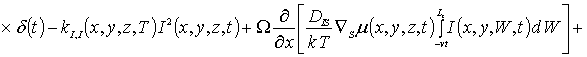
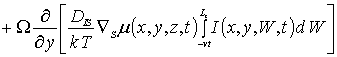 (3а)
(3а)
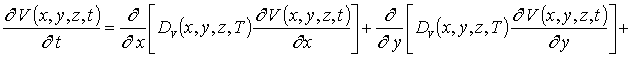
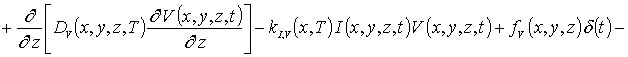
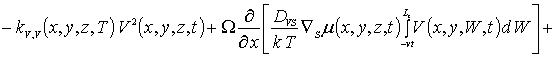
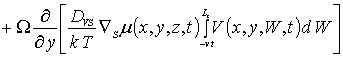
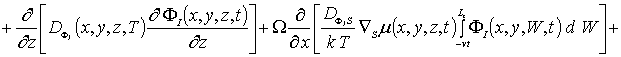
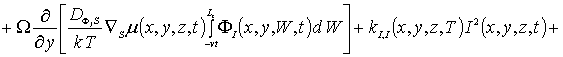
![]() (5а)
(5а)
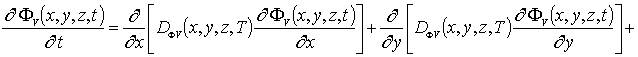
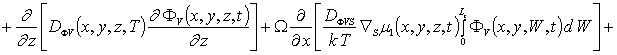
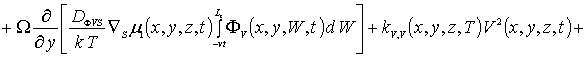
![]() .
.
Далее заменим искомые функции в правых частях уравнений (1а), (3а) и (5а) на их пока неизвестные значения a1r. В результате получим уравнения для первых приближений искомых концентраций в следующей форме
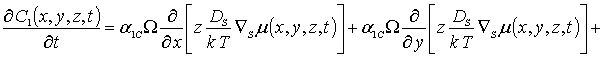
![]() (1б)
(1б)
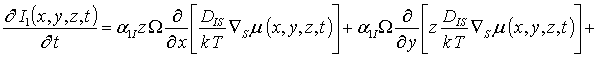
![]() (3б)
(3б)
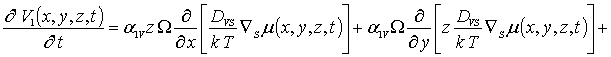
![]()
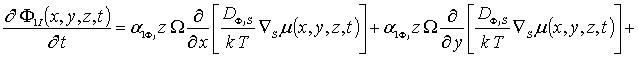
![]() (5б)
(5б)
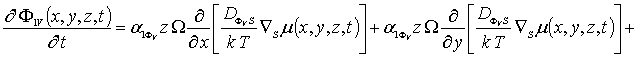
![]() .
.
Интегрирование левых и правых частей уравнений (1б), (3б) и (5б) позволяет получить соотношения для первых приближений искомых концентраций в окончательной форме
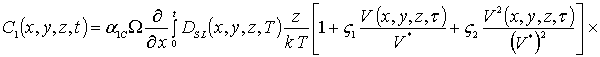
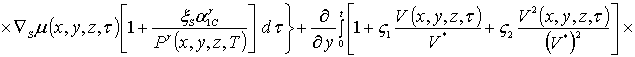
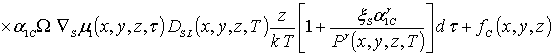 (1в)
(1в)
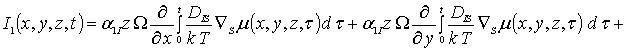
![]() (3в)
(3в)
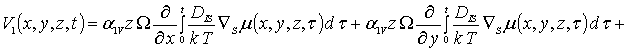
![]()
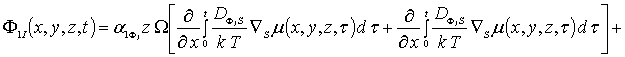
![]() (5в)
(5в)
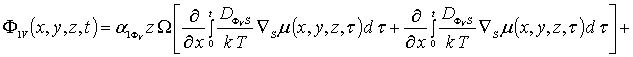
![]() .
.
Средние значение первых приближений искомых функций определим с помощью стандартного соотношения [16-22]
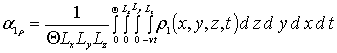 . (9)
. (9)
Подстановка соотношений (1в), (3в) и (5в) в соотношение (9) позволяет получить искомые средние значения в следующей форме
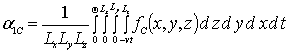 ,
, 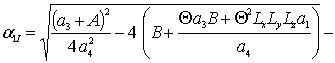
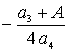 ,
, 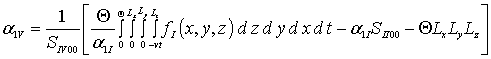 ,
,
где ![]() ,
, ![]()
![]() ,
, ![]() ,
, ![]()
![]()
![]() ,
, ![]() ,
,
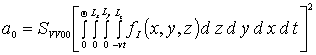 ,
, 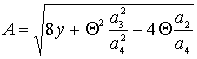 ,
, 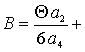
![]() ,
, 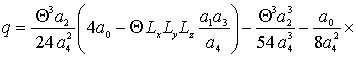
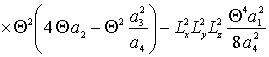 ,
, 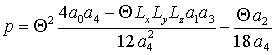 ,
,
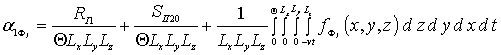
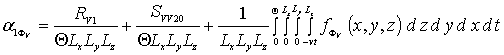 ,
,
где ![]() .
.
Приближения второго и более высокого порядков концентраций примеси и радиационных дефектов определим в рамках стандартной итерационной процедуры метода осреднения функциональных поправок [16-22]. В рамках данной процедуры для нахождения приближения n-го порядка концентраций примеси и радиационных дефектов заменим в правых частях уравнений (1а), (3а), (5а) искомые распределения концентраций C(x,y,z,t), I(x,y,z,t), V(x,y,z,t), FI(x,y, z,t) и FV(x,y,z,t) на сумму среднего значения n-го приближения и n-1-го приближения данных функций, т.е. на сумму anr+r n-1(x,y,z,t). После такой замены получаем соотношения для вторых приближений искомых концентраций
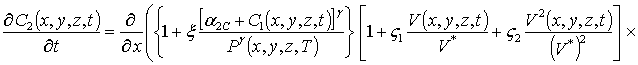
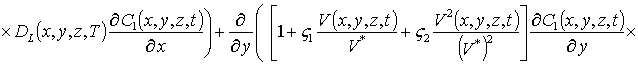
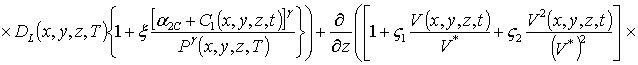
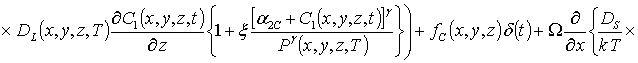
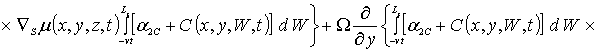
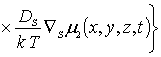 (1г)
(1г)
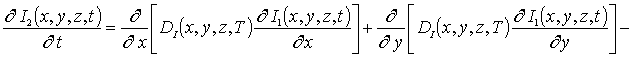
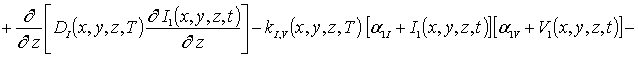
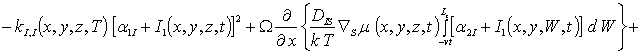
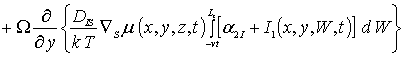 (3г)
(3г)
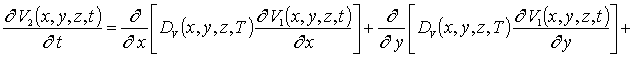
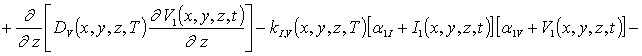
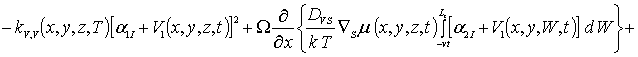
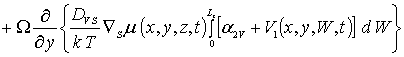
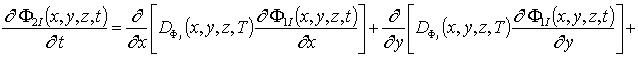
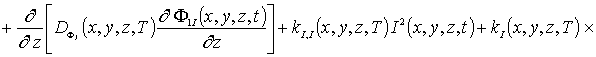
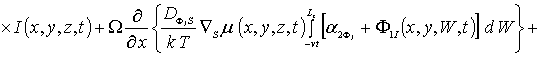
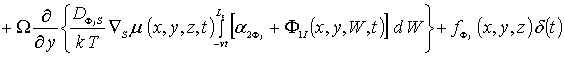 (5г)
(5г)
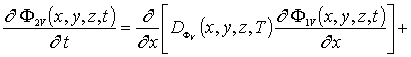
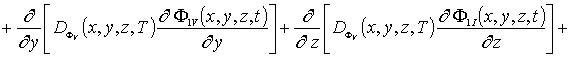
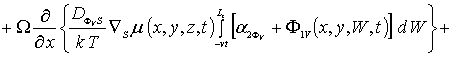
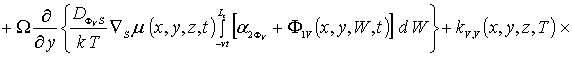
![]() .
.
Интегрирование левой и правой части уравнений (1г), (3г) и (5г) позволяет получить соотношения для второго приближения искомых концентраций примеси и радиационных дефектов в следующей форме
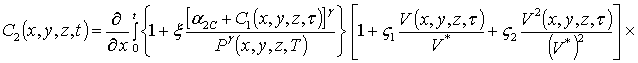
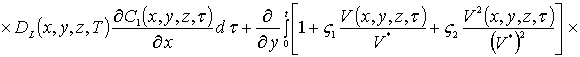
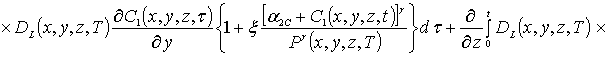
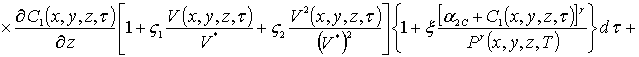
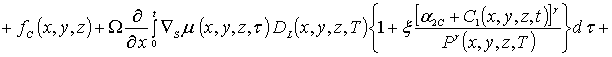
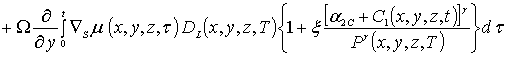 (1д)
(1д)
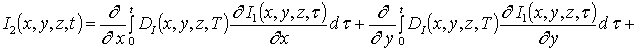
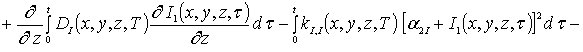
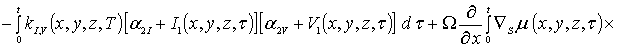
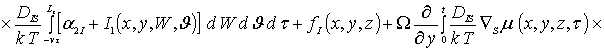
![]() (3д)
(3д)
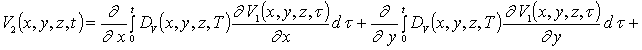
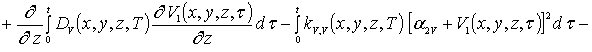
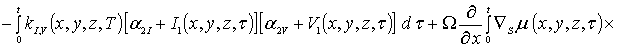
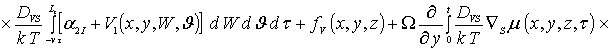
![]()
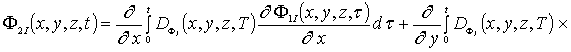
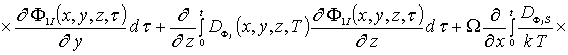
![]()
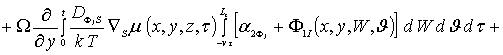
![]() (5д)
(5д)
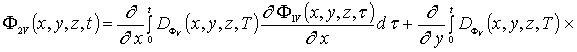
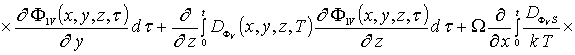
![]()
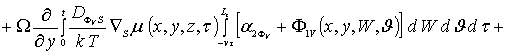
![]() .
.
Средние значение вторых приближений искомых функций определим с помощью стандартного соотношения [16-22]
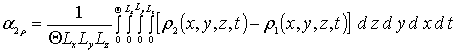 . (10)
. (10)
Подстановка соотношений (1д), (3д), (5д) в соотношение (10) позволяет получить соотношения для искомых величин a 2r
a2C=0, a2FI =0, a2FV =0, 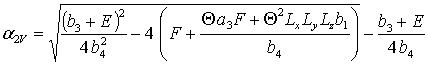 ,
,
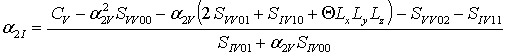 ,
,
где 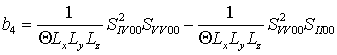 ,
, ![]()
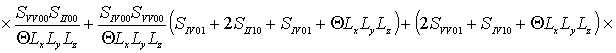
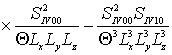 ,
, 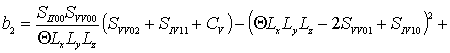
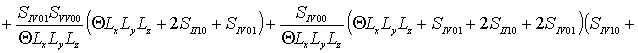
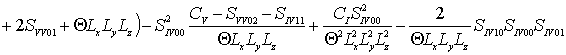 ,
, ![]()
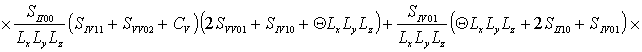
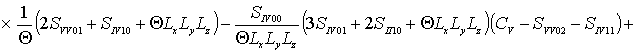
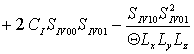 ,
, 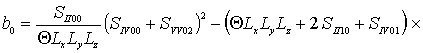
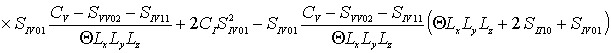 ,
,
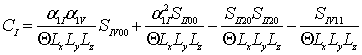 ,
, ![]()
![]() ,
, 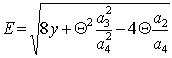 ,
, 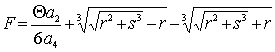 ,
, 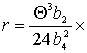
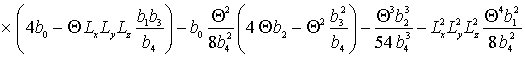 ,
, 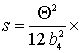
![]() .
.
Далее определим решения уравнений системы (8), решения которых являются компонентами вектора смещений. Для определения первых приближений искомых компонент в рамках метода осреднения функциональных поправок подставим в правую часть рассматриваемых уравнений пока неизвестные средние значения a1i. Такая подстановка приводит к следующему результату
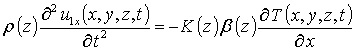 ,
, 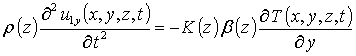 ,
,
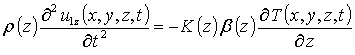 .
.
Интегрирование правых и левых частей полученных соотношений по времени t приводит к следующему результату
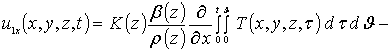
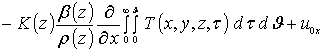 ,
,
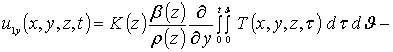
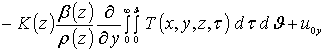 ,
,
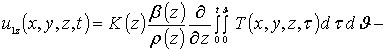
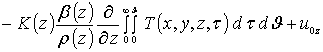 .
.
Приближения второго и более высоких порядков компонент вектора смещений определяются с помощью стандартной замены искомых функций в правой части уравнений (8) на следующую сумму a1i+ui(x,y,z,t) [19]. Такая замена приводит к следующему результату
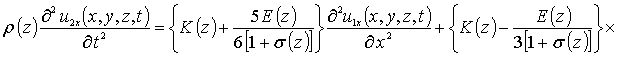
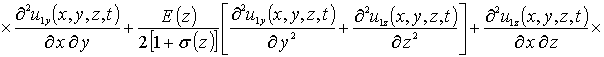
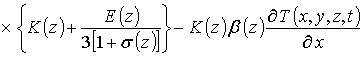
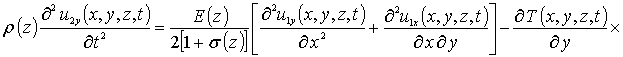
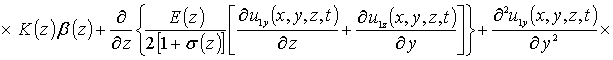
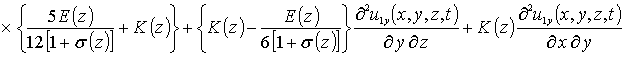
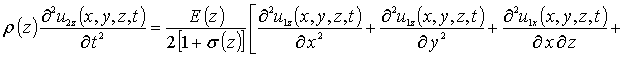
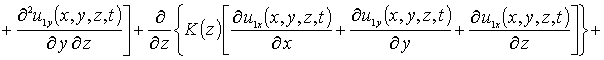
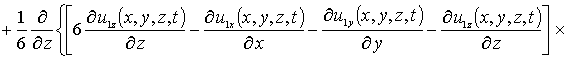
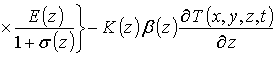 .
.
Интегрирование правых и левых частей полученных соотношений по времени t приводит к следующему результату
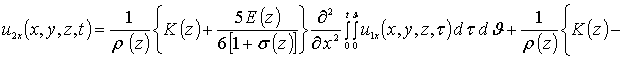
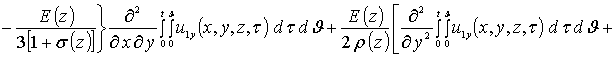
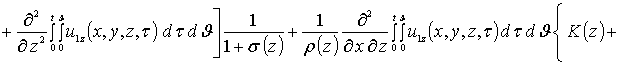
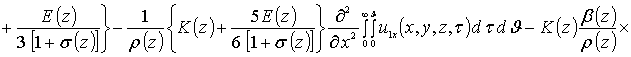
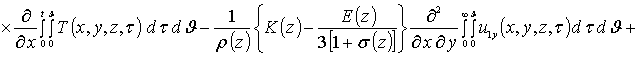
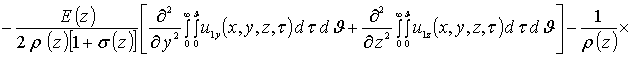
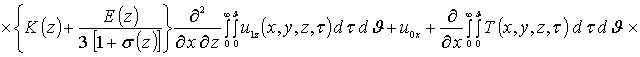
![]()
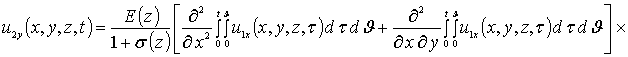
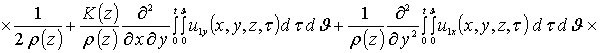
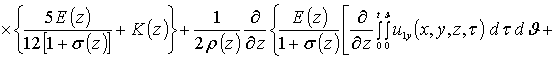
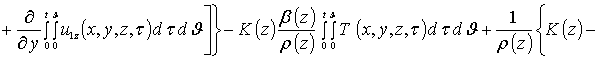
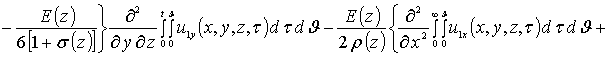
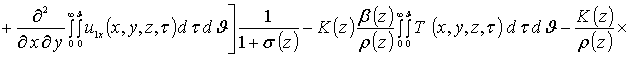
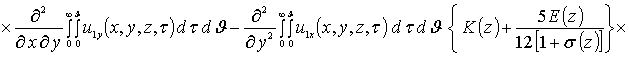
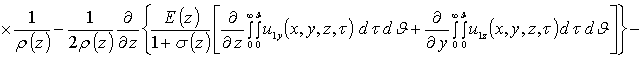
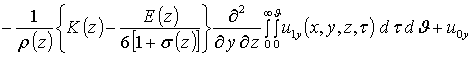
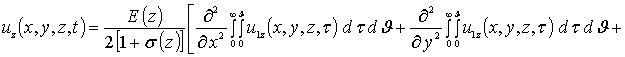
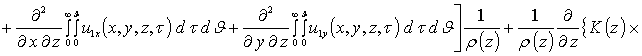
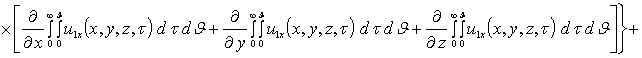
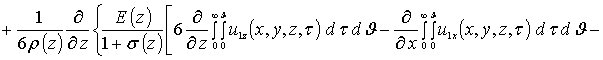
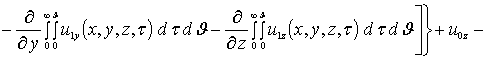
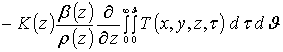 .
.
В рамках данной работы искомые концентрации примеси и радиационных дефектов, а также компонент вектора смещения определены во втором приближении по методу осреднения функциональных поправок. Данного приближения обычно достаточно для получения качественных выводов и получения некоторых количественных результатов. Результаты аналитических расчетов проверялись путем их сопоставления с результатами численного моделирования.
Результаты анализа
В данном разделе проведем анализ перераспределения примеси (в случае ионного легирования рассматриваемой гетероструктуры) с учетом перераспределения и взаимодействия между собой радиационных дефектов. В случае, когда скорость роста покровного слоя мала (v t<D1/ v) он будет полностью легирован примесью, введенной в эпитаксиальный слой. В противном случае будет легирована только приповерхностная область покровного слоя. Если коэффициент диффузии покровного слоя и подложки имеют меньшее значение, чем в эпитаксиальном слое, а их тип проводимости противоположен типу проводимости эпитаксиального слоя, тогда формируется биполярный транзистор с более резкими p-n-переходами (по сравнению с однородным материалом с усредненным коэффициентом диффузии) и более равномерным распределением концентрации примеси в обогащенной ею области (см. рис. 2 для ионного легирования).
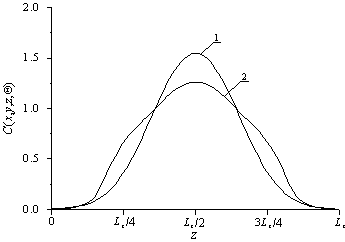
Рис. 2. Расчетные пространственные распределения
концентрации имплантированной примеси в однородном материале (кривая 1)
и представленной
на рис. 1 трехслойной структуре (кривая 2) после отжига с одинаковой
длительностью.
Границы раздела между слоями имеет координаты a1=Lz/4 и a2=3Lz/4
Качественно близкие распределения концентрации примеси возникают и при диффузионном легировании. Если коэффициент диффузии примеси покровного слоя больше, чем у легированного эпитаксиального слоя, левый p-n-переход становится более плавным с увеличением равномерности распределения концентрации примеси в покровном слое (см. рис. 3).
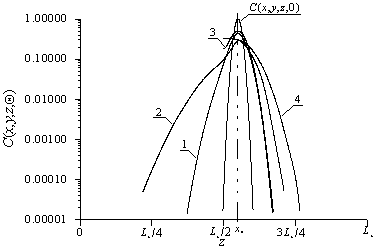
Рис.3. Расчетные пространственное распределение
концентрации имплантированной примеси
в покровном и эпитаксиальном слоях (кривые
1 и 2) и только в эпитаксиальном слое (кривые 3 и 4).
Увеличение номера кривой
соответствуют увеличению отношения D1/D2.
Границы раздела между слоями имеет координаты a1=Lz/4 и a2=3Lz/4
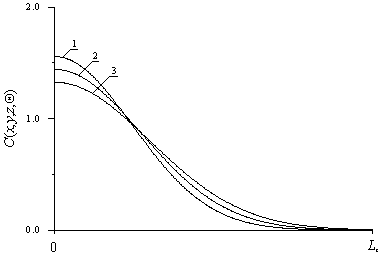
Рис. 4. Пространственные распределения концентрации примеси
в диффузионном p-n-переходе
после отжига с одинаковой
длительностью.
Кривая 1 соответствует e0<0.
Кривая 2 соответствует e0=0. Кривая 3 соответствует e0>0
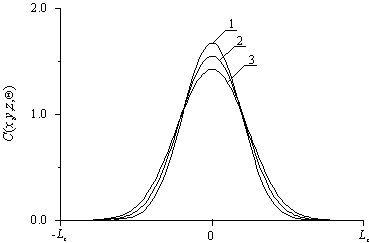
Рис. 5. Пространственные распределения концентрации
примеси в имплантационном p-n-переходе
после отжига с одинаковой
длительностью.
Кривая 1 соответствует e0<0.
Кривая 2 соответствует e0=0. Кривая 3 соответствует e0>0
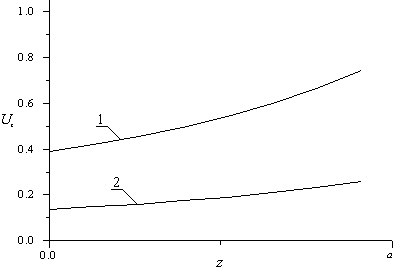
Рис.6. Нормированные зависимости компоненты вектора
смещений uz от координаты z
для эпитаксиальных слоев
до радиационной обработки (кривая 1)
и после радиационной обработки (кривая 2)
Далее проведем анализ влияния механических напряжений на распределения примесей. В результате проведенного анализа получено, что при условии формирования p-n-перехода в окрестности границы раздела между слоями гетероструктуры происходит увеличение резкости p-n- перехода и увеличение равномерности распределения примеси в обогащенной ею области. В направлениях, параллельных границе раздела, также происходит изменение формы распределения примеси, вызванное механическими напряжениями структуры. Например, при e0<0 распределение примеси в направлениях x и y становится более компактным (см. рис. 4). При e0>0 достигается противоположный эффект (см. рис. 5). Следует также заметить, что радиационная обработка материалов гетероструктуры при ионном легировании позволяет уменьшить величину механических напряжений (см. рис. 6).
Заключение
В данной работе исследовано влияние заращивания диффузионно и ионно легированных областей гетероструктуры на распределения концентраций примесей в ней. Определены условия увеличения резкости формируемых в данном технологическом процессе p-n-переходов (одиночных и в составе биполярных транзисторов). Одновременно исследовано влияние скорости заращивания областей и механических напряжений в рассматриваемой гетероструктуре на распределения концентраций примесей в ней.
Работа выполнена при поддержке соглашения между Министерством Образования и Науки РФ и Нижегородского госуниверситета от 27 августа 2013 г. № 02.В.49.21.0003, стипендиями правительств РФ и Министерством Образования и Науки Нижегородской области, а также Нижегородского архитектурно- строительного университета.
Литература
[1] В.И. Лачин, Н.С. Савелов. Электроника. Ростов-на-Дону: Феникс, 2001.
[2] D. Fathi, B. Forouzandeh. Nano. Vol. 4 (3). P. 171-176 (2009).
[3] D. Fathi, B. Forouzandeh, N. Masoumi. Nano. Vol. 4 (4). P. 233-238 (2009).
[4] S.A. Chachuli, P.N.A. Fasyar, N. Soin, N.M. Karim, N. Yusop. Mat. Sci. Sem. Proc. Vol. 24. P. 9-14 (2014).
[5] Jung-Hui Tsai, Shao-Yen Chiu, Wen-Shiung Lour, Der-Feng Guo. ФТП. Т. 43 (7). С. 971-974 (2009).
[6] J.Y. Choi, Ch. Park. Circuits and Systems. Vol. 2 (3). P. 170-182 (2011).
[7] M.J. Kumar, T.V. Singh. Int. J. Nanoscience. Vol. 7 (2-3). P. 81-84 (2008).
[8] P. Sinsermsuksakul, K. Hartman, S.B. Kim, J. Heo, L. Sun, H.H. Park, R. Chakraborty, T. Buonassisi, R.G. Gordon. Appl. Phys. Lett. Vol. 102 (5). P. 053901-053905 (2013).
[9] R. Laajimi, M. Masmoudi. Circuits and Systems. Vol. 3 (4). P. 311-316 (2012).
[10] A. Ghorbani, A. Ghanaatian. Circuits and Systems. Vol. 3 (3). P. 263-268 (2012).
[11] Y.W. Zhang, A.F. Bower. Journal of the Mechanics and Physics of Solids. Vol. 47 (11). P. 2273-2297 (1999).
[12] P.M. Fahey, P.B. Griffin, J.D. Plummer. Rev. Mod. Phys. Vol. 61. № 2. P. 289-388 (1989).
[13] V.L. Vinetskiy, G.A. Kholodar', Radiative physics of semiconductors. ("Naukova Dumka", Kiev, 1979, in Russian).
[14] З.Ю. Готра. Технология микроэлектронных устройств. - М.: Радио и связь. 1991. 528с.
[15] Л.Д. Ландау, Е.М. Лифшиц. Теоретическая физика. Т. 7 (Теория упругости). М.: ФИЗМАТЛИТ, 2001.
[16] Ю.Д. Соколов. Прикладная Механика. Т.1 (1). С. 23-35 (1955).
[17] E.L. Pankratov, E.A. Bulaeva. Reviews in Theoretical Science. Vol. 1 (1). P. 58-82 (2013).
[19] E.L. Pankratov, E.A. Bulaeva. Int. J. Nanoscience. Vol. 11 (5). P. 1250028-1-1250028-8 (2012).
[20] E.L. Pankratov, E.A. Bulaeva. J. Comp. Theor. Nanoscience. Vol. 10 (4). P. 888-893 (2013).
[21] E.L. Pankratov, E.A. Bulaeva. Int. J. Micro-Nano Scale Transp. Vol. 4 (1). P. 17-31 (2014).
[22] E.L. Pankratov, E.A. Bulaeva. J. Comp. Theor. Nanoscience. Vol. 11 (1). P. 91-101 (2014).