"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 11, 2000

contents

discussion

SMART ANTENNA BASE STATION BEAMFORMER FOR MOBILE COMMUNICATIONS

 V. Zaharov, F. Casco, O. Amin

 Departamento de Ingeniería Eléctrica,
Universidad Autónoma  Metropolitana - Iztapalapa
México D.F., México

Received November 13, 2000

A novel RLS beamforming algorithm with low complexity and high accuracy for applying in mobile communications smart antenna array processor is presented. The proposed pipelined structure has a higher performing that conventional RLS algorithm because require only  vector operation and can be easy implemented en VLSI. As result proposed pipelined architecture can operate en N/k times faster than conventional RLS structure, where N and k are numbers of antenna elements and training samples respectively, and more, this algorithm have a minimum variance problem in finite precision implementation because one use  the Householder transform procedure of weight vector updating. 

1. INTRODUCTION

The technology of smart antennas for mobile communications systems has received widely interest in the last couple of years [1],[2],[3]. The principle reason for applying smart antennas is the possibility for a large increase in capacity due to control and reduce interferences. This is accomplish through the use of narrow beams at the base site and as result  the users separations at the space.

A smart antenna combines antenna array with digital signal processing unit that optimize reception and radiation patterns dynamically in response to the signal environment, e.i. mobile moving about the coverage area. It is obvious that a smart antenna base station system is much more complex that traditional omnidirectional one because must include  very powerful numeric processors and beamforming control systems.

In acordens with  [4] digital  processor is structured in four main sections

1.      Direction of arrival (DOA) estimation. From the received input data in uplink the number of incoming wavefronts and their DOAs is estimated.

2.      DOA classification. In a next step are identified those wavefronts that are originated from the user: First, the spatially resolved wavefronts, each incident from an estimated DOA  extract from the input data, with a spatial pre-filter. Then, a user identification decides whether a wavefront (DOA) belongs to a user or to an interfere.

3.      Tracking. The user DOAs are tracked to increase the reliability of the DOA estimates.

4.      Signal reconstruction - beamforming.  Finally a beamforming algorithm forms an antenna pattern with a main beam steered into the direction of the user, while minimizing the influence of the interfering wavefronts.

The weights of beamforming algorithm can be optimized from two criteria: maximization of received signal from the desired user or maximization of the SIR (MSIR) by suppressing the signal from interference sources. In case of SIR maximization is to be used, the optimum weight vector W_opt is given by 

                                                                                                    ,                                                          (1)

where  R is N´N correlation matrix of the total received signal, P is cross - correlation vector between input vector  and desirable signal. 

Even with the powerful signal processor available today it is a very challenging task to perform  eq.(1) in real time because the computational complexity of this operation sufficiently large and depends of number of  antenna elements and applied algorithm category. There will be a growing need for development of efficient algorithms for real time weights optimizing and signal tracking. 

In this paper we propose economically vector operations RLS algorithm for beamforming and tracking which allows decrease complexity of smart antenna base station. We present the architecture of proposed algorithm and comparison of computational complexity with conventional RLS algorithm.

2.THE GENERAL FORM OF ADAPTIVE  BEAMFORMING ALGORITHMS

 We will consider the block diagram of the beamformer as shown at figure1.

Figure 1. Block diagram of the beamformer

The signal at the input of L antenna elements  is given 

                                                                                                  ,                                              (2)

where is signal from i-th  user which satisfy the "narrowband assumption",  ,  is angle of i-th user arrival signal, are element space and wave length respectively, n(t) is zero-mean thermal noise present in the receiver, M is number of users.

Matrix of beamforming presents as N row of the steering vectors 

                                                                ,                                        (3)

where , , is i-th reference angle.

The output signal of the Batler matrix  is 

                                                                                                                       (4)

And the output signal of the i-th user beamformer is given by 

                                                                      ,                                                        (5)

 where is weigh vector  of  i-th beamformer.

The recursive adaptive beamforming algorithm takes the general form         

                                                                                    (6)

 where   is vector which minimize the mean square error (MSE) between a reference signal  a_k  and its linear estimation   based on an observed input vector of  k-th sample time  , correlated with a_k , , T,H  are  signs of transpose and conjugate transpose accordingly.

In this case for  MSE and MSIR criterions the optimal vector W_opt is given by the same form [5]

                                                                                                                        (7)

 where

When one used finite sample size then formula (7) can be rewritten as 

                                                                                                                        (8)

 where , .

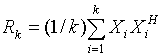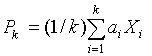The increment  depends on the algorithm.  The popular least mean square (LMS) algorithm has a form

                                                                                               (9) 

This algorithm has good performers but when covariance matrix  has large eigenvalue spread, LMS algorithm has a rather slow convergence[5]. The situation are changed if one should use in the increment a inverse sampling matrix   which is close to . In this case is obtained recursive least square algorithm (RLS) and least square solution

                                                                                      (10)

The convergence rate of this algorithm more fast and not depends of eigenvalue spreading, but the computational complexity of this algorithm is large. Consider RLS algorithm given by one rank matrix modification formula

                                                                                          (11) 

where m is forgetting factor,  . It is well known that  is computed without matrix division using the matrix inversion lemma.                                      

                                                                (12) 

This updating algorithm (12) requires  complex multiplication per one iteration because the base operation is multiplication of matrix on vector with dimension N and high sensitivity to computational errors.   

3. SYNTHESIS OF THE ALGORITHM

We consider beamforming algorithm which has a computational complexity and high accuracy implementation, where k is number of samples in matrix R_k .For this purpose the matrix R_k  in (11) we  write as follows  

                                  (13)

where X  is matrix N´k consisted from k input vectors, and matrix T is a k´k  square matrix  .   

In (11) make a substitution and given 

                                                                                             (14)

According to matrix inversion lemma 

                                                    (15)

 If  then

                                                     (16)

We may rewrite eq.(15) as 

                                                                                          (17)

 where

                                                                                                 (18)

 Matrix A  may be present  as L - factorization 

                                                                                                                       (19)

where   L and are (k´ k) lower and upper triangular matrixes accordingly. Omitting scale factor  in  eq.(17) we get 

                                                                   (20)

 where  is matrix N´k which can be obtain solving system 

                                                                                                                      (21)

Using eq.(8) and eq.(20) the optimal vector can be obtained in form    

                                                                  ,                                (22)

4. RECURSIVE PERFORMENS OF WEIGHT VECTOR

 If input data are a sliding windows with N elements then matrix X for the m-th  window has a structure

              (23)

 where       .

Matrix  for the (m+1)-th  window can be obtain as 

                                                                                                      (24)

where - matrix  without 1-th  column,  .

In this  case matrix  A  from eq.(18) has the following structure   (here shown only lower triangular part and diagonal for k=3 because matrix A is eremite  and upper part will be conjugated

As follows from eq. (25)

                         (26)

 From the matrix  can be obtained recursively  the matrix    (see part 5). 

Its easy that matrix  has a following structure

                                                                                                                     (28)

 where      is k-th row of matrix . is matriz  without 1^th column.  Solving the system of linear eq. (21) we obtain  the  vector , j=1,2,...,k 

                                                                      (29)

Using eq. (8),(22) and eq.(29) we have following recursion for updating the value of adaptive vectors W_j,   j = 1,2,…,k .

                                      ,      (30)

 5. RECURSIVE UPDATING OF MATRIX .

The matrixes  and   can be obtain using Cholesky factorization [6].Then the elements of matrix   is defined by

                                                                        (31)

How follows from eq.(28)  for matrix  no need  calculate all elements but only for i=k, becouse other elements was calculated at privies matrix .  The elements of k-th row could be calculate as 

                                                                       (32)

However in case of obtaining matrix  using  Choletsky factorization  improvement of numerical stability is insignificant and the matrix R should be formed in an obvious form (i.e.  it requires additional memory). Then must be made it  factorization that requires also additional  computational complexity.  

The proposed algorithm allows to make recursive updating of vector W  no form a matrix R in an obvious form but  elements of a matrix L to receive directly from a matrix of input data  X using Householder transform [7]. In this case the algorithm will have a minimum variance problem in finite precision implementation because the Householder transform has a big immunity against the computational errors [8].

Let us consider recursive procedure of updating of elements of a matrix  with Householder transform application. We  assume, that the matrix X is presented as  

                                                                                                                               (33)

so that .  Then 

                                                                           ,                                                (34)

where Q - (N+k)´ (N+k)  orthogonal Householder matrix. From eq.(34) follows, that the elements of a matrix  can be received using orthogonal transformation above a matrix X, not forming in an obvious form of a matrix A.  

We present a matrix Q in factorized  form as  . Then eq.(34) can be rewrite as  

                                                                       ,                                       (35)

 where , ,  

i=1,2..., k, thus column , j=1,2...,k of  matrix have passed the orthogonalization by matrixes Q₁, Q₂..., Q_i-1  (i-1) times.  The matrixes Q_i according to [7] are determined as follows 

                                                              , i = 1,2..., k,                             (36)

 where  is (N+k)´ (N+k)  identity matrix. In eq.(36) scalar C_i is determined as follows 

                                                               , i = 1,2..., k ,                                (37)

 where  is i-th  column of a matrix . The column vector U_i in eq.(36) has dimension N+k and is determined by expression 

                                                                ,                                               (38)

where 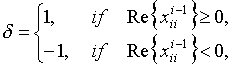,  is the real part of an element ,  is column-vector  which dimension same as a vector ,where unit is  in  the

i-th  place. The value u_i in (36) is i-th element of a vector U_i. Then i-th  step of column ortogonalization of a matrix will  be 

                                                                       .                                                   (39)

 We will present expression eq.(39) with the account eq.(36) as operations above vectors  

                                     .     (40)

 With the account eq.(38) we  present eq.(40) as         

                                                          ,            (41)

 where ,     .    

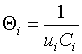The expression eq.(41) determines vector algorithm of reception of elements l_ij and orthogonalization of vectors  using Householder transform.  Proceeding from eq.(41) we obtain expression for elements l_ij of a matrix  as

                                                          ,              (42)

where i = 1,2..., k,  j = i,i+1..., k.

Expression for  vectors orthogonalization yielding     

                                                           .                     (43)

Thus  recursive computing process of reception of elements l_ij of a matrix  with use of Householder transform on i-th  iteration (i = 1,2..., k) consists of the following stages:

a)  Forming of a scalar C_i according to expression (37);

b)  Forming of a vector U_i agrees eq.(38);

c)  The calculation l_ij agrees eq.(42);  

d)  Ortogonalization of vectors  according to eq. (43).    

6. THE COMPUTATIONAL COMPLEXITY AND ARCHITECTURE OF ALGORITHM

The computational steps of adaptive weighting modifications algorithm could be presented as follows

1. Inicialization  W0 =1,. R0 = IN, Z0 = X1 for  i=1,2,3,… for  j=1,2,…k 2. Compute of  triangular decomposition     elements 2.1. Choletsky factorization                     1.                a) Obtain of i-th row of matrix A  (eq.26)  b) Obtain of i-th row of matrix L   (eq.32) 2.2. Householder transform    a)Obtain of i-th row of matrix L   (eq.42) 3. Calculate of vector Z elements 4. Update of adaptive vectors elements Wj,

Figure 2. The architecture of the tracking algorithm

 Figure 2 illustrates the architecture of the proposed algorithm and its computational complexity in terms of multiplications and adders. As it can be observed from the figure 3 the number of operations on the each stage no more than N and total computational complexity equal 3N+k multiplicationes and adders per one iteration. It means that pipelined architecture will operate N/k times faster then conventional structure. 

7. SUMMARY 

Presented beamforming adaptive algorithm for computing the optimum weight vector in accordance with MSIR criterion for mobile communications smart antenna base station beamformer. The proposed algorithm can be implemented with a linear complexity using only vector operations and can be easy implemented en VLSI. Pipelined architecture can operate en N/k times faster than conventional RLS structure. The novel algorithm has a minimum variance problem in finite precision implementation because one use in the procedure of weight vector updating well known stable Householder transform which has a big immunity against the computational errors.  

8. REFERENCES 

1. Liberti J.C., Rappaport T.S., Smart Antennas for Wireless Communications: IS-95 and Third-Generation CDMA Applications. Prentice Hall, NJ, 1999.

2. Barrett M., Arnott R. "Adaptive Antennas for Mobile Communications". Electronics and Communications Engineering Journal, Aug, 1994, pages 203­214.

  3. Winters J.H. “Smart antennas for wireless systems". IEEE Personal Com. Magazine, pages 23 -27, Feb, 1998.

4. Kuchar A. at all “Real-time smart antenna processing for GSM1800 base station” in IEEE Vehicular Technology Conference '99, Houston, Texas.

5.     Haykin S. ”Adaptive Filter Theory”, Prentice Hall, NJ, 1996.

6. Golub G.H., Van Loan C. F. ”Matrix Computations”. 2nd edition, The Johns Hop-kins University Press, North Oxford   Academic Publishing Co., Baltimore and London, 1989.

7. Householder A.S. “A class of method for inverting matrices”.J. Sos.  Indust. Appl. Math, 1958, V.6, # 2, pages 189-195.

8. Wilkinson J..H. The algebraic eigenvalue problem: monographs in Numerical   Analysis. Clarendon Press, Oxford, 1988.

Authors:
Zaharov Viktor Vasilevich , Fausto Casco Sanches,  Omar Amin
vick@xanum.uam.mx, Victor307@yahoo.com 
Departamento de Ingeniería Eléctrica, Universidad Autónoma  Metropolitana - Iztapalapa
México D.F., México

contents

discussion