| "ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 11 , 2000 |
ДИНАМИЧЕСКАЯ НЕУСТОЙЧИВОСТЬ ДВИЖЕНИЯ
ЗАРЯЖЕННЫХ ЧАСТИЦ В ПОСТОЯННОМ НЕОДНОРОДНОМ МАГНИТНОМ ПОЛЕ
С.В.
Поршнев
Нижнетагильский
государственный педагогический институт
Получена 15 ноября 2000 г.
| "ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 11 , 2000 |
ДИНАМИЧЕСКАЯ НЕУСТОЙЧИВОСТЬ ДВИЖЕНИЯ
ЗАРЯЖЕННЫХ ЧАСТИЦ В ПОСТОЯННОМ НЕОДНОРОДНОМ МАГНИТНОМ ПОЛЕ
С.В.
Поршнев
Нижнетагильский
государственный педагогический институт
Получена 15 ноября 2000 г.
Получены численные решения уравнения движения электрического заряда в постоянном неоднородном магнитном поле, параметры которого соответствуют параметрам магнитного поля Земли. Обнаружено существование хаотических решений уравнений движения, получены условия их существования.
Задача об описании движения электрических зарядов (в частности, вычислении траектории) в постоянном неоднородном магнитном поле относится к числу классических задач. Интерес к ней стимулировался в первую очередь активными исследованиями в области управляемого термоядерного синтеза, где требовалось найти ответ на вопрос о возможности удержания частиц в магнитных ловушках, имеющих различные конфигурации магнитных полей [1-3]. Кроме того, данная задача возникает в космической астрофизике [3-5] при объяснении причины существования радиационных поясов у космических тел, обладающих магнитным полем.
Для
однозначного описания траектории движения нерелятивистского электрического
заряда q в постоянном неоднородном магнитном поле
напряженностью ![]() необходимо при
заданных начальных условиях (
необходимо при
заданных начальных условиях (![]() ) решить систему уравнений движения:
) решить систему уравнений движения:
где
m
– масса заряда, ![]() – радиус-вектор, проведенный из начала координат в текущее
положение заряда, с – скорость света.
– радиус-вектор, проведенный из начала координат в текущее
положение заряда, с – скорость света.
Необходимо
отметить, что аналитические решения системы дифференциальных уравнений второго
порядка (1) удается найти только для нескольких случаев: 1) для постоянного
однородного магнитного поля (![]() ), в котором заряд движется по спирали, т.е. траектория
движения представляет собой сумму двух движений: вращения с равномерной угловой
скоростью
), в котором заряд движется по спирали, т.е. траектория
движения представляет собой сумму двух движений: вращения с равномерной угловой
скоростью ![]() по ларморовской
окружности радиуса
по ларморовской
окружности радиуса ![]() в плоскости,
перпендикулярной к направлению вектора напряженности магнитного поля
в плоскости,
перпендикулярной к направлению вектора напряженности магнитного поля ![]() , (
, (![]() – проекция вектора скорости
– проекция вектора скорости ![]() на плоскость,
перпендикулярную вектору
на плоскость,
перпендикулярную вектору ![]() ) и равномерного перемещения вдоль вектора
) и равномерного перемещения вдоль вектора ![]() [3]; 2) для аксиально-симметричного магнитного поля,
создаваемого короткой катушкой с постоянным электрическим током (магнитной
линзы) [3]; 3) для неоднородных магнитных полей, величина напряженности
которых медленно меняется вдоль пути частицы
[2,3,6,7]. Условие медленности
состоит в том, что ларморовский радиус
[3]; 2) для аксиально-симметричного магнитного поля,
создаваемого короткой катушкой с постоянным электрическим током (магнитной
линзы) [3]; 3) для неоднородных магнитных полей, величина напряженности
которых медленно меняется вдоль пути частицы
[2,3,6,7]. Условие медленности
состоит в том, что ларморовский радиус ![]() должен быть мал по
сравнению с размерами области, в пределах которой вектор напряженности
магнитного поля заметно меняется по величине или по направлению:
должен быть мал по
сравнению с размерами области, в пределах которой вектор напряженности
магнитного поля заметно меняется по величине или по направлению:
Отметим, что
аналитические решения во втором и третьем случаях оказываются приближенными.
Так, при расчете магнитных линз предполагается, что магнитное поле, действующее
на электрический заряд, сосредоточено в относительно узкой области
пространства, т.е. в области движения заряда продольная составляющая
напряженности магнитного поля ![]() (
(![]() –цилиндрические координаты) зависят только
от переменной z (z – расстояние, отсчитываемое от центра магнитной катушки вдоль оси
симметрии магнитного поля).
–цилиндрические координаты) зависят только
от переменной z (z – расстояние, отсчитываемое от центра магнитной катушки вдоль оси
симметрии магнитного поля).
Задача описания движения электрического заряда в слабо неоднородном магнитном поле решается методом усреднения, называемого “дрейфовым приближением” [8]. Используя этот метод, в [2] показано, что движение электрического заряда в неоднородном магнитном поле представляет суперпозицию следующих движений:
1. Вращения по ларморовской окружности со скоростью ![]() .
.
2. Движения центра ларморовской окружности вдоль силовой линии со
cкоростью ![]() , при этом
, при этом ![]() в силу закона
сохранения
в силу закона
сохранения
энергии.
3. Дрейфового движения центра ларморовской окружности со скоростью
![]() (
(![]() ||
|| ![]() ),
),
![]() – радиус-вектор
заряда,
– радиус-вектор
заряда, ![]() – ларморовская
частота, соответствующая напряженности магнитного поля в точке положения
заряда.
– ларморовская
частота, соответствующая напряженности магнитного поля в точке положения
заряда.
Другой подход к решению данной задачи основан на том, что слабая неоднородность магнитного поля порождает мало изменяющиеся адиабатические инварианты, количество которых совпадает с числом степеней свободы исследуемой системы. Для рассматриваемой задачи существование адиабатических инвариантов обусловлено, каждым из перечисленных выше движений [2,8]. Вопрос о сохранении адиабатических инвариантов наиболее подробно рассматривался для открытых магнитных ловушек: в [9] получено экспериментальное подтверждение сохранения адиабатического инварианта, связанного с вращением заряда по ларморовской окружности; в [10] доказано вечное сохранение данного адиабатического инварианта в идеальной осесимметричной ловушке с двумерным движением зарядов; в [11] исследовано изменение инвариантов, обусловленное взаимодействием трех степеней свободы.
Модель слабо
неоднородного поля принято также использовать для объяснения движения
заряженных частиц, захваченных магнитосферой Земли
[2,3,8]. При этом вопрос об
адекватности данной модели либо не обсуждается [2,8], либо приводится оценка
параметра ![]() для протонов и электронов с энергией 10 Мэв, находящихся в
магнитном поле напряженностью 0,3 э
[3]. Такой подход, с нашей точки зрения, не вполне
правомерен: во-первых, энергетический спектр частиц, захваченных магнитосферой
Земли, простирается от 100 кэв до 100
Мэв. Во-вторых, в процессе движения
расстояние между заряженной частицей и Землей будет изменяться. Учитывая, сильную зависимость напряженности
геомагнитного поля от расстояния (напряженность геомагнитного поля убывает
расстоянием по кубическому закону), представляется более правильным вычислять
значение коэффициента
для протонов и электронов с энергией 10 Мэв, находящихся в
магнитном поле напряженностью 0,3 э
[3]. Такой подход, с нашей точки зрения, не вполне
правомерен: во-первых, энергетический спектр частиц, захваченных магнитосферой
Земли, простирается от 100 кэв до 100
Мэв. Во-вторых, в процессе движения
расстояние между заряженной частицей и Землей будет изменяться. Учитывая, сильную зависимость напряженности
геомагнитного поля от расстояния (напряженность геомагнитного поля убывает
расстоянием по кубическому закону), представляется более правильным вычислять
значение коэффициента
![]() в каждой точке траектории движения заряда.
в каждой точке траектории движения заряда.
Другой не менее существенный недостаток подходов к решению задачи о движении заряженных частиц в постоянных неоднородных магнитных полях, основанных использовании дрейфового приближения и адиабатических инвариантов, состоит в невозможности точного вычисления законов изменения координат частицы во времени и, как следствие, невозможности детального описания особенностей движения и магнитотормозного излучения электрических зарядов. Отмеченный недостаток не позволяет получить ответы и на другие не менее важные с физической точки зрения вопросы: существуют ли у рассматриваемой системы уравнений (1) хаотические решения, обнаруженые у многих динамических систем, поведение которых описывается нелинейными дифференциальными уравнениями [12,13]; при каких условиях они возникают; каков механизм перехода от детерминированного поведения к динамическому хаосу?
Целью данной работы является исследование особенностей движения электрических зарядов в постоянных неоднородных магнитных полях. Здесь, в условиях отсутствия точного аналитического решения системы нелинейных дифференциальных уравнений (1) представляется естественным находить и анализировать ее численное решение.
1. Математическая модель движения заряженной частицы в магнитном поле
Земли
Как известно [8], по своей геометрии магнитное поле Земли оказывается близким к полю магнитного диполя, наклоненного под углом 11,5° к оси вращения Земли (рис. 1). Центр магнитного диполя смещен приблизительно на 400 км относительно центра Земли. В связи с тем, что данное расстояние оказывается значительно меньше радиуса Земли (6,4×103 км) далее в математической модели указанным смещением можно пренебречь и считать, что магнитный диполь находится в начале прямоугольной декартовой системы координат, ось оZ, которой направлена вдоль оси вращения Земли (рис. 1).
Рис.1.
Для получения замкнутой системы дифференциальных уравнений необходимо дополнить систему уравнений (1) аналитическим выражением для напряженность магнитного поля диполя, которая имеет следующий вид [14]:
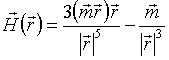 , (4)
, (4)
где
![]() – вектор магнитного диполя,
– вектор магнитного диполя, ![]() – радиус-вектор точки текущего положения электрического
заряда. Задание начальных условий: радиус-вектора
– радиус-вектор точки текущего положения электрического
заряда. Задание начальных условий: радиус-вектора ![]() и начальной скорости
и начальной скорости ![]() позволяет решить
задачу Коши для системы уравнений движения
(1).
позволяет решить
задачу Коши для системы уравнений движения
(1).
Для проведения дальнейших численных расчетов удобно переписать систему
дифференциальных уравнений (1) и выражение для напряженности магнитного поля
(4) в безразмерных переменных. В качестве единиц измерения расстояния
естественно выбрать модуль радиус-вектора ![]() и модуль магнитного момента
и модуль магнитного момента ![]() и ввести следующие безразмерные переменные
и ввести следующие безразмерные переменные ![]() ,
, ![]() (как очевидно,
(как очевидно, ![]() – единичный вектор). В выбранных единицах измерения уравнение (4)
принимает следующий вид:
– единичный вектор). В выбранных единицах измерения уравнение (4)
принимает следующий вид:
где ![]() – модуль
напряженности магнитного поля в точке начального положения заряда.
– модуль
напряженности магнитного поля в точке начального положения заряда.
Из (5) видно, что наиболее естественно в качестве единицы измерения
напряженности магнитного поля использовать величину ![]() . Тогда выражение для безразмерной напряженности магнитного поля
. Тогда выражение для безразмерной напряженности магнитного поля ![]() имеет следующий вид
имеет следующий вид
Выбрав в
качестве единиц измерения времени ![]() – период движения заряда по ларморовской окружности в
магнитном поле в плоскости перпендикулярной вектору напряженности
– период движения заряда по ларморовской окружности в
магнитном поле в плоскости перпендикулярной вектору напряженности ![]() и используя ранее
введенные безразмерные переменные, можно записать систему уравнений движения,
состоящую из 6 уравнений, в следующем виде
и используя ранее
введенные безразмерные переменные, можно записать систему уравнений движения,
состоящую из 6 уравнений, в следующем виде
где безразмерные начальные условия вычисляются по следующим выражениям:
Отметим, что условие (2) в безразмерных переменных принимает следующий вид:
где ![]() .
.
Анализ
выражений (6)–(9) показывает: 1) система безразмерных уравнений движения оказывается
универсальной: коэффициенты системы не зависят от конкретных параметров заряда
(массы и величины заряда) и напряженности магнитного поля; 2) безразмерный
радиус-вектор, проведенный из начала координат в точку начального положения
заряда, – есть единичный вектор; 3) траектория движения заряда в постоянном
неоднородном поле, создаваемом магнитным диполем, определяется не отдельными
значениями параметров заряда и магнитного поля, но комбинацией этих параметров:
![]() ; 3) при выполнении условия
; 3) при выполнении условия ![]() траектории движения
электрических зарядов в постоянных неоднородных полях, создаваемых магнитными
диполями различной величины, оказываются одинаковыми; 4) для исследования особенностей
движения заряда в неоднородном магнитном поле достаточно провести вычисления
при различных значениях безразмерной начальной скорости.
траектории движения
электрических зарядов в постоянных неоднородных полях, создаваемых магнитными
диполями различной величины, оказываются одинаковыми; 4) для исследования особенностей
движения заряда в неоднородном магнитном поле достаточно провести вычисления
при различных значениях безразмерной начальной скорости.
2. Особенности движения заряженных частиц в постоянном неоднородном магнитном поле
В связи с тем, что наибольший практический интерес представляет решение системы уравнений (7) для элементарных частиц, движущихся в магнитных полях, создаваемых космическими объектами, в частности, в магнитном поле Земли, далее приводится анализ результатов численного моделирования движения протона, находящегося в геомагнитной ловушке.
Для численного решения системы уравнений (7) был использован метод Рунге-Кутта 4-го порядка. Правильность работы программы контролировалась по величине кинетической энергии заряда, которая в магнитном поле является интегралом движения. При этом оказалось, что максимальное значение относительной погрешности вычислений не превосходило 10-3%.
Непосредственным результатом работы программы являются зависимости соответствующих декартовых координат от времени (![]() ). Наличие зависимостей
). Наличие зависимостей ![]() позволяет провести
вычисление значений параметра
позволяет провести
вычисление значений параметра ![]() , характеризующего неоднородность магнитного поля, для каждой
точки траектории, а также значений любого из адиабатических инвариантов. Для
анализа особенностей движения заряда оказывается более удобным использовать
зависимость радиус-вектора заряда от времени (
, характеризующего неоднородность магнитного поля, для каждой
точки траектории, а также значений любого из адиабатических инвариантов. Для
анализа особенностей движения заряда оказывается более удобным использовать
зависимость радиус-вектора заряда от времени (![]() ). Это позволяет проводить анализ поведения динамической
системы в двумерном фазовом пространстве вместо анализа в 6-ти мерном пространстве.
). Это позволяет проводить анализ поведения динамической
системы в двумерном фазовом пространстве вместо анализа в 6-ти мерном пространстве.
В качестве
примера рассмотрим результаты расчетов для следующих параметров модели:
электрический заряд – протон (m=1,672×10-24 г, q=4,803×10-10
ед. СГСЭq);
радиус-вектор начального положения точечного заряда ![]() =(0,6,4×109,0)
см; модуль напряженности магнитного
поля
=(0,6,4×109,0)
см; модуль напряженности магнитного
поля ![]() в точке с радиус-вектором
в точке с радиус-вектором ![]() равен 60g (g = 10-5 э) [15]; вектор магнитного диполя
равен 60g (g = 10-5 э) [15]; вектор магнитного диполя ![]() наклонен под углом
11,5° к оси оZ (рис. 1). Выбранные параметры, с одной стороны, соответствуют
параметрам магнитного поля Земли на расстоянии, отсчитываемом от ее центра,
равном 10 радиусам Земли, с другой, позволяют выявить наиболее важные
особенности движения зарядов. В качестве изменяемого параметра модели использовалось
абсолютное значение начальной скорости заряда при неизменном направлении
вектора скорости.
наклонен под углом
11,5° к оси оZ (рис. 1). Выбранные параметры, с одной стороны, соответствуют
параметрам магнитного поля Земли на расстоянии, отсчитываемом от ее центра,
равном 10 радиусам Земли, с другой, позволяют выявить наиболее важные
особенности движения зарядов. В качестве изменяемого параметра модели использовалось
абсолютное значение начальной скорости заряда при неизменном направлении
вектора скорости.
Анализ
зависимостей R(t), полученных при различных значениях
безразмерной начальной скорости и фиксированной в пространстве ориентации радиус-вектора,
и нормированных амплитудно-частотных спектров (далее спектров) зависимостей R(t) показал, что функция R(t) является некоторой периодической функцией,
амплитуда которой зависит от величины безразмерной начальной скорости.
(Типичные зависимости радиус-вектора заряда от времени, спектры функции R(t), а также зависимости ![]() (фазовые траектории) представлены на
рис. 2.)
(фазовые траектории) представлены на
рис. 2.)
Эти результаты
показывают, что траектория движения заряда в неоднородном магнитном поле,
создаваемом магнитным диполем, в координатном пространстве является финитным
квазипериодическим движением: заряд движется по поверхности тора (радиус
большой окружности тора ![]() , радиус малой окружности тора
, радиус малой окружности тора ![]() ). Увеличение значения абсолютной
скорости приводит к увеличению радиусов большой и малой окружностей тора. Данный вывод справедлив также для 6-ти
мерного фазового пространства, в котором движение заряда является
квазипериодическом движением по поверхности 6-ти мерного тора. Этот результат
понятен: существование для каждого начального условия тороидальной поверхности
является следствием сохранения энергии
заряда, движущегося в постоянном магнитном поле.
). Увеличение значения абсолютной
скорости приводит к увеличению радиусов большой и малой окружностей тора. Данный вывод справедлив также для 6-ти
мерного фазового пространства, в котором движение заряда является
квазипериодическом движением по поверхности 6-ти мерного тора. Этот результат
понятен: существование для каждого начального условия тороидальной поверхности
является следствием сохранения энергии
заряда, движущегося в постоянном магнитном поле.
В связи с тем, что наибольший интерес представляют не отдельные
значения параметра ![]() , но его максимальная величина для данной траектории, а также
не отдельные значения адиабатических инвариантов
Ii, но параметры
, но его максимальная величина для данной траектории, а также
не отдельные значения адиабатических инвариантов
Ii, но параметры ![]() , значения которых показывает степень
сохранения инварианта Ii,
указанные характеристики для различных значений начальной скорости представлены
в табл. 1. (Здесь вместе со значениями безразмерной начальной скорости мы также указываем при выбранных параметрах
магнитного поля значения соответствующей кинетической энергии, и ограничиваемся
величиной, характеризующей сохранение адиабатического инварианта
, значения которых показывает степень
сохранения инварианта Ii,
указанные характеристики для различных значений начальной скорости представлены
в табл. 1. (Здесь вместе со значениями безразмерной начальной скорости мы также указываем при выбранных параметрах
магнитного поля значения соответствующей кинетической энергии, и ограничиваемся
величиной, характеризующей сохранение адиабатического инварианта ![]() ). Кроме указанных величин в табл.
1 приведены значения
радиусов большой и малой окружностей тора.
). Кроме указанных величин в табл.
1 приведены значения
радиусов большой и малой окружностей тора.
|
|
|
E, Мэв |
|
A, % |
|
|
1. |
0,3×10-2 |
4,22×10-3 |
2,0×10-3 |
1,6 |
0,014 |
|
2. |
0,6×10-2 |
16,9×10-3 |
4,3×10-3 |
3,1 |
0,019 |
|
3. |
1,2×10-2 |
67,5×10-2 |
1,3×10-2 |
6,4 |
0,028 |
|
4. |
2,4×10-2 |
0,27 |
2,3×10-2 |
12,1 |
0,045 |
|
5. |
4,8×10-2 |
1,08 |
8,1×10-2 |
23,5 |
0,078 |
|
6. |
7,0×10-2 |
2,30 |
1,3×10-1 |
33,4 |
0,106 |
|
7. |
9,0×10-2 |
3,80 |
1,7×10-1 |
42,1 |
0,129 |
|
8. |
1,5×10-1 |
10,55 |
3,1×10-1 |
68,4 |
0,190 |
|
9. |
2,0×10-1 |
18,76 |
4,4×10-1 |
82,9 |
0,228 |
|
10. |
3,0×10-1 |
42,21 |
1,13 |
199,7 |
0,406 |
Анализ
результатов, представленных в табл. 1 показывает, что увеличение безразмерной
скорости движения заряда, достигаемое увеличением абсолютного значения скорости
при неизменных характеристиках магнитного поля, происходит монотонное
увеличение коэффициента ![]() при одновременном
разрушении адиабатического инварианта
при одновременном
разрушении адиабатического инварианта ![]() . При этом оказывается, что точность сохранения адиабатического инварианта А уже при значениях
. При этом оказывается, что точность сохранения адиабатического инварианта А уже при значениях ![]() »9×10-2, (т.е. по устоявшемуся мнению
удовлетворяющих условию применимости дрейфового приближения
»9×10-2, (т.е. по устоявшемуся мнению
удовлетворяющих условию применимости дрейфового приближения ![]() <<1) составляет не более 23,5%. Следовательно,
использование модели сохраняющихся адиабатических инвариантов для описания
движения в магнитном поле Земли протонов с энергией более 2 Мэв неправомерно. Более того, как будет
показано ниже, даже для протонов, имеющих значительно меньшие кинетические
энергии, данная модель не позволяет выявить ряд особенностей движения
электрических зарядов в поле магнитного диполя.
<<1) составляет не более 23,5%. Следовательно,
использование модели сохраняющихся адиабатических инвариантов для описания
движения в магнитном поле Земли протонов с энергией более 2 Мэв неправомерно. Более того, как будет
показано ниже, даже для протонов, имеющих значительно меньшие кинетические
энергии, данная модель не позволяет выявить ряд особенностей движения
электрических зарядов в поле магнитного диполя.
Рассмотрим
более подробно трансформацию спектров зависимостей
R(t) и фазовых траекторий, полученных по
зависимости R(t), при последовательном увеличении значений
безразмерной начальной скорости (рис.
2).
При ![]() = (0,1,5×10-2,0) (
= (0,1,5×10-2,0) (![]() »2,1×10-3, А»1,6%) движение частицы согласуется с моделью сохраняющихся
адиабатических инвариантов: вращение частицы по ларморовской окружности,
движения центра ларморовской окружности вдоль силовой линии, дрейфа центра
ларморовской окружности в плоскости XoY (рис. 2а). Отметим, не касаясь деталей, что здесь и далее на рис. 2.
вследствие особенностей цифровых методов спектрального анализа, подробно
рассмотренных в [16], при выбранных длительностях временного интервала для
поиска решения системы уравнений движения (7) в спектре функции R(t) не удается разрешить гармоники,
соответствующие наиболее медленному из перечисленных выше движений – дрейфу частицы в плоскости XоY, поскольку на выбранном временном интервале
укладывается менее одного периода дрейфового движения. Указанный недостаток
легко устранить, увеличив при неизменном шаге интегрирования временной
интервал, на котором ищется решение системы уравнений движения
(7). Однако
этого не требуется, поскольку, скорость дрейфового движения при выбранных
начальных условиях (
»2,1×10-3, А»1,6%) движение частицы согласуется с моделью сохраняющихся
адиабатических инвариантов: вращение частицы по ларморовской окружности,
движения центра ларморовской окружности вдоль силовой линии, дрейфа центра
ларморовской окружности в плоскости XoY (рис. 2а). Отметим, не касаясь деталей, что здесь и далее на рис. 2.
вследствие особенностей цифровых методов спектрального анализа, подробно
рассмотренных в [16], при выбранных длительностях временного интервала для
поиска решения системы уравнений движения (7) в спектре функции R(t) не удается разрешить гармоники,
соответствующие наиболее медленному из перечисленных выше движений – дрейфу частицы в плоскости XоY, поскольку на выбранном временном интервале
укладывается менее одного периода дрейфового движения. Указанный недостаток
легко устранить, увеличив при неизменном шаге интегрирования временной
интервал, на котором ищется решение системы уравнений движения
(7). Однако
этого не требуется, поскольку, скорость дрейфового движения при выбранных
начальных условиях (![]() ) оказывается значительно меньше скоростей ларморовского
вращения и движения центра ларморовской окружности, в чем легко убедится,
записав (3) в безразмерном виде и учтя, что при выбранных начальных условиях
:
) оказывается значительно меньше скоростей ларморовского
вращения и движения центра ларморовской окружности, в чем легко убедится,
записав (3) в безразмерном виде и учтя, что при выбранных начальных условиях
:
где ![]() , поэтому влиянием смещения, обусловленного дрейфом заряда,
на особенности движения заряда в первом приближении можно пренебречь.
, поэтому влиянием смещения, обусловленного дрейфом заряда,
на особенности движения заряда в первом приближении можно пренебречь.
Анализ зависимости R(t) и соответствующей фазовой траектории при (0,0,3×10-2,0) позволяет сделать вывод о существовании у системы (7) простого или регулярного аттрактора. При этом необходимо отметить, особенность движения, не выявляемую при использовании модели сохраняющихся адиабатических инвариантов. В спектре функции R(t) помимо гармоник, соответствующим движению заряда вдоль силовых линий (f1) и вращения заряда по ларморовской окружности (f2), присутствуют две дополнительные гармоники с частотами f2±f1. Их существование обусловлено взаимодействием рассматриваемых движений: перемещение заряда вдоль силовой линии приводит к изменению скорости вращения по ларморовской окружности вследствие изменения напряженности магнитного поля.
Для ![]() = (0,6,1×10-2,0) (
= (0,6,1×10-2,0) (![]() »1,3×10-2, А»6,4%) при
сохранении в целом регулярности аттрактора происходит усложнение движения:
во-первых, появляется удвоенная гармоника (2f2),
соответствующая вращению заряда по ларморовской окружности, во-вторых, в
спектре помимо описанных выше гармоник
появляются дополнительные боковые гармоники c с частотами f2±2f1, 2f2±f1, 2f2±2f1 (рис. 2б). Данный результат обусловлен
увеличением "степени нелинейности" рассматриваемой динамической системы:
увеличение начальной скорости заряда приводит к более быстрому смещению в
область сильно неоднородного магнитного поля, и, как следствие, большему
взаимовлиянию рассматриваемых движений друг на друга.
»1,3×10-2, А»6,4%) при
сохранении в целом регулярности аттрактора происходит усложнение движения:
во-первых, появляется удвоенная гармоника (2f2),
соответствующая вращению заряда по ларморовской окружности, во-вторых, в
спектре помимо описанных выше гармоник
появляются дополнительные боковые гармоники c с частотами f2±2f1, 2f2±f1, 2f2±2f1 (рис. 2б). Данный результат обусловлен
увеличением "степени нелинейности" рассматриваемой динамической системы:
увеличение начальной скорости заряда приводит к более быстрому смещению в
область сильно неоднородного магнитного поля, и, как следствие, большему
взаимовлиянию рассматриваемых движений друг на друга.
При ![]() = (0, 1,23×10-1, 0) (
= (0, 1,23×10-1, 0) (![]() »2,3×10-2, А»12,1%) в
спектре появляется дополнительная гармоника с частотой, равной утроенной
частоте вращения заряда по ларморовской окружности и боковых гармоник, имеющих
частоты 3f1±f2. Дальнейшее увеличение начальной скорости приводит к увеличению амплитуды
данных гармоник (см. рис. 2г). При
начальной скорости при
»2,3×10-2, А»12,1%) в
спектре появляется дополнительная гармоника с частотой, равной утроенной
частоте вращения заряда по ларморовской окружности и боковых гармоник, имеющих
частоты 3f1±f2. Дальнейшее увеличение начальной скорости приводит к увеличению амплитуды
данных гармоник (см. рис. 2г). При
начальной скорости при ![]() = (0, 3,59×10-1, 0) (
= (0, 3,59×10-1, 0) (![]() »1,25×10-1, А»33,4%) в
спектре появляются гармоники, имеющие частоты 4f1±f2, при дальнейшем увеличении начальной скорости повторяется описанный
сценарий (см. рис. 2д–2ж).
»1,25×10-1, А»33,4%) в
спектре появляются гармоники, имеющие частоты 4f1±f2, при дальнейшем увеличении начальной скорости повторяется описанный
сценарий (см. рис. 2д–2ж).
Наиболее
интересный результат получается для начальных скоростей, превышающих по
абсолютному значению 0,3. Анализ спектра функции
R(t) при ![]() = (0, 1,54, 0) (
= (0, 1,54, 0) (![]() »1,1, А»200%), представленный на рис. 2з, показывает, что спектр функции
становится непрерывным. Траектория движения заряда в координатном пространстве
для данных начальных условий представлена на
рис.3, зависимость расстояния
между траекториями близкими в начальный момент времени представлена на
рис.4.
»1,1, А»200%), представленный на рис. 2з, показывает, что спектр функции
становится непрерывным. Траектория движения заряда в координатном пространстве
для данных начальных условий представлена на
рис.3, зависимость расстояния
между траекториями близкими в начальный момент времени представлена на
рис.4.
Из рис. 4 видно, что расстояние между двумя траекториями, устойчивыми по Пуассону, меняется по случайному закону, т.е. решения системы нелинейных дифференциальных уравнений (7) при данных начальных условиях оказываются неустойчивыми по Ляпунову. Таким образом, совокупность результатов, представленных на рис. 2з, 3, 4, позволяет сделать вывод о возникновении в изучаемой системе динамического хаоса при условии
где ![]() .
.
Особо отметим, что полученные результаты в полной мере относятся и к случаю движения в постоянном неоднородном магнитном поле заряженных частиц с релятивистскими скоростями. Как известно [17], уравнение движения в данном случае имеет вид
где
сила Лоренца,
действующая на частицу направлена так, что всегда ![]() , поэтому работа внешней силы, пропорциональная величине
, поэтому работа внешней силы, пропорциональная величине ![]() , равна нулю. Следовательно, энергия частицы, а вместе с ней
и абсолютное значение скорости остаются постоянными. Поэтому можно сказать, что
движение релятивистской частицы в постоянном магнитном поле описывается
классическими уравнениями движения заряженной частицы с постоянной массой
, равна нулю. Следовательно, энергия частицы, а вместе с ней
и абсолютное значение скорости остаются постоянными. Поэтому можно сказать, что
движение релятивистской частицы в постоянном магнитном поле описывается
классическими уравнениями движения заряженной частицы с постоянной массой ![]() . Этот вывод позволяет обобщить полученные результаты для
частиц, движущихся с релятивистскими скоростями. Для этого при выборе единиц
измерения достаточно заменить в соответствующих выражениях массу частицы
m
на
. Этот вывод позволяет обобщить полученные результаты для
частиц, движущихся с релятивистскими скоростями. Для этого при выборе единиц
измерения достаточно заменить в соответствующих выражениях массу частицы
m
на ![]() . С учетом этой замены выражение (9) принимает вид
. С учетом этой замены выражение (9) принимает вид
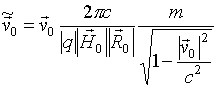 . (15)
. (15)
Подставив выражение (12) в (15), найдем абсолютное значение скорости движения релятивистской заряженной частицы в постоянном неоднородном магнитном поле, при которой возникает динамический хаос:
где
Подставив, (16) в известное выражение для энергии релятивистской частицы, получим выражение для энергии, соответствующей хаотическому движению
Для
электронов, двигающихся в магнитного поле Земли, ![]() , т.е. движение электронов с энергией большей
, т.е. движение электронов с энергией большей ![]() является хаотическим.
является хаотическим.
Заключение
В проведенных численных исследованиях особенностей движения электрических зарядов в постоянном неоднородном поле, создаваемом магнитным диполяем, обнаружены хаотические решения системы дифференциальных уравнений (1). Для магнитного поля, параметры которого соответствуют параметрам магнитного поля Земли, определены условия возникновения динамического хаоса в рассматриваемой системе и описан механизм перехода к хаотическому режиму. Показано, что условия возникновения хаоса реализуются для нерелятивистских протонов с кинетической энергией ³ 84 Мэв и релятивистских электронов с энергией ³ 50 Мэв.
В то же время необходимо проведение дальнейших исследований в этом направлении, в частности, более подробное исследование структуры хаоса: получить численные оценки показателя Ляпунова, исследовать возможность появление фрактальных структур и получить оценку их размерностей и др.
ЛИТЕРАТУРА
1. Арцимович Л.А. Замкнутые плазменные конфигурации. М.:Наука, 1969.
2. Арцимович Л.А., Сагдеев Р.З. Физика плазмы для физиков. М.: Атомиздат, 1979.
3. Арцимович Л.А., Лукьянов С.Ю. Движение заряженных частиц в электрических и магнитных полях. М.: Наука, 1978.
4. Альвен Х. Космическая электродинамика. М.: Изд-во иностранной литературы, 1952.
5. Пилькенер С.Б. Основы космической электродинамики. М.: Физматгиз, 1961.
6. Сивухин Д.В.// Вопросы теории плазмы М.: Госатомиздат, 1963. Вып. 1. С. 7.
7. Морозов А.И., Соловьев Л.С.// Вопросы теории Плазмы М.: Госатомиздат, 1963. Вып. 2.
8. Заславский Г.М., Сагдеев Р.З. Введение в нелинейную физику: От маятника до турбулентности и хаоса. М.: Наука, 1988.
9. Родионов М.С.// Атомная энергия. 1959. Т. 6. С. 623.
10. Арнольд В.И.// Доклады АН СССР. 1962. Т. 142. С. 758.
11. Чириков Б.В.// Вопросы теории плазмы. М.: Энергоатомиздат, 1983. Вып. 13. С. 3.
12. Анищенко В.С. Сложные колебания в простых системах: Механизмы возникновения, структура и свойства динамического хаоса в радиофизических системах. М.: Наука, 1990.
13. Шустер Г. Детерминированный хаос. Введение. М.: Мир, 1988.
14. Тамм И.Е. Основы теории электричества. М.: Наука, 1976.
15. Веденов А.А. Задачник по физике плазмы. М.: Атомиздат, 1981.
16. Марпл-мл. С.П. Цифровой спектральный анализ и его приложения. М.: Мир, 1990.
17. Угаров В.А. Специальная теория относительности. М.: Наука, 1977.
Автор:
Поршнев
Сергей Владимирович, доктор
технических наук, доцент,
e-mail: ntr20@ntgpi.e-burg.ru, зав. кафедрой информатики и
вычислительной техники Нижнетагильского
государственного педагогического
института.