| "ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 10, 2001 |
|
Алгоритм синтеза диаграммы направленности осесимметричной двухзеркальной антенны
ГКБ "СВЯЗЬ", Ростов-на-Дону
Получена 19 ноября 2001 г.
Рассмотрен алгоритм синтеза диаграммы направленности осесимметричной двухзеркальной антенны, удовлетворяющей рекомендациям UTI-R, основанный на оптимизации формы амплитудного распределения в апертуре двухзеркальной антенны, заданной функцией, обеспечивающей возможность аналитического вычисления интеграла излучения.
Современные приемо-передающие зеркальные антенны для земных станций спутниковых систем (ЗССС) с высокими электрическими характеристиками: коэффициентом усиления и коэффициентом использования поверхности (КИП), должны удовлетворять международным и национальным нормам и параметрам. Согласно рекомендациям UTI-R S.580 для антенн, вводимых в эксплуатацию после 1995 г., необходимо, чтобы их усиление (по крайней мере, более 90% пиков диаграммы направленности) не превышало значение:
где
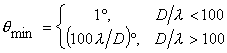 .
.
Проектирование таких антенн обычно сводится к решению задачи геометрооптического (ГО) синтеза профилей поверхностей зеркал по заданному амплитудному распределению поля в апертуре антенны [1,2]. Выбор формы амплитудного распределения в апертуре в конечном счете и определяет характер бокового излучения антенны, оценка которого основывается на вычислении поля в дальней зоне антенны токовым или апертурным методом.
Для двухзеркальных антенн (ДЗА) (рис. 1) расчет диаграммы
направленности связан с вычислением интеграла излучения для основного
рефлектора и для контррефлектора, что сопряжено, обычно, с достаточно большими
как алгоритмическими, так и чисто вычислительными трудностями. Поэтому
предварительную оценку бокового излучения имеет смысл проводить на основе
апертурного метода. Из [3, 4] известно, что для антенн с диаметром апертуры
![]() расчеты поля в дальней
зоне эквивалентны для методов физической оптики и оценок поля по апертурному
распределению.
расчеты поля в дальней
зоне эквивалентны для методов физической оптики и оценок поля по апертурному
распределению.
Рис. 1. Двухзеркальная осесиммметричная антенна.
Целью настоящей статьи является анализ возможности оптимизации формы амплитудного распределения в апертуре основного зеркала ДЗА для получения уровня бокового излучения антенны, удовлетворяющего международным нормам, при минимизации снижения коэффициента использования поверхности (КИП) антенны.
Близкая к оптимальной форма амплитудного распределения в апертуре осесимметричной ДЗА с учетом затенения в центре, обеспечивающая низкий уровень боковых лепестков и максимально возможный КИП, может быть описана выражением:
где
![]() - нормированная координата функции
амплитудного распределения,
- нормированная координата функции
амплитудного распределения,
![]() - относительный радиус затененной
центральной области,
- относительный радиус затененной
центральной области,
![]() -
относительные радиусы переходных областей,
-
относительные радиусы переходных областей,
![]() - коэффициент, определяющий уровень поля
на краю апертуры (рис. 2).
- коэффициент, определяющий уровень поля
на краю апертуры (рис. 2).
Рис. 2. Распределение поля в апертуре ДЗА.
Такое представление апертурного распределения может быть использовано для расчета геометрии синтезируемых профилей зеркал в приближении ГО. Однако при этом КИП осесимметричной ДЗА и ее диаграмма направленности не могут быть рассчитаны аналитически. Поэтому решение оптимизационной задачи по выбору оптимальных параметров амплитудного распределения, обеспечивающих проектирование антенны удовлетворяющей международным требованиям, требует значительных временных затрат.
Как известно, поле в дальней зоне при апертурном подходе определяется соотношением:
где
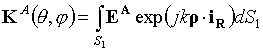 ,
,
![]() - волновое число,
- волновое число,
![]() - проекция поверхности зеркала
- проекция поверхности зеркала
![]() на плоскость апертуры
рефлектора,
на плоскость апертуры
рефлектора,
![]() -
радиус вектор в точку интегрирования,
-
радиус вектор в точку интегрирования,
![]() .
.
Интеграл (3) для круглых апертур сводится к интегралу Гюйгенса-Грина [5]:
где
![]() ,
,
![]() - нормированные координаты интегрирования
в полярной системе координат, совмещенной с плоскостью апертуры.
- нормированные координаты интегрирования
в полярной системе координат, совмещенной с плоскостью апертуры.
Представление амплитудного
распределения в виде (2) не позволяет получить аналитическое решение интеграла
(4). Однако, из литературы известно [6], что наилучшая аппроксимация функций
поля
![]() в апертуре
зеркала, позволяющая получить на основании свойств функций Бесселя
аналитическое решение интеграла (4), описывается рядом:
в апертуре
зеркала, позволяющая получить на основании свойств функций Бесселя
аналитическое решение интеграла (4), описывается рядом:
Как утверждается в работе [6], для
амплитудных распределений, плавно спадающих к краю апертуры, рассмотренное
представление позволяет аппроксимировать функцию поля в апертуре с точностью
![]() для очень
ограниченного числа точек (
для очень
ограниченного числа точек (![]() ). При этом:
). При этом:
где
![]() - гамма функция,
- гамма функция,
![]() - функция Бесселя.
- функция Бесселя.
Для случая осевой симметрии функции возбуждения апертуры аппроксимация (5) упрощается:
и функция диаграммы направленности
![]() принимает вид
принимает вид
Непосредственная апроксимация амплитудного распределения (2)
рядом вида (7) приводит к значительным искажениям формы функции амплитудного
распределения в области
![]() (см. рис. 3). Однако, если выражение (2)
переписать в виде:
(см. рис. 3). Однако, если выражение (2)
переписать в виде:
где
то каждая из функций может быть аппроксимирована рядом (7) без существенных искажений формы амплитудного распределения для каждого из слагаемых:
где
![]() - коэффициенты аппроксимации функций
- коэффициенты аппроксимации функций
![]() , соответственно.
, соответственно.
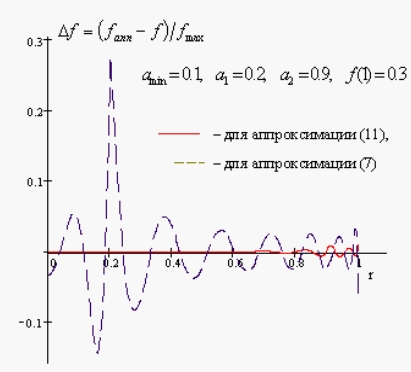
На рис. 3 представлены графики функций
![]() отклонения аппроксимированного
амплитудного распределения от распределения, заданного теоретически функцией
(1), для аппроксимаций (7) и (11). Число членов ряда для графиков,
представленных на рис. 3,
отклонения аппроксимированного
амплитудного распределения от распределения, заданного теоретически функцией
(1), для аппроксимаций (7) и (11). Число членов ряда для графиков,
представленных на рис. 3,
![]() . Узловые точки аппроксимации совпадают с
нулями полинома Чебышева
. Узловые точки аппроксимации совпадают с
нулями полинома Чебышева
![]() . Точность аппроксимации для рядов с
. Точность аппроксимации для рядов с
![]() при использовании
функции (11) даже для областей перехода
при использовании
функции (11) даже для областей перехода
![]() оказывается не хуже 0.1, максимальные
ошибки аппроксимации получаются на границах переходных областей.
оказывается не хуже 0.1, максимальные
ошибки аппроксимации получаются на границах переходных областей.
Результирующее выражение для
![]() принимает вид
принимает вид
где
![]() .
.
Рис. 3. Отклонение аппроксимированного апертурного распределения от распределения, заданного теоретически.
В случае если геометрооптический синтез поверхностей ДЗА проводится для амплитудного распределения, заданного функцией (9), то выражение (10) описывает диаграмму направленности ДЗА без потерь точности.
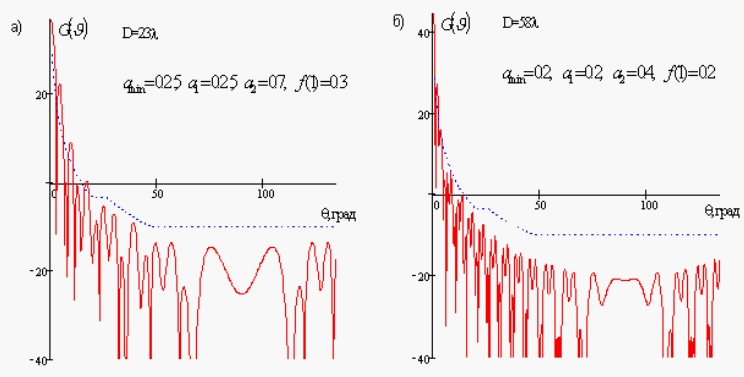
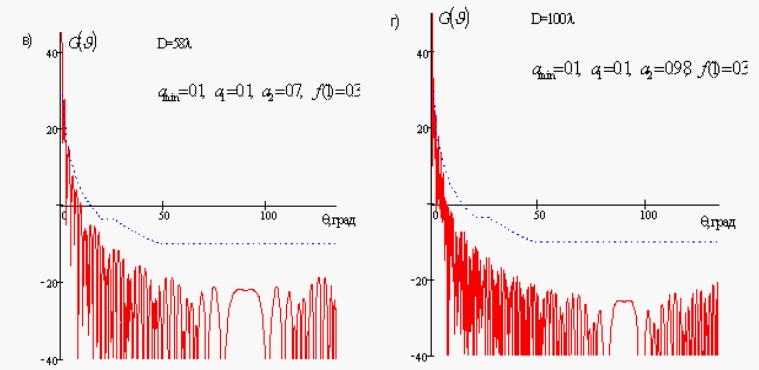
На рис. 4 представлены рассчитанные зависимости
![]() для ДЗА с различными
диаметрами апертуры и параметрами амплитудного распределения в сравнении с
нормативным уровнем бокового излучения (1).
для ДЗА с различными
диаметрами апертуры и параметрами амплитудного распределения в сравнении с
нормативным уровнем бокового излучения (1).
Анализ представленных графиков показывает, что у ДЗА с
диаметрами
![]() структура
бокового излучения для углов
структура
бокового излучения для углов
![]() удовлетворяет требованиям норм с
достаточно большим запасом (даже для антенны с размером затененной области:
удовлетворяет требованиям норм с
достаточно большим запасом (даже для антенны с размером затененной области:
![]() , как на
рис. 4б).
Поэтому основное внимание следует уделять анализу бокового излучения в области
углов
, как на
рис. 4б).
Поэтому основное внимание следует уделять анализу бокового излучения в области
углов ![]() .
.
Для ДЗА с диаметрами апертуры ![]() (рис. 4а) становится проблематичным
обеспечение заданного апертурного распределения поля в результате
геометрооптического синтеза поверхностей зеркал, так как даже для
(рис. 4а) становится проблематичным
обеспечение заданного апертурного распределения поля в результате
геометрооптического синтеза поверхностей зеркал, так как даже для
![]() диаметр контррефлектора
оказывается меньше 10
диаметр контррефлектора
оказывается меньше 10![]() и дифракционные токи на кромке контррефлектора могут значительно исказить
картину результирующего апертурного распределения и, следовательно, диаграмму
направленности антенны. Поэтому, в этом случае, анализ свойств апертурного
распределения представляет чисто теоретический интерес.
и дифракционные токи на кромке контррефлектора могут значительно исказить
картину результирующего апертурного распределения и, следовательно, диаграмму
направленности антенны. Поэтому, в этом случае, анализ свойств апертурного
распределения представляет чисто теоретический интерес.
Рис. 4. Диаграммы направленности ДЗА
ДЗА с диаметрами
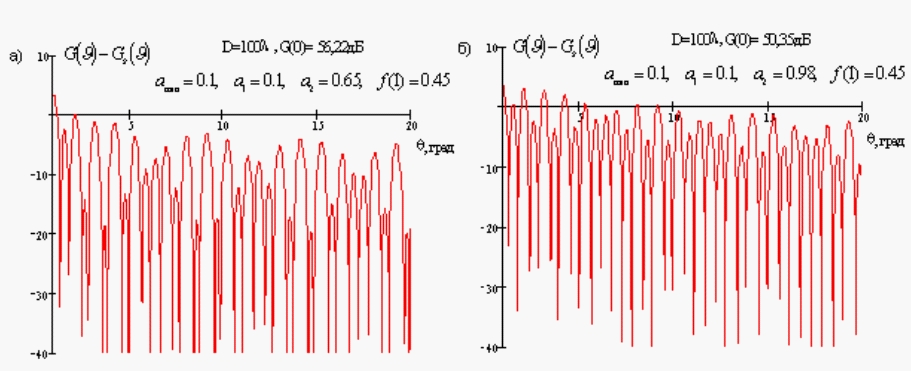
![]() имеют структуру ближнего бокового излучения,
удовлетворяющую требованиям норм, для практически столообразных апертурных
распределений. Графики, демонстрирующие отклонение ближней боковой структуры
диаграммы направленности от предельно допустимой, представлены на рис. 5.
Однако реальная диаграмма направленности из-за потерь, связанных с дифракцией
на опорах контррефлектора, ошибках в юстировке положения облучателя и
контррефлектора, может обладать несколько худшей структурой ближних боковых
лепестков.
имеют структуру ближнего бокового излучения,
удовлетворяющую требованиям норм, для практически столообразных апертурных
распределений. Графики, демонстрирующие отклонение ближней боковой структуры
диаграммы направленности от предельно допустимой, представлены на рис. 5.
Однако реальная диаграмма направленности из-за потерь, связанных с дифракцией
на опорах контррефлектора, ошибках в юстировке положения облучателя и
контррефлектора, может обладать несколько худшей структурой ближних боковых
лепестков.
Рис. 5. Отклонение ближней
боковой структуры от
![]() .
.
Поэтому, при проектировании ДЗА имеет смысл ужесточать требования (1) на ближнюю боковую структуру (рис. 6):
Рис. 6. Оптимизация
ближней боковой структуры для
![]() .
.
Ужесточение требований приводит к необходимости решения оптимизационной задачи поиска оптимальных значений параметров функции амплитудного распределения (9) для достижения требований технического задания на КИП проектируемой антенны.
Выводы
Предложенное представление амплитудного распределения поля в апертуре ДЗА в виде разности рядов аппроксимирующих поле круглых апертур с единичным радиусом и относительным радиусом контррефлектора позволяет аналитически рассчитывать интеграл излучения антенны. Предложенная форма аппроксимации апертурного распределения позволяет с высокой точностью аппроксимировать практически столообразную функцию апертурного распределения. Синтез поверхностей зеркал антенной системы в соответствии с полученной при аппроксимации функцией апертурного распределения позволяет избавиться от ошибок связанных с точностью аппроксимации при расчете диаграммы направленности антенны.
Анализ боковой структуры рассчитанной диаграммы направленности позволяет подобрать оптимальные характеристики амплитудного распределения в апертуре ДЗА.
Литература
-
Айзенберг Г.З., Ямпольский В.Г., Терешин О.Н. Антенны УКВ. – М: "Связь". - Ч. 2. – 1977 – С. 58-74.
-
М.В. Романенко. Единый подход к проектированию осесимметричных двухзеркальных систем с модифицированными поверхностями. Антенно-фидерные устройства, системы и средства радиосвязи (ICARSM-97). Сборник трудов 3 международной научно-технической конференции. – Т. 1. – С. 204-214.
-
В.А. Боровиков, Б.К. Кинбер. О пределах приближения Кирхгоффа для расчета зеркальных антенн. – М: "Радиотехника и электроника".- №3. – 1976. – С. 997-1006.
-
Yaghjian. Equivalence of surface current and aperture field integration for reflector antennas. – IEEE Trans. Antennas Propagat. – V. AP-32. – Pp. 1355-1358. – 1984.
-
S. Silver. Microwave Antenna Theory and Design. – MIT Series. – V. 12. – McGraw Hill. – 1949. – P. 192.
-
K. Hongo, H. Matsuura. Simplified Technique for Evaluating the Radiation Integrals. – IEEE Trans. Antennas Propagat. – V. AP-34. – Pp. 732-737. – No. 5. - May. – 1986.
Автор:
Романенко Марина Витальевна, ГКБ "Связь", Ростов-наДону, научный сотрудник, e-mail: mvrom@aaanet.ru
 , (1)
, (1)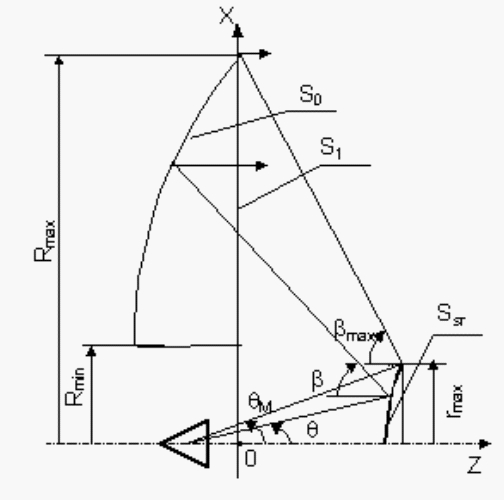
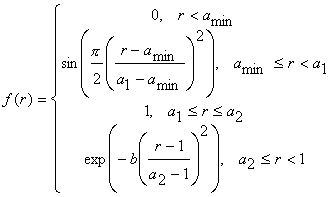 , (2)
, (2)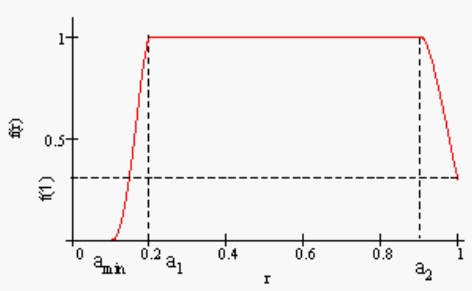
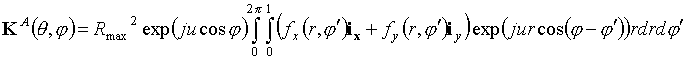 , (4)
, (4)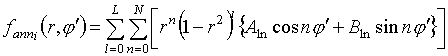 . (5)
. (5)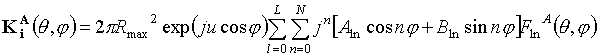 , (6а)
, (6а)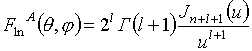 , (6б)
, (6б)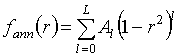 , (7)
, (7)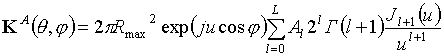 , (8)
, (8)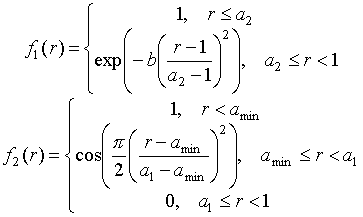 , (10)
, (10)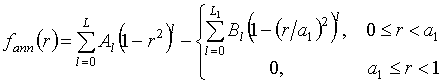
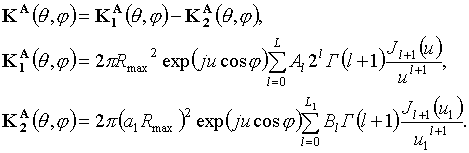 (12)
(12)