В работе разработана новая математическая модель динамики коммутатора Gigabit Ethernet – одного из основных узлов современных телекоммуникационных систем. При синтезе модели был применен оригинальный подход, отличный от широко распространенного подхода на основе теории систем массового обслуживания. Созданная модель учитывает переменный размер кадра и вариацию межкадрового интервала, а также уровень загрузки коммутационного устройства. В работе показана адекватность модели реальному коммутатору Gigabit Ethernet, и выявлена частичная некорректность применения обобщенного параметра – уровня загрузки канала при анализе динамических характеристик телекоммуникационных сетей на основе технологии Gigabit Ethernet.

1. ВВЕДЕНИЕ

Современные телекоммуникационные системы передают как правило конвергированный трафик данных, голоса и видео. Основная причина этого – экономическая выгода. В числе основных требований предъявляемых к широкополосным цифровым сетям с интеграцией служб (Ш-ЦСИС), является гарантия определенного качества обслуживания (Quality of Service, QoS) каждого соединения [1]. До сих пор необходимые многим современным приложениям дифференцированные услуги и гарантии качества обслуживания у широко распространенной технологии Ethernet – отсутствовали, так как сети на основе Ethernet создавались для передачи в первую очередь информации содержащей как правило данные.

Появление новых механизмов управления приоритетом трафика, потоком кадров и виртуальными каналами, вкупе с технологией многопротокольной коммутации с заменой меток (Multiprotocol Label Switching, MPLS), делает очевидной возможность применения Ethernet в мультисервисных корпоративных и городских сетях, а с развитием технологии плотного волнового мультиплексирования (Density Wave De-Multiplexing, DWDM) и с принятием стандарта на 10 Гб/с и в сетях территориального уровня [2].

Требуемое качество обслуживания в сети MPLS/Ethernet не может быть обеспечено только методами построения оптимального маршрута передачи данных [3]. Помимо этого требуются эффективные протоколы и алгоритмы управления классами, очередями и потоками в устройствах коммутации трафика, разработать которые без комплексного исследования динамических характеристик коммутаторов Gigabit Ethernet – не представляется возможным. Поэтому сегодня, при растущих масштабах использования технологии Ethernet в сетях с новыми приложениями, такими как передача компрессированного голоса, высококачественного видео, банковских транзакций, трафика Интернет – задача комплексного исследования динамических характеристик коммутаторов Gigabit Ethernet, остается безусловно актуальной.

Специфика эксплуатации реальных сетей не позволяет входить в режим активного эксперимента. Существующие теоретические методы анализа на основе систем массового обслуживания не учитывают переменный размер кадра и вариацию межкадровой паузы, а оперируют обобщенным параметром – уровнем загрузки канала [4-7]. Применение имитационного моделирования в чистом виде осложнено, так как требует создания асинхронной дискретно-временной модели [8-10]. В связи с этим требуется разработка подхода к моделированию динамики коммутаторов Gigabit Ethernet свободного от этих недостатков. Представляет интерес также исследование правомочности применения обобщенного параметра – уровня загрузки канала при исследовании вероятностно-временных характеристик (ВВХ) устройств Gigabit Ethernet.

Структура данной работы такова. В секции 2, мы представляем новую модель коммутирующего устройства и показываем ее адекватность. Результаты исследования возможности применения уровня загрузки канала при анализе вероятностно-временных характеристик устройств Gigabit Ethernet приведены в секции 3. Выводы, и рекомендации к дальнейшим исследованиям, приведены в секции 4.

2. ПОСТРОЕНИЕ МОДЕЛИ ДИНАМИКИ КОММУТАТОРА GIGABIT ETHERNET

2.1. Постановка задачи

Для правильного проектирования и управления коммутатором Gigabit Ethernet необходима адекватная функциональная модель этого устройства. Реальный коммутатор может быть представлен различными моделями в зависимости от степени и полноты детализации процессов и конечной задачи исследования.

Базовую функциональную модель узла коммутации трафика (УКТ) можно создать на основе положений теории массового обслуживания [11, 12]. При этом коммутатор в первом приближении представляется одноканальной системой массового обслуживания (СМО), с конечным входным буфером и дисциплиной обслуживания заявок FIFO (first input/first output). Функциональная модель системы приведена на рис. 2.1.

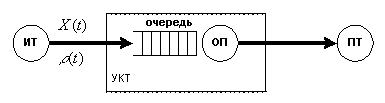
Рис. 2.1. Функциональная схема коммутатора в терминах СМО

В терминах теории массового обслуживания, коммутационная матрица и процессор представляются как обслуживающий прибор (ОП), входной буфер как очередь, кадры как заявки, которые генерирует источник трафика (ИТ). Нагрузкой коммутатора является потребитель трафика (ПТ). Уровень загрузки входного канала выражается через интенсивность потока заявок. Вектор состояния канала обозначим через.

Если принять допущение об однородности трафика, тогда каждое состояние канала– номер сгенеренного кадра, будет состоять из двух фаз: "p-" – межкадровая пауза, и "p+" – передача кадра. Длительность межкадрового интервала обозначим, а длительность передачи кадра. Процесс передачи кадров показан на рис. 2.2.

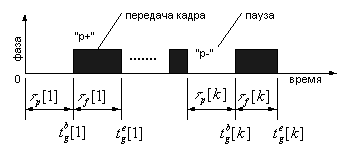
Рис. 2.2. Функциональная диаграмма
процесса передачи кадров в канале

Длительность фазы "p+" связана с размером кадра, соотношением

, (2.1)

где– битовая скорость канала, постоянный аппаратный параметр. Начало передачи кадрахарактеризуется временной отметкой, а окончание отметкой. Технология Gigabit Ethernet передает кадры переменной длины при переменном межпакетном интервале, поэтому минимальный вектор состояния канала при допущении об изотропности кадров характеризуется двумя компонентами [13]:

. (2.2)

Кадр Gigabit Ethernet состоит из преамбулы (служит для синхронизации передатчика и приемника физического уровня), служебной части и полезной нагрузки [13]. Размер преамбулы зафиксирован в 512 бит, а служебной части в 144 бит. Минимальное значение “чистого” межкадрового интервала в точности равно времени передачи 96 бит и составляет для Gigabit Ethernet 96 нс, а максимальное значение не ограниченно. Учитывая что преамбула на канальном уровне не обрабатывается, получаем значение “реального” минимального межкадрового интервала в 608 нс.

Таблица 2.1
Параметры канального уровня Gigabit Ethernet

Параметр	Кадр минимальной длины	Кадр максимальной длины
Размер кадра без преамбулы	64 байта	1 518 байт
Полезная нагрузка	368 бит	12 000 бит
Доля полезной нагрузки	71,88%	98,81%
Минимальный период следования кадров	1,120 мкс	12,752 мкс
Максимальная частота следования кадров	892 857 кадр/с	78 419 кадр/с
Максимальная полезная пропускная способность	328,571 Мб/с	941,028 Мб/с

Наиболее важные параметры канального уровня Gigabit Ethernet приведены в табл. 2.1. В итоге получаем, что компонентавекторадискретна по своей природе и определена на битовом отрезке

, (2.3)

с дискретой в 8 бит. Компонентанепрерывна и определена на наносекундном полуинтервале

. (2.4)

С точностью достаточной для инженерных расчетов, компонентуможно также представить дискретной, с интервалом дискретизации в 1нс. Ошибка дискретизации в этом случае составляет менее. Тогда процесс порождающий минимальный вектор состояния канала, будет дискретен и по времени и по уровню.

Период следования кадров в канале есть величина. Отношение минимального периода к текущему, есть текущий уровень загрузки канала. С учетом вышеизложенного, уровень загрузки канала будет зависеть и от размера кадра и от межкадровой паузы следующим образом:

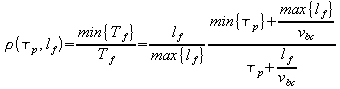. (2.5)

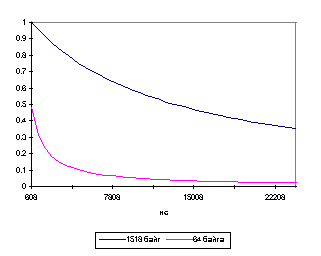
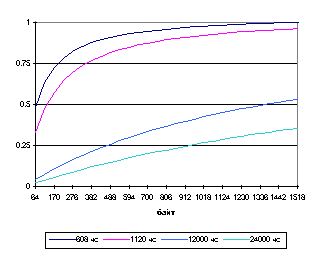
На рис. 2.3а изображен график функции (2.5) в зависимости от значения межкадрового интервала для двух размеров кадров: 64 байта и 1518 байт, а на рис. 2.3б в зависимости от размера кадра для четырех значений межкадровой паузы: 608нс, 1120нс, 12000нс и 24000нс.

а) б)
Рис. 2.3. Зависимость уровня загрузки канала

Из рис. 2.3б наглядно видно, что одному и тому же уровню загрузки канала, соответствуют разные комбинации размера кадра и межкадровой паузы. Возникает закономерный вопрос, как будут вести себя динамические характеристики коммутатора, если уровень загрузки канала будет оставаться постоянным, но размер кадра и длительность межкадровой паузы будут изменяться. Дать ответ на этот вопрос оставаясь в рамках классических моделей на основе СМО, не представляется возможным, поэтому требуется разработка и изучение модели, учитывающей эти особенности.

2.2. Разработка математической модели коммутатора

Для составления математической модели, детализируем исходную функциональную модель устройства коммутации трафика (см. рис. 2.1). Развернутая функциональная модель представлена на рис. 2.4.

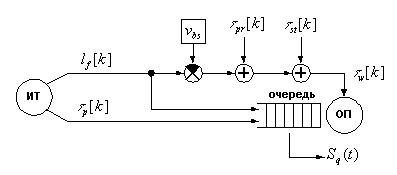
Рис. 2.4. Детализированная модель коммутатора

На вход СМО поступает поток заявок (см. подраздел 2.1), который описывается двумя случайными величинами:– длительность межкадрового интервала, и– размер кадра. Битовая скорость коммутациипринимается постоянной, так как является аппаратным параметром. Время обработкив общем случае зависит от размера кадра, времени обработки заголовкапроцессором (производится проверка контрольной суммы и определяется выходной порт по записи “адрес-порт” в таблице коммутации) и времени остающегося до освобождения выходного порта занятого другими процессами. Две последние величины в нашей модели принимаем случайными, они зависят от конкретной технической реализации коммутатора и от режима его функционирования.

Так как входной буфер коммутатора имеет ненулевую и конечную емкость, СМО относится к классу систем с ожиданием и потерями [11]. Для этого класса систем СМО справедлив закон баланса, выражающийся в равенстве количества поступивших в систему заявок сумме количеств обслуженных, потерянных, и находящихся в буфере. Потерянные заявки возникают в силу конечной емкости буфера, при его переполнении. В качестве математической модели закона баланса, используем выражение

, (2.6)

которое определяет текущую длину очередив битах, через функции– количество поступивших битов,– количество скоммутированных битов и– количество потерянных битов.

Так как функцииопределяют количество битов к моменту времени, определим их как интегралы от функций состоянияв промежутке:

, (2.7)

, (2.8)

. (2.9)

Знакозначает неопределенность параметров функций на данном этапе синтеза модели. На основании свойств интеграла и формул (2.7) – (2.9), выражение (2.6) перепишем в следующем виде:

. (2.10)

Дальнейший синтез модели подразумевает определение функций,и, как по аргументам, так и по внутренней структуре.

Функцияопределяет состояние источника трафика следующим образом:

при фазе "p-" (межкадровая пауза), и при фазе "p+" (передача кадра). Процесс переключения состояний иллюстрируется рис. 2.2.

Учитывая дискретность процесса генерации кадров, моменты времени наступленияи окончанияфазы "p+", выразятся следующим образом:

, (2.11)

, (2.12)

где– номер обрабатывающегося кадра,.

Из (2.11) и (2.12) следует, что функцияимеет единичное значение внутри промежутка, вне его она равна нулю. В этом случае функция состояния источника трафика в терминах непрерывного временивыразится следующим образом:

, (2.13)

где– функция Хевисайда.

Через функциюопределяется состояние коммутатора теряющего (сбрасывающего) входящие кадры из-за переполнения его входного буфера емкостью. Состояние сброса характеризуется единичным значением функции:, а нормальный режим нулевым значением функции:. Состояние сброса характеризуется истинностью выражения, в этом случае потеря кадра начинается в момент времении заканчивается в момент.

Принимая во внимание вышесказанное, функцию сброса кадров определим так:

. (2.14)

Функцию состояния коммутационной матрицыпостроим для режима коммутации с буферизацией (“store-and-forward”), так как именно этот режим применяется в большинстве магистральных коммутаторов Gigabit Ethernet. При коммутации с буферизацией, входящий кадр при приеме полностью помещается во входной буфер порта. Затем процессор проверяет буферезированый кадр на наличие ошибок (проверка производится по контрольной сумме) и обрабатывает заголовок – определяя выходной порт. И только если ошибки не были обнаружены и канал коммутирующей матрицы оказывается свободным, то начинается собственно процесс коммутации – кадр передается на выходной порт (выходной буфер). Этот режим коммутации гарантирует полную фильтрацию ошибочных кадров и позволяет управлять всеми кадрами, проходящими через коммутирующее устройство.

Время собственно коммутации определяется размером кадраи битовой скоростью коммутации. Выразим

. (2.15)

Как уже указывалось выше, время обработки кадрав общем случае зависит от времени коммутации, времени обработки заголовкапроцессором (производится проверка контрольной суммы и определяется выходной порт по записи “адрес-порт” в таблице коммутации) и времени остающегося до освобождения выходного порта занятого другими процессами. Если же данный кадр был сброшен (потерян), то он отсутствует во входном буфере и время его обработки естественно равно нулю. Отсюда время обработки выразим

. (2.16)

Принимая во внимание вышеизложенные принципы функционирования коммутатора в режиме “store-and-forward” и учитывая дискретность процесса коммутации кадров, моменты времени началаи окончанияобработки кадров можно выразить следующим образом:

, (2.17)

. (2.18)

С учетом формул (2.15), (2.17) и (2.18) моменты времени начала и окончания собственно процесса коммутации кадра, выразятся следующим образом:

, (2.19)

. (2.20)

Состояние коммутатора в режиме собственно коммутации кадра характеризуется единичным значением функции:, в иных состояниях функция принимает нулевое значение:.

В этом случае, с учетом (2.16), (2.19) и(2.20) функция состояния коммутационной матрицы (функция коммутации) в терминах непрерывного времени определится так:

. (2.21)

На данном этапе синтез математической модели динамики коммутатора можно считать успешно завершенным, так как все функции раскрыты как по аргументам, так и по структуре, т.е. выявлены все функциональные зависимости (на нашем уровне точности описания). Полная структура математической модели изображена на рис. 2.6.

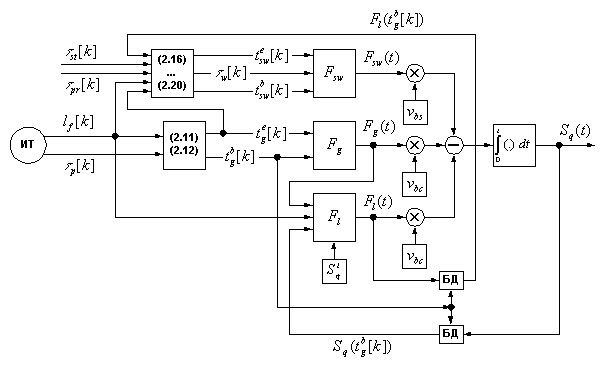
Рис. 2.6. Полная структура математической модели коммутатора

БД – обозначает дискретизацию функции по временной отметке.

Основными динамическими характеристиками коммутирующих устройств, задающими качество обслуживания, являются следующие величины:

– текущая длина очереди [бит].

– вероятность потери кадра из-за переполнения входного буфера:

. (2.22)

– величина задержки при коммутации кадра [сек]:

. (2.23)

– отклонение в задержках соседних кадров (Джиттер) [сек]:

. (2.24)

– рост межкадрового интервала [сек]:

. (2.25)

Эти величины и являются выходными параметрами разработанной модели.

Решение полученной математической модели, в силу наличия обратных связей в системе, в аналитическом виде не представляется возможным, поэтому требуется преобразование модели к виду, пригодному для численного решения. В основе этого преобразования лежит дискретизация непрерывного временного аргументас шагом в 1 нс., при этом максимальная ошибка дискретизации не превышает.

2.3. Проверка адекватности математической модели
реальным коммутаторам Gigabit Ethernet

Прежде чем применять полученную математическую модель для комплексного исследования динамических характеристик коммутаторов Gigabit Ethernet требуется оценить адекватность полученной математической модели реальным коммутаторам Gigabit Ethernet.

В качестве реального объекта исследования используем широко распространенный коммутатор “Cajun P550”, производства компании “Avaya”. Необходимые для численного моделирования аппаратные параметры этого устройства приведены в табл. 2.2. Необходимо заметить, что параметры приводятся для конфигурации коммутатора включающей 24 порта Gigabit Ethernet в полнодуплексном режиме работы.

Таблица 2.2

Параметры коммутатора Gigabit Ethernet

Параметр	Эффективное значение на один порт
Производительность коммутационного ядра	1,638 Гб/с
Производительность процессора	1 375 461 кадров/с
Объем памяти входного буфера	256 КВ

В табл. 2.3, представлены для сравнительного анализа усредненные результаты тестирования и моделирования. Результаты тестирования по одиночным пакетам взяты из [14], данные по реальному трафику получены самостоятельно. Мы видим (см. табл. 2.3), что максимальная ошибка моделирования не превышает 10%, это говорит о достаточной адекватности модели исследуемому объекту в части оценки его вероятностно-временных характеристик. Данная точность вполне приемлема для практических, инженерных исследований.

Таблица 2.3

Результаты тестов и моделирования

Параметр	Тест	Модель	Ошибка
Задержка одиночного кадра, 64 байта	3,42 мкс	3,64 мкс	6,43%
Задержка одиночного кадра, 1518 байт	10,15 мкс	9,62 мкс	5,51%
Задержка (реальный трафик, 200 пакетов)	7,12 мкс	6,93 мкс	2,74%
Джиттер (реальный трафик, 200 пакетов)	1,66 мкс	1,78 мкс	7,23%

3. ИССЛЕДОВАНИЕ ЗАВИСИМОСТИ ДИНАМИКИ КОММУТАТОРА GIGABIT ETHERNET
ОТ УРОВНЯ ЗАГРУЗКИ КАНАЛА

3.1. Постановка задачи

Вероятностно-временные характеристики трафика голоса, видео и данных в установившихся режимах существенно отличаются. Видео передается кадрами большого размера, а при передачи голоса используются кадры малого размера. Трафик передачи данных имеет весьма неравномерный во времени (спорадический) характер [15]. Как уже было показано в разделе 2.1, одному и тому же уровню загрузки канала, соответствуют разные комбинации размера кадра и межкадровой паузы. Анализ на основе уровня загрузки канала потенциально может приводить к неоднозначной оценке динамики коммутаторов при передачи разных видов трафика. Применим разработанную модель для выяснения этого обстоятельства. Учитывая, что в установившемся режиме вероятностно-временные характеристики коммутатора зависят от длительности режима будем оперировать первыми производными по времени и по количеству пакетов от следующих параметров:

· размер очереди;

· задержка кадра;

· приращение межкадрового интервала.

3.2. Результаты численного моделирования

Численное моделирование проводилось при тех же самых аппаратных параметрах модели, что и оценка ее адекватности. Данное обстоятельство позволяет привязать результаты моделирования к коммутатору “Cajun P550”, и тем самым повысить практическую значимость результатов работы.

В данной работе не рассматривается влияние уровня загрузки устройства и алгоритмов управления классами, потоками и очередями на его динамические показатели.

Моделирование установившихся режимов приводилось для последовательности длиной в 100 кадров. Данная величина получена после интерпретации данных приведенных в работе [16]. Результаты проведенного численного эксперимента показывают, что в установившемся режиме вторые производные динамических параметров равны нулю. Сводные данные эксперимента приведены в табл. 3.1.

Таблица 3.1

Зависимость динамических параметров от уровня загрузки канала

	байт	нс	бит/нс	бит/кадр	нс/нс	нс/кадр	нс/нс	нс/кадр
0,17	64	2 708	47,58	153,2	1,92	6 184	0,35	1 117
0,17	604	23 408	17,08	482,4	0,21	5 919	0,11	3 007
0,48	64	608	366,25	410,2	13,96	15 634	2,68	3 007
	388	3 608	46,13	309,6	0,75	5 055	0,31	2 057
	1 518	14 108	46,23	1 213,6	0,36	9 575	0,27	7 029
0,78	226	608	398,26	962,2	5,53	13 366	1,3	3 136
0,78	1 518	4 208	74,22	1 213,6	0,58	9 575	0,43	7 029

3.3. Анализ результатов

Современные сети передают высокую долю трафика критичного к качеству обслуживания, а оно в свою очередь напрямую зависит от динамических характеристик коммутаторов. Сравнительный анализ данных представленных в табл. 3.1 показывает, что оперирование уровнем загрузки канала при исследовании динамики коммутирующих устройств Ethernet может приводить к неоднозначным выводам, так как значения динамических параметров при фиксированном уровне загрузки, существенным образом зависят от комбинации размера пакета и межкадровой паузы. Поэтому оперирование только уровнем загрузки канала при описании трафика и динамики коммутаторов и/или сетей не способствует проектированию более оптимальных устройств и сетей.

4. ВЫВОДЫ

В процессе проведенных в работе исследований получены следующие основные результаты:

1. Разработан новый подход к созданию моделей динамики устройств коммутации трафика телекоммуникационных систем.

2. На основе нового подхода создана математическая модель коммутатора Gigabit Ethernet учитывающая переменный размер кадра и вариацию межкадрового интервала, а также уровень загрузки коммутационного устройства. Учет данных параметров позволяет точнее исследовать динамику различных режимов функционирования коммутатора, что способствует проектированию более оптимальных устройств и сетей.

3. Выполненная проверка разработанной модели показала ее достаточную точность и адекватность реальным исследуемым объектам в части оценки их вероятностно-временных характеристик.

4. По результатам численного эксперимента определен ряд динамических параметров коммутатора Gigabit Ethernet в установившихся режимах функционирования. Для адекватной оценки этих режимов введены новые параметры, а именно первые производные известных вероятностно-временных показателей. Введение этих параметров позволило избавиться от неоднозначности (вероятностно-временных характеристики зависят от длительности режима). Также показано, что в установившемся режиме, вторые производные динамических параметров равны нулю.

5. Показана частичная некорректность применения обобщенного параметра – уровня загрузки канала при моделировании коммутирующих устройств Ethernet. При использовании данного параметра анализ систем возможен лишь обобщенный, и особенности отдельных режимов остаются без внимания.

В настоящий момент проводится дополнительное расширение модели для учета влияния ею алгоритмов управления классами, потоками и очередями на динамику коммутатора. Также проводится исследование динамики стохастических режимов по уровню потерь кадров и джиттеру.

ЛИТЕРАТУРА

1. Нетес В. А. Качество обслуживания на сетях связи. Обзор рекомендаций МСЭ-Т. – “Журнал “Сети и системы связи”, №3, 1999. – 66-71 стр.

2. Энди Дорнани. Ethernet выходит в глобальные сети. – Журнал “LAN. Сетевые решения”, №11, 2000. – 52-57 стр.

3. Rosen E., 'Cisco Systems'; Viswanathan A., 'Force10 Networks'; Callon R., 'Juniper Networks'; “Multiprotocol Label Switching Architecture”. RFC3031, Jan. 2001.

4. Whitt W. Performance of the queuing network analizer, Bell Syst. Tech. J., vol. 62., pp. 2816-2843, July/Aug. 1980.

5. Башарин Г. П., Бочаров П. П., Коган Я. А. Анализ очередей в вычислительных сетях. Теория и методы расчета. – М.: Наука, 1989.

6. Kramer W., Langenbach-Belz. Approximation for the delay in the queuing systems GI|GI|1. Congressbook, 8^th ITC, Melbourne, 1976.

7. Клейнрок Л. Вычислительные системы с очередями. – М.: Мир, 1979.

8. Исследование операций: Модели и применение: Пер. с англ. / Под ред. Дж. Моудера, С. Элмаграби. – М.: Мир, 1981. – 712 с.

9. Ларионов А. М., Майоров С. А., Новиков Г. И. Вычислительные комплексы, системы и сети. – Л.: Энергоатомиздат. Ленингр. отделение, 1987. – 288 с.

10. Марков А. А., Моделирование информационно-вычислительных процессов. – М.: Изд-во МГТУ им. Э. Баумана, 1999. – 360 с., ил.

11. Гнеденко Б. В., Коваленко И. Н., Введение в теорию массового обслуживания. – Изд-во “Наука”, М., 1966. – 432 стр.

12. Ивченко Г. И., Каштанов В. А., Коваленко И. Н. Теория массового обслуживания. – М.: Высшая школа, 1982.

13. IEEE 802.3z. 1998 Edition. IEEE standards for Local Area Networks: Gigabit Ethernet.

14. Report 180998, September 1998, Mier Communications Inc.

15. Leland W. E., Taqqu M. S., Willinger W., Wilson D., “On the self-similar nature of ethernet traffic”, Proc. ACM SIGCOMM'93, pp. 183-193, 1993.

16. Ata S., Murata M., Miyahara H., “Analysis of Network Traffic and its Application to Design of High-speed Routers”, IEICE Trans. Inf. & Syst., Vol. E83-D, No. 5 May 2000, p. 988.

Автор: Макаренко Андрей Викторович, с.н.с. информационного центра СКГТУ, E-mail: compdep@nosu.ru