Рассмотрим приемную
радиотехническую систему, предназначенную для измерения временной задержки и
доплеровского сдвига частоты сигнала, отраженного от цели. Такая система
является многоканальной и имеет в каждом канале дальности набор цифровых
фильтров с фиксированными значениями доплеровских частот.
Корреляционно-фильтровой матрицей (КФМ) будем называть совокупность приемных
каналов для различных дальностей и доплеровских частот. Такая матрица
получается, например, путем оптимальной обработки принятого сигнала при
использовании алгоритма быстрого преобразования Фурье.
Соседние численные
значения элементов КФМ могут отличатся на достаточно малую величину, что
приводит к появлению отраженного от цели сигнала в двух и более элементах
матрицы. Представляет практический интерес вычисление характеристик обнаружения
сигнала в n элементах КФМ из m (m³2) с учетом корреляционных связей
между огибающими выходных значений смежных элементов данной матрицы. Знание
указанных характеристик позволит определить вероятность того, что сигнал от
одной цели занимает n элементов при заданном отношении сигнал/помеха и
фиксированном уровне ложных тревог, который обеспечивает идеально
функционирующая шумовая АРУ.
Считаем, что на вход
приемной системы поступает аддитивная смесь сигнала и флуктуационной помехи.
Сигнал является когерентной пачкой дружно флуктуирующих радиоимпульсов с
релевским законом распределения огибающих и равномерным распределением
начальных фаз.
Мгновенные значения
сигнала на выходе линейной части приемной системы имеют нормальное
распределение с параметрами (0, 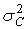 ). Флуктуационная помеха в полосе
пропускания приемной системы является стационарным нормальным случайным
процессом с параметрами (0,
). Флуктуационная помеха в полосе
пропускания приемной системы является стационарным нормальным случайным
процессом с параметрами (0, 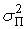 ).
).
Вероятность обнаружения сигнала
в n элементах КФМ из m равна [1]
|
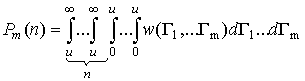 , ,
|
(1)
|
где 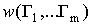 - совместная плотность
распределения огибающих на выходах элементов КФМ,
- совместная плотность
распределения огибающих на выходах элементов КФМ,
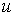 - пороговое значение, которое
связано с
- пороговое значение, которое
связано с 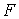 -
вероятностью ложной тревоги в одном элементе КФМ выражением
-
вероятностью ложной тревоги в одном элементе КФМ выражением
|
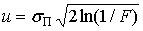 . .
|
(2)
|
В дальнейшем отношение сигнал / шум
считаем равным
|
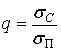 . .
|
(3)
|
Из выражения (1) следует,
что для вычисления вероятности обнаружения сигнала в нескольких элементах КФМ
необходимо определить функцию совместной плотности распределения 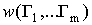 . Для ее
получения может быть использована методика, изложенная в [2]. При этом
выражение для m – мерной функции плотности распределения огибающих
представляют в виде произведения показательных и бесселевых функций.
Интегрирование данного произведения при разложении бесселевых функций в ряд по
коэффициентам корреляции не позволяет получить соотношения, удобного для
вычисления вероятности обнаружения сигнала в n элементах матрицы КФМ из m.
. Для ее
получения может быть использована методика, изложенная в [2]. При этом
выражение для m – мерной функции плотности распределения огибающих
представляют в виде произведения показательных и бесселевых функций.
Интегрирование данного произведения при разложении бесселевых функций в ряд по
коэффициентам корреляции не позволяет получить соотношения, удобного для
вычисления вероятности обнаружения сигнала в n элементах матрицы КФМ из m.
Введем эмпирическую
аппроксимацию, которая путем незначительного искажения корреляционных связей
между огибающими аддитивной смеси сигнала и помехи в смежных элементах КФМ 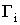 ,
, 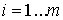 дает возможность
достаточно просто вычислять интеграл в выражении (1). Представим вероятность
обнаружения сигнала в n элементах КФМ из m в следующем виде
дает возможность
достаточно просто вычислять интеграл в выражении (1). Представим вероятность
обнаружения сигнала в n элементах КФМ из m в следующем виде
|
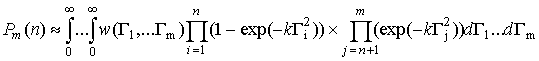 . .
|
(4)
|
В формуле (4)
интегрирование по каждой переменной ведется от нуля до бесконечности, а
значения порога учитывается в показательных функциях с помощью коэффициентов 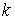 , которые
введены в подынтегральное выражения. Выбор показательных функций основан на
предположении, что с ростом значений огибающей
, которые
введены в подынтегральное выражения. Выбор показательных функций основан на
предположении, что с ростом значений огибающей 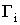 и вероятности превышения порога
умножение подынтегрального выражения в соотношении (1) на функцию вида
и вероятности превышения порога
умножение подынтегрального выражения в соотношении (1) на функцию вида
|
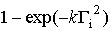 , ,
|
(5)
|
не изменяет характера
этой зависимости. Аналогичные рассуждения можно провести для случая не превышения
порога в 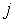 -
м элементе КФМ, где соответствующая вероятность с ростом значения огибающей
-
м элементе КФМ, где соответствующая вероятность с ростом значения огибающей 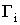 уменьшается и,
следовательно, выбирается функция вида
уменьшается и,
следовательно, выбирается функция вида
|
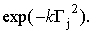
|
(6)
|
Значение коэффициента 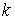 в выражениях
(5) и (6) может быть найдено из условия совпадения соотношений (1) и (4) для
одномерного случая m=1. Согласно предложенной аппроксимации имеем
в выражениях
(5) и (6) может быть найдено из условия совпадения соотношений (1) и (4) для
одномерного случая m=1. Согласно предложенной аппроксимации имеем
|
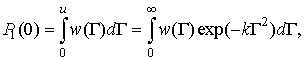
|
(7)
|
|
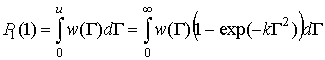 . .
|
(8)
|
Для введенных выше статистических
характеристик сигнала и помехи распределение огибающей аддитивной смеси сигнала
и помехи 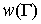 совпадает
с релеевской функцией [1]
совпадает
с релеевской функцией [1]
|
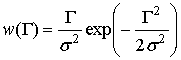 , ,
|
(9)
|
при 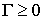 ,
, 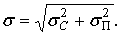
Подставим формулу (9) в
выражения (7) и (8)
|
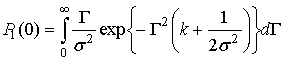 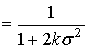 , ,
|
(10)
|
|
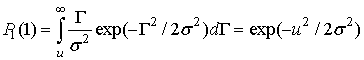 . .
|
(11)
|
Учитывая, что вероятности 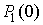 и
и 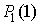 образуют полную группу событий,
т.е.
образуют полную группу событий,
т.е.
|
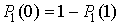 . .
|
(12)
|
Из соотношений (10)-(12) находим
|
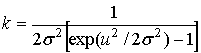 . .
|
(13)
|
В формуле (4) заменим
плотность распределения огибающих аддитивной смеси сигнала и помехи на
совместную плотность распределения квадратурных составляющих этой смеси 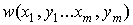 . Представим совместную
плотность распределения
. Представим совместную
плотность распределения 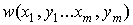 в виде 2m-мерной нормальной
плотности распределения
в виде 2m-мерной нормальной
плотности распределения
|
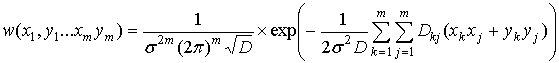 , ,
|
(14)
|
где 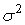 - дисперсия
квадратурной составляющей смеси сигнала и помехи,
- дисперсия
квадратурной составляющей смеси сигнала и помехи,
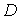 - детерминант
корреляционной матрицы
- детерминант
корреляционной матрицы 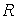 , соответствующей данной плотности
распределения,
, соответствующей данной плотности
распределения,
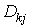 - алгебраическое
дополнение элемента
- алгебраическое
дополнение элемента 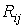 в матрице
в матрице 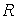 .
.
Подставим соотношение
(14) в выражение (4)
|
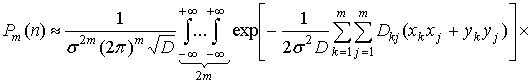
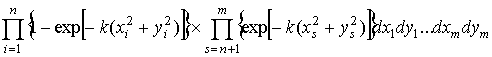 . .
|
(15)
|
Введем обозначение
|
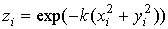 . .
|
(16)
|
Используя формулу
произведения двучленов [3], получаем
|
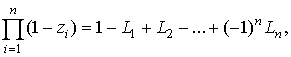
|
(17)
|
где 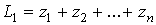 ,
,
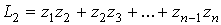 ,
,
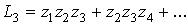 ,
,
и в общем виде 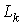 есть сумма
всевозможных произведений
есть сумма
всевозможных произведений 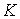 чисел
чисел 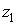 ,
, 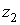 , …
, …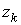 . Предположим, что величина
. Предположим, что величина 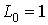 , соотношение
(17) можно представить в виде
, соотношение
(17) можно представить в виде
|
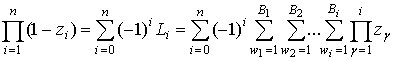 , ,
|
(18)
|
при 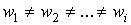 ,
,
где 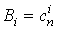 число сочетаний из n
по i.
число сочетаний из n
по i.
Подставим выражение (18)
в формулу (15) с учетом соотношения (16), меняя местами в формуле (15) операции
интегрирования и суммирования, а также учитывая независимость квадратурных
составляющих огибающих аддитивной смеси сигнала и помехи 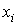 и
и 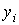 ,
, 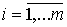 в совпадающие моменты
времени, получаем
в совпадающие моменты
времени, получаем
|
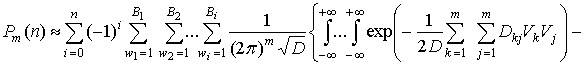
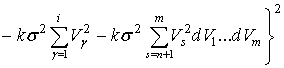 , ,
|
(19)
|
при 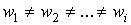 ,
,
где 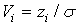 .
.
Из анализа правой части
соотношения (19) следует, что выражение вида
соответствует вероятности не превышения
порога в (m+i-n) элементах матрицы КФМ. Тогда вероятность
обнаружения сигнала в n элементах матрицы КФМ из m может быть
определена в виде
|
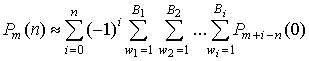 , ,
|
(20)
|
при 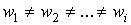 .
.
Из выражения (20)
следует, что для определения вероятности обнаружения сигнала в n
элементах КФМ из m необходимо вычислить вероятности непревышения порога 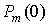 для любого m.
При n=0 из соотношения (19) получаем
для любого m.
При n=0 из соотношения (19) получаем
|
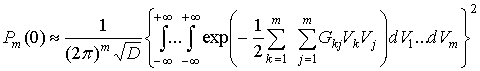 , ,
|
(21)
|
|
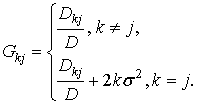
|
(22)
|
В векторной форме
выражение (21) имеет вид
|
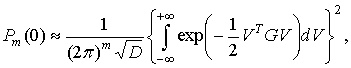
|
(23)
|
где 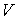 - вектор столбец
размерности [1´m],
- вектор столбец
размерности [1´m],
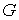 - положительно
определенная матрица размера [m´m].
- положительно
определенная матрица размера [m´m].
Интеграл в правой части
соотношения (23) равен [3]
|
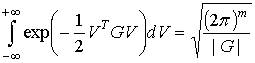 . .
|
(24)
|
Вероятность непревышения
порога в m элементах матрицы КФМ с учетом соотношения (24) равна
|
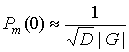 . .
|
(25)
|
Подставляя выражение (25)
в формулу (20), получаем итоговое соотношение для определения вероятности обнаружения
сигнала в n элементах КФМ из m
|
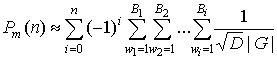 , ,
|
(26)
|
при 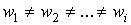 ,
,
где
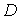 - детерминант
корреляционной матрицы
- детерминант
корреляционной матрицы
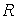 , а элементы матрицы
, а элементы матрицы
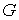 определяются по формуле
(22).
определяются по формуле
(22).
В качестве примера
рассмотрим КФМ, состоящую из четырех элементов – m=4 (см. рис. 1). Для
каждого столбца или строки этой матрицы (при m=2) корреляционная
матрица, соответствующая совместному распределению квадратурных составляющих
огибающих аддитивной смеси сигнала и помехи в совпадающие моменты времени,
имеет вид
|
 , ,
|
(27)
|
где 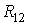 - коэффициент
корреляции между значениями огибающих аддитивной смеси сигнала и помехи в
строке или столбце матрицы.
- коэффициент
корреляции между значениями огибающих аддитивной смеси сигнала и помехи в
строке или столбце матрицы.
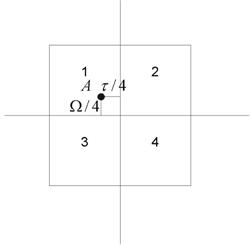
Рис. 1
Детерминант
корреляционной матрицы 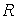 равен
равен
|
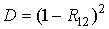 . .
|
(28)
|
Вычислим матрицу 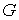 по формуле
(22). Детерминант этой матрицы равен
по формуле
(22). Детерминант этой матрицы равен
|
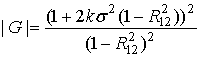 . .
|
(29)
|
Подставляя соотношения
(28) и (29) в формулу (26), получаем
|
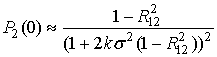 . .
|
(30)
|
В выражении (30) при 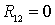 имеем точное
равенство
имеем точное
равенство
|
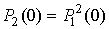 , ,
|
(31)
|
где 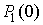 вероятность
непревышения порога в одном элементе КФМ вычисляется по формуле (10).
вероятность
непревышения порога в одном элементе КФМ вычисляется по формуле (10).
Аналогично вероятности 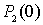 могут быть
определены вероятности непревышения порога для трех и четырех элементов КФМ,
соответственно,
могут быть
определены вероятности непревышения порога для трех и четырех элементов КФМ,
соответственно, 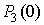 и
и 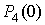 . Полученные значения вероятностей
непревышения порога -
. Полученные значения вероятностей
непревышения порога - 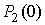 ,
, 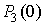 ,
, 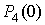 необходимо подставить в выражение (20).
Например, вероятность превышения порога в двух или трех элементах КФМ их
четырех равна
необходимо подставить в выражение (20).
Например, вероятность превышения порога в двух или трех элементах КФМ их
четырех равна
|
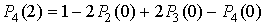 , ,
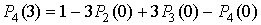 . .
|
(32)
|
Пусть параметры сигнала
цели соответствуют положению точки 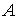 на рис. 1, т.е. отстоят от центра элемента
1 по времени на
на рис. 1, т.е. отстоят от центра элемента
1 по времени на 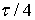 и частоте на
и частоте на 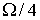 , где
, где 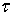 и
и  - размеры элемента КФМ.
Если опрос элементов КФМ проводится в один и тот же момент времени, то
коэффициенты корреляции в этих элементах равны
- размеры элемента КФМ.
Если опрос элементов КФМ проводится в один и тот же момент времени, то
коэффициенты корреляции в этих элементах равны
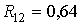 ,
, 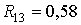 ,
, 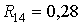 .
.
На рис. 2 представлены
зависимости (сплошные кривые) обнаружения сигнала в трех из четырех и необнаружения сигнала в четырех элементах КФМ от отношения сигнал / помеха 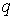 (см. формулу
(3)) при фиксированной вероятности ложной тревоги в одном элементе. Выбранные
примеры характеризуются большим диапазоном изменения вероятностей и удобны для
сравнения результатов расчета и цифрового моделирования.
(см. формулу
(3)) при фиксированной вероятности ложной тревоги в одном элементе. Выбранные
примеры характеризуются большим диапазоном изменения вероятностей и удобны для
сравнения результатов расчета и цифрового моделирования.
Цифровое моделирование
многоканальной системы проведено с помощью метода комплексной огибающей в
матричной форме [4]. В основу данного подхода положены метод комплексных
огибающих и уравнения метода пространства состояний, которые записываются в
матричной форме и позволяют получить основные зависимости в компактном виде,
удобном для программирования на ЦВМ. При этом, задав в качестве компонент
вектора состояний значения огибающих выходных напряжений элементов КФМ рассматриваемой
системы, можно одновременно проанализировать всю совокупность данных элементов.
На рис. 2 представлены
результаты цифрового моделирования (пунктирные кривые) при условиях, описанных
выше.
Рис. 2.
Как видно из рис. 2 погрешность между результатами
расчета и цифрового моделирования не превосходит 10-15%, что свидетельствует об
удовлетворительной аппроксимации многомерной плотности распределения огибающих
в элементах КФМ на основе соотношения (26).
Список
Литературы:
-
Тихонов В.И.
Статистическая радиотехника. – 2-изд., перераб. и доп. – М.: Радио и связь,
1982.
-
Пугачев В.П.
Теория вероятностей и математическая статистика: Учеб. пособие для вузов. –
М.: Мир, 1995.
-
Бронштейн И.Н.,
Семендяев К.А. Справочник по математике. – 10-изд. стереотипное. – М.: Наука,
1964.
-
Субботин С.В.,
Большаков Д.Ю. Цифровое моделирование многоканальных радиотехнических устройств
с помощью метода комплексной огибающей в матричной форме. ОАО "Концерн ПВО "Алмаз-Антей" - Вычислительные
устройства и ПО РЛС (тематический сборник) 2003, с. 105-109.
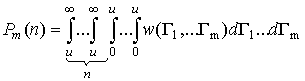 ,
,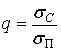 .
.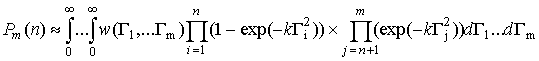 .
.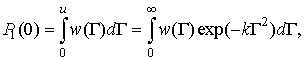
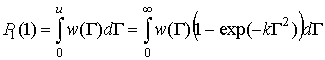 .
.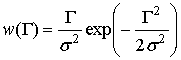 ,
,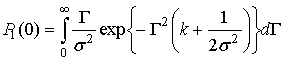
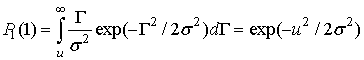 .
.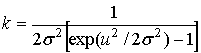 .
.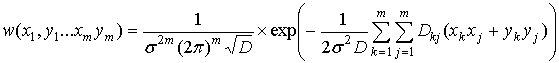 ,
,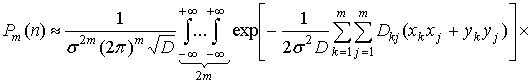
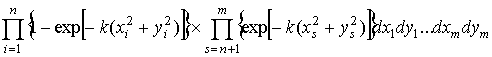 .
.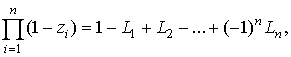
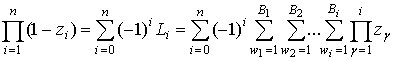 ,
,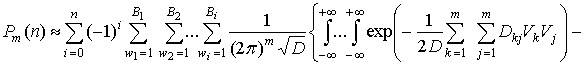
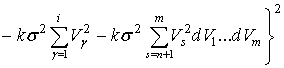 ,
,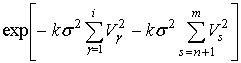
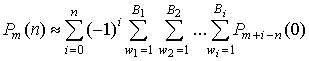 ,
,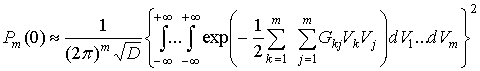 ,
,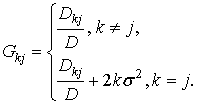
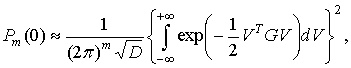
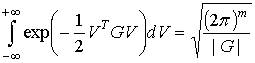 .
.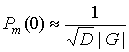 .
.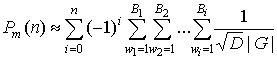 ,
, ,
,
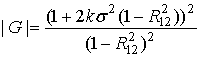 .
.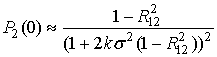 .
.