|
|
"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 5, 2006 |
|
ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ ДВУМЕРНЫХ ФОТОННЫХ КРИСТАЛЛОВ
А.Н. Боголюбов, И.А. Буткарев, Ю.С. Дементьева,
Московский государственный университет им. М. В. Ломоносова, Физический факультет
Получена 23 ноября 2006 г.
В статье строится численный алгоритм для исследования двумерных волноведущих систем. Для построения этого алгоритма используется метод конечных разностей во временной области (FDTD), метод TS/SF и метод идеального согласованного слоя (PML). Этот алгоритм применяется для исследования двумерных фотонных кристаллов и основанных на них устройств.
Фотонные кристаллы
В конце 80-х годов прошлого века была впервые предложена концепция фотонных кристаллов (ФК) [1].
Фотонные кристаллы это оптические материалы, для которых характерны следующие два свойства: диэлектрическая проницаемость меняется периодически с периодом, сравнимым с длиной волны света, и наличие связанной с периодичностью кристалла полной запрещённой зоны в спектре собственных электромагнитных состояний кристалла.
Рис. 1 Структура двумерного фотонного кристалла
Второе свойство отличает фотонный кристалл от обычной дифракционной решетки. Оно означает, что в определенном спектральном диапазоне свет любой поляризации не может распространяться в ФК ни в каком направлении в одном, двух или трех измерениях. Это и есть уникальное свойство фотонного кристалла, с которым принято связывать возможные революционные события в технике оптической связи, физике лазеров и оптической компьютерной технологии [2].
Фотонные кристаллы предоставляют новые возможности управления световыми потоками благодаря наличию полной запрещенной зоны в плотности электромагнитных состояний в заданной области частот. Внесение искажений в структуру кристалла позволяет создавать различные устройства, например волноводы, резонаторы, фильтры, разветвители, и др. [3,4,5,6,7].
Из-за отсутствия природных фотонных кристаллов первоочередной задачей является создание искусственных фотонно-кристаллических структур [8,9].
В данной работе рассматривается двумерный фотонный кристалл, диэлектрическая проницаемость в нём периодически меняется в двух направлениях. Он представляет собой набор диэлектрических стержней выставленных в узлах прямоугольной решетки с шагом H (рис. 1). Толщина стержней составляет h, а диэлектрическая проницаемость — e2. Удалив ряд стержней в таком кристалле можно создать фотонно-кристаллический волновод.
Распространение электромагнитного поля в таком кристалле описывается уравнениями Максвелла. Для исследования фотонных кристаллов и устройств, основанных на них, строится численный алгоритм, позволяющий вычислять распространение электромагнитного импульса через такую структуру. Вычислив спектр падающего поля и спектр прошедшего поля, удается сразу определить спектральные свойства волноведущей системы в определенном диапазоне частот, что является преимуществом перед рассмотрением данной задачи в частотной области.
FDTD-метод
FDTD-метод, возможно, самый популярный численный метод решения нестационарных задач электродинамики (см., например, [10]). Впервые этот метод был предложен К.С.Е в 1966 году [11]. В данный момент существует большое число модификаций данного метода. Рассмотрим вариант основанный на явной разностной схеме. Этот метод позволяет явно выразить значения компонент электромагнитного поля на следующем временном слое через значения на текущем слое. Недостатком метода является ограничение шага по времени и требование больших вычислительных ресурсов.
Рассмотрим уравнения Максвелла в ТМ случае (Ex=Ez=Hy=0) в отсутствие токов и свободных зарядов:
Задача решается в прямоугольной двумерной области S={(x, z): 0£x£a, 0£z£b}. Введём в этой области разностную сетку [12] wh={xi=ihx, zj=jhz, i=0,1,…,Nx, j=0,1,…,Nz}. Отрезок времени, на котором рассматривается решение задачи, также разбивается на конечное число интервалов — вводится сетка по временной переменной ws={ts=st, s=0,1,…}. Значение сеточной функции F в некотором узле сетки (xi, zj) в момент времени ts обозначим через
. Компонента поля Ey рассматривается в узловых точках области (i, j) и в моменты времени s, а компоненты Hx, Hz — в промежуточных точках области (i, j+0.5), (i+0.5, j) и в промежуточные моменты времени s+0.5.
Такое рассмотрение позволяет записать пространственные и временные производные в уравнениях через центральные разности. Например, для функции F в точке xi=ihx, zj=jhz в момент времени t=st производные по x и по t будут иметь вид:
Представляя в таком виде все производные в уравнениях (1)-(3), их можно переписать в следующем виде:
Уравнения (6)-(8) позволяют явно выразить значения компонент электромагнитного поля на следующем временном слое через значения на текущем слое:
Аналогично рассматривается ТЕ случай (Hx=Hz=Ey=0). Уравнения Максвелла в отсутствие токов и свободных зарядов имеют вид
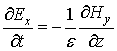
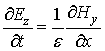
Разностный аналог этих уравнений:
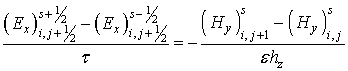
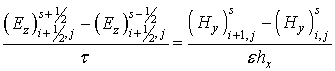
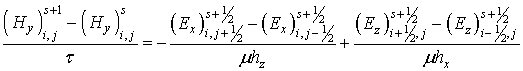
Разностная схема в данном случае принимает следующий вид:
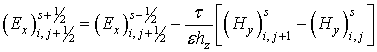
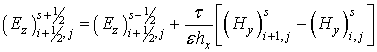
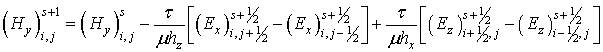
Данные схемы имеют второй порядок аппроксимации по времени и пространственным координатам. Условие сходимости этих схем:
.
PML-метод
Одной из важных проблем численного моделирования волноведущих систем, особенно открытых, является проблема ограничения области, в которой строится решение [13]. При решении нестационарных задач для ограничения области обычно используются поглощающие граничные условия.
Для постановки поглощающих граничных условий используется PML-метод (Perfectly Matched Layer) [14].
В соответствии с данным методом каждая компонента электромагнитного поля разделяется на две части. В декартовых координатах 6 компонент поля Ex, Ey, Ez, Hx, Hy, Hz заменяются на 12 подкомпонент: Exy, Exz, Eyx, Eyz, Ezx, Ezy, Hxy, Hxz, Hyx, Hyz, Hzx, Hzy, удовлетворяющих уравнениям:
В двумерном случае, из-за симметрии задачи, получается четыре уравнения и только одна компонента разделяется на две части. В случае TM поля разделяется компонента Ey на подкомпоненты Eyx, Eyz и рассматриваются уравнения
В случае TE поля компонента Hy разделяется на Hyx, Hyz и рассматриваются уравнения
Применяя к уравнениям (12)-(15) и (16)-(19) FDTD-метод, получим соответствующие разностные схемы (20)-(23) и (24)-(27):
Чтобы получить значения исходных компонент поля, нужно сложить значения соответствующих подкомпонент:
Значения параметров
зависят от расположения точки в области: внутри PML-слоя они отличны от нуля, а вне — равны нулю (рис. 2).
Параметры s* и s связанны соотношением:
.
Исследование параметров PML-слоя
Рассмотрим двумерную прямоугольную область (рис. 3).
Рис. 3. Схема области, в которой исследуются граничные условия PML
На границах z=0 и z=b введены PML-слои. Значения параметра sz заданы следующим образом:
,
где z1=hzN0, z2=hz(Nz-N0).
Численно моделирование показало, что при увеличении ширины N0 PML-слоя коэффициент отражения от границы уменьшается. При увеличении параметра smax до определённого значения коэффициент отражения уменьшается, а при дальнейшем увеличении — растёт. В таблицах 1 и 2 приведены результаты измерений коэффициента отражения от границы двумерной прямоугольной области с размерами a=b=10, Nx=Nz=500, hx=hz=0.02 для различных значений параметров PML-слоя smax и ширины N0:
smax
N0
R
smax
N0
R
10
10
0,482
10
50
0,024
10
20
0,205
102
50
0,007
10
50
0,029
103
50
0,002
10
100
0,015
104
50
0,011
10
200
0,011
105
50
0,037
Таблица 1. Зависимость коэффициента отражения R от ширины PML-слоя
Таблица 2. Зависимость коэффициента отражения R от параметра smax
Возбуждение поля. TF/SF – метод
Для возбуждения волноведущей системы используется метод total-field/scattered-field (TF/SF) [15]. Данный метод состоит в разделении расчетной области на две подобласти: область общего поля и область рассеянного поля (рис. 4).
Рис. 4. Схема разделения расчетной области при применении метода TF/SF
Так как уравнения Максвелла линейные, то электромагнитное поле можно представить в виде суммы падающего и рассеянного полей:
,
где индекс пад означает падающее поле, рас — рассеянное поле, общ — общее поле.
Область общего поля выбирается так, чтобы в ней полностью находился рассеивающий объект (существуют варианты TF/SF метода, в которых преодолено это ограничение), вся оставшаяся часть — это область рассеянного поля. В области рассеянного поля рассматривается только рассеянное поле, а в области общего — рассеянное и падающее. На границе между этими областями ставятся специальные граничные условия. Например, для одномерного TМ-случая эти условия на левой границе между областями общего и рассеянного полей имеют вид:
,
.
Аналогично на правой границе:
,
.
В двумерном случае условия на левой и правой границах совпадают с одномерными, а условия на нижней и верхней границах имеют следующий вид:
,
,
,
.
Индексы jлев, jправ, iнижн, iверхн соответствуют левой, правой, нижней и верхней координатам границы между областями общего и рассеянного полей.Задавая падающее поле специальным образом, можно рассматривать рассеяние электромагнитных волн на объекте, расположенном в области общего поля. Падающее поле можно получить, например, решая вспомогательную одномерную задачу, возбуждение которой осуществляется током.
В данном случае возбуждение поля осуществляется при помощи заданного тока:
,
где
,
, t0=2pw, w=p(fmax+fmin), fmax, fmin — изменяемые параметры. Спектр импульса, образованного таким током меняется в частотной области от fmin до fmax.
Численные результаты
Описанные методы были применены для моделирования прохождения электромагнитного импульса через фотонный кристалл.
Двумерный фотонный кристалл рассматривается в области S={(x, z): 0£x£a, 0£z£b} (рис. 5). В этой области моделируется электромагнитный импульс, распространяющийся в положительном направлении оси z и падающий на кристалл.
Рис. 5. Область, в которой проводились численные расчеты
Кристалл характеризуется параметрами H — постоянная решётки кристалла, ε1, ε2 — диэлектрические проницаемости, Npc характеризует размер кристалла. Во всех измерениях диэлектрические проницаемости ε1 и ε2 равны соответственно 1 и 8, h=0.05, H=0.1, Npc =40. Размеры расчетной области составляют: a=8, b=10. Расчеты велись на разностной сетке c hx=hz=0.025, Nx=320, Nz=400 и шаге по времени t=0.012. На границе расчетной области поставлены поглощающие граничные условия типа PML с параметрами: smax=1000, толщина PML-слоя составляет 10% от размеров области: рядом с границами z=0 и z=b — 1, x=0 и x=a — 0.8. Область общего поля имеет размеры 6.3×6.3 и расположена симметрично в центре расчетной области. Параметры, определяющие спектр импульса, падающего на кристалл, выбраны следующим образом fmin=0, fmax=10.
После прохождения импульса через фотонный кристалл, в спектре появляются запрещённые зоны — области, в котороых коэффициент пропускания близок к нулю. При увеличении размера кристалла Npc эти зоны имеют более чёткий вид (рис. 6).
Рис. 6. Спектр поля, прошедшего через фотонный кристалл: а — Npc=10, б — Npc=50
Запрещённые зоны существуют для различных поляризаций. Электромагнитные импульсы, имеющие различные поляризации, после прохождения через фотонный кристалл имеют спектры, в которых есть общие запрещённые зоны. На рис. 7 показаны соответствующие спектры для TМ-поля (Ex=Ez=Hy=0) — рис. 7а и TE-поля (Hx=Hz=Ey=0) — рис. 7б.
Рис. 7. Спектры поля разной поляризации, прошедшего через фотонный кристалл: а — ТМ, б — ТЕ
Удаляя ряд стержней из фотонного кристалла можно создать фотонно-кристаллический волновод, работающий в диапазоне запрещенных зон (рис. 8).
Рис. 8. Модель фотонно-кристаллического волновода
Из рис. 9 видно, что падающая на границу фотонного кристалла плоская волна частично втягивается в волновод с области большей, чем сечение волновода. Следовательно, в данном случае, управляя характеристиками фотонного кристалла на границе (положением стержней), можно изменять степень проникновения электромагнитного поля в волновод.
Рис. 9. Спектр поля внутри фотонно-кристаллического волновода: а — в точке А, б — в точке В
Управлять направлением распространения света можно при помощи волноводных изгибов.
На рис. 10 изображена модель фотонно-кристаллического волновода с изгибом.
Рис. 10. Модель фотонно-кристаллического волновода с изгибом
Спектр рассеянного поля на выходе из этого изгиба изображён на рис. 11а. Если сравнить этот спектр со спектром поля, рассеянного аналогичным кристаллом без изгиба (рис. 7а), то видно, что в запрещённой зоне возникла полоса пропускания.
Из рис. 7б и рис. 11б видно, что аналогичные свойства наблюдаются и для другой поляризации.
Рис. 11. Спектр поля в изгибе фотонно-кристаллического волновода (точка В): а — ТМ-поле, б — ТЕ-поле
Еще одним вариантом волновода, основанного на фотонных кристаллах, является волновод связанных резонаторов (CCW) рис. 12а. На рис. 12б и 13б приведены вычисленные характеристики этого волновода и изгиба такого волновода, параметры фотонного кристалла и разностной сетки оставлены прежние.
Рис. 12. Результаты расчета CCW: а — схема CCW, б — результаты
Рис. 13. Результаты расчета изгиба CCW: а — схема изгиба, б — результаты
На рис. 14 приведены результаты расчета разветвления волновода связанных резонаторов.
Рис. 14. Результаты расчета разветвления CCW: а — схема разветвления, б — результаты
Заключение
Построенный численный алгоритм позволяет рассчитывать различные волноведущие системы, в частности, системы основанные на фотонных кристаллах. Проведен анализ эффективности поглощающих граничных условий PML. Применение комбинации PML и TF/ST методов даёт возможность существенно сократить вычислительные затраты за счёт уменьшения расчётной области.
Полученные численные результаты для волноводного изгиба показывают, что фотонные кристаллы являются очень удобными объектами для управления распространением света. Фотонные кристаллы позволяют существенно уменьшить размеры устройств, управляющих распространением электромагнитных волн, и являются перспективными объектами для применения в интегрально оптических устройствах. Рассмотрение задачи во временной области позволяет сразу получить характеристики волноведущей системы в определённом диапазоне частот, определяемом спектром падающих волн.
Литература
Yablonovitch E. Inhibited spontaneous emission in solid-state physics and electronics // Phys. Rev. Lett., 58, P.2059-2062 (1987).
Наний О.Е., Павлова Е.Г. Фотонно-кристаллические волокна // LIGHTWAVE Russian edition, 2004, №3, С.47-53.
Fan S., Villeneuve P.R., Joannopoulos J.D., Haus H.A. Channel drop filters in photonic crystals // Optics Express, 3, No.1, P.4-11 (06.07.1998).
Bayindir M., Ozbay E. Band-dropping via coupled photonic crystal waveguides // Optics Express, 10, No.22, P.1279-1284 (04.11.2002).
Wang Z., Fan S. Compact all-pass filters in photonic crystals as the building block for high-capacity optical delay lines // Physical Review, 68, 066616 (2003).
Harbers R., Moll N., Mahrt R.F., Ernil D., Bachtold W. Enhancement of the mode coupling in photonic-crystal-based organic lasers // Journal Of Optics A: Pure And Applied Optics, 7, P.S230-S234 (2005).
Cowan B.M. Two-dimensional photonic crystal accelerator structures // Physical Review Special Topics - Accelerators And Beams, 6, 101301 (2003).
Toader O., Berciu M., John S. Photonic Band Gaps Based on Tetragonal Lattices of Slanted Pores // Physical Review Letters, 90, No.23, 233901 (13.07.2003).
Noda S., Tomoda K., Yamamoto N., Chutinan A. Full Three-Dimensional Photonic Bandgap Crystals at Near-Infrared Wavelengths // Science, 289, P.604-606 (28.07.2000).
Tentzeris E., Krumpholz M., Dib N., Yook J-G., Katehi L. FDTD Characterization of Waveguide-Probe Structures // IEEE Trans. Microwave Theory Tech., 46, No.10, P.1452-1460 (October 1998).
Yee K.S. Numerical solution of initial boundary value problems involving Maxwell’s equations in isotropic media // IEEE Trans. Antennas Propagat., AP-14, P.302–307 (May 1966).
Ильгамов М.А., Гильманов А.Н. Неотражающие условия на границах расчетной области. М.: ФИЗМАТЛИТ, 2003.
Berenger J.-P. Three-Dimensional Perfectly Matched Layer for the Absorption of Electromagnetic Waves // Journal of Computational Physics, 127, P.363-379 (1996).
Anantha V., Taflove A. Efficient Modeling of Infinite Scatterers Using a Generalized Total-Field/Scattered-Field FDTD Boundary Partially Embedded Within PML // IEEE Trans. Antennas Propagat., 50, No.10. P.1337-1349 (October 2002).
Авторы: Боголюбов Александр Николаевич, Буткарев Иван Андреевич, e-mail: butkarev@phys.msu.ru, Дементьева Юлия Сергеевна, Московский Государственный Университет им. М.В. Ломоносова, Физический факультет.