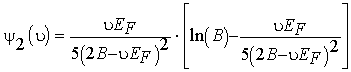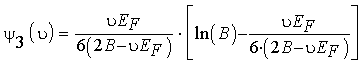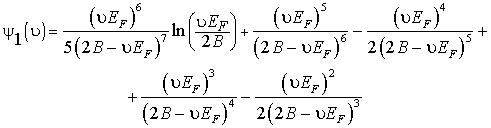|
|
"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 5, 2006 |
|
электрон-электронные взаимодействия в умеренно
легированном
гетеропереходе AlxGa1-x/GaAs
А. Б. Дюбуа
Рязанский институт открытого обраования
Получена 28 ноября 2006 г.
Исследован вклад внутризонной электрон-электронной релаксации в затухание квантования Ландау осцилляций поперечного магнитосопротивления. Получены выражения параметрических зависимостей
от температуры
, которые объясняют экспериментальные зависимости для умеренно легированного гетероперехода
(x=0.3), аппроксимированного треугольным потенциальным профилем, при условии заполнения основной подзоны размерного квантования.
Электрон – электронные ("е-е") взаимодействия играют определяющую роль в кинетических явлениях, среди которых следует отметить эффекты горячих электронов, квантовые поправки к проводимости и затухание (разрушение) квантования Ландау в объемных и двумерных полупроводниковых соединениях с вырожденными электронами [1]. Необходимость создания сильноточных высокочастотных электронных устройств стимулировало теоретические и экспериментальные исследования в области физики низкоразмерных полупроводниковых наноструктур. Для корректной теоретической интерпретации экспериментов необходимо нахождение явного вида зависимостей времени электрон - электронных взаимодействий от температуры
в приближении хаотических фаз [2].
Суть метода состоит в следующем. Роль внешнего возмущения играет потенциал экранирования, в который входит диэлектрическая функция электронного газа. Далее, Фурье – образ внешнего возмущения (обычно ограничиваются вторым членом разложения) подставляется в уравнение Больцмана, результатом решения которого является время "е-е" релаксации. Решение этого интегро – дифференциального уравнения представляет большие математические сложности. В первую очередь это связано с необходимостью точного учета потенциального профиля квантовой ямы. Чаще всего (см. например [3]) используется в качестве аппроксимации бесконечная прямоугольная квантовая яма, что делает все последующие преобразования неприменимыми для исследования более сложных квантовых структур.
Зонные диаграммы исследованных наноструктур были рассчитаны методом самосогласованного решения уравнений Шредингера
с граничными условиями
,
, (3)
с граничными условиями
,
(4)
где- диэлектрическая функция.
Самосогласованное решение системы (1)-(4) представляет определенные трудности из-за неопределенности распределения плотности заряда
.
В ряде работ (см. напр. [4]) уже были предприняты попытки расчета зонных структур гетеропереходов, однако авторы ограничились численным методом и не получили аналитического решения. Кроме того, в решении системы (1)-(4) могут возникнуть разного рода расходимости, существенно влияющие на конечный результат.
Так как суммарный интеграл
то в первом приближении должны существовать две области положительного и отрицательного зарядов:
и
с условием
. Так как
(
- уровень легирования), то простейшая аппроксимация
, (6)
Подставляя систему (6) в (5) и интегрируя, получим:
.
Далее, подставив (6) в (3) и после простых преобразований получим распределение потенциала:
Моделирование потенциала имеет существенный недостаток: произвол в определении постоянных
и
. Кроме того, используя данный метод, не удается решить уравнение Шредингера (1). В какой-то мере произвол можно снять с помощью граничного условия (4).
Откуда следует связь
.
Для решения уравнения (1) преобразуем его к виду:
где
- уровень Ферми, связанный с волновым вектором
соотношением
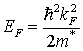
Для 2D-электронного газа справедливо
, где
- концентрация 2D-электронов.
Систему уравнений (1)-(4) удобно решать в новых безразмерных переменных:
,
,
,
,
.
Исходная система в новых переменных запишется как
где
.
В отсутствии внешних полей интеграл в (14) равен нулю.
Будем искать решение уравнения (12) в виде
где
- некоторые подлежащие определению константы, а
определяется из граничных условий как
.
Из уравнения (12) получим
,
а затем будем варьировать
в известных пределах и построим параметрическую зависимость функции
от
(рис.1). На этом же рисунке изображено решение системы (7)-(8). Подгоночными параметрами были выбраны
и
. Анализ показал, что зависимость
достаточно слабая.
Решение уравнения (11) представим как
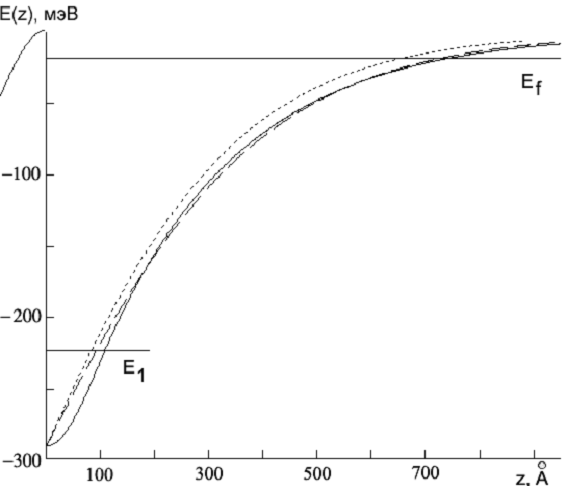
Рис. 1. Профиль потенциальной ямы: сплошная – решение системы (7)-(8); пунктирная – зависимость (16) при
,
; штриховая - зависимость (16) при
,
.
где
будет определяться из условий нормировки
Представляя (17) в виде
И подставляя в уравнение Шредингера (11) получим
(20)
где
, которое определяется из условия нормировки (18).
Фазовый сдвиг определяется суммой
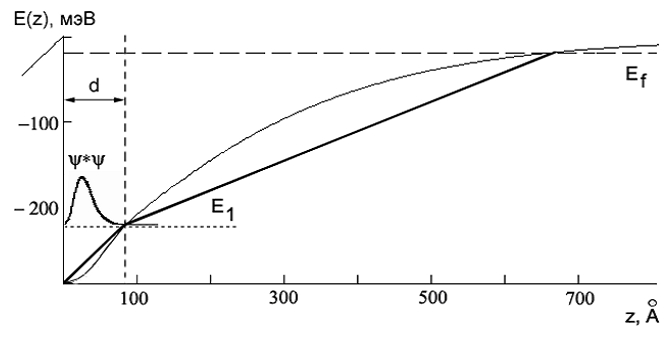
На рис.2 показана зависимость
, квадрат модуля волновых функций электронов на энергетическом уровне основной
подзоны размерного квантования. Для решения поставленной задачи реальный профиль
зоны проводимости гетероперехода аппроксимируем треугольной ямой, так как это представлено на рис.2. Рассмотрим двумерный электронный газ, находящийся в треугольной потенциальной яме. Представляя в области
потенциальный профиль в сферической системе координат как
(24)
с граничными условиями
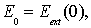
.
Рис. 2. Фрагмент
гетероперехода при
=6.3∙1011 см-2. Показана аппроксимация реального распределения потенциала треугольным профилем с изломом в точке пересечения с уровнем
.
Фурье-образ кулоновской экранировки будет иметь вид:
где
,
- линейные размеры системы, а Фурье-образ полной экранировки
Где диэлектрическая функция в приближении хаотических фаз (ПХФ) имеет вид (27).
В соответствии с теорией возмущений
где
— матричный элемент полного потенциала экранирования, а
- функция Ферми-Дирака. В случае одной заполненной подзоны имеем i=j=k=l=1. Здесь отступим от традиционного (численного) метода решения задачи, использовав нормировку вероятности электрон - электронных переходов на δ – функцию. В результате в процессе интегрирования (28) встречаются лишь сингулярные члены. Это позволило проинтегрировать (28) в элементарных функциях и получить результат, удобный для анализа. Воспользовавшись в процессе вычисления тождественным преобразованием
где
, а
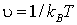
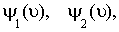
- зависящие от температуры функции, их явный вид приведен в Приложении. Приходим к окончательному выражению
При вычислении времени взаимодействия удобнее выражать энергию Ферми через концентрацию —
.
Проанализируем последнее выражение. По смыслу входящих в него величин можно указать, что основными факторами, влияющими на интенсивность электрон — электронного взаимодействия, являются 1) температура и 2) параметры потенциальной ямы. Оценим вклад каждого из них. Преобразуем (30) к виду
где функции
зависят только от параметров ямы и являются безразмерными, а
— от температуры и имеют размерность времени. Вышеуказанные функции представлены на рис.3 и 4, а
Рис. 3 Характер воздействия на
суммы (9) параметров
и
для реальных гетероструктур при
=225мэВ. Сплошные кривые —
,
при
Å, штриховые кривые —
,
при d=100Å
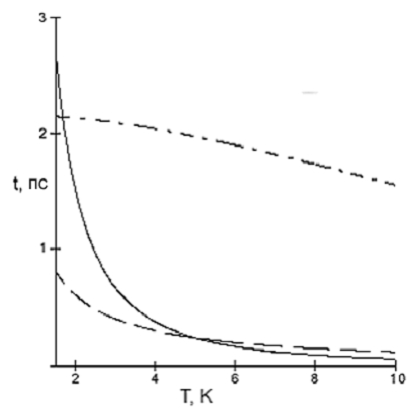
Рис. 4. Вариационный вклад в температурную зависимость компонентов Pn в (9) при
мэВ,
мэВ, d=86Å. P1 — сплошная кривая, Р2 — штриховая, P3 — штрих - пунктирная.
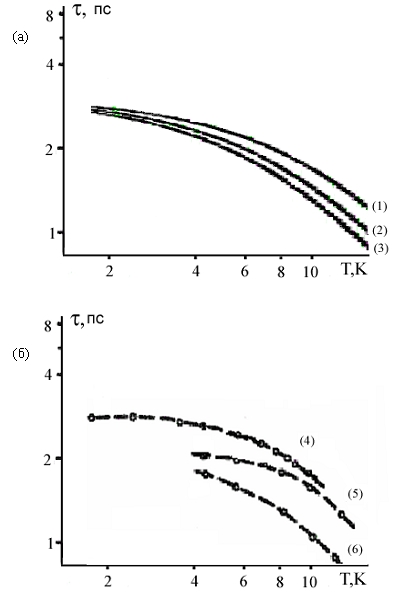
зависимость времени релаксации от температуры на рис.5. Сравним выражение (31) с экспериментальными данными [4] (рис.5). Варьируя параметры ямы в известных пределах (см. табл. 1), возможно добиться удовлетворительного согласия с экспериментальной работой [4]. Как видно из рис.2, имеются три параметра, задающих треугольную яму. Зафиксируем один из них
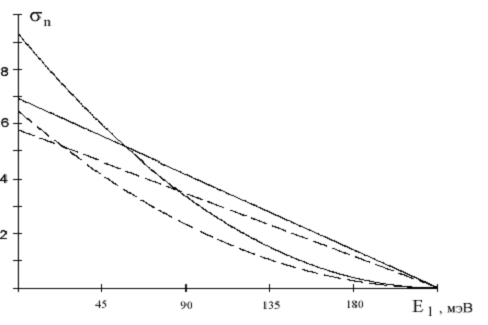
Рис. 5. Сопоставление теоретических (а) и экспериментальных (б) зависимостей для
=8∙1011 см-2 — (1) и (4),
=6.9∙1011 см-2 — (2) и (5),
=6.3∙1011 см-2—(3) и (6).
(пусть это будет
) и будем варьировать два других (ширина ямы
и
). Из рис.2 следует, что влияние первых двух слагаемых в (31) при значениях
мэВ будет несущественным и ход температурной зависимости времени "е-е" взаимодействия полностью определяется третьим слагаемым –
, повторяющим экспериментальные кривые.
Таким образом, аппроксимируя реальный профиль гетероперехода треугольной ямой, когда под уровнем Ферми имеется лишь одна заполненная подзона размерного квантования, удается добиться хорошего согласия результатов расчета
- времени внутриподзонной релаксации с экспериментальной зависимостью. Подгоночными параметрами служила лишь характеристика потенциальной ямы наноструктуктуры.
Параметры треугольной ямы, аппроксимирующей реальный профиль для трех образцов.
№ обр.
, 1011 см-2
, мэВ
, мэВ
d, Ǻ
1
6.3
225
165
86.0
2
6.9
225
162
87.5
3
8.0
225
161
87.0
Приложение
Литература
Т.Андо, А. Фаулер, Ф. Стерн. Электронные свойства двумерных систем. М.: "Мир", 416 с., (1985).
Д. Пайнс, Ф. Нозьер, Теория квантовых жидкостей, М., "Мир", 382 с., (1967).
M. Slutzky, O. Entin-Wohlman, Y. Berk, and A. Palevsky // Phys. Rev. B, 53, (7) 4065, (1996).
V.I. Kadushkin, E.L. Shangina, F.M. Tsahhaev // Phys. Low-Dim. Struct. 11/12, 43, (1998).
Автор: Дюбуа Александр Борисович, e-mail:
abd@rioo.ru, Рязанский институт открытого
образования.
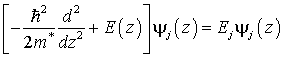
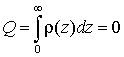 ,
(5)
,
(5)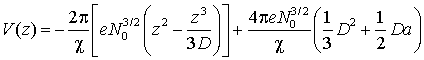 ,
,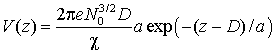 ,
,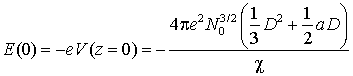 .
(9)
.
(9)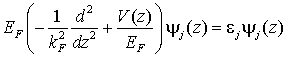 (10)
(10)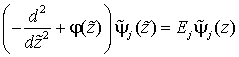 ,
(11)
,
(11)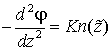 ,
(12)
,
(12)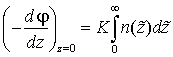 ,
(14)
,
(14)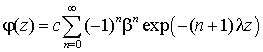 ,
(16)
,
(16)
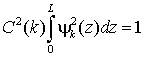 .
(18)
.
(18)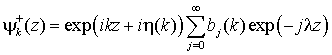 (19)
(19)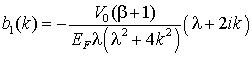 (21)
(21)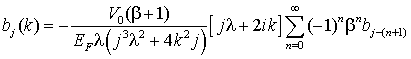 (22)
(22)
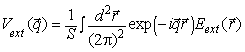
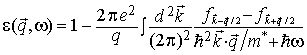 .
(27)
.
(27)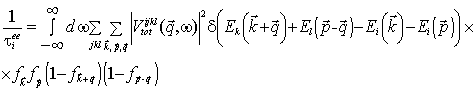 (28)
(28)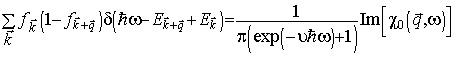 , (29)
, (29)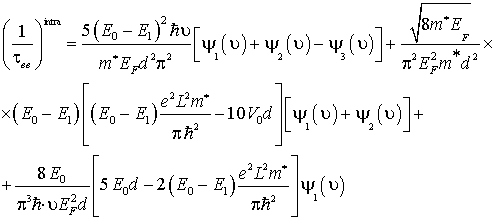 (30)
(30)