ВЫВОД УРАВНЕНИЯ ТИПА УРАВНЕНИЯ ГИНЗБУРГА-ЛАНДАУ ДЛЯ НАНОПРОВОЛОКИ ВБЛИЗИ КРИТИЧЕСКОГО МАГНИТНОГО ПОЛЯ
А. В. Семенов1, И. А. Девятов2, И. В. Третьяков1 , Ю. В. Лобанов1, Р. В. Ожегов1, Д. В. Петренко1, С. В. Селиверстов1, М. И. Финкель1
1 Московский педагогический государственный университет
2 НИИЯФ им. Д. В. Скобельцина МГУ им. М.В. Ломоносова
Получена 14 октября 2011 г.
Аннотация. В пределе больших магнитных полей выведено нелинейное уравнение Гинзбурга-Ландау, описывающее состояние одномерной «грязной» нанопроволоки.
Ключевые слова: сверхпроводимость, нанопроволока, уравнение Гинзбурга-Ландау.
Abstract. Nonlinear Ginzburg-Landau equation for dirty supercondicting 1D wire is derived in the limit of high magnetic field.
Keywords: superconductivity, nanowire, Ginzburg-Landau equation.
В ряде современных экспериментов [1, 2] исследуются одномерные сверхпроводниковые нанопроволоки (сверхпроводники, размер которых в сечении меньше или порядка длины когерентности ξ), помещённые во внешнее магнитное поле. Наложение внешнего магнитного поля позволяет управлять сверхпроводниковыми свойствами нанопроволоки, например, изменять частоту проскальзываний фазы или время жизни квазичастиц [Anthore2], не меняя температуры нанопроволоки, что представляет интерес как для фундаментальных исследований, так и для применений в микроэлектронике.
При достижении магнитным полем некоторого критического значения нанопроволока испытывает фазовый переход второго рода, при котором параметр порядка обращается в ноль. Эти обстоятельство позволяет вблизи критического магнитного поля свести уравнения микроскопической теории, описывающие состояние нанопроволоки, (в случае «грязной» нанопроволоки – уравнения Узаделя) к замкнутому уравнению для параметра порядка, аналогичному уравнению Гинзбурга-Ландау. Линеаризованное уравнение Гинзбурга-Ландау для сверхпроводника второго рода вблизи второго критического поля было получено в [3]. В одномерном случае одновременно с обращением в ноль параметра порядка расходится характерный пространственный масштаб ξ, на котором происходят изменения параметра порядка, благодаря чему, как мы покажем в настоящей работе, оказывается возможным получить полный аналог уравнения Гинзбурга-Ландау, содержащий нелинейный член. В идейном отношении процедура производится так же, как при предельном переходе от уравнений Узаделя к уравнению Гинзбурга-Ландау вблизи критической температуры перехода из сверхпроводящего в нормальное состояние [4].
Рассмотрим сначала пространственно-однородную ситуацию. Состояние нанопроволоки может быть описано уравнением Узаделя [5]
где G и F – функции Грина, связанные условием нормировки
![]() , (2)
, (2)
Δ – параметр порядка, ω – мацубаровская частота, а Γ – т.н. энергия распаривания, описывающая влияние магнитного поля. В случае, когда нанопроволока представляет собой полоску шириной w, а поле H ориентировано перпендикулярно поверхности полоски, Γ=e2DH2w2/6 (D – коэффициент диффузии). Параметр порядка выражается через функции Грина уравнением самосогласования
![]() , (3)
, (3)
Будем искать решение уравнения (1) разложением F в ряд по малому Δ. В нулевом порядке по Δ имеем, очевидно, G(0)=1, F(0)=0
1-й порядок. Уравнение Узаделя, записанное в первом порядке по Δ
![]() , (1.1)
, (1.1)
имеет решением
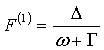 . Из условия нормировки (2), записанного в первом
порядке,
. Из условия нормировки (2), записанного в первом
порядке, ![]() , следует
, следует ![]() .
.
Подставив F(1) в уравнение самосогласования (3), имеем равенство
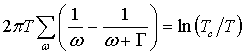 , (2.1)
, (2.1)
которое должно выполняться точно при критическом
значении энергии распаривания Γ=Γc. Взяв сумму по мацубаровским
частотам, 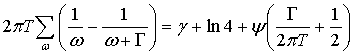 , в пределе T<<Γc получаем Γc=½Δ0. Здесь использованы асимптотическое поведение
дигамма-функции при больших значениях аргумента, ψ(x)≈lnx, и
известное соотношение между критической температурой и модулем параметра
порядка при нулевой температуре Tc=(eγ/π)Δ0.
, в пределе T<<Γc получаем Γc=½Δ0. Здесь использованы асимптотическое поведение
дигамма-функции при больших значениях аргумента, ψ(x)≈lnx, и
известное соотношение между критической температурой и модулем параметра
порядка при нулевой температуре Tc=(eγ/π)Δ0.
Для дальнейшего удобно переписать уравнение самосогласования вблизи Γc в виде
Во втором порядке
из уравнения Узаделя получается F(2)=0, а условие нормировки ![]() даёт
даёт
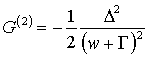 .
.
В третьем порядке решением уравнения Узаделя
![]() , (1.3)
, (1.3)
является
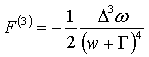 . Подставив это в уравнение самосогласования в форме (2а) и
взяв сумму по мацубаровским частотам (которую в пределе T<<Tc естественно заменить интегралом),
получаем формулу, дающую закон обращения в нуль Δ вблизи Γc:
. Подставив это в уравнение самосогласования в форме (2а) и
взяв сумму по мацубаровским частотам (которую в пределе T<<Tc естественно заменить интегралом),
получаем формулу, дающую закон обращения в нуль Δ вблизи Γc:
![]() . (3)
. (3)
В пространственно-неоднородной ситуации в левую часть уравнения Узаделя (1) добавляется слагаемое
![]()
(![]() означает дифференцирование по координате вдоль нанопроволоки). В силу
упомянутой выше малости градиентов, оно даст вклад лишь в третьем порядке по Δ. Теперь вместо (1.3) будем иметь
означает дифференцирование по координате вдоль нанопроволоки). В силу
упомянутой выше малости градиентов, оно даст вклад лишь в третьем порядке по Δ. Теперь вместо (1.3) будем иметь
![]() , (1.3а)
, (1.3а)
откуда
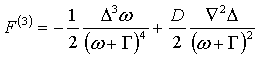 . Подставив это в (2а), приходим к уравнению для параметра
порядка
. Подставив это в (2а), приходим к уравнению для параметра
порядка
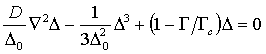 , (4)
, (4)
вполне аналогичному уравнению Гинзбурга-Ландау.
Работа выполнена при поддержке Министерства образования и науки, мероприятие 2011-1.9-519-005, государственный контракт № 11.519.11.4005, и в рамках реализации ФЦП «Научные и научно-педагогические кадры инновационной России» на 2009-2013.
Литература