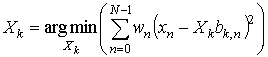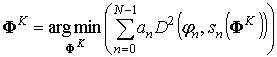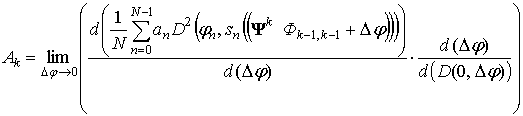УДК 004.932
МЕТОД WLSF ДЛЯ ПОСТРОЕНИЯ ДЕСКРИПТОРОВ ОКРЕСТНОСТЕЙ КЛЮЧЕВЫХ ТОЧЕК ИЗОБРАЖЕНИЙ
Д. А. Пиманкин
Нижегородский государственный технический университет им. Р.Е. Алексеева
Получена 6 ноября 2012 г.
Аннотация. Предлагается метод построения признакового описания окрестностей ключевых точек изображения на основе анализа ориентаций векторов градиента изображения с помощью метода наименьших взвешенных квадратов (метод WLSF). Показано, что для широкого класса изображений две модификации предлагаемого подхода могут быть с успехом применены для решения задачи сопоставления ключевых точек. Показано преимущество метода WLSF перед методом SURF при анализе зашумленных изображений.
Ключевые слова: метод наименьших взвешенных квадратов, ортогональное преобразование, признаковое пространство, сопоставление ключевых точек.
Abstract. Feature description build-up method for feature points neighborhoods based on image gradient vectors orientation analysis by weighted least squares (WLSF-method) is proposed. It is shown, that two modifications of this approach can be successfully applied for the task of feature points matching for a large class of images. The advantage of the WLSF-method over SURF-method in the case of noisy image analysis is shown.
Key words: Weighted least squares, orthogonal transformation, feature space, feature point matching.
Введение
Для успешного решения целого ряда задач компьютерного зрения и распознавания образов необходимо осуществление отображения исходного множества измерений в новое множество признаков. На сегодняшний день проблема генерации признаков, особенно на основе нелинейных преобразований, остается открытой. Целью такой генерации является сокращение информации об анализируемом объекте до «значимой», необходимой для решения конкретной задачи.
Под извлечением признака будем понимать отображение f : P → Qf, где P — множество измерений (множество всех изображений), Qf — множество допустимых значений признака. Достаточно хорошо изучены методы извлечения на основе различных ортогональных преобразований, таких как дискретное преобразование Фурье (ДПФ), дискретное косинусное преобразование (ДКП) и др., входного сигнала (изображения).
Количество признаков стремятся уменьшать по ряду причин. Одна из них состоит в следующем. Часто признаковое описание изображения состоит в представлении его в виде точки в N-мерном метрическом признаковом пространстве. Для эффективного поиска по большой базе данных используются специфические структуры данных, например M-деревья. С увеличением размерности пространства скорость обработки запросов типа ближайший сосед или k-ближайших соседей сокращается [3, 4].
Извлечение признаков на основе ортогональных преобразований
Известным методом анализа сигнала является его анализ в частотной области [1].
Рассмотрим некоторое ортогональное преобразование входного сигнала в самом общем случае. Пусть анализируемый сигнал xn. Разложим xn по базисным векторам bk, n. Если сигнал состоит из N отсчетов, то он может быть полностью описан N коэффициентами разложения. Иначе говоря, xn однозначно восстановим по N коэффициентам. Пусть базис B ортонормирован. Т. е. ||bn|| = 1 и bm ∙ bn = 0 (m ≠ n). Тогда проекцию сигнала на k-й базисный вектор можно записать следующим образом:
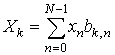 . (1)
. (1)
Очевидно, что при выше описанных условиях и по определению проекции Xk можно записать как:
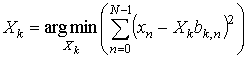 . (2)
. (2)
Т. е. при разложении сигнала по ортогональному базису, минимизируется сумма квадратов разностей компонент сигнала и базисного вектора, умноженного на коэффициент разложения.
В качестве компонент искомого вектора признаков обычно используются K низкочастотных коэффициентов разложения.
Метод наименьших взвешенных квадратов
При обычном ортогональном разложении сигнала все отсчеты входят в преобразование с одинаковыми коэффициентами, т. е. все отсчеты равнозначны. Идеей предлагаемого метода является построение такого преобразования, в котором различные отсчеты входили бы с различными коэффициентами [1]. Наибольший вес должен быть у наиболее информативных участков сигнала, наименьший — у наименее информативных.
Зависимость величины вклада некоторого участка сигнала от информативности этого участка достигается тем, что каждый из коэффициентов разложения Xk находится путем минимизации не суммы квадратов отклонений отсчетов сигнала xn и базисного вектора bk, n, а путем минимизации суммы взвешенных квадратов отклонений — методом наименьших взвешенных квадратов (МНВК):
Рис. 1 иллюстрирует проекцию двумерного сигнала на базисный вектор при одинаковых и разных (w0 < w1) весах компонент x1 и x2.
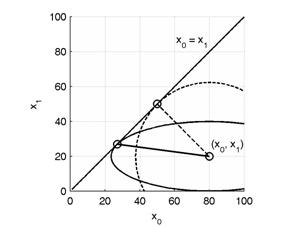
Рис. 1. Иллюстрация расстояния в МНК (пунктирная линия) и МНВК (сплошная линия).
Распишем метод наименьших взвешенных квадратов для суммы первых двух функций Хаара (Уолша). В данном случае будем минимизировать сумму взвешенных квадратов отклонений анализируемого сигнала и суммы базисных векторов, умноженных на коэффициенты разложения X0 и X1. Обозначим B0, n = X0 ∙ |b0, n| и B1, n = X1 ∙ |b1, n|.
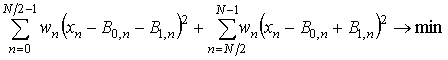 . (4)
. (4)
Продифференцируем левую часть выражения (4) по B0, n:
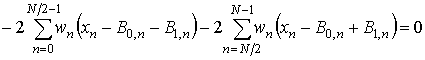 , (5)
, (5)
после раскрытия скобок имеем:
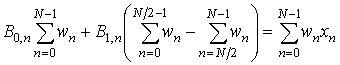 . (6)
. (6)
Аналогично, продифференцировав левую часть выражения (4) по B1, n после раскрытия скобок имеем:
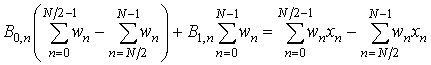 . (7)
. (7)
Из (6) и (7) видно, что коэффициенты X0 и X1 для МНВК (в отличие от МНК) независимы только в случае если:
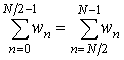 . (8)
. (8)
Т. е. в общем случае минимум СКО сигнала и каждого из векторов Xk ∙ bk, n по отдельности не соответствует минимуму СКО сигнала и суммы этих векторов. Этот вывод важен для понимания последующих рассуждений.
На рис 2 показан пример дискретного сигнала, его некоторой весовой функции wn и его аппроксимации первыми двумя функциями Хаара (Уолша) умноженными на коэффициенты разложений по формулам (2) и (3).
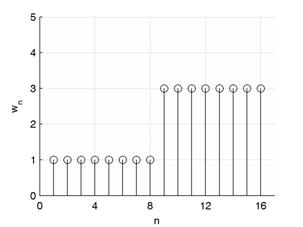
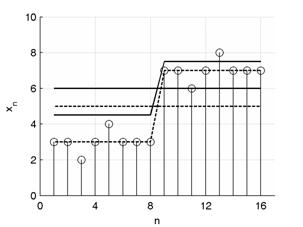
Рис. 2. График wn (слева); график xn (справа) и его разложение МНК (пунктирная линия) и последовательным МНВК (сплошная линия).
При разложении МНВК, перед нахождением X1, из анализируемого сигнала вычитается X0 ∙ bk, n (последовательная схема разложения). Очевидно, что при разложении в соответствии с (2) вычитание излишне. Здесь wn = 1 при n = 1, 2, …, 8; wn = 3 при n = 9, 10, …, 16.
Применение МНВК для описания областей изображения
Определим прямоугольную область изображения как двумерную функцию fm, n пространственных координат m и n. Значение функции в каждой точке, задаваемой парой координат, соответствует интенсивности изображения в этой точке. В цифровом представлении координаты m и n принимают дискретные значения: m = 0, 1, …, H – 1, n = 0, 1, …, W – 1. W и H — ширина и высота области изображения в пикселях, соответственно.
Для функции изображения в некоторой точке (m, n) можно определить градиент как двумерный вектор-столбец. Компонентами этого вектора являются частные производные функции fm, n по m и n. Значение вектора градиента в каждой точке можно представить в виде комплексного числа gm, n = gnm, n + j ∙ gmm, n. gm соответствует частной производной вдоль оси m, а gn — частной производной вдоль оси n. Таким образом, функции fm, n соответствует комплексная функция gm, n. Значение градиента в каждой точке можно также записать через его длину и угол (действительные функции двух переменных am, n и φm, n).
Для простоты анализа эффекты перекрытия при движении дифференцирующих масок учитываться в дальнейшем не будут. На рис. 3 приведено тестовое изображение и визуализация амплитуды поля градиента.


Рис 3. Область тестового изображения (слева), визуализация амплитуды градиента (справа).
Разделим комплексную функцию значений градиента изображения от координат на «сигнальную» составляющую, в качестве которой будем использовать φm, n, и «весовую» составляющую, в качестве которой будем использовать am, n. Идея анализа ориентаций градиентов для выделения дескрипторов областей изображений не нова, различные подходы описаны в работах [2, 5-8].
Теперь необходимо, во-первых, адаптировать МНВК для разложения аргумента градиента, т. е. для разложения сигнала с областью значений [– π, π), а во-вторых, т. к. полутоновое изображение является двумерным сигналом, описанное выше преобразование обобщить на двумерный случай.
Попытаемся построить некоторое отображение функции gm, n, компактно описывающее распределение ориентаций градиента в пределах исследуемой области изображения. При этом должна быть учтена и амплитуда градиента: подобласти с высоким значением амплитуды градиента должны вносить больший вклад, чем подобласти с малым значением.
Для начала рассмотрим одномерный сигнал xn.
Будем искать выходной вектор искомого отображения в виде:
![]() . (9)
. (9)
Внесем несколько замечаний по поводу используемых в дальнейшем обозначений. Здесь и далее будем обозначать aq = |xq|, φq = arg(xq), Aq = |Xq|, Φq = arg(Xq). Также будем считать каждое комплексное число xq эквивалентным вектору:
![]() . (10)
. (10)
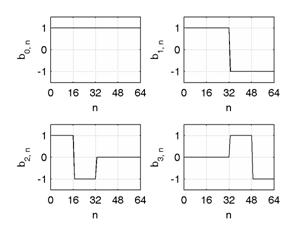
В качестве базисных векторов могут быть использованы базисные вектора ДКП, дискретного преобразования Уолша и др. Также можно использовать метод главных компонент. Наиболее простыми с точки зрения обоснования являются функции Хаара, их и будем использовать. На рис. 4 (слева) показаны графики первых 4-х функций Хаара.
Рис 4. Графики первых 4-х функций Хаара (слева) и их двумерный вариант (справа).
Найдем Φk.
Для начала необходимо определение адекватной метрики для множества комплексных чисел с единичным модулем.
Воспользуемся представлением комплексных чисел в виде векторов в декартовой системе координат и определим расстояние между двумя числами, через скалярное произведение. Найдем такое значение угла вектора, при котором максимизируется среднее значение скалярных произведений анализируемых векторов и единичного вектора u:
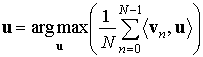 . (11)
. (11)
Приведем (11) к виду формулы (3):
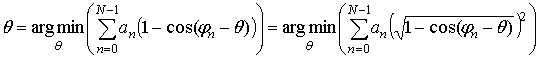 , (12)
, (12)
где: θ = arg(u).
Тогда выражение для расстояния между двумя числами (метрики) запишется следующим образом:
Для любого K ≤ N можно найти вектор ΦK = (ΦK – 1, 0, ΦK – 1, 1, …, ΦK – 1, K – 1):
где:
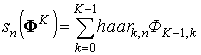 , (15)
, (15)
где: haar — функция Хаара с множеством значений {0, 1, –1}.
Введем для удобства следующие величины:
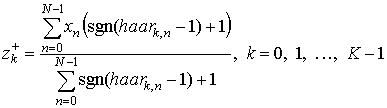 ; (16)
; (16)
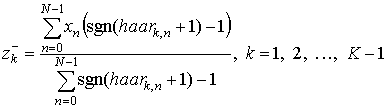 . (17)
. (17)
Из (14) нас в первую очередь будут интересовать Φk, k. Φ0, 0 может быть расписан следующим образом:
![]() . (18)
. (18)
Φk, k, k ≠ 0, запишется следующим образом:
![]() . (19)
. (19)
Найдем Ak.
Введем вектор ΨK = (ΨK – 1, 0, ΨK – 1, 1, …, ΨK – 1, K – 2):
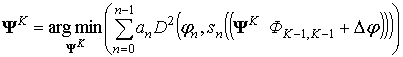 . (20)
. (20)
Теперь определим Ak как:
Из формулы (19) следует, что при расчете Φk сигнал может быть эквивалентным образом представлен двумя комплексными числами. Это также следует из области значений функций Хаара. Найдем для двух произвольных комплексных чисел коэффициенты Φ0 и Φ1. Изменим Φ1 на бесконечно малую величину Δφ и зафиксируем. Найдем новое значение для Φ0 выполнением условия (14) при условии неизменности Φ1. Тогда Δφk = Δφk+ + Δφk–. Зафиксируем Δφk. Из (13) и (20) следует:
![]() . (22)
. (22)
Продифференцировав по Δφk+ получим:
![]() . (23)
. (23)
Т. к. Δφk бесконечно мало, то в пределе получим:
![]() . (24)
. (24)
Отсюда и из условия Δφk = Δφk+ + Δφk– получаем выражения для Δφk+ через Δφk:
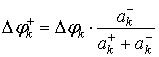 , (25)
, (25)
аналогично для Δφk– получим:
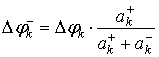 . (26)
. (26)
Теперь подставим Δφk+ и Δφk– в левую часть (22) и продифференцируем по Δφk. В пределе получим:
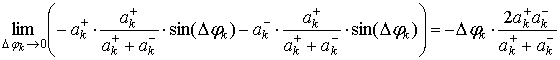 . (27)
. (27)
Сравнивая (13), (21) и (27) получим выражение для Ak:
![]() ; (28)
; (28)
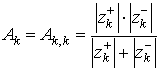 . (29)
. (29)
С учетом введенных выше обозначений предлагаемое преобразование можно записать следующим образом:
![]() ; (30)
; (30)
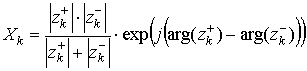 . (31)
. (31)
В качестве компонент искомого вектора признаков используются K низкочастотных коэффициентов описанного разложения. Т. е. каждому анализируемому изображению ставится в соответствие K-компонентный вектор признаков (X1, X2, …, XK) или точка в K-мерном метрическом пространстве (пространстве признаков). Коэффициенты |Xkq| перед расчетом D можно нормировать.
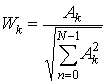 . (32)
. (32)
В качестве меры близости двух областей изображений будем использовать следующую величину:
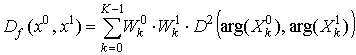 . (33)
. (33)
Для устранения эффекта обнуления меры близости только за счет весов, в формулу (33) добавим «стабилизирующее» слагаемое:
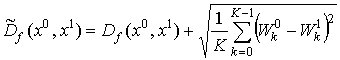 . (34)
. (34)
Обобщение преобразования на двумерный случай заключается лишь в замене функций Хаара на их двумерные аналоги. Рис. 4 (справа) иллюстрирует визуализацию 16 первых двумерных функций Хаара.
В дальнейшем будем называть описанное преобразование методом WLSF (Weighted Least Squares Features). В ряде задач требуется учитывать ориентацию градиента с точностью до π (т. е. не различать переходы от светлого к темному и от темного к светлому), для этого введем две модификации метода — WLSF2π и WLSFπ. Разница между WLSF2π и WLSFπ заключается в следующем:
1. в WLSF2π угол ориентирования квадратной окрестности анализируемой области может принимать значения в интервале [0, 2π), в WLSFπ — [0, π);
2. в WLSFπ нулевой коэффициент X0 рассчитывается по следующей формуле:
![]() . (35)
. (35)
Экспериментальные исследования и сравнительный анализ
На основе описанного преобразования был реализован алгоритм описания областей изображений в окрестностях ключевых точек для задачи их сопоставления. Сравнение проводилось с методом SURF [2].
Эксперимент ставился следующим образом. В качестве входных данных выступали изображения — оригинальные и зашумленные, с различной дисперсией гауссова шума. Гауссов шум был выбран как наиболее часто встречающийся на практике.
Примеры оригинальных и зашумленных (σ = 0.07 и σ = 0.15) изображений приведены на рис. 5.






Рис. 5. Пример искажений тестовых изображений.
Ключевые точки, размеры и ориентации анализируемых окрестностей искались по оригинальному изображению методом, также описанным в работе [2]. Отметим, что основным предметом тестирования являлось качество предложенного описания окрестностей точек, поэтому для чистоты эксперимента (чтобы исключить влияние алгоритма поиска ключевых точек) точки на исходном и зашумленном изображениях одни и те же — найденные по оригинальному изображению.
Вектора признаков окрестностей ключевых точек в первом случае получались методом SURF, а во втором случае методом, предлагаемым в данной работе (K = 16).
Примеры найденных ключевых точек представлены на рис. 6.


Рис. 6. Тестовые изображения и ключевые точки, полученные методом SURF.
Графики зависимостей процента неправильно сопоставленных ключевых точек от среднеквадратического отклонения гауссова шума для методов SURF и WLSF2π приведены на рис. 7 (сверху). Аналогичные графики для методов SURF и WLSFπ приведены на рис. 7 (снизу).
Очевидно, что WLSFπ в условиях только шумовых искажений будет давать несколько худшие результаты, чем WLSF2π, однако из сравниваемых методов лишь WLSFπ устойчив к градационным преобразованиям изображения с кусочно (или полностью) убывающей функцией преобразования интенсивности. Например, при дополнительной инверсии интенсивности одного из двух изображений (для которых ищутся соответствия точек) результат сопоставления точек не меняется.
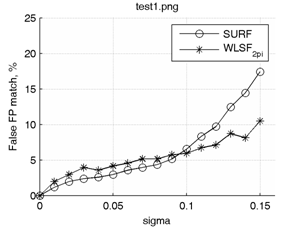
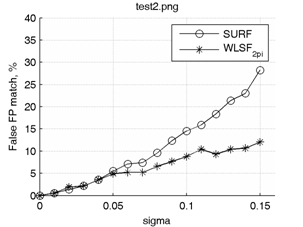
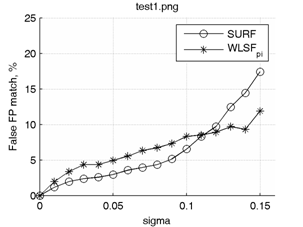
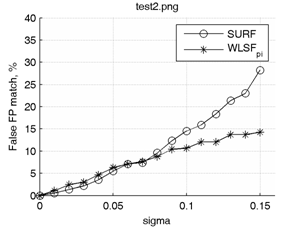
Рис. 7. Графики зависимостей процента неправильно сопоставленных ключевых точек от среднеквадратического отклонения гауссова шума.
Из графиков видно, что наибольший выигрыш точности от использования предложенного метода достигается при анализе сильно зашумленных изображений (σ > 0.1). При слабом уровне шумов методы SURF и WLSF в среднем показывают схожие результаты.
Итак, в ходе экспериментов был выявлен ряд позитивных и негативных особенностей метода.
К минусам метода можно отнести:
- сильная чувствительность к изменению масштаба по одной из осей (при повороте 3D сцены);
К плюсам относятся:
- слабая чувствительность к различным градационным преобразованиям изображений;
- слабая чувствительность к гауссову шуму.
Описанный метод с успехом может быть использован для построения признакового описания областей изображений в различных задачах компьютерного зрения, в том числе в задаче поиска изображений по содержанию.
1. Пиманкин Д. А. Построение признакового описания изображения на основе анализа распределения ориентаций векторов градиента. // Информационные системы и технологии-2012: Тезисы докл. – Нижний Новгород, 2012.
2. Bay, H., Tuytelaars, T., and Van Gool, L. (2006). SURF: Speeded up robust features. In Ninth European Conference on Computer Vision (ECCV 2006), pp. 404–417.
3. Berchtold S., Keim, D. A., and Kriegel H.-P. (1996) The X-Tree: An Index Structure for High-Dimensional Data. Proceedings of the 22nd International Conference on Very Large Data Bases (VLDB), Bombay, India: 28–39.
4. Ciaccia, P., Patella, M., and Zezula, P. (1997). M-tree An Efficient Access Method for Similarity Search in Metric Spaces. Proceedings of the 23rd VLDB Conference Athens, Greece. pp. 426–435.
5. Ke, Y., and Sukthankar, R. (2004). PCA-SIFT: a more distinctive representation for local image descriptors. In IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’2004), pp. 506–513, Washington, DC.
6. Lowe, D. G. (1999). Object recognition from local scale-invariant features. In Seventh International Conference on Computer Vision (ICCV’99), pp. 1150–1157, Kerkyra, Greece.
7. Lowe, D. G. (2004). Distinctive image features from scale-invariant keypoints. International Journal of Computer Vision, 60(2):91–110.
8. Mikolajczyk, K. and Schmid, C. (2005). A performance evaluation of local descriptors. IEEE Transactions on Pattern Analysis and Machine Intelligence, 27(10):1615–1630.