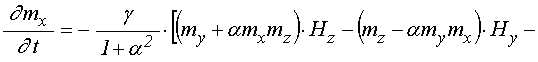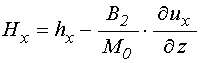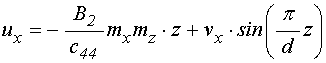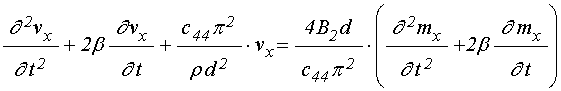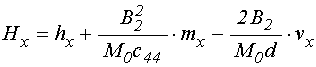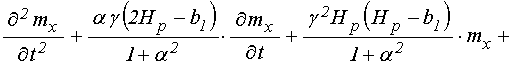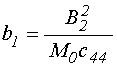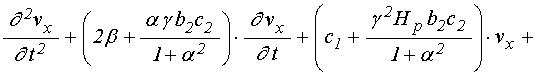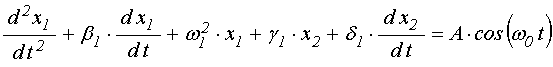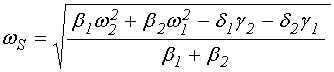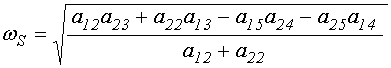УДК 537.874; 537.624
АНАЛИЗ ЛИНЕЙНОГО ВОЗБУЖДЕНИЯ ГИПЕРЗВУКОВЫХ КОЛЕБАНИЙ МАГНИТОСТРИКЦИОННОГО ПРЕОБРАЗОВАТЕЛЯ НА ОСНОВЕ МОДЕЛИ СВЯЗАННЫХ ОСЦИЛЛЯТОРОВ
В. С. Власов 1 , А. П. Иванов 1, В. Г. Шавров 2, В. И. Щеглов 2
1 Сыктывкарский государственный университет, Сыктывкар
2 ИРЭ им.
В.А.Котельникова РАН, Москва
Статья получена 19 ноября 2013 г.
Аннотация. Рассмотрено возбуждение гиперзвуковых колебаний переменным магнитным полем в геометрии плоскопараллельной нормально намагниченной ферритовой пластины. Предложена укороченная система уравнений, основанная на модели связанных осцилляторов. Выявлены два режима вынужденных колебаний, соответствующие спаду и нарастанию амплитуды во времени. Найдены аналитические критерии, определяющие критическое значение константы связи и частоту резонансных колебаний в точке перехода между режимами. Показано, что точка перехода, для модельной системы соответствующая бесконечному росту амплитуды колебаний, для случая железоиттриевого граната эквивалентна точке переориентации вектора намагниченности.
Ключевые слова: гиперзвук, нелинейные колебания, магнитоупругость.
Abstract. The hypersound vibrations excitation by alternating magnetic field in geometry of normal magnetized ferrite plate is investigated. It is suggested the reduced equation system based on connected oscillators model. It is found two forced vibration regimes corresponded to decrease and increase of amplitude in the time. The analytical criterions of connection constant critical meaning and resonance frequency in transition point are found. It is shown that the bifurcation point between regimes corresponded to infinite growth of model system vibrations amplitude for the case of yttrium iron garnet is equivalent to reorientation transition point of magnetization vector.
Key words: hypersound, nonlinear vibrations, magnetoelasticity.
Введение
Возбуждение гиперзвуковых колебаний в диапазоне СВЧ является актуальной задачей как для общей физики, так и для технической акустики [1-3], в том числе для аналоговой обработки информации [4-9]. Весьма перспективными здесь являются магнитострикционные преобразователи на основе ферритов, использующие возбуждение упругих колебаний в условиях ферромагнитного резонанса (ФМР) [10,11], что позволяет повысить частоту возбуждаемого гиперзвука до десятков ГГц без заметного роста затухания. Особенно перспективными материалами для таких преобразователей являются железоиттриевый гранат (ЖИГ), имеющий рекордно низкие потери как упругих, так и магнитных колебаний, а также тербиевый феррит-гранат (ТбФГ), имеющий весьма высокое значение константы магнитоупругого взаимодействия в сочетании со сравнительно невысокой намагниченностью насыщения [11].
В ферритах значительной помехой на пути повышения мощности возбуждаемого гиперзвука является рост потерь за счет параметрического возбуждения обменных спиновых волн [12-14]. Однако, в работах [15-19] показано, что при выборе геометрии преобразователя в виде нормально намагниченного тонкого диска частота ФМР приходится на дно спектра обменных волн, вследствие чего их возбуждение исключается.
В работе [20] показано, что в подобной геометрии амплитуда гиперзвука может превышать таковую в линейном режиме более чем в 30 раз, что открывает путь для создания магнитоакустических преобразователей высокой мощности.
Расчет свойств работы таких преобразователей в условиях ФМР требует привлечения весьма сложного аналитического аппарата, успешно реализуемого только ценой ряда упрощающих предположений. В простейшем варианте задача сводится к системе семи нелинейных дифференциальных уравнений первого порядка, разрешимой только численными методами [20].
Условия практики однако требуют создания достаточно простого расчетного аппарата, позволяющего оценить возможности и рассчитать основные параметры преобразователя без привлечения сложных аналитических и численных методов. Настоящая работа посвящена созданию такого аппарата на основе модели связанных осцилляторов. На данном этапе рассмотрение проведено только для линейных колебаний, однако даны некоторые рекомендации для обобщения задачи на случай нелинейности, подробное рассмотрение которого предполагается в дальнейшем.
1. Геометрия задачи и основные уравнения
Геометрия задачи, совпадающая с
принятой в [20], показана на рис.1. В ее основе лежит плоскопараллельная
пластина толщины ![]() , обладающая магнитными,
упругими и магнитоупругими свойствами. Материал пластины имеет кубическую
кристаллографическую симметрию, плоскость (100) которой совпадает с плоскостью
пластины.
, обладающая магнитными,
упругими и магнитоупругими свойствами. Материал пластины имеет кубическую
кристаллографическую симметрию, плоскость (100) которой совпадает с плоскостью
пластины.
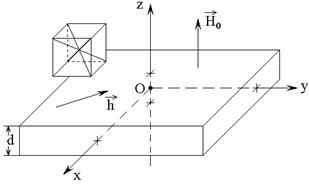
Рис.1. Геометрия задачи. Слева – схема кристаллографической ячейки.
Внешнее постоянное магнитное поле
![]() приложено перпендикулярно плоскости пластины,
переменное магнитное поле
приложено перпендикулярно плоскости пластины,
переменное магнитное поле ![]() действует в плоскости
пластины. Задача решается в декартовой системе координат
действует в плоскости
пластины. Задача решается в декартовой системе координат ![]() , плоскость
, плоскость ![]() которой
совпадает с плоскостью пластины, а оси
которой
совпадает с плоскостью пластины, а оси ![]() ,
, ![]() и
и ![]() параллельны
ребрам куба кристаллографической ячейки. Центр системы координат
параллельны
ребрам куба кристаллографической ячейки. Центр системы координат ![]() находится в центре пластины, ее плоскости
соответствуют координатам
находится в центре пластины, ее плоскости
соответствуют координатам ![]() .
.
Основная система уравнений движения для нормированных компонент намагниченности имеет вид [20]:
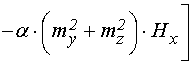 ; (1)
; (1)
где уравнения для ![]() и
и ![]() получаются
циклической перестановкой
получаются
циклической перестановкой ![]() ,
, ![]() ,
, ![]() , а эффективные
поля
, а эффективные
поля ![]() определяются формулами (11) работы [20].
определяются формулами (11) работы [20].
Уравнения для компонент упругого
смещения ![]() имеют вид [20]:
имеют вид [20]:
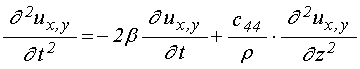 ;
(2)
;
(2)
граничные условия [20]:
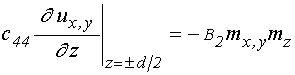 .
(3)
.
(3)
Таким образом здесь имеются три уравнения первого порядка для компонент намагниченности и два уравнения второго порядка для компонент упругого смещения, что эквивалентно системе из семи уравнений первого порядка. Анализ развития колебаний в такой системе методом фазового пространства [21,22] требует нахождения координат особых точек, что сводится к решению линейного алгебраического уравнения седьмой степени. Сложность решения такой задачи стимулирует поиск возможностей уменьшения общего числа уравнений, одна из которых рассматривается далее.
2. Линейное приближение
Рассмотрим задачу в линейном
приближении, то есть положим ![]() ,
, ![]() и далее будем оставлять члены только
первого порядка по
и далее будем оставлять члены только
первого порядка по ![]() . В отношении упругих колебаний,
аналогично [20], примем следующие предположения:
. В отношении упругих колебаний,
аналогично [20], примем следующие предположения: ![]() ,
продольные упругие волны отсутствуют:
,
продольные упругие волны отсутствуют: ![]() ,
упругие волны распространяются только вдоль оси
,
упругие волны распространяются только вдоль оси ![]() :
: ![]() ;
; ![]() .
Дополнительно будем считать, что упругие смещения вдоль оси
.
Дополнительно будем считать, что упругие смещения вдоль оси ![]() отсутствуют, то есть:
отсутствуют, то есть: ![]() . Такое предположение не является безупречно
корректным, однако в ряде случаев будучи примененным на первом этапе, позволяет
существенно сократить требуемый объем вычислений [23,24].
. Такое предположение не является безупречно
корректным, однако в ряде случаев будучи примененным на первом этапе, позволяет
существенно сократить требуемый объем вычислений [23,24].
Входящие в уравнения (1) эффективные поля с учетом линеаризации принимают вид:
![]() ;
(5)
;
(5)
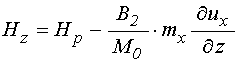 ,
(6)
,
(6)
где введено вспомогательное обозначение:
![]() .
(7)
.
(7)
В эти выражения входит
производная от смещения ![]() по координате
по координате ![]() . Найдем эту производную.
. Найдем эту производную.
Согласно [20], в рассматриваемой
задаче ![]() -компонента упругого смещения для первой
моды колебаний может быть представлена в виде (формула (51)):
-компонента упругого смещения для первой
моды колебаний может быть представлена в виде (формула (51)):
При этом производная от смещения ![]() по координате
по координате ![]() имеет
вид (формула (62)):
имеет
вид (формула (62)):
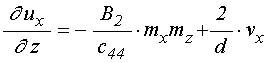 ;
(9)
;
(9)
где ![]() –
функция, удовлетворяющая уравнению (формула (53)):
–
функция, удовлетворяющая уравнению (формула (53)):
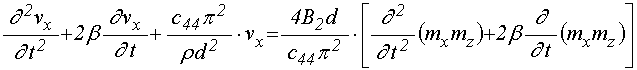 (10)
(10)
Полагая ![]() , из
(9) получаем:
, из
(9) получаем:
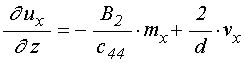 , (11)
, (11)
а уравнение (10) принимает вид:
Возвращаясь к полям (4)-(6) и полагая
![]() , получаем:
, получаем:
![]() ;
(14)
;
(14)
![]() .
(15)
.
(15)
3. Уравнение для намагниченности
Преобразуем теперь уравнения для
намагниченности (1). Полагая ![]() , третье уравнение опускаем,
а в оставшихся двух, полагая
, третье уравнение опускаем,
а в оставшихся двух, полагая ![]() , оставляем только
члены первого порядка по
, оставляем только
члены первого порядка по ![]() :
:
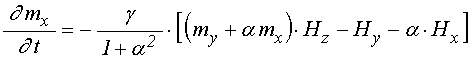 ;
(16)
;
(16)
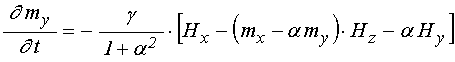 .
(17)
.
(17)
Раскрывая скобки, выражая из первого
уравнения ![]() и подставляя во второе, получаем
уравнение для
и подставляя во второе, получаем
уравнение для ![]() :
:
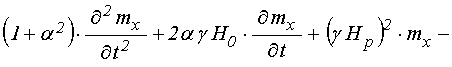
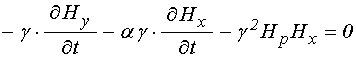 . (18)
. (18)
Это – одно уравнение второго порядка
для ![]() , полученное через посредство
, полученное через посредство ![]() , то есть оно эквивалентно двум уравнениям
первого порядка для
, то есть оно эквивалентно двум уравнениям
первого порядка для ![]() и
и ![]() .
Такое же уравнение второго порядка можно получить для
.
Такое же уравнение второго порядка можно получить для ![]() ,
однако в этом необходимости нет, так как оно дублирует полученное уравнение для
,
однако в этом необходимости нет, так как оно дублирует полученное уравнение для
![]() .
.
Подставляя в (18) поля (13)-(15),
получаем уравнение для ![]() в виде:
в виде:
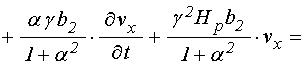
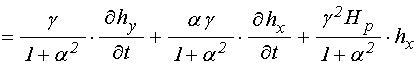 , (19)
, (19)
где введены вспомогательные обозначения:
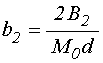 .
(21)
.
(21)
4. Уравнение для упругого смещения
Рассмотрим теперь уравнение (12)
для упругого смещения ![]() .
.
Вводя упрощенные обозначения:
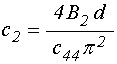 .
(23)
.
(23)
и подставляя в (12) вторую
производную от намагниченности в соответствии с (19), получаем уравнение для ![]() :
:
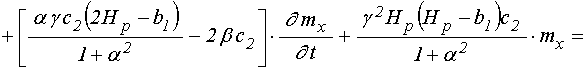
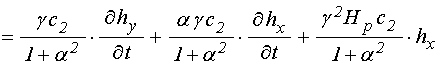 . (24)
. (24)
Уравнения (19) и (24) составляют искомую систему.
5. Проверка применимости линейного приближения
Рассмотрим степень приближения,
обеспечиваемого линеаризованной системой (19)-(24) по сравнению с исходной
нелинейной системой (1)-(3). На рис.2 показаны зависимости поперечной
компоненты намагниченности (а) и упругого смещения (б) от амплитуды переменного
поля при параметрах ЖИГ, принятых в работе [20]. Кривые 1 соответствуют решению
полной системы (1)-(3), кривые 2 – решению линеаризованной системы (19)-(24)
(смещение ![]() получено из
получено из ![]() в
соответствии с формулой (8) при
в
соответствии с формулой (8) при ![]() ).
).
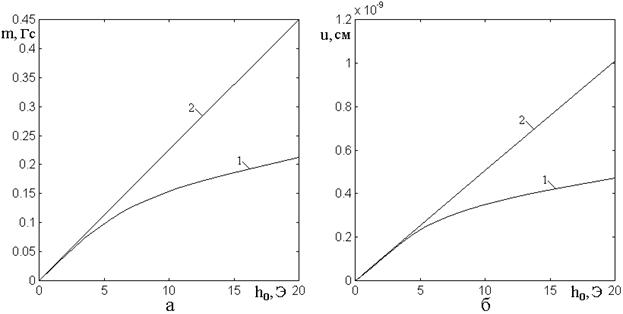
Рис.2. Зависимости поперечной компоненты
намагниченности (а) и упругого смещения (б) от амплитуды переменного поля.
Параметры – соответствуют ЖИГ (![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
;![]() ;
; ![]() );
);
толщина пластины: ![]() .
.
1 – решение нелинейной системы (1)-(3);
2 – решение линеаризованной системы (19)-(24).
Из рисунка видно, что
приближенная линеаризованная система (19)-(24) описывает точную картину до
амплитуды переменного поля 2 Э (то есть до ![]() ) с точностью
не менее 1%, до амплитуды 5 Э (до
) с точностью
не менее 1%, до амплитуды 5 Э (до ![]() ) – с точностью
порядка 10%, а для амплитуды 10 Э (до
) – с точностью
порядка 10%, а для амплитуды 10 Э (до ![]() ) – с
точностью около 30%.
) – с
точностью около 30%.
6. Система уравнений для намагниченности и упругого смещения в обобщенном виде
Таким образом, вместо исходной системы (1)-(2), эквивалентной семи уравнениям первого порядка с граничными условиями (3), получена более простая система (19)-(24), содержащая два уравнения второго порядка без граничных условий. Эта система в общем случае описывает колебания двух связанных гармонических осцилляторов, где связь осуществляется не только через сами переменные, но и через их производные.
Запишем уравнения для намагниченности (19) и упругого смещения (24) в обобщенном виде:
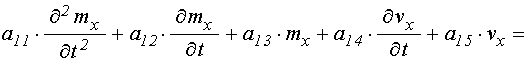
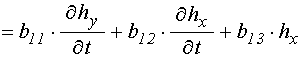 ; (25)
; (25)
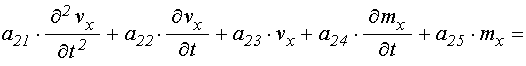
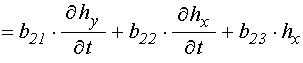 , (26)
, (26)
где с учетом (20)-(21) и (22)-(23) введены обозначения:
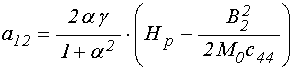 ;
(28)
;
(28)
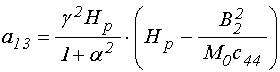 ;
(29)
;
(29)
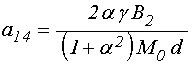 ;
(30)
;
(30)
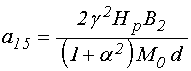 ;
(31)
;
(31)
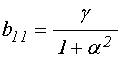 ;
(32)
;
(32)
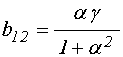 ;
(33)
;
(33)
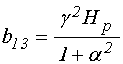 ;
(34)
;
(34)
![]() ; (35)
; (35)
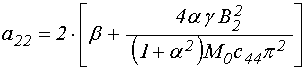 ;
(36)
;
(36)
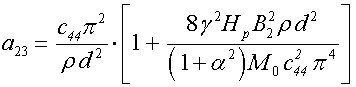 ;
(37)
;
(37)
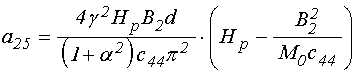 ;
(39)
;
(39)
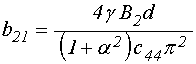 ;
(40)
;
(40)
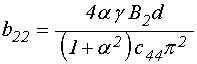 ;
(41)
;
(41)
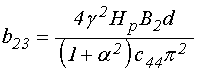 .
(42)
.
(42)
7. Упрощение коэффициентов на основе численного анализа
Полученные коэффициенты (27)-(42)
имеют довольно сложный вид, так ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() содержат
два слагаемых, а
содержат
два слагаемых, а ![]() – три. Однако при реальных
значениях параметров материалов, используемых для магнитострикционных
преобразователей, таких как ЖИГ и ТбФГ, относительная роль этих слагаемых
различна, что позволяет произвести определенные упрощения.
– три. Однако при реальных
значениях параметров материалов, используемых для магнитострикционных
преобразователей, таких как ЖИГ и ТбФГ, относительная роль этих слагаемых
различна, что позволяет произвести определенные упрощения.
Рассмотрим, например параметры,
соответствующие монокристаллу ЖИГ [11]: ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() . В таблице приведены значения
коэффициентов, рассчитанные с этими параметрами при двух значениях постоянного
поля: 2850 Э и 1850 Э. В этих случаях поле
. В таблице приведены значения
коэффициентов, рассчитанные с этими параметрами при двух значениях постоянного
поля: 2850 Э и 1850 Э. В этих случаях поле ![]() принимает
значения 1000 Э и 100 Э, а частота ФМР в отсутствие магнитоупругости равна 2800
МГц и 280 МГц соответственно. Все коэффициенты в таблице рассчитаны в системе
СГС (Гаусса), размерные единицы опущены для упрощения записи.
принимает
значения 1000 Э и 100 Э, а частота ФМР в отсутствие магнитоупругости равна 2800
МГц и 280 МГц соответственно. Все коэффициенты в таблице рассчитаны в системе
СГС (Гаусса), размерные единицы опущены для упрощения записи.
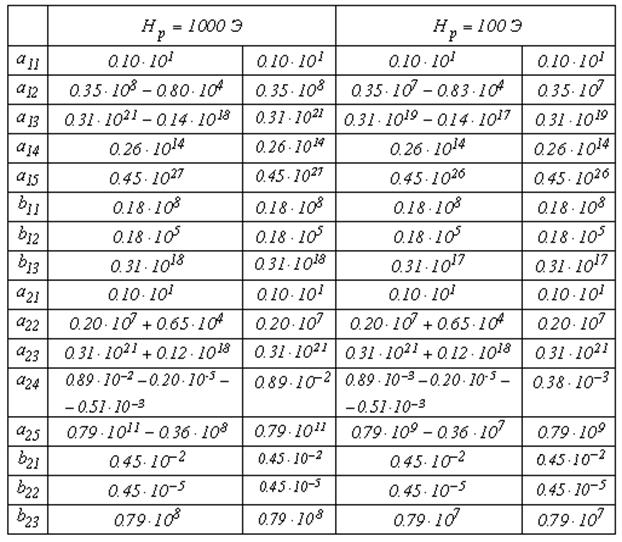
В первом столбце таблицы
приведены наименования коэффициентов. Второй и третий столбцы соответствуют
полю ![]() , равному 1000 Э, четвертый и пятый – 100
Э. Во втором и четвертом столбцах приведены численные значения коэффициентов,
причем составляющие их слагаемые выделены отдельно.
, равному 1000 Э, четвертый и пятый – 100
Э. Во втором и четвертом столбцах приведены численные значения коэффициентов,
причем составляющие их слагаемые выделены отдельно.
Из второго и четвертого столбцов таблицы видно, что в большинстве случаев одно из слагаемых преобладает над другими на порядок и более. В третьем и пятом столбцах приведены численные значения коэффициентов, полученные в пренебрежении меньшими слагаемыми.
Аналогичный расчет коэффициентов, исходящий из параметров ТбФГ, показывает, что полученные при этом коэффициенты ведут себя подобным образом.
В соответствии с полученными
данными, в аналитических выражениях для коэффициентов (27)-(42) можно
пренебречь слагаемыми, дающими малый вклад, а также учесть, что ![]() , в результате чего эти коэффициенты принимают
значительно более простой вид:
, в результате чего эти коэффициенты принимают
значительно более простой вид:
![]() ;
(44)
;
(44)
![]() ;
(45)
;
(45)
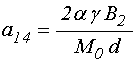 ;
(46)
;
(46)
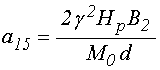 ;
(47)
;
(47)
![]() ;
(48)
;
(48)
![]() ;
(49)
;
(49)
![]() ; (50)
; (50)
![]() ;
(51)
;
(51)
![]() ;
(52)
;
(52)
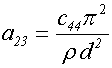 ;
(53)
;
(53)
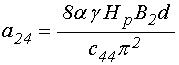 ;
(54)
;
(54)
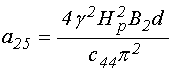 ;
(55)
;
(55)
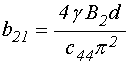 ;
(56)
;
(56)
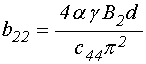 ;
(57)
;
(57)
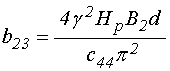 .
(58)
.
(58)
Так как производные от переменных
полей дают в качестве множителя частоту, то вблизи резонанса вклад в уравнения
(19) и (24) от слагаемых, определяемых коэффициентами ![]() ,
имеет примерно тот же порядок, что и от остальных слагаемых. Структура коэффициентов
,
имеет примерно тот же порядок, что и от остальных слагаемых. Структура коэффициентов
![]() довольно сложна, однако следует учесть,
что коэффициенты
довольно сложна, однако следует учесть,
что коэффициенты ![]() и
и ![]() меньше
соответствующих коэффициентов
меньше
соответствующих коэффициентов ![]() и
и ![]() в
в ![]() раз,
то есть – на три порядка, поэтому ими можно пренебречь. Слагаемые, содержащие
производные от компонент переменных полей, в сумме со слагаемыми, содержащими
сами эти поля, дают не более чем сдвиг фазы примерно на четверть периода,
поэтому их также можно опустить. Далее, поскольку возбуждение системы в целом
происходит через магнитный осциллятор, а действие возбуждающей силы на упругий
осциллятор, определяемое коэффициентом
раз,
то есть – на три порядка, поэтому ими можно пренебречь. Слагаемые, содержащие
производные от компонент переменных полей, в сумме со слагаемыми, содержащими
сами эти поля, дают не более чем сдвиг фазы примерно на четверть периода,
поэтому их также можно опустить. Далее, поскольку возбуждение системы в целом
происходит через магнитный осциллятор, а действие возбуждающей силы на упругий
осциллятор, определяемое коэффициентом ![]() ,
пропорционально величине константы магнитоупругого взаимодействия
,
пропорционально величине константы магнитоупругого взаимодействия ![]() , которая может быть достаточно малой,
роль коэффициента
, которая может быть достаточно малой,
роль коэффициента ![]() а процессе возбуждения колебаний
также можно считать второстепенной. В результате решающим для возбуждения
остается только коэффициент
а процессе возбуждения колебаний
также можно считать второстепенной. В результате решающим для возбуждения
остается только коэффициент ![]() , а в первом
приближении остальные коэффициенты
, а в первом
приближении остальные коэффициенты ![]() можно положить равными
нулю.
можно положить равными
нулю.
Заметим, что связь между
осцилляторами, обусловленная самими переменными, то есть определяемая
коэффициентами ![]() и
и ![]() , в
обоих случаях пропорциональна величине магнитного параметра затухания
, в
обоих случаях пропорциональна величине магнитного параметра затухания ![]() , что в какой-то мере является
несимметричным. Действительно, упругий осциллятор тем больше влияет на
магнитный, чем затухание магнитного осциллятора больше, то есть чем магнитный
осциллятор является более «мягким». Исходя из симметрии задачи естественно
предположить, что и магнитный осциллятор тем сильнее влияет на упругий, чем
затухание упругого больше. С этой точки зрения коэффициент
, что в какой-то мере является
несимметричным. Действительно, упругий осциллятор тем больше влияет на
магнитный, чем затухание магнитного осциллятора больше, то есть чем магнитный
осциллятор является более «мягким». Исходя из симметрии задачи естественно
предположить, что и магнитный осциллятор тем сильнее влияет на упругий, чем
затухание упругого больше. С этой точки зрения коэффициент ![]() должен быть пропорционален не магнитному
параметру затухания
должен быть пропорционален не магнитному
параметру затухания ![]() , а упругого
, а упругого ![]() . Действительно, в полном выражении для
. Действительно, в полном выражении для ![]() (38) параметр
(38) параметр ![]() входит
в роли самостоятельного слагаемого. Однако в реальном случае ЖИГ при поле 2750
Э, то есть на частоте 2800 МГц, представляющей наибольший интерес для практики,
значение этого слагаемого на порядок меньше, чем определяемого параметром
входит
в роли самостоятельного слагаемого. Однако в реальном случае ЖИГ при поле 2750
Э, то есть на частоте 2800 МГц, представляющей наибольший интерес для практики,
значение этого слагаемого на порядок меньше, чем определяемого параметром ![]() . При понижении поля до 1850 Э, то есть
частоты до 280 МГц, как видно из таблицы, порядок вклада от обоих слагаемых
становится одинаковым, то есть в этом случае к сделанным приближениям надо относиться
с некоторой осторожностью.
. При понижении поля до 1850 Э, то есть
частоты до 280 МГц, как видно из таблицы, порядок вклада от обоих слагаемых
становится одинаковым, то есть в этом случае к сделанным приближениям надо относиться
с некоторой осторожностью.
Более того, при увеличении параметра
затухания ![]() , начиная с
, начиная с ![]() при
том же значении
при
том же значении ![]() последнее слагаемое в
коэффициенте
последнее слагаемое в
коэффициенте ![]() (38) уже преобладает над первыми двумя, в
результате чего этот коэффициент принимает вид:
(38) уже преобладает над первыми двумя, в
результате чего этот коэффициент принимает вид:
то есть влияние магнитного
осциллятора на упругий сказывается тем сильнее, чем затухание упругого
осциллятора больше. То есть система относительно связи через переменные обретает
определенную симметричность. Таким образом, при получении приближенных
аналитических выражений следует следить за относительными величинами обоих параметров
затухания ![]() и
и ![]() .
.
8. Модель осцилляторов, связанных через производные
Как показано в предыдущем разделе, задача о линейном возбуждении гиперзвуковых колебаниях в магнитной пластине, обладающей магнитоупругими свойствами, может быть сведена к системе двух линейных дифференциальных уравнений второго порядка с постоянными коэффициентами, связанных через переменные и производные от переменных по времени.
В обозначениях, традиционно принятых для рассмотрения подобной системы связанных осцилляторов, систему уравнений (19)-(24) можно записать в виде:
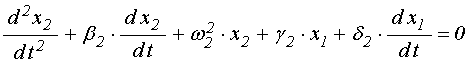 ,
(61)
,
(61)
где: ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
;
![]() , а
также положено:
, а
также положено: ![]() .
.
В отсутствие вынуждающей силы (![]() ), эти уравнения могут описывать только
затухающие колебания. Однако, поскольку каждое из уравнений кроме слагаемого с
производной от основной переменной содержит еще слагаемое с производной от
другой переменной, то затухание одного осциллятора может зависеть от колебаний
другого. Можно полагать, что при наличии вынуждающей силы это обстоятельство способно
привести к частичной или даже полной компенсации затухания каждого из
осцилляторов, то есть колебания могли бы как убывать во времени, так и
нарастать. Во втором случае можно считать, что колебательная система приобретает
«отрицательное сопротивление», то есть становится активной, а нарастание колебаний
ограничивается только нелинейными свойствами системы, здесь не
рассматриваемыми.
), эти уравнения могут описывать только
затухающие колебания. Однако, поскольку каждое из уравнений кроме слагаемого с
производной от основной переменной содержит еще слагаемое с производной от
другой переменной, то затухание одного осциллятора может зависеть от колебаний
другого. Можно полагать, что при наличии вынуждающей силы это обстоятельство способно
привести к частичной или даже полной компенсации затухания каждого из
осцилляторов, то есть колебания могли бы как убывать во времени, так и
нарастать. Во втором случае можно считать, что колебательная система приобретает
«отрицательное сопротивление», то есть становится активной, а нарастание колебаний
ограничивается только нелинейными свойствами системы, здесь не
рассматриваемыми.
Для проверки такого предположения в рамках линейного приближения рассмотрим далее модель связанных осцилляторов в наиболее общем виде, описываемом уравнениями (60)-(61). Параметры задачи выберем исходя из максимальной наглядности представления результатов.
9. Численный анализ развития вынужденных колебаний
Для анализа действия затухания
колебательных систем друг на друга система уравнений (60)-(61) решалась численно
методом Рунге-Кутта четвертого порядка [25]. Исследовался характер возбуждаемых
колебаний при различной величине связи осцилляторов через производные ![]() и
и ![]() .
Собственные частоты осцилляторов были положены равными и рассматривались два
случая: равенства частоты возбуждения собственным частотам и ее отличия.
.
Собственные частоты осцилляторов были положены равными и рассматривались два
случая: равенства частоты возбуждения собственным частотам и ее отличия.
На рис.3 показано развитие колебаний во времени для двух осцилляторов с равными частотами. Рис.3а соответствует равенству частоты возбуждения собственным частотам осцилляторов, рис.3б – ее отличию от частот осцилляторов (единицы – относительные, принятые, исходя из наглядности рисунка).
Из рис.3а видно, что при возбуждении системы на собственной частоте осцилляторов в отсутствие связи через производные (верхняя эпюра) колебания довольно быстро (через время около 40) приходят к стационарной амплитуде около 28 и дальше не меняются. Картина соответствует обычному экспоненциальному насыщению, характерному для положительного затухания.
При связи 0.1 (средняя эпюра) колебания нарастают почти линейно. Наблюдаемое незначительное отклонение от линейности в нижнюю сторону, возможно, означает приближение к какой-то стационарной амплитуде, но если это и происходит, то где-то далеко за временем 100. Амплитуда заметно превышает предыдущую и при времени 100 составляет около 75. Близкий к линейному рост амплитуды можно интерпретировать как экспоненту с нулевым показателем.
При связи 0,2 (нижняя эпюра) амплитуда колебаний до времени порядка 40-60 слегка увеличивается, составляя не более нескольких сотен, после чего рост ее резко усиливается и при времени 100 амплитуда достигает 2000, имея тенденцию увеличиваться еще больше. Картина напоминает экспоненциальный рост, характерный для отрицательного затухания.
Таким образом, можно полагать, что при частоте возбуждения равной собственной, из-за связи через производные знак показателя экспоненты, описывающей затухание, меняется с положительного, проходя через нуль, на отрицательный.
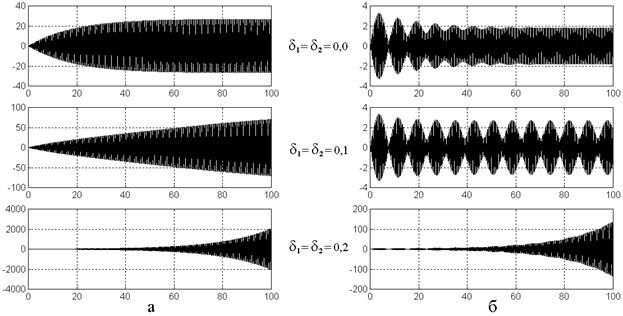
Рис.3. Развитие вынужденных колебаний во времени при различной величине связи.
Параметры: ![]() ;
;
![]() ;
; ![]() ;
значения
;
значения ![]() приведены на рисунке; амплитуда
возбуждения:
приведены на рисунке; амплитуда
возбуждения: ![]() .
.
а – частота возбуждения: ![]() ; б – частота возбуждения:
; б – частота возбуждения: ![]() .
.
Рассмотрим теперь, что происходит при отстройке частоты возбуждения от резонансной. Полученные зависимости показаны на рис.3б, построенном при тех же параметрах, что и рис.3а, кроме частоты возбуждения, теперь отличной от собственных частот осцилляторов.
Из рис.3б видно, что в отсутствие связи через производные наблюдается модуляция амплитуды, обусловленная биениями с частотой, равной разности частот возбуждения и собственной, однако такие модуляционные колебания, как и полагается биениям, быстро затухают при времени около 60. Эта картина полностью соответствует обычному установлению вынужденных колебаний при экспоненциальном затухании с положительным показателем.
При связи равной 0,1 (средняя эпюра) модуляционные колебания не затухают и амплитуда их имеет постоянное значение, равное 2,9. Модуляция опять обусловлена разностью частот возбуждения и собственной, то есть биениями, а затухание отсутствует, что соответствует нулевому показателю экспоненты.
При связи равной 0,2 (нижняя эпюра) модуляционные колебания есть, однако их размах на фоне резкого роста общей амплитуды теряется, то есть биения, хотя и остаются, но роль их в общей картине колебаний становится весьма незначительной. Рост амплитуды опять соответствует экспоненте с отрицательным показателем.
Наблюдаемое во всех трех случаях уменьшение амплитуды колебаний примерно на порядок по сравнению с рис.3а, обусловлено отстройкой частоты возбуждения от резонансной.
Таким образом, можно полагать, что в случае связи через производные, по мере увеличения величины связи, мы имеем картину уменьшения затухания от положительного значения, через нулевое до отрицательного. То есть наблюдаются три различных режима вынужденных колебаний: режим спада амплитуды, режим ее нарастания, и между нами – режим стационарной амплитуды. При этом автоколебания как самоподдерживающийся процесс полностью отсутствуют, а наблюдаемая модуляция амплитуды обусловлена биениями.
Замечание. Вообще говоря, экспоненциальный рост амплитуды колебаний, наблюдаемый на нижних эпюрах на рис.3, не может продолжаться до бесконечности, так как это соответствовало бы бесконечному нарастанию энергии колебаний. В реальном случае такой экспоненциальный рост неизбежно ограничивается при достаточной амплитуде колебаний из-за нелинейной расстройки, приводящей к выходу системы из резонанса [26]. Механизм нелинейной расстройки выходит за рамки настоящей работы и будет отдельно рассмотрен в другом случае.
10. Аналитический критерий изменения характера колебаний
Система уравнений (60)-(61) в ряде случаев допускает аналитическое решение. Рассмотрим, например, частный случай свободных колебаний без вынуждающей силы. В этом случае система (60)-(61) принимает вид:
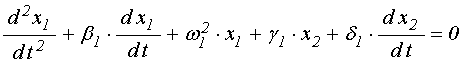 ;
(62)
;
(62)
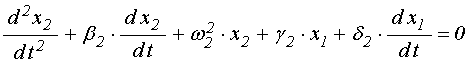 .
(63)
.
(63)
Введем дополнительные переменные:
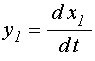 ;
(64)
;
(64)
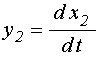 .
(65)
.
(65)
Подставляя новые переменные и их производные в исходные уравнения (62)-(63), получаем систему уравнений первого порядка:
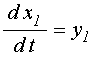 ;
(66)
;
(66)
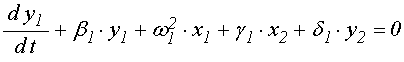 ;
(67)
;
(67)
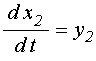 ;
(68)
;
(68)
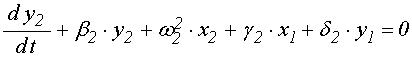 .
(69)
.
(69)
Будем искать решение этой системы в виде:
![]() ;
(70)
;
(70)
![]() ;
(71)
;
(71)
![]() ;
(72)
;
(72)
![]() .
(73)
.
(73)
Подставляя (70)-(73) в (66)-(69), можно видеть, что уравнения (66) и (68) удовлетворяются тождественно, а уравнения (67) и (69) образуют систему:
![]() ;
(74)
;
(74)
![]() ,
(75)
,
(75)
детерминант которой имеет вид:
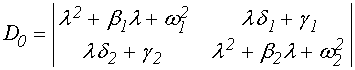 .
(76)
.
(76)
Условие нетривиальности решения
системы ![]() дает уравнение для
дает уравнение для ![]() :
:
![]() .
(77)
.
(77)
Решение этого уравнения в аналитическом виде довольно громоздко, поэтому рассмотрим упрощенный частный случай.
11. Комплексный показатель экспоненциального изменения амплитуды
Предположим, что ![]() имеет вид:
имеет вид:
![]() ,
(78)
,
(78)
где ![]() ,
, ![]() – действительные, то есть
– действительные, то есть ![]() соответствует изменению амплитуды колебаний
во времени, а
соответствует изменению амплитуды колебаний
во времени, а ![]() – частоте этих колебаний.
– частоте этих колебаний.
Подставляя (78) в (77) и выделяя действительную и мнимую части, получаем:
![]() ,
(79)
,
(79)
где:
![]()
![]()
![]() ;
(80)
;
(80)
![]()
![]()
![]() . (81)
. (81)
Уравнение (79) выполняется только в том случае, когда как действительная, так и мнимая части равны нулю. При этом из (80) получаем:
![]()
![]()
![]() ;
(82)
;
(82)
Из (81), разделяя ![]() на
на ![]() и
группируя относительно
и
группируя относительно ![]() , получаем:
, получаем:
![]()
![]()
![]() . (83)
. (83)
Уравнения (82) и (83) составляют
систему относительно ![]() и
и ![]() ,
которая должна быть решена совместно. Так (83) содержит
,
которая должна быть решена совместно. Так (83) содержит ![]() только
в квадрате и только в качестве линейного сомножителя в левой части, поэтому из
этого уравнения можно выразить
только
в квадрате и только в качестве линейного сомножителя в левой части, поэтому из
этого уравнения можно выразить ![]() через
через ![]() , после чего подставить в (82), в
результате чего будет получено уравнение, содержащее только
, после чего подставить в (82), в
результате чего будет получено уравнение, содержащее только ![]() . Это уравнение будет шестой степени и его
решение, по-видимому, будет не проще, чем решение исходного уравнения (77).
. Это уравнение будет шестой степени и его
решение, по-видимому, будет не проще, чем решение исходного уравнения (77).
Поэтому рассмотрим частный
случай, соответствующий постоянству амплитуды во времени, то есть ![]() . При этом из (82) и (83) получаем два
уравнения для
. При этом из (82) и (83) получаем два
уравнения для ![]() , которые должны удовлетворяться
одновременно:
, которые должны удовлетворяться
одновременно:
![]() ;
(84)
;
(84)
![]() .
(85)
.
(85)
Из (85) при условии ![]() получаем:
получаем:
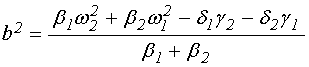 ,
(86)
,
(86)
Это соотношение позволяет найти частоту собственных колебаний системы при условии сохранения постоянства амплитуды:
При этом (84) также соответствует условию сохранения амплитуды постоянной, то есть при его нарушении в ту или другую сторону амплитуда растет или спадает. Введем вспомогательную функцию:
![]() ,
(88)
,
(88)
с помощью которой получаем критерий перехода от нарастания амплитуды к ее убыванию:
Таким образом, главным критерием постоянства амплитуды является (89), а если он выполняется, то частота определяется соотношением (87). При этом выполняется равенство:
![]() .
(90)
.
(90)
Этот критерий позволяет
определить возможные значения параметров ![]() ,
, ![]() ,
, ![]() ,
соответствующие такому переходу.
,
соответствующие такому переходу.
Проверим условия (89) и (87)
численно. Зависимость функции ![]() от частоты иллюстрируется
рис.4.
от частоты иллюстрируется
рис.4.
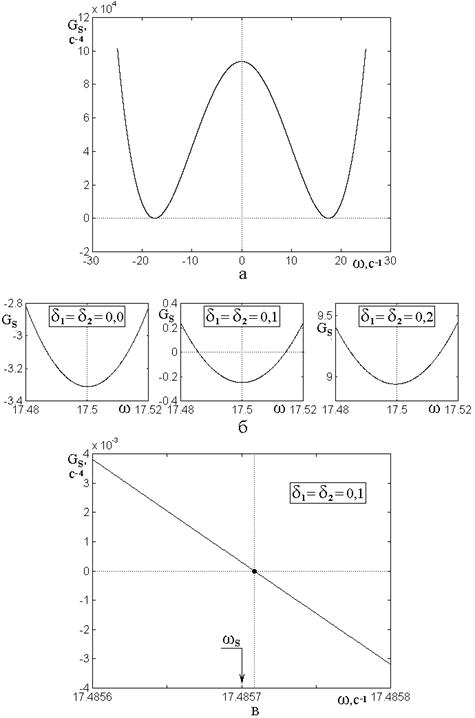
Рис.4. Зависимость функции ![]() от частоты
от частоты ![]() .
.
Параметры: ![]() ;
;
![]() ;
; ![]() ;
; ![]() .
.
а – общий характер зависимости;
б – зависимость при различных значениях параметров связи;
в – зависимость вблизи главного нуля в крупном масштабе.
На рис.4а представлен общий
характер зависимости ![]() . Видно, что она представляет
собой параболу четвертого порядка, симметричную относительно оси ординат. Функция
. Видно, что она представляет
собой параболу четвертого порядка, симметричную относительно оси ординат. Функция
![]() имеет два минимума при
имеет два минимума при ![]() , разделенные максимумом при
, разделенные максимумом при ![]() .
.
Реальный физический смысл имеет
правый минимум, окрестность которого представлена на рис.4б в более крупном
масштабе при трех характерных значениях параметров связи ![]() . Так левый из этих рисунков построен при
. Так левый из этих рисунков построен при ![]() , что в случае свободных колебаний соответствует
их затуханию во времени, средний рисунок построен при
, что в случае свободных колебаний соответствует
их затуханию во времени, средний рисунок построен при ![]() ,
то есть при сохранении амплитуды свободных колебаний постоянной, а правый
рисунок, построенный при
,
то есть при сохранении амплитуды свободных колебаний постоянной, а правый
рисунок, построенный при ![]() , соответствует
экспоненциальному нарастанию амплитуды. При вынужденных колебаниях эти случаи
соответствуют показанным на рис.3а трем режимам: установления стационарного
значения (верхняя эпюра), линейного (средняя эпюра) и экспоненциального (нижняя
эпюра) роста амплитуды колебаний.
, соответствует
экспоненциальному нарастанию амплитуды. При вынужденных колебаниях эти случаи
соответствуют показанным на рис.3а трем режимам: установления стационарного
значения (верхняя эпюра), линейного (средняя эпюра) и экспоненциального (нижняя
эпюра) роста амплитуды колебаний.
Из рис.4б видно, что во всех
случаях минимум зависимости ![]() приходится на
приходится на ![]() , однако значение этой функции в минимуме
находится вблизи нуля (около -0.21) только при
, однако значение этой функции в минимуме
находится вблизи нуля (около -0.21) только при ![]() (средний
рисунок), тогда как при
(средний
рисунок), тогда как при ![]() (левый рисунок) это значение
является отрицательным и составляет -3.3, а при
(левый рисунок) это значение
является отрицательным и составляет -3.3, а при ![]() (правый
рисунок) – положительным, равным 0.89. Таким образом, нули функции
(правый
рисунок) – положительным, равным 0.89. Таким образом, нули функции ![]() находятся вблизи минимума только при
находятся вблизи минимума только при ![]() , тогда как при
, тогда как при ![]() они
отнесены в разные стороны на значительные расстояния, а в случае
они
отнесены в разные стороны на значительные расстояния, а в случае ![]() – вообще отсутствуют.
– вообще отсутствуют.
На рис.4в показан левый нуль правой
ветви функции ![]() (где
(где ![]() )
в еще более крупном масштабе. Видно, что он приходится на
)
в еще более крупном масштабе. Видно, что он приходится на ![]() . Рассчитанное по формуле (87) значение
частоты резонанса системы составляет
. Рассчитанное по формуле (87) значение
частоты резонанса системы составляет ![]() и показано стрелкой.
Видно, что оно весьма близко к частоте, при которой функция
и показано стрелкой.
Видно, что оно весьма близко к частоте, при которой функция ![]() проходит через нуль.
проходит через нуль.
Таким образом, можно видеть, что оба условия постоянства амплитуды (89) и (87) выполняются с весьма высокой степенью точности (до шести значащих цифр).
Выполненная численная проверка
показывает, что из четырех возможных корней уравнения (89) только один
соответствует частоте (87). Таким образом, условие (87) дополняет основной
критерий (89) тем, что позволяет определить, какой именно из четырех корней
уравнения (89) действительно соответствует переходу от убывания амплитуды к ее
нарастанию. Из рис.4в видно, что этот корень соответствует убыванию функции ![]() в области
в области ![]() . То
есть для выбора корня можно использовать условие отрицательности производной функции
. То
есть для выбора корня можно использовать условие отрицательности производной функции
![]() по частоте:
по частоте:
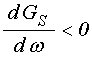 ,
(91)
,
(91)
или в развернутом виде:
![]() .
(92)
.
(92)
Для частоты можно записать:
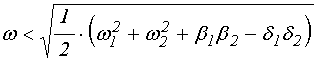 ,
(93)
,
(93)
причем это соотношение должно быть дополнено условием:
![]() ,
(94)
,
(94)
которое накладывает ограничение на величины параметров связи через производные.
Замечание. Приведенные условия (91)-(94) получены на основе анализа численного примера с конкретными заданными значениями параметров, то есть не исключена возможность необходимости коррекции этих условий при других таких значениях. Однако полное исследование подобной задачи, требующее вариации восьми параметров, является крайне громоздким, поэтому в рамки настоящей работы не входит и должно быть проделано отдельно. На практике в простейшем случае можно рекомендовать прямую проверку дополняющих друг друга соотношений (89) и (87), позволяющих выбрать корень уравнения (89) непосредственно.
12. Критерии для магнитоупругих колебаний
Запишем полученное значение частоты и критерия перехода для магнитоупругой колебательной системы, приведенной на рис.1.
Так из (87) и (88) получаем:
![]() , (96)
, (96)
а условие (89) принимает вид:
где величины ![]() определяются
формулами (27)-(42) или (43)-(59).
определяются
формулами (27)-(42) или (43)-(59).
Получение явного вида выражений (95)-(97) тривиально, однако довольно громоздко, поэтому здесь не приводится.
13. Критерии трех режимов на примере реальных материалов
Рассмотрим предсказанную линеаризованной системой (19)-(24) возможность существования трех режимов – стационарной амплитуды, ее роста и убывания на примере реальных материалов типа ЖИГ и ТбФГ. Параметры этих материалов можно найти, например, в [2,11], эти же параметры использованы в работах [20,27].
На рис.5 представлены зависимости
функции ![]() от частоты
от частоты ![]() для
ферритов двух различных составов: ЖИГ (а) и ТбФГ (б).
для
ферритов двух различных составов: ЖИГ (а) и ТбФГ (б).
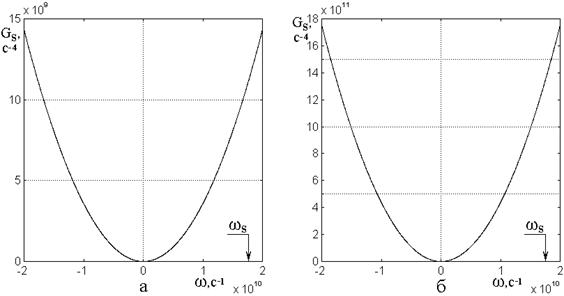
Рис.5. Зависимости функции ![]() от частоты
от частоты ![]() для
ферритов двух различных составов: ЖИГ (а) и ТбФГ (б).
для
ферритов двух различных составов: ЖИГ (а) и ТбФГ (б).
Параметры общие: ![]() ;
; ![]() ;
;![]() ;
; ![]() ;
; ![]() .
.
Параметры специфические:
ЖИГ(а): ![]() ;
; ![]() ;
;![]() ;
;
ТбФГ(б): ![]() ;
; ![]() ;
; ![]() .
.
Из рис.5 видно, что в обоих
случаях функция ![]() представляет собой параболу, симметричную
относительно оси ординат, с единственным нулем при
представляет собой параболу, симметричную
относительно оси ординат, с единственным нулем при ![]() . Ветви
параболы для ТбФГ поднимаются вверх значительно круче (на два порядка), чем
ветви параболы для ЖИГ, что, по-видимому, связано с большим значением константы
. Ветви
параболы для ТбФГ поднимаются вверх значительно круче (на два порядка), чем
ветви параболы для ЖИГ, что, по-видимому, связано с большим значением константы
![]() для этого материала. Однако критические
частоты, определяемые формулой (95) с учетом (27)-(42), для обоих ферритов близки
друг к другу и составляют:
для этого материала. Однако критические
частоты, определяемые формулой (95) с учетом (27)-(42), для обоих ферритов близки
друг к другу и составляют: ![]() ,
, ![]() . Видно, что в обоих случаях эти частоты
весьма далеки от нуля функции
. Видно, что в обоих случаях эти частоты
весьма далеки от нуля функции ![]() , то есть критерий
постоянства амплитуды не выполняется. Контрольная проверка развития колебаний
во времени показывает, что в обоих случаях свободные колебаний затухают со
временем релаксации порядка
, то есть критерий
постоянства амплитуды не выполняется. Контрольная проверка развития колебаний
во времени показывает, что в обоих случаях свободные колебаний затухают со
временем релаксации порядка ![]() , а амплитуда вынужденных
колебаний принимает постоянное значение со временем установления той же длительности.
, а амплитуда вынужденных
колебаний принимает постоянное значение со временем установления той же длительности.
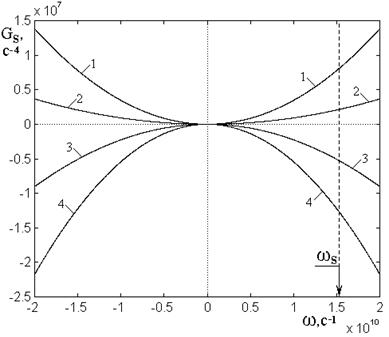
Рис.6. Зависимость функции ![]() от частоты
от частоты ![]() при
различных значениях
при
различных значениях ![]() , близких к критическому.
, близких к критическому.
Параметры: ![]() ;
;
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
;
1 –![]() ; 2
–
; 2
–![]() ;
;
3 –![]() ; 4
–
; 4
–![]() .
.
Представляет интерес найти
условия, максимально близкие к реальности, при которых оба критерия (97) и (95)
выполняются. Реальные материалы предоставляют в этом плане широкий выбор
величины константы магнитоупругого взаимодействия ![]() .
Проверка зависимости вида функции
.
Проверка зависимости вида функции ![]() от величины этой
константы при всех остальных параметрах, соответствующих ЖИГ, показала, что
резкое изменение
от величины этой
константы при всех остальных параметрах, соответствующих ЖИГ, показала, что
резкое изменение ![]() происходит при переходе
значения
происходит при переходе
значения ![]() через критическую величину
через критическую величину ![]() , превышающую
, превышающую ![]() для
ЖИГ в 46,86532 раза, то есть, если считать значение
для
ЖИГ в 46,86532 раза, то есть, если считать значение ![]() точным,
то при
точным,
то при ![]() . При этом ветви параболы переходят от
стремления вверх к стремлению вниз, причем переворот происходит при весьма критичном
значении такой константы.
. При этом ветви параболы переходят от
стремления вверх к стремлению вниз, причем переворот происходит при весьма критичном
значении такой константы.
Соответствующее изменение вида
функции ![]() при переходе величины константы
при переходе величины константы ![]() через критическое значение
через критическое значение ![]() иллюстрируется рис.6. Из рисунка видно,
что по мере роста значения
иллюстрируется рис.6. Из рисунка видно,
что по мере роста значения ![]() в седьмой значащей
цифре на единицу, ветви параболу первоначально стремящиеся вверх, резко
перескакивают вниз. При этом частота, определяемая критерием (95), равна
в седьмой значащей
цифре на единицу, ветви параболу первоначально стремящиеся вверх, резко
перескакивают вниз. При этом частота, определяемая критерием (95), равна ![]() . Ввиду крайней резкости перескока ветвей
параболы сверху вниз, определить точное значение константы
. Ввиду крайней резкости перескока ветвей
параболы сверху вниз, определить точное значение константы ![]() , превышающее семь значащих цифр, в
настоящей работе не представилось возможным, однако очевидно, что переход
ветвей происходит через их выстраивание вдоль горизонтальной оси, то есть на
частоте
, превышающее семь значащих цифр, в
настоящей работе не представилось возможным, однако очевидно, что переход
ветвей происходит через их выстраивание вдоль горизонтальной оси, то есть на
частоте ![]() правая ветвь должна приблизиться к нулю
на величину бесконечно малую, что и обеспечит одновременное выполнение обоих
критериев (97) и (95).
правая ветвь должна приблизиться к нулю
на величину бесконечно малую, что и обеспечит одновременное выполнение обоих
критериев (97) и (95).
14. Развитие во времени колебаний магнитной и модельной систем
Рассмотрим теперь, в какой степени колебания осцилляторов, описываемые упрощенной системой (19)-(24), соответствуют колебаниям намагниченности, описываемым полной системой (1)-(3). Для сравнения обратимся к рис.7.
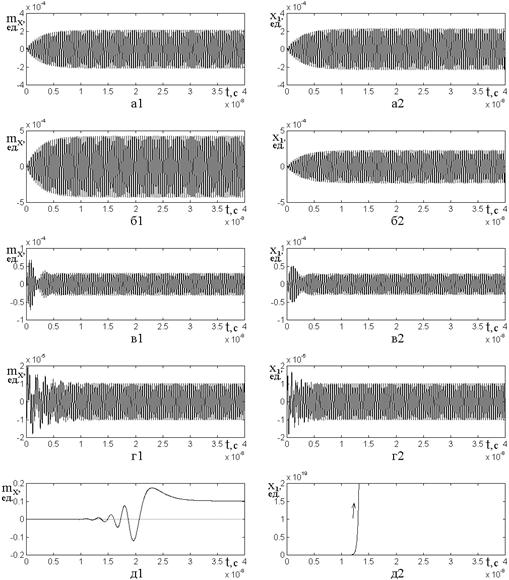
Рис.7. Развитие колебаний компонент ![]() (1) и
(1) и ![]() (2) во
времени при различных коэффициентах константы магнитоупругого взаимодействия:
(2) во
времени при различных коэффициентах константы магнитоупругого взаимодействия: ![]() . Частота возбуждения
. Частота возбуждения ![]() .
.
Условия возбуждения: а – ![]() ,
, ![]() ;
; ![]() ;
; ![]() ;
;
б, в, г, д – ![]() ,
,
![]() ; везде
; везде ![]() .
.
Коэффициент константы магнитоупругого взаимодействия:
а – ![]() ; б
–
; б
– ![]() ; в –
; в – ![]() ; г
–
; г
– ![]() ; д –
; д – ![]() .
.
На рис.7 показано развитие
колебаний компонент ![]() (1) и
(1) и ![]() (2)
во времени при различных коэффициентах константы магнитоупругого
взаимодействия:
(2)
во времени при различных коэффициентах константы магнитоупругого
взаимодействия: ![]() . Кривые в левом столбце
соответствуют полной системе (1)-(3), кривые в правом столбце – укороченной
системе (19)-(24).
. Кривые в левом столбце
соответствуют полной системе (1)-(3), кривые в правом столбце – укороченной
системе (19)-(24).
Кривая а1 построена при
возбуждении магнитной системы по одной координате ![]() . Из
сравнения с кривой а2, соответствующей возбуждению первого осциллятора
упрощенной системы, видно совпадение установившейся амплитуды в обоих случаях с
точностью до единиц процентов. Однако при увеличении константы
. Из
сравнения с кривой а2, соответствующей возбуждению первого осциллятора
упрощенной системы, видно совпадение установившейся амплитуды в обоих случаях с
точностью до единиц процентов. Однако при увеличении константы ![]() установившаяся амплитуда
установившаяся амплитуда ![]() падает несколько быстрее, чем амплитуда
падает несколько быстрее, чем амплитуда ![]() и при
и при ![]() это
различие достигает почти двух раз. В этом случае с точки зрения совпадения
установившихся амплитуд более удобным становится возбуждение магнитной системы
сразу по двум координатам
это
различие достигает почти двух раз. В этом случае с точки зрения совпадения
установившихся амплитуд более удобным становится возбуждение магнитной системы
сразу по двум координатам ![]() и
и ![]() . Однако в этом случае при
. Однако в этом случае при ![]() амплитуда
амплитуда ![]() становится
больше амплитуды
становится
больше амплитуды ![]() почти в два раза, как это
показано на рис.7б1 и 7б2.
почти в два раза, как это
показано на рис.7б1 и 7б2.
Тем не менее, при увеличении
константы ![]() до
до ![]() и
более вплоть до
и
более вплоть до ![]() , установившиеся амплитуды
, установившиеся амплитуды ![]() и
и ![]() совпадают
с точностью до единиц процентов, как это видно из рис.7в1-7в2 и 7г1-7г2.
совпадают
с точностью до единиц процентов, как это видно из рис.7в1-7в2 и 7г1-7г2.
При дальнейшем увеличении
константы ![]() , начиная с
, начиная с ![]() вектор
намагниченности претерпевает переориентацию к направлению более близкому к плоскости
пластины, что происходит через посредство нескольких затухающих осцилляций, как
это видно из рис.7д1, соответствующего
вектор
намагниченности претерпевает переориентацию к направлению более близкому к плоскости
пластины, что происходит через посредство нескольких затухающих осцилляций, как
это видно из рис.7д1, соответствующего ![]() . Более
подробно процесс переориентации описан в работе [27]. При таких же значениях
константы
. Более
подробно процесс переориентации описан в работе [27]. При таких же значениях
константы ![]() амплитуда осциллятора
амплитуда осциллятора ![]() , как показано на рис.7д2, устремляется к
бесконечности, что соответствует переходу через критическое значение
, как показано на рис.7д2, устремляется к
бесконечности, что соответствует переходу через критическое значение ![]() , рассмотренное в предыдущем разделе.
, рассмотренное в предыдущем разделе.
Таким образом, можно видеть, что
переориентация вектора намагниченности в исходной магнитоупругой системе и уход
на бесконечность амплитуды колебаний модельной системы осцилляторов происходит
при одном и том же значении константы магнитоупругого взаимодействия ![]() .
.
15. Сравнение амплитуд колебаний магнитной и модельной систем при изменении константы магнитоупругого взаимодействия
Рассмотрим поведение полной и
укороченной колебательных систем при изменении константы магнитоупругого
взаимодействия ![]() более подробно.
более подробно.
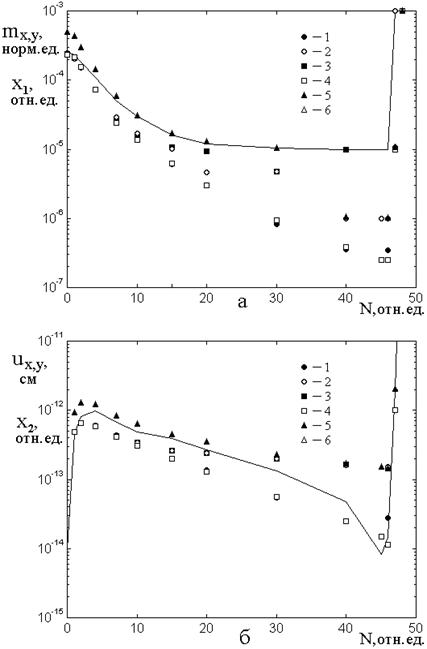
Рис.8. Зависимости амплитуд компонент намагниченности (а) и упругого смещения (б) от отношения константы магнитоупругого взаимодействия к той же константе для ЖИГ. Точки – результаты расчета по полным уравнениям (1)-(3), сплошная линия – расчет по укороченной системе (19)-(24).
1 – ![]() ,
, ![]() при
при ![]() ,
, ![]() ; 2 –
; 2 – ![]() ,
, ![]() при
при ![]() ,
, ![]() ;
;
3 – ![]() ,
, ![]() при
при ![]() ,
, ![]() ; 4 –
; 4 – ![]() ,
, ![]() при
при ![]() ,
, ![]()
5 – ![]() ,
, ![]() при
при ![]() ,
, ![]() ; 6 –
; 6 – ![]() ,
, ![]() при
при ![]() ,
, ![]() . Положения точек 5 и 6 совпадают, то
есть эти точки полностью накладываются друг на друга. Сплошная линия построена
при
. Положения точек 5 и 6 совпадают, то
есть эти точки полностью накладываются друг на друга. Сплошная линия построена
при ![]() .
.
На рис.8 показаны зависимости
амплитуд компонент намагниченности (а) и упругого смещения (б) от отношения
константы магнитоупругого взаимодействия к той же константе для ЖИГ, то есть от
![]() . Точками показаны результаты расчета по
полным уравнениям (1)-(3), сплошной линией – расчет по укороченной системе
(19)-(24).
. Точками показаны результаты расчета по
полным уравнениям (1)-(3), сплошной линией – расчет по укороченной системе
(19)-(24).
Из рисунка видно, что укороченная
система в общем довольно близко описывает поведение полной системы во всем
диапазоне изменения константы ![]() . При небольших значениях
. При небольших значениях
![]() от 1 до 2 значения амплитуд как
магнитных, так и упругих колебаний, рассчитанные по укороченной системе,
наиболее близко подходят к амплитудам, рассчитанным по полной системе при
возбуждении только одной компонентой переменного поля:
от 1 до 2 значения амплитуд как
магнитных, так и упругих колебаний, рассчитанные по укороченной системе,
наиболее близко подходят к амплитудам, рассчитанным по полной системе при
возбуждении только одной компонентой переменного поля: ![]() ,
,
![]() (точки 1). Различие здесь не превышает
20%. Однако при больших значениях
(точки 1). Различие здесь не превышает
20%. Однако при больших значениях ![]() от 2 до 30 лучшее
совпадение наблюдается с возбуждением обеими компонентами переменного поля:
от 2 до 30 лучшее
совпадение наблюдается с возбуждением обеими компонентами переменного поля: ![]() ,
, ![]() (точки
5, 6), где различие не превышает 10%. Для амплитуды магнитных колебаний (а)
такое совпадение продолжается вплоть до
(точки
5, 6), где различие не превышает 10%. Для амплитуды магнитных колебаний (а)
такое совпадение продолжается вплоть до ![]() , что
соответствует значению константы
, что
соответствует значению константы ![]() , при котором
происходит переориентация вектора намагниченности. Однако для упругих колебаний
(б) значения амплитуд, рассчитанные по укороченной системе, от
, при котором
происходит переориентация вектора намагниченности. Однако для упругих колебаний
(б) значения амплитуд, рассчитанные по укороченной системе, от ![]() вплоть до
вплоть до ![]() лучше
соответствуют полным значениям при возбуждении только по одной координате,
однако другой по сравнению со случаем малых
лучше
соответствуют полным значениям при возбуждении только по одной координате,
однако другой по сравнению со случаем малых ![]() :
: ![]() ,
, ![]() (точки
4). В этом случае различие также не превышает 30%. Смена координатных компонент
переменного поля, обеспечивающих оптимальное возбуждение упругих колебаний при
(точки
4). В этом случае различие также не превышает 30%. Смена координатных компонент
переменного поля, обеспечивающих оптимальное возбуждение упругих колебаний при ![]() , по-видимому, обусловлено гиротропией
полной системы, у укороченной системы отсутствующей. При достижении
, по-видимому, обусловлено гиротропией
полной системы, у укороченной системы отсутствующей. При достижении ![]() значения вблизи 47 укороченная система
уходит на бесконечность, что также соответствует критическому значению
константы
значения вблизи 47 укороченная система
уходит на бесконечность, что также соответствует критическому значению
константы ![]() .
.
Таким образом, укороченная
система описывает свойства полной системы во всем интервале изменения константы
![]() от
от ![]() до
до ![]() с точностью не хуже 30%, причем уход
укороченной системы на бесконечность эквивалентен переориентации вектора
намагниченности и оба они происходят при одном и том же значении константы
с точностью не хуже 30%, причем уход
укороченной системы на бесконечность эквивалентен переориентации вектора
намагниченности и оба они происходят при одном и том же значении константы ![]() .
.
Заключение
Основные результаты настоящей работы сводятся к следующему.
В применении к задаче анализа работы магнитострикционного преобразователя СВЧ диапазона на частоте ферромагнитного резонанса рассмотрено возбуждение гиперзвуковых колебаний переменным магнитным полем в геометрии плоскопараллельной нормально намагниченной ферритовой пластины.
Записаны связанные уравнения движения вектора намагниченности и упругого смещения с граничными условиями и возбуждением переменным магнитным полем.
Для упрощения задачи предложена линеаризованная система уравнений, основанная на модели связанных осцилляторов, в результате чего полная система, содержащая семь уравнений первого порядка и четыре граничных условия, сведена к системе четырех уравнений первого порядка без граничных условий.
Введены эквивалентные параметры укороченной системы, выраженные через параметры материала исходной ферритовой пластины. На основе анализа соотношения составляющих эквивалентных параметров для реального случая железоиттриевого граната (ЖИГ), получены укороченные выражения, описывающие параметры задачи с точностью не менее двух порядков.
Укороченная система уравнений приведена к виду, соответствующему модельной системе из двух осцилляторов, связанных через производные от переменных.
Обе системы уравнений, полная и укороченная, решены методом Рунге-Кутта четвертого порядка, получено развитие колебаний во времени.
Показано, что в зависимости от величины параметров связи возможны два режима вынужденных колебаний, соответствующие спаду и нарастанию амплитуды во времени, разделенные третьим режимом (точкой бифуркации), в котором амплитуда вынужденных колебаний сохраняет постоянное значение, причем критичность порога перехода от одного режима к другому по константе связи составляет не менее шести значащих цифр.
Рассмотрено аналитическое решение укороченной системы в режиме постоянной амплитуды колебаний. Найдены два критерия, один из которых определяет критическое значение константы связи, соответствующее переходу между режимами, а другой дает частоту резонансных колебаний системы в точке перехода.
Результаты рассмотрения укороченной системы применены к реальному случаю возбуждения пластины из ЖИГ. Выявлены условия перехода от режима убывания амплитуды к режиму ее нарастания. Отмечено, что в реальном случае железоиттриевого граната амплитуда нарастающих колебаний ограничивается на достаточно высоком постоянном уровне, обусловленном нелинейной расстройкой магнитной колебательной системы.
Показано, что точка перехода между режимами, соответствующая бесконечному росту амплитуды колебаний модельной системы, для случая ЖИГ эквивалентна точке переориентации вектора намагниченности, причем тот и другой переходы происходят при одном и том же критическом значении константы магнитоупругого взаимодействия.
Отмечено, что модельная система связанных осцилляторов описывает как развитие во времени, так и стационарное значение амплитуды установившихся колебаний реального материала во всем допустимом интервале изменения величины константы магнитоупругого взаимодействия с точностью не хуже 30%.
Работа выполнена при финансовой поддержке РФФИ (гранты №12-02-01035-а, №13-02-01401-а).
Литература
1. Физическая энциклопедия. Т.1. М.: Советская энциклопедия. 1988. Статья «Гиперзвук».
2. Физическая акустика. Под ред. Мэзона У., Терстона Р. Т.1-7. М.: Мир. 1966-1974.
3. Такер Дж., Рэмптон В., Гиперзвук в физике твердого тела. М.: Мир. 1975.
4. Поверхностные акустические волны. Под ред. Олинера А. М.: Мир. 1981.
5. Викторов И.А. Звуковые поверхностные волны в твердых телах. М.: Наука. 1981.
6. Bleustein J.L. // Appl. Phys. Lett. 1968. V.13. P.412.
7. Гуляев Ю.В. // ПЖЭТФ. 1969. Т.9. С.63.
8. Кикучи Е. Ультразвуковые преобразователи. М.: Мир. 1972.
9. Голямина И.П. // Магнитострикционные излучатели из ферритов. В кн.: Физика и техника мощного ультразвука. Кн.1. Источники мощного ультразвука. М., Наука, 1967.
10. Comstock R.L., LeCraw R.C. // J. Appl. Phys. 1963. V.34. № 10. P.3022.
11. Ле-Кроу Р., Комсток Р. // В кн.: Мэзон У. (ред.): Физическая акустика. Т.3Б. Динамика решетки. М.: Мир. 1968. С.156.
12. Suhl H. // J. Phys. Chem. Sol. 1957. V.1. №4. P.209.
13. Моносов Я.А. // Нелинейный ферромагнитный резонанс. М.: Наука. 1971.
14. Захаров В.Е., Львов В.С., Старобинец С.С. // УФН. 1974. Т.114. №4. С.609.
15. Temiryazev A.G., Tikhomirova M.P., Zilberman P.E. // J. Appl. Phys. 1994. V.76. №12. P.5586.
16. Зильберман П.Е., Темирязев А.Г., Тихомирова М.П. // ЖЭТФ. 1995. Т.108. №1. С.281.
17. Гуляев Ю.В., Зильберман П.Е., Темирязев А.Г., Тихомирова М.П. // РЭ. 1999. Т.44. № 10. С.1262.
18. Гуляев Ю.В., Зильберман П.Е., Темирязев А.Г., Тихомирова М.П. // ФТТ. 2000 Т.42. №6. С.1062.
19. Gerrits Th., Schneider M.L., Kos A.B., Silva T.J. // Phys.Rev.B. 2006. V.73. №9. P.094454(7).
20. Власов В.С., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2009. Т.54. №7. С.863.
21. Заславский Г.М., Сагдеев Р.З. Введение в нелинейную физику. М.: Наука. 1988.
22. Карлов Н.В., Кириченко Н.А. Колебания, волны, структуры. М.: Физматлит. 2003.
23. Власов В.С. Исследование релаксационной и нелинейной динамики магнитных и магнитоупругих колебаний пленок и частиц. Диссертация на соискание ученой степени канд. физ.-мат. наук. МГУ. 2007.
24. Vlasov V.S., Kotov L.N., Asadullin F.F. // J. of Magnetism and Magnetic Materials. 2006.V.300. №1. P. e48-e51.
25. Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Наука. 1973.
26. Мигулин В.В., Медведев В.И., Мустель Е.Р., Парыгин В.Н. Основы теории колебаний. М.: Наука. 1978.
27. Власов В.С., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2010. Т.55. №6. С.689.