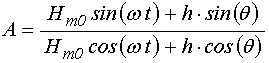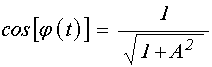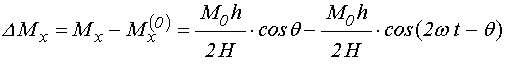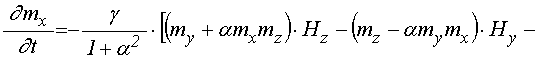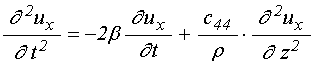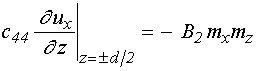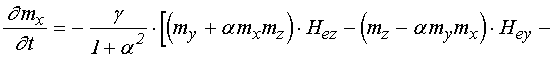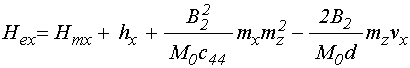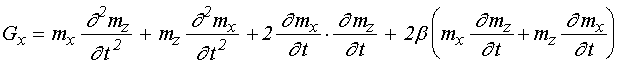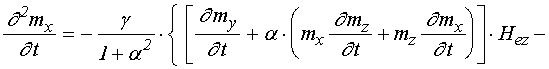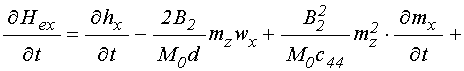УДК 537.874; 537.624
ФОРМИРОВАНИЕ МАГНИТНОГО ЗАТУХАНИЯ ЗА СЧЕТ УПРУГОЙ ДИССИПАЦИИ В СХЕМЕ РОТАЦИОННОГО МАГНЕТОМЕТРА
П. М. Ветошко, В. Г. Шавров, В. И. Щеглов
Институт
радиотехники и электроники РАН, Москва, Россия
Статья
получена 21 октября 2014 г.
Аннотация. Рассмотрена классическая схема ротационного магнетометра, предназначенного для измерения слабых магнитных полей. Показана важность механизма формирования магнитного затухания за счет возбуждения упругих волн в магнитоупругой среде. Рассмотрена нелинейная задача о возбуждении прецессии намагниченности в ферритовой пластине, обладающей магнитоупругими свойствами. Показано, что затухание ферромагнитного резонанса в значительной степени формируется за счет связи с упругой системой. Выявлено расщепление резонансной кривой, тем более ярко выраженное, чем константа магнитоупругой связи больше. Для ротационного магнетометра указано на возбуждение вращающимся полем шлейфа магнитных колебаний, затухание которых формируется за счет возбуждения упругих волн.
Ключевые слова: слабые магнитные поля, ротационный магнетометр, магнитоупругое взаимодействие, магнитное затухание.
Abstract. The classic rotational magnetometer scheme intended for weak magnetic field measuring is considered. It is shown the importance of magnetic relaxation formation mechanism at elastic waves excitation expense in magnetoelastic medium. It is investigated the nonlinear task about the magnetization precession excitation in ferrite plate having the magnetoelastic properties. It is shown that the ferromagnetic resonance dissipation in the great degree is formed by the connection with elastic medium. It is found the resonance line splitting the more pronounced the more the magnetoelasticity constant is larger. For rotational magnetometer there is shown the magnetic vibrations train excitation by rotational field where the dissipation is formed by the elastic waves excitation.
Key words: weak magnetic field, rotational magnetometer, magnetoelastic interaction, magnetic dissipation.
Введение
Задача измерения слабых магнитных полей является важнейшей областью исследования магнитных явлений и самых разнообразных проявлений магнетизма [1]. Наиболее широко применяемым инструментом для таких исследований является СКВИД-магнетометр [2], основанный на использовании эффекта Джозефсона в сверхпроводнике [3]. Основным неудобством СКВИД-магнетометров является требование для их работы низких температур, в традиционном варианте – гелиевых, а при использовании высокотемпературных сверхпроводников – азотных. Поэтому применяются и находятся в разработке многие конструкции высокочувствительных магнетометров, работающих при комнатной температуре, некоторые из которых описаны в обзорах [4,5].
Среди таких магнетометров своей высокой чувствительностью в сочетании с относительной простотой реализации выделяется ротационный магнетометр [6-16], представляющий собой магнитный диск с приложенным в его плоскости вращающимся магнитным полем. Измеряемое поле нарушает вращательную симметрию системы, в результате чего в отклике, регистрируемом надетой на диск катушкой, появляется вторая гармоника от частоты вращения.
Уровень чувствительности такого
магнетометра при комнатной температуре для постоянных и медленно меняющихся
полей составляет ![]() , что позволяет весьма успешно
применять его для исследования магнитных полей в задачах биологии [13].
, что позволяет весьма успешно
применять его для исследования магнитных полей в задачах биологии [13].
Поскольку, как показано в работе
[12] и дополнительно отмечено в [16], уровень шума ротационного магнетометра,
обусловленный температурными флуктуациями намагниченности, пропорционален ширине
линии ферромагнитного резонанса (ФМР) ![]() , то
наилучшим материалом для такого магнетометра считается железоиттриевый гранат
(ЖИГ) [9,15], обладающий рекордно низкими магнитными потерями [17-21] (
, то
наилучшим материалом для такого магнетометра считается железоиттриевый гранат
(ЖИГ) [9,15], обладающий рекордно низкими магнитными потерями [17-21] (![]() ).
).
Другим механизмом, ограничивающим чувствительность ротационного магнетометра, являются скачки Баркгаузена на дефектах, неизбежно присутствующих в любом магнитом материале, в том числе в какой-то степени и в ЖИГ. Влияние этого механизма частично упомянуто в работе [16], хотя проведенное там рассмотрение является существенно не полным. Так остается в стороне связь этого механизма с параметром магнитного затухания.
Таким образом, как можно видеть из перечисленных работ, важнейшим фактором, определяющим чувствительность ротационного магнетометра, являются свойства релаксации магнитных колебаний.
Природа процессов релаксации в магнитных диэлектриках исследуется с давних времен. В качестве основного механизма, формирующего затухание прецессии намагниченности в таких средах, обычно считается двухмагнонное рассеяние, то есть процесс, при котором возбужденные в образце магноны теряют свою энергию за счет столкновения с дефектами [22-29].
Однако рассмотренный в этих работах двухмагнонный процесс, как правило, обеспечивает лишь небольшую часть затухания прецессии намагниченности, наблюдаемого в эксперименте.
В работе [30], по-видимому, впервые обращено внимание на возможность обеспечения магнитного затухания за счет передачи энергии магнонов возбуждаемым на неоднородностях фононам, энергия которых в свою очередь уходит в решетку, то есть явно указано о возможности формирования магнитного затухания за счет упругого.
В работе [31] рассчитано затухание колебаний намагниченности за счет генерации сдвиговых упругих волн в магнитоупругой среде, обладающей упругой вязкостью.
Однако в работе [32] утверждается, что полученный в обеих этих работах коэффициент затухания магнитных колебаний мал по сравнению с экспериментальными величинами. В качестве альтернативы предложена собственная модель возбуждения фононов в пленке на подложке, в результате рассмотрения которой показано, что при больших частотах коэффициент затухания обратно пропорционален кубу частоты, а при малых – прямо пропорционален квадрату частоты. Какая-либо экспериментальная проверка полученных соотношений в этой работе отсутствует.
В работе [33] предпринята попытка исследования динамики намагниченности с учетом термального резервуара упругих мод. Для магнитной пленки на немагнитной подложке получено уравнение движения, в котором параметр магнитного затухания является тензором и зависит от намагниченности. Показано, что этот параметр и ширина линии ФМР пропорциональны произведению квадрата константы магнитоупругого взаимодействия на толщину пленки.
В работе [34] в рамках термодинамики проведено рассмотрение магнитного затухания с учетом магнитоупругого взаимодействия на основе флуктуацонно-диссипационной теоремы. Показано, что параметр магнитного затухания имеет тензорный характер и пропорционален намагниченности.
В работе [35] указано на аналогию между феноменологическими уравнениями движения в магнитной и электрически поляризованной средах, обусловленную сходной природой электронного энергетического спектра. Показано, что магнитное затухание определяется вязкостью упругой системы.
Однако экспериментальная проверка результатов, полученных в работах [33-35], опять отсутствует.
Наконец в работе [36] рассматривается формирование магнитной релаксации за счет упругой, то есть внесение упругого затухания как данного в затухание колебаний намагниченности, причем еще раз постулируется представление параметра магнитного затухания в виде тензора второго ранга. Далее проводится подробное сравнение полученных результатов с экспериментами предшествующих авторов, выполненными на десяти различных составах: от магнитных диэлектриков – ферритов до хороших проводников – металлов. Результаты сравнения показывают соответствие между теорией и экспериментом с точностью не хуже полутора-двух раз, хотя всегда в меньшую сторону.
Будучи выполненной в чисто феноменологических рамках, эта работа микроскопические механизмы, рассмотренные в работах [30-35], не затрагивает.
С другой стороны, даже феноменологический подход здесь проведен не полностью: так учет имеющей место в реальности прецессии намагниченности заменен термодинамическим рассмотрением вклада магнитострикционной добавки к потенциалу, а выражение для параметра магнитного затухания получено исходя из аналогии с подобным выражением для затухания упругих колебаний.
Таким образом, развитие подхода, использованного в работе [36], требует детального рассмотрения прецессии намагниченности с учетом магнитоупругого взаимодействия в рамках модели, учитывающей кристаллографическую симметрию, каковой обладает используемый для построения магнетометра монокристаллический ЖИГ.
Важным вопросом является также роль в формировании магнитного затухания соотношения между ферромагнитным и упругим резонансами, в случае их возбуждения в магнитной пластине магнетометра.
Ферромагнитный резонанс (ФМР) в различных его проявлениях является основой для создания многочисленных устройств обработки информации в СВЧ диапазоне [37-42]. Вопрос о теоретической интерпретации затухания прецессии ФМР обычно решается путем феноменологического введения в уравнение движения для намагниченности Ландау-Лифшица «диссипативного члена», чаще всего используемого в форме, первоначально предложенной Гильбертом [43].
При этом природа диссипации движения намагниченности обычно рассматривается в рамках «двухмагнонных» процессов рассеяния возбуждаемых при ФМР магнонах на дефектах кристаллической решетки [22-29]. При высоком уровне мощности сигнала СВЧ возникают процессы параметрического возбуждения обменных спиновых волн, сильно увеличивающие потери однородной прецессии [44-46].
Механизм передачи энергии магнитных колебаний упругим [30-36], по-видимому, описывает магнитные потери при ФМР более адекватно, однако его подробное рассмотрение с учетом специфики монокристаллического ЖИГ в геометрии ротационного магнетометра отсутствует.
Настоящая работа посвящена рассмотрению перечисленных вопросов. Сначала вкратце обсуждается схема ротационного магнетометра и механизм формирования второй гармоники. Затем проводится анализ ограничения его чувствительности за счет скачков Баркгаузена и тепловых флуктуаций намагниченности. Основное внимание уделяется формированию магнитного затухания за счет упругого, в том числе в условиях как магнитного, так и упругого резонансов. В заключение приводятся некоторые рекомендации для постановки экспериментов и повышения чувствительности ротационного магнетометра.
1. Схема ротационного магнетометра
Рассмотрим сначала общую схему ротационного магнетометра и получение в нем второй гармоники от частоты вращения поля. Конструкция ротационного магнетометра, впервые заявленная в патентах [6,7], впоследствии была многократно описана в работах [8-16]. Однако механизм получения второй гармоники от частоты вращающегося поля в работах [8-15] в должной мере освещен не был. Только в работе [16] был приведен схематичный вывод выражений, описывающих физические процессы, лежащие в его основе.
Ввиду важности рассматриваемого механизма, следуя, в основном, работе [16], приведем его здесь в более подробном варианте.
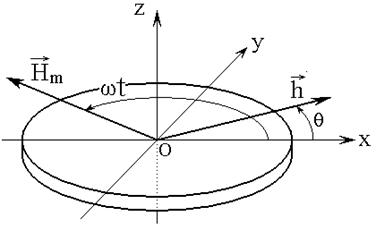
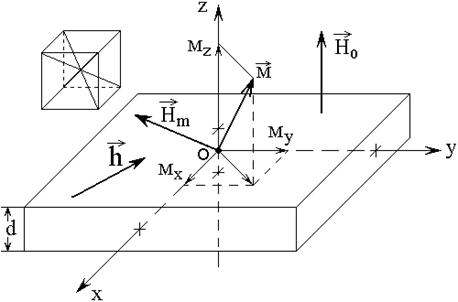
Схема чувствительно элемента
магнетометра [16] показана на рис.1. Основу элемента составляет пленка
железоиттриевого граната (ЖИГ) круглой формы. В плоскости пленки приложено
переменное поле ![]() , вращающееся с частотой
, вращающееся с частотой ![]() . Измеряемое поле
. Измеряемое поле ![]() неизменно
во времени и приложено также в плоскости пленки. Декартова система координат
неизменно
во времени и приложено также в плоскости пленки. Декартова система координат ![]() ориентирована таким образом, что
плоскость
ориентирована таким образом, что
плоскость ![]() совпадает с плоскостью пленки, а ось
совпадает с плоскостью пленки, а ось ![]() этой плоскости перпендикулярна. Поле
этой плоскости перпендикулярна. Поле ![]() составляет угол
составляет угол ![]() с
осью
с
осью ![]() .
.
Вращающееся поле ![]() создается парой надетых на пленку взаимно
перпендикулярных катушек, плоскости витков которых параллельны плоскостям
создается парой надетых на пленку взаимно
перпендикулярных катушек, плоскости витков которых параллельны плоскостям ![]() и
и ![]() .
Катушки питаются переменным током частоты
.
Катушки питаются переменным током частоты ![]() со
сдвигом фаз на
со
сдвигом фаз на ![]() относительно друг друга.
относительно друг друга.
Рис.1. Схема чувствительного элемента магнетометра.
Измерение поля ![]() осуществляется с помощью измерительной
катушки, надетой на пленку таким образом, что плоскость ее витков параллельна
плоскости
осуществляется с помощью измерительной
катушки, надетой на пленку таким образом, что плоскость ее витков параллельна
плоскости ![]() . Измерение состоит в регистрации сигнала
двойной частоты
. Измерение состоит в регистрации сигнала
двойной частоты ![]() , снимаемого с измерительной
катушки, который наводится в ней вращающимся вектором намагниченности.
, снимаемого с измерительной
катушки, который наводится в ней вращающимся вектором намагниченности.
2. Получение сигнала двойной частоты
Следуя [16], поясним, как
получается сигнал двойной частоты более подробно. Пусть компоненты поля ![]() имеют вид:
имеют вид:
![]() ;
(1)
;
(1)
![]() .
(2)
.
(2)
Компоненты поля ![]() положим в виде:
положим в виде:
![]() ;
(3)
;
(3)
![]() .
(4)
.
(4)
Полное поле ![]() равно
сумме этих полей:
равно
сумме этих полей:
![]() ,
(5)
,
(5)
а его компоненты имеют вид:
![]() ;
(6)
;
(6)
![]() .
(7)
.
(7)
Предполагается, что амплитуда
поля ![]() больше поля насыщения пленки ЖИГ. Такое
поле вызывает вращение вектора намагниченности в плоскости
больше поля насыщения пленки ЖИГ. Такое
поле вызывает вращение вектора намагниченности в плоскости ![]() с частотой
с частотой ![]() . Будем
полагать, что компоненты вращающегося вектора намагниченности
. Будем
полагать, что компоненты вращающегося вектора намагниченности ![]() имеют вид:
имеют вид:
![]() ,
(9)
,
(9)
где ![]() –
зависящее от времени угловое положение вектора намагниченности, синхронное с
вращающимся полем
–
зависящее от времени угловое положение вектора намагниченности, синхронное с
вращающимся полем ![]() .
.
Будем полагать, что вектор
намагниченности точно следует за полем ![]() , то
есть его компоненты соответствуют компонентам поля (6)-(7). Такое предположение
означает, что частота вращения поля
, то
есть его компоненты соответствуют компонентам поля (6)-(7). Такое предположение
означает, что частота вращения поля ![]() настолько мала, что в
каждый момент времени вектор
настолько мала, что в
каждый момент времени вектор ![]() успевает установиться
вдоль поля, то есть период поля
успевает установиться
вдоль поля, то есть период поля ![]() значительно больше
времени релаксации намагниченности.
значительно больше
времени релаксации намагниченности.
При этом компоненты вектора намагниченности принимают вид:
![]() ;
(10)
;
(10)
![]() ,
(11)
,
(11)
где ![]() –
магнитная восприимчивость, которую для простоты полагаем скалярной.
–
магнитная восприимчивость, которую для простоты полагаем скалярной.
Сравнивая (10)-(11) с (8)-(9), получаем:
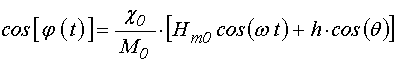 ;
(12)
;
(12)
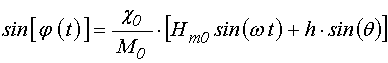 ;
(13)
;
(13)
Из этих соотношений находим ![]() :
:
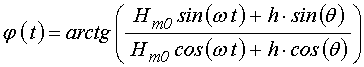 .
(14)
.
(14)
Введем вспомогательное обозначение:
при котором (14) принимает вид:
![]() .
(16)
.
(16)
На данном этапе главной задачей
поставим нахождение компоненты намагниченности ![]() ,
которая, в соответствии с (8), выражается через
,
которая, в соответствии с (8), выражается через ![]() :
:
Для исключения арктангенса, найдем выражение косинуса через тангенс. Для получения такого выражения обе части известного соотношения
![]() (18)
(18)
разделим на ![]() ,
в результате чего получаем:
,
в результате чего получаем:
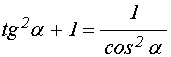 , (19)
, (19)
откуда находим:
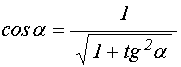 ,
(20)
,
(20)
Подставляя вместо ![]() выражение
выражение ![]() и
учитывая, что
и
учитывая, что ![]() , получаем:
, получаем:
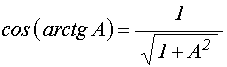 .
(21)
.
(21)
Используя соотношение (16), из (21) получаем:
Преобразуем (22) в предположении,
что ![]() . Для упрощения записи индекс «
. Для упрощения записи индекс «![]() » у
» у ![]() опустим,
то есть будем полагать
опустим,
то есть будем полагать ![]() .
.
При этом из (15) получаем:
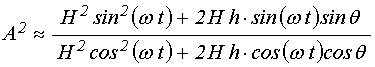 .
(23)
.
(23)
Далее получаем:
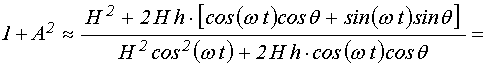
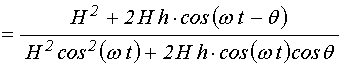 .
(24)
.
(24)
Извлекая квадратный корень из
числителя и знаменателя этого выражения, с учетом малости ![]() , получаем:
, получаем:
![]() ;
(25)
;
(25)
![]() .
(26)
.
(26)
Извлекая из (24) квадратный корень, с учетом (25)-(26), получаем:
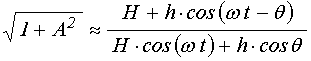 .
(27)
.
(27)
Используем (27) для нахождения правой части выражения (22):
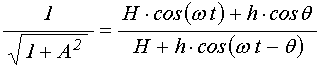 .
(28)
.
(28)
Учитывая малость ![]() , воспользуемся приближенным соотношением:
, воспользуемся приближенным соотношением:
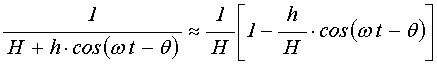 .
(29)
.
(29)
Подставляя (29) в (28) и выполняя умножение, получаем:
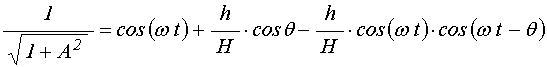 .
(30)
.
(30)
Раскрывая произведение косинусов и приводя подобные члены, получаем:
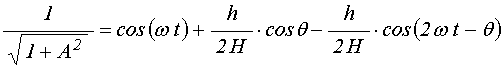 .
(31)
.
(31)
Подставляя в (17) с учетом (22)
соотношение (31), получаем ![]() -компоненту намагниченности
в виде:
-компоненту намагниченности
в виде:
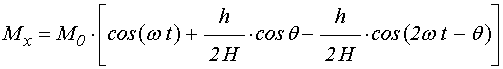 .
(32)
.
(32)
В отсутствие измеряемого поля эта компонента равна:
![]() .
(33)
.
(33)
Таким образом, приращение
намагниченности за счет включения поля ![]() равно:
равно:
Здесь первое слагаемое
представляет собой постоянную во времени добавку, определяемую углом ![]() : так при
: так при ![]() , то
есть когда измеряемое поле направлено вдоль оси
, то
есть когда измеряемое поле направлено вдоль оси ![]() , эта
добавка равна нулю. Второе слагаемое меняется во времени с двойной частотой
, эта
добавка равна нулю. Второе слагаемое меняется во времени с двойной частотой ![]() . Изменение компоненты
. Изменение компоненты ![]() происходит аналогично.
происходит аналогично.
Полагая, что изменение компоненты
намагниченности ![]() вида (32) создает в измерительной
катушке напряжение
вида (32) создает в измерительной
катушке напряжение ![]() , получаем:
, получаем:
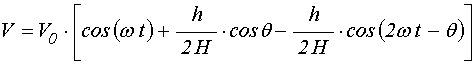 ,
(35)
,
(35)
где ![]() , а
, а ![]() – коэффициент пропорциональности,
определяемый конструкцией катушки.
– коэффициент пропорциональности,
определяемый конструкцией катушки.
Раскрывая скобки в выражении (35), получаем:
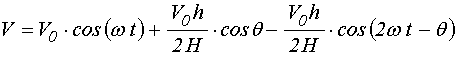 ,
(36)
,
(36)
где первое слагаемое соответствует
составляющей на частоте вращающегося поля, второе – небольшой постоянной
составляющей, получаемой за счет нарушения круговой симметрии вращения
намагниченности за счет поля ![]() , третье – переменной
составляющей на двойной частоте, обусловленное тем же нарушением симметрии.
, третье – переменной
составляющей на двойной частоте, обусловленное тем же нарушением симметрии.
Таким образом, сигнал на двойной частоте имеет вид:
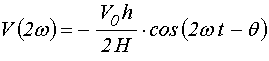 .
(37)
.
(37)
Амплитуда этого сигнала
определяет величину измеряемого поля ![]() , а его фаза
, а его фаза ![]() – направление поля
– направление поля ![]() относительно оси
относительно оси ![]() (рис.1).
(рис.1).
Именно это слагаемое,
пропорциональное величине поля ![]() , будучи пропущенным через
селективный фильтр, настроенный на двойную частоту, позволяет измерить поле
, будучи пропущенным через
селективный фильтр, настроенный на двойную частоту, позволяет измерить поле ![]() .
.
3. Обоснование математического аппарата
Основной целью настоящей работы будет оценка возможности формирования магнитного затухания за счет упругого. Для решения такой задачи можно эффективно использовать математический аппарат, развитый в работе [47] для решения нелинейной задачи о возбуждении гиперзвука в магнитной пластине, обладающей магнитоупругими свойствами. Такой аппарат удобен тем, что выбранная там геометрия нормально намагниченной пластины исключает параметрическое возбуждение обменных спиновых волн, давая тем самым возможность возбуждения прецессии намагниченности с отклонением от нормали к пластине, достигающим десятков градусов [48-53]. В схеме ротационного магнетометра движение вектора намагниченности происходит в плоскости пластины, где этот угол составляет девяносто градусов. Таким образом, развитый в работе [47] нелинейный математический аппарат как раз подходит для решения рассматриваемой задачи.
4. Геометрия задачи и основные уравнения
Геометрия задачи совпадает с
принятой в работе [47] и показана на рис.2. В ее основе лежит
плоскопараллельная пластина толщины ![]() , обладающая магнитными,
упругими и магнитоупругими свойствами. Внешнее постоянное магнитное поле
, обладающая магнитными,
упругими и магнитоупругими свойствами. Внешнее постоянное магнитное поле ![]() приложено перпендикулярно плоскости
пластины. Введение такого нормального поля не является обязательным, так в
приведенной на рис.1 схеме ротационного магнетометра оно равно нулю, здесь же
это поле сохранено для общности задачи. Вращающееся поле
приложено перпендикулярно плоскости
пластины. Введение такого нормального поля не является обязательным, так в
приведенной на рис.1 схеме ротационного магнетометра оно равно нулю, здесь же
это поле сохранено для общности задачи. Вращающееся поле ![]() приложено в плоскости пластины.
Измеряемое поле
приложено в плоскости пластины.
Измеряемое поле ![]() в общем случае может быть
приложено в произвольном направлении относительно пластины, в схеме же
ротационного магнетометра (рис.1) оно также лежит в плоскости пластины.
в общем случае может быть
приложено в произвольном направлении относительно пластины, в схеме же
ротационного магнетометра (рис.1) оно также лежит в плоскости пластины.
Задача решается в декартовой
системе координат ![]() , плоскость
, плоскость ![]() которой совпадает с плоскостью пластины,
а оси
которой совпадает с плоскостью пластины,
а оси ![]() ,
, ![]() и
и ![]() параллельны ребрам куба кристаллографической
ячейки. Центр системы координат
параллельны ребрам куба кристаллографической
ячейки. Центр системы координат ![]() находится в центре
пластины, так что ее плоскости соответствуют координатам
находится в центре
пластины, так что ее плоскости соответствуют координатам ![]() . Показан также вектор намагниченности
. Показан также вектор намагниченности ![]() и кубическая ячейка, соответствующая
кристаллографической ориентации (100).
и кубическая ячейка, соответствующая
кристаллографической ориентации (100).
В схеме магнетометра движение
вектора намагниченности под действием вращающегося поля предполагается
квазистатическим, то есть как вращающееся ![]() , так и
измеряемое
, так и
измеряемое ![]() поля вместе с полем
поля вместе с полем ![]() можно считать постоянными.
можно считать постоянными.
Рис.2. Геометрия задачи.
Полагая полную плотность энергии
пластины ![]() в поле
в поле ![]() равной
сумме плотностей магнитной, упругой и магнитоупругой энергий [47], получаем
(оставлены только члены, важные для дальнейшего рассмотрения):
равной
сумме плотностей магнитной, упругой и магнитоупругой энергий [47], получаем
(оставлены только члены, важные для дальнейшего рассмотрения):
![]()
![]() . (38)
. (38)
где: ![]() -
нормированный вектор намагниченности,
-
нормированный вектор намагниченности, ![]() -
намагниченность насыщения;
-
намагниченность насыщения; ![]() - константа (модуль)
упругости;
- константа (модуль)
упругости;
![]() -
константа магнитоупругого взаимодействия.
-
константа магнитоупругого взаимодействия.
Аналогично [47] для упрощения решения сделаем два предположения.
Во-первых, будем считать, что прецессия намагниченности в пластине является однородной, то есть от координат не зависит.
Во-вторых, предположим, что
продольные колебания вдоль оси ![]() с намагниченностью не
связаны, то есть можно полагать
с намагниченностью не
связаны, то есть можно полагать ![]() .
.
Первое из этих предположений имеет право на существование благодаря однородности постоянного поля внутри нормально намагниченной плоскопараллельной пластины [19-21,54], однако неоднородные типы прецессии [19-21,55,56] при этом из рассмотрения исключаются.
Второе, согласно численной оценке,
выполненной в работе [47], достаточно корректно при углах прецессии до ![]() . При больших углах, вплоть до
. При больших углах, вплоть до ![]() , типичных для ротационного магнетометра,
оно означает, что из рассмотрения исключаются продольные упругие волны,
оставляя только поперечные. Подобное предположение, хотя и без подробного
обоснования, было принято в работе [31], что позволило значительно упростить
полученные выражения. Поскольку на данном этапе нашей целью является также
упрощение выкладок, примем его как данное, не забывая однако о необходимости в
дальнейшем более точной его проверки.
, типичных для ротационного магнетометра,
оно означает, что из рассмотрения исключаются продольные упругие волны,
оставляя только поперечные. Подобное предположение, хотя и без подробного
обоснования, было принято в работе [31], что позволило значительно упростить
полученные выражения. Поскольку на данном этапе нашей целью является также
упрощение выкладок, примем его как данное, не забывая однако о необходимости в
дальнейшем более точной его проверки.
Итак, при упомянутых предположениях аналогично [47] получаем полную систему уравнений и граничных условий:
уравнения для намагниченности:
![]() ; (39)
; (39)
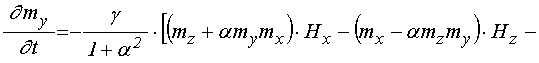
![]() ; (40)
; (40)
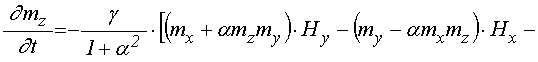
![]() ;
(41)
;
(41)
где эффективные поля равны:
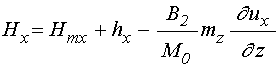 ;
(42)
;
(42)
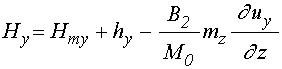 ;
(43)
;
(43)
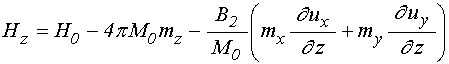 (44)
(44)
уравнения для упругого смещения:
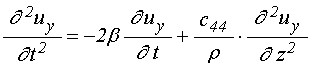 ;
(46)
;
(46)
граничные условия:
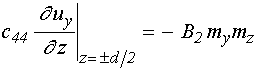 .
(48)
.
(48)
В этих уравнениях: ![]() – гиромагнитная постоянная (
– гиромагнитная постоянная (![]() ),
), ![]() – параметр
затухания для намагниченности,
– параметр
затухания для намагниченности, ![]() – плотность материала
пластины,
– плотность материала
пластины, ![]() – параметр затухания для упругого
смещения.
– параметр затухания для упругого
смещения.
5. Общий ход решения
Таким образом, полная система состоит из трех уравнений первого порядка для намагниченности (39)-(41), двух уравнений второго порядка (45)-(46), эквивалентных четырем уравнениям первого порядка для упругого смещения, а также четырех граничных условий (47)-(48) для упругого смещения. Уравнения для упругого смещения (45)-(46) с намагниченностью не связаны, а само упругое смещение связано с намагниченностью только через граничные условия (47)-(48). Таким образом, для упругого смещения можно выделить независимые четыре уравнения первого порядка и четыре граничных условия, зависящие от намагниченности, то есть часть полной системы, определяющая упругое смещение, полностью определена и ее можно выделить в отдельную задачу, которая решается независимо. В этой задаче имеются однородные уравнения (45)-(46) и неоднородные граничные условия (47)-(48).
Для решения этой задачи аналогично [47, 57-59] воспользуемся приемом переноса неоднородности из граничных условий в уравнения [60], который состоит в следующем. Решение ищется в виде суммы линейной функции от координаты и отклонения от этой линейной функции. Параметры линейной функции выбираются таким образом, чтобы граничные условия для функции отклонения стали однородными. При этом уравнение для функции отклонения становится неоднородным. Его решение ищется в виде разложения в ряд по функциям, являющимся решением однородного уравнения с однородными граничными условиями. Учет однородных граничных условий приводит к бесконечной системе уравнений для членов разложения в ряд функции отклонения. При этом полное решение для упругого смещения получается зависящим от координаты и намагниченности. Если полученное решение продифференцировать по координате и подставить в оставшиеся три уравнения для намагниченности (39)-(41), то в результате получим систему, состоящую из трех нелинейных дифференциальных уравнений первого порядка для намагниченности, в совокупности с бесконечным числом уравнений второго порядка для упругого смещения. Граничных условий никаких не будет, так как колебания намагниченности в пространстве предполагаются однородными, а граничные условия для упругого смещения уже учтены в виде разложения в ряд по собственным функциям однородной задачи.
В простейшем случае вместо бесконечного ряда можно ограничиться рассмотрением только одной первой упругой моды. При этом получаем систему из трех уравнений первого порядка для намагниченности в совокупности с двумя уравнениями второго порядка для упругого смещения, которые эквивалентны четырем уравнениям первого порядка. Таким образом, полная система будет содержать семь нелинейных дифференциальных уравнений первого порядка.
6. Полная система уравнений
Полная система уравнений рассматриваемой задачи имеет вид:
![]() ; (49)
; (49)
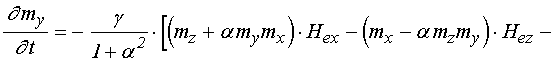
![]() ; (50)
; (50)
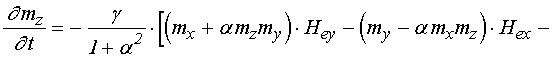
![]() ; (51)
; (51)
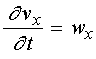 ;
(52)
;
(52)
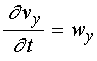 ;
(53)
;
(53)
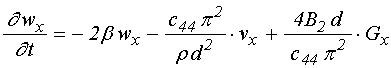 ;
(54)
;
(54)
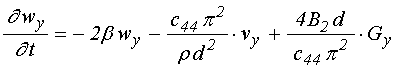 .
(55)
.
(55)
Входящие в уравнения (49)-(51) эффективные поля определяются следующими выражениями:
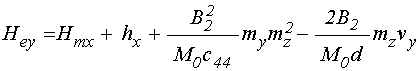 ;
(57)
;
(57)
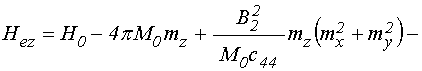
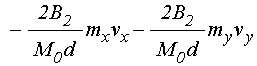 . (58)
. (58)
Входящие в уравнения (54), (55) функции
![]() и
и ![]() определяются
следующими выражениями:
определяются
следующими выражениями:
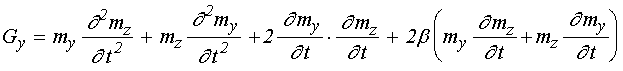 (60)
(60)
Входящие в (59) и (60) первые производные от намагниченности по времени определяются выражениями (49)-(51), а вторые производные от намагниченности определяются следующими выражениями:
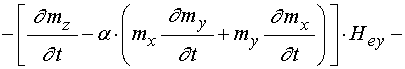
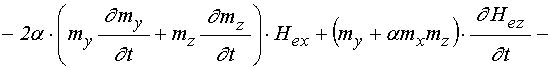
 (61)
(61)
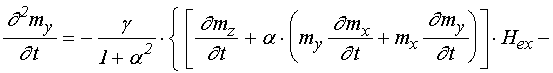
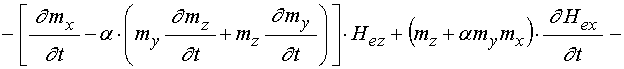
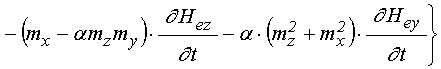 ;
(62)
;
(62)
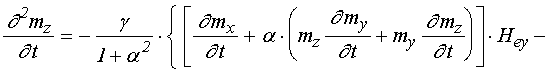
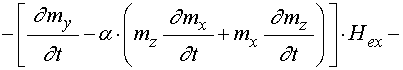
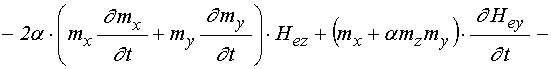
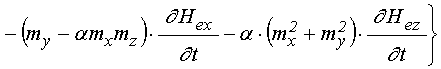 .
(63)
.
(63)
Входящие в (61)-(63) первые производные от полей по времени определяются следующими выражениями:
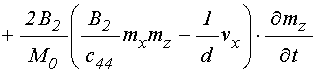 ; (64)
; (64)
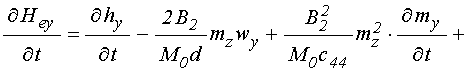
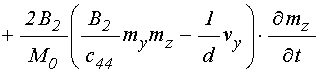 ; (65)
; (65)
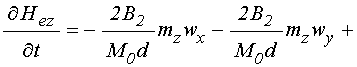
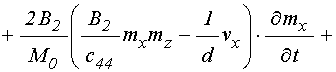
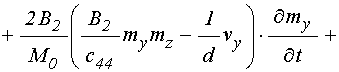
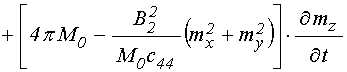 . (66)
. (66)
Эта система уравнений была положена в основу решения поставленной задачи исследования роли упругого затухания в формировании колебаний намагниченности. Решение проводилось методом Рунге-Кутта четвертого порядка [61]. Результаты расчетов излагаются далее.
7. Основные алгоритмы численного решения
Численное решение системы уравнений (49)-(66) позволило рассмотреть две задачи:
1) свободные колебания намагниченности, происходящие после начального возмущения, что можно было рассматривать как установление намагниченности на нуль после одиночного скачка Баркгаузена.
2) вынужденные колебания намагниченности под действием переменного поля в условиях близких к резонансным для магнитной и упругой систем.
Для характеристики релаксационных свойств магнитной системы рассматривалось установление намагниченности как в режиме свободных колебаний, так и при непрерывном возбуждении. При этом система уравнений (49)-(66) решалась непосредственно методом Рунге-Кутта, давая развитие колебаний во времени.
Для более подробного выявления степени воздействия упругой системы на магнитную исследовалось амплитудно-частотные характеристики (АЧХ) связанной системы. Для получения таких АЧХ использовался следующий алгоритм. Сначала устанавливалось какое-то фиксированное значение частоты возбуждения, после чего наблюдалось развитие колебаний за промежуток времени, значительно превосходящий время их установления. При этом амплитуда колебаний принимала стационарное значение, которое и фиксировалось как соответствующее заданной частоте. Затем частота менялась на некоторую величину и возбуждение колебаний наблюдалось снова опять до установления стационарного режима, после чего полученное новое значение амплитуды фиксировалось как соответствующее измененной частоте. Повторение такого процесса с определенным шагом по частоте позволяло получить амплитудно-частотную характеристику в заданном диапазоне частот.
Результаты расчетов с использованием описанных алгоритмов излагаются далее.
8. Развертка колебаний во времени
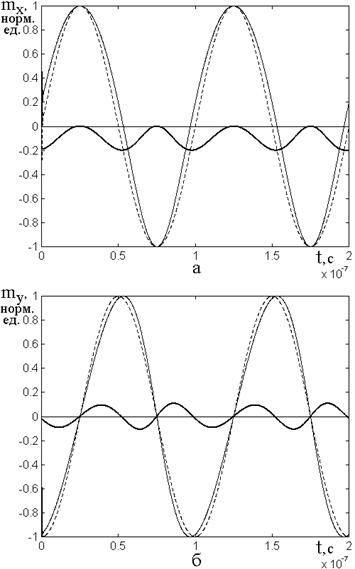
Рассмотрим теперь, как получается вторая гармоника в процессе развертки колебаний во времени, для чего обратимся к рис.3.
На рисунке пунктирная линия –
колебания намагниченности в отсутствие измеряемого поля. Сплошная линия –
колебания намагниченности при наличии измеряемого поля. Утолщенная линия –
разность между колебаниями при наличии измеряемого поля и в его отсутствие, для
компоненты ![]() соответствующая формуле (34).
соответствующая формуле (34).
Из рисунка видно, что в
отсутствие измеряемого поля обе компоненты намагниченности колеблются по
правильному синусоидальному закону (пунктирные линии). При включении
измеряемого поля синусоиды искажаются. Для компоненты ![]() искажение
происходит симметрично относительно точек максимума и минимума: кривые
несколько расширяются. Для компоненты
искажение
происходит симметрично относительно точек максимума и минимума: кривые
несколько расширяются. Для компоненты ![]() искажение
происходит не симметрично относительно точек максимума и минимума: кривые
несколько наклоняются вперед по времени.
искажение
происходит не симметрично относительно точек максимума и минимума: кривые
несколько наклоняются вперед по времени.
Рис.3. Развертка во времени колебаний вектора намагниченности при возбуждении полем, вращающимся в плоскости пленки.
Материал – ЖИГ. Частота вращающегося
поля – ![]() , его амплитуда –
, его амплитуда – ![]() .
Магнитоупругое взаимодействие отсутствует. Параметр затухании колебаний намагниченности:
.
Магнитоупругое взаимодействие отсутствует. Параметр затухании колебаний намагниченности:
![]() . Параметры измеряемого поля: напряженность
–
. Параметры измеряемого поля: напряженность
– ![]() , ориентация – вдоль оси
, ориентация – вдоль оси ![]() .
.
а – компонента ![]() ; б – компонента
; б – компонента ![]() .
.
В обоих случаях разностная кривая
имеет характер близкий к синусоидальному и четко выраженную двойную частоту.
Для компоненты ![]() разностная кривая сдвинута
вниз, что соответствует отрицательной постоянной составляющей. Постоянная
составляющая имеется только для компоненты
разностная кривая сдвинута
вниз, что соответствует отрицательной постоянной составляющей. Постоянная
составляющая имеется только для компоненты ![]() , тогда
как для
, тогда
как для ![]() отсутствует, что отражает симметрию
измеряемого поля, направленного вдоль оси
отсутствует, что отражает симметрию
измеряемого поля, направленного вдоль оси ![]() .
.
9. Ограничение чувствительности магнетометра за счет шума
Чувствительность магнетометра ограничивается рядом факторов, из которых, по-видимому, важнейшими можно считать скачки Баркгаузена и тепловые флуктуации намагниченности [16].
Скачки Баркгаузена обусловлены дефектами образца, представляющими собой локальные макроскопические нарушения кристаллической структуры магнитной пленки. При вращении вектора намагниченности перемагничивание таких локальных участков пленки приводит к скачкообразному изменению намагниченности вблизи дефекта, в результате чего в приемной катушке наводится импульс тока. Хаотическое чередование последовательности таких импульсов приводит к шуму на выходе магнетометра, полностью маскирующему измеряемое поле.
Поскольку распределение дефектов
в образце является стационарным во времени и пространстве, то увеличение
частоты вращения поля приводит к учащению скачкообразного изменения тока, то
есть к увеличению шума. Поэтому для уменьшения влияния такого шума частоту
вращения поля целесообразно снижать. Так в работе [16] использовалась частота
порядка ![]() , а в работе [12] –
, а в работе [12] – ![]() ,
,
Однако столь низкие частоты
вращения поля, с учетом требования квазистационарного изменения
намагниченности, ограничивают частоты измеряемых полей на уровне по крайней
мере на один-два порядка меньшем, то есть не выше ![]() .
.
Стремление измерять более высокие
частоты требует увеличения частоты вращения поля, что приводит к уменьшению
промежутка времени между следующими друг за другом скачками Баркгаузена. Так
при частоте ![]() и линейной плотности дефектов
и линейной плотности дефектов ![]() на
на ![]() при
размере образца
при
размере образца ![]() такое время составляет порядка
такое время составляет порядка ![]() , а при частоте
, а при частоте ![]() уменьшается
до
уменьшается
до ![]() .
.
Другим важнейшим фактором, ограничивающим чувствительность магнетометра, являются температурные флуктуации намагниченности. Согласно [12], из термодинамических соображений с учетом гиромагнитной восприимчивости материала магнетометра, минимальный уровень поля флуктуаций намагниченности определяется формулой:
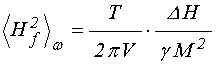 , (67)
, (67)
где ![]() –
температура,
–
температура, ![]() – объем рабочего элемента магнитометра,
– объем рабочего элемента магнитометра, ![]() – его намагниченность насыщения,
– его намагниченность насыщения, ![]() – гиромагнитное отношение,
– гиромагнитное отношение, ![]() – полуширина линии ферромагнитного
резонанса, связанная с параметром магнитного затухания Гильберта
– полуширина линии ферромагнитного
резонанса, связанная с параметром магнитного затухания Гильберта ![]() соотношением:
соотношением: ![]() . Эта
же формула в работе [16] представлена в следующем эквивалентном виде:
. Эта
же формула в работе [16] представлена в следующем эквивалентном виде:
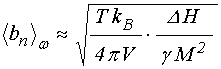 ,
(68)
,
(68)
где ![]() –
константа Больцмана.
–
константа Больцмана.
Таким образом, можно видеть, что
чувствительность магнетометра прямо пропорциональна величине параметра
магнитного затухания ![]() , то есть для повышения чувствительности
этот параметр надо уменьшать.
, то есть для повышения чувствительности
этот параметр надо уменьшать.
Рассмотрим теперь одновременное действие этих обоих факторов. Очевидно, при непрерывном режиме работы минимальная величина поля, измеряемого магнетометром, не может быть меньше скачка намагниченности, вызываемого дефектом. Однако, если скачки достаточно редки, то вторую гармонику частоты вращения поля можно зарегистрировать между двумя следующими друг за другом скачками. При этом время установления квазистатического движения намагниченности должно быть значительно меньше промежутка времени между скачками. Поскольку время установления намагниченности определяется параметром магнитного затухания в соответствии с экспонентой в отрицательной степени, то для уменьшения времени установления параметр магнитного затухания должен увеличиваться.
Таким образом, выделение второй гармоники из последовательности скачков Баркгаузена требует увеличения параметра магнитного затухания, а уменьшение флуктуаций намагниченности – его уменьшения.
То есть вопрос об оптимальной величине этого параметра приобретает решающее значение. Рассмотрим механизмы, определяющие величину магнитного затухания в магнитоупругой среде несколько более подробно.
10. Установление колебаний при наличии магнитоупругой связи
Как показано в предыдущих разделах, измерение поля требует успешного выделения из шума второй гармоники частоты вращения, для чего необходим режим квазистационарного следования вектора намагниченности за вращающимся полем. Однако такое квазистационарное движение в случае реального образца может нарушаться следующими друг за другом с определенными промежутками скачками Баркгаузена.
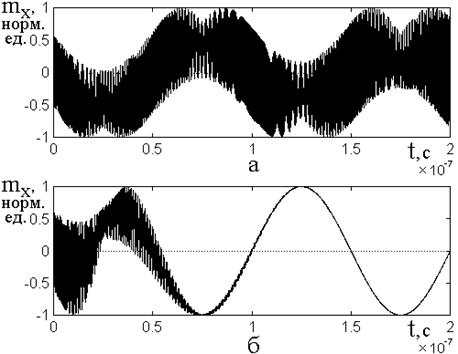
Рассмотрим теперь этот процесс при наличии в образце магнитоупругого взаимодействия, для чего обратимся к рис.4.
Следует отметить, что при
построении разверток колебаний на рис.4 толщина пластины ![]() выбрана той же, что в работе [47] для
удобства сравнения при использовании далее идентичного математического
аппарата. Параметр затухания упругих колебаний
выбрана той же, что в работе [47] для
удобства сравнения при использовании далее идентичного математического
аппарата. Параметр затухания упругих колебаний ![]() и
константа магнитоупругости
и
константа магнитоупругости ![]() выбраны больше
аналогичных величин для ЖИГ:
выбраны больше
аналогичных величин для ЖИГ: ![]() ,
, ![]() . В свою очередь параметр затухания
колебаний намагниченности
. В свою очередь параметр затухания
колебаний намагниченности ![]() выбран несколько
меньшим такого же параметра для ЖИГ:
выбран несколько
меньшим такого же параметра для ЖИГ: ![]() . Такой выбор
параметров, не меняя дела по существу, обусловлен не более чем удобством и
наглядностью изображения развития процессов на рис.4.
. Такой выбор
параметров, не меняя дела по существу, обусловлен не более чем удобством и
наглядностью изображения развития процессов на рис.4.
Рис.4. Развертка во времени колебаний ![]() -компоненты
вектора намагниченности при отсутствии (а) и наличии (б) магнитоупругого
взаимодействия.
-компоненты
вектора намагниченности при отсутствии (а) и наличии (б) магнитоупругого
взаимодействия.
Толщина пластины: ![]() . Параметры затухания:
. Параметры затухания: ![]() ,
, ![]() . Остальные
параметры совпадают с параметрами ЖИГ.
. Остальные
параметры совпадают с параметрами ЖИГ.
Частота вращающегося поля – ![]() , его амплитуда –
, его амплитуда – ![]() .
.
Напряженность измеряемого поля – ![]() , ориентация – вдоль оси
, ориентация – вдоль оси ![]() .
.
а – ![]() ; б
–
; б
– ![]() .
.
Итак, на рис.4а показано развитие
во времени магнитных колебаний сразу после включения переменного поля при
заданном начальном значении ![]() -компоненты намагниченности
(
-компоненты намагниченности
(![]() ,
, ![]() ,
, ![]() ). Можно полагать, что такая ситуация
аналогична прохождению намагниченности через скачок Баркгаузена, приводящий к
ее мгновенному ступенчатому изменению. Дальнейшее развитие колебаний
намагниченности происходит путем вынужденной прецессии под действием
вращающегося поля, причем установление квазистационарного режима вращения сопровождается
постепенно затухающими свободными колебаниями намагниченности, приобретающими
здесь шумовой характер. Постоянная затухания свободных колебаний, вносящих шумовую
составляющую, определяется параметром магнитного затухания
). Можно полагать, что такая ситуация
аналогична прохождению намагниченности через скачок Баркгаузена, приводящий к
ее мгновенному ступенчатому изменению. Дальнейшее развитие колебаний
намагниченности происходит путем вынужденной прецессии под действием
вращающегося поля, причем установление квазистационарного режима вращения сопровождается
постепенно затухающими свободными колебаниями намагниченности, приобретающими
здесь шумовой характер. Постоянная затухания свободных колебаний, вносящих шумовую
составляющую, определяется параметром магнитного затухания ![]() .
.
Наблюдаемый шумоподобный характер
колебаний при принятых значениях параметров продолжается до времени порядка ![]() , после чего за правым краем рисунка
(ограничен для удобства изображения) переходит в плавный синусоидальный с
постоянной амплитудой, подобный показанному на рис.3.
, после чего за правым краем рисунка
(ограничен для удобства изображения) переходит в плавный синусоидальный с
постоянной амплитудой, подобный показанному на рис.3.
Вторую гармонику можно успешно
выделить только после установления квазистационарных колебаний, то есть при
времени большем ![]() . Если следующий скачок Баркгаузена
произойдет раньше этого времени, то возникшие после него новые колебания
намагниченности опять будут иметь шумовой характер и выделение второй гармоники
станет невозможным.
. Если следующий скачок Баркгаузена
произойдет раньше этого времени, то возникшие после него новые колебания
намагниченности опять будут иметь шумовой характер и выделение второй гармоники
станет невозможным.
Таким образом, для успешного измерения поля надо сделать так, чтобы шумовые колебания намагниченности заканчивались как можно раньше после произошедшего скачка Баркгаузена. То есть параметр магнитного затухания должен по возможности быть увеличен.
На рис.4б показано развитие
колебаний намагниченности в тех же условиях, но при наличии в образце магнитоупругой
связи. При этом магнитные колебания возбуждают упругие, которые сами в свою
очередь как-то затухают, передавая свою энергию в решетку кристалла. Таким
образом, введение магнитоупругой связи нагружает магнитную колебательную
систему, приводя к увеличению ее параметра затухания. Из рисунка видно, что при
принятых параметрах шумовые колебания намагниченности прекращаются при времени
порядка ![]() , после чего устанавливается
квазистационарный режим, то есть успешное выделение второй гармоники становится
вполне возможным.
, после чего устанавливается
квазистационарный режим, то есть успешное выделение второй гармоники становится
вполне возможным.
Таким образом, магнитоупругое взаимодействие, увеличивая параметр затухания магнитных колебаний, обеспечивает условия измерения поля даже при наличии достаточно часто следующих друг за другом скачков Баркгаузена.
Резюмируя сказанное, можно сделать вывод, что вклад упругого затухания в формирование магнитного весьма высок и для обеспечения требуемого уровня чувствительности ротационного магнетометра может иметь решающее значение. Поэтому дальнейшие разделы настоящей работы посвящены рассмотрению именно этого вопроса.
11. Ограничение колебаний намагниченности за счет упругого затухания
В силу важности вопроса о роли упругого затухания в формировании магнитного дальнейшее рассмотрение проведем не напрямую на базе ротационного магнитометра, а в более общем виде на примере вынужденной прецессии намагниченности в условиях, близких к резонансным. Можно полагать, что такое рассмотрение вблизи резонанса позволит выявить основные особенности вклада упругого затухания в магнитное более рельефно, чем в случае ротационного магнитометра, работающего в условиях, от резонанса довольно удаленных.
Рассмотрим сначала роль различных
механизмов затухания в формировании установившегося режима прецессии
намагниченности в магнитоупругой среде. Основными механизмами будем считать
магнитный, релаксационные возможности которого задаются параметром ![]() и упругий, характеризуемый параметром
и упругий, характеризуемый параметром ![]() .
.
12. Роль параметра упругого затухания
Рассмотрим сначала вклад упругого затухания в общее в зависимости от соотношения между параметрами магнитного и упругого затухания.
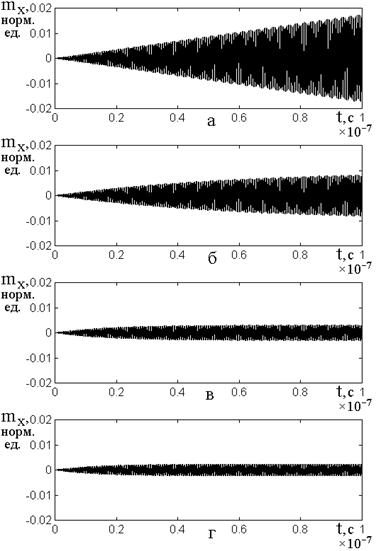
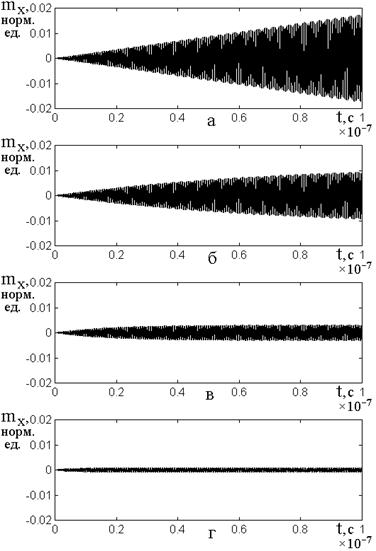
Рис.5. Развитие колебаний
намагниченности ![]() во времени при различных
значениях параметров затухания.
во времени при различных
значениях параметров затухания.
а – ![]() ,
, ![]() ,
, ![]() ; б
–
; б
– ![]() ,
, ![]() ,
, ![]() ;
;
в – ![]() ,
, ![]() ,
, ![]() ;
;
г – ![]() ,
, ![]() ,
, ![]() .
.
На рис.5 показано развитие во
времени колебаний компоненты намагниченности ![]() при
различных вариантах затухания. Характер колебаний другой компоненты намагниченности
при
различных вариантах затухания. Характер колебаний другой компоненты намагниченности
![]() , а также обеих компонент упругих колебаний
, а также обеих компонент упругих колебаний
![]() и
и ![]() полностью
подобен приведенному, поэтому здесь не рассматривается. При расчете
использовались параметры материала, типичные для монокристалла ЖИГ [57]:
полностью
подобен приведенному, поэтому здесь не рассматривается. При расчете
использовались параметры материала, типичные для монокристалла ЖИГ [57]: ![]() ;
; ![]() ;
; ![]() . Параметр затухания магнитной подсистемы
был выбран также типичным для ЖИГ:
. Параметр затухания магнитной подсистемы
был выбран также типичным для ЖИГ: ![]() . Параметр затухания
упругой подсистемы был взят равным
. Параметр затухания
упругой подсистемы был взят равным ![]() , то есть несколько
большим типичного значения для ЖИГ
, то есть несколько
большим типичного значения для ЖИГ ![]() , что было сделано для
исключения мешающего наглядности рассмотрения расщепления резонансной кривой
(описанного далее). Остальные параметры задачи были выбраны такими, чтобы в
отсутствие магнитоупругой связи при линейных колебаниях резонансные частоты однородной
прецессии и первой моды упругих колебаний совпадали и равнялись
, что было сделано для
исключения мешающего наглядности рассмотрения расщепления резонансной кривой
(описанного далее). Остальные параметры задачи были выбраны такими, чтобы в
отсутствие магнитоупругой связи при линейных колебаниях резонансные частоты однородной
прецессии и первой моды упругих колебаний совпадали и равнялись ![]() . При этом постоянное поле составило
. При этом постоянное поле составило ![]() , а толщина магнитной пластины равнялась
, а толщина магнитной пластины равнялась ![]() . Рассматривались линейные колебания
намагниченности, возбуждаемые полем круговой поляризации с компонентами
. Рассматривались линейные колебания
намагниченности, возбуждаемые полем круговой поляризации с компонентами ![]() ,
, ![]() .
Развитие колебаний рассматривалось во временном интервале
.
Развитие колебаний рассматривалось во временном интервале ![]() с шагом
с шагом ![]() .
.
Рис.5а соответствует развитию
колебаний в отсутствие затухания обеих как магнитной, так и упругой подсистем.
Магнитоупругая связь тоже отсутствует, чтобы упругая подсистема не нагружала
магнитную и колебания намагниченности можно было рассмотреть в чистом виде. В
приведенном случае амплитуда колебаний нарастает во всем исследованном
интервале времени практически линейно, достигая при времени ![]() величины
величины ![]() от
от ![]() .
.
Рис.5б соответствует наличию
магнитного затухания при отсутствии как затухания, так и связи с упругой
подсистемой. Видно, что в этом случае колебания намагниченности выходят на
насыщение при времени около ![]() , где амплитуда
составляет
, где амплитуда
составляет ![]() от
от ![]() .
.
Рис.5в соответствует отсутствию
магнитного затухания при наличии магнитоупругой связи. Здесь выход на насыщение
магнитных колебаний при времени ![]() и амплитуде
и амплитуде ![]() от
от ![]() обусловлен
чисто упругой подсистемой. Видно, что при принятом значении параметра упругого
затухания вклад его в затухание колебаний намагниченности является весьма
значительным.
обусловлен
чисто упругой подсистемой. Видно, что при принятом значении параметра упругого
затухания вклад его в затухание колебаний намагниченности является весьма
значительным.
Рис.5г соответствует совокупному
действию как магнитного, так и упругого затухания при наличии магнитоупругой
связи. Этот случай наиболее близок к реальным условиям для ЖИГ. Видно, что
здесь выход на насыщение магнитных колебаний происходит при времени ![]() и амплитуде
и амплитуде ![]() от
от ![]() , причем обе из этих величин заметно
меньше, чем в обоих предыдущих случаях.
, причем обе из этих величин заметно
меньше, чем в обоих предыдущих случаях.
Таким образом, можно сделать вывод, что реально наблюдаемая ширина линии ФМР в ЖИГ обусловлена совокупным вкладом как чисто магнитных, так и дополняющих их упругих потерь.
13. Роль параметра магнитоупругой связи
Рассмотрим теперь вклад упругого затухания в общее в зависимости от связи между магнитными и упругими колебаниями.
На рис.6 показано развитие
колебаний намагниченности ![]() во времени при постоянных
параметрах затухания
во времени при постоянных
параметрах затухания ![]() ,
, ![]() и
различных значениях константы магнитоупругого взаимодействия
и
различных значениях константы магнитоупругого взаимодействия ![]() . В качестве нормирующего эталона
используем значение этой константы для ЖИГ:
. В качестве нормирующего эталона
используем значение этой константы для ЖИГ: ![]() .
Поскольку
.
Поскольку ![]() , то магнитное затухание отсутствует, то
есть все затухание прецессии намагниченности формируется за счет нагружения
магнитной подсистемы упругой, причем величина упругого затухания остается
постоянной, а величина связи через посредство константы
, то магнитное затухание отсутствует, то
есть все затухание прецессии намагниченности формируется за счет нагружения
магнитной подсистемы упругой, причем величина упругого затухания остается
постоянной, а величина связи через посредство константы ![]() изменяется.
изменяется.
Рис.6. Развитие колебаний
намагниченности ![]() во времени при постоянных
параметрах затухания
во времени при постоянных
параметрах затухания ![]() ,
, ![]() и
различных значениях константы магнитоупругой связи. Остальные параметры – те
же, что на рис.5.
и
различных значениях константы магнитоупругой связи. Остальные параметры – те
же, что на рис.5.
а –![]() ; б
–
; б
–![]() ;
;
в –![]() ; г
–
; г
–![]() .
.
Рис.6а соответствует развитию
колебаний в отсутствие магнитоупругой связи. При этом, хотя константа упругого
затухания отлична от нуля, упругие колебания отсутствуют и никакого влияния на
магнитные колебания на оказывают. Этот рисунок соответствует рис.2а, то есть и
здесь амплитуда колебаний нарастает линейно, достигая при времени ![]() величины
величины ![]() от
от ![]() .
.
Рис.6б соответствует величине
связи магнитной подсистемы с упругой на уровне половины от константы ![]() для ЖИГ. Видно, что в этом случае колебания
намагниченности выходят на насыщение при времени около
для ЖИГ. Видно, что в этом случае колебания
намагниченности выходят на насыщение при времени около ![]() ,
где амплитуда составляет
,
где амплитуда составляет ![]() от
от ![]() .
.
Рис.6в соответствует связи между
подсистемами, обеспечиваемой точным значение константы ![]() ,
характерным для ЖИГ. Здесь магнитные колебания выходят на насыщение раньше, чем
в предыдущем случае – при времени
,
характерным для ЖИГ. Здесь магнитные колебания выходят на насыщение раньше, чем
в предыдущем случае – при времени ![]() , ограничиваясь на
уровне
, ограничиваясь на
уровне ![]() от
от ![]() .
.
Рис.6г соответствует значению
константы магнитоупругой связи в два раза превышающей ее значение для ЖИГ.
Теперь магнитные колебания достигают насыщения при времени ![]() и амплитуде
и амплитуде ![]() от
от ![]() .
.
Можно видеть, что по мере увеличения степени связи магнитной и упругой подсистем вклад в затухание магнитной системы за счет упругой с увеличением величины константы взаимодействия растет тем быстрее, чем больше величина связи.
14. Амплитудно-частотные характеристики колебаний намагниченности
Рассмотрим теперь характер резонансной кривой колебаний намагниченности при различных видах затухания. Будем менять величину связи между магнитным и упругим резонаторами путем изменения константы магнитоупругого взаимодействия, а также взаимную расстройку резонаторов путем изменения толщины магнитной пластины.
15. Изменение константы магнитоупругости
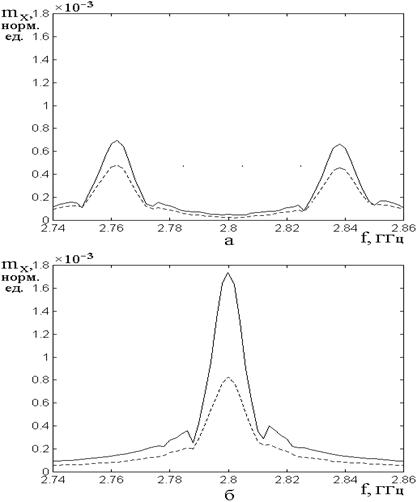
На рис.7 показаны
амплитудно-частотные характеристики (АЧХ) связанной системы: ферромагнитный
резонанс – упругий резонанс при различных значениях константы магнитоупругого
взаимодействия ![]() .
.
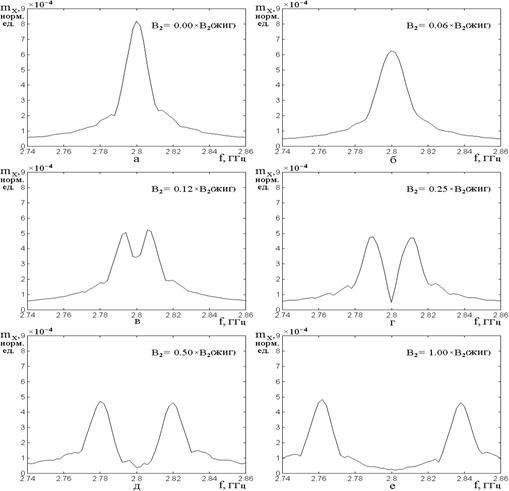
Рис.7. Амплитудно-частотные
характеристики связанной системы: ферромагнитный резонанс – упругий резонанс
при различных значениях константы магнитоупругого взаимодействия ![]() .
.
Параметры затухания: ![]() ;
; ![]() .
Остальные параметры совпадают с приведенными на предыдущих рисунках.
.
Остальные параметры совпадают с приведенными на предыдущих рисунках.
а – ![]() ;
б –
;
б – ![]() ;
;
в – ![]() ; г
–
; г
– ![]() ;
;
д – ![]() ; е
–
; е
– ![]() .
.
Рассмотрен случай равенства
частот ферромагнитного и упругого резонансов, имеющих место в отсутствие связи.
Оба параметра затухания магнитного и упругого положены постоянными, меняется
только связь между магнитной и упругой подсистемами. Рисунки 7а-7е
соответствуют постепенному увеличению константы ![]() от
нуля до значения, соответствующего ЖИГ, причем начиная с рис.7б, для каждого
последующего рисунка значение константы увеличивается в два раза по сравнению с
предыдущим.
от
нуля до значения, соответствующего ЖИГ, причем начиная с рис.7б, для каждого
последующего рисунка значение константы увеличивается в два раза по сравнению с
предыдущим.
Из рис.7а, соответствующего
отсутствию магнитоупругой связи, то есть ферромагнитному резонансу в чистом
виде, следует, что при принятом параметре магнитного затухания ![]() ширина резонансной кривой на половине высоты
составляет около
ширина резонансной кривой на половине высоты
составляет около ![]() , что соответствует полуширине
линии по магнитному полю
, что соответствует полуширине
линии по магнитному полю ![]() порядка
порядка ![]() – типичному значению для ЖИГ [19-23].
Высота резонансной кривой при этом составляет
– типичному значению для ЖИГ [19-23].
Высота резонансной кривой при этом составляет ![]() от
от ![]() .
.![]()
Рис.7б соответствует наличию
небольшой магнитоупругой связи, здесь упругая система уже немного нагружает
магнитную, в результате чего амплитуда магнитных колебаний в максимуме падает
до ![]() от
от ![]() , а
ширина возрастает до
, а
ширина возрастает до ![]() , что соответствует
, что соответствует ![]() .
.
Рис.7в соответствует двукратному
увеличению значения ![]() по сравнением с предыдущим. В
этом случае на резонансной кривой между двумя максимумами появляется небольшой
провал. Максимумы расходятся друг от друга на
по сравнением с предыдущим. В
этом случае на резонансной кривой между двумя максимумами появляется небольшой
провал. Максимумы расходятся друг от друга на ![]() , что
соответствует по полю около
, что
соответствует по полю около ![]() , то есть их полная раздвижка
несколько (на
, то есть их полная раздвижка
несколько (на ![]() ) превышает ширину линии в
отсутствие связи (рис.7а). Амплитуды максимумов составляют
) превышает ширину линии в
отсутствие связи (рис.7а). Амплитуды максимумов составляют ![]() и
и ![]() от
от ![]() , амплитуда в провале равна
, амплитуда в провале равна ![]() от
от ![]() .
.
Рис.7г соответствует следующему
двукратному увеличению ![]() . Видно что максимумы
раздвигаются до
. Видно что максимумы
раздвигаются до ![]() (
(![]() ), а
провал между максимумами прорезается до
), а
провал между максимумами прорезается до ![]() от
от ![]() . Ширина каждого из максимумов на половине
высоты составляет
. Ширина каждого из максимумов на половине
высоты составляет ![]() (
(![]() ), что
близко к исходному значению в отсутствие связи (рис.7а). Амплитуды максимумов
по сравнению с предыдущим случаем меняются мало и составляют
), что
близко к исходному значению в отсутствие связи (рис.7а). Амплитуды максимумов
по сравнению с предыдущим случаем меняются мало и составляют ![]() от
от ![]() .
.
При дальнейшем двукратном
увеличении ![]() , иллюстрируемом рис.7д, максимумы еще
больше разъезжаются до
, иллюстрируемом рис.7д, максимумы еще
больше разъезжаются до ![]() (
(![]() ), их
амплитуда остается прежней
), их
амплитуда остается прежней ![]() от
от ![]() , ширина также сохраняется на уровне
, ширина также сохраняется на уровне ![]() (
(![]() ),
глубина провала остается прежней порядка
),
глубина провала остается прежней порядка ![]() от
от ![]() .
.
Рис.7е соответствует равенству
константы ![]() характерному значению для ЖИГ, то есть
наиболее близко приближается к реальности. Видно, что здесь картина расщепления
резонансной линии ФМР за счет связи с упругой подсистемой становится еще более
яркой. Максимумы разъезжаются до
характерному значению для ЖИГ, то есть
наиболее близко приближается к реальности. Видно, что здесь картина расщепления
резонансной линии ФМР за счет связи с упругой подсистемой становится еще более
яркой. Максимумы разъезжаются до ![]() (
(![]() ), значительно (до
), значительно (до ![]() раз)
превышая исходную ширину линии ФМР в отсутствие связи (рис.4а), причем их
амплитуда остается прежней
раз)
превышая исходную ширину линии ФМР в отсутствие связи (рис.4а), причем их
амплитуда остается прежней ![]() от
от ![]() и ширина также сохраняется на уровне
и ширина также сохраняется на уровне ![]() (
(![]() ), а
глубина провала несколько увеличивается, приближаясь к
), а
глубина провала несколько увеличивается, приближаясь к ![]() от
от
![]() .
.
16. Параметры резонансных кривых
Рассмотрим теперь, как меняются основные
параметры резонансных кривых при непрерывном изменении константы
магнитоупругого взаимодействия ![]() . Соответствующие
зависимости иллюстрируются рис.8.
. Соответствующие
зависимости иллюстрируются рис.8.
На рис.8а показана зависимость
частоты максимумов (сплошные линии) и краев (пунктир) резонансных кривых от
величины константы магнитоупругой связи ![]() .
Видно, что с увеличением
.
Видно, что с увеличением ![]() , начиная с
, начиная с ![]() , происходит расширение резонансной кривой,
переходящее с
, происходит расширение резонансной кривой,
переходящее с ![]() в расщепление резонансной
кривой на две линии, частоты которых меняются далее вверх и вниз по линейному
закону с угловым коэффициентом
в расщепление резонансной
кривой на две линии, частоты которых меняются далее вверх и вниз по линейному
закону с угловым коэффициентом ![]() (при
(при ![]() ). Общая резонансная кривая до расщепления
при
). Общая резонансная кривая до расщепления
при ![]() расширяется примерно в два раза, а после
расщепления ширина каждого из отдельных пиков не меняется, оставаясь близкой к
начальной ширине общей линии при
расширяется примерно в два раза, а после
расщепления ширина каждого из отдельных пиков не меняется, оставаясь близкой к
начальной ширине общей линии при ![]() , равной
, равной ![]() или
или ![]() , что
составляет полуширину резонансной линии по полю
, что
составляет полуширину резонансной линии по полю ![]() (типичная
величина для ЖИГ при принятом параметре чистого магнитного затухания
(типичная
величина для ЖИГ при принятом параметре чистого магнитного затухания ![]() ).
).
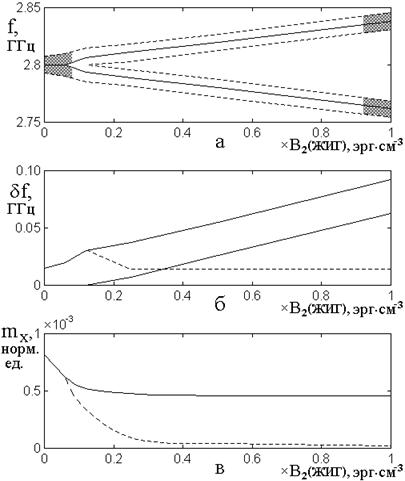
Рис.8. Зависимости параметров
резонансных кривых от константы магнитоупругой связи ![]() .
Параметры – те же, что на предыдущем рисунке.
.
Параметры – те же, что на предыдущем рисунке.
а – частоты максимумов (сплошные
линии) и краев (пунктир) резонансных кривых; б – ширина резонансной
характеристики на половине высоты по внешним и внутренним краям общей кривой
(сплошные линии), а также по внешним краям каждого пика (пунктир); в –
амплитуда ![]() -компоненты намагниченности в максимумах
резонансных пиков (сплошная линия) и в минимуме провала между ними (пунктир).
-компоненты намагниченности в максимумах
резонансных пиков (сплошная линия) и в минимуме провала между ними (пунктир).
На рис.8б показана именно ширина
резонансной характеристики ![]() на половине ее высоты
по внешним и внутренним краям общей кривой (сплошные линии), а также по внешним
краям каждого пика (пунктир). Видно, что ширина общей кривой по внешним
(верхняя сплошная линия) и внутренним (нижняя сплошная линия) границам пиков сначала
до
на половине ее высоты
по внешним и внутренним краям общей кривой (сплошные линии), а также по внешним
краям каждого пика (пунктир). Видно, что ширина общей кривой по внешним
(верхняя сплошная линия) и внутренним (нижняя сплошная линия) границам пиков сначала
до ![]() увеличивается примерно в два раза, после
чего обе зависимости растут по линейному закону с тем же угловым коэффициентом,
что на рис.8а. При этом после расщепления ширина каждого из отдельных пиков не
меняется, оставаясь близкой к начальному значению
увеличивается примерно в два раза, после
чего обе зависимости растут по линейному закону с тем же угловым коэффициентом,
что на рис.8а. При этом после расщепления ширина каждого из отдельных пиков не
меняется, оставаясь близкой к начальному значению ![]() .
.
На рис.8в показана зависимость
нормированной амплитуды ![]() -компоненты намагниченности
-компоненты намагниченности
![]() в максимумах резонансных пиков (сплошная
линия) и в минимуме провала между ними (пунктир). Видно, что до расщепления
амплитуда еще единого пика резонансной кривой по намагниченности постепенно
спадает с
в максимумах резонансных пиков (сплошная
линия) и в минимуме провала между ними (пунктир). Видно, что до расщепления
амплитуда еще единого пика резонансной кривой по намагниченности постепенно
спадает с ![]() до
до ![]() , а после
расщепления амплитуда каждого пика далее не меняется, оставаясь на уровне
, а после
расщепления амплитуда каждого пика далее не меняется, оставаясь на уровне ![]() . Учитывая квадратичность энергии
колебаний по намагниченности, можно видеть, что такое соотношение амплитуд
примерно соответствует равному распределению энергии между двумя степенями
свободы системы (так как
. Учитывая квадратичность энергии
колебаний по намагниченности, можно видеть, что такое соотношение амплитуд
примерно соответствует равному распределению энергии между двумя степенями
свободы системы (так как ![]() ). На долю же
колебаний между пиками остается энергии ничтожно мало, вследствие чего
пунктирная кривая на рис.8в после расщепления сильно спадает и по мере увеличения
). На долю же
колебаний между пиками остается энергии ничтожно мало, вследствие чего
пунктирная кривая на рис.8в после расщепления сильно спадает и по мере увеличения
![]() выше
выше ![]() стремится
к нулю.
стремится
к нулю.
Таким образом, можно видеть, что при совпадении исходных частот магнитного и упругого резонансов, увеличение связи между ними приводит к расщеплению резонансной кривой тем более сильному, чем величина константы магнитоупругого взаимодействия больше.
17. Изменение толщины пластины
В предыдущем разделе рассмотрено формирование резонансной линии ФМР за счет нагружения магнитной подсистемы упругой при условии совпадения частот магнитного и упругого резонансов. Рассмотрим теперь, как деформируется резонансная кривая ФМР при выходе упругой подсистемы из резонанса.
Для этого рассмотрим
иллюстрируемое рис.9 изменение толщины магнитной пластины ![]() в сторону ее увеличения от резонансного
значения
в сторону ее увеличения от резонансного
значения ![]() до
до ![]() с
шагом
с
шагом ![]() , что соответствует понижению частоты
упругого резонанса с
, что соответствует понижению частоты
упругого резонанса с ![]() до
до ![]() с
шагом в
с
шагом в ![]() и обеспечивает шесть рисунков от 9а до 9е.
и обеспечивает шесть рисунков от 9а до 9е.
На рис.9а показана резонансная
кривая ФМР при совпадении частот магнитного и упругого резонансов. Эта кривая
соответствует приведенной на рис.7е. Видно сильно выраженное расщепление
резонансной кривой с пиками при ![]() и
и ![]() с провалом между ними на частоте
с провалом между ними на частоте ![]() . Высоты обоих пиков практически одинаковы
и составляют
. Высоты обоих пиков практически одинаковы
и составляют ![]() от
от ![]() .
.
Рис.9б соответствует отстройке
частоты упругого резонанса от магнитного за счет увеличения толщины пластины до
величины ![]() , что соответствует снижению частоты
упругого резонанса до
, что соответствует снижению частоты
упругого резонанса до ![]() , которая находится между
пиками. Видно, что столь малое (
, которая находится между
пиками. Видно, что столь малое (![]() ) изменение частоты
упругого резонанса привело к несколько меньшему по порядку величины изменению резонансной
кривой для ФМР: расщепление осталось, хотя частоты обоих пиков несколько
уменьшились: нижнего с
) изменение частоты
упругого резонанса привело к несколько меньшему по порядку величины изменению резонансной
кривой для ФМР: расщепление осталось, хотя частоты обоих пиков несколько
уменьшились: нижнего с ![]() до
до ![]() (
(![]() ), то есть на
), то есть на ![]() , тогда
как верхнего еще меньше с
, тогда
как верхнего еще меньше с ![]() до
до ![]() – на
– на ![]() (
(![]() ). Амплитуда нижнего пика уменьшилась до
). Амплитуда нижнего пика уменьшилась до ![]() от
от ![]() , верхнего
– увеличилась до
, верхнего
– увеличилась до ![]() от
от ![]() .
.
Резонансные кривые на рис.9в-9е
проявляют ту же тенденцию. По мере увеличения толщины пластины частота нижнего
пика значительно понижается, для рис.9е (при ![]() ),
составляя
),
составляя ![]() , при этом амплитуда его падает до
, при этом амплитуда его падает до ![]() от
от ![]() , тогда
как частота верхнего пика также понижается, стремясь к частоте исходного ФМР и
составляет
, тогда
как частота верхнего пика также понижается, стремясь к частоте исходного ФМР и
составляет ![]() , амплитуда же его возрастает, также
стремясь к исходному значению и составляет
, амплитуда же его возрастает, также
стремясь к исходному значению и составляет ![]() от
от ![]() . Ширина каждого из пиков ФМР меняется мало
и на всем рассмотренном интервале изменения толщины пластины остается близкой к
. Ширина каждого из пиков ФМР меняется мало
и на всем рассмотренном интервале изменения толщины пластины остается близкой к
![]() .
.
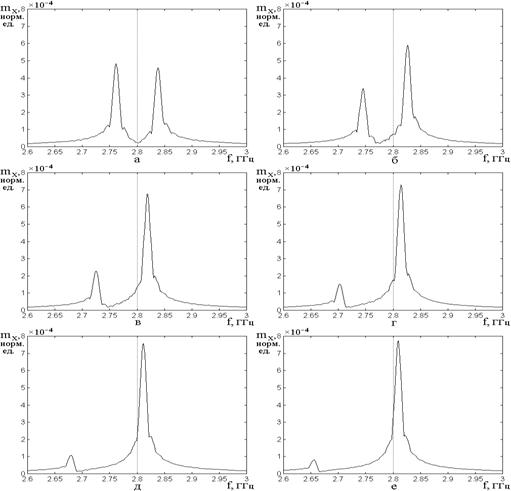
Рис.9. Амплитудно-частотные
характеристики связанной системы: ферромагнитный резонатор – упругий резонатор
при различных значениях нормированной толщины пластины ![]() при
при
![]() (резонанс при
(резонанс при ![]() ).
).
Константа магнитоупругого
взаимодействия:![]() . Параметры затухания:
. Параметры затухания: ![]() ;
; ![]() .
Остальные параметры – те же.
.
Остальные параметры – те же.
а – ![]() ; б
–
; б
– ![]() ; в –
; в – ![]() ;
;
г – ![]() ; д
–
; д
– ![]() ; е –
; е – ![]() .
.
Из сказанного можно видеть, что при отстройке вниз частоты резонанса упругой подсистемы от резонанса магнитной, частоты обоих расщепленных пиков понижаются, причем для низкочастотного пика значительно сильнее, чем для высокочастотного, амплитуда низкочастотного пика падает, а высокочастотного растет, причем частота, высота и ширина выделившегося высокочастотного пика стремятся к таковым параметрам резонансной кривой ФМР в отсутствие магнитоупругой связи.
Таким образом, влияние упругой подсистемы на магнитную, состоящее в расщеплении резонансной кривой, проявляется особенно сильно только вблизи совпадения частоты и упругого резонанса с частотой магнитного, а при удалении от этого значения уменьшается.
18. Параметры резонансных кривых
Рассмотрим теперь, как меняются
основные параметры резонансных кривых при непрерывном изменении толщины
пластины ![]() . Соответствующие зависимости иллюстрируются
рис.10.
. Соответствующие зависимости иллюстрируются
рис.10.
На рис.10а показана зависимость
частоты максимумов (сплошные линии) и краев (пунктир) резонансных кривых от
нормированной толщины пластины ![]() .
.
Из рис.10а видно, что при
удалении значения толщины от резонансного в обе стороны, то есть ниже ![]() и выше
и выше ![]() от
от ![]() , частоты обеих линий резонансной кривой
(1 и 2) остаются близкими к частотам магнитного (4) и упругого (3) резонансов.
В области толщин между
, частоты обеих линий резонансной кривой
(1 и 2) остаются близкими к частотам магнитного (4) и упругого (3) резонансов.
В области толщин между ![]() и
и ![]() от
от ![]() наблюдается расталкивание ветвей,
настолько сильное, что линии отдельных резонансов не перекрываются. При этом по
мере изменения толщины пластины низкочастотный и высокочастотный максимумы как
бы меняются ролями: при
наблюдается расталкивание ветвей,
настолько сильное, что линии отдельных резонансов не перекрываются. При этом по
мере изменения толщины пластины низкочастотный и высокочастотный максимумы как
бы меняются ролями: при ![]() высокочастотный
максимум соответствует преимущественно упругому резонансу, а низкочастотный –
магнитному, тогда как при
высокочастотный
максимум соответствует преимущественно упругому резонансу, а низкочастотный –
магнитному, тогда как при ![]() высокочастотный максимум
становится преимущественно магнитным, а низкочастотный – упругим.
высокочастотный максимум
становится преимущественно магнитным, а низкочастотный – упругим.
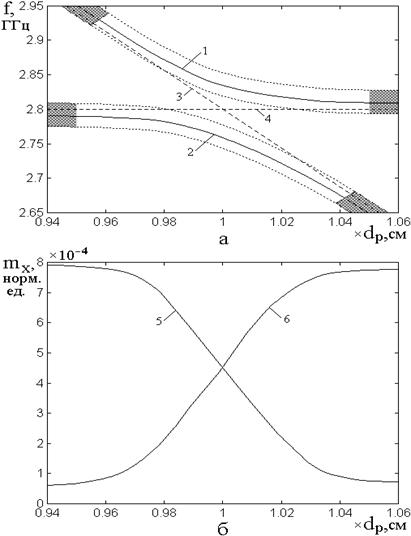
Рис.10. Зависимости частот двух
максимумов резонансных кривых (а) и амплитуд ![]() -компоненты
намагниченности (б) обоих максимумов от нормированной толщины пластины
-компоненты
намагниченности (б) обоих максимумов от нормированной толщины пластины ![]() , где
, где ![]() .
.
1, 5 – низкочастотный максимум; 2, 6 – высокочастотный максимум;
3 – упругий резонанс; 4 – магнитный резонанс.
Такое соотношение вкладов
магнитной и упругой составляющих в общую резонансную кривую иллюстрируется рис.10б,
где показана зависимость амплитуд ![]() -компоненты
намагниченности для обоих максимумов резонансной кривой от толщины пластины.
-компоненты
намагниченности для обоих максимумов резонансной кривой от толщины пластины.
В области ![]() частота
низкочастотного максимума близка к частоте магнитного резонанса (4), поэтому
его амплитуда (5) велика, а амплитуда высокочастотного (6), далекого от частоты
магнитного резонанса – мала. В области
частота
низкочастотного максимума близка к частоте магнитного резонанса (4), поэтому
его амплитуда (5) велика, а амплитуда высокочастотного (6), далекого от частоты
магнитного резонанса – мала. В области ![]() частота
низкочастотного максимума удаляется от частоты магнитного резонанса (4),
поэтому его амплитуда (5) падает. При этом частота высокочастотного максимума
(6) приближается к частоте магнитного резонанса (4), так что его амплитуда (6)
увеличивается.
частота
низкочастотного максимума удаляется от частоты магнитного резонанса (4),
поэтому его амплитуда (5) падает. При этом частота высокочастотного максимума
(6) приближается к частоте магнитного резонанса (4), так что его амплитуда (6)
увеличивается.
Таким образом, можно видеть, что в области пересечения ветвей исходных резонансов магнитного и упругого происходит их расталкивание, в результате чего магнитная и упругая ветви меняются местами.
19. Сравнение с классической колебательной системой с двумя степенями свободы
Описанное здесь поведение магнитной и упругой ветвей в основном соответствует классической картине поведения колебательной системы с двумя степенями свободы, образованной двумя связанными резонаторами. В данном случае роль одного резонатора играет прецессионное движение намагниченности, а роль другого – первая мода стоячей упругой волны по толщине пластины.
Отличие состоит в том, что в классическом случае колебания описываются двумя уравнениями второго порядка, эквивалентными четырем уравнениям первого порядка, что соответствует двум степеням свободы. Тогда как в рассматриваемой здесь ситуации процесс описывается тремя уравнениями первого порядка для намагниченности и двумя уравнениями второго порядка для упругого смещения, что эквивалентно семи уравнениям первого порядка или трем с половиной степеням свободы. Такое различие в количестве степеней свободы колебательных систем должно особенно проявляться при высоком уровне возбуждения, давая повод разнообразным нелинейным режимам автомодуляционного характера [53,58,59,62-67].
На уровне настоящего рассмотрении специфика состоит в нелинейности магнитной системы, а также механизме формирования магнитного затухания за счет упругого, что приводит к особенностям свойств расщепления резонансной кривой, кратко перечисленным в следующем разделе.
20. Свойства расщепления резонансной кривой
Перечислим некоторые свойства расщепления резонансной кривой ФМР за счет магнитоупругой связи, выявленные в результате дополнительного исследования.
Величина расщепления по частоте
(или по полю) определяется только значением коэффициента связи (константы
магнитоупругости ![]() ) и от затухания (магнитного
) и от затухания (магнитного ![]() или упругого
или упругого ![]() ) не
зависит. При изменении затухания, того или другого, меняется только высота АЧХ
– при увеличении затухания высота уменьшается, но частоты пиков расщепления
остаются неизменными.
) не
зависит. При изменении затухания, того или другого, меняется только высота АЧХ
– при увеличении затухания высота уменьшается, но частоты пиков расщепления
остаются неизменными.
Для начала расщепления константа
связи (магнитоупругости ![]() ) должна достигать
критического значения (порога). Порог расщепления можно определить как
изменение выпуклости середины резонансной кривой с положительной на
отрицательную. Поскольку выпуклость определяется знаком второй производной от
резонансной кривой в точке максимума (где первая производная равна нулю), то
критерием порогового значения константы магнитоупругости, необходимым для
появления расщепления, можно считать равенство нулю этой второй производной.
) должна достигать
критического значения (порога). Порог расщепления можно определить как
изменение выпуклости середины резонансной кривой с положительной на
отрицательную. Поскольку выпуклость определяется знаком второй производной от
резонансной кривой в точке максимума (где первая производная равна нулю), то
критерием порогового значения константы магнитоупругости, необходимым для
появления расщепления, можно считать равенство нулю этой второй производной.
Критическое значение (порог)
константы с увеличением частоты уменьшается, при ее изменении от ![]() до
до ![]() оно
меняется приблизительно в два раза, то есть как бы константа, если она измерена
на низких частотах, то с повышением частоты – увеличивается. Возможно, это
можно интерпретировать как «динамическое» значение константы. То есть
«динамическая» константа магнитоупругости с увеличением частоты увеличивается.
оно
меняется приблизительно в два раза, то есть как бы константа, если она измерена
на низких частотах, то с повышением частоты – увеличивается. Возможно, это
можно интерпретировать как «динамическое» значение константы. То есть
«динамическая» константа магнитоупругости с увеличением частоты увеличивается.
21. Формирование АЧХ по намагниченности за счет диссипации по упругости
Рассмотрим теперь, как формируется резонансная кривая ФМР в условиях, когда частота упругого резонанса значительно ниже частоты магнитного, что более соответствует реальным экспериментам, в том числе с ротационным магнетометром. Вид получающихся резонансных кривых представлен на рис.11.
Рис.11. Формирование АЧХ по
намагниченности при различной толщине пластины ![]() и
различном магнитном затухании.
и
различном магнитном затухании.
Сплошные линии – ![]() , пунктир –
, пунктир – ![]() .
Параметры:
.
Параметры: ![]() ,
, ![]() . Остальные
параметры – те же.
. Остальные
параметры – те же.
а – ![]() ; б
–
; б
– ![]() .
.
На рис.11а показан вид
резонансной кривой ФМР при толщине пластины ![]() ,
соответствующей резонансной при ФМР (
,
соответствующей резонансной при ФМР (![]() ). Здесь, как и ранее,
резонансные кривые имеют расщепленный характер, причем как при наличии магнитного
затухания (пунктир), так и в его отсутствие (сплошная линия) резонансная кривая
по высоте ограничена, то есть в отсутствие магнитного затухания ограничение
колебаний намагниченности происходит за счет затухания упругой подсистемы.
Можно также видеть, что при выбранных параметрах роль магнитного затухания
ниже, чем упругого, так как уменьшение амплитуды пиков при включении магнитного
затухания (пунктир в сравнении со сплошной линией) составляет менее трети общей
высоты резонансной кривой.
). Здесь, как и ранее,
резонансные кривые имеют расщепленный характер, причем как при наличии магнитного
затухания (пунктир), так и в его отсутствие (сплошная линия) резонансная кривая
по высоте ограничена, то есть в отсутствие магнитного затухания ограничение
колебаний намагниченности происходит за счет затухания упругой подсистемы.
Можно также видеть, что при выбранных параметрах роль магнитного затухания
ниже, чем упругого, так как уменьшение амплитуды пиков при включении магнитного
затухания (пунктир в сравнении со сплошной линией) составляет менее трети общей
высоты резонансной кривой.
Теперь пусть толщина пластины
превышает резонансную в ![]() раз, то есть
составляет
раз, то есть
составляет ![]() . Тогда частота упругого резонанса будет
равна
. Тогда частота упругого резонанса будет
равна ![]() , то есть также станет в 10 раз ниже частоты
магнитного. Этому случаю соответствует рис.11б. Видно, что здесь расщепление
резонансной кривой полностью отсутствует, пики обеих резонансных кривых (как
пунктирной, так и сплошной) приходятся точно на
, то есть также станет в 10 раз ниже частоты
магнитного. Этому случаю соответствует рис.11б. Видно, что здесь расщепление
резонансной кривой полностью отсутствует, пики обеих резонансных кривых (как
пунктирной, так и сплошной) приходятся точно на ![]() . Как и
ранее обе кривые по высоте ограничены, причем роль магнитного затухания в
совокупном действии обоих затуханий здесь несколько увеличивается: добавка к
высоте пунктирной кривой при выключении магнитного затухания составляет около
половины общей высоты кривой. Однако абсолютная величина магнитного резонанса
значительно (примерно в два раза) увеличивается, как при наличии, так и при
отсутствии упругого затухания. Такое увеличение амплитуды магнитных колебаний
при сильной отстройке частоты упругого резонанса от частоты магнитного,
по-видимому, обусловлено уменьшением в этом случае влияния упругих колебаний на
магнитные, то есть «нагружение» магнитной подсистемы системой упругой
уменьшается, что и приводит к росту амплитуды магнитных колебаний.
. Как и
ранее обе кривые по высоте ограничены, причем роль магнитного затухания в
совокупном действии обоих затуханий здесь несколько увеличивается: добавка к
высоте пунктирной кривой при выключении магнитного затухания составляет около
половины общей высоты кривой. Однако абсолютная величина магнитного резонанса
значительно (примерно в два раза) увеличивается, как при наличии, так и при
отсутствии упругого затухания. Такое увеличение амплитуды магнитных колебаний
при сильной отстройке частоты упругого резонанса от частоты магнитного,
по-видимому, обусловлено уменьшением в этом случае влияния упругих колебаний на
магнитные, то есть «нагружение» магнитной подсистемы системой упругой
уменьшается, что и приводит к росту амплитуды магнитных колебаний.
22. Замечание об эксперименте
Выбранные здесь параметры
магнитной пластины близки к типичным параметрам для ЖИГ. Однако сообщения о
наблюдении в эксперименте описанного здесь расщепления резонансной кривой за
счет взаимодействия с упругой подсистемой отсутствует. По-видимому, это связано
с тем, что в экспериментах на объемных образцах ЖИГ толщина образца составляет
единицы миллиметров и редко снижается до ![]() из-за
крайне низкой механической прочности пластины такой толщины. В экспериментах на
пленках толщина пленки составляет единицы и доли микрометров, то есть вполне
согласуется с описываемыми здесь размерами. Однако пленка ЖИГ, как правило,
находится на достаточно толстой подложке из гадолиний-галлиевого граната (ГГГ),
типичная толщина которой составляет порядка
из-за
крайне низкой механической прочности пластины такой толщины. В экспериментах на
пленках толщина пленки составляет единицы и доли микрометров, то есть вполне
согласуется с описываемыми здесь размерами. Однако пленка ЖИГ, как правило,
находится на достаточно толстой подложке из гадолиний-галлиевого граната (ГГГ),
типичная толщина которой составляет порядка ![]() . По
упругим же свойствам пленка и подложка, как правило, весьма близки (отличаются
на доли процента и менее), поэтому резонансная частота упругой подсистемы здесь
определяется суммарной толщиной пленки и подложки и составляет единицы
. По
упругим же свойствам пленка и подложка, как правило, весьма близки (отличаются
на доли процента и менее), поэтому резонансная частота упругой подсистемы здесь
определяется суммарной толщиной пленки и подложки и составляет единицы ![]() . Таким образом, экспериментальная
ситуация обычно близка к показанной на рис.9е при условии, что частота упругого
резонанса еще намного ниже, то есть видимое расщепление резонансной кривой ФМР
отсутствует.
. Таким образом, экспериментальная
ситуация обычно близка к показанной на рис.9е при условии, что частота упругого
резонанса еще намного ниже, то есть видимое расщепление резонансной кривой ФМР
отсутствует.
Не та ситуация однако наблюдается в режиме бегущих магнитостатических волн (МСВ) в магнитоупругой среде, где резонансные условия определяются не размерами образца, а совпадением длины магнитостатической волны с длиной возбуждаемой на той же частоте упругой. В этом случае в области пересечения ветвей дисперсионных кривых магнитной и упругой волн в эксперименте наблюдается сильное взаимодействие, проявляющееся не только во взаимном расталкивании ветвей (аналог описанного здесь расщепления), но и в интенсивной перекачке энергии из магнитной ветви в упругую, что может явиться весьма эффективным источником возбуждения гиперзвуковых волн в диапазоне сверхвысоких частот [47,57].
С другой стороны, при использовании магнитостатических волн для построения линий задержки [38-42,57,62,63], затухание магнитостатических волн также может в значительной степени формироваться за счет затухания одновременно возбуждаемых упругих волн, что может приводить к росту потерь МСВ на распространение.
Отметим дополнительно, что для эксперимента было бы весьма интересным исследовать ФМР именно в условиях совпадения его частоты с частотой упругого резонанса. При этом толщина магнитной пластины должна составлять десятки и сотни нанометров, что могло бы позволить создать магнитострикционный генератор гиперзвука СВЧ диапазона нанометровых размеров. Ключевым вопросом здесь могло бы явиться выполнение магнитной пленки соответствующей толщины на механически достаточно прочной подложке с резко отличными от ЖИГ упругими свойствами, чтобы упругий резонанс в магнитной пленке возбуждался бы независимо от свойств подложки.
23. Применение полученных результатов к схеме ротационного магнетометра
Проведенное в последних разделах рассмотрение относится к случаю линейных колебаний намагниченности главным образом в условиях, довольно близких к резонансным. Однако ротационный магнетометр в его классическом варианте [6-16] работает в условиях развернутой в плоскости прецессии, то есть при сильной ее нелинейности, причем вращение намагниченности происходит в квазистационарном режиме, то есть вдали от резонанса. С другой стороны, напряженность вращающегося поля, по условиям работы магнитометра должна превышать поле насыщения пластины, что составляет сотни и тысячи эрстед то есть как раз соответствует частоте ФМР, лежащей в СВЧ диапазоне.
Поэтому даже медленное вращение столь большого поля, благодаря его изменению во времени, можно рассматривать как механизм, возбуждающий собственную прецессию намагниченности в условиях, близких к резонансным. То есть вращающееся поле «тащит за собой» конус резонансной прецессии, время затухания которой должно быть достаточно малым, чтобы процесс оставался квазистационарным. Такая вращающаяся затухающая прецессия сопровождается соответствующими упругими деформациями, которые уносят ее энергию, переводя ее в решетку. То есть вращающаяся намагниченность тянет за собой «шлейф» магнитных колебаний, энергия которых за счет упругих уносится в решетку. Такая ситуация, по-видимому, весьма близка к формированию магнитного затухания за счет упругого в условиях, близких к резонансным.
С другой стороны, ротационный магнетометр, как правило, работает в условиях, когда постоянное подмагничивающее поле, перпендикулярное плоскости пластины, достаточно мало или вообще отсутствует. Такая ситуация в сильно нелинейном режиме соответствует условиям возбуждения прецессии второго порядка, частота которой может быть на несколько порядков ниже частоты ФМР [64-69]. То есть мы попадаем как раз в диапазон частот вращающегося поля ротационного магнетометра. В этом случае за счет магнитоупругого взаимодействия может не только формироваться затухание магнитных колебаний, но и при достаточной его величине происходить переориентация вектора намагниченности [70], приводящая к специфическим автомодуляционным режимам [64-69], могущим повысить уровень шума магнетометра.
Таким образом, можно полагать, что роль магнитоупругого взаимодействия в схеме ротационного магнетометра является чрезвычайно важной и требует более подробного изучения, в том числе в условиях сильной нелинейности.
Итак, на данном этапе можно сделать предварительный вывод, что магнитоупругое взаимодействие в схеме ротационного магнетометра является фактором, в известной степени, мешающим. В этом плане для построения магнетометра следует выбирать ферриты с как можно меньшей величиной константы магнитоупругой связи, чего можно добиться, возможно, выбором легирующих добавок, как это делается для изменения анизотропии в смешанных ферритах гранатах [71]. Заметим однако, что этот вопрос до конца не ясен и требует дополнительного исследования.
Заключение
Рассмотрена классическая схема ротационного магнетометра, предназначенного для измерения слабых магнитных полей. На основе модели квазистатического вращения намагниченности приведена схема расчета, иллюстрирующего возбуждение сигнала второй гармоники от частоты вращающегося поля. Обращено внимание на два главных механизма, ограничивающих чувствительность магнетометра: скачки Баркгаузена и тепловые флуктуации намагниченности. Показано, что уменьшение затухания магнитной прецессии, приводя к снижению шума магнетометра, обусловленного флуктуациями намагниченности, ухудшает возможность выделения второй гармоники в условиях скачков Баркгаузена.
На основе краткого анализа литературы по процессам магнитной релаксации, сделан вывод о важности для работы ротационного магнетометра механизма формирования затухания колебаний намагниченности за счет возбуждения упругих волн в магнитоупругой среде.
Применительно к схеме ротационного магнетометра рассмотрена нелинейная задача о возбуждении прецессии намагниченности переменным магнитным полем в ферритовой пластине, обладающей упругими свойствами и магнитострикцией. Приведены уравнения движения и граничные условия для компонент намагниченности и упругого смещения в случае произвольного угла прецессии вектора намагниченности. Выполнено численное решение полученной системы методом Рунге-Кутта.
Показано, что наблюдаемое в эксперименте затухание ферромагнитного резонанса в значительной степени формируется за счет связи с упругой системой, нагружающей магнитную через посредство магнитоупругой связи, то есть даже в отсутствие затухания в магнитной системе, амплитуда вынужденных колебаний намагниченности все равно ограничивается за счет затухания в упругой системе.
Показано, что при совпадении собственных частот магнитного и упругого резонансов совокупная резонансная кривая претерпевает расщепление на два пика, тем более ярко выраженное, чем константа магнитоупругой связи больше.
Показано, что при отстройке вниз частоты упругого резонанса от частоты магнитного, например при увеличении толщины магнитной пластины, частоты обоих пиков расщепленной резонансной кривой понижаются, причем частота низкочастотного пика уходит резко вниз до собственной частоты упругого резонанса, а его амплитуда уменьшается, тогда как частота высокочастотного пика стремится к собственной частоте магнитного резонанса и его амплитуда увеличивается, в результате чего расщепленный характер резонансной кривой сменяется единственным пиком, частота которого стремится к собственной частоте ФМР.
Обсуждено соотношение полученных результатов с картиной ФМР, реально наблюдаемой в эксперименте. Причина отсутствия в эксперименте расщепления резонансной кривой ФМР указана в несоответствии большинства экспериментов условию упругого резонанса. Отмечена аналогия предсказанного расщепления кривой ФМР с наблюдаемым в эксперименте расталкиванием ветвей бегущих магнитостатических и упругих волн в диапазоне СВЧ.
Рассмотрено применение полученных результатов к условиям работы ротационного магнетометра. Указано на возможность возбуждения вращающимся полем шлейфа магнитных колебаний, затухание которых формируется за счет возбуждения упругих волн в условиях, близких к резонансным. Отмечена важность рассмотренных магнитоупругих явлений в работе магнетометра и даны рекомендации для дальнейших исследований.
Работа выполнена при финансовой поддержке за счет гранта Российского Научного Фонда (проект № 14-22-00279).
Литература
1. Вонсовский С.В. Магнетизм. М.: Наука. 1971.
2. Физическая энциклопедия. Т.4. М.: Советская энциклопедия. 1994. С.539. Статья «Сквид».
3. Физическая энциклопедия. Т.1. М.: Советская энциклопедия. 1988. С.602. Статья «Джозефсона эффект».
4. Robbes D. // Sensors and Actuators A. 2006. V.129. P.86.
5. Korepanov V., Marusenkov A. // Surv Geophys. 2012. V.33. P.1059.
6. Ветошко П.М. // Магнитометр. Патент № 21000819. Приоритет от 30.09.1996.
7. Никитин П.И., Ветошко П.М. // Измеритель магнитной восприимчивости. Патент РФ № 2177611. Приоритет от 09.03.2000.
8. Vetoshko P.M., Volkovoy V.B., Zalogin V.N., Toporov A.Yu. // J. Appl. Phys. 1991. V.70. №10. P.6298.
9. Perlov A.Ya., Vetoshko P.M., Volkovoy V.B. // J. Appl. Phys. 1994. V.75. №10. P.5922.
10. Валейко М.В., Ветошко П.М., Перлов А.Я., Топоров А.Ю. // ФТТ. 1994. Т.36. №10. С.3067.
11. Nikitin P.I., Kasatkin S.I., Muravjov A.M., Vetoshko P.M., Valeiko M.V., Konov V.I., Meydan T. // Sensors and Actuators A. 2003. V.106. №1-3. P.26.
12. Vetoshko P.M., Valeiko M.V., Nikitin P.I. // Sensors and Actuators A. 2003. V.106. №1-3. P.270.
13. Nikitin P.I., Vetoshko P.M., Ksenevich T.I. // J. Magn. Magn. Mat. 2007. V.311. P.445.
14. Skidanov V., Vetoshko P. // Procedia Enineering. 2010. V.5. P.989.
15. Vetoshko P., Skidanov V., Stempkovskiy A. // Sensor Letters. 2013. V.11. P.59.
16. Dufay B., Saez S., Cordier C., Dolabdjian C., Dubic C., Hristoforou E., Ubizskii S. // IEEE Sensors Journal. 2011. V.11. №12. P.3211.
17. LeCraw R.C., Spencer E.G., Porter C.S. // Phys. Rev. 1958. V.110. №6. P.1311.
18. ЛеКроу Р., Спенсер Е., Портер К. // В сб. «Ферриты в нелинейных сверхвысокочастотных устройствах». Ред.: Гуревич А.Г. // М.: ИЛ. 1961. С.433.
19. Гуревич А.Г. Ферриты на сверхвысоких частотах. М.: Гос.Изд.физ.-мат.лит. 1960.
20. Гуревич А.Г. Магнитный резонанс в ферритах и антиферромагнетиках. М.: Наука. 1973.
21. Гуревич А.Г., Мелков Г.А. Магнитные колебания и волны. М.: Физматлит. 1994.
22. Clogston A.M., Suhl H., Walker L.R., Anderson P.W. // J. Phys. Chem. Solids. 1956. V.1. №3. P.129.
23. Клогстон А., Сул Г., Уокер Л., Андерсон П. // В сб. «Ферриты в нелинейных сверхвысокочастотных устройствах». Ред.: Гуревич А.Г. // М.: ИЛ. 1961. С.598.
24. Sparks M., Loudon R., Kittel C. // Phys. Rev. 1961. V.122. P.791.
25. Sparks M. Ferromagnetic relaxation theory. McGraw-Hill Book Co. 1964.
26. Hurben M.J., Patton C.E. // J. Appl. Phys. 1998. V.83. P.4344.
27. McMichael R.D., Stiles M.D., Chen P.J., Egelhoff W.F. // J. Appl. Phys. 1998. V.83. P.7037.
28. Arias R., Mills D.L. // Phys. Rev. B. 1999. V.60. P.7395.
29. Safonov V.L., Bertram H.N. // Phys. Rev. B. 2001. V.63. P.094419.
30. Abrahams E., Kittel C. // Phys. Rev. 1952. V.88. P.1200.
31. Suhl H. // IEEE Trans on Magn. 1998. V.34. №4. P.1834.
32. McMichael E.D., Kunz A. // J. Appl. Phys. 2002. V.91. №10. P.8650.
33. Rossi E., Heinonen O.G., MacDonald A.H. // Phys. Rev. B. 2005. V.72. №17. P.174412(11).
34. Widom A., Vittoria C., Yoon S. // J. Appl. Phys. 2010. V.108. №7. P.073924(4).
35. Widom A., Sivasubramanian S., Vittoria C., Yoon S., Srivastava Y.N. // Phys. Rev. B. 2010. V.81. №21. P.212402(4).
36. Vittoria C., Yoon S.D., Widom A. // Phys. Rev. B. 2010. V.81. №1. P.014412(6).
37. Вашковский А.В., Стальмахов В.С., Шараевский Ю.П. Магнитостатические волны в электронике сверхвысоких частот. Саратов. Изд.Саратовского университета. 1993.
38. Адам Дж.Д. // ТИИЭР. 1988. Т.76. №2. С.73.
39. Исхак В.С. // ТИИЭР. 1988. Т.76. №2. С.86.
40. Adam J.D., Davis L.E., Dionne G.F., Schloemann E.F., Stitzer S.N. // IEEE Trans. on Micr. Theor. and Tech. 2002. V.50. №3. P.721.
41. Курушин Е.П., Нефедов Е.И. // Микроэлектроника. 1977. Т.6. №6. С.549.
42. Гуляев Ю.В., Зильберман П.Е. // РЭ. 1978. Т.23. №5. С.897.
43. Gilbert T.L. // IEEE Trans. on Magn. V.40. №6. P.3443.
44. Suhl H. // J. Phys. Chem. Sol. 1957. V.1. №4. P.209.
45. Сул Г. // В сб. «Ферриты в нелинейных сверхвысокочастотных устройствах». Ред.: Гуревич А.Г. // М.: ИЛ. 1961. С.163.
46. Моносов Я.А. // Нелинейный ферромагнитный резонанс. М.: Наука. 1971.
47. Власов В.С., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2009. Т.54. №7. С.863.
48. Temiryazev A.G., Tikhomirova M.P., Zilberman P.E. // J. Appl. Phys. 1994. V.76. №12. P.5586.
49. Зильберман П.Е., Темирязев А.Г., Тихомирова М.П. // ЖЭТФ, 1995. Т.108. №1. С.281.
50. Гуляев Ю.В., Зильберман П.Е., Темирязев А.Г., Тихомирова М.П. // РЭ. 1999. Т.44. № 10. С.1262.
51. Гуляев Ю.В., Зильберман П.Е., Темирязев А.Г., Тихомирова М.П. // ФТТ. 2000 Т.42. №6. С.1062.
52. Gerrits Th., Schneider M.L., Kos A.B., Silva T.J. // Phys.Rev.B. 2006. V.73. №9. P.094454(7).
53. Семенцов Д.И., Шутый А.М. // УФН. 2007. Т.177. № 8. С.831.
54. Kittel C. // Phys. Rev. 1948. V.73. № 2. P.155.
55. Walker L.R. // Phys. Rev. 1957. V.105. № 2. P.390. С.470.).
56. Уокер Л. // В сб. «Ферриты в нелинейных сверхвысокочастотных устройствах». Ред.: Гуревич А.Г. // М.: ИЛ. 1961. С.470.
57. Ле-Кроу Р., Комсток Р. В кн.: У. Мэзон (ред.): Физическая акустика. Т.3Б. Динамика решетки. М.: Мир. 1968. С.156.
58. Карпачев С.Н., Власов В.С., Котов Л.Н. // Вестник МГУ. Сер.3. 2006. № 6. С.60.
59. Власов В.С. // Исследование релаксационной и нелинейной динамики магнитных и магнитоупругих колебаний пленок и частиц. Диссертация на соискание ученой степени канд. физ.-мат. наук. М.: МГУ. 2007.
60. Тихонов А.Н., Самарский А.А. Уравнения математической физики. М.: Наука. 1972.
61. Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Наука. 1973.
62. Schlömann E., Joseph R.I., Kohane T. // Proc. IEEE. 1965. V.53. №10. P.1495.
63. Шлёман, Джозеф, Кохейн // ТИИЭР. 1965. Т.53. №10. С.1685.
64. Власов В.С., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2011. Т.56. №1. С.84.
65. Власов В.С., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2011. Т.56. №6. С.719.
66. Власов В.С., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2011. Т.56. №9. С.1120.
67. Власов В.С., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2012. Т.57. №5. С.501.
68. Власов В.С., Кирушев М.С., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2013. Т.58. №8. С.806.
69. Власов В.С., Кирушев М.С., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2013. Т.58. №9. С.857.
70. Власов В.С., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2010. Т.55. №6. С.689.
71. Малоземов А., Слонзуски Дж. Доменные стенки в материалах с цилиндрическими магнитными доменами. М.: Мир. 1982.