УДК 519.676 + 621.391
Новые методы анализа воздействия эрланговских дельта-импульсов в задачах радиотехники [*]
Т. А. Аверина1,2, К. А. Рыбаков3
1 Институт вычислительной математики и математической геофизики СО РАН
2 Новосибирский государственный университет
3 Московский авиационный институт (национальный исследовательский университет)
Получена 10 ноября 2014 г.
Аннотация. В статье рассматриваются стохастические системы при импульсных воздействиях, образующих эрланговские потоки событий и приводящих к разрывам траекторий системы. Решается задача нахождения плотности вероятности вектора состояния. В основе предлагаемых методов лежит использование метода статистического моделирования и спектральной формы математического описания систем управления.
Ключевые слова: задача анализа, импульсные воздействия, метод статистического моделирования, обобщенные уравнения Фоккера–Планка–Колмогорова, спектральный метод, стохастическая система, эрланговский поток событий, эрланговский процесс.
Abstract: The article deals with the stochastic systems with impulses generated by Erlang flow of events and lead to discontinuities of the system trajectories. We solve the problem of finding the probability density function for the system state. The solution is based on using the statistical simulation method and spectral form of mathematical description for control systems.
Key words: analysis, Erlang flow of events, Erlang process, generalized Fokker–Planck–Kolmogorov equations, impulse signals, spectral method, statistical simulation method, stochastic system.
Введение
Случайные возмущения, действующие на систему, могут иметь различную природу, действовать постоянно (непрерывно) или время от времени (в виде импульсов). Удобной математической моделью для описания процессов, подверженных непрерывным и импульсным возмущениям, являются стохастические дифференциальные уравнения с диффузионной и скачкообразной компонентами [1–4].
В работе [5] были предложены новые методы анализа воздействия пуассоновских дельта-импульсов в стохастических системах, в частности в электрических цепях. Однако случай, рассмотренный в [5], подразумевает описание импульсных воздействий с помощью общего пуассоновского процесса, т.е. в предположении, что промежутки времени между двумя последовательными импульсами задаются показательным законом распределения. Это в некоторой степени сужает класс решаемых прикладных задач, поэтому в данной работе рассматривается более общий тип импульсных воздействий, для которых промежутки времени между двумя последовательными импульсами задаются эрланговским законом распределения.
Решаются задачи нахождения вероятностных характеристик процессов, описываемых стохастическими дифференциальными уравнениями с диффузионной и скачкообразной компонентами, причем скачкообразная компонента задается общим эрланговским процессом.
В статье приведена математическая постановка задачи, описаны разработанные методы и алгоритмы приближенного анализа – нахождения вероятностных характеристик вектора состояния системы с помощью метода статистического моделирования [6–13] и спектральной формы математического описания систем управления [14–17].
Преимущества предлагаемых подходов к анализу стохастических систем при импульсных воздействиях состоят в простоте реализации и универсальности. Они могут применяться как для линейных, так и для нелинейных систем, для различных законов распределения величин приращений вектора состояния. Как и в [5], апробация предлагаемых методов проводится на модельных примерах анализа воздействия импульсов на электрические цепи.
1. Математическая модель систем с эрланговской составляющей
Будем рассматривать стохастическое дифференциальное уравнение Ито со скачкообразной (эрланговской) компонентой [2]:
где ![]() –
вектор состояния;
–
вектор состояния; ![]() ,
, ![]() –
отрезок времени функционирования системы;
–
отрезок времени функционирования системы; ![]() –
вектор-функция размера
–
вектор-функция размера ![]() ,
, ![]() –
матричная функция размера
–
матричная функция размера ![]() ;
; ![]() –
– ![]() -мерный
стандартный винеровский процесс, не зависящий от начального состояния
-мерный
стандартный винеровский процесс, не зависящий от начального состояния ![]() .
.
Слагаемое ![]() описывает случайные
импульсные воздействия на систему, а именно
описывает случайные
импульсные воздействия на систему, а именно
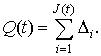
Здесь ![]() –
эрланговский процесс порядка
–
эрланговский процесс порядка ![]() ,
, ![]() – независимые случайные величины из
– независимые случайные величины из ![]() , распределение которых задано плотностью
вероятности
, распределение которых задано плотностью
вероятности ![]() , т.е. вектор состояния получает случайные
приращения в моменты времени
, т.е. вектор состояния получает случайные
приращения в моменты времени ![]() ,
, ![]() , …, образующие эрланговский поток событий
[1, 2, 16]:
, …, образующие эрланговский поток событий
[1, 2, 16]:
![]()
Если величина приращения зависит от вектора состояния, то
используется условная плотность вероятности ![]() ,
характеризующая распределение
,
характеризующая распределение ![]() при условии
при условии ![]() . В частном случае
. В частном случае ![]() .
.
Эрланговский поток событий формируется в результате пропуска
подряд ![]() события пуассоновского потока, который в
свою очередь определяется интенсивностью
события пуассоновского потока, который в
свою очередь определяется интенсивностью ![]() следования
событий и задает пуассоновский процесс
следования
событий и задает пуассоновский процесс ![]() . При
. При ![]() процессы
процессы ![]() и
и ![]() совпадают, этот случай подробно рассматривался
в работе [5].
совпадают, этот случай подробно рассматривался
в работе [5].
Для стохастической системы (1) эквивалентное уравнение в смысле Стратоновича имеет вид
где функции ![]() и
и
![]() связаны соотношением
связаны соотношением
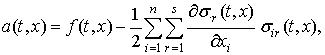
в котором ![]() –
–
![]() -й столбец матрицы
-й столбец матрицы ![]() .
Если
.
Если ![]() не зависит от
не зависит от ![]() , то
функции
, то
функции ![]() и
и ![]() совпадают.
совпадают.
Для дальнейшего изложения введем случайный процесс ![]() с конечным множеством состояний
с конечным множеством состояний ![]() . Они сменяются последовательно, начиная
с 1, в соответствии с кольцевым графом состояний (рис. 1),
. Они сменяются последовательно, начиная
с 1, в соответствии с кольцевым графом состояний (рис. 1), ![]() – интенсивность смены состояний:
– интенсивность смены состояний:
![]()
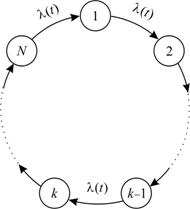
Рис. 1. Граф
состояний случайного процесса ![]()
При переходе из состояния с номером ![]() в
состояние с номером 1 вектор состояния
в
состояние с номером 1 вектор состояния ![]() системы
(1) получает случайное приращение, что соответствует разрыву (скачку) траектории
процесса
системы
(1) получает случайное приращение, что соответствует разрыву (скачку) траектории
процесса ![]() (рис. 2).
(рис. 2).
Введение дополнительного процесса ![]() позволяет
представить плотность вероятности
позволяет
представить плотность вероятности ![]() вектора
вектора ![]() в виде суммы:
в виде суммы:
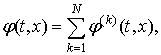
где функции ![]() удовлетворяют
системе обобщенных уравнений Фоккера–Планка–Колмогорова [1,
2, 15]:
удовлетворяют
системе обобщенных уравнений Фоккера–Планка–Колмогорова [1,
2, 15]:
в которой
где ![]() –
элементы матрицы диффузии
–
элементы матрицы диффузии ![]() .
.
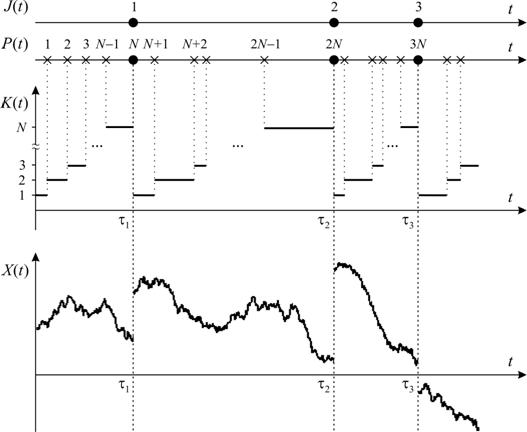
Рис. 2. Пример
траекторий случайных процессов ![]() и
и ![]()
Начальное состояние ![]() определяется
заданной плотностью вероятности
определяется
заданной плотностью вероятности ![]() . Для процесса
. Для процесса ![]() начальное состояние
фиксировано:
начальное состояние
фиксировано: ![]() , следовательно,
, следовательно,
![]()
Задача анализа стохастических систем с эрланговской составляющей заключается в нахождении вероятностных характеристик вектора состояния (плотности вероятности, моментных характеристик) в соответствии с заданной математической моделью.
2. Статистический алгоритм численного решения стохастических систем с разрывами траекторий
В работе [5] был описан статистический алгоритм
моделирования стохастических систем при импульсных воздействиях, образующих
пуассоновский поток событий интенсивности ![]() и
приводящих к разрывам траекторий системы. Алгоритм был построен для переменной
интенсивности и использовал эффективные алгоритмы моделирования пуассоновских
ансамблей [6–8]. В данной статье мы построим статистический алгоритм
моделирования траекторий решения (1) или (2) для постоянной интенсивности
и
приводящих к разрывам траекторий системы. Алгоритм был построен для переменной
интенсивности и использовал эффективные алгоритмы моделирования пуассоновских
ансамблей [6–8]. В данной статье мы построим статистический алгоритм
моделирования траекторий решения (1) или (2) для постоянной интенсивности ![]() .
.
Известно [18], что плотность распределения времени появления
![]() -й точки в точечном пуассоновском потоке событий
интенсивности
-й точки в точечном пуассоновском потоке событий
интенсивности ![]() имеет эрланговский закон
распределения
имеет эрланговский закон
распределения ![]() -го порядка с параметром
-го порядка с параметром ![]() :
:
Поэтому статистический алгоритм моделирования решения стохастических систем с разрывами траекторий вида (1) или (2) можно построить с использованием алгоритма моделирования точечного пуассоновского потока постоянной интенсивности и численных методов решения стохастических дифференциальных уравнений [9].
Статистический
алгоритм моделирования траекторий процесса ![]() для стохастических систем (1) или (2)
для стохастических систем (1) или (2)
0) ![]() ;
; ![]() ;
; ![]() ;
моделируем
;
моделируем ![]() согласно заданной плотности вероятности
согласно заданной плотности вероятности ![]() ;
;
1) моделируем момент разрыва траекторий ![]() , где
, где ![]() –
случайная величина с плотностью (7), моделируемая по формуле
–
случайная величина с плотностью (7), моделируемая по формуле ![]() , где
, где ![]() –
независимые равномерно распределенные на интервале
–
независимые равномерно распределенные на интервале ![]() случайные
величины; если
случайные
величины; если ![]() , то
, то ![]() и
и ![]() ;
;
2) решаем стохастическое дифференциальное уравнение в смысле Ито
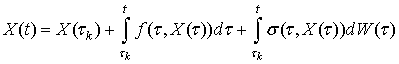
или эквивалентное ему стохастическое дифференциальное уравнение в смысле Стратоновича
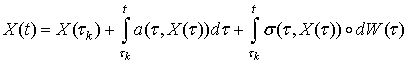
на интервале ![]() численным
методом с шагом h и находим
численным
методом с шагом h и находим ![]() – решение в момент
– решение в момент ![]() , при этом шаг должен быть согласован с
интенсивностью, например,
, при этом шаг должен быть согласован с
интенсивностью, например, ![]() ; если
; если ![]() , то процесс моделирования завершается;
, то процесс моделирования завершается;
3) моделируем случайную величину X согласно
плотности ![]() и полагаем
и полагаем ![]() ; или
моделируем величину скачка
; или
моделируем величину скачка ![]() согласно плотности
согласно плотности ![]() и полагаем
и полагаем ![]() ;
;
4) если ![]() , то
, то ![]() и переходим к п. 1, иначе процесс моделирования
завершается.
и переходим к п. 1, иначе процесс моделирования
завершается.
Выбор численного
метода решения конкретного стохастического дифференциального уравнения и шага
интегрирования ![]() определяются видом системы (1)
или (2) и требуемой точностью вычисления вероятностных характеристик выходных
процессов. Сетка по времени
определяются видом системы (1)
или (2) и требуемой точностью вычисления вероятностных характеристик выходных
процессов. Сетка по времени ![]() является суперпозицией
равномерной сетки с шагом
является суперпозицией
равномерной сетки с шагом ![]() и моментов разрыва
траекторий. Немного усложнив алгоритм моделирования моментов разрывов [5–8],
можно рассматривать случай переменной интенсивности
и моментов разрыва
траекторий. Немного усложнив алгоритм моделирования моментов разрывов [5–8],
можно рассматривать случай переменной интенсивности ![]() .
.
В работе [12] для численного решения стохастического дифференциального уравнения в смысле Стратоновича (2) построено семейство численных методов. При численных расчетах использовался устойчивый метод из этого семейства [13]:
где ![]() – значение приближенного решения в
узле сетки по времени
– значение приближенного решения в
узле сетки по времени ![]() ;
; ![]() – единичная
матрица размера
– единичная
матрица размера ![]() ;
; ![]() – шаг
интегрирования в узле
– шаг
интегрирования в узле ![]() ,
, ![]() –
вектор независимых между собой случайных величин
–
вектор независимых между собой случайных величин ![]() ,
, ![]() , имеющих стандартное нормальное
распределение с нулевым математическим ожиданием и единичной дисперсией. Сетка
, имеющих стандартное нормальное
распределение с нулевым математическим ожиданием и единичной дисперсией. Сетка ![]() на отрезке
на отрезке ![]() строится
для каждой траектории численного решения и включает все моменты скачков.
строится
для каждой траектории численного решения и включает все моменты скачков.
Аналогично работе [19] для построенного алгоритма можно доказать, что
1) для
достижения требуемой погрешности ![]() вычисления
функционалов от решения условно-оптимальными значениями параметров численного метода
являются
вычисления
функционалов от решения условно-оптимальными значениями параметров численного метода
являются
![]() и
и ![]() ;
;
2) для вычисления
гистограммы решения с точностью ![]() в норме пространства
в норме пространства ![]() условно-оптимальными значениями
параметров численного метода являются
условно-оптимальными значениями
параметров численного метода являются
![]() ,
, ![]() и
и ![]() ,
,
где ![]() – число узлов гистограммы на интервале [a,b],
– число узлов гистограммы на интервале [a,b], ![]() – объем выборки,
– объем выборки, ![]() –
шаг численного метода.
–
шаг численного метода.
Асимптотически несмещенный метод (8) имеет 1-й порядок сходимости
в среднеквадратичном для произвольных систем стохастических дифференциальных
уравнений и 2-й – для систем с одним шумом, а также в случае систем с
постоянной матрицей ![]() . В рассматриваемых ниже
тестовых примерах матрицы
. В рассматриваемых ниже
тестовых примерах матрицы ![]() постоянны, поэтому
порядок сходимости метода
постоянны, поэтому
порядок сходимости метода ![]() и
и
1) для достижения
погрешности ![]() вычисления математического ожидания и
дисперсии условно-оптимальными значениями параметров численного метода являются
вычисления математического ожидания и
дисперсии условно-оптимальными значениями параметров численного метода являются
![]() и
и ![]() ;
;
2) для вычисления
гистограммы решения с точностью ![]() в норме пространства
в норме пространства ![]() условно-оптимальными значениями
параметров численного метода являются
условно-оптимальными значениями
параметров численного метода являются
![]() ,
, ![]() и
и ![]() .
.
Так как вероятностные моменты и гистограмма считались одновременно, то полагали
Стандартные нормальные случайные величины моделировались по формуле
![]()
где ![]() –
равномерные на интервале
–
равномерные на интервале ![]() случайные величины,
для моделирования которых использовался датчик псевдослучайных чисел RAND [6].
случайные величины,
для моделирования которых использовался датчик псевдослучайных чисел RAND [6].
3. Спектральный метод анализа стохастических систем с эрланговской составляющей
Спектральный метод анализа базируется на применении спектральной формы математического описания систем управления [14], в основе которой лежит представление функций их спектральными характеристиками – упорядоченными совокупностями коэффициентов разложения в ряды по подходящей системе ортонормированных функций. Применение спектральной формы математического описания позволяет перейти от операторных уравнений – системы, включающей интегро-дифференциальное уравнение (3) и дифференциальные уравнения (4), – к алгебраическим уравнениям для коэффициентов разложения, которые представляются в матричной форме.
Будем использовать те же обозначения, что и в [5], а именно ![]() – ортонормированный базис пространства
– ортонормированный базис пространства ![]() , причем функции
, причем функции ![]() порождаются
всевозможными произведениями функций, образующих ортонормированные базисы
порождаются
всевозможными произведениями функций, образующих ортонормированные базисы ![]() и
и ![]() пространств
пространств
![]() и
и ![]() соответственно,
т.е.
соответственно,
т.е.
![]()
Подробный вывод спектрального аналога системы обобщенных уравнений Фоккера–Планка–Колмогорова (3) и (4) содержится в [16], поэтому приведем лишь основные соотношения – уравнения обобщенных характеристических функций:
где ![]() –
спектральная характеристика оператора дифференцирования по времени с учетом
значения функции в начальный момент;
–
спектральная характеристика оператора дифференцирования по времени с учетом
значения функции в начальный момент; ![]() и
и ![]() – спектральные характеристики операторов
– спектральные характеристики операторов ![]() и
и ![]() ,
определенных выражениями (5) и (6) соответственно;
,
определенных выражениями (5) и (6) соответственно; ![]() –
спектральная характеристика оператора умножения на функцию
–
спектральная характеристика оператора умножения на функцию ![]() ;
; ![]() –
спектральные характеристики функций
–
спектральные характеристики функций ![]() ,
, ![]() . Все перечисленные спектральные характеристики
определены относительно системы функций
. Все перечисленные спектральные характеристики
определены относительно системы функций ![]() .
Далее,
.
Далее, ![]() – матрица-столбец значений функций
базисной системы
– матрица-столбец значений функций
базисной системы ![]() в точке
в точке ![]() ;
;
![]() – спектральная характеристика плотности вероятности
– спектральная характеристика плотности вероятности
![]() начального состояния
начального состояния ![]() , определенная относительно системы
функций
, определенная относительно системы
функций ![]() .
.
Спектральная характеристика ![]() плотности
вероятности
плотности
вероятности ![]() , называемая также обобщенной
характеристической функцией [15], выражается следующим образом (
, называемая также обобщенной
характеристической функцией [15], выражается следующим образом (![]() – многомерная гиперстолбцовая матрица, образованная
искомыми коэффициентами разложения
– многомерная гиперстолбцовая матрица, образованная
искомыми коэффициентами разложения ![]() ):
):
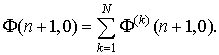
Спектральные характеристики функций и линейных операторов определены в [5], подробнее теория спектрального метода изложена в [14, 15].
Уравнения (10), (11) линейны относительно спектральных
характеристик ![]() , поэтому ее решение нетрудно
получить методом исключения неизвестных. Тогда [16]
, поэтому ее решение нетрудно
получить методом исключения неизвестных. Тогда [16]
или
где
![]()
Отметим, что в частном случае ![]() , т.е.
при воздействии пуассоновских дельта-импульсов на систему, формулы (12) и (13)
могут быть записаны в виде соотношения
, т.е.
при воздействии пуассоновских дельта-импульсов на систему, формулы (12) и (13)
могут быть записаны в виде соотношения
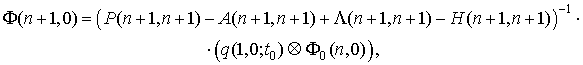
полученного в [5].
После нахождения обобщенной характеристической функции ![]() плотность вероятности
плотность вероятности ![]() вектора состояния может быть представлена
в виде ряда
вектора состояния может быть представлена
в виде ряда
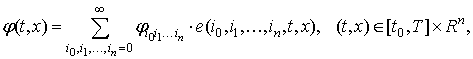
или при приближенном решении задачи анализа в виде частичной суммы этого ряда:
где числа ![]() –
порядки усечения спектральных характеристик [14, 15]. В последнем случае (10) и
(11) – матричная запись системы конечного числа линейных алгебраических
уравнений (число уравнений и число неизвестных:
–
порядки усечения спектральных характеристик [14, 15]. В последнем случае (10) и
(11) – матричная запись системы конечного числа линейных алгебраических
уравнений (число уравнений и число неизвестных: ![]() ).
).
По найденной спектральной характеристике ![]() могут быть определены маргинальные
плотности вероятности (при
могут быть определены маргинальные
плотности вероятности (при ![]() ) и моментные характеристики
вектора состояния с использованием свойств спектральных характеристик линейных
функционалов [15]. Для определения маргинальных плотностей вероятности
спектральным методом достаточно, чтобы функции базисной системы
) и моментные характеристики
вектора состояния с использованием свойств спектральных характеристик линейных
функционалов [15]. Для определения маргинальных плотностей вероятности
спектральным методом достаточно, чтобы функции базисной системы ![]() порождались всевозможными произведениями
функций базисных систем
порождались всевозможными произведениями
функций базисных систем ![]() , …,
, …, ![]() пространства
пространства ![]() , т.е.
, т.е. ![]() ,
, ![]()
Алгоритм приближенного решения задачи анализа стохастических систем с эрланговской составляющей спектральным методом
1. Выбрать базисные системы ![]() и
и ![]() (или
(или ![]() , …,
, …, ![]() ), сформировать базисную систему
), сформировать базисную систему ![]() . Выбрать порядки усечения спектральных
характеристик
. Выбрать порядки усечения спектральных
характеристик ![]() ,
, ![]() , …,
, …, ![]() .
.
2. Вычислить спектральные характеристики оператора
дифференцирования ![]() по времени и оператора
умножения
по времени и оператора
умножения ![]() на интенсивность
на интенсивность ![]() ,
спектральные характеристики
,
спектральные характеристики ![]() и
и ![]() операторов
операторов ![]() и
и ![]() соответственно (см. [5]), спектральную
характеристику
соответственно (см. [5]), спектральную
характеристику ![]() плотности вероятности начального
состояния
плотности вероятности начального
состояния ![]() ; сформировать матрицу-столбец
; сформировать матрицу-столбец ![]() .
.
3. Найти решение (12) или (13) уравнений обобщенных характеристических функций.
4. Представить плотность вероятности ![]() в виде (14).
в виде (14).
В качестве базисных систем ![]() ,
, ![]() , …,
, …, ![]() могут
применяться подходящие для конкретных задач системы ортонормированных функций:
полиномиальные, тригонометрические, кусочно-постоянные и др. [14,
15, 17].
могут
применяться подходящие для конкретных задач системы ортонормированных функций:
полиномиальные, тригонометрические, кусочно-постоянные и др. [14,
15, 17].
4. Примеры анализа воздействия импульсов на электрические цепи
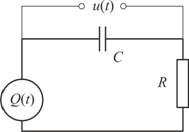
Возьмем за основу задачи, приведенные в [5]. В качестве первого примера рассмотрим задачу определения вероятностных характеристик напряжения на конденсаторе в RC-цепи (интегрирующей цепи; рис. 3, а).
|
|
|
Рис. 3. RC-цепь и RCL-цепь с генераторами импульсов
Уравнение, описывающее динамику изменения напряжения на конденсаторе, задается в виде
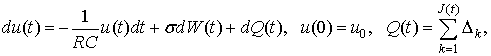
где ![]() –
сопротивление,
–
сопротивление, ![]() – емкость конденсатора,
– емкость конденсатора, ![]() – параметр, характеризующий интенсивность
помехи,
– параметр, характеризующий интенсивность
помехи, ![]() – начальное напряжение,
– начальное напряжение, ![]() – амплитуды скачков напряжения;
– амплитуды скачков напряжения; ![]() ,
, ![]() –
время окончания процесса. Параметры эрланговского процесса
–
время окончания процесса. Параметры эрланговского процесса ![]() :
: ![]() –
порядок,
–
порядок, ![]() – интенсивность.
– интенсивность.
Для численных расчетов положим ![]() Ом
(8 кОм),
Ом
(8 кОм), ![]() ф (250 мкф),
ф (250 мкф), ![]() , начальное напряжение
, начальное напряжение ![]() имеет нормальное распределение с
параметрами
имеет нормальное распределение с
параметрами ![]() В,
В, ![]() В
(дисперсия
В
(дисперсия ![]() ), случайные величины
), случайные величины ![]() имеют логарифмически нормальное
распределение с параметрами
имеют логарифмически нормальное
распределение с параметрами ![]() и
и ![]() – математическое ожидание и
среднеквадратическое отклонение для
– математическое ожидание и
среднеквадратическое отклонение для ![]() . Будем решать задачу
при
. Будем решать задачу
при ![]() и интенсивности
и интенсивности ![]() ,
т.е. задавать нормированный эрланговский закон распределения порядка
,
т.е. задавать нормированный эрланговский закон распределения порядка ![]() для обеспечения постоянства среднего
числа импульсов в единицу времени и изучения влияния закона распределения длины
промежутка времени между двумя последовательными импульсами на вероятностные
характеристики напряжения на конденсаторе.
для обеспечения постоянства среднего
числа импульсов в единицу времени и изучения влияния закона распределения длины
промежутка времени между двумя последовательными импульсами на вероятностные
характеристики напряжения на конденсаторе.
При решении задачи методом статистических испытаний
нормальная случайная величина ![]() моделировалась по
формуле
моделировалась по
формуле ![]() , где
, где ![]() –
стандартная нормальная случайная величина с нулевым математическим ожиданием и
единичной дисперсией; моделирование времени между скачками осуществлялось по
формуле
–
стандартная нормальная случайная величина с нулевым математическим ожиданием и
единичной дисперсией; моделирование времени между скачками осуществлялось по
формуле ![]() , где
, где ![]() –
независимые равномерно распределенные на интервале
–
независимые равномерно распределенные на интервале ![]() случайные
величины; моделирование величин скачков осуществлялось по формуле
случайные
величины; моделирование величин скачков осуществлялось по формуле ![]() , где
, где ![]() – стандартная
нормальная случайная величина; на интервалах между скачками решение моделировалось
по методу (8). Как было отмечено выше, параметры метода задавались согласно (9).
Сетка по времени была суперпозицией равномерной сетки с шагом
– стандартная
нормальная случайная величина; на интервалах между скачками решение моделировалось
по методу (8). Как было отмечено выше, параметры метода задавались согласно (9).
Сетка по времени была суперпозицией равномерной сетки с шагом ![]() и моментов скачков.
и моментов скачков.
При решении задачи спектральным методом в качестве базисной
системы ![]() были выбраны полиномы Лежандра [14,
15],
а в качестве базисной системы
были выбраны полиномы Лежандра [14,
15],
а в качестве базисной системы ![]() – функции Эрмита [15,
17] с параметрами
– функции Эрмита [15,
17] с параметрами ![]() и
и ![]() ,
порядки усечения
,
порядки усечения ![]() ; для удобства вычислений
предварительно была сделана линейная замена переменной:
; для удобства вычислений
предварительно была сделана линейная замена переменной: ![]() .
.
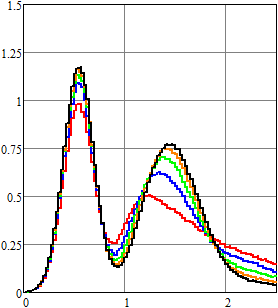
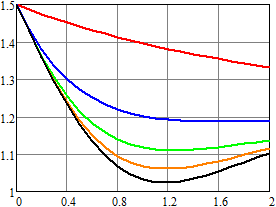
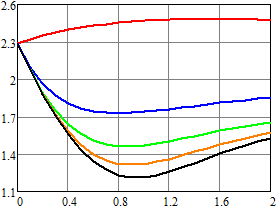
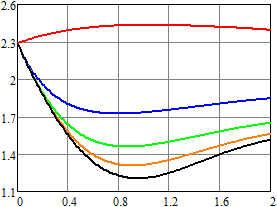
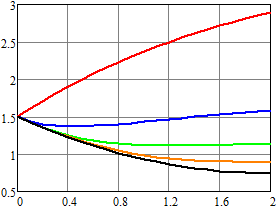
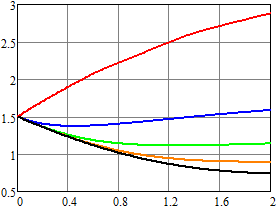
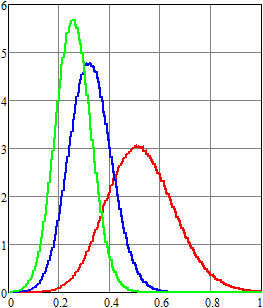
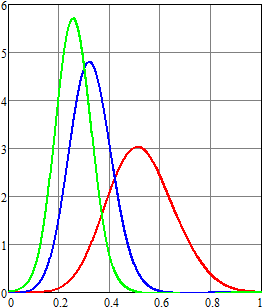
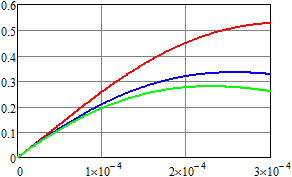
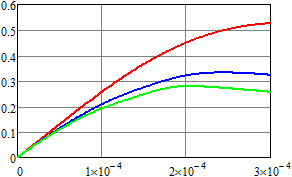
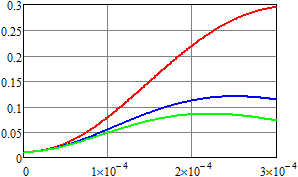
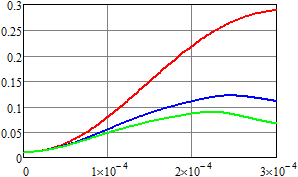
Результаты вычислений для плотности вероятности и первых
двух моментов напряжения приведены на рис. 4–6. Для ![]() ,
, ![]() (воздействие пуассоновских дельта-импульсов)
результаты показаны красным;
(воздействие пуассоновских дельта-импульсов)
результаты показаны красным; ![]() ,
, ![]() – синим;
– синим; ![]() ,
, ![]() – зеленым;
– зеленым; ![]() ,
, ![]() – оранжевым;
– оранжевым; ![]() ,
, ![]() – черным. Рисунки слева соответствуют
результатам, которые получены методом статистических испытаний, а справа – спектральным
методом.
– черным. Рисунки слева соответствуют
результатам, которые получены методом статистических испытаний, а справа – спектральным
методом.
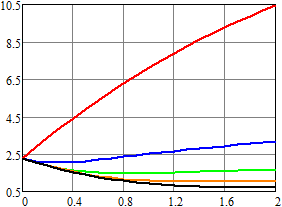
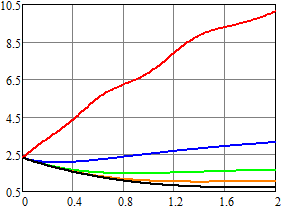
Нетрудно видеть, что даже при одинаковом среднем числе импульсов в единицу времени математическое ожидание и второй начальный момент существенно отличаются за счет изменения статистических характеристик длины промежутка времени между двумя последовательными импульсами.
|
|
|
Рис. 4.
Оценка плотности вероятности напряжения для RC-цепи
в конечный момент времени
|
|
|
Рис. 5. Оценка математического ожидания напряжения для RC-цепи
|
|
|
Рис. 6. Оценка второго начального момента напряжения для RC-цепи
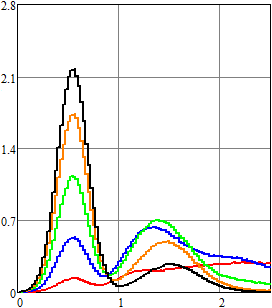
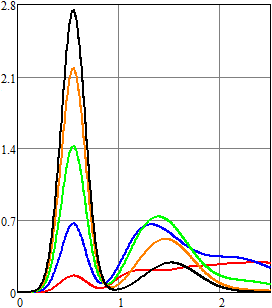
Дополнительно были проведены расчеты для ![]() и интенсивности
и интенсивности ![]() ,
т.е. для ненормированного эрланговского закона распределения. При применении
метода статистических испытаний использовались те же параметры, а для
спектрального метода в качестве базисной системы
,
т.е. для ненормированного эрланговского закона распределения. При применении
метода статистических испытаний использовались те же параметры, а для
спектрального метода в качестве базисной системы ![]() были
выбраны косинусоиды [14, 15], а в качестве базисной системы
были
выбраны косинусоиды [14, 15], а в качестве базисной системы ![]() – функции Эрмита [15,
17] с параметрами
– функции Эрмита [15,
17] с параметрами ![]() и
и ![]() для
для ![]() ; с параметрами
; с параметрами ![]() и
и
![]() для
для ![]() .
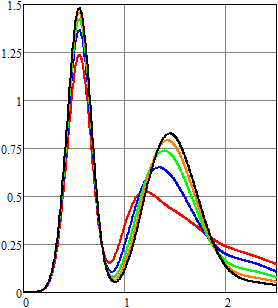
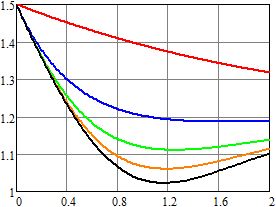
Порядки усечения такие же, как и ранее. Результаты вычислений отражены на рис.
7–9.
.
Порядки усечения такие же, как и ранее. Результаты вычислений отражены на рис.
7–9.
С ростом порядка ![]() для ненормированного
эрланговского закона распределения среднее число импульсов в единицу времени
становится меньше, что оказывает существенное влияние как на оценку плотности
вероятности, так и на моментные характеристики.
для ненормированного
эрланговского закона распределения среднее число импульсов в единицу времени
становится меньше, что оказывает существенное влияние как на оценку плотности
вероятности, так и на моментные характеристики.
|
|
|
Рис. 7.
Оценка плотности вероятности напряжения для RC-цепи
в конечный момент времени
|
|
|
Рис. 8. Оценка математического ожидания напряжения для RC-цепи
|
|
|
Рис. 9. Оценка второго начального момента напряжения для RC-цепи
Отличия в оценках плотности вероятности напряжения, по-видимому, вызваны погрешностью расчетов спектральным методом, результаты при применении которого достаточно чувствительны к изменению параметров базисных систем.
Далее рассмотрим задачу определения вероятностных характеристик силы тока в RCL-цепи (колебательном контуре; рис. 3, б), используя математическую модель
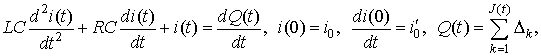
где ![]() –
сопротивление,
–
сопротивление, ![]() – емкость конденсатора,
– емкость конденсатора, ![]() – индуктивность,
– индуктивность, ![]() и
и
![]() – начальные данные,
– начальные данные, ![]() – амплитуды скачков;
– амплитуды скачков; ![]() ,
, ![]() с
– время окончания процесса. Эрланговский процесс
с
– время окончания процесса. Эрланговский процесс ![]() задается
порядком
задается
порядком ![]() и постоянной интенсивностью
и постоянной интенсивностью ![]() .
.
Зададим числовые значения для параметров контура, начальных
данных и параметров источника импульсов: ![]() Ом,
Ом,
![]() ф (1.2 мкф),
ф (1.2 мкф), ![]() Гн (15 мГн),
Гн (15 мГн), ![]() ,
, ![]() .
Начальная сила тока
.
Начальная сила тока ![]() случайна и имеет нормальное распределение
с параметрами
случайна и имеет нормальное распределение
с параметрами ![]() А и
А и ![]() А;
А; ![]() имеет
нормальное распределение с параметрами
имеет
нормальное распределение с параметрами ![]() А/с,
А/с,
![]() А/с. Случайные величины
А/с. Случайные величины ![]() имеют нормальное распределение с параметрами
имеют нормальное распределение с параметрами
![]() А
А![]() с,
с, ![]() А
А![]() с
(дисперсия
с
(дисперсия ![]() ).
).
Предварительно уравнение было преобразовано к эквивалентной
системе двух уравнений: ![]() ,
, ![]() ; кроме того, для увеличения точности
расчетов был выбран другой масштаб времени, чтобы коэффициенты в уравнении,
описывающем динамику изменения силы тока, были одного порядка:
; кроме того, для увеличения точности
расчетов был выбран другой масштаб времени, чтобы коэффициенты в уравнении,
описывающем динамику изменения силы тока, были одного порядка: ![]() ,
, ![]() ).
).
При решении задачи методом статистических испытаний были
использованы те же правила для моделирования случайных величин, что и в предыдущем
примере. Параметры метода (8) задавались согласно (9). Сетка по времени
является суперпозицией равномерной сетки с шагом ![]() и
моментов скачков. Задача также была просчитана при числе узлов гистограммы
и
моментов скачков. Задача также была просчитана при числе узлов гистограммы ![]() . Согласно условно-оптимальным значениям
параметров метода (9), увеличение числа узлов гистограммы не улучшает оценку
плотности в норме пространства
. Согласно условно-оптимальным значениям
параметров метода (9), увеличение числа узлов гистограммы не улучшает оценку
плотности в норме пространства ![]() , но вид графика
становится более плавным. Полученные гистограммы при
, но вид графика
становится более плавным. Полученные гистограммы при ![]() приведены
на рис. 10.
приведены
на рис. 10.
При решении задачи спектральным методом в качестве базисной
системы ![]() были выбраны полиномы Лежандра [14,
15],
а в качестве базисных систем
были выбраны полиномы Лежандра [14,
15],
а в качестве базисных систем ![]() и
и ![]() – функции Эрмита [15,
17] с параметрами
– функции Эрмита [15,
17] с параметрами ![]() и
и ![]() , порядки
усечения
, порядки
усечения ![]() .
.
Результаты вычислений для
плотности вероятности и первых двух моментов силы тока приведены на рис. 10–12.
Для ![]() (воздействие пуассоновских
дельта-импульсов) результаты показаны красным,
(воздействие пуассоновских
дельта-импульсов) результаты показаны красным, ![]() –
синим,
–
синим, ![]() – зеленым. Рисунки слева соответствуют
результатам, которые получены методом статистических испытаний, а справа –
спектральным методом.
– зеленым. Рисунки слева соответствуют
результатам, которые получены методом статистических испытаний, а справа –
спектральным методом.
|
|
|
Рис. 10.
Оценка плотности вероятности силы тока для RCL-цепи
в конечный момент времени
Как показали численные эксперименты, в приведенных примерах получены сопоставимые по точности оценки вероятностных характеристик параметров электрических цепей. Предлагаемые методы ориентированы на применение современных вычислительных средств и эффективны при анализе стохастических систем с эрланговской составляющей.
|
|
|
Рис. 11. Оценка математического ожидания силы тока для RCL-цепи
|
|
|
Рис. 12. Оценка второго начального момента силы тока для RCL-цепи
Литература
1. Артемьев В.М., Ивановский А.В. Дискретные системы управления со случайным периодом квантования. – М.: Энергоатомиздат, 1986.
2. Пугачев В.С., Синицын И.Н. Стохастические дифференциальные системы. Анализ и фильтрация. – М.: Наука, 1990.
3. Тихонов В.И., Харисов В.Н. Статистический анализ и синтез радиотехнических устройств и систем. – М.: Радио и связь, 1991.
4. Тихонов В.И., Миронов М.А. Марковские процессы. – М.: Советское радио, 1977.
5. Аверина Т.А., Рыбаков К.А. Новые методы анализа воздействия пуассоновских дельта-импульсов в задачах радиотехники // Журнал радиоэлектроники. – 2013. № 1. URL: http://jre.cplire.ru/jre/jan13/13/text.html
6. Ермаков С.М., Михайлов Г.А. Статистическое моделирование. – М.: Наука, 1982.
7. Михайлов Г.А., Аверина Т.А. Алгоритм «максимального сечения» в методе Монте-Карло // Докл. АН. – 2009. Т. 428. № 2. – С. 163–165.
8. Аверина Т.А. Методы статистического моделирования неоднородного пуассоновского ансамбля // Сиб. журн. вычисл. матем. – 2009. Т. 12. № 4. – С. 361–374.
9. Artemiev S.S., Averina T.A. Numerical Analysis of Systems of Ordinary and Stochastic Differential Equations. – VSP, 1997.
10. Аверина Т.А., Михайлов Г.А. Алгоритмы точного и приближенного статистического моделирования пуассоновских ансамблей // Журн. вычисл. матем. и матем. физ. – 2010. Т. 50. № 6. – С. 1005–1016.
11. Соболь И.М. Численные методы Монте-Карло. – М.: Наука, 1973.
12. Аверина Т.А., Артемьев С.С. Новое семейство численных методов решения стохастических дифференциальных уравнений // Докл. АН СССР. – 1986. Т. 288. № 4. – С. 777–780.
13. Аверина Т.А. Устойчивые численные методы решения стохастических дифференциальных уравнений в смысле Стратоновича // Вестник Бурятского гос. унив. – 2012. № 9. – C. 91–94.
14. Солодовников В.В., Семенов В.В. Спектральная теория нестационарных систем управления. – М.: Наука, 1974.
15. Пантелеев А.В., Рыбаков К.А., Сотскова И.Л. Спектральный метод анализа нелинейных стохастических систем управления. – М.: Вузовская книга, 2006. (Дифференциальные уравнения и процессы управления. – 2013. № 1. URL: http://www.math.spbu.ru/diffjournal).
16. Кожевников А.С., Рыбаков К.А. Анализ нелинейных стохастических систем управления с импульсными воздействиями, образующими эрланговские потоки событий // Научный вестник МГТУ ГА. – 2012. № 184 (10). – С. 37–45.
17. Рыбаков К.А. Многопараметрические базисные системы для представления функций в неограниченных областях // Научный вестник МГТУ ГА. – 2013. № 195 (9). – С. 45–50.
18. Королюк В.С., Портенко Н.И., Скороход А.В., Турбин А.Ф. Справочник по теории вероятностей и математической статистике. – М.: Наука, 1985.
19. Аверина Т.А., Рыбаков К.А. Два метода анализа стохастических мультиструктурных систем с распределенными переходами // Сиб. журн. вычисл. матем. – 2008. Т. 11. № 1. – С. 1–18.
[*] Работа выполнена при финансовой поддержке грантов РФФИ (проекты № 14-01-00787, 12-08-00892) и НШ – 5111.2014.1.
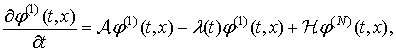
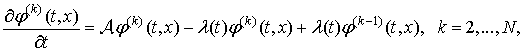
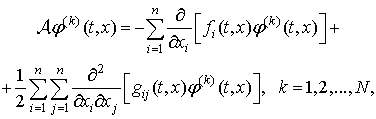
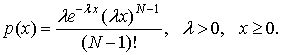
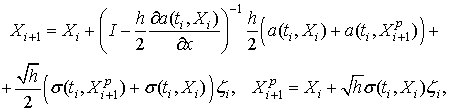
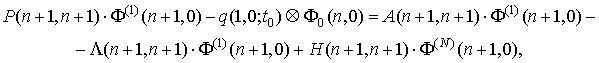
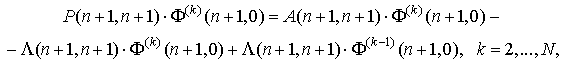
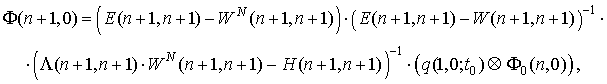
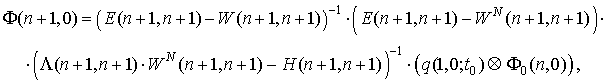
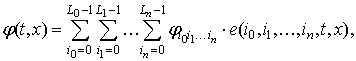
 а)
а)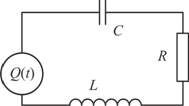 б)
б)