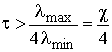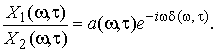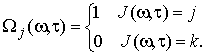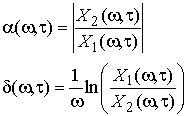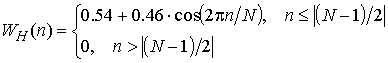УДК 681.513.6
МНОГОКАНАЛЬНАЯ АДАПТИВНАЯ КОМПЕНСАЦИЯ УЗКОПОЛОСНЫХ ПОМЕХ С ИХ ПРЕДВАРИТЕЛЬНЫМ СЛЕПЫМ РАЗДЕЛЕНИЕМ В ОПОРНЫХ КАНАЛАХ
А. Е. Манохин
Институт радиоэлектроники и информационных технологий
- РТФ
УрФУ им. первого Президента РФ Б.Н.Ельцина,
кафедра радиоэлектронных и
телекоммуникационных систем, Екатеринбург
Статья поступила в редакцию 15 октября 2015 г., после доработки – 17 ноября 2015 г.
Аннотация. В работе решается задача многоканальной компенсации узкополосных помех с их предварительным разделением в опорных каналах. Отличительной особенностью компенсатора является использование алгоритма слепого разделения DUET, благодаря которому, во-первых, увеличивается скорость сходимости адаптивного алгоритма наименьших квадратов, а во-вторых, используются всего два опорных канала для компенсации более двух помех. При этом выигрыш в скорости сходимости при использовании алгоритма слепого разделения DUET составляет не менее 8 раз.
Ключевые слова: слепое разделение сигналов, многоканальный адаптивный компенсатор, алгоритм DUET, скорость сходимости.
Введение
В [1] решалась задача повышения скорости сходимости адаптивного алгоритма наименьших квадратов (МНК) при многоканальной адаптивной компенсации помех с использованием предварительного слепого разделения помех в опорных каналах (рис. 1).
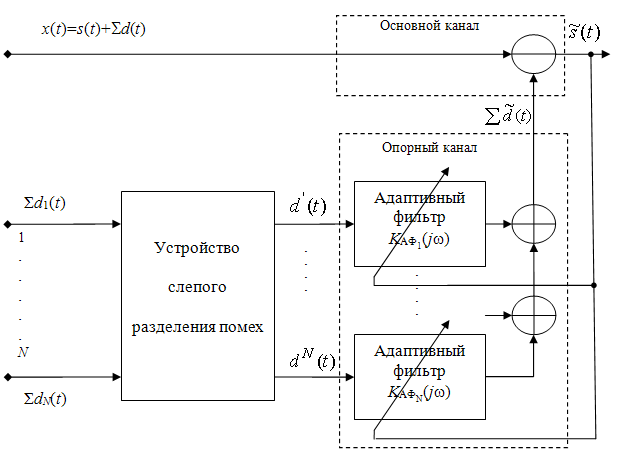
Рис. 1. Структурная схема компенсатора помех на основе многоканальной адаптивной обработки с предварительным слепым разделением помех в опорном канале.
В качестве алгоритма слепого разделения применялся простой в вычислительном плане модифицированный алгоритм Жуттена-Эро. Однако этот алгоритм имеет существенный недостаток – для его работоспособности необходимо обеспечивать когерентность (равенство задержек) однотипных помех в каналах приема.
Алгоритм DUET лишен этого недостатка. Он функционирует в частотной области, а число разделяемых помех может быть больше числа приемных датчиков. Фактически алгоритм работоспособен в условиях произвольного числа разделяемых помех. Обязательным условием разделения является взаимная ортогональность и разбросанный по частоте спектр помех в любой момент времени [2].
Постановка задачи
Как известно, обусловленность (т.е. обратимость) матрицы влияет на постоянную времени обучающей кривой и, как следствие, на скорость сходимости алгоритма [3]. Максимальное значение постоянной времени обучающей кривой (τ) алгоритма наименьших квадратов не может быть меньше четверти отношения максимального и минимального собственных чисел корреляционной матрицы или четверти ее числа обусловленности[1] [1]:
где λmax — максимальное собственное число корреляционной матрицы;
λmin — минимальное собственное число корреляционной матрицы;
χ — число обусловленности корреляционной матрицы.
Рассматривается корреляционная матрица входных сигналов адаптивных фильтров (или корреляционная матрица помех), являющаяся квадратной, эрмитовой и теплицевой.
Как и в случае применения алгоритма Жуттена-Эро [1], найдем время сходимости без предварительного разделения помех (для смеси из двух узкополосных процессов). Для этого выведем значение постоянной времени обучающей кривой для многоканального адаптивного фильтра через отношение собственных значений корреляционной матрицы помех. Аналогично возьмем для рассмотрения двухканальный вариант реализации фильтра.
Пусть в опорном канале действует смесь двух узкополосных нормальных процессов d1(n) и d2(n) c шириной полосы a1 и a2 и центральными частотами Ω1 и Ω2 соответственно:
![]() —
в 1 опорном канале; (2)
—
в 1 опорном канале; (2)
![]() —
во 2 опорном канале, (3)
—
во 2 опорном канале, (3)
где k и ![]() — СКО помех в каналах (k<1).
— СКО помех в каналах (k<1).
Составим корреляционную матрицу помех для многоканального фильтра в виде клеточной матрицы [3, с.77]:
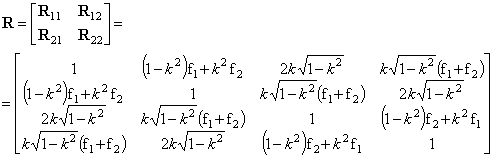 , (4)
, (4)
где ![]() ;
; ![]() .
.
Тогда уравнение собственных значений ![]() :
:
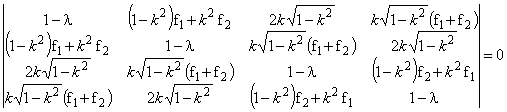 (5)
(5)
Находим определитель (5):
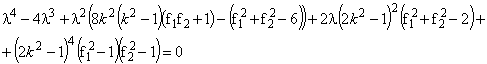 (6)
(6)
Решая уравнение (4) порядка (6) относительно l с помощью метода Феррари [4], получаем:
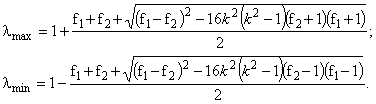 (7)
(7)
Подставляя собственные значения (7) в (1), получаем значение постоянной времени обучающей кривой:
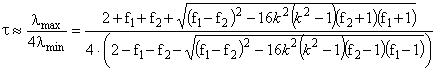 (8)
(8)
Рисунок 2 демонстрирует наихудшую обусловленность матрицы (т.е. матрица становится вырожденной, χ→∞) и как следствие наибольшую постоянную времени обучающей кривой при равных мощностях помех на каждом входе адаптивных фильтров, поэтому сначала необходимо разделить помехи, а только потом подать на опорные входы компенсатора (см. рис. 1).
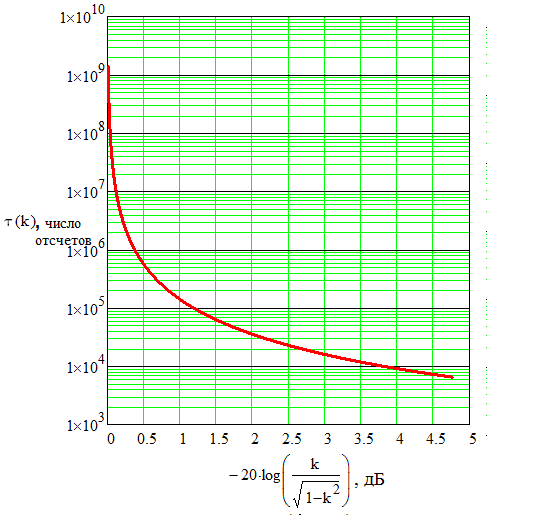
Рис. 2. Зависимость времени сходимости от отношения мощностей двух узкополосных помех в каналах (α1=α2=0.001; Ω1=0.0078, Ω2=0.016).
Алгоритм DUET
Рассмотрим классический алгоритм слепого разделения DUET. Пусть имеются результаты измерений с двух приемных датчиков, в которых действуют смеси сигналов, распространяющихся без переотражений и интерференции. В этом случае можно выразить эти смеси от первого и второго датчиков следующим образом:
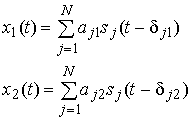 (9)
(9)
где aj1, aj2 и δj1, δj2 — амплитуды и задержки j-сигналов, действующих в первом и втором датчиках; N — число источников сигналов.
Для удобства представления можно выразить ф. 9 через относительные амплитуды и задержки:
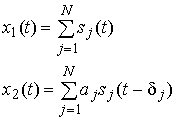 (10)
(10)
где aj = aj1/aj2 и δj = δj1–δj2 — смешивающие параметры.
В частотной области смеси сигналов с датчиков могут быть записаны:
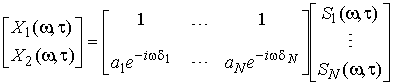 (11)
(11)
где X1(ω,τ) и X2(ω,τ) — смеси сигналов от первого и второго датчиков в частотной области;
S1(ω,τ)… SN(ω,τ) — источники сигналов в частотной области.
Идея алгоритма DUET состоит в том, что в каждый момент времени отношение частотных компонент смесей с двух датчиков зависит только от смешивающих параметров aj и δj [5]:
Поэтому можно определить набор пар смешивающих параметров aj и δj при тех значения частоты, на которых присутствуют частотные компоненты искомых сигналов. Эти пары и будут истинными значениями смешивающих параметров этих сигналов.
Для поиска истинных значений смешивающих параметров в [6] предложен функционал:
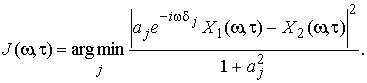 (13)
(13)
Функционал (13) есть не что иное, как номер пары смешивающих параметров, принадлежащих искомому источнику сигнала. Минимизация функции:
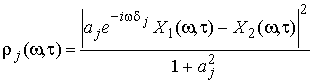 (14)
(14)
показывает, что найденная пара смешивающих параметров принадлежит j-му источнику сигнала. Выражение (14) принимает нулевое значение на всех частотах, где присутствуют компоненты выделяемого сигнала.
Тогда можно сформировать частотно-временную маску, изолирующую искомый источник сигнала от других сигналов в смеси:
Если частотно-временная компонента принадлежит j-му источнику (искомому), то маска принимает единичное значение, если k-му источнику, то нулевое. Соответственно эта бинарная маска локализует соответствующие максимумы в двумерной спектрограмме (рис. 3):

Рис. 3. Процесс выделения одного источника из смеси трех сигналов (обозначены «x», «+», «-»)
Математически операцию выделения источника сигнала из смеси можно записать:
Оценка смешивающих параметров производится путем построения двумерной гистограммы и поиска ее максимумов и их расположения относительно aj и δj. (рис. 4).
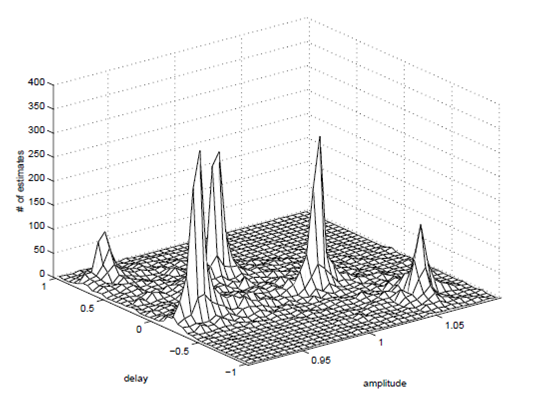
Рис. 4. Двумерная гистограмма оценок смешивающих параметров при приеме двумя датчиками аддитивной суммы пяти сигналов [7].
Гистограмма находится по формуле [5]:
где ![]() — фильтрующая функция.
— фильтрующая функция.
I(α,δ) принимает значения (ω,τ), при которых смешивающие параметры α(ω,τ) и δ(ω,τ) не выходят за заданные пределы amax и dmax (максимальное значение осей гистограммы). Смешивающие параметры α(ω,τ) и δ(ω,τ) из (12) можно получить:
Ограничивая предел изменения смешивающих параметров, можно путем интегрирования модуля произведения спектров смесей с двух датчиков получить гистограмму, содержащую максимумы в точках с координатами (αj,δj), соответствующими искомым смешивающим параметрам каждого сигнала.
Рассмотрим зависимости смешивающих параметров α(ω,τ) и δ(ω,τ) от частоты для смеси трех стационарных узкополосных нормальных процессов с центральными частотами 256, 512, 1024 и относительной полосой 0.001. Для получения оконных преобразований Фурье используется окно Хэмминга[2] шириной 8192 отсчета, а величина сдвига окна равна 128.
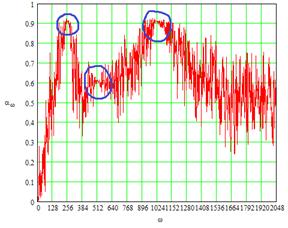
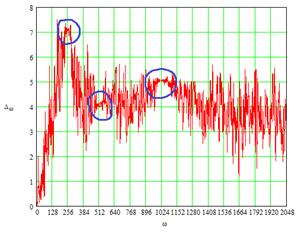
Рис. 5. Зависимости смешивающих параметров α(ω) и δ(ω) от частоты ω.
На рис. 5 синим цветом выделены истинные значения, которые принимают смешивающие параметры. Для того чтобы их найти необходимо построить по ф. 17 двумерную гистограмму (рис. 6), реализованную в алгоритме в среде Mathcad (рис. 7).
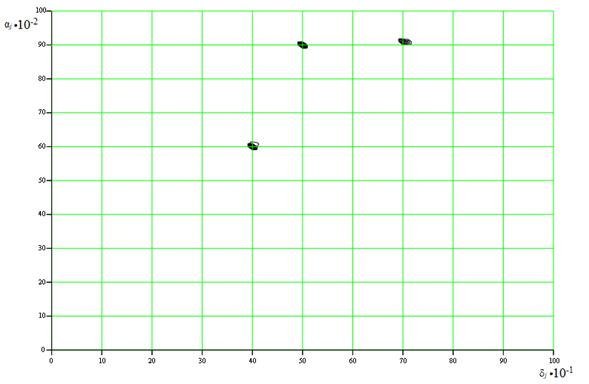
Рис. 6. Двумерная гистограмма оценок смешивающих параметров при приеме двумя датчиками аддитивной суммы трех узкополосных процессов с коэффициентами смешивания αj = (0.9; 0.6; 0.9), δj = (7; 4; 5).

Рис. 7. Программная реализация формулы 16 (Fx1ω
и Fx2ω — спектры смесей сигналов,
Δa и Δδ —
масштабы осей гистограммы, N — размер выборки
смесей).
С помощью разнообразных алгоритмов кластеризации (например, К-средних или FOREL [8]) можно определить координаты максимумов гистограммы, которые являются искомыми смешивающими параметрами αj и δj. В алгоритме FOREL (см. приложение) вычисляются центры тяжести кластеров, в качестве которых рассматриваются элементы, находящиеся внутри круга радиусом r с центром в точке С (алгоритм на рис. П.1). После нахождения центра тяжести кластера его элементы вырезаются из анализируемой выборки (алгоритм на рис. П.2), и аналогично находится центр тяжести следующего кластера. В целом алгоритм FOREL реализован в среде Mathcad и изображен на рис. П.4.
Определенной сложностью использования алгоритма FOREL является задание фиксированного значения радиуса кластера. Можно рекомендовать выбор параметра исходя из максимального размера кластера (считывается из гистограммы и делится на 2) или минимального расстояния между центрами кластеров, определяющего минимально возможные отличия смешивающих параметров. В этом случае радиус кластера находится по формуле:
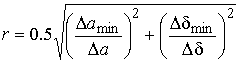 . (19)
. (19)
где Damin , Ddmin — минимальные отличия амплитуд и задержек сигналов в смеси, когда они еще могут быть разделены.
Например, если ожидается, что в смешиваемых сигналах амплитуды будут отличаться на 0.1 (при масштабе амплитудной оси гистограммы Da равным 0.01), а задержки — в 1 отсчет (при Dd=0.1), тогда радиус кластера составит r=7.
Достоинством алгоритма FOREL является возможность кластеризации параметров в условиях априорной неопределенности относительно количества кластеров и гарантированная сходимость [8]. Именно этот алгоритм используется автором и реализован в среде Mathcad (см. приложение).
Таким образом, алгоритм DUET можно составить из нескольких этапов. На первом этапе выполняется прямое оконное преобразование Фурье смесей от двух датчиков. На втором этапе находятся наборы смешивающих параметров по формуле (18) и применяется фильтрующая функция I(α,δ) для определения масштабов по осям гистограммы. На третьем этапе по ф. (17) формируется гистограмма, по которой определятся расположение ее максимумов. Координаты этих максимумов будут являться искомыми смешивающими параметрами (αj,δj) каждого j-источника. На четвертом этапе создается маска (ф. 15) и выделяется каждый источник по ф. (16) в спектральной области. На пятом этапе производится обратное оконное преобразование Фурье спектра каждого сигнала.
Алгоритм DUET представлен в среде Mathcad на рис. 8. Для разделения моделируется аддитивная смесь объемом выборки 32768 отсчетов из четырех узкополосных нормальных процессов с центральными частотами 256, 512, 1024, 2048 и одинаковой относительной полосой α=0.001 и смешивающими параметрами αj = (0.9; 0.6; 0.9; 0.3), δj = (7; 4; 5; 2). В связи со стационарностью и непрерывностью разделяемых процессов, оконное преобразование Фурье не используется.
Качество разделения контролировалось по отношению мощностей сигналов в каналах после их разделения (qi out), результаты отображены в таблице 1 при amax=1, Δa=0.01, δmax=10, Δδ=0.1.
Таблица 1.
|
Число разделяемых помех |
q1 out, дБ |
q2 out, дБ |
q3 out, дБ |
q4 out, дБ |
|
2 |
18.91 |
18.89 |
– |
– |
|
3 |
17.38 |
16.58 |
14.76 |
– |
|
4 |
17.42 |
15.82 |
16.5 |
14.77 |

Рис. 8. Программная реализация алгоритма DUET (NSTFT — размер окна, Nshift — величина сдвига окна).
Очевидно, что сходимость классического алгоритма DUET будет определяться сходимостью алгоритма кластеризации FOREL. Процедура алгоритма FOREL является сходящейся за конечное число шагов в евклидовом пространстве любой размерности при произвольном расположении точек и любом выборе радиуса [9]. При этом будем исходить из того, что радиус кластера выбирается таким образом, чтобы сходимость была обеспечена при формировании маски на обрабатываемой выборке. В этой связи время сходимости будет не больше длины обрабатываемой выборки, на которой происходит поиск маски.
Согласно рис. 2 при отношении мощностей двух узкополосных помех в каналах 0.5 дБ, время сходимости составит порядка 600000 отсчетов. Соответственно с использованием классического алгоритма DUET время сходимости градиентного алгоритма наименьших квадратов с учетом табличных значений (таблица 1) отношения мощности помех в каналах 18.9 дБ составит не более 800 отсчетов.
При этом выигрыш в скорости сходимости при использовании слепого разделения двух помех алгоритмом DUET и объеме выборки смесей 32768 отсчетов равен:
![]() (20)
(20)
Компьютерное моделирование работы многоканального адаптивного компенсатора помех со слепым разделением помех по алгоритму DUET
Был проведен эксперимент с аддитивной смесью из трех узкополосных помех и одной квазигармонической помехи с выделением полезного сигнала — М-последовательности с помощью многоканального адаптивного фильтра без предварительного слепого разделения помех в каналах. В каждом канале действует преобладающая (т.е. превосходящая по мощности остальные) помеха и другие помехи, равные по мощности. Отношение мощностей помех в каждом канале устанавливается одинаковым и задается по формуле:
 , (21)
, (21)
где ![]() — мощность преобладающей помехи
в i-канале;
— мощность преобладающей помехи
в i-канале; ![]() —
мощность не преобладающей k-помехи в i-канале; L — число
помех.
—
мощность не преобладающей k-помехи в i-канале; L — число
помех.
Другие параметры моделирования отображены в таблице 2, результаты моделирования — на рис. 9.
Таблица 2.
|
Параметр |
Значение |
|
Период М-последовательности |
25-1 |
|
Формирующий полином М-последовательности |
|
|
Центральная частота и ширина полоса первой узкополосной помехи |
300; 10-6 |
|
Центральная частота и ширина полоса второй узкополосной помехи |
500; 10-6 |
|
Центральная частота и ширина полоса третьей узкополосной помехи |
1000; 10-6 |
|
Центральная частота квазигармонической помехи |
100 |
|
Входное отношение сигнал-помеха, дБ |
–10.8 |
|
Число весовых коэффициентов адаптивного фильтра |
2 |
|
Коэффициент адаптации АКП |
0,0001 |
|
Алгоритм адаптации АКП |
МНК |
|
Общий объем выборки |
1114112 |
|
Объем выборки для оценки рош |
32768 |
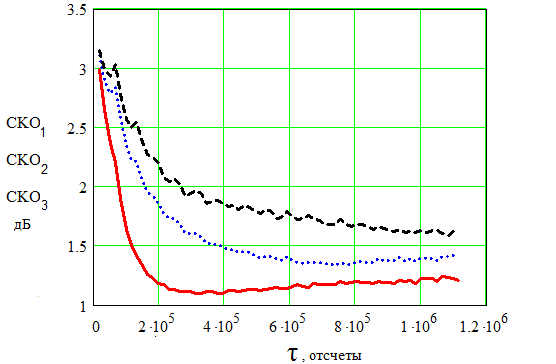
Рис. 9. Изменение нормированного[3] среднего квадрата выходного сигнала многоканального адаптивного компенсатора помех во времени без предварительного разделения помех при отношении мощностей помех в каналах 0 дБ (сплошная, СKO1), минус 3 дБ (точечная, СKO2), минус 4.77 дБ (пунктирная, СKO3).
Для четырех помех, действующих в опорном канале, критическим отношением в соответствии с ф. 21 является минус 4.77 дБ (на рис. 9 соответствует СКО3), так как в этом случае помехи имеют одинаковый уровень, а процесс адаптации — максимальное время сходимости. С увеличением отношения qi in время сходимости уменьшается (см. рис. 9).
Результаты моделирования (параметры в табл. 2) с предварительным разделением помех с помощью алгоритма DUET отображены в таблицах 3, 4 и на рис. 10. Качество выделения сигнала компенсатором контролировалось через значения вероятности ошибки приема отсчета полезного сигнала (pош) и выигрыша по отношению сигнал-помеха на выходе АКП (G).
Кроме того, на рис. 10 для сравнения построен нормированный средний квадрат выходного сигнала многоканального адаптивного компенсатора помех без разделения помех. Отношение qi in установлено минус 3 дБ.
Таблица 3.
|
Отношение мощностей квазигармонической помехи к остальным помехам в 1 канале после разделения q1 out, дБ |
16,7 |
|
Отношение мощностей 1 узкополосной помехи к остальным помехам во 2 канале после разделения q2 out, дБ |
19,3 |
|
Отношение мощностей 2 узкополосной помехи к остальным помехам в 3 канале после разделения q3 out, дБ |
12,8 |
|
Отношение мощностей 3 узкополосной помехи к остальным помехам в 3 канале после разделения q4 out, дБ |
18,0 |
Таблица 4.
|
qi in, дБ |
Без слепого разделения помех |
С разделением помех |
||
|
pош |
G, дБ |
pош |
G, дБ |
|
|
–3.0 |
0.05 |
15.5 |
0.02 |
22.1 |
|
–4.77 |
0.2 |
12.1 |
0.033 |
22.1 |
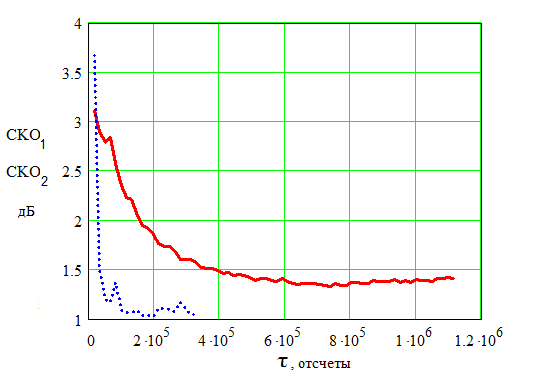
Рис. 10. Изменение нормированного среднего квадрата выходного сигнала многоканального адаптивного компенсатора помех во времени без предварительного разделения помех (сплошная, СKO1) и с предварительным разделением помех (точечная,CKO2) при отношении мощностей помех в каналах минус 3 дБ.
Оценивая результаты применения предварительного слепого разделения помех, можно сделать вывод, что выигрыш в скорости сходимость составляет не менее 8 раз. Кроме того, при фиксированной длине выборки и наихудшем для многоканального фильтра случае (когда уровень помех в каналах одинаков) вероятность ошибки может быть снижена в 6 раз. При этом, в опорном канале для приема 4 помех используется всего два приемных датчика, что упрощает аппаратную реализацию многоканального адаптивного компенсатора.
Выводы
1. Использование многоканального адаптивного компенсатора с предварительным слепым разделением помех в опорных каналах позволяет повысить скорость сходимости алгоритма адаптации наименьших средних квадратов при плохой обусловленности корреляционной матрицы помех.
2. Доказано, что при использовании алгоритма слепого разделения DUET можно увеличить скорость сходимости не менее чем в 8 раз, что превосходит модифицированный алгоритм Жуттена-Эро.
3. Продемонстрировано, что при выделении М-последовательности многоканальным адаптивным компенсатором со слепым разделением на фоне помех с отношением сигнал-помеха минус 10.8 дБ и заданным в эксперименте объемом выборки 1114112 отсчетов можно снизить вероятность ошибки в 6 раз по сравнению с многоканальным компенсатором Уидроу.
4. Преимущества алгоритма DUET перед алгоритмом Жуттена-Еро состоят в использовании всего двух каналов для приема смеси помех и учете их взаимных задержек.
Формула определения расстояния между точками гистограммы:
![]() (П.1)
(П.1)
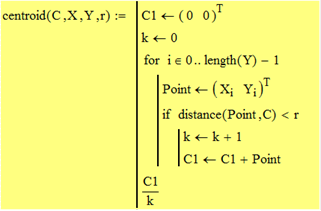
Рис. П.1. Алгоритм поиска центра тяжести кластера с центром С и радиусом не более r.

Рис. П.2. Алгоритм удаления кластера с центром С и радиусом не более r.

Рис. П.3. Алгоритм формирования массивов X и Y координат элементов гистограммы (max(H) — максимальное значение гистограммы).

Рис. П.4. Алгоритм FOREL.
Литература
1. Манохин А.Е. Многоканальный адаптивный компенсатор со слепым разделением помех в опорных каналах // Журнал радиоэлектроники [Электронный ресурс]. – 2014.- №11(12) – Режим доступа: http://jre.cplire.ru/jre/ oct14/4/text.pdf.
2. Gavelin R., Klomp H., Priddle C., Uddenfeldt M. Blind Source Separation Report for Adaptive Signal Processing Project //Department of Engineering Sciences, Uppsala University, Sweden, June, 2004.
3. Джиган В.И. Адаптивная фильтрация: теория и алгоритмы. – Москва : Техносфера, 2013. – 528 с.
4. Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. — Наука, 2003. — 832 с.
5. Rickard S., Makino S., Lee, T.-W., Sawada, H. The DUET Blind Source Separation Algorithm. In: Blind Speech Separation. Springer-Verlag, pp. 217-237, 2007.
6. Yilmaz O., Rickard S. Blind Separation of Speech Mixtures via Time-Frequency Masking November 2002: IEEE Transactions on Signal Processing.
7. Jourjine A., Rickard S., and O. Yilmaz. Blind Separation of Disjoint Orthogonal Signals: Demixing N Sources from 2 Mixtures. In Proc. ICASSP2000, June 5–9, 2000, Istanbul, Turkey, June 2000.
8. Лепский А.Е., Броневич А.Г. Математические методы распознавания образов: Курс лекций. – Таганрог: Изд-во ТТИ ЮФУ, 2009. – 155 с.
9. Алгоритмы Форель и Форель 2. [Электронный ресурс]. – Режим доступа: www.aiportal.ru/articles/autoclassification/forel.html.