"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ"  N 9, 2001

оглавление

дискуссия

 

алгоритмы адаптации параметров фильтрационных оценок сигналов на основе процедур стохастической аппроксимации с ограничением траектории

 

 

Получена 10 октября 2001 г.

 

Рассматривается задача параметрической адаптации фильтрационных оценок случайных процессов методом стохастической аппроксимации в скалярном варианте, когда эти оценки определены с точностью до одного параметра. Приводятся модификации процедуры Роббинса-Монро для случая, когда известен некоторый конечный интервал, внутри которого лежит оптимальное значение этого параметра. В предложенных вариантах осуществляется ограничение траектории, определяемой традиционной процедурой, что позволяет ослабить условия сходимости. Дается доказательство сходимости. Приведен иллюстративный пример.

 

введение

 

Методы стохастической аппроксимации [1] нашли свое применение для решения задач радиотехники и радиоэлектроники, связанных с адаптацией алгоритмов оптимального оценивания случайных процессов, обучением фильтров и т. п. [2 - 7]. В последнее время наблюдается возобновление интереса к этому направлению исследований.

В этих задачах неточное знание моделей оцениваемых процессов приводит к неопределенности алгоритмов оценивания, характер которой практически всегда сводится к параметрическому типу. Вследствие неопределенности относительно значений параметров алгоритмов фильтрации синтезируемые на их основе оценки можно считать также зависящими, в общем случае, от вектора параметров.

К одним из наиболее известных методов стохастической аппроксимации относится метод Роббинса-Монро [8] отыскания корней уравнений регрессии, в виде которых в отмеченных задачах часто записываются условия оптимальности параметров фильтрационных оценок. Являясь относительно простым и в то же время достаточно эффективным аппаратом решения широкого класса задач оптимизации в условиях априорной неопределенности [9, 10], процедуры Роббинса-Монро имеют ограниченную область применения, прежде всего, из-за необходимости соблюдения известных требований сходимости [11]. При этом на практике имеют место случаи, когда априорная информация о справедливости некоторых из них отсутствует. Неучет условий сходимости при синтезе алгоритмов адаптивного оценивания может привести к неработоспособности последних.

Отсюда возникает задача разработки алгоритмов стохастической аппроксимации, сходящихся при более слабых условиях и позволяющих при априорной неопределенности относительно выполнимости некоторых из традиционных требований сходимости гарантированно получать корни соответствующих уравнений регрессии.

Возможность синтеза таких алгоритмов исходит из особенностей условий практического применения стохастической аппроксимации. Например, допустимые значения параметров на практике всегда можно считать содержащимися внутри конечных интервалов.

В настоящей работе предлагаются возможные варианты решения сформулированной задачи при условии, что известен некоторый конечный интервал, внутри которого находится подлежащий определению корень.

 

 

постановка задачи

 

Рассмотрим для простоты скалярный вариант задачи.

Пусть некоторая оценка полезного сигнала, являющегося одномерным случайным процессом, в силу неопределенности его априорной модели зависит от параметра  и является оптимальной в соответствии с выбранным критерием при .

Неизвестное оптимальное значение  параметра , доставляя экстремум некоторому показателю качества

 

 (1)    ,

 

где  - доступная измерению функция потерь оценивания, явный вид которой не может быть определен,

 - стационарный случайный процесс,

является единственным корнем уравнения регрессии:

(2)     ,

в котором .

Так как аналитическое решение уравнения (2) невозможно, для определения его корня могут быть использованы вычислительные процедуры на основе стохастической аппроксимации:

(3)      ,

где k – номер итерации;

 - соответствующее ему вычисленное значение параметра ;

            - последовательность положительных действительных чисел, удовлетворяющая известным условиям [11];

 - случайная величина, условное распределение которой при данных  совпадает с распределением случайной величины .

Применимость данного метода определяют условия сходимости процедуры Роббинса-Монро (3). Практика показывает, что необходимость удовлетворения требования [11]:

(4)        для всех  и некоторых

нередко становится фактором, значительно ограничивающим область успешного применения метода.

Отсюда возникает задача построения процедур стохастической аппроксимации, сходящихся при более слабых, чем (4), ограничениях.

Рассмотрим возможные варианты ее решения, полагая, что известен некоторый конечный интервал, внутри которого лежит искомое оптимальное значение  параметра .

 

процедуры стохастической аппроксимации с ограничением траектории

 

Сущность предлагаемого метода решения задачи сформулирована в виде следующей теоремы.

Теорема. Пусть выполнены условия:

1)       - действительная случайная величина, зависящая от параметра , такая, что ее математическое ожидание  и дисперсия  - действительные измеримые функции действительного аргумента ;

2)      , < ;

3)      >0 при >, <0 при <,

 

;

4)       (5)      ;

5)       - функция ограничения траектории такая, что:

       (6)      =

6)  - последовательность положительных действительных чисел такая,     что:

     , ;

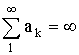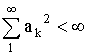7)  - случайная последовательность действительных чисел, определяемая рекуррентным соотношением:

 

       (7)      ,

 

где  - произвольное действительное число.

Тогда .

 

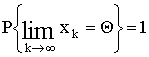Доказательство. Сопоставив (7) с процедурой Роббинса-Монро (3) отыскания корня уравнения регрессии (2), заметим, что (7) есть процедура поиска корня уравнения

,

который, очевидно, равен , если удовлетворено условие 4) теоремы.

Из условий 1) и 5) теоремы следует, что величина  ограничена для всех .

Значит, 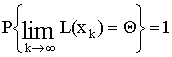 [11]. Отсюда в силу (5), (6) получим, что  с вероятностью 1. Теорема доказана.

Следствие. В условиях 1) - 6) доказанной теоремы с вероятностью 1 к  сходится случайная последовательность действительных чисел , определяемая рекуррентным соотношением:

 

(8)       .

Доказательство. Действительно, (8) можно представить в виде системы:

 

 

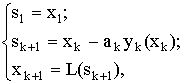
 Подставив (10) в (9), получим процедуру:

 

,

сходимость которой уже доказана.

Замечание. Из ограниченности величины  непосредственно следует сходимость к  последовательности случайных чисел , определяемой рекуррентным соотношением:

 

(11)        .

При этом выбор значений величин  и  в (6) не должен противоречить условию:

 

>0 при >, <0 при <,

где . Это условие выполняется, например, при , .

Таким образом, при соблюдении сформулированных условий и отсутствии априорной информации о справедливости ограничения роста (4) процедуры (7), (8), (11) сходятся с вероятностью 1 к корню  уравнения регрессии (2), тогда как для сходимости традиционной процедуры Роббинса-Монро условие (4) является необходимым.

 

пример

 

Пусть оптимальное значение  параметра  доставляет минимум показателю качества:

(12)     ,

где  - стационарный случайный процесс, условное одномерное распределение которого при данном  нормально с параметрами , .

Проиллюстрируем алгоритмические способы определения  на основе процедур стохастической аппроксимации, задав , где  - коэффициенты.

Единственный корень уравнения регрессии

 

,

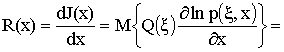
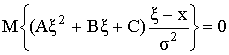где  - плотность вероятности случайной величины , легко определятся аналитически: .

Нетрудно убедиться в том, что функции  и

 

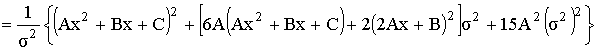
 удовлетворяют условиям доказанной теоремы и не удовлетворяют ограничению роста (4).

Следовательно, утверждать о сходимости с вероятностью 1 процедуры Роббинса-Монро:

 

(13)     

в данном случае нельзя:

Этот вывод подтверждается результатами моделирования алгоритма (13) в среде MathCAD при исходных данных: , , , , , , представленными таблицей, из которых видно, что приведенная реализация процесса (13) расходится.

 

Таблица - Результаты моделирования

реализации процедуры (13)

 

 

 

Запишем в соответствии с (7), (8), (11) процедуры поиска с ограничением траектории:

 

(14)      ,

(15)      ,

(16)      ,

где  - случайная величина, условное распределение которой при данном  нормально с параметрами . При этом для соблюдения условия 4) теоремы выберем согласно (6) функцию , например, следующего вида:

  

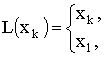
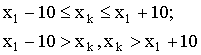
для алгоритма (14),

  

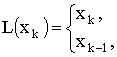
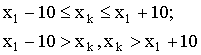
для алгоритма (15) и

=

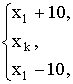
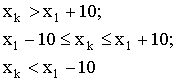
для алгоритма (16). Так как  заведомо должно принадлежать интервалу , где , , зададим .

Результаты моделирования представлены рисунками 1 - 9.

На рисунках 1, 2, 3 изображены типичные траектории процессов (14), (15), (16) соответственно, асимптотически сходящиеся к .

Усредненные по 1000 реализаций процессов (14), (15), (16) траектории показаны на рисунках 4, 5, 6 соответственно.

Графики выборочных дисперсий приведены на рисунках 7, 8, 9.

 

 

 

 

 

Итак, приведенный пример наглядно проиллюстрировал эффект сходимости процедур стохастической аппроксимации с ограничением траектории в условиях, когда получение аналогичного результата с вероятностью 1 алгоритмом Роббинса-Монро невозможно.

 

заключение

 

Таким образом, синтезированы процедуры стохастической аппроксимации, сходящиеся с вероятностью 1 в условиях неопределенности относительно справедливости ограничения (4). Предлагаемые алгоритмы применимы в том случае, когда известен конечный интервал, содержащий искомый оптимум показателя качества (1).

На частном примере показано, что процедура Роббинса-Монро не может быть использована в адаптивных задачах с квадратичным критерием оптимальности вида (12) ввиду ее расходимости для этого случая. Алгоритмы с ограничением траектории сходятся к оптимальному значению  с вероятностью 1.

По-видимому, скорости сходимости процессов (7), (8), (11) будут различными, а приведенную теорему можно обобщить на многомерный случай. Исследованию этих вопросов будут посвящены последующие работы.

 

литература

 

1.      Логинов Н. В. // Автоматика и телемеханика. 1966. № 4. С. 185.

2.      Семушин И. В. // Изв. вузов. Приборостроение. 1969. № 10. С.

3.      Понырко С. А., Семушин И. В. // Изв. АН СССР. Техническая кибернетика. 1971. № 1. С.

4.      Понырко С. А., Семушин И. В. // Изв. АН СССР. Техническая кибернетика. 1971. № 5. С.

5.      Семушин И. В. // Изв. АН СССР. Техническая кибернетика. 1975. № 5. С. 192.

6.      Сосулин Ю. Г., Паршин Ю. Н. // Радиотехника и электроника. 1986. № 5. С. 904.

7.      Сосулин Ю. Г., Паршин Ю. Н., Гусев С. И. // Радиотехника. 1999. № 10. С. 67.

8.      Robbins H., Monro S. // Ann. math. statist. 1951. T. 22. P. 400.

9.      Цыпкин Я. З. // Автоматика и телемеханика. 1976. № 4. С. 78.

10.  Цыпкин Я. З. // Автоматика и телемеханика. 1979. № 6. С. 94.

11.  Гладышев Е.Г. // Теория вероятностей и ее применения. 1965. Т. 10. № 2. С. 297.

---

Авторы:

Расщепляев Юрий Семенович - доктор технических наук, профессор кафедры антенных устройств и теоретических основ радиоэлектронных систем Ростовского военного института ракетных войск, email: chernat@don.sitek.net

Пирогов Сергей Петрович – адъюнкт, Ростовский военный институт ракетных войск, email: chernat@don.sitek.net

 

оглавление

дискуссия