| "ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 9, 2001 |  |
УСЛОВИЯ ПРИМЕНЕНИЯ МАТРИЧНЫХ ИГР ДЛЯ ОПТИМИЗАЦИИ УПРАВЛЕНИЯ МНОГОПОЗИЦИОННОЙ РЛС
Ростовский военный институт ракетных войск
Получена 23 октября 2001 г.
В статье рассмотрены необходимые и достаточные условия применения смешанного расширения матричных игр "неклассического" типа для решения задачи поиска оптимального управления многопозиционной РЛС в условиях конфликта, в которой разыгрывание ситуаций предполагается ограниченное количество раз.
Введение. Многообразие действующих факторов,
сложность поиска оптимального управления многопозиционными РЛС (МПРЛС) в
условиях конфликта делают актуальной разработку новых моделей принятия решений.
В [1] рассмотрено применение аппарата смешанного расширения матричных игр
"неклассического" типа (игры
![]() ) для решения задачи оптимизации управления
МПРЛС в условиях ограниченного числа реализаций игровой ситуации с матрицей
игры не содержащей седловых точек. В этих условиях классические модели
матричных игр не адекватны сложившейся проблемной ситуации, а применение игры
) для решения задачи оптимизации управления
МПРЛС в условиях ограниченного числа реализаций игровой ситуации с матрицей
игры не содержащей седловых точек. В этих условиях классические модели
матричных игр не адекватны сложившейся проблемной ситуации, а применение игры
![]() позволяет выполнить
оптимизацию управления МПРЛС на основе гибкого учёта в моделях предпочтения
игроков фактора числа реально проводимых разыгрываний.
позволяет выполнить
оптимизацию управления МПРЛС на основе гибкого учёта в моделях предпочтения
игроков фактора числа реально проводимых разыгрываний.
Однако открытым остаётся вопрос о понятии малости
числа реализаций, при котором следует отказаться от применения модели
классического смешанного расширения матричной игры (игры
![]() ) и следует применять модель игры
) и следует применять модель игры
![]() (поскольку
игра
(поскольку
игра
![]() в
некотором смысле обобщает классические модели матричных игр и при
в
некотором смысле обобщает классические модели матричных игр и при
![]() игры
игры
![]() и
и
![]() эквивалентны [2], то далее,
говоря об условиях применения игры
эквивалентны [2], то далее,
говоря об условиях применения игры
![]() , будем иметь в виду условия применения
этой модели игры при
, будем иметь в виду условия применения
этой модели игры при
![]() ).
).
Таким образом, вывод условий применения модели
смешанного расширения матричных игр "неклассического" типа
![]() , является актуальной
задачей.
, является актуальной
задачей.
1. Постановка задачи. Рассматривается система
вооружения, включающая в качестве информационной подсистемы МПРЛС. Для этой
системы задана математическая модель, позволяющая для некоторого управления
МПРЛС (первого игрока)
![]() ,
,
![]() , где
, где
![]() - множество возможных вариантов управления
МПРЛС, и некоторого варианта действий противника (второго игрока)
- множество возможных вариантов управления
МПРЛС, и некоторого варианта действий противника (второго игрока)
![]() ,
,
![]() , где
, где
![]() - множество возможных вариантов
действий противника, определить значение показателя эффективности МПРЛС
- множество возможных вариантов
действий противника, определить значение показателя эффективности МПРЛС
![]() . Порядок получения
. Порядок получения
![]() рассмотрен, например, в [1]. Таким образом, задана матрица игры А с элементами
рассмотрен, например, в [1]. Таким образом, задана матрица игры А с элементами
![]() ,
,
![]() ,
,
![]() . Первый игрок имеет n чистых стратегий, а
второй - m.
Определены множества
. Первый игрок имеет n чистых стратегий, а
второй - m.
Определены множества
![]() и
и
![]() , являющиеся
множествами смешанных стратегий
, являющиеся
множествами смешанных стратегий
![]() ,
,
![]() в исходной матричной игре, соответственно,
для первого и второго игроков. При этом
в исходной матричной игре, соответственно,
для первого и второго игроков. При этом
![]() ,
,
![]() и
и
![]() ,
,
![]() таковы, что
таковы, что
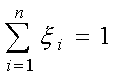 ,
,
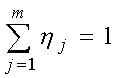 .
.
Положим, что матрица игры А не имеет седловых точек, а игровая ситуация будет реализована К раз.
Требуется на основе анализа матрицы игры А и значения К определить условия
применения модели смешанного расширения матричных игр
"неклассического" типа
![]() .
.
2. Условия применения модели смешанного расширения
матричной игры "неклассического" типа
![]() . Для вывода необходимых
условий применения игры
. Для вывода необходимых
условий применения игры
![]() требуется найти для заданной
матрицы игры такой интервал значений числа реализаций игровой ситуации (K), при котором
по некоторому критерию применение классического смешанного расширения матричной
игры обоими игроками было бы неприемлемо.
требуется найти для заданной
матрицы игры такой интервал значений числа реализаций игровой ситуации (K), при котором
по некоторому критерию применение классического смешанного расширения матричной
игры обоими игроками было бы неприемлемо.
Обозначим через
средний выигрыш первого игрока после К реализаций игровой ситуации, в которых стороны
придерживались оптимальных смешанных стратегий
![]() ,
,
![]() для игры
для игры
![]() , где
, где
![]() - частоты применения соответствующими
игроками своих чистых стратегий после К реализаций игровой ситуации.
- частоты применения соответствующими
игроками своих чистых стратегий после К реализаций игровой ситуации.
Дополним модели предпочтения игроков вероятностными критериями
отказа их от модели игры
![]() и переходу к модели игры
и переходу к модели игры
![]() :
:
- для первого игрока
- для второго игрока
где
![]() ,
,![]() - нижнее и верхнее
значение игры, соответственно,
- нижнее и верхнее
значение игры, соответственно,
![]() ,
,![]() - пороги
чувствительности игроков к получению ими результатов хуже гарантированных.
- пороги
чувствительности игроков к получению ими результатов хуже гарантированных.
Рассмотрим случай, когда значение К таково, что случайную величину
![]() можно считать
распределённой по нормальному закону.
можно считать
распределённой по нормальному закону.
Тогда
где
![]() ,
,
![]() - пороговые значения
числа реализаций для первого и второго игрока, соответственно,
- пороговые значения
числа реализаций для первого и второго игрока, соответственно,
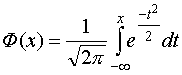 ,
,
При этом несложно получить зависимость значений
![]() ,
,
![]() от
от
![]() ,
,
![]() , соответственно:
, соответственно:
где значения
![]() ,
,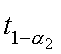 определяются как
решения уравнений
определяются как
решения уравнений
![]() ,
,
![]() .
.
Следовательно, принятие тем или иным игроком модели игры
![]() зависит от
соответствующего значения
зависит от
соответствующего значения
![]() или
или
![]() , а также от матрицы игры, и в общем случае
может быть не обоюдным. Отметим, что для равенства
, а также от матрицы игры, и в общем случае
может быть не обоюдным. Отметим, что для равенства
![]() и
и
![]() даже при
даже при
![]() необходимо выполнения условия
необходимо выполнения условия
![]() .
.
Таким образом, если при заданных
![]() ,
,
![]() ,
,
![]() для матрицы игры А выполняются неравенства
для матрицы игры А выполняются неравенства
то игрокам в соответствии с критериями (2) и (3) следует применять модель
игры
![]() .
.
Если выполняются неравенства
то игрокам в соответствии с критериями (2) и (3) следует применять модель
игры
![]() (со
значением параметра
(со
значением параметра
![]() ).
).
Если неравенства (12), (13) не выполняются, то позиции
игроков становятся не антагонистическими и модель игры
![]() не применима.
не применима.
В случае, когда величина
![]() мала настолько, что закон распределения величины
мала настолько, что закон распределения величины
![]() не является
нормальным, значения вероятностей
не является
нормальным, значения вероятностей
![]() и
и
![]() могут быть найдены путём имитационного
моделирования выбора чистых стратегий игроков в соответствии с
могут быть найдены путём имитационного
моделирования выбора чистых стратегий игроков в соответствии с
![]() ,
,
![]() и подсчёта частот наступления
событий
и подсчёта частот наступления
событий
![]() и
и
![]() .
.
Кроме того, при малых n, m и K возможен непосредственный подсчёт этих
вероятностей с учётом того, что
![]() определяется по выражению (1), где
определяется по выражению (1), где
![]() ,
,
![]() ,
,
Обозначим через
![]() ,
,
![]() множества допустимых наборов частот
множества допустимых наборов частот
![]() ,
,
![]() , удовлетворяющих условиям
, удовлетворяющих условиям
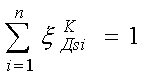 ,
,
![]() ,
,
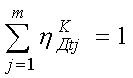 ,
,
![]() .
.
Тогда возможные значения
![]() и их вероятности можно определить по
выражениям
и их вероятности можно определить по
выражениям
Следовательно,
Для определения
![]() и
и
![]() можно воспользоваться приближением распределения
можно воспользоваться приближением распределения
![]() по двойному
нормальному распределению (ДНР), которое было разработано В.П. Котельниковым в [3]-[5]. Это распределение является четырёхпараметрическим
(задаётся математическое ожидание, дисперсия и два параметра формы
по двойному
нормальному распределению (ДНР), которое было разработано В.П. Котельниковым в [3]-[5]. Это распределение является четырёхпараметрическим
(задаётся математическое ожидание, дисперсия и два параметра формы
![]() и
и
![]() ) и имеет большое число форм.
Отличительной особенностью ДНР является учёт при определении
) и имеет большое число форм.
Отличительной особенностью ДНР является учёт при определении
![]() и
и
![]() границ интервала возможных
значений случайной величины, что соответствует условиям решаемой задачи,
поскольку эти границы могут быть определены по выражениям
границ интервала возможных
значений случайной величины, что соответствует условиям решаемой задачи,
поскольку эти границы могут быть определены по выражениям
Кроме того, это распределение при
![]() и
и
![]() стремиться к нормальному.
стремиться к нормальному.
Следовательно, согласно [3]-[5]
где функция распределения вероятностей
В (25)
![]() -
функция, обратная к функции
-
функция, обратная к функции
где
![]() - обратная
функция стандартного нормального распределения.
- обратная
функция стандартного нормального распределения.
Практические расчёты с использованием приближений распределения
вероятностей
![]() по
нормальному и двойному нормальному распределениям показали, что при расчёте
по
нормальному и двойному нормальному распределениям показали, что при расчёте
![]() и
и
![]() они дают завышенные значения,
поскольку не в полной мере учитывают структуру решаемой задачи и не учитывают
большую зависимость этих значений от K.
они дают завышенные значения,
поскольку не в полной мере учитывают структуру решаемой задачи и не учитывают
большую зависимость этих значений от K.
Изменив в ДНР выражение для параметра формы (27) на
![]() :
:
получим пятипараметрическое модифицированное ДНР. При
![]() оно соответствует ДНР,
а при
оно соответствует ДНР,
а при
![]() обеспечивает
с ростом K
большее уменьшение значений
обеспечивает
с ростом K
большее уменьшение значений
![]() и
и
![]() .
.
Таким образом, полученные неравенства (13) представляют
необходимые условия применения модели игры
![]() . В (13)
. В (13)
![]() и
и
![]() определяются по выражениям (10), (11) или
как решение уравнений
определяются по выражениям (10), (11) или
как решение уравнений
где
![]() и
и
![]() определяются
в зависимости от условий задачи путём имитационного моделирования или
непосредственным подсчётом по выражениям (14)-(21), или с использованием (22)-(29).
определяются
в зависимости от условий задачи путём имитационного моделирования или
непосредственным подсчётом по выражениям (14)-(21), или с использованием (22)-(29).
Достаточные условия применения игры
![]() могут быть получены на основе
определения допустимых областей изменения b
и
могут быть получены на основе
определения допустимых областей изменения b
и
![]() для
заданных уровней
для
заданных уровней
![]() ,
,
![]() .
.
Для этого необходимо разработать процедуру определения верхних
граничных значений
![]() для
заданных уровней
для
заданных уровней
![]() ,
,
![]() или нижних
граничных значений
или нижних
граничных значений
![]() для
этих уровней.
для
этих уровней.
Воспользуемся соотношениями (2) - (9) и методикой решения игр
![]() , основанной на
построении и решении двойственных задач линейного программирования [2], и
получим процедуру построения
, основанной на
построении и решении двойственных задач линейного программирования [2], и
получим процедуру построения
![]() :
:
где
![]() ,
,
![]() ,
,![]() ,
,
![]() - решения следующих задач линейного
программирования.
- решения следующих задач линейного
программирования.
Найти
при ограничениях
Найти
при ограничениях
где
![]() ,
,
![]() ,
,
![]() ,
,
![]() и
и
![]() - векторы, соответствующей размерности,
каждая компонента которых равна единице,
- векторы, соответствующей размерности,
каждая компонента которых равна единице,
![]() - вектор-столбец с компонентами
- вектор-столбец с компонентами
![]() .
.
Для
малых значений К,
при которых закон распределения величины
![]() не является нормальным, значения
не является нормальным, значения
![]() определяются как
решения уравнений (30) и (31), где
определяются как
решения уравнений (30) и (31), где
![]() и
и
![]() могут быть найдены различными способами,
как и при выводе необходимых условий.
могут быть найдены различными способами,
как и при выводе необходимых условий.
Таким
образом, задаваясь различными значениями параметра
![]() , получим нижнюю границу области
применения игры
, получим нижнюю границу области
применения игры
![]() по
числу реализаций игровой ситуации для заданной матрицы игры и значений порогов
чувствительности игроков
по
числу реализаций игровой ситуации для заданной матрицы игры и значений порогов
чувствительности игроков
![]() и
и
![]() . Отметим, что
. Отметим, что
![]() , причём при
, причём при
![]() игра
игра
![]() эквивалента матричной игре в
чистых стратегиях [1].
эквивалента матричной игре в
чистых стратегиях [1].
3. Пример определения условий применения игры
![]() для оптимизации
управления МПРЛС. В [6] рассмотрена система вооружения, которая включает
МПРЛС воздушного базирования для обнаружения групповых наземных целей и систему
высокоточного оружия. Для этой системы в [1] построена методика применения
аппарата смешанного расширения матричной игры "неклассического" типа,
в качестве примера для
для оптимизации
управления МПРЛС. В [6] рассмотрена система вооружения, которая включает
МПРЛС воздушного базирования для обнаружения групповых наземных целей и систему
высокоточного оружия. Для этой системы в [1] построена методика применения
аппарата смешанного расширения матричной игры "неклассического" типа,
в качестве примера для
![]() построена матрица игры
построена матрица игры
и получены
решения задачи для различных значений параметра
![]() .
.
Пусть
требуется определить условия применения модели
![]() для матрицы игры (43) при
для матрицы игры (43) при
![]() и
и
![]() . Результаты решения приведены в
табл. 1. При этом
. Результаты решения приведены в
табл. 1. При этом
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Из
анализа табл.1 следует, что в условиях примера игра
![]() при
при
![]() и
и
![]() может применяться при числе реализаций от
9 и более. При таком значении K применение нормального распределения и ДНР даёт
завышенные значения
может применяться при числе реализаций от
9 и более. При таком значении K применение нормального распределения и ДНР даёт
завышенные значения
![]() и
и
![]() . Это, в свою
очередь, в значительной мере необоснованно увеличивает граничное значение
. Это, в свою
очередь, в значительной мере необоснованно увеличивает граничное значение
![]() , определяемое для
применения игры
, определяемое для
применения игры
![]() .
С другой стороны модифицированное ДНР с параметром формы
.
С другой стороны модифицированное ДНР с параметром формы
![]() достаточно точно позволяет
определить минимальное число реализаций игры, при котором модель игры
достаточно точно позволяет
определить минимальное число реализаций игры, при котором модель игры
![]() удовлетворяет
требованиям. При применении этого распределения граничное значение
удовлетворяет
требованиям. При применении этого распределения граничное значение
![]() составляет 10
реализаций.
составляет 10
реализаций.
Таким образом, если число реализаций игровой ситуации с матрицей игры
(43) более 8, то игра
![]() при
при
![]() и
и
![]() применима. Если же K менее 9, то следует применять модель игры
применима. Если же K менее 9, то следует применять модель игры
![]() с
с
![]() или понизить требования,
определяемые значениями
или понизить требования,
определяемые значениями
![]() .
.
Таблица 1. Результаты решения игры
|
Показатель вероятностной гарантии |
Число реализаций игровой ситуации К |
|||||
|
1 |
5 |
8 |
9 |
10 |
20 |
|
|
Имитационное моделирование с числом итераций 1 000 000 |
||||||
|
|
0,483791 |
0,011237 |
0,000514 |
0,000247 |
0,000080 |
0,000000 |
|
|
0,516209 |
0,015970 |
0,001458 |
0,000523 |
0,000268 |
0,000000 |
|
Нормальное распределение |
||||||
|
|
0,244303 |
0,060746 |
0,025070 |
0,018874 |
0,014263 |
0,000977 |
|
|
0,268400 |
0,083620 |
0,040318 |
0,031943 |
0,025397 |
0,002870 |
|
Двойное нормальное распределение |
||||||
|
|
0,299781 |
0,059912 |
0,022189 |
0,016143 |
0,011795 |
0,000585 |
|
|
0,308667 |
0,08801 |
0,041649 |
0,032729 |
0,025818 |
0,002717 |
|
Модифицированное
двойное нормальное распределение с
|
||||||
|
|
0,299781 |
0,013713 |
0,000941 |
0,000359 |
0,000132 |
0,000000 |
|
|
0,308667 |
0,028930 |
0,003875 |
0,001888 |
0,000898 |
0,000000 |
Заключение. В статье рассмотрены пути формирования условий применения аппарата смешанного расширения матричных игр "неклассического" типа для решения задачи оптимизации управления МПРЛС. Показано, что для получения этих условий с низкими вычислительными затратами и приемлемой точностью можно воспользоваться модифицированным двойным нормальным распределением.
СПИСОК ЛИТЕРАТУРЫ
-
Строцев А.А. Оптимизация управления многопозиционной РЛС на основе применения аппарата смешанного расширения матричных игр "неклассического" типа. - Интернет-публикация, М.: Журнал радиоэлектроники , № 9, 2001.
-
Строцев А.А. Построение смешанного расширения матричной игры "неклассического" типа / Изв.АН. Теория и системы управления, 1998, №3.
-
Котельников В.П. Предельное распределение суммы неоднородных и коррелированных индикаторов. - В сб.: Вторая Всероссийская школа-коллоквиум по стохастическим методам. Тезисы докладов.: М.: ТВП, 1995.
-
Котельников В.П. Предельное распределение суммы коррелированных случайных величин. - В сб.: Третья Всероссийская школа-коллоквиум по стохастическим методам. Тезисы докладов.: М.: ТВП, 1996.
-
Котельников В.П. О распределениях степенной функции с коррелированными аргументами. - Обозрение прикладной и промышленной математики, серия вероятн. и статист., 2001, т. 8, в. 1.
-
Керков В.Г. Скабаров М.М. Методика комплексной оценки эффективности радиолокационной системой в условиях конфликтного противодействия. - Интернет-публикация, М.: Журнал радиоэлектроники , №12, 2000.
Автор:
Строцев Андрей Анатольевич, к.т.н., доцент Ростовского военного института ракетных войск, email: apl@aaanet.ru
 |
 |
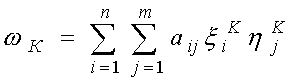 (1)
(1)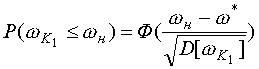 ,
(4)
,
(4)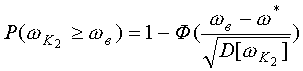 ,
(5)
,
(5)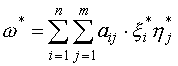 ,
, 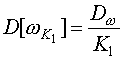 ,
, 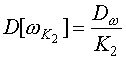 ,
, 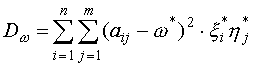 .
. 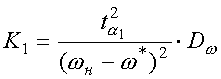 ,
(10)
,
(10)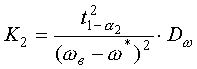 ,
(11)
,
(11)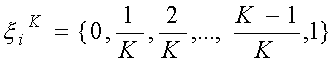 ,
,
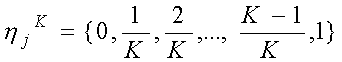 ,
,
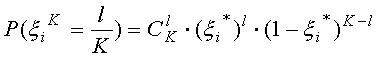 ,
,
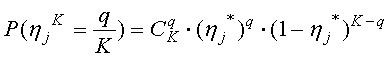 ,
,
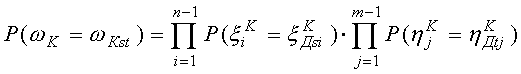 .
(19)
.
(19)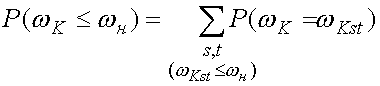 ,
(20)
,
(20)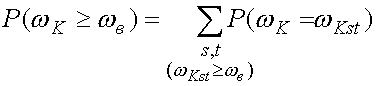 .
(21)
.
(21)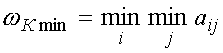 ,
,
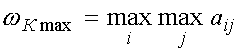 . (22)
. (22)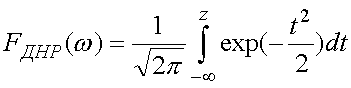 .
(25)
.
(25)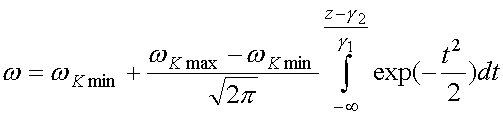 ,
(26)
,
(26)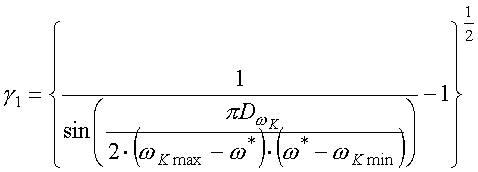 ,
(27)
,
(27)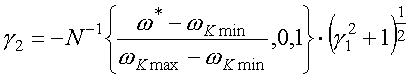 ,
(28)
,
(28)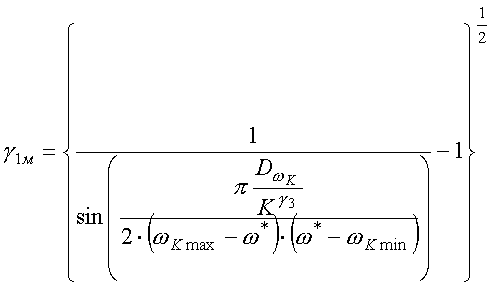 ,
(29)
,
(29)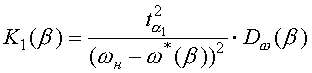 ,
(33)
,
(33)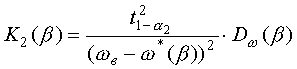 ,
(34)
,
(34)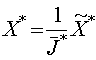 ,
,
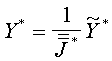 ,
(38)
,
(38)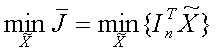 (39)
(39)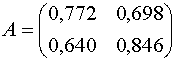 (43)
(43)