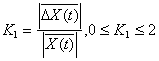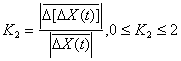|
|
"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 4, 2006 |
|
УДК 621.396
КОЛИЧЕСТВЕННАЯ ОЦЕНКА СВОЙСТВ "РЕГУЛЯРНОСТИ-ХАОТИЧНОСТИ" СИГНАЛОВ
Ю.Н. Кликушин
Омский государственный технический университет
Получена 26 октября 2006 г.
Предлагается новый подход к формированию количественных оценок таких свойств сигналов, которые характеризуются понятиями "регулярность" и "хаотичность". Данный поход основан на теории и технологиях идентификационных шкал и использует идею измерения частотного распределения отсчетов выборочной реализации сигнала.
ВВЕДЕНИЕ
При разработке интеллектуальных средств измерения, контроля и диагностики возникает необходимость в автоматическом разделении исходной группы сигналов на некоторое количество классов, объединяющих, попавшие в них реализации, по определенному качественному признаку. Для примера можно привести задачу кардиологического обследования пациентов, при котором требуется классифицировать кардиограммы по 4-5 диагностическим признакам, описывающим различные состояния человека из диапазона понятий "здоровый - больной". Подобная ситуация имеет место и в задачах оптимальной фильтрации, когда структура и параметры интеллектуального фильтра должны автоматически подстраиваться к виду входного "зашумленного" сигнала.
Одним из вариантов решения указанных задач может служить применение некоего инструмента, позволяющего количественно оценивать текущее состояние анализируемого объекта или процесса, но так, чтобы упорядочение этих оценок приводило бы к соответствующему упорядочению исследуемого свойства. В таком случае можно было бы говорить об измерении качественной характеристики объекта или процесса. При этом под измерением понимается отображение множества, например, временного ряда наблюдений, в число.
Подобные числа, названные "идентификационными параметрами" (IdP), были предложены в работах [1-3]. Результаты исследования свойств и методика связывания значений IdP с такими качественными характеристиками, как форма случайных и периодических сигналов, изложены в монографии [4]. Инструменты, осуществляющие цепочку преобразований вида "сигнал – число (IdP) – имя (качественная характеристика) сигнала", называются "идентификационными шкалами" (ИШ). Такой подход позволил применить методологию теории измерений к задачам распознавания образов и, таким образом, сделать "метризуемыми" некоторые качественные понятия.
В данной работе предлагается такой количественный показатель, который позволяет измерять те свойства выборочных реализаций сигнала, которые характеризуются понятиями "регулярный – хаотический" сигнал.
ТЕОРЕТИЧЕСКИЕ МОДЕЛИ И ХАРАКТЕРИСТИКИ ИДЕНТИФИКАЦИОННЫХ ИНСТРУМЕНТОВ
Идея возникновения этого показателя (назовем его коэффициентом вариабельности, K) связана с моделью роста популяции. В исследованиях, связанных с нелинейной динамикой, процесс Ферхюльста, описывающий рост популяции во времени [5], занимает важное место по ряду причин.
Во-первых, этот процесс является хорошим примером для изучения явления, называемого детерминированным хаосом, который порождает фрактальные структуры, присущие многим природным объектам.
Во-вторых, процесс Ферхюльста служит наглядной иллюстрацией существования различных нестационарных эффектов, имеющих место в замкнутых системах управления.
В-третьих, модель роста популяции достаточно проста, носит итерационный характер и удобна для моделирования на персональном компьютере.
Алгоритмически
динамика Ферхюльста описывается соотношением:
где: ![]() - начальная численность
популяции,
- начальная численность
популяции, ![]() -
ее численность через n лет,
-
ее численность через n лет, ![]() - численность популяции в n+1 год, r
≥0 – коэффициент, называемый параметром роста. Этот коэффициент управляет
динамикой процесса таким образом, что, если 0<r<2
при
- численность популяции в n+1 год, r
≥0 – коэффициент, называемый параметром роста. Этот коэффициент управляет
динамикой процесса таким образом, что, если 0<r<2
при![]() >0 , то
процесс с ростом номера итерации приближается к нужному конечному устойчивому
состоянию
>0 , то
процесс с ростом номера итерации приближается к нужному конечному устойчивому
состоянию ![]() При
2<r<2,570 состояние x=1
является неустойчивым, в результате чего возникают периодические колебания,
форма которых зависит от значения параметра роста. Наконец, при r=2,570, процесс перестает быть периодическим, и колебания
приобретают хаотический характер.
При
2<r<2,570 состояние x=1
является неустойчивым, в результате чего возникают периодические колебания,
форма которых зависит от значения параметра роста. Наконец, при r=2,570, процесс перестает быть периодическим, и колебания
приобретают хаотический характер.
Таким образом, уравнение (1) можно рассматривать как модель некоторого генератора сигналов, характер и форма которых зависят от значения управляющего параметра r.
В связи с
этим, рассмотрим обратную задачу, возникающую при анализе сигнала, когда
известными являются его дискретные отсчеты ![]() . Требуется, используя модель роста
популяции (1), оценить эмпирическое значение параметра r
роста и установить его логическую связь с качественным признаком сигнала.
Другими словами, если параметр r роста
отображает переменное состояние модели (1), то, можно ли его использовать для
идентификации состояния любой другой модели?
. Требуется, используя модель роста
популяции (1), оценить эмпирическое значение параметра r
роста и установить его логическую связь с качественным признаком сигнала.
Другими словами, если параметр r роста
отображает переменное состояние модели (1), то, можно ли его использовать для
идентификации состояния любой другой модели?
Для ответа на
этот вопрос решим уравнение (1) относительно параметра роста и запишем его в
форме (2):
Выражение (2)
представляет собой преобразованную и линеаризованную форму модели (1), аналогичную
той, которая была использована при анализе процесса Ферхюльста в работе [5].
Чтобы прояснить физический смысл параметра роста, модернизируем уравнение (2),
проведя следующие замены:
Из (3) следует, что идентификационный параметр роста (К) измеряет отношение среднего модуля приращений сигнала к среднему модулю сигнала X(t).
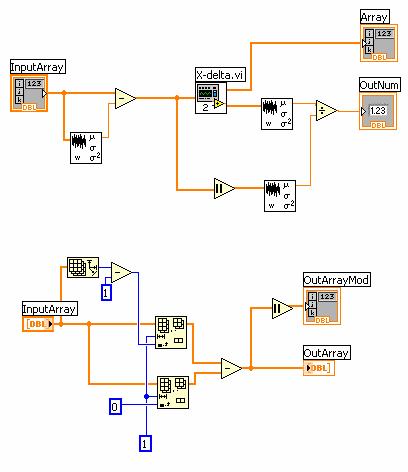
Программная реализация модели (3) в виде структурной схемы виртуального прибора (K-тестера), выполненной в среде LabVIEW – 7.1 представлена на рис. 1.
Анализ физического смысла данного идентификационного параметра показывает, что показания К-тестера пропорциональны относительной средней скорости сигнала.
Если известна
аналитическая форма записи входного сигнала X(t), то можно получить (точно или приближенно) формулу для
расчета коэффициента вариабельности. Так, например, для синусоидального
сигнала, модель которого ![]() , параметр К равен круговой частоте ω
входного сигнала
, параметр К равен круговой частоте ω
входного сигнала ![]() =
2πf.
=
2πf.
Рис. 1. Структура программного кода K-тестера (верхний рисунок)
и его модуля X-delta (нижний рисунок)
В процессе исследований были изучены две основные идентификационные характеристики (ИХ) K-тестера: распознавательная (рекогнитивная, РИХ) и частотная (ЧИХ).
1. Рекогнитивная– такая ИХ, которая связывает значение идентификационного параметра с формой сигнала. При этом сама "форма" рассматривается в пределе как непрерывная величина, задаваемая из некоторого диапазона значений. Например, периодическая система химических элементов Д.И. Менделеева является рекогнитивной ИХ, поскольку связывает имя и, соответственно, свойства химического элемента (или его порядковый номер) с атомным весом (числовым идентификационным параметром) [6].
2. Частотная ИХ – такая ИХ, в которой значение идентификационного параметра зависит от частоты входного сигнала при постоянстве его формы. Аналогом ЧИХ является частотная характеристика электрической цепи, например, двух или четырехполюсника.
Результаты измерения РИХ для случайных стационарных сигналов с симметричными распределениями (2mod – двумодальным, asin – арксинусным, even – равномерным, simp – треугольным, gaus – нормальным, lapl – двусторонним экспоненциальным, kosh – Коши) представлены в табл.1. Средние значения (mean) коэффициента вариабильности (K) и его случайной среднеквадратической погрешности (error,%) оценивались для различных объемов (N) выборок и числа (L) реализаций случайных сигналов.
В табл. 2 представлены результаты измерения РИХ и ЧИХ для периодических сигналов прямоугольной (squ), синусоидальной (sin), треугольной (tri) и пилообразной (saw) формы.
Полученные результаты позволяют сформулировать три основных положения, определяющих информационное содержание коэффициента вариабельности как идентификационного параметра:
1. Значение K=1 разделяет множество сигналов на два класса. Первый класс (0≤K<1) образуют периодические (преимущественно регулярные) сигналы. Второй класс (1≤K≤2) – случайные (преимущественно хаотические) сигналы.
2. Увеличение частоты периодического сигнала приводит к тому, что при малом разрешении, соответствующем 4-5 отсчетам на периоде, система начинает воспринимать периодический сигнал как случайный, поскольку значение коэффициента вариабельности становится равным или большим 1.
3. При известной и постоянной частоте периодического сигнала значение коэффициента вариабельности несет информацию о форме этого сигнала, что отражено данными табл. 3.
4. При
известной и постоянной форме периодического сигнала значение коэффициента
вариабельности несет информацию о частоте этого сигнала, причем эта зависимость
носит преимущественно линейный характер.
|
IdP=K |
Вид распределения мгновенных значений случайного сигнала |
||||||
|
2mod |
asin |
even |
simp |
gaus |
lapl |
kosh |
|
|
Mean (K), N=1000,L=1000 |
1 |
1,273 |
1,333 |
1,4 |
1,414 |
1,5 |
1,63 |
|
Error (р=0,95),% |
6,5 |
4,6 |
4,2 |
4 |
3,7 |
3,4 |
21 |
|
Mean (K), N=10000,L=100 |
0,999 |
1,274 |
1,333 |
1,4 |
1,414 |
1,5 |
1,67 |
|
Error (р=0,95),% |
1,84 |
1,44 |
1,2 |
1,24 |
1,18 |
1,1 |
23 |
|
Mean (K), N=100000,L=10 |
0,999 |
1,274 |
1,333 |
1,4 |
1,414 |
1,5 |
1,61 |
|
Error (р=0,95),% |
0,62 |
0,4 |
0,33 |
0,3 |
0,2 |
0,4 |
36 |
|
IdP=K |
Количество периодов сигнала в объеме наблюдаемой выборки N=10000 |
|||||
|
1 |
10 |
100 |
1000 |
2000 |
4000 |
|
|
Sin |
6,28E-4 |
6,28E-3 |
6,28E-2 |
0,618 |
1,236 |
2 |
|
Tri |
8E-4 |
8E-3 |
8E-2 |
0,67 |
1,333 |
2 |
|
Squ |
2E-4 |
3,8E-3 |
3,98E-2 |
0,4 |
0,833 |
1,667 |
|
Saw |
8E-4 |
8E-3 |
8E-2 |
0,72 |
1,333 |
2 |
|
№ п/п |
Форма периодического сигнала |
Уравнение измерения |
Примечание |
|
1 |
Прямоугольная |
|
P – число периодов сигнала, укладывающихся в объеме N выборки |
|
2 |
Синусоидальная |
|
|
|
3 |
Треугольная или пилообразная |
|
Перспективы предлагаемого подхода связаны со следующими направлениями использования:
· Измерение формы периодических сигналов (при известной частоте).
· Измерение частоты периодических сигналов (при известной форме).
· Преобразование формы сигналов (в том числе периодических в случайные и наоборот) путем их компарированмя по идентификационному параметру.
· Измерение степени хаотичности квазипериодических сигналов – чем сложнее форма сигнала и выше его частота, тем более "хаотичным" этот сигнал является.
· Измерение нелинейных искажений периодических сигналов произвольной (в спектральном методе только синусоидальной) формы и, как следствие, возможность автоматической регулировки формы сигналов.
· Измерение формы распределения мгновенных значений случайных сигналов.
·
Классификация сигналов по свойствам регулярность – хаотичность".
ПРИМЕР ПРИМЕНЕНИЯ
ИДЕНТИФИКАЦИОННЫХ ИНСТРУМЕНТОВ
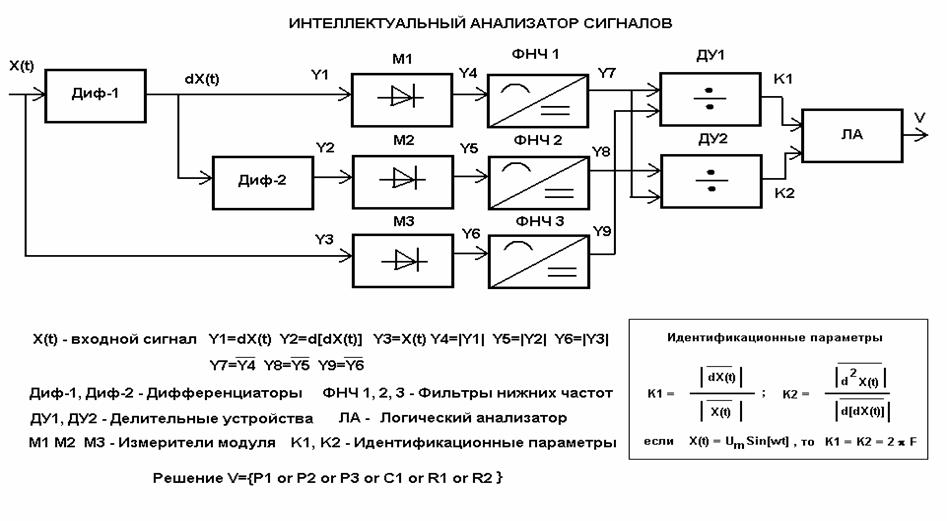
В качестве примера рассмотрим решение классификационной задачи. На рис. 2 представлена структурная схема интеллектуального анализатора (ИА), позволяющего полностью автоматизировать процедуру классификации.
Исходный непрерывный во времени сигнал X(t) представляется, после аналого-цифрового преобразования, в виде дискретной выборочной реализации, объема N, и записывается в файловом формате в память компьютера. Операции дифференцирования (Диф-1, Диф-2), определения модуля (М1, М2, М3), усреднения (ФНЧ1, ФНЧ2, ФНЧ3) и вычисления (ДУ1, ДУ2) идентификационных параметров K1 и K2 реализуются на программном уровне. Математические модели и физический смысл используемых идентификационных параметров отражены в табл. 4.
Математические
и физические модели идентификационных параметров
|
№ п/п |
Имя IdP |
Обозначение IdP |
Физический смысл IdP |
Математическая модель |
|
1 |
Коэффициент вариабельности |
K-1 |
Измерение среднего значения модуля относительной скорости сигнала |
|
|
2 |
Коэффициент вариабельности |
K-2 |
Измерение среднего значения модуля относительного ускорения сигнала |
|
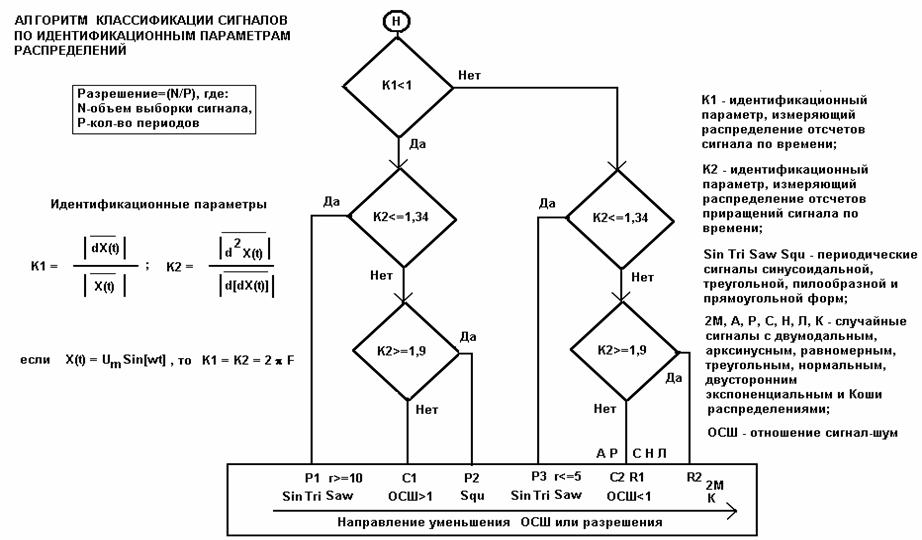
В логическом анализаторе (ЛА) реализован алгоритм классификации, структурная схема которого представлена на рис. 3. В структурном отношении ЛА представляет собой обычную реляционную базу данных (БД), записями которой являются имена файлов выборочных реализаций сигналов, а полями – имена идентификационных параметров (K1, K2). В ячейки БД (на пересечении строк и столбцов) записываются численные оценки идентификационных параметров. Анализ сочетаний значений идентификационных параметров позволяет определить – по какому из 6-ти направлений (P1, C1, P2, P3, R1, R2) фильтруется данная запись. Каждое направление имеет свой собственный адрес. Адрес образуется путем перечисления единиц и нулей, соответствующих выполнению условий (Да → «1», Нет → «0») при прохождении алгоритма (рис. 3) от входа до выхода.
Разрядность адреса определяет "длину пути" прохождения анализа. Чем больше разрядность адреса, тем более "точно" определяется некоторое свойство сигнала, например, в том смысле, что увеличивается число различимых градаций интенсивности проявления данного свойства. Если разрядность адресов всех выходных направлений одинакова, то подобный алгоритм будем называть алгоритмом с равномерной дискретизацией (квантованием) свойств.
Таким образом, можно утверждать, что адрес записи является количественной характеристикой данного классификационного алгоритма. Соответственно, появляется возможность объективно и автоматически сравнивать между собой эффективность различных классификационных алгоритмов, работающих с одной и той же БД.
Если в БД имеется множество записей, идентификационные параметры которых полностью покрывают диапазон возможных значений IdP 0≤(K1, K2)≤2, то такую БД будем называть представительной. Сигналы, на основе анализа которых формируется представительная БД, называются эталонами БД. Подразумевается, что для эталонов известны не только оценки их идентификационных параметров, но также другие характеристики, в том числе и качественные.
Чтобы проиллюстрировать основные особенности предлагаемого алгоритма, рассмотрим технологию его использования, заключающуюся в следующем.
Создадим эталонную БД, состоящую из списка сигналов, состояние которых охватывает максимально возможный диапазон в направлении эволюции этих сигналов - от случайных до периодических (табл. 1 и 2, соответственно), включая аддитивные смеси типа сигнал-шум. Фрагмент (из 30 первых файлов сигналов) исходной базы данных, состоящей из 114 образцов сигналов, изображен в табл.5.
Выявление закономерностей в структуре созданной БД проводим путем применения стандартных операций упорядочения и фильтрации записей по идентификационным параметрам K1, K2. В табл. 6 показан фрагмент БД, соответствующий реализации двух условий (K1<1 → Да, K2<=1,34 → Да, адрес направления P1→ 11) алгоритма.
Анализ выходного состояния БД показывает, что:
· По направлению P1 действительно фильтруются периодические сигналы синусоидальной (Sin), треугольной (Tri) и пилообразной (Saw) формы с числом периодов от 1 до 10000, что соответствует разрешению r>=10. Эта часть БД представляет идеальное (желаемое) ее состояние.
· Отклонения от идеальности проявляются в наличии "посторонних" записей, представляющих сигналы аддитивных смесей типа gaus+tri-100-(500-400-300). Здесь gaus – шумовая компонента с нормальным распределением и действующим значением, равным 1, tri-100-(500-400-300) – периодическая компонента треугольной формы, имеющая 100 периодов и соответствующую амплитуду (500-400-300). Данную ситуацию можно интерпретировать таким образом, что классификационная система при таких больших отношениях сигнал-шум ОСШ>=300, нечувствительна к наличию шумовой компоненты и воспринимает эти смеси как чисто периодические сигналы треугольной формы.
· Возможность фильтрации "посторонних" записей связана с введением дополнительного условия по идентификационному параметру, отличному от K1, K2, например, в виде их отношения. Введение дополнительных условий на выходах алгоритма позволяет увеличить количество направлений и, соответственно, провести более детальную классификацию сигналов.
Характеристики выходных направлений алгоритма (рис. 3) даны в табл. 7. Расположение направлений и симметрия структуры алгоритма позволяют выделить общее направление (при движении слева – направо) эволюции сигналов от чисто периодических к случайным. В качестве упорядочивающего фактора выступает отношение сигнал-шум для смесей или разрешение для периодических сигналов.
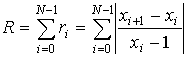 .
. 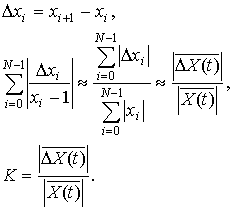 (3)
(3)