ПЕРИОДИЧЕСКИЙ ПОТОК СО СЛУЧАЙНОЙ НЕЗАВИСИМОЙ ДЕЦИМАЦИЕЙ
Ф. В. Голик, Е. А. Порхунов
Новгородский государственный университет им. Ярослава Мудрого
Получена 25 сентября 2008 г
Анализируется поток точек, следующих с постоянным неизвестным периодом, содержащий конечное, но неизвестное число точек, каждая из которых может быть децимирована (потеряна) с неизвестной вероятностью. Предложена процедура преобразования потока, позволяющая обнаружить поток и оценить его параметры – период следования, вероятность децимации, число точек в исходном потоке и координату центра потока. Построены рабочие характеристики обнаружения и найдены характеристики оценок параметров потока. Исследуемый процесс может служить адекватной моделью обнаружения пачки импульсных радиосигналов на фоне некоррелированной помехи, принимаемых пассивным радиолокатором, реализующим критерий обнаружения Неймана-Пирсона при задании предельно низкой (практически нулевой) вероятности ложного обнаружения одиночного сигнала.
Ключевые слова: обнаружение сигналов, обработка сигналов, радиолокация.
Постановка
задачи
Формально поток точек может быть представлен вектором
![]() (1)
(1)
где ![]() - момент возникновения i-й точки, а N –
количество точек или размер потока[1].
- момент возникновения i-й точки, а N –
количество точек или размер потока[1].
Положим, что отсчет времени ведется с
момента начала наблюдения ![]() . Тогда поток с постоянным периодом T есть вектор
. Тогда поток с постоянным периодом T есть вектор
![]() . (2)
. (2)
Каждая точка потока ![]() может быть потеряна с
вероятностью q и сохранена с вероятностью
может быть потеряна с
вероятностью q и сохранена с вероятностью ![]() . Тогда децимированному
потоку соответствует вектор
. Тогда децимированному
потоку соответствует вектор
По условию задачи децимация точек взаимно независима, т. е.
![]() .
.
Априори период следования T, размер N потока и вероятность q децимации неизвестны.
Цель настоящей работы состоит в разработке процедуры обнаружения децимированного потока и нахождения оценок его параметров.
Обнаружение периодичности
Периодический поток без потерь
В отличие от общеизвестных методов обнаружения пачки сигналов (потока точек) в настоящей работе предложен подход, основанный на обнаружении периодичности исследуемого процесса. Действительно, если удастся доказать, что наблюдаемый поток периодический, то можно утверждать, что он порожден некоторым источником детерминированного, а не случайного процесса. То есть обнаружение периодичности равносильно обнаружению цели.
Процедуры, предназначенные для выявления периодичности, базируются на общем подходе, заключающемся в таком преобразовании анализируемого процесса, при котором максимально усиливаются периодические составляющие и подавляются апериодические [1].
Поставим в соответствие каждой точке
потока дельта-функцию и представим поток ![]() следующим образом:
следующим образом:
Косинус-преобразование Фурье потока (4) равно:
Точки потока ![]() появляются в моменты
появляются в моменты ![]() , следовательно [2, 1.341.3]:
, следовательно [2, 1.341.3]:
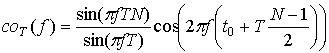 .
.
Совместив начало интервала наблюдения
с моментом появления первой точки потока, т. е. приняв ![]() и, тем самым, компенсировав
эпоху, получаем:
и, тем самым, компенсировав
эпоху, получаем:
Следует подчеркнуть, что компенсация
эпохи таким способом возможна далеко не всегда. Действительно, в случае анализа
суперпозиции потоков можно компенсировать эпоху только одного потока (если
вероятностью появления в момент ![]() точек, принадлежащих двум и более потока
можно пренебречь). В настоящей работе исследуются потоки, для которых эпоха
может быть компенсирована указанным способом, т. е. потоки с нулевой эпохой.
точек, принадлежащих двум и более потока
можно пренебречь). В настоящей работе исследуются потоки, для которых эпоха
может быть компенсирована указанным способом, т. е. потоки с нулевой эпохой.
Функция (6) принимает максимальные
значения, равные N, при ![]() Откуда следует, что найдя точку
максимума
Откуда следует, что найдя точку
максимума ![]() и
его номер k, определим и период потока:
и
его номер k, определим и период потока: ![]() . Нетрудно убедиться,
что производная функции (6) в точках
. Нетрудно убедиться,
что производная функции (6) в точках ![]() равна нулю. Следовательно, оценка периода
несмещенная.
равна нулю. Следовательно, оценка периода
несмещенная.
Таким образом, признаком наличия
периодичности является существование глобальных максимумов функции (6) в точках
![]() .
.
Периодический поток с независимой децимацией
Рассмотрим поток с потерей точек.
Выполнив для потока (3) преобразования, аналогичные (4, 5), получаем косинус-преобразование потока:
где n – количество точек, потерянных подряд в начале потока.
Множитель 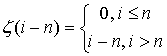 позволяет
исключить отклики от точек, потерянных в начале потока.
позволяет
исключить отклики от точек, потерянных в начале потока.
Функция (7) случайна. Для исследования ее свойства найдем ее математическое ожидание.
Поскольку по определению случайные
множители ![]() взаимно
независимы, то случайная величина n распределена
по «ограниченному» геометрическому закону:
взаимно
независимы, то случайная величина n распределена
по «ограниченному» геометрическому закону:
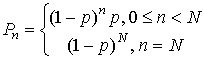 (8)
(8)
Выполнив необходимые преобразования с
учетом (8) получаем, что среднее значение функции ![]() равно:
равно:
где
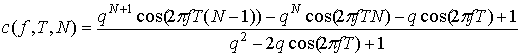 ;
;
 .
.
Полное аналитическое исследование
функции (9) затруднено. Однако можно показать, что глобальные максимумы
расположены в точках ![]() и
оценка периода потока равна
и
оценка периода потока равна ![]() . Подставив в (9)
. Подставив в (9) ![]() , убеждаемся, что функция (9)
принимает максимальное значение, равное Np. Это
в точности соответствует математическому ожиданию распределения Бернулли,
модель которого, по существу, и реализуется в потоке с независимой децимацией.
Численные расчеты показывают, что производная по f
среднего значения косинус-преобразования при
, убеждаемся, что функция (9)
принимает максимальное значение, равное Np. Это
в точности соответствует математическому ожиданию распределения Бернулли,
модель которого, по существу, и реализуется в потоке с независимой децимацией.
Численные расчеты показывают, что производная по f
среднего значения косинус-преобразования при ![]() равна нулю и не зависит от вероятности p. Следовательно, оценка периода T
несмещенная. Точность измерения периода зависит только от шага дискретизации частоты
f .
равна нулю и не зависит от вероятности p. Следовательно, оценка периода T
несмещенная. Точность измерения периода зависит только от шага дискретизации частоты
f .
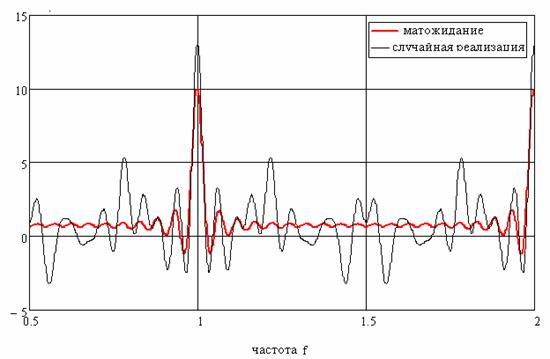
Рис. 1. Математическое ожидание косинус-преобразования и косинус-преобразование случайной реализации при p=0.5 и N=20. Период следования точек T=1
Таким образом, и в случае
децимированного потока существует возможность обнаружения периодичности по
наличию глобальных максимумов косинус-преобразования (7) в точках ![]() .
.
Обнаружение потока
В отличие от общепринятых понятий
обнаружения сигнала в рассматриваемом случае под правильным обнаружением потока
понимается фиксация двух событий: 1) поток содержит больше z
точек и 2) глобальные максимумы косинус-преобразования (7) находятся в точках ![]() . Первое условие не
требует пояснений. Выполнение второго требования связано с тем, что существуют
такие комбинации точек децимированного потока, при которых глобальные максимумы
функции (7) возникают не только на частотах
. Первое условие не
требует пояснений. Выполнение второго требования связано с тем, что существуют
такие комбинации точек децимированного потока, при которых глобальные максимумы
функции (7) возникают не только на частотах ![]() , но и на кратных частотах
, но и на кратных частотах ![]() , где d – произведение наименьших общих делителей номеров
точек, сохранившихся в потоке. В принципе не важно, на какой именно частоте
появился ложный глобальный максимум. Достаточно убедиться, что он есть (d > 1) или его нет (d = 1). При d = 1 частота
следования точек оценивается по положению первого глобального максимума и равна
1/T. Таким образом, будем считать, что:
, где d – произведение наименьших общих делителей номеров
точек, сохранившихся в потоке. В принципе не важно, на какой именно частоте
появился ложный глобальный максимум. Достаточно убедиться, что он есть (d > 1) или его нет (d = 1). При d = 1 частота
следования точек оценивается по положению первого глобального максимума и равна
1/T. Таким образом, будем считать, что:
- поток обнаружен правильно, если число точек r потока больше z и d = 1 (поток обнаружен и частота оценена верно);
- произошло ложное обнаружение, если r > z и d > 1 (поток обнаружен, но частота оценена неверно);
- поток не обнаружен, если ![]() .
.
Характеристики обнаружения
При расчете вероятностей обнаружения
основная сложность состоит в определении вероятности того, что произведение
общих делителей номеров сохранившихся точек, равно 1. Нам не удалось получить
решение в общем виде. Поэтому вероятностные характеристики найдены с путем
статистического моделирования. Оценки вероятностей получены по 104
реализациям, что гарантирует их высокую надежность. При моделировании параметры
потока изменялись в следующих пределах: вероятность сохранения точки p = 0.1, 0.2,…0.9; размер потока N
= 10, 15,…50. Порог обнаружения z принимался
равным z =2, 3, 4. Шаг квантования функции ![]() меньше
меньше ![]() . Ограничения на
дискретизацию частоты f не накладывались.
. Ограничения на
дискретизацию частоты f не накладывались.
После обработки статистических данных оказалось, что вероятность D правильного обнаружения хорошо аппроксимируется функцией (10) при коэффициенте детерминации не менее 0.9998.
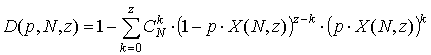 (10)
(10)
где ![]() .
.
Значения коэффициентов функции X приведены в табл. 1
Таблица 1
|
z |
a |
b |
|
2 |
1.0147 |
-0.0485 |
|
3 |
1.0241 |
-0.0247 |
|
4 |
1.0221 |
-0.0099 |
На рис. 2 приведен график зависимости
вероятности правильного обнаружения D от вероятности p при N
=30, рассчитанной по формуле (10) и ее статистические оценки ![]() при пороге обнаружения z
= 2.
при пороге обнаружения z
= 2.
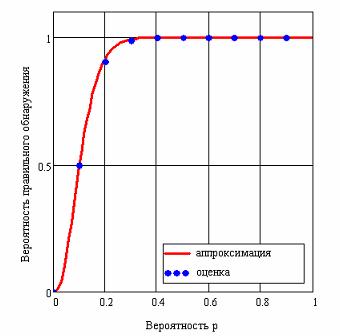
Рис. 2. Вероятность D правильного обнаружения потока в зависимости от вероятности p при N=30 и пороге z=2
Вероятность пропуска, очевидно, равна
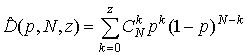 , (11)
, (11)
а вероятность ложного обнаружения определяется из условия вероятности полной группы событий:
![]() (12)
(12)
Вероятность ошибки ![]() равна сумме вероятностей
пропуска и ложного обнаружения или:
равна сумме вероятностей
пропуска и ложного обнаружения или:
![]() (13)
(13)
На рис. 3…6 приведены зависимости вероятностей (10)…(13) от p при разных значениях N.
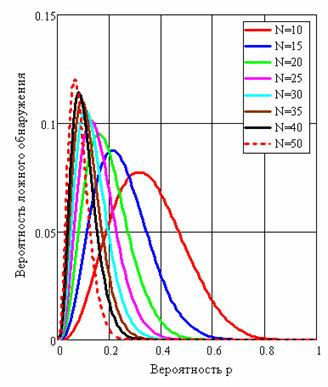
Рис. 3. Вероятность F ложного обнаружения потока в зависимости от вероятности p при разных размерах N и пороге z=2
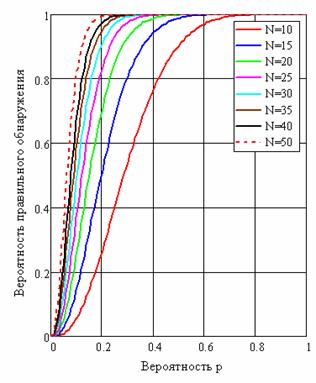
Рис. 4. Вероятность D правильного обнаружения потока в зависимости от вероятности p при разных размерах N и пороге z=2
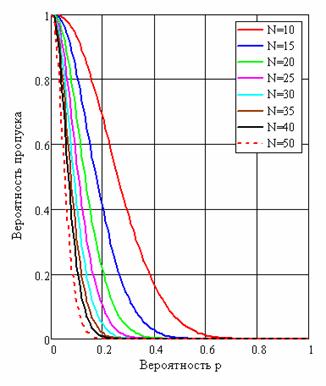
Рис. 5. Вероятность пропуска потока в зависимости от вероятности p при разных размерах N и пороге z=2
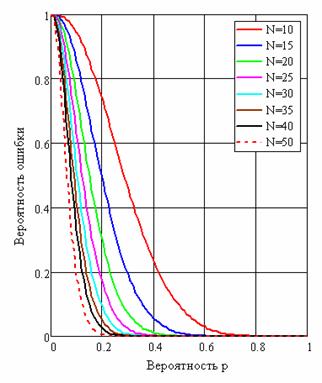
Рис. 6. Вероятность суммарной вероятности E ошибки обнаружения потока в зависимости от вероятности p при разных размерах N и пороге z=2
Рабочие характеристики по вероятностям правильного и ложного обнаружения можно найти из (10), (12), решая уравнения
![]() (14)
(14)
относительно
параметров потока p и N. Здесь ![]() - заданные значения соответствующих
вероятностей.
- заданные значения соответствующих
вероятностей.
На основании численного решения
уравнений (14) построены рабочие характеристики для значений порога обнаружения
z =2, 3, 4 при ![]() = 0.95, 0.99, 0.999, 0.9999 и при
= 0.95, 0.99, 0.999, 0.9999 и при ![]() = 10-3, 10-4,
10-5, 10-6, графики которых при z
=2 приведены на рис. 7 и 8.
= 10-3, 10-4,
10-5, 10-6, графики которых при z
=2 приведены на рис. 7 и 8.
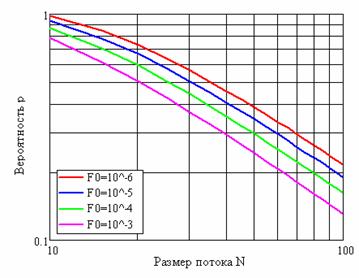
Рис. 7. Зависимость вероятности p от размера N потока при заданных вероятностях F0 ложного обнаружения и пороге z=2

Рис. 8. Зависимость вероятности p от размера N потока при заданных вероятностях D0 правильного обнаружения и пороге z=2
Из графиков следует, что с увеличением размера потока N требования по величине вероятности p существенно снижаются. Так при N = 30 и p = 0.5 вероятность правильного обнаружения больше 0.9999, а вероятность ложного обнаружения равна 10-5. При N = 60 те же характеристики можно получить уже при вероятности p = 0.2.
Рабочие характеристики хорошо аппроксимируются функцией вида
Значения коэффициентов c, d, e, g приведены в Приложении.
Оптимизация порога обнаружения
Постановка задачи обнаружения потока, рассматриваемая в настоящей работе, отличается от классической задачи обнаружения сигнала. Во-первых, в нашем случае под правильным обнаружением понимается выполнение двух условий одновременно: число точек потока больше z и период потока оценен верно. То есть, совмещены две процедуры – обнаружения и оценки. Во-вторых, предполагается, что поток присутствует всегда, то есть априорная вероятность «наличия цели» равна единице.
Тогда критерий идеального наблюдателя сводится к минимизации вероятности суммарной ошибки, равной
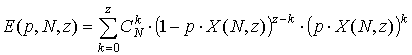 (16)
(16)
Вероятность E является неубывающей функцией порога z. Следовательно, вероятность ошибки будет минимальна при наименьшем значении порога, при котором в принципе возможно получение однозначной оценки периода следования точек. Таким значением является z = 2.
Вероятность E
зависит и от параметров потока N и p, которые априори неизвестны.
Полагая, что вероятность p равномерно
распределена на интервале (0,1], а размер потока так же равномерно распределен
на интервале [N0, N1], можно найти средние значения вероятностей
ошибки при разных z. Численные расчеты дают следующие
значения средних вероятностей суммарной ошибки при ![]() :
:
Таблица 2
|
N1 |
Порог z |
||
|
2 |
3 |
4 |
|
|
50 |
0.140 |
0.170 |
0.202 |
|
100 |
0.095 |
0.114 |
0.134 |
Наименьшее значение средней вероятности ошибки оказываются при минимально допустимом пороге. Таким образом, оптимальным порогом обнаружения можно считать z0 = 2.
Оценка параметров потока
Оценки размера потока и вероятности децимации
При идентификации источника,
порождающего поток, в качестве дополнительной информации полезно использовать
оценки параметров потока. Так, если известно примерное число ![]() импульсов в пачке
радиолокационного сигнала и обнаруженным импульсам пачки соответствуют точки
потока, то после обнаружения потока можно найти оценку
импульсов в пачке
радиолокационного сигнала и обнаруженным импульсам пачки соответствуют точки
потока, то после обнаружения потока можно найти оценку ![]() его размера. Если окажется, что
его размера. Если окажется, что ![]() , то это может служить
дополнительным подтверждением правильности принятого решения об обнаружении цели.
, то это может служить
дополнительным подтверждением правильности принятого решения об обнаружении цели.
Обозначим моменты появления первой и
последней точки соответственно ![]() . Между этими крайними точками имеется n позиций. Очевидно
. Между этими крайними точками имеется n позиций. Очевидно 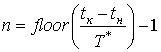 , где
, где ![]() - ближайшее меньшее целое
- ближайшее меньшее целое ![]() ,
, ![]() - оценка периода.
- оценка периода.
На n позициях может оказаться k точек. Поток можно обнаружить, если общее число точек k + 2 больше порога z. Откуда следует, что k = z-1…n.
Допустим, что наблюдатель имеет возможность
регистрировать только две величины – r=k+2 и n. На основании этих
данных найдем максимально правдоподобные оценки вероятности ![]() сохранения точки потока и
размера
сохранения точки потока и
размера ![]() исходного
потока.
исходного
потока.
Функция правдоподобия равна
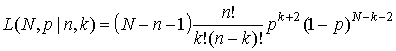 (17)
(17)
Полагая N непрерывной величиной, можно показать, что функция (17) почти
при всех допустимых значениях n
и k имеет единственный максимум, в точке
которого производные по p и N
равны нулю. Исключение составляет случай, когда ![]() При этом функция правдоподобия достигает
максимума в точке
При этом функция правдоподобия достигает
максимума в точке ![]() ,
координаты которой являются максимально правдоподобными оценками для
рассматриваемого частного случая.
,
координаты которой являются максимально правдоподобными оценками для
рассматриваемого частного случая.
При ![]() для нахождения оценок параметров p и N применимы
стандартные процедуры метода максимального правдоподобия.
для нахождения оценок параметров p и N применимы
стандартные процедуры метода максимального правдоподобия.
Найдем логарифм функции правдоподобия
![]()
и вычислим его частные производные по p и N:
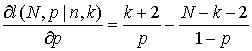
![]()
Приравняв производные нулю, получаем систему уравнений:
К сожалению, система уравнений (18), (19)
не имеет решения в замкнутой форме. Для приближенного решения представим ![]() первыми членами ряда [2, 1.512]
первыми членами ряда [2, 1.512]
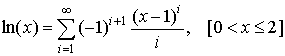 (20)
(20)
Используя приближение первым членом ряда (20), получаем уравнение:
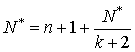 ,
,
корень которого равен:
![]() (21)
(21)
При приближении двумя членами ряда (20) получаем
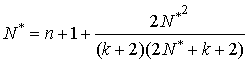
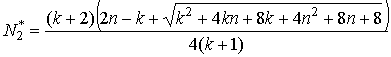 (22)
(22)
При аппроксимации тремя членами ряда формула для оценки размера потока слишком громоздка и не дает заметного выигрыша по точности.
Строго говоря, для оценки ![]() не существует
точного решения, поскольку N - целочисленная
величина, а выражения (18, 19) и связанные с ними получены в предположении ее
непрерывности. Поэтому оценки
не существует
точного решения, поскольку N - целочисленная
величина, а выражения (18, 19) и связанные с ними получены в предположении ее
непрерывности. Поэтому оценки ![]() приходится округлять. Приведем расчетные
формулы для максимально правдоподобных оценок длины потока и вероятности
сохранения точки в потоке:
приходится округлять. Приведем расчетные
формулы для максимально правдоподобных оценок длины потока и вероятности
сохранения точки в потоке:
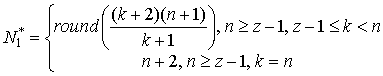
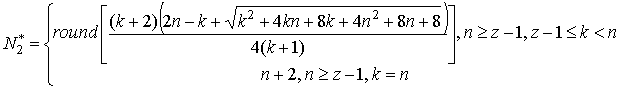
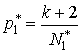 ,
, 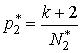 .
.
Здесь ![]() - функция
округления числа x до ближайшего целого.
- функция
округления числа x до ближайшего целого.
С помощью статистического
имитационного моделирования найдены средние значения и дисперсии оценок ![]() и
и ![]() при следующих
параметрах исходного потока:
при следующих
параметрах исходного потока: ![]() . Порог обнаружения z = 2. Число реализаций 104. На основании
результатов моделирования можно утверждать, что оценки
. Порог обнаружения z = 2. Число реализаций 104. На основании
результатов моделирования можно утверждать, что оценки ![]() и
и ![]() смещенные и
состоятельные по размеру N потока
– с увеличением N смещение и дисперсия монотонно
убывают и стремятся к нулю.
смещенные и
состоятельные по размеру N потока
– с увеличением N смещение и дисперсия монотонно
убывают и стремятся к нулю.
Зависимость вероятности p, при которой модуль относительной ошибки не превышает
заданного значения ![]() %, хорошо аппроксимируется функцией (23)
при коэффициенте детерминации больше 0.995.
%, хорошо аппроксимируется функцией (23)
при коэффициенте детерминации больше 0.995.
![]() . (23)
. (23)
Значения коэффициентов приведены в табл. 3, а графики на рис. 9.
Таблица 3
|
Относительная ошибка % |
Оценка вероятности p |
Оценка размера N |
||
|
a |
b |
a |
b |
|
|
5 |
-0.2706 |
1.3723 |
-0.2367 |
1.2117 |
|
10 |
-0.2392 |
1.1299 |
-0.1661 |
0.8115 |

Рис. 9. Зависимость вероятности p от размера N потока при заданных относительных ошибках оценок вероятности p и размера N
Из графиков рис. 9 видно, что уже при сравнительно небольших размерах N потока можно получить достаточно точные оценки его параметров. Так при N = 30 и вероятности p = 0.4 относительные погрешности не превышают 5%.
Оценка координаты центра потока
Положим, что поток обнаружен, следовательно, известен его период T. Тогда координату центра достаточно выразить через номера точек, т. е. получить нормированную по T координату.
Отметим, что задача оценки координаты центра потока эквивалентна задаче оценки азимута цели по пачке двоично-квантованных сигналов при воздействии некоррелированной помехи. Известны эвристические и оптимальные алгоритмы оценки азимута [3].
Рассмотрим простейший алгоритм оценки
по номерам первой ![]() и последней
и последней ![]() точек:
точек:
![]() .
(24)
.
(24)
Характеристики оценки можно найти,
используя распределение ![]() общего числа v
точек, потерянных в начале и конце потока, при условии, что в потоке сохранилось
больше z точек:
общего числа v
точек, потерянных в начале и конце потока, при условии, что в потоке сохранилось
больше z точек:
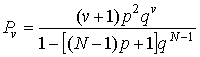 .
.
Математическое ожидание оценки координаты
центра ![]() потока
вычисляется по формуле
потока
вычисляется по формуле
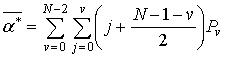 ,
,
которая преобразуется к виду:
![]()
Откуда следует, что оценка координаты центра потока несмещенная.
Дисперсия оценки равна:
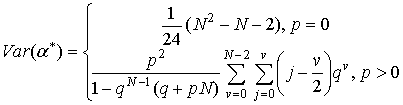
Можно показать, что дисперсия уменьшается с ростом N, следовательно, оценка (24) состоятельная по размеру потока.
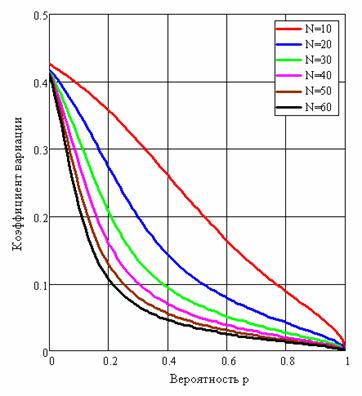
Рис. 10. Зависимость коэффициента вариации оценки координаты центра потока от вероятности p при различных размерах N
На рис. 10 приведены графики
зависимости коэффициента вариации оценки ![]() от вероятности p
при различных значениях размера потока N.
от вероятности p
при различных значениях размера потока N.
Распределение координаты ![]() центра можно
найти с помощью расчетной формулы:
центра можно
найти с помощью расчетной формулы:
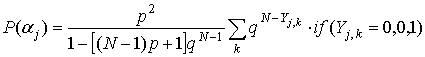
где 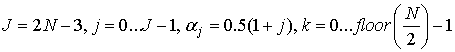 ,
,
![]() - матрица количества
точек, сохранившихся в потоке.
- матрица количества
точек, сохранившихся в потоке.
Распределение координаты центра потока симметричное, эксцесс положительный.
Заключение
Полученные результаты могут служить основой для построения алгоритма обнаружения пачки радиоимпульсов, поступающей на вход пассивного радиолокатора, а также оценки параметров – периода следования радиоимпульсов, длительности пачки, координаты ее центра. При этом предполагается, что вероятность ложного обнаружения одиночного сигнала пренебрежимо мала и отсутствует многолучевое распространение сигнала от источника излучения. Кроме того, принято, что погрешность оценки временного положения радиоимпульсов мала. Перечисленные ограничения достаточно строги и редко выполняются на практике в полном объеме. Однако, на наш взгляд, развитие предложенного подхода может оказаться продуктивным для решения и более сложных задач.
Литература
1. Серебренников М. Г., Первозванский А. А. Выявление скрытых периодичностей. - М.: Наука, 1965. - 244 с.: ил.
2. Градштейн И. С., Рыжик И. М.: Таблицы интегралов, сумм, рядов и произведений. М.: Наука, 1971. - 1108 с.: ил.
3. Кузьмин С. З. Основы проектирования систем цифровой обработки радиолокационной информации. – М.: Радио и связь, 1986.- 352 с.: ил.
Приложение. Коэффициенты функции (15), аппроксимирующей рабочие характеристики обнаружения децимированного потока
Таблица П1
|
Порог обнаружения z = 2 |
||||
|
Вероятность D0 |
c |
d |
e |
g |
|
0.95 |
7.12608 |
-0.97329 |
-8.51202 |
-1.63158 |
|
0.99 |
14.04819 |
-1.02771 |
-17.50963 |
-1.43442 |
|
0.999 |
19.44982 |
-1.02910 |
-27.58727 |
-1.42917 |
|
0.9999 |
54.78414 |
-1.09737 |
-65.26045 |
-1.27006 |
|
Вероятность F0 |
c |
d |
e |
g |
|
0.001 |
14.80789 |
-0.99159 |
-22.64423 |
-1.49599 |
|
0.0001 |
443.51862 |
-1.16250 |
-453.31324 |
-1.18459 |
|
0.00001 |
923.70361 |
-1.15916 |
-937.07397 |
-1.17178 |
|
0.000001 |
1327.69522 |
-1.14839 |
-1344.02532 |
-1.15821 |
Таблица П2
|
Порог обнаружения z = 3 |
||||
|
Вероятность D0 |
c |
d |
e |
g |
|
0.95 |
7.90419 |
-0.98229 |
-13.11693 |
-1.82490 |
|
0.99 |
11.51148 |
-1.00015 |
-20.00618 |
-1.67354 |
|
0.999 |
24.33768 |
-1.06213 |
-35.20249 |
-1.43689 |
|
0.9999 |
614.75939 |
-1.19346 |
-628.09420 |
-1.21266 |
|
Вероятность F0 |
c |
d |
e |
g |
|
0.001 |
24.73151 |
-1.06081 |
-31.94967 |
-1.37412 |
|
0.0001 |
379.96994 |
-1.17930 |
-391.42719 |
-1.20766 |
|
0.00001 |
900.82214 |
-1.18103 |
-916.72380 |
-1.19546 |
|
0.000001 |
1517.70456 |
-1.16913 |
-1536.56843 |
-1.17855 |
Таблица П3
|
Порог обнаружения z = 4 |
||||
|
Вероятность D0 |
c |
d |
e |
g |
|
0.95 |
7.90419 |
-0.98229 |
-13.11693 |
-1.82490 |
|
0.99 |
13.21021 |
-1.01376 |
-25.60585 |
-1.71160 |
|
0.999 |
22.30745 |
-1.05049 |
-38.23678 |
-1.53057 |
|
0.9999 |
805.86559 |
-1.21268 |
-822.75440 |
-1.22974 |
|
Вероятность F0 |
c |
d |
e |
g |
|
0.001 |
9.76386 |
-0.93933 |
-39.61348 |
-1.95658 |
|
0.0001 |
13.42641 |
-0.95394 |
-46.00445 |
-1.82916 |
|
0.00001 |
612.19299 |
-1.19246 |
-630.49297 |
-1.21522 |
|
0.000001 |
1339.90551 |
-1.18148 |
-1360.64605 |
-1.19277 |
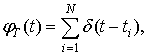 (4)
(4)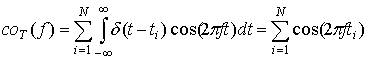 . (5)
. (5)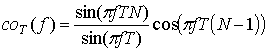 . (6)
. (6)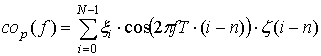 (7)
(7)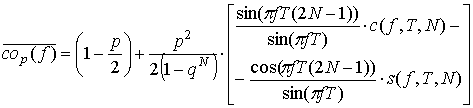 (9)
(9)
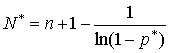 (19)
(19)