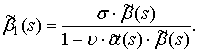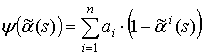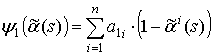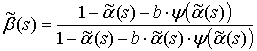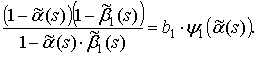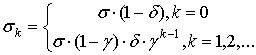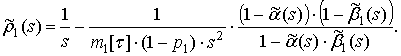УДК 621.391.14:621.396
ХАРАКТЕРИСТИКИ ПРОРЕЖЕННЫХ СЛУЧАЙНЫХ ПОТОКОВ ПРЯМОУГОЛЬНЫХ ИПУЛЬСОВ
Ф. В. Голик
Новгородский государственный университет им. Ярослава
Мудрого
Получена 29 сентября 2010 г.
Аннотация. Исследуется влияние случайного прореживания (децимации) на характеристики случайных потоков прямоугольных импульсов. Определены условия устойчивости автокорреляционной функции потока к процедуре прореживания. Предложена методика расчета характеристик децимированных потоков. Найдены характеристики потоков на выходе параметрического селектора, обнаружителя и одноканальной системы обслуживания.
Ключевые слова. Случайный поток прямоугольных импульсов, прореживание, обнаружение, селекция, обслуживание, автокорреляция, время корреляции.
Введение
Случайные потоки прямоугольных импульсов (СППИ) широко используются в качестве моделей при исследовании систем передачи и обработки информации, радиолокационных систем и систем управления. В одной из первых работ [1], посвященных исследованию СППИ, рассмотрены методы анализа потоков. В [2, 3] предложены методы синтеза потоков с заданными корреляционными свойствами. Целью настоящей работы является исследование характеристик СППИ, подвергшихся прореживанию в результате селекции, обнаружения и обслуживания. При этом решаются следующие задачи:
- разработка методов расчета характеристик прореженных СППИ;
- анализ влияния прореживания на корреляционные свойства потока и поиск процедур децимации, не влияющих на автокорреляционную функцию (АКФ) выходного потока;
- расчет характеристик потоков на выходе параметрического селектора, на выходе обнаружителя одиночных сигналов на фоне коррелированной помехи и на выходе системы массового обслуживания с внутренней и внешней параметрической зависимостью.
Основные соотношения
Пусть поток задан плотностями распределения
длительностей импульсов ![]() и пауз
и пауз ![]() . Обозначим их преобразования
Лапласа
. Обозначим их преобразования
Лапласа ![]() и
и
![]() соответственно.
После прохождения очередного импульса через аппарат прореживания с вероятностью
соответственно.
После прохождения очередного импульса через аппарат прореживания с вероятностью
![]()
![]() теряется
теряется ![]() импульсов.
Тогда изображения плотностей распределения длительностей импульсов
импульсов.
Тогда изображения плотностей распределения длительностей импульсов ![]() и пауз
и пауз ![]() выходного
потока соответственно равны:
выходного
потока соответственно равны:
![]() ,
,
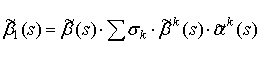
Последнее выражение следует из стохастического
уравнения для длительности ![]() паузы выходного потока при потере
паузы выходного потока при потере ![]() импульсов
подряд
импульсов
подряд
где ![]() - длительности пауз и импульсов
входного потока соответственно.
- длительности пауз и импульсов
входного потока соответственно.
Эти соотношения справедливы при зависимом и независимом прореживании. Отметим, что аналогичные результаты получены при рекуррентной децимации потоков однородных событий [4]. Рассмотрим частные случаи.
Независимое одиночное прореживание
В этом случае каждый импульс сохраняется в потоке с
вероятностью ![]() и
теряется с вероятностью
и
теряется с вероятностью ![]() .
.
Тогда ![]() и
и 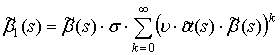
или
Начальные моменты ![]() -го порядка длительности пауз
выходного потока равны
-го порядка длительности пауз
выходного потока равны
![]() ,
,
здесь ![]() - производная
- производная ![]() - го порядка.
- го порядка.
В частности математическое ожидание длительности пауз прореженного потока равно
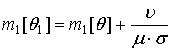
где ![]() - средние длительность пауз,
импульсов и частота следования импульсов входного потока.
- средние длительность пауз,
импульсов и частота следования импульсов входного потока.
Вероятность того, что случайный момент времени окажется в пределах импульса выходного потока (вероятностный параметр)[1] равна
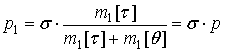 .
.
где ![]() - вероятностный параметр
входного потока.
- вероятностный параметр
входного потока.
Итак, определены все исходные данные, необходимые для вычисления корреляционной функции прореженного потока по общей формуле для АКФ обобщенного потока [3]
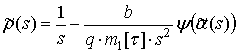 (3).
(3).
где b – постоянный коэффициент, ![]() ,
, ![]() - порождающая функция
потока [3].
- порождающая функция
потока [3].
Отметим важное свойство независимой одиночной децимации.
Оно заключается в эквивалентности многофазного (последовательного) прореживания
с параметрами ![]() однофазному прореживанию с параметром
однофазному прореживанию с параметром 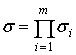 .В
справедливости этого утверждения легко убедиться путем поочередного использования
формулы (2) при вычислении изображения плотности
распределения длительности пауз потока на выходе последовательно включенных
аппаратов прореживания.
.В
справедливости этого утверждения легко убедиться путем поочередного использования
формулы (2) при вычислении изображения плотности
распределения длительности пауз потока на выходе последовательно включенных
аппаратов прореживания.
Устойчивость АКФ обобщенных
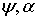 -потоков
к независимому одиночному прореживанию
-потоков
к независимому одиночному прореживанию
При проектировании систем, в которых СППИ выполняют
функцию управляющих сигналов, [3] желательно, чтобы в
процессе преобразования потоков не возникали дополнительные корреляционные
связи. Этого можно добиться, если использовать потоки, автокорреляционные
функции которых устойчивы к преобразованиям. По отношению к независимому
одиночному прореживанию свойством устойчивости обладают обобщенные ![]() - потоки [3],
что следует из приведенной ниже теоремы.
- потоки [3],
что следует из приведенной ниже теоремы.
Теорема. Пусть поток ![]() с
порождающей функцией
с
порождающей функцией
подвергается независимому одиночному прореживанию
с параметром ![]() .
.
Тогда выходной поток ![]() есть
есть ![]() -поток с порождающей
функцией
-поток с порождающей
функцией
где
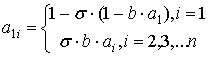
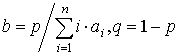 .
.
Доказательство. Подставив в (2) изображение плотности распределения пауз [3]
получаем
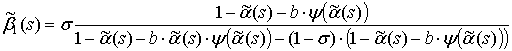 .
(7)
.
(7)
Обозначим
После подстановки (7) в (8) и выполнения необходимых преобразований, имеем:
![]()
или с учетом (4)
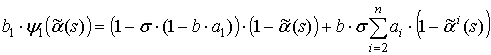
Подставив последнее выражение в (2)
и выполнив необходимые преобразования, убеждаемся, что ![]() . Следовательно,
выражение (5) справедливо и теорема доказана.
. Следовательно,
выражение (5) справедливо и теорема доказана.
Следствие 1. Время корреляции ![]() -потока в результате независимого
одиночного прореживания не изменяется. Известно [3], что
время корреляции обобщенного потока равно
-потока в результате независимого
одиночного прореживания не изменяется. Известно [3], что
время корреляции обобщенного потока равно
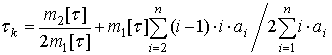 .
.
Подставив коэффициенты ![]() из (5)
убеждаемся, что время корреляции прореженного потока равно времени корреляции входного.
из (5)
убеждаемся, что время корреляции прореженного потока равно времени корреляции входного.
Следствие 2. Нормированная АКФ ![]() -геометрического потока [3] не изменяется в
результате независимого одиночного прореживания. Действительно,
-геометрического потока [3] не изменяется в
результате независимого одиночного прореживания. Действительно, ![]() -геометрический
поток является частным случаем
-геометрический
поток является частным случаем ![]()
![]() -потока при
-потока при
Подставив в (3) поочередно выражения
(9), (10) и учитывая, что вероятностный параметр выходного потока ![]() , убеждаемся,
что изображение
, убеждаемся,
что изображение ![]() АКФ прореженного потока равно изображению
АКФ прореженного потока равно изображению ![]() входного
потока.
входного
потока.
Оценим устойчивость АКФ потоков к другим видам децимации.
Биномиальное прореживание
Вид децимации определяется законом распределения ![]() . В
рассматриваемом случае
. В
рассматриваемом случае ![]() . Тогда изображение плотности распределения
длительности пауз прореженного потока равно:
. Тогда изображение плотности распределения
длительности пауз прореженного потока равно:
![]() .
.
Если входной поток ![]() -геометрический [2],
то
-геометрический [2],
то ![]() и
и
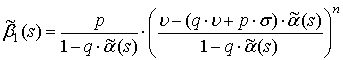 .
(11)
.
(11)
Выражение (11) не приводится к виду (6).
Следовательно, выходной поток не принадлежит к классу ![]() -потоков и
-потоков и ![]() -геометрический
поток неустойчив к биномиальному прореживанию.
-геометрический
поток неустойчив к биномиальному прореживанию.
Пуассоновское прореживание
В этом случае 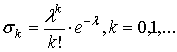
Тогда ![]() .
.
Для ![]() -геометрического потока
-геометрического потока
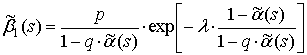 .
.
Как и в предыдущем случае изображение плотности
распределения не приводится к виду (6) и, следовательно, ![]() -геометрический
поток неустойчив к пуассоновскому прореживанию.
-геометрический
поток неустойчив к пуассоновскому прореживанию.
В заключение еще раз подчеркнем, что из всех рассмотренных случаев устойчивость АКФ обеспечивается только при независимом одиночном прореживании.
Селекция импульсов по длительности
Пусть ![]() - случайная неотрицательная величина с
плотностью распределения
- случайная неотрицательная величина с
плотностью распределения ![]() . Селекция осуществляется следующим
образом. Если длительность
. Селекция осуществляется следующим
образом. Если длительность ![]() импульса входного потока
импульса входного потока ![]() больше
больше ![]() , то импульс
передается на выход без изменений и тем самым включается в состав выходного
потока
, то импульс
передается на выход без изменений и тем самым включается в состав выходного
потока ![]() .
При
.
При ![]() импульс
теряется. Вследствие независимости длительностей импульсов процедура селекции является
частным случаем независимого одиночного прореживания с вероятностью
импульс
теряется. Вследствие независимости длительностей импульсов процедура селекции является
частным случаем независимого одиночного прореживания с вероятностью
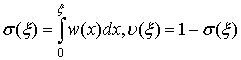 .
.
Поэтому характеристики выходного потока определяются
по приведенным выше формулам, при условии, что вероятность прореживания ![]() . На конечном
этапе расчета характеристики выходного потока следует усреднить по случайной
величине
. На конечном
этапе расчета характеристики выходного потока следует усреднить по случайной
величине ![]() .
.
Заметим, что аналогичные рассуждения применимы при селекции потока и по другим параметрам, например, по амплитуде или периоду следования (паузе).
Марковское прореживание
Пусть на вход устройства прореживания с вероятностью ![]() поступил
импульс входного потока
поступил
импульс входного потока ![]() . Этот импульс без изменений передается на
выход. Следующий входной импульс с вероятностью
. Этот импульс без изменений передается на
выход. Следующий входной импульс с вероятностью ![]() сохраняется в составе выходного
потока
сохраняется в составе выходного
потока ![]() и
с вероятностью
и
с вероятностью ![]() теряется. После потерянного следующий
входной импульс сохраняется с вероятностью
теряется. После потерянного следующий
входной импульс сохраняется с вероятностью ![]() и теряется с вероятностью
и теряется с вероятностью ![]() . Таким
образом, процесс прореживания описывается цепью Маркова с матрицей вероятностей
. Таким
образом, процесс прореживания описывается цепью Маркова с матрицей вероятностей
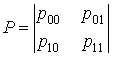 .
.
Заметим, что процедура Марковской децимации может служить моделью обнаружения одиночных сигналов на фоне коррелированной помехи.
Для упрощения последующих записей обозначим
![]()
При принятых обозначениях вероятность потери ![]() импульсов
подряд равна
импульсов
подряд равна
Из условия нормировки
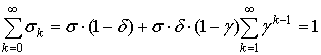
следует, что ![]() . Это согласуется с
описанной процедурой, поскольку цикл прореживания начинается только после
поступления первого импульса входного потока.
. Это согласуется с
описанной процедурой, поскольку цикл прореживания начинается только после
поступления первого импульса входного потока.
Длительность ![]() паузы выходного потока при потере
паузы выходного потока при потере ![]() импульсов
подряд описывается стохастическим уравнением (1), на
основании которого с учетом (12) можно записать:
импульсов
подряд описывается стохастическим уравнением (1), на
основании которого с учетом (12) можно записать:
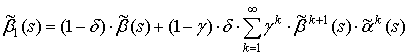
или
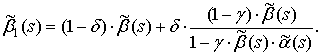
Среднее значение длительности пауз прореженного потока равно
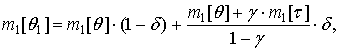
а средняя частота следования
импульсов ![]() и
вероятностный параметр
и
вероятностный параметр ![]() соответственно равны:
соответственно равны:
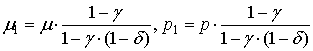 .
.
Изображение АКФ равно [3]
Прореживание с внутренней зависимостью (ресурсное обслуживание)
![]() В этом случае, как и раньше, после поступления
на вход аппарата прореживания импульса входного потока с вероятностью
В этом случае, как и раньше, после поступления
на вход аппарата прореживания импульса входного потока с вероятностью ![]() теряется
теряется ![]() импульсов, но
при этом вероятность
импульсов, но
при этом вероятность ![]() зависит от параметров входного потока.
Введем неотрицательную случайную величину
зависит от параметров входного потока.
Введем неотрицательную случайную величину ![]() с плотностью распределения
с плотностью распределения ![]() . Будем
считать, что теряется ровно
. Будем
считать, что теряется ровно ![]() импульсов входного потока, если выполняется
система стохастических неравенств:
импульсов входного потока, если выполняется
система стохастических неравенств:
![]()
Это означает, что теряются все импульсы, попавшие на
интервал длиной ![]() , начало которого совпадает с моментом
окончания некоторого произвольного импульса входного потока. Следовательно,
такое прореживание можно рассматривать как обслуживание требований одноканальной
системой с потерями. При этом под требованиями понимаются импульсы входного
потока, а время обслуживания равно
, начало которого совпадает с моментом
окончания некоторого произвольного импульса входного потока. Следовательно,
такое прореживание можно рассматривать как обслуживание требований одноканальной
системой с потерями. При этом под требованиями понимаются импульсы входного
потока, а время обслуживания равно ![]() . Очевидно, что вероятность
. Очевидно, что вероятность ![]() потери
потери ![]() импульсов зависит
от
импульсов зависит
от ![]() и
равна [5]
и
равна [5]
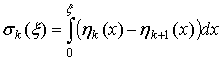 .
.
Здесь ![]() - плотность распределения момента появления
- плотность распределения момента появления
![]() -го
импульса
-го
импульса
![]()
вычисляется как свертка плотностей распределения длительностей импульсов и пауз. Тогда изображение плотности распределения длительностей пауз прореженного потока равно
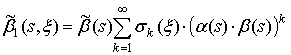 ,
,
а математическое ожидание длительности пауз определяется соотношением
![]()
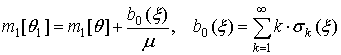 .
.
![]() На каждый обслуженный импульс с
вероятностью
На каждый обслуженный импульс с
вероятностью ![]() приходится
приходится
![]() потерянных.
Поэтому среднее число потерянных в одном цикле импульсов равно
потерянных.
Поэтому среднее число потерянных в одном цикле импульсов равно ![]() , а среднее
число импульсов в цикле обслуживания на единицу больше. Тогда стационарная
вероятность обслуживания равна отношению этих величин
, а среднее
число импульсов в цикле обслуживания на единицу больше. Тогда стационарная
вероятность обслуживания равна отношению этих величин 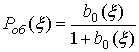 , а параметры
обслуженного потока вычисляются по формулам:
, а параметры
обслуженного потока вычисляются по формулам:
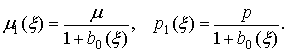
Преобразование Лапласа нормированной АКФ находим по формуле (13).
При практических расчетах параметров реальной системы
все характеристики обслуженного потока необходимо усреднить по ![]() .
.
Отметим, что случайная величина ![]() может определяться
только свойствами системы и не зависеть от параметров входного потока. Однако
предложенная методика анализа применима при анализе систем, в которых время
обслуживания
может определяться
только свойствами системы и не зависеть от параметров входного потока. Однако
предложенная методика анализа применима при анализе систем, в которых время
обслуживания ![]() зависит
от длительности импульса (ресурса), поступившего на обслуживание (накопление).
Такую модель можно использовать при исследовании систем накопления ресурсов или
систем обработки информации. В последнем случае время обслуживания
зависит
от длительности импульса (ресурса), поступившего на обслуживание (накопление).
Такую модель можно использовать при исследовании систем накопления ресурсов или
систем обработки информации. В последнем случае время обслуживания ![]() пропорционально
длине информационного блока, интерпретируемой как длительность
пропорционально
длине информационного блока, интерпретируемой как длительность ![]() импульса входного потока.
Например, можно принять
импульса входного потока.
Например, можно принять ![]() , где
, где ![]() - случайная величина, зависящая
от «сложности» поступившей на обработку информации.
- случайная величина, зависящая
от «сложности» поступившей на обработку информации.
Заключение
Анализ характеристик потоков, подвергшихся
прореживанию, показал, что независимое одиночное прореживание не изменяет
корреляционных свойств обобщенного ![]() -потока. При других видах прореживания (пуассоновском,
биномиальном) АКФ выходного потока отличается от АКФ входного вследствие
возникновения дополнительных корреляционных связей.
-потока. При других видах прореживания (пуассоновском,
биномиальном) АКФ выходного потока отличается от АКФ входного вследствие
возникновения дополнительных корреляционных связей.
Предложенные методы анализа могут быть применены при исследовании параметрических селекторов, обнаружителей одиночных импульсных сигналов на фоне коррелированной помех и одноканальных систем массового обслуживания с потерями. При этом во всех случаях единственным ограничением, накладываемым на входной поток, является требование независимости длительностей импульсов и пауз.
Литература
1. Седякин Н.М. Элементы теории случайных импульсных потоков. М.: Сов. радио, -1965.
2. Голик Ф.В. Потоки прямоугольных импульсов с «хорошей» автоковариационной функцией //Радиотехника и электроника. - 1991. - т. 36, № 11, с. 2141-2147.
3. Голик Ф.В. Случайные потоки импульсов с заданными корреляционными свойствами // Журнал Радиоэлектроника , – 2000. - № 7, http://jre.cplire.ru/jre/jul00/index.html.
4. Климов Г.П. Стохастические системы обслуживания. - М.: Наука , - 1966.
5. Голик Ф.В. Многомерные импульсные потоки в теории асинхронных радиотехнических систем //Радиотехника, № 2 - 1991. - с. 18-19.