EVALUATION OF THE STATISTICAL CHARACTERISTICS OF THE SIGNAL FADING IN SATELLITE RADIOLINKS
Adán Espinoza Millán 1, Esaú Vicente Vivas 2, Vladimir M. Shakhparonov 1
1 Lomonosov Moscow State University, 2 Universidad Nacional Autónoma de México (UNAM)
Received October 3, 2011
ÎÖÅÍÊÀ ÑÒÀÒÈÑÒÈ×ÅÑÊÈÕ ÕÀÐÀÊÒÅÐÈÑÒÈÊ ÇÀÌÈÐÀÍÈÉ ÑÈÃÍÀËΠ ÑÈÑÒÅÌÀÕ ÑÏÓÒÍÈÊÎÂÎÉ ÐÀÄÈÎÑÂßÇÈ
À. Ýñïèíîñà Ìèëüàí 1, Å. Âèñåíòå Âèâàñ 2, Â. Ì. Øàõïàðîíîâ 1
1Ìîñêîâñêèé Ãîñóäàðñòâåíèûé Óíèâåðñèòåò Èìåíè Ì. Â. Ëîìîíîñîâà
2 Óíèâåðñèòåò Ìåêñèêè (ÓÍÀÌ)
Abstract. The main objective of this paper is to find and identify the fading fluctuations in telemetry signals caused by no homogeneities of the communication channel. The employed methodology follows the next steps: remove the envelope of the signal amplitude; identifying the Gaussian component; identifying the non-Gaussian component and obtaining the statistical characteristics from Gaussian and non-Gaussian components. Then, the results are statistically treated in order to obtain a diffusion K parameter of Rician fading which are associated with fading in atmosphere and ionosphere layers. In this way the communications channel among satellite and ground station is characterized and a BER parameter can be obtained. The methodology is applied to telemetry signals of the Moscow State University microsatellite better known as “Universitetsky-Tatiana” and the results are discussed.
Keywords: ionosphere, fading, wavelets, satellite.
Àííîòàöèÿ. Îñíîâíîé öåëüþ ñòàòüè ÿâëÿåòñÿ îáíàðóæåíèå çàìèðàíèé ñèãíàëà, îáóñëîâëåííûõ íåîäíàðîäíîñòÿìè â êàíàëå òåëåêîìóíèêàöèé. Ïðèìåíÿåìàÿ ìåòîäîëîãèÿ îòâå÷àåò ñëåäóþùèì ýòàïàì: óäàëåíèå îãèáàþùåé ñèãíàëà; îáíàðóæåíèå ãàóññîâñêèõ è íåãàóññîâñêèõ êîìïîíåíò è ïîëó÷åíèå èõ ñòàòèñòè÷åñêèõ õàðàêòåðèñòèê. Òàêèì îáðàçîì ìîæíî îõàðàêòåðèçîâàòü êàíàë êîììóíèêàöèé è ïîëó÷èòü ïàðàìåòð âåðîÿòíîñòè îøèáêè (BER). Ìåòîäîëîãèÿ ïðèìåíÿåòñÿ ê òåëåìåòðè÷åñêèì ñèãíàëàì ìèêðîñïóòíèêà Ìîñêîâñêîãî ãîñóäàðñòâåííîãî óíèâåðñèòåòà «Óíèâåðñèòåòñêèé-Òàòüÿíà».
Êëþ÷åâûå ñëîâà: èîíîñôåðà, çàìèðàíèÿ, âåéâëåò, ñïóòíèê.
Introduction
In a satellite-Earth link it is common to find some factors that affect the transmission of signals. First of all an important factor is the free space loss, this factor depends on the distance between the satellite and the ground station (GS) as well as of the wavelength of the transmitted signal. Therefore, the attenuation of the signal can be predicted at each moment of the transmission as well as the final waveform of the signal. Other considerable affecting factors are the thermal noise present in the transmitter and a Gaussian noise present in the communications channel. In spite of the previous affecting factors, it is possible to foresee the characteristics of the signal in the receiver. Another factor that generates serious fluctuations in all parameters that define the signal (phase, amplitude and frequency) is the multipath propagation or multipath fading.
The multipath fading is a good indicator of fluctuations both in ionosphere and troposphere, [1], [2] and [3]. The study we aim to carry out is based in the observation of both the characteristics and changes of the transmission channel. The classical idea to model a radio communication channel includes the free lose effect as well as the Gaussian and thermal noise in the carrier signal. However, for some more detailed modeling it is necessary to considerer the presence of path fading. In this case we considered the use of statistical models.
Statistical models of fading fluctuations
The fading phenomenon occurs when the signal travels over several refractive and reflective paths generating multiple interfering signals. When all these signals arrive to the receiver, the signal experiment fluctuations in amplitude and phase. This process can be described through its impulse response [4]:
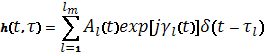 (1)
(1)
Where: ![]() and
and ![]() are independent random processes
representative of the fading amplitude and phase. Then the received signal
are independent random processes
representative of the fading amplitude and phase. Then the received signal ![]() can be modeled by:
can be modeled by:![]() , where
, where ![]() , is the transmitted signal.
The impulse response
, is the transmitted signal.
The impulse response ![]() and the received signal
and the received signal ![]() are random processes and
their statistical behavior depends on the number of interfering signals.
Several statistical models have been proposed to characterize fading channels.
These models are based in the amplitude probability density function of the
are random processes and
their statistical behavior depends on the number of interfering signals.
Several statistical models have been proposed to characterize fading channels.
These models are based in the amplitude probability density function of the ![]() or
or![]() .
.
In general in a radio link the fading process can be divided in two types: large scale fading and small scale fading [5]. The large scale fading can be characterized by a shadowing model. In this type of fading the amplitude density function is normal when the amplitude is measured in decibels and becomes log normal when the amplitude is measured in watts. The normal standard distribution is defined as follows [4]:
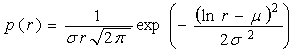 (2)
(2)
Where
![]() is the mean value of
is the mean value of
![]() and
and ![]() is
the standard deviation of
is
the standard deviation of
![]() .
.
The small scale fading is the result of signal scattering or interference from other signals with similar frequencies. If the small fading in a radio link is significant enough, the amplitude distribution of the signal becomes a Rayleigh distribution. Besides, it is common to use the Rayleigh distribution for narrow band non-line-of sight (NLOS) channels. The Rayleigh´s probability density function of the signal amplitude, [4], is given as:
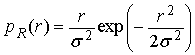 (3)
(3)
Where
![]() the amplitude of the signal and
the amplitude of the signal and
![]() is the average energy of the signal.
is the average energy of the signal.
When the channel has a
predominant signal component (this commonly occurs in a line of sight, LOS,
channel) the distribution will become a Rician distribution. The ratio between
the predominant power signal and the multipath power is known as the Rician K
factor. The K factor is a measure of the multipath fading of the channel. When![]() , there is not multipath fading, however,
when
, there is not multipath fading, however,
when![]() , the channel is only multipath and the
distribution becomes Rayleigh.
, the channel is only multipath and the
distribution becomes Rayleigh.
The probability density function of the signal amplitude in Rician fading is given by:
 (4)
(4)
Where s is the magnitude
of the predominant signal component,
![]() is the power of the
predominant component,
is the power of the
predominant component,
![]() is the power of the scattered component and
is the power of the scattered component and
![]() is the modified first kind and zero order
Bessel function. The K factor could be expressed as [4]:
is the modified first kind and zero order
Bessel function. The K factor could be expressed as [4]:
![]() (5)
(5)
Because in a LEO satellite link the channel model changes frequently, the probability distribution of the signal amplitude data also changes repetitively. Actually, in most of the cases we find that this distribution is a mixture of some distributions because of the large path the signal should cover. The Susuki, Loo and log normal Rician models are described by a mixture of distributions and they were developed for different fading environments. The Susuki’s distribution combines the Rayleigh distribution and the log normal distribution. While the Loo distribution is the sum of the log normal and Rayleigh phasors. In addition, the rice log normal model is the multiplication of the Rician and log normal phasors [4].
In LEO satellite communications it is clear that the channel changes not only in each overpass, but also at each moment during this overpass. If a satellite is located in the horizon, there exists NLOS and then the multipath fading probably corresponds to a Rayleigh Fading. On the other hand when the satellite is located in the zenith there is LOS and the multipath fading could be Rician or Log Normal according to the ionosphere and whether conditions. The conclusion is that we have a dynamic channel that constantly changes its characteristics and it is necessary to obtain these characteristics during the data transmission in order to improve the BER values.
Review of proposals for study the fading phenomenon in radio-communication systems
Fading channels represent a big problem when a radio link is designed, especially in mobile communication systems such as mobile telephony, mobile radio networks, and so on. Therefore, the study of fading channels is a current issue in the Radio communications field, and several papers report on the modeling of the fading channel and propose possible solutions. In the publication of Michael Monnerat et al. [6], a simulation is performed around 3 types of specific modulations (SRC, BPSK and BOC). In addition, three types of channels were chosen: AWGN, Rician and Rayleigh. Besides, a determinate bandwidth was proposed. The obtained results in that paper describe the transmission behavior for each type of modulation over all chosen fading channels. However, there were no considerations about the possible changes in the channel. Its channel model was a static model that only solved specific transmission cases in multipath fading. In the work exposed by V. Sridjara et al. [7] a simulation of urban fading channel is analyzed. In this paper all fluctuations in an urban channel are included. The obtained results are much more reliable than the ordinary 2 ray model or free-space model. The considerations made in this work are the considerations that should be made when trying to design a wireless mobile communication system, taking into account slow and fast fading, reflections, diffractions, scattering, delays, and so on. V. Sridjara proposes a simulation tool which is a good instrument to model realistic propagation channels; however, the considerations that should be done and the required calculation time, increase the complexity of the simulation. Therefore, in this paper we present the first step to create a dynamic system in order to practically characterize the communication channel in real time, as well as the parameters that determinate its fluctuations, which in this case are obtained from the signal itself.
Kohei Ohata et al. [8] examine the scheme of a broadband mobile satellite communication system for networks. This proposal considers the Rician channel as the worst case multipath fading; it compares the principal multiplexing types (FDMA, CDMA and TDMA) and use the multi-frequency reuse strategy. However, it does not consider the changes in the channel. In addition, in the paper written by Seher Sener et al. [9] presents a performance study of multitone DS-CDMA system and the orthogonal MC DS-CDMA system over Nakagami fading channels for different fading values, where the convenience of one system or another depends on this parameter and the signal to noise ratio. These two papers describe possible solutions to avoid transmission problems in wireless satellite networks due to fluctuations in the mean channel. Though, this is a specific fading channel and it does not consider changes. Although it is common in satellite communication systems to calculate the signals amplitude under determinate fluctuations; this work assumes this calculation as insufficient.
Other authors studied different adaptive techniques in fading channels such as coding, adaptive modulation and diversity techniques, that is the case of the work performed by Ali F. Almutairi et al., [10]. The main results of this work shows that the effects of these techniques are dissimilar for different fading noises and it is necessary to perform a dynamic system that works with channel changes. By this reason, the channel should be characterized frequently at each moment of the transmission. From the point of view of the authors, the optimal solution is the application of correction coding techniques for fading channels [11, 12] to reduce the BER when the transmission takes place.
By its side, V. I. Zakharov and A. C, Zienko [13] completed an ionosphere fluctuation detection method based on the study of the statistical characteristics of the wavelet signal transform. Once the wavelet transform is calculated, the maximums and minimums of each scale are obtained to deduce the time periods and poly-periods at each frequency. When a signal component was identified, for subsequent analysis the component was filtrated and isolated from other components corresponding to the mean signal. In contrast with Zakharov’s method, this paper discusses the separation of the signal components that correspond with a fast fading and slow fading fluctuations.
Based on these results, a diagnosis of the ionosphere conditions could be formulated.
Considering that the goal of this work is to determine the multipath fading effect within every one of the signals records captured at the satellite GS as well as to associate the fading process with transmission errors. The authors used a method to carry out this analysis consisting in obtaining the probability distribution of the signal amplitude. In case the distribution becomes a non-parametric distribution the signal has to be decomposed in multiple signals with the help of wavelet techniques. With these results the fading distributions contained into the total distribution of the signal amplitude data have to be found. In this way the communication channel can be modeled and a BER can be found for each data transmission when the satellite overpasses its GS.
Wavelet theory
Wavelet signals have limited duration and an average value of zero. To perform a wavelet transformation it is required not only a wavelet but also a family of wavelets. The mathematical expression for a wavelet family function, [14], is:
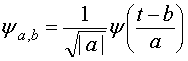 (6)
(6)
Where, values “a” and “b” are both real and positive.
In the time domain, other function members of a wavelet family are created when a translation, delay or width change of the wavelet mother is performed. The wavelet mother is the mean wavelet of the family, then, in order to perform the wavelet transformation the next expression has to be solved [14].
![]()
Where, parameters “a” and “b” are functions of both time and frequency.
The CWT is defined by the expression 7:
![]() (7)
(7)
The result of the wavelet transform is a group of wavelet coefficients C, which are a function of both scale and position. It is possible to understand these coefficients like a result of many correlations between a signal and the wavelet mother, shifted and scaled many times.
CWT could be difficult to obtain or could demand big computational resources, so in some cases when it is required a fast calculation, CWT is not efficient. To reduce the calculation work we can choose a subset of scales and positions to make calculations easier. Choosing scales and positions based on powers of two (so-called dyadic scales and positions) makes the analysis much more efficient and accurate, this process is named discrete wavelet transform (DWT)
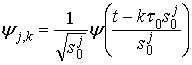 (8)
(8)
The discrete form of expression 6 is shown in expression 8; evidently S0 should be equal to 2 in order to obtain a dyadic sampling. It is possible indeed to reconstruct a signal from the decomposition of its wavelet series.
In 1988 Mallat developed an efficient way to obtain DWT using filters. The Mallat algorithm, [15], is a classical scheme known in the signal processing community as a two-channel sub-band. This very practical filtering algorithm yields a fast wavelet transform, in other words, it is a box where signal passes, and out of which wavelet coefficients quickly emerge. DWT deals with approximations and details. The approximations are the high-scale, low-frequency components of the signal, while details are the low-scale, high-frequency components.
The DWT property to get decomposition in high and low frequencies is employed for separating LOS and NLOS fading from the signal amplitude. The coefficients with slow changes are associated with the LOS and those that change quickly are associated with NLOS. For this purpose a wavelet that changes faster and requires fewer levels of decomposition is needed to detect NLOS components, therefore, the LOS components also can be detected. In this way the approximations can be recovered and fitted with the expected distributions.
With the purpose of obtaining the fading components of the signal it is necessary to use a wavelet threshold technique suitable for heavy tail distribution noises. The problem is that practically all the wavelet threshold techniques were created for removing Gaussian noise from noisy data and others kind of noises are no considered. In the last two decades several authors have been studied new wavelet threshold methods that work well for some kind of non-Gaussian noises especially in images processing [16, 17]. Bayesian, Level Dependent Cross Validation and Two Fold Cross Validation [18, 19] methods are very efficient in image processing to remove non-Gaussian noise. In this paper the Two Fold Cross Validation method has been chosen since this method provides the best results for heavy tail distribution noises [18].
Methods
In this paper it is proposed a method to detect fading components within the signal amplitude. The methodology requires the application of a group of statistical techniques that allow comparing the data with the Rayleigh, Rician or Log normal distributions. In fact, before any data processing is performed, the application of a Gaussian test is necessary to know if the signal amplitude distribution corresponds to a simple shadow fading. In case that the signal amplitude data does not correspond with shadow fading then the application of a different test is necessary to evaluate if the data correspond to a Rician or Rayleigh fading. Whenever the data information does not correspond to any of these distributions the data decomposition will be started. Once data processing and decomposition are completed, the application of tests has to be applied again.
In order to evaluate if data fitted a Gaussian distribution, the Lillilifors test [20] was selected. Lillilifors test is based in calculating the mean value and the variance of data series and then calculating the cumulative distribution function (CDF) of the data. Later, the theoretical Gaussian CDF with the mean and variance of the data is calculated. The next step consists in obtaining the maximum discrepancy between the CDF data and the theoretical CDF. The value of the maximum discrepancy confirms if the data distribution corresponds with a Gaussian distribution.
In addition, in order to know if the data distributions corresponded with Rician or Rayleigh distributions, the Kolmogorov-Smirnov test [20] was employed in this paper. This test works in the same way as the Lillilifors test; however the referred distribution should be established in advance.
The criterion to accept the hypothesis that the data distributions correspond to a Log normal, Rician or Rayleigh distribution is the value of the maximum discrepancy of the tests. A common value used in the literature is 5 %. This work considers that data distributions fit with the already mentioned Log normal, Rician or Rayleigh distributions when the maximum discrepancy value is less than 5%.
To achieve the detection of multipath fading a first step has to be achieved to decompose the signal amplitude into fading components with the help of DWT. Then the detection of Rician, Rayleigh or Lognormal components of all signal amplitude fluctuations data is performed. To systematize the previous analysis the use of wavelet packets was proposed. Figure 1 shows the signal amplitude fluctuations and their distributions, from this figure it is seen that the distribution is not a regular distribution, so, it is necessary to decompose it. The signal amplitude is given in dBm.
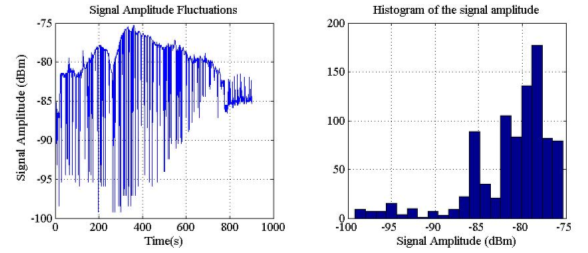
Figure 1. Amplitude graphics of telemetry signals from Universitietsky satellite: signal amplitude vs. time and histogram of signal amplitude.
In order to decompose the signal amplitude fluctuations it was employed DWT using the wavelet “DMeyer” with 2 levels of decomposition. The decomposition in wavelet package is necessary to establish the best wavelet tree. In this case the best wavelet tree matches up with the wavelet tree of the common DWT.
Figure 2 shows signal LOS fading and NLOS fading. In this case the LOS fading follows a Gaussian distribution, while the NLOS fading is in fact a Rician noise with a low value of K factor. The distributions are given in figures 3 and 4, where a sharp fit of decomposition data with the expected distributions is seen.
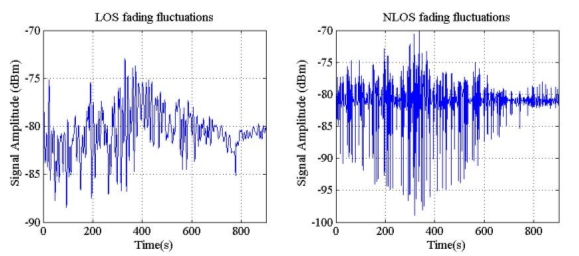
Figure 2. Decomposition of signal in: LOS large scale fading and NLOS small scale fading.
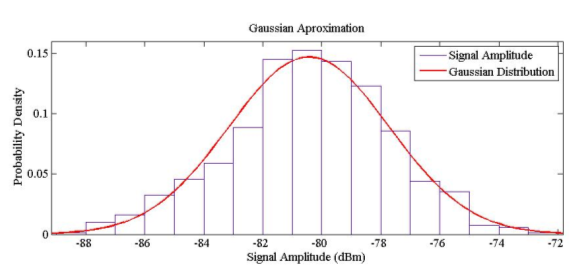
Figure 3. Approximation of NLOS fading data to Gaussian distribution.
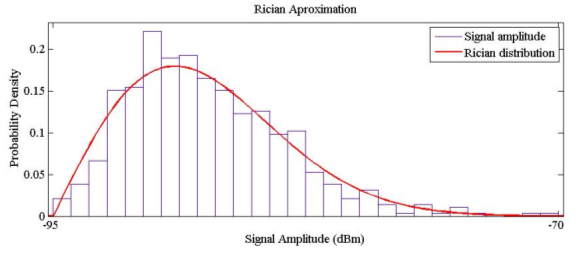
Figure 4. Approximation of LOS fading to Rician distribution.
The performed analysis showed that the mean of the Gaussian distribution component is equal to -81.2 dBm and the standard deviation is equal to 2.95 dBm and for the Rician distribution component the K factor is less than 10-3. It should be highlighted that this distribution is practically a Rayleigh distribution.
Examining the results obtained for this signal, it is seen that there are certain components of the signal that accomplish a Rayleigh distribution, therefore, it is concluded that the path of the transmitted signal was completely dispersive at some instants of the satellite trajectory.
The full study was performed with 7500 signals as well as with software written in Matlab. First of all, the software checked for fluctuations in all amplitude signals with no Gaussian distribution. Therefore, when fluctuations in the signal amplitude became Gaussian the program considered that fluctuations represented only a log normal fading. When the distribution is not Gaussian the analysis continues with the signal amplitude decomposition in a Rician and Rayleigh fading components. Finally, the fading distribution and the statistical characteristics, that model the channel, are obtained by the program. The software employs. The Lillilifors test [20] is employed to evaluate if data are Gaussian (signal amplitude is measured in dBm). When the test fails after signal decomposition the Kolmogorov-Smirnov test is employed by the program to identify which distribution approaches better the data.
In conclusion, the software performs the Gaussian test, the decomposition of the signal amplitude, the distributions fitting, and the calculation of statistical parameters that characterize the channel and also displays the power spectrum of the large scale and small scale fading. The exposed analysis was performed over 7500 recorded signals.
Results and discussion
This paper shows the data analysis performed on multiple satellite telemetry signals. From them, 256 signals were unable to be analyzed because of their low amount of data. About 960 decompositions of signals fit with normal distribution, 853 fit with Rician distribution and 2100 signals decompositions fit with Rayleigh distribution.
The K factor values of the Rician fading for 853 signals decompositions is shown in figure 5. In addition, the mean power values of the Rayleigh fading for 2100 signals decompositions is shown in figure 6.
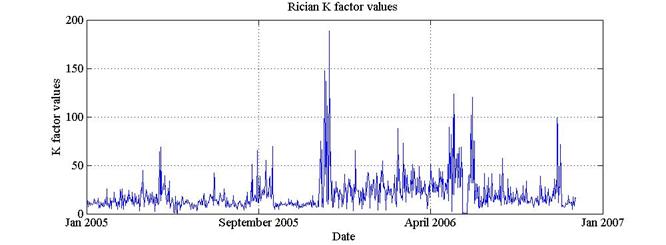
Figure 5. K factor for 853 decompositions of signals in Rician fading.
We can make few observations about the obtained results. When certain components of the analyzed signals are consistent with a Rayleigh distribution it is clear that a dispersive medium is present at some point in the trajectory among satellite and GS, however, it is also possible to find present more than one single medium in this route. Actually, this phenomenon could be repeated several times at various points in the communications path. Then, in order to detect areas where highly dispersive media are presented it is possible to perform the analysis by dividing the trajectory into several parts and then observing the results. The size of the dispersive areas that can be detected depends on the sampling frequency with which the signal amplitude is measured. If the sampling rate is high, relatively small areas can be detected. If the frequency is low, large areas could be detected.
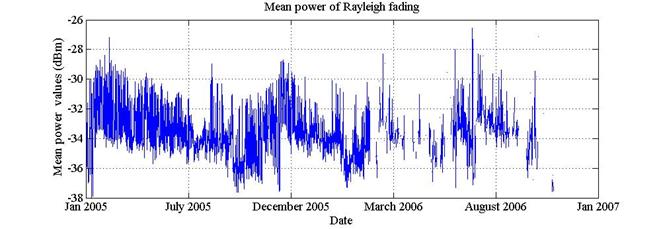
Figure 6. Values of mean power of 2100 signals decompositions in Rayleigh fading.
The same reflections
can be formulated for Rician distribution components. Different dispersive
media with different degrees of dispersion could exist in the signal
trajectory. However, in this case and for applications in radio communications
it is not strictly necessary to know the changes of the dispersion coefficient
in the fading environment, if and only if this ratio remains within the
accepted range for good transmission. However, the fading coefficient can be a
measure of ionosphere activity. Changes in the values of the fading coefficient
may be used to investigate variations in the concentration of charged particles
in the ionosphere plasma. For example, on the basis of the K Rician factor
scintillation index ![]() in each satellite
overpass can be calculated by the expression:
in each satellite
overpass can be calculated by the expression:
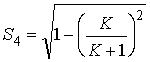 (9)
(9)
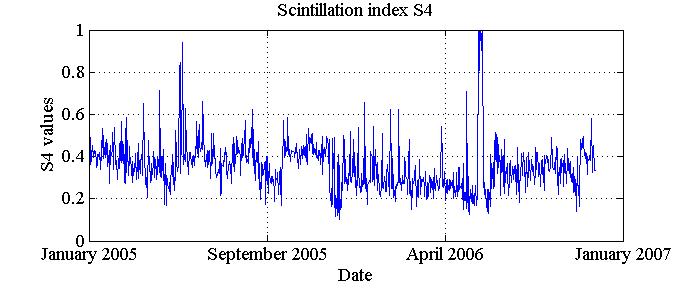
Figure 7. Scintillation index![]() Values related with the K Rician factor values from figure 5.
Values related with the K Rician factor values from figure 5.
If we strictly talk about the ionosphere, highly dispersive media can occupy large areas during long time. They can also occupy small areas during some minutes. The difference between the dispersive effect due to non-homogeneities in the ionosphere and the dispersive effects due other sources such as the presence of large buildings or wooded areas could be detected after analyzing the fading components of the signal amplitude in these areas and comparing it with the ionosphere fading. The fading due to urban and wooded zones has been already studied and some models have been suggested to understand this process. The characteristics of these models can be used to separate the fading fluctuations due to Ionosphere activity from those due to other sources.
Then, an associated BER can be obtained with the fading results obtained from each satellite overpass. These results show a type of multipath fading noise and its data transmission effects from the Universitetsky-Tatiana satellite.
The graphics of BER vs Eb/No for Universitetsky-Tatiana satellite telemetry signals in Log normal, Rician and Rayleigh fading channels is shown in figure 8.
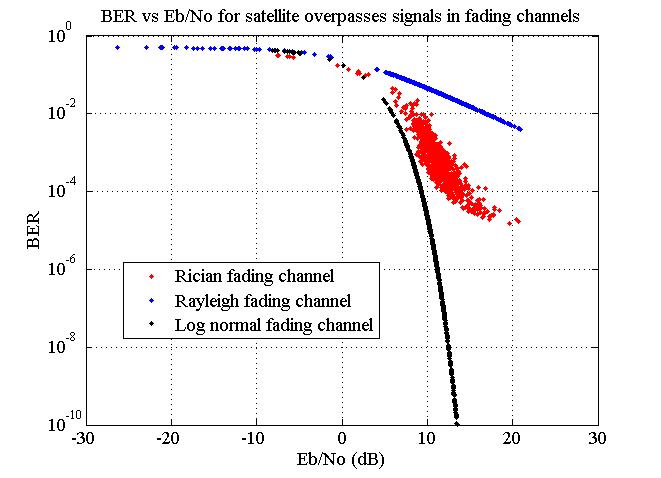
Figure 8. Graphics of BER vs. Eb/No for satellite telemetry signals in log normal, Rician and Rayleigh fading.
The BER value is the most important parameter to considerate in wireless communication systems, therefore, the system design should accomplish the transmission process with a determinate BER. The solutions that fulfill this requirement are generally the implementations of some: anti-noise codes, expansion of the bandwidth or, a special type of modulation. The channel fluctuations in satellite systems are varied and could change at the time of transmission. The results presented here show that at each satellite overpass, the channel could behave as Rician, log normal, Rayleigh or a mixture of them. Besides, changes were observed in the SNR ratio. These problems might be found during the operation of the next satellites from Moscow State University, so this paper is focused to find an optimal solution to improve the channel BER. A technique proposed in [5], consists in placing an array of antennas and receivers to make correlations of the received signals as well as corrections. However, in terms of cost this solution is not optimal especially for a University project.
A different method is the adaptive modulation [10] which is utilized in wireless systems. It changes the modulation type according with the channel characteristics. This solution is more feasible and more convenient although its satellite implementation could be complex.
According with the experience of authors, the best solution is error coding [10, 11-12]. In this technique, the channel code utilized in the transmission can be changed according with changes in the channel characteristics.
Figure 9 shows the relationship between the Eb/No and BER parameter for different error correction codes.
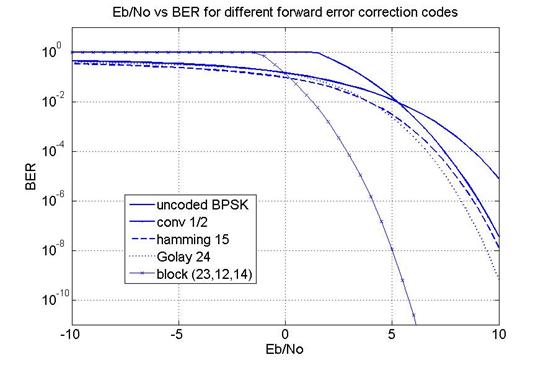
Figure 9. BER vs. Eb/No for different forward error correction codes.
It should be highlighted that some codes work better to determinate Eb/No values. Besides, adaptive error coding schemes can improve the transmission quality in satellite links when changes in the channel characteristics are known. In future works the authors will propose a system based in adaptive error coding schemes and characteristic channel detection which will be very useful for next generations of small satellites.
Concluding Remarks
This paper has made a deep study of the communications channel fluctuations due to fading phenomena for the “Universitetsky-Tatiana” microsatellite through wavelet techniques. The telemetry signals from the 30 Kg microsatellite were decomposed both in LOS and NLOS fluctuations to find the parameters of each distribution. The results of this analysis are of great importance for channel characterization in future satellite missions.
Particularly, the K factor was obtained for the LOS Rician distribution as well as the density for its NLOS Rayleigh distribution in order to determinate the degree of signal dispersion. With this information the signal dispersion was associated with changes in the communications channel. Above all, the observed K variations of the Rician distribution, obtained from the signal analysis, represent physical variations in the atmosphere layers. The K factor was also associated with the BER parameter obtained at each satellite overpass. In this case the authors found that the bigger the K variation the smaller the BER.
Conversely, the density of the Rayleigh distribution showed information losses generated by multipath fading in urban regions. In addition, as a solution to the problem, the paper commented about possible solutions such as: arrays of antennae and receivers as well as adaptive modulation and adaptive error coding.
Furthermore, the authors believe that the best solution to reduce data errors due to multipath fading is to use adaptive error coding schemes along with real time channel analyzer algorithms. The authors also suggest the utilization of such channel analyzer algorithms to implement the theory exposed in this paper.
References
[1] O. I. Yakovlev, J. Wickert, A. G. Pavelyev, S. S. Matyugov, V. A. Anufriev, Sporadic structures in equatorial ionosphere as revealed from GPS occultation data, Acta Astronautica, Volume 63, Issues 11-12, December 2008, Pages 1350-1359
[2] Michela Muñoz Fernández, Victor A. Vilnrotter. Coherent optical array receiver for PPM signals under atmospheric turbulence, Acta Astronautica (2006), vol. 58, 633 – 641
[3] Masashi Hayakawa, VLF/LF Radio Sounding of Ionospheric Perturbations Associated with Earthquakes, Sensors 2007, vol. 7, 1141-1158, Switzerland
[4] Matthias Pätzold, Mobile fading channels, John Wiley & Sons, Ltd. 2002 ISBN: 0-471-49549-2
[5] Claude Oestges, Bruno Clerckx, MIMO wireless communications, Hardbound, March 2007, Academic Press, pp. 480
[6] Michel Monnerat, Bruno Lobert, Impact of the transmission channel on galileo signal performance, Acta Astronautica (2002), vol. 51, No. l-9, 285-293
[7] Vinay Sridhara, Stephan Bohacek, Realistic propagation simulation of urban mesh networks, Computer Networks (2007), vol. 51, 3392–3412.
[8] Kohei Ohata, Kiyoshi Kobayashi, Katsuya Nakahira, Masazumi Ueba, Broadband and scalable mobile satellite communication system for future access networks, Acta Astronautica (2005),vol. 57, 239 - 249
[9] Seher Sener, Ibrahim Develi , Nurhan Karaboga, Further performance analysis of the generalized MC DS-CDMA system in Nakagami-m fading channels, Computers and Electrical Engineering (2009), vol. 35, 1–8
[10] Ali F. Almutairi , Salem Salamah, Spectral efficiency improvement for LMDS systems using adaptive techniques in fading channels, Computers and Electrical Engineering (2006), vol. 32, 299–311
[11]Vidhyacharan Bhaskar, and Laurie L. Joiner, Adaptive rate coding using convolutional codes for asynchronous code division multiple access communications over slowly fading channels, Computers & Electrical Engineering Volume 31, Issue 3, May 2005, Pages 217-240
[12]Alex Grant, Co-channel interference reduction in Rayleigh fading channels, Digital Signal Processing Volume 16, Issue 5, September 2006, Pages 619-627 Special Issue on DASP 2005
[13] V. I. Zakharov and A. C, Zienko, A method for statistical wavelet analysis of ionospheric GPS signals, Moscow University Physics Bulletin, Vol. 62, no. 2, April de 2007, pp. 108-112.
[14]. Cohen A. Wavelets and multiscale signal processing, Chapman and Hall. 1995, pp. 238
[15] Mallat, S. A theory for multiresolution signal decomposition: the wavelet representation, IEEE Pattern Analysis and Machine Intelligence (1989), vol. 11, no. 7, 674–693
[16] Saraswathi Janaki Samusarma, Mary Brinda, “Denoising” Of Mixed Noise in Ultrasound Images, IJCSI International Journal of Computer Science Issues, Vol. 8, Issue 4, No 1, July 2011. 517-523.
[17] H. Rabbani, Statistical Modeling of Low SNR Magnetic Resonance Images in Wavelet Domain Using Laplacian Prior and Two-Sided Rayleigh Noise for Visual Quality Improvement, Measurement Science Review, Volume 11, No. 4, 2011. 125-130
[18] Alsaidi M. Altaher, Mohd T. Ismail, A Comparison of Some Thresholding Selection Methods for Wavelet Regression, World Academy of Science, Engineering and Technology Issue 62 2010. 119-125
[19] Guangfen Wei, Feng Su and Tao Jian, Study on the Robust Wavelet Threshold
Technique for Heavy-tailed Noises, Journal of computers, vol. 6, no. 6, June 2011. 1246-1253
[20] Lilliefors, H.W., On the Komogorov-Smirnov test for normality with mean and variance unknown, J.Am.Stat.Assoc. (1967), vol. 62, 399-402.