ОЦЕНКА СРЕДНЕГО КВАДРАТА ИНТЕНСИВНОСТИ СВЕТА ИЗ ФОТОЭЛЕКТРОННЫХ СТАТИСТИК
Е.
С. Саркисян
Институт радиотехники и электроники им. В.А.Котельникова РАН,
Институт радиофизики и электроники НАН Армении
Получена 21 сентября 2011 г., после доработки – 18 октября 2011 г.
Аннотация. Рассмотрены следствия двух способов обработки выхода фотоэлектронного умножителя, касающиеся дисперсии производимых оценок. Рассмотрение касается детектирования излучения, производящего в среднем менее одного одноэлектронного импульса за время корреляции флуктуаций интенсивности излучения. Отличие соответствующих дисперсий тем больше, чем более выражен импульсный характер излучения.
Ключевые слова: детектирование слабого света, статистика интенсивности света.
Abstract. Consequence of two methods of processing a photomultiplier output is considered, related to the variance of the estimates obtained. Detection of a radiation producing in the average less than one photoelectron per radiation intensity correlation time is presumed. Distinction between the variance of the respective estimates proves to become greater as pulsations of the light intensity grow.
Keywords: detection of weak light, light intensity statistics.
Вопрос статистической точности измерения вероятностных характеристик света привлек достаточное внимание уже в первые годы развития техники счета фотонов. Преимущественно рассматривалось измерение первых двух моментов и простейшей корреляционной функции числа регистрируемых фотоэмиссий или соответствующих характеристик интенсивности света [1, 2, 3]. Ниже сравниваются статистические точности для двух процедур определения среднего квадрата интенсивности слабого света. Такая задача возникает в разных экспериментах [1, 2]. Обращение к этому вопросу, связано с рассмотрением в [4] двух процедур обработки значений реализации случайной функции при измерении среднего квадрата этой функции и вызвано, в сущности, необходимостью обойти особенность детектирования слабого света, состоящую в отсутствии возможности считывания мгновенных значений интенсивности. (Обсуждение связи вероятностных характеристик света и производимого им тока является неотъемлемой частью современных спецкурсов статистической оптики, например, [5].)
Рассмотрим фотоэлектронный умножитель (ФЭУ) с пренебрежимым уровнем собственных шумов, детектирующий свет флуктуирующей во времени t интенсивности I(t). Последнюю будем предполагать реализацией некоторого, удовлетворяющего условию эргодичности, процесса [6] с одномерной плотностью распределения вероятностей (ПРВ) p0(I).
Освещенная площадь фотокатода и спектральная ширина света полагаются достаточно малыми, что позволяет говорить о постоянной поверх катода эффективности η преобразования света приемником. Выход ФЭУ представляется последовательностью импульсов от отдельных фотоэмиссий. В последующем будем оперировать отсчитанным числом (фотоотсчетом) n одноэлектронных (ОЭ) импульсов, зарегистрированных на аноде в отдельном временном интервале счета длительности Т много меньшей времени корреляции флуктуаций интенсивности.
Положение повторяющихся интервалов счета на временной оси может быть произвольным, обеспечивающим взаимную независимость чисел n, или привязанным к определенным временным отметкам. Для факториальных моментов n(к) (к- целое положительное число) независимых отсчетов имеет место соотношение (см. напр. [1, 6] )
где I – значение интенсивности на отдельном интервале счета, угловые скобки означают операцию вероятностного усреднения по всему множеству значений величины в них, а цифровой индекс при скобке (а в дальнейшем–и при n и I ) устанавливает, если не указано иное, соответствие величины в скобках вероятностному процессу (или его реализации), характеризуемому ПРВ с тем же цифровым индексом. Рассматривается важный для практики случай, когда среднее число отсчетов за время корреляции интенсивности исследуемого света меньше единицы.
Пусть за достаточно протяженное время Тe на анод ФЭУ поступает N (много большее единицы) OЭ импульсов. При таком же числе произведенных за указанное время независимых отсчетов обычная оценка среднего квадрата интенсивности, как следует из (1) есть (ср. [1] )
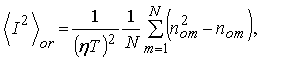 (2)
(2)
где nom отсчет в m-ом интервале счета.
Пропорциональность вероятности регистрации ОЭ импульса в малых (меньших Т) временных интервалах значению интенсивности на них ведет [4] к ПРВ интенсивности в малой окрестности моментов наступления этих импульсов вида p1(I) = I p0(I) / á I ñ0 со средним á I ñ1 = á I2 ñ0 / á I ñ0 , что позволяет писать
где á n ñ1 есть среднее отсчетов n1 для множества интервалов Т, лежащих в указанной окрестности. За оценку величины á n ñ0 разумно брать NT / Te , что обеспечивает существенно меньший относительный разброс ее вокруг среднего значения в сравнении с соответствующим разбросом стандартной оценки величины á n ñ1, используемой ниже в формуле (4). Тогда при пренебрежении разбросом указанной оценки величины á n ñO вокруг истинной формула (3) предписывает следующую процедуру получения оценки значения áI2ñ0
где суммируются отсчеты в привязанных интервалах счета (здесь может обнаружиться краевой эффект- близость последних ОЭ импульсов к концу времени Те - и потребоваться время большее Те на величину порядка Т).
Дисперсия величины á I2 ñor есть
Дисперсия суммы в (4) содержит
N(N-1)/2 средних произведений отсчетов для всех пар интервалов счета, лежащих
в указанных выше окрестностях, с заданными порядковыми номерами, но не с
заданным положением во времени. Положение каждого из этих интервалов случайно.
Поэтому вычисление среднего каждого произведения должно проводиться в два
приема: усреднение произведения при фиксированном положении выбранных двух
интервалов счета, а затем - усреднение по множеству положений с учетом
ограничения, накладываемого конечным (возможным в конкретном случае) положением
интервалов счета. Среднее произведения n1i n1k отсчетов в двух фиксированных интервалах счета есть ![]() < I1i I1k> (см. например, [1]), где в угловой скобке перемножаются интенсивности в
моменты ti
и tk наступления i-го и k-го импульсов. В
рассматриваемом случае двумерная плотность распределения вероятностей
соответствующих интенсивностей I1i и I1k есть u1(I1i , I1k) = I1i u0(I1i , I1k) / <I>0
,
где u0 – соответствующее распределение рассматриваемого
(исходного) процесса.
< I1i I1k> (см. например, [1]), где в угловой скобке перемножаются интенсивности в
моменты ti
и tk наступления i-го и k-го импульсов. В
рассматриваемом случае двумерная плотность распределения вероятностей
соответствующих интенсивностей I1i и I1k есть u1(I1i , I1k) = I1i u0(I1i , I1k) / <I>0
,
где u0 – соответствующее распределение рассматриваемого
(исходного) процесса.
Таким образом, общее среднее < n1i n1k> задается дополнительным усреднением величины
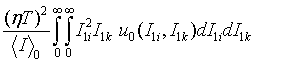
по совместному распределению времен ti и tk.
Ввиду сказанного получение выражения для дисперсии указанной суммы математически строгим путем оказывается сложной вычислительной задачей.
Несложно получить результат при пренебрежении корреляциями n1i в (4) . На практике слабая коррелированность фотоотсчетов имеет место, например, при детектировании рассеянного на флуктуациях плотности среды лазерного излучения или при приеме луча, прошедшего через атмосферу. В этих случаях подавляющий вклад в разброс чисел фотоотсчетов вносит дробовой шум детектирования, и поэтому моменты отсчитываемых ОЭ импульсов близки к соответствующим моментам простого пуассоновского распределения с заданным средним.
При игнорировании упомянутых корреляций дисперсия суммы в формуле (4) равна сумме дисперсий чисел n1. Выражая моменты n1 через моменты n0 с использованием соотношения аналогичного (1) и связи распределений p1 и p0 и произведя необходимые преобразования имеем
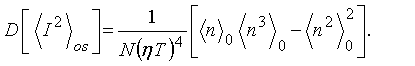 (6)
(6)
Необходимо отметить, что в отличие от (5) наивысший момент фотоотсчетов в (6) – <n3>0.
Представление о соотношении дисперсий оценок в
(4) и (5) при
коррелированных отсчетах можно получить упростив (несколько загрубив) подход к
задаче. Ввиду обстоятельства, что среднее число ОЭ импульсов за время корреляции
интенсивностей меньше единицы, допустимо следующее: учитывать только попарные
корреляции отсчетов на интервалах счета с порядковыми номерами 2i- 1 и 2i ( i = 1, 2 ... N/2; для
простоты N можно полагать четным) и одновременно завышать результат
для <I2>0S, считая, что для каждой пары интервалов
значения интенсивности света на обоих интервалах одинаковы (полная коррелированность
интенсивностей). В таком случае к дисперсии суммы в (6) прибавится (с
удвоением) величина 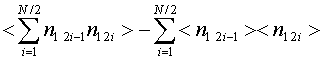 , которая выражается через моменты значений nօ до третьего включительно. Наличие <n4>0
в (5) обусловливает
большее значение
дисперсии в (5), причем, отличие ее от значения (6) растет (до меры, зависящей
от средней интенсивности) с ростом (средней) высоты выбросов интенсивности.
, которая выражается через моменты значений nօ до третьего включительно. Наличие <n4>0
в (5) обусловливает
большее значение
дисперсии в (5), причем, отличие ее от значения (6) растет (до меры, зависящей
от средней интенсивности) с ростом (средней) высоты выбросов интенсивности.
Применяя формулу (6), как приближенную, к случаю детектирования слабомодулированного по интенсивности света и используя в (5) и (6) моменты отсчетов для дробового шума имеем
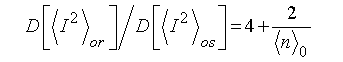 (7)
(7)
с очевидной выгодой для случая
измерений с привязкой интервалов счета к фотоэлектронным импульсам. Причем,
проводить измерение án(n-1)ñ через
измерение án2ñ0, полагая оценку величины á n ñ0 заданной, нецелесообразно, так как правая часть (7)
преобразуется в таком случае в 4 + 6 / á n ñ0
+ 1 / á n ñ20 с существенным увеличением численных значений ее при
фиксированном á n ñ0. Можно убедиться, что в рассматриваемом случае при
выборе для одной лишь формулы (5) наибольшего возможного при выбранном Т числа
выборок ![]() ,
соответствующего допустимому,
но сложнее реализуемому (к тому же, при худшей электронной совместимости
требуемой конструкции) непрерывному стробированию (т.е. отсчетам на примыкающих
один к другому интервалах T) импульсной последовательности на выходе ФЭУ, отношение
рассматриваемых дисперсий не менее двух.
,
соответствующего допустимому,
но сложнее реализуемому (к тому же, при худшей электронной совместимости
требуемой конструкции) непрерывному стробированию (т.е. отсчетам на примыкающих
один к другому интервалах T) импульсной последовательности на выходе ФЭУ, отношение
рассматриваемых дисперсий не менее двух.
Заключение
Сравнение точностей, проведенное для определенных условий, указывает на предпочтительность измерений с привязкой интервалов счета к каждому ОЭ импульсу выхода ФЭУ. Автоматически обнаруживается и возможность измерения среднего квадрата независимых фотоэлектронных отсчетов с меньшей в сравнении со способом прямых измерений случайной ошибкой.
Формулы, аналогичные (3), содержащие средние отсчеты для организованных определенным образом выборок, могут быть выписаны для произвольных моментов интенсивности. Тем самым, могут быть заданы упрощенные алгоритмы измерений их через арифметические средние отсчетов в соответствующих выборках.
Проведенное рассмотрение основано, помимо общих “физических” суждений, на общепринятой формуле ([1], [6]) для распределения числа ОЭ импульсов, образующих сложный пуассоновский процесс, ведущей к формуле (1), и на определенном свойстве временных отметок, задаваемых таким процессом, ведущем к соотношению (3). Поэтому для оговоренных условий результат рассмотрения приложим к процессам упомянутого типа любой природы (импульсы в зрительном нерве, акты радиоактивного распада и т.п.)
Автор выражает благодарность руководителю лаборатории проф. В.Г.Шаврову за поддержку данной работы.
ЛИТЕРАТУРА
[1] Е. Джейкман, Корреляция фотонов, в кн. «Спектроскопия оптического смешения и корреляция фотонов», Мир, Москва, 1976, с.71-145 (пер. с англ. под ред. Ф.В. Бункина).
[2] Ф.Т. Арекки, Распределение фотоотсчетов и статистика поля, в сб. Квантовые флуктуации излучения лазера, Мир, Москва, 1974, с.7-85 (пер. с англ. под ред. А.П. Казанцева)
[3] V. Degiorgio and J.B. Lastovka, Intensity-Correlation Spectroscopy, Phys. Re v.A, 4, p.2033-2050 (1971)
[4] Е.С. Саркисян, О статистической погрешности измерения среднего квадрата случайной функции. «Журнал Радиоэлектроники», декабрь 2006 [Электронный ресурс] // URL: http://jre.cplire.ru/jre/dec06/3/text.html.
[5] П.В.Короленко, А.И.Одинцов, Спецкурс по статистической оптике (кафедра оптики и спектроскопии Московского государственного университета) [Электронный ресурс] // URL: http://optics.sinp.msu.ru.
[6] М. Бертолотти, Статистика фотонов, в кн. Спектроскопия оптического смешения и корреляция фотонов», Мир, Москва, 1976, с.46-70 (пер. с англ. под ред. Ф.В.Бункина).
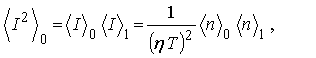 (3)
(3)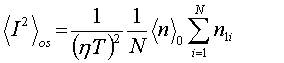 (4)
(4)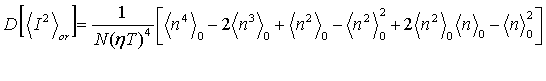 (5)
(5)